Costs for switching partners reduce network dynamics but not cooperative behaviour

Abstract

Social networks represent the structuring of interactions between group members. Above all, many interactions are profoundly cooperative in humans and other animals. In accordance with this natural observation, theoretical work demonstrates that certain network structures favour the evolution of cooperation. Yet, recent experimental evidence suggests that static networks do not enhance cooperative behaviour in humans. By contrast, dynamic networks do foster cooperation. However, costs associated with dynamism such as time or resource investments in finding and establishing new partnerships have been neglected so far. Here, we show that human participants are much less likely to break links when costs arise for building new links. Especially, when costs were high, the network was nearly static. Surprisingly, cooperation levels in Prisoner's Dilemma games were not affected by reduced dynamism in social networks. We conclude that the mere potential to quit collaborations is sufficient in humans to reach high levels of cooperative behaviour. Effects of self-structuring processes or assortment on the network played a minor role: participants simply adjusted their cooperative behaviour in response to the threats of losing a partner or of being expelled.

1. Introduction

One common way to deal with an unpleasant peer is to get out of her or his way and to become friends with someone else. In fact, the breaking of links serves as an effective mechanism to control cheating in social relationships and the evolution of cooperation among unrelated individuals [1–5]. The process of finding new friends leads to assortment and populations with a social structure. First, this means that not all but only subsets of individuals interact with each other. Second, the social structure is dynamic. As such, dynamism in social networks has, for instance, been described in humans [6,7], bottlenose dolphins [8] or chacma baboons [9]. Recent experiments [10–12] show that human cooperation is substantially higher in dynamic networks compared with static ones. For that matter, static network structures—though in theory impacting cooperation positively ([13–15, but see [16])—have trouble producing cooperative outcomes in experimental settings [17–22]. It has to be noted that while most of the mentioned research assume that individuals make one decision for all partners, we allow them to choose freely for each of their partners, as in [10]. This set-up seems to be more realistic for human societies.

Conscious care of one's partnerships is beneficial for cooperation in humans. Both evolutionary models and experiments show that the directed breaking of social links to cheaters or so-called defectors in joint endeavours eventually leads to cooperative outcomes [2,5,10–12,23–25]; further, long-term relationships occur between like-minded cooperators [1,4,5,10,12,26]. However, not only humans make use of partner switching as control mechanism to achieve cooperative outcomes: long-nosed parrotfishes stop interacting (at least temporarily) with their cleaner wrasses and choose a different cleaner station when being cheated on [27].

Real-world interactions offer a large variety of potential costs of partner switching in terms of resources such as food, grooming or money. Further, psychological, effort- and time-based costs may also occur. Theoretical evidence is sparse in regard to modelling link-related or partner switching-related costs and their effects on the evolution of cooperation. When costs in terms of distance—the further away a partner the larger associated (e.g. contacting or travelling) costs—arise for individuals, they are prone to choose those in close reach and hence with lower associated costs [28]. Other approaches impacting the evolution of cooperation include the introduction of migration costs [29], participation costs [30,31] and time-related costs [32]. Surprisingly, present experiments on cooperative behaviour in dynamic human networks [10–12,23] assume that altering partners is cost-free. In summary, exploring the consequences of partner-switching costs on cooperation needs to be investigated as the experimental evidence is lagging behind of insights of natural observations and the development of models.

While partner-switching costs might impact the positive effect of dynamic social networks on cooperative behaviour, they can also affect the dynamism per se. Conflicting work exists on the question of how much partner switching in dynamic networks is optimal. On the one hand, higher rates of network dynamism should generally lead to more cooperation [1,4,11,12]. On the other hand, recent work suggests that the optimal rate of changing partners must be in medium ranges [2,23,24] or the maximum number of partners has to be limited [33]. If defective individuals switch their partners too rapidly, they can exploit newly linked partners and thus will outcompete cooperative individuals. According to [34], another reason may be that defectors need to stay connected to cooperators in order to learn and adopt their strategy, yet recent experimental data suggest that humans imitate only selfish behaviour, but not cooperative behaviour [35]. Former studies [1,2,12,23] approach this question by controlling for how often partners can be exchanged. Instead, we will keep the opportunity to switch partners at a maximum and constant throughout treatments, but expect that varying levels of costs influence partner-switching rates—with a so far unexplored impact on cooperative behaviour in humans.

Here, we examine the cooperative behaviour of human participants while either a static social structure or dynamic social structures define interaction partners. The switching of partners in dynamic networks occurs at (i) no, (ii) low or (iii) high costs (i.e. breaking of social links is cost-free; however, costs occur for setting up a new link). Participants interact with three partners and play independent Prisoner's Dilemma games (PD; [36,37] and see electronic supplementary material for a game description). Only if the game allows for repeated interactions then direct reciprocity [38–40] can produce cooperative outcomes. In general, as our experimental set-up permits repeated interactions without a known endpoint, we expect cooperative behaviour of participants in both social structures. In particular, cooperation levels are predicted to be higher in the three dynamic networks (despite possible costs for partner switching). Especially, we address the impact of costs of partner switching in dynamic networks: as costs for new partners increase, we expect participants' tendency to end partnerships will decrease and hence reduce the dynamism in the network. We therefore infer reduced cooperative behaviour under low and high costs compared with no costs for partner switching. Nonetheless, we predict to find directed link breaking in all dynamic network set-ups: mainly to unwanted, that is to defective, participants. In addition, we examine the specific link-breaking behaviour that occurs along with no, low or high costs of setting new partnerships.

2. Material and methods

(a). The participants

We conducted computerized experiments with 400 students, tested in autumn 2009 and 2012. Students were recruited from a German University via the online recruitment system ORSEE [41] and came from a broad range of disciplines. They were composed of 49% females and were aged 22.07 ± 3.194 (mean ± s.d.). Upon arrival, participants were randomly seated in front of computers separated by opaque partitions. Participants were informed via written instructions about the game rules (available upon request) and came to know that their decisions were made anonymously towards other participants and the experimenters. They were forbidden to communicate except via computers. To allow for in-game identification while ensuring anonymity in regard to their real identity participants were given pseudonyms (randomly assigned names of moons of the solar system). These pseudonyms were also used to ensure anonymous payment at the end (as described in [42]; known by participants from written instructions). Sessions lasted approximately 90 minutes and participants earned 17.53€ ± 5.02.

(b). Static-network treatment and three dynamic-network treatments

We ran 10 sessions for each of our four treatments with 10 participants in each session, respectively: STATIC, DYNAMIC, DYNAMIC10 and DYNAMIC50 (see electronic supplementary material, figure S1–S5).

For the STATIC interaction, partners of participants were defined by the structure of the so-called Petersen graph [43]. This graph consists of 10 nodes (vertices; here players), and each node is linked to exactly three other nodes summing up to a total of 15 interaction links. Importantly, players have identical starting positions in terms of network properties. Note that participants did not receive any information regarding the network nor their position within. At the beginning of each session, participants were randomly assigned to one of these nodes. With each of their three linked partners, participants played independent PD games (i.e. different decisions could be made for different partners). Each of the three games lasted 30 rounds. To avoid end-round effects, participants were not informed about the duration. In each PD round, participants simultaneously decided whether to cooperate or to defect. However, instead of saying ‘to cooperate’ and ‘to defect’, we used the terms ‘ORANGE’ and ‘BLUE’ to avoid morally burdened language (cf. [10]). After all decisions in a PD round were made, participants were shown their own and their partners' decisions and pay-offs. For mutual cooperation (defection), the players received 0.25€ (0.00€) and if one player cooperated and the other defected, the former received −0.10€, whereas the latter received 0.40€. Participants received only local information, that is, they were not informed about the outcomes and pay-offs resulting from their partners' interactions with others. Thereafter, the next round of PD games started. This treatment is called STATIC, because the network did not change throughout the experiment (no partner switching allowed).

Generally, in the three dynamic treatments, the initial network in form of the Petersen graph could change over time owing to link breaking (in all treatments, the maximum number of partners remained limited to three). DYNAMIC followed the set-up of STATIC. Participants played three independent PD games, but, in addition, they were given the option to quit any of their partnerships after learning the results of the current PD round. Independent link-breaking decisions were made. For a link to be broken, at least one player had to decide to end the partnership. Thereafter, participants were informed about their and their partners' decisions. For each broken link, participants were randomly reassigned to any other participant with less than three partners. Afterwards, the next round would start. Because of the random relinking procedure, occasionally, no partner could be found and participants had less than three partners (known by participants from written instructions; this situation generates the same pay-off as mutual defection in partnerships, 0.00€). Further, depending on the total number of broken links in the network, there was a chance to get relinked to the same partner (which could be noted by pseudonyms).

In DYNAMIC10 and DYNAMIC50, participants made PD decisions followed by link-breaking decisions and, additionally, were asked—if they had less than three partners—whether they would like to buy a new link at the cost of 0.10€/0.50€, respectively, or not. Thus, there was no automatic relinking to other available participants. The programme randomly assigned partners to those willing to buy a new link; otherwise, participants did not receive a new partner in the current round. If no new partner could be connected, the costs were not deducted. Note that only in DYNAMIC10 participants could immediately compensate the costs of a new link either owing to mutual cooperation (0.25€ pay-off—0.10€ costs) or owing to exploitation of the new partner (0.40€ pay-off—0.10€ costs). However, DYNAMIC50 would require either the sum of pay-offs of at least two partners or the sum of pay-offs of at least two rounds with the new partner to compensate the initial costs for a new link.

(c). Statistical analysis

We conducted group-level analyses as the behaviour of participants within each session was interdependent and thus required the unit of analysis to be groups rather than to be individuals. For statistical analysis, R v. 2.15.2 [44] was used. Probabilities are reported as two-tailed at a 5% significance level. Pairwise comparisons were corrected using the Bonferroni method (reported below are corrected probabilities for significant results).

3. Results

(a). Link-breaking behaviour in dynamic networks

Overall, the experiment showed that costs for setting new links affected the willingness of participants to break them. We found significant differences in the link-breaking rate between each of the three dynamic treatments: the higher the costs, the lower the link-breaking rate (figure 1a; Wilcoxon rank-sum test: DYNAMIC versus DYNAMIC10: W = 0, n_1,2 = 10, p < 0.001; DYNAMIC versus DYNAMIC50: W = 0, n_1,2 = 10, p < 0.001, DYNAMIC10 versus DYNAMIC50: W = 17, n_1,2 = 10, p < 0.05; see the electronic supplementary material, table S1). Additionally, we found that links were broken mostly during the first few rounds of the experiment (figure 2; comparing link-breaking rates of the average of rounds 1–10 against rounds 21–30, Wilcoxon signed-rank test: DYNAMIC: V = 0, n = 10, p < 0.01; DYNAMIC10: V = 0, n = 10, p < 0.01; DYNAMIC50: V = 1, n = 10, p < 0.01).

Figure 1.

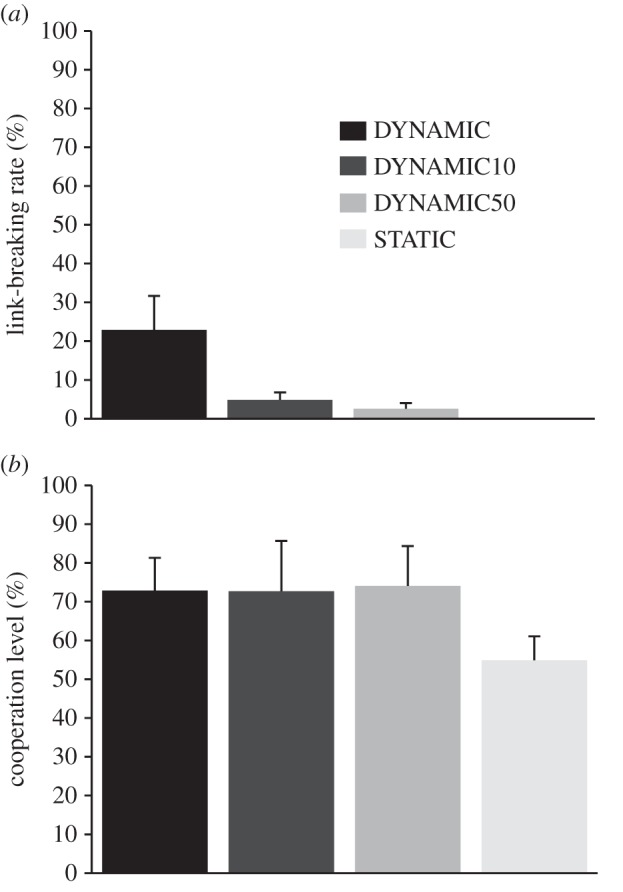
(a) Average rates of link breaking in the dynamic networks and (b) average cooperation levels in the Prisoner's Dilemma games. Interactions occurred either on a static structure (STATIC) or on dynamic structures. Here, social links could be broken after each round. Setting new links was either cost-free (DYNAMIC), or else low costs of 0.10€ (DYNAMIC10) or high costs of 0.50€ (DYNAMIC50) arose.

Figure 2.

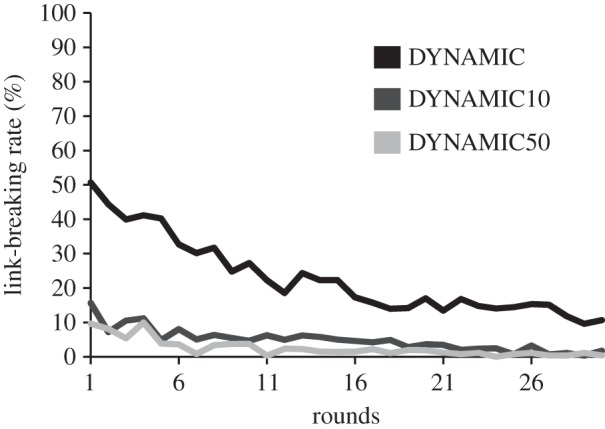
Average link-breaking rates over rounds. Participants played Prisoner's Dilemma games with three partners and could break social links after each round. Setting new links was either cost-free (DYNAMIC), or else low costs of 0.10€ (DYNAMIC10) or high costs of 0.50€ (DYNAMIC50) arose. Average link-breaking rates differed significantly between treatments (p values < 0.05) and link-breaking rates significantly decreased over time (p values < 0 0.01).

Now, we asked which behaviour was likely to trigger link breaking. Generally, within all dynamic treatments, significantly more links were broken to defectors than to cooperators (break rate to defectors: DYNAMIC: 82.9% ± 8.3; DYNAMIC10 89.5% ± 7.0; DYNAMIC50: 91.3% ± 7.5; Wilcoxon signed-rank test: V = 0, n = 10, p < 0.01 for all dynamic treatments). Here, we also found that the link-breaking rates to defectors marginally significantly differed between the dynamic treatments (Kruskal–Wallis test: χ₂² = 5.17, p = 0.075). Moreover, when taking the participants own behaviour into account, we observed that if both players cooperated, participants almost never broke such a link. Of a total of 4706 mutually cooperative PD outcomes in DYNAMIC50, only one link was broken (DYNAMIC10: one of 4828; DYNAMIC: 12 of 5040).

(b). Cooperative behaviour in the Prisoner's Dilemma games

Next, we examined the cooperative behaviour of participants as well as its relation to link-breaking behaviour. The overall cooperation levels between the four treatments were significantly different. Detailed analysis revealed that cooperation levels were significantly lower in STATIC compared with all dynamic treatments (figure 1b; Wilcoxon rank-sum test: STATIC versus DYNAMIC: W = 4, n_1,2 = 10, p < 0.001; STATIC versus DYNAMIC10: W = 13, n_1,2 = 10, p < 0.05; STATIC versus DYNAMIC50: W = 5, n_1,2 = 10, p < 0.01, for a round-by-round figure, see the electronic supplementary material, figure S2). However, we did not find significant differences between the dynamic treatments themselves (see the electronic supplementary material, table S2).

To understand the high levels of cooperation in the dynamic treatments despite very different dynamism in the networks (note the network structure in DYNAMIC50 was nearly static), we first looked at the readiness to cooperate when a participant received a newly linked partner (i.e. participants who had no current partnership, but who might have met each other before; behaviour of the first round was excluded). We found significantly higher cooperation levels of participants with a new link in DYNAMIC50 than in DYNAMIC (figure 3; Wilcoxon rank-sum test: W = 10, n_1,2 = 10, p < 0.01; see the electronic supplementary material, table S3). Second, we examined the willingness of participants to reciprocate defection, that is, to defect when a link to a defector remained in place (note this required the approval of both players; level of defection in DYNAMIC 64.9% ± 8.1; DYNAMIC50: 72.2% ± 8.5; DYNAMIC10: 74.8% ± 4.3). We found significant higher levels of reciprocating a defection in DYNAMIC compared with DYNAMIC10 (Wilcoxon rank-sum test: W = 11, n_1,2 = 10, p < 0.05; see the electronic supplementary material, table S4).

Figure 3.

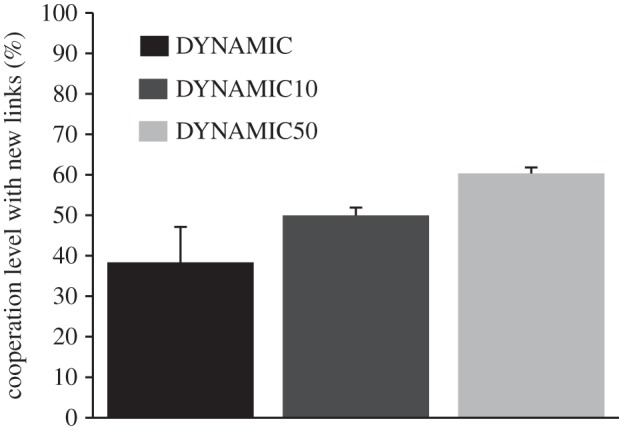
Average cooperation level in the Prisoner's Dilemma (PD) game of two newly linked participants. After each PD round, participants could break social links. Setting new links was either cost-free (DYNAMIC), or else low costs of 0.10€ (DYNAMIC10) or high costs of 0.50€ (DYNAMIC50) arose.

4. Discussion

In accordance with a previous series of experiments [10–12,23], we contribute evidence on the beneficial effects of dynamic networks on cooperative behaviour in humans. More specifically, we build upon a rather new approach introduced in [10] where participants can choose independent actions for each partner. Here, cooperation in dynamic networks went beyond the purely reciprocity-guided cooperation of static networks. We advance previous findings by introducing costs that arise when one is in search of new partners. The willingness to break social links was clearly reduced when low costs arose. When costs were so high that they could not be compensated within a single interaction, participants further reduced their link-breaking behaviour. Nonetheless, high levels of cooperation in PD games were achieved (i.e. cost treatments did not differ from a treatment without costs). Interestingly, though participants of dynamic networks with no, low or high costs differed quantitatively in their link-breaking behaviour, they followed similar strategies. In all dynamic treatments, link-breaking rates decreased over time, participants mostly broke links to defective players and under mutual cooperation participants almost never broke links.

Contrary to our assumption, we found no impact of reduced dynamism on cooperative behaviour. This notion supports the view that the mere option to end partnerships is enough to maintain cooperation. The option of link breaking provides (i) the possibility to get rid of defectors, (ii) the threat of losing a partnership, as well as (iii) the option to stay with like-minded cooperative partners. While avoiding link breaking when costs occurred, participants adjusted their behaviour in the PD games in response: participants under high costs were more willing to cooperate with a newly linked partner compared with participants who did not have to pay for new links, and participants under low costs reacted themselves with higher levels of defection when a link to a defective partner remained in place compared with participants who did not have to pay for new links. These behavioural adjustments played an important role for maintaining high levels of cooperation.

Currently, there is an on-going debate of how much partner switching is necessary to achieve the highest possible level of cooperation [1,2,12,23]. Previously, different rates of partner-switching were achieved by actively controlling them (e.g. partner-switching every round versus every fifth round of an evolutionary game). Contrasting, our dynamic-network treatments, in principle, allowed for the same rates of switching. However, rates varied greatly across treatments owing to different incentives resulting from costs. In fact, in our high-cost dynamic networks, participants broke only 2.5% of the existing links and still cooperated 20% more than in the static networks. Our study implies that it is important to investigate effects which constrain or lead to network dynamics naturally, in addition to the approach of setting different rates exogenously. Thus, our findings can inspire this debate by showing a different perspective of partner-switching.

In our experiment, assignment of new partners was random. As such, we have implemented active link breaking but not active link seeking. Both models and experimental findings support the view that partner-choice based on behavioural [12,23] or reputational information [1,45,46] fosters cooperation. Future research will have to address questions like whether costly partner choice will increase individuals' willingness to break social links as they are given more control over future partners as well as whether this will make partner-switching mechanisms faster and more efficient in achieving cooperative outcomes.

Furthermore, our experiment also included a more implicit form of costs as we constrained the maximum number of partners to three (true for all treatments). Time might be such a factor limiting ones interactions, but theoretically, have not been found to derogate cooperative incentives of individuals [32]. Moreover, while our study provides important first insights into the impact of costs as of seeking new interaction partners, further experiments should investigate the impact of different types of costs on cooperation. As discussed in the theoretical literature [28,29] such costs may, for instance, relate to geographical distance or migration.

The mechanism of costly link breaking demonstrated here can also be seen as punitive incentive. Related cheater-control mechanisms are ostracism [47,48] and costly punishment [49] of defective individuals. An advantage of link-breaking mechanisms lies in the fact that they are based on individual decisions that lead to assortment and self-organizing processes on the level of the network [10]. Hence, unlike ostracism they achieve isolation or even final exclusion of defectors without the necessary cooperative and coordinated decision of all group members. Further, costly punishment often suffers from ongoing retaliations and antisocial punishment [50,51]. Such detrimental behaviour is avoided in settings where links can simply be broken. Which of the two—partner switching or costly punishment—is the more favourable behaviour most likely depends on the environmental or social ecology of individuals. The interspecies mutualism of the cleaner wrasse and their clients (i.e. various reef-fish species) provides an example: clients switch to a new cleaner after defection by their current one if they have access to several cleaners [27]. This forces the cleaner to be more cooperative [52]. Whereas clients with access to only one cleaner make use of punishment by chasing defective cleaners [53].

To conclude, we emphasize that the mere option to break the social link to a partner promotes cooperation among humans. Despite being reluctant to pay costs for seeking new partners and reducing link-breaking behaviour, participants cooperated at very high levels. Owing to the minuscule network dynamics, there was barely any room left for participants to assort and to alter their social environment. Thus, the difference in cooperation levels between the ‘nearly static’ and the static network is even more remarkable. Hence, besides assortment, making relationships costly, and therefore valuable, is an additional way to achieve cooperative outcomes in dynamic networks.

Data accessibility

The data used for this article can be accessed online at http://datadryad.org/, doi:10.5061/dryad.tp582. We are happy to provide more information on request.

Funding statement

The research is supported by the German Initiative of Excellence of the German Science Foundation (DFG).