Programmable chemical controllers made from DNA

Abstract

Biological organisms use complex molecular networks to navigate their environment and regulate their internal state. The development of synthetic systems with similar capabilities could lead to applications such as smart therapeutics or fabrication methods based on self-organization. To achieve this, molecular control circuits need to be engineered to perform integrated sensing, computation and actuation. Here we report a DNA-based technology for implementing the computational core of such controllers. We use the formalism of chemical reaction networks as a 'programming language', and our DNA architecture can, in principle, implement any behaviour that can be mathematically expressed as such. Unlike logic circuits, our formulation naturally allows complex signal processing of intrinsically analogue biological and chemical inputs. Controller components can be derived from biologically synthesized (plasmid) DNA, which reduces errors associated with chemically synthesized DNA. We implement several building-block reaction types and then combine them into a network that realizes, at the molecular level, an algorithm used in distributed control systems for achieving consensus between multiple agents.

Molecular devices have captured the imagination of chemists and engineers for at least 30 years (1). Rationally designed “active” molecules include nanoparticles for the targeted delivery of drugs and imaging agents (2), or molecular motors that move along tracks and deliver cargo (3). DNA nanotechnology (4, 5) is in a unique position among the many actively pursued strategies for constructing molecular nano-robots, demonstrating progress towards the rational design of all the required elements: sensors and amplifiers (6–11), circuits (12–25), motors (26–30), and structures (4, 31, 32). A rationally designed molecular robot even combined structural elements with sensing and actuation, though it lacked complex embedded control (33). The DNA-only construction of digital logic circuits and Boolean neural networks with over a hundred rationally designed parts forms possibly the most dramatic demonstration of a systematic engineering approach to building molecular circuits (16, 17). However, these approaches to constructing molecular information processing systems do not realize the full spectrum of analog and temporal dynamics naturally present in chemistry, and that can be harnessed to control active molecular devices.

We experimentally demonstrate a design strategy for building DNA-only chemical controllers capable of being programmed to execute analog temporal dynamics. The technology is designed around a signalling protocol based on short single-stranded DNA sequences. Molecular sensors (e.g. aptamer switches) can release or expose such short sequences, and actuators (e.g. antisense drugs or ribozymes) can be triggered by them. MicroRNAs can also be used as inputs to DNA circuits (18, 34). The control system we design sits in between, receiving inputs in the form of DNA sequences, and producing outputs in the form of other sequences (Fig. 1a). The treatment of controller, sensor and actuator as independent modules has proved indispensible in other fields of engineering.

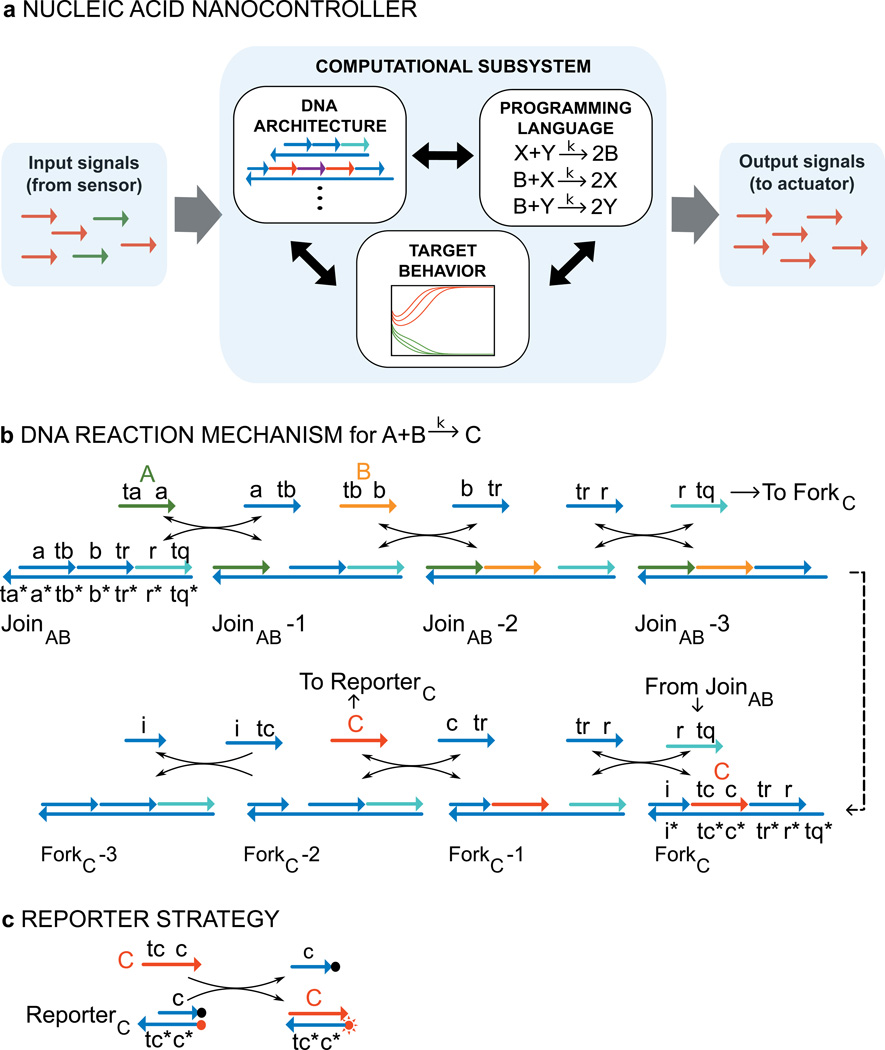
Figure 1. DNA realization of a formal CRN.

a, A standardized signalling protocol based on short single strands of DNA enables the components of the nano-controller to communicate with each other. The formalism of chemical reaction networks serves as a programming language that specifies the desired behaviour for the computational subsystem. The target behaviour is experimentally realized by the DNA architecture. b, Reaction mechanism. DNA strands are drawn as lines with arrows at the 3’ end. Functional domains are labelled with lowercase letters; “*” indicates Watson-Crick complement. Species A, B and C of the formal reaction are represented by DNA signal strands A (<ta a>, green), B (<tb b>, orange), and C (<tc c>, red), respectively. Implementation of the bimolecular reaction A+B->C requires two multi-stranded gate complexes Join_AB and Fork_C as well as the auxiliary strands <tr r>, <c tr>, and <i tc>. The reaction proceeds through a sequence of six stand displacement reactions where each step provides a toehold for initiation of the next one. c, Reporting strategy for reaction kinetics used in this paper. The reporter consists of two strands, one labelled with fluorophore (red dot), the other with a quencher (black dot). Fluorescence is quenched when fluorophore and quencher are co-localized; displacement of the quencher-labelled strand by signal C leads to an increase in fluorescence proportional to the amount of C detected.

Our DNA components are, in principle, capable of realizing the entire diversity of dynamic behaviours of chemical kinetics as mathematically captured by a chemical reaction network (CRN) (12, 19). Although CRNs started out as a tool to understand experimental observations of elementary chemical reactions, they form a general framework to model systems with many interacting components such as gene regulatory networks, animal populations and sensor networks. CRNs can embody a wide range of digital and analog behaviours including temporal pattern generation, multi-stability and memory, Boolean logic, signal processing, control systems, or distributed algorithms (13, 35–40). Moreover, viewed as a programming language, CRNs provide a natural and intuitive formalism for delineating and reasoning about molecular interactions, without making underlying physical details explicit.

We use the familiar language of chemistry to write programs for our DNA architecture (Fig. 1a). The “instruction” A+B->C+D means that the signals A and B are transformed into the signals C and D, where A,B,C,D are DNA strands we design. The reaction is not elementary – rather it is systematically “compiled” into a sequence of DNA strand displacement reactions. Our use of this chemical programming language is not gratuitous: A central contribution of this paper is to provide experimental evidence that our DNA architecture produces the expected stoichiometry and mass action kinetics of chemical reactions, so that our algorithms can behave similarly to what one might naively expect.

We test the major reaction classes --- non-catalytic, catalytic, and autocatalytic reactions. Then we combine multiple such building blocks into a network implementing a distributed control algorithm for achieving consensus between multiple agents. While the connection between distributed computing and chemistry has been noted multiple times in the literature (e.g. Petri nets (41)), the sophistication of molecular engineering required has deterred experimental implementations. Our experiments corroborate that we can realize complex behaviours previously out of reach of synthetic molecular systems.

Among the many proposed architectures for strand displacement computation (2, 10–13, 15–19), ours is unique in that it relies exclusively on linear, double-stranded DNA complexes (processed by “nicking” one of the strands) (10). Because this structure is compatible with natural DNA, we are able to produce our computational elements in a highly pure form by bacterial cloning. Thus, we bypass the practical limitations in the length and purity of synthetic strands.

Signal transduction mechanism

We identify signals (A,B,C…) with single-stranded DNA molecules (signal strands, Fig. 1b). Nicked double-stranded DNA (ndsDNA) gate complexes mediate interactions between these signal strands with the help of additional auxiliary single-stranded species. All signal strands have the same sequence domain structure (see e.g. signal strands A (<ta a>, green), B (<tb b>, orange) and C (<tc c>, red) in Fig. 1b) with a short toehold domain (labels ta, tb, …) that initiates binding to a gate, followed by a long domain (a, b, …) that determines signal identity.

The reaction A+B->C is implemented with two gates (called Join_AB and Fork_C in Fig. 1b). The join gate consumes (and thus “joins”) the two signals A and B and the fork gate releases the signal C, which is initially bound to the fork gate Fork_C, and thus inactive. (The name “fork gate” derives from the fact that multiple signal strands can be released, as shown in later examples.) The complete triggering of a join and a fork gate --- corresponding a single formal reaction A+B->C --- is a cascade of strand displacement reactions in which each reaction exposes a toehold for the subsequent reaction (Fig. 1b, Supplementary Information (SI), Section S1). The displacing strand is either a signal strand, an auxiliary strand, or a strand previously released in the cascade (e.g. “translator” strand <r tq> is released by the join gate and triggers the fork gate). We use a fluorescent reporter strategy to detect specific strands and follow the reactions (Fig. 1c).

Each reaction is reversible until the very last displacement step involving the fork gate. The reversibility of the first step is essential to ensure stoichiometric correctness: the first formal reactant (A) should not be consumed in the absence of the second (B). Reversibility allows A to be re-released if the cascade does not complete.

The two-gate design and use of auxiliary strands ensures that all signal strands have the same domain structure and independent sequence, which guarantees composability (12). Signal strands can thus be shared between multiple reactions to create a coupled system. Without these constraints, we can implement an individual bimolecular reaction with many fewer species, but we would lose the ability to compose reactions into arbitrary CRNs.

Plasmid encoding of DNA gates

The performance of strand displacement systems is currently limited by undesirable side reactions: leaks (the spontaneous “firing” of a reaction cascade in the absence of the intended molecular trigger), or sub-stoichiometric completion levels (unintentional sequestration of the signal leading to reduced product yield). These problems can at least in part be traced to errors in chemical DNA synthesis (42). Biologically synthesized DNA is a useful alternative to synthetic DNA even in non-biological applications where large quantities of highly pure DNA are required (43–45).

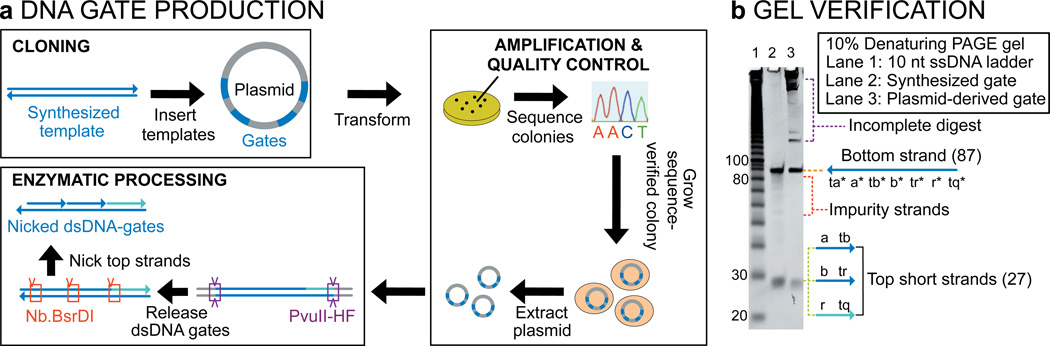
Our gates consist entirely of nicked double stranded DNA (12), which makes them uniquely compatible with plasmid DNA as a starting material. Plasmid-derived gates have the additional advantage that they can be replicated and stored as bacterial glycerol stocks (before enzymatic processing). Gate production is detailed in Fig. 2a. Correct processing was tested using gel electrophoresis (Fig. 2b and S7). Enzyme selection and additional design criteria are detailed in the SI, Sections S2 and S3. The sequence constraints imposed by the use of nicking enzymes do not limit the generality of our method. Signals can be made orthogonal to one another by designing the sequences surrounding the nicking sites to be different. All data shown in the paper was collected with plasmid-derived ndsDNA gates except where otherwise indicated. Externally added signal and auxiliary strands, as well as the reporter gates used for following reaction kinetics were chemically synthesized.

Figure 2. DNA gate production.

a, Highly pure ndsDNA gates can be produced from plasmid DNA. Multiple copies of a double stranded ndsDNA gate template are inserted into a plasmid and transformed into E. coli cells. Clones are picked and plasmid sequence is verified. A clonal population is grown up and plasmid DNA is extracted using standard molecular techniques. Finally, the restriction enzyme PvuII-HF is used to release the gate from the plasmid, and the nicking enzyme Nb.BsrDI is used to generate nicks in the top strand. b, Analysis by 10% denaturing-PAGE of the enzymatically processed gate. Lane 1: 10 nt ladder; lane 2: Synthesized control gate; lane 3: Plasmid-derived gate. The long bottom strand (87-mer) and short top strands (27-mer) are visible on the D-gel.

Testing fundamental reaction types

The modular nature of our design makes it easy to create reactions with multiple products of unconstrained sequence, allowing us to engineer the three major reaction classes: non-catalytic, catalytic, and autocatalytic. These are the building blocks for composition of complex CRNs.

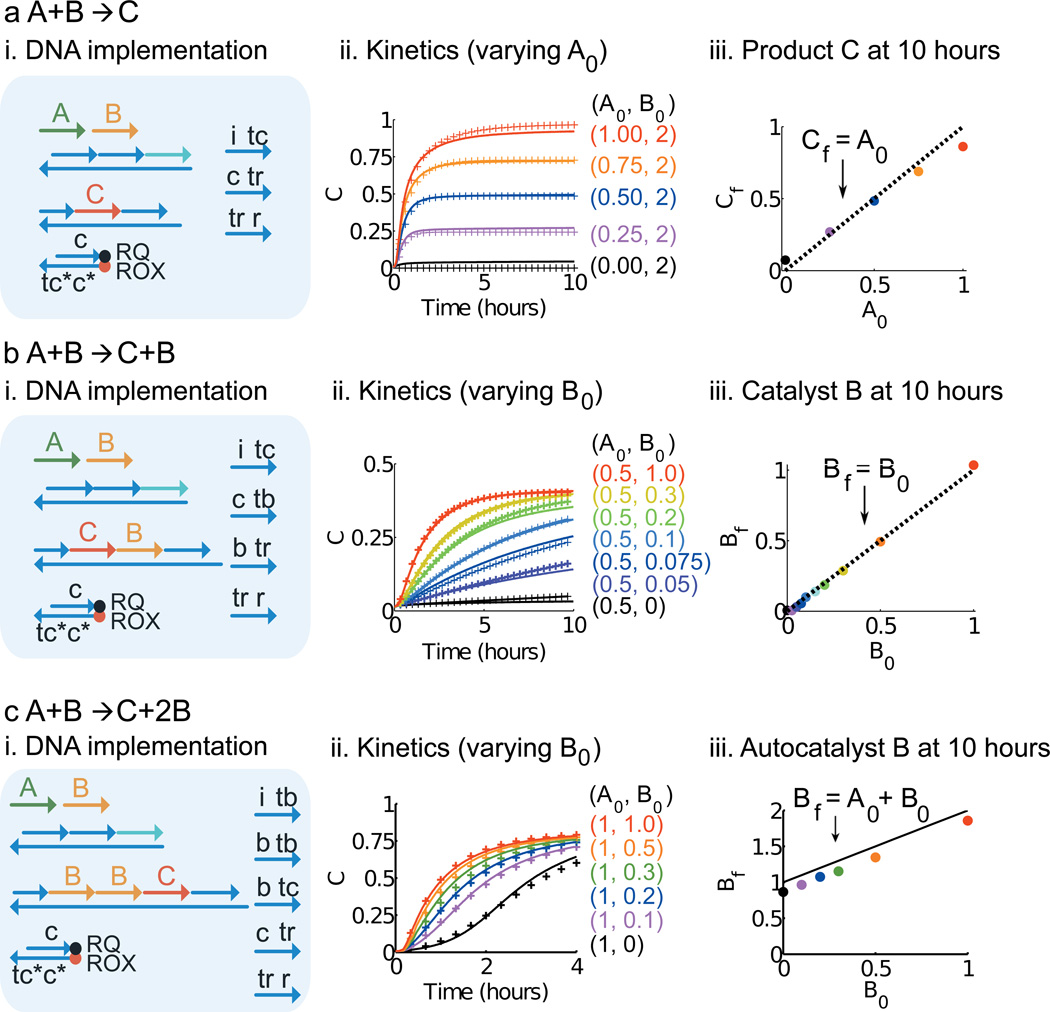
Extensive tests of the most basic reaction A+B->C verified correct stoichiometry (are the correct amounts of reactants used up and products generated? Fig. 3a) and kinetics (are the reactants and products being generated according to the target rate law?, Section “Verification of the bimolecular rate law”). In the catalytic reaction A+B->C+B, even a small amount of B effectively “converts” all of A to C, but B remains conserved (Fig. 3b). Catalytic reactions are ubiquitous in biological chemical controllers (e.g. transcriptional networks, kinase networks) as well as man-made artificial systems (6–11). In Fig. S10, we quantitatively analyse the catalytic turnover --- showing that a single catalyst can trigger multiple reaction cycles.

Figure 3. Testing fundamental reaction types.

Panel (i) shows a simplified representation of the gates, auxiliary strands, and signal strands used for the corresponding experiments. Experimental kinetics data are shown in panel (ii) as full coloured lines. Concentrations of the signal strands are indicated in the same colour, 1×=50nM. All join and fork gates were at 1.5×, and auxiliary strands were at 2×. Best fits of the strand displacement-level model to the data are shown as crossed lines. Panel (iii) shows data confirming the correct reaction stoichiometry. a, Non-catalytic bimolecular reaction A+B->C. Signal B was at 2× and different amounts of signal strand A were added. Panel (iii) shows that levels of (product) signal C at the measurement end point (10 hrs) are very close to the amounts of limiting inputs as expected for a stoichiometrically correct bimolecular reaction. b, Bimolecular catalytic reaction A+B->C+B. Signal A was at 0.5× and different amounts of the catalytic signal B were introduced into the system. Panel (iii) shows that the final amount of free catalyst B_f is equal to the initial amount B₀. The amount of catalyst signal B at 10 hrs was measured by adding a fluorescent reporter for B. c, Autocatalytic reaction A+B->C+2B. Signal A was at 1× and the amount of signal B was varied. Panel (iii) shows that the final amount of the autocatalyst signal B is equal to the sum of the initial amounts of A and B as expected for autocatalysis. The amount of autocatalyst signal B was measured at 10 hrs by adding a fluorescent reporter for B.

In the autocatalytic reaction A+B->C+2B even a small amount of B effectively “converts” all of A to itself (C acts as a “read-out”), resulting in the typical sigmoidal kinetic curves (Fig. 3c). Because of the exponential growth kinetics, autocatalytic reactions are common in settings where rapid (self-)amplification is observed such as replication or apoptosis. These properties also make autocatalysis a key ingredient to propagate information in proposed chemical algorithms (46) (see also Section “Consensus algorithm”). Because autocatalysis is extremely sensitive to leaks (9–11), it provides a good measurement of reactant quality. The estimated amount of autocatalyst B leaked (black trace, Fig. 3c,ii) is less than 2% (Supplementary Table S3), however this leak is exponentially amplified.

To compare the performance of plasmid-derived gates to that of synthesized gates, we re-implemented the catalytic and autocatalytic reactions with synthesized gates using the same sequences. We observed that catalytic turnover is at least twice as high for the plasmid-derived gates. This observation is indicative of incomplete triggering due to unknown side reactions sequestering the catalyst in the synthesized system. Comparing autocatalytic reactions, we found that plasmid-derived gates suffered from noticeably less un-triggered amplification characteristic of a lower leak rate (Fig. S10). These data are consistent with the observation that there are fewer truncated strands detected in a gel analysis of the plasmid-derived gates than for the synthetic gates (Figs. 2b and S3.3).

We tested bimolecular reactions with one, two, or three products, but our approach can be generalized to different numbers of products and reactants. Unimolecular reactions can be implemented with a single-input join gate, while higher order reactions can be implemented using join gates with multiple inputs.

Verification of the bimolecular rate law

The reaction specification A+B->C delineates not only the production/consumption relationships between A,B,C, but also the dynamics. Despite the overall complex reaction mechanism (which, for A+B->C, involves 5 reversible and 1 irreversible stand displacement reactions, Fig. 1b), an analytical argument shows that the overall kinetics should be well approximated by the mass-action rate law expected of the formal reaction (i.e. d[C]/dt=−d[A]/dt=−d[B]/dt=k[A][B]). As the derivation in S5 shows, the regime of best correspondence (“CRN regime”) is one in which gates and auxiliary strands, including “backward” auxiliary strands <a tb> and <b tr>, are sufficiently in excess over the signal strands (Fig. 4a).

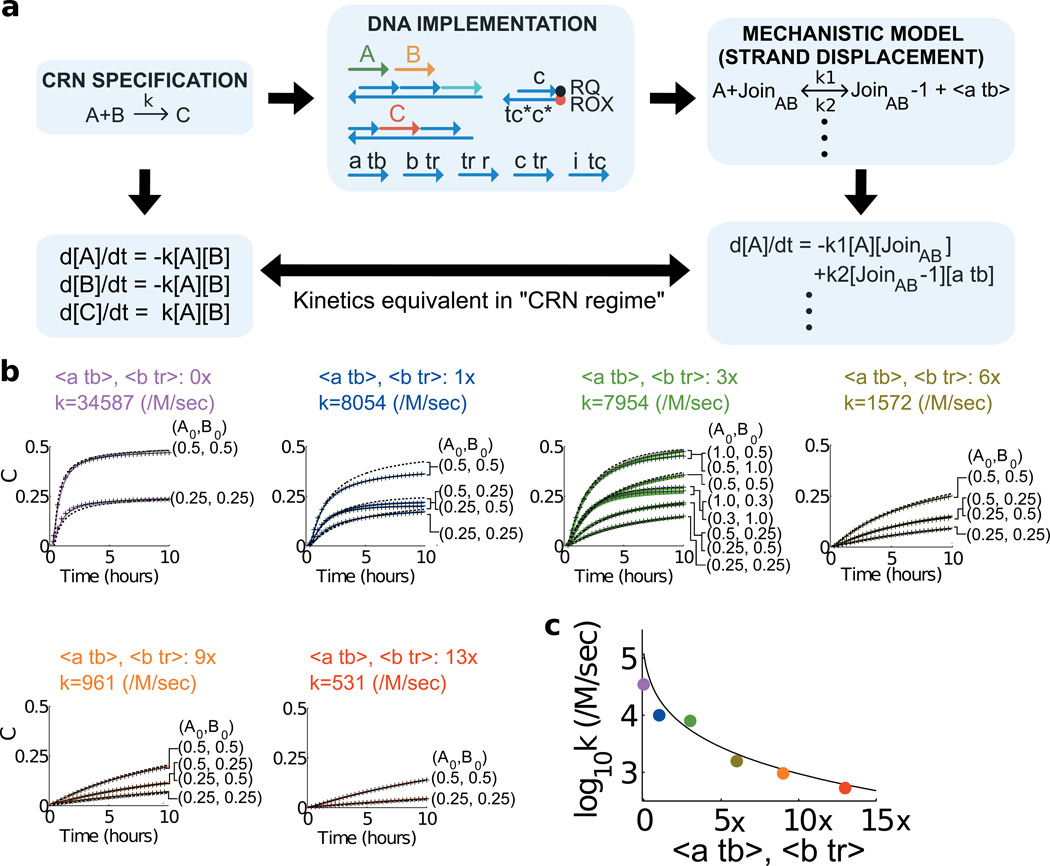
Figure 4. Tuning the rate of the bimolecular reaction A+B->C.

a, Approximating the bimolecular rate law. The CRN program is executed by a DNA architecture that can be quantitatively modelled at a mechanistic level. We view strand displacement reactions (e.g. A + Join_AB -> Join_AB−1+<a tb>, see Fig. 1b for component names) as the elementary reaction steps and the formal bimolecular reaction (e.g. A+B->C) as the complex reaction pathway decomposed into these elementary reactions. In the “CRN regime” (see text) the mechanistic model closely approximates the dynamics of the target program. The rate constant k of the formal system can be tuned by changing the concentrations of gates and auxiliary strands. b, Reactions with varying concentrations of the backward auxiliary strands <a tb> and <b tr>. The data (solid traces) show the time-evolution of C: Purple traces (0× <a tb> and <b tr>), blue (1×), green (3×), olive green (6×), orange (9×) and red (13×), 1×=40nM. Gates were at 3× and initial concentration of the signals A and B are indicated in each panel. Black dashed lines are fits to the bimolecular rate law in (a). Best-fit rate constants to the bimolecular rate law are indicated in each panel. Black crossed lines are fits to the mechanistic strand displacement-level model. c, Fitted bimolecular rate constant vs. analytic prediction. The dashed line is obtained from an analytic predication for the dependence of the expected rate constant on the concentrations of the backward auxiliary strands <a tb> and <b tr> (Eq. 8, S5). The coloured dots show the rate constants fitted to experimental data from (b).

We experimentally confirmed that the multi-step strand displacement level mechanism implements the expected rate law for A+B->C, and that the rate constant can be tuned by adjusting the concentrations of gates and auxiliary species. Fig. 4b shows six sets of experimental data for the reaction A+B->C in or near the CRN regime. Each set was obtained with a different concentration of the backward auxiliary strands <a tb> and <b tr> and contains kinetics traces corresponding to at least two different combinations of the signals A and B. We chose to vary the concentration of the backward auxiliary strands because our analysis suggests that the formal rate constant can be effectively tuned in this way (see Sections S5). We then fit the data from each set to a bimolecular rate law; the best fit rate constants varied over about two orders of magnitude from 3.5*10⁴/M/s to 5.3*10²/M/s as the concentration of backward auxiliary strands increased from 0× to 13× (see also Section S5). The data show that the reactions are symmetrical with regard to the two signals as required by the bimolecular rate law although the signal strands A and B react sequentially with the join gate (see e.g. traces with A, B at 1×, 0.3× and 0.3×, 1× respectively).

Mechanistic strand displacement-level model

Each individual strand displacement step can be well modelled as a bimolecular reaction between a signal or auxiliary strand and a gate complex with a matching open toehold (47). We used the Visual DSD (14, 48) software to develop a quantitatively constrained model of the dynamics of our system on this mechanistic level. We allowed each strand displacement step to occur at a different rate depending on the sequences of the toeholds and adjacent domains. The model includes a phenomenological treatment of the erroneous leak reactions (Supplementary text S7.3). We fit all the data that we obtained for the non-catalytic, catalytic and autocatalytic reactions (Figs. 3 and 4), and independent measurements of a large number of intermediate reaction steps (Figs. S16–S17). These 104 data traces yielded a highly constrained set of strand displacement rate constants, with values ranging from 10⁴/M/s to 1.44×10⁶/M/s (Table S3), consistent with previously reported data (47). The mechanistic strand displacement-level model fitted the data for all reaction conditions, including leak reactions, exceptionally well (crossed lines in Fig. 3 and 4b, see also SI Section S7).

The strand displacement rate constants can be used to predict the effective bimolecular rate constant for the target formal reaction A+B->C (SI S5). We compared this predicted rate constant to that obtained by direct fitting of the data in Fig. 4b to a bimolecular rate law. Fig. 4c shows that our prediction is in good agreement as long as the concentration of the backward strands is 3× or higher. Divergence is expected at lower concentrations since the approximation we made to derive the analytic result does not hold. These results demonstrate that we can systematically vary the formal rate constant through quantitative control over the underlying reaction mechanism.

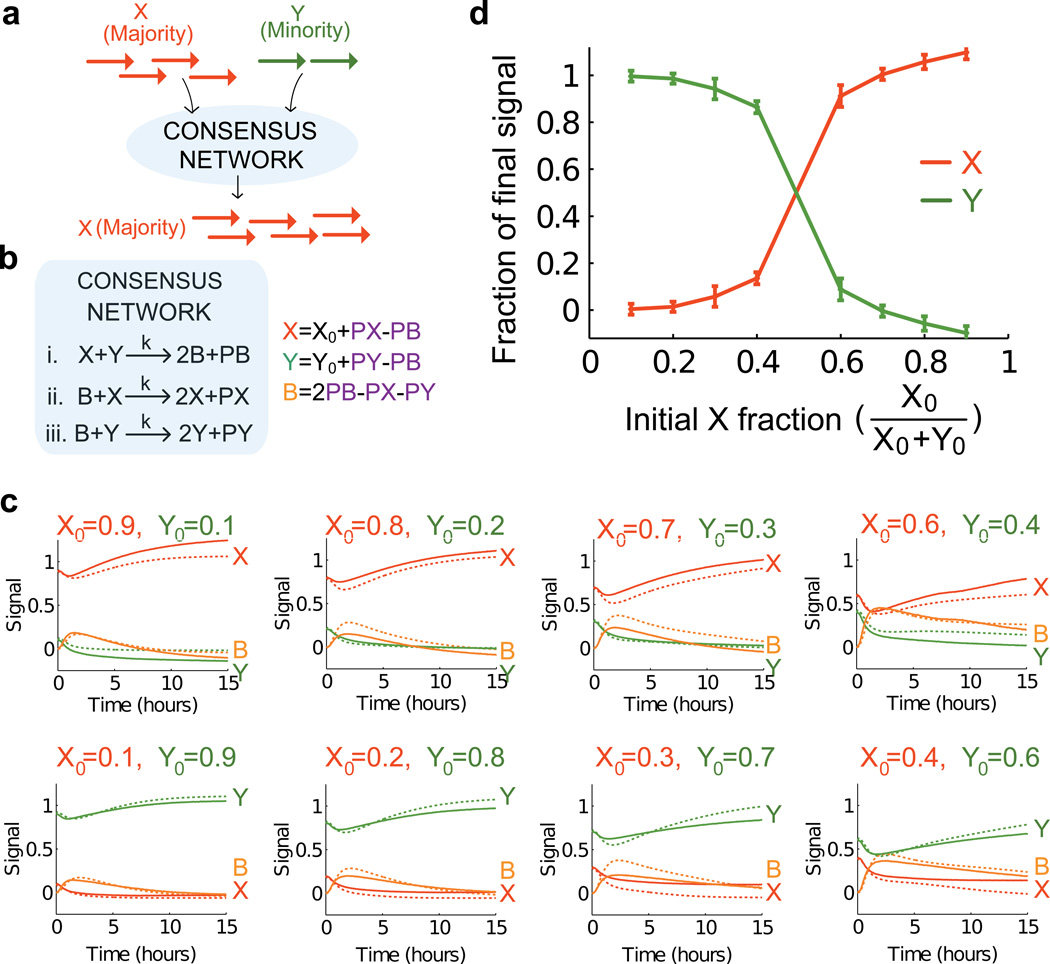
Consensus network

An important function of molecular controllers is their ability to make decisions by comparing concentrations of input signals (Fig. 5a). We engineered such a decision-making controller by implementing a consensus algorithm that operates on two signals (X and Y). The signal that is initially in the minority is completely eliminated and replaced by the signal that is initially in the majority (in any given experiment the sum of all signal concentrations is constant) (SI Section S8.1). In distributed computing parlance, we implement an algorithm that allows picomole (10¹¹) quantities of agents, each with vote X or Y, to agree on a majority decision (46, 49). The classification into minority and majority is thus unequivocal, distinguishing this network from previous proposals for DNA-based molecular classifiers (50) where the resulting signal was proportional to the difference in the initial concentrations (which can be small when concentrations are close). Consensus is a basic distributed computing problem and provides for us a proof-of-principle that CRN algorithms are directly translatable to our DNA controllers.

Figure 5. Consensus network.

a, Given arbitrary amounts of signal strands X (red) and Y (green), the consensus network converts the minority signal to the majority signal. b, The formal chemical reactions for the consensus network. Signals PX, PY, and PB were used to follow the reaction kinetics without interfering with the dynamics of X, Y, and B. Reporters for PX, PY, and PB each used a different fluorophore such that all three signals could be detected in the same reaction. The values of X, Y, and B were calculated from the measured values of PX, PY, and PB as indicated. c, Time-evolution of the signals X (red), Y (green), and B (yellow). Initial concentrations of signals X and Y are indicated in each panel, 1×=80nM. Reporters were at 3×, auxiliary strands at 2× and gates at 2× for reactions (i) and (ii). Gates and auxiliary strands for reaction (iii) B+Y->2Y were at 2.4× to balance the rates of the two autocatalytic reactions. The DNA implementation for the consensus network consisted of 3 join gates, 3 fork gates, 3 reporters, 13 auxiliary strands and 3 signal strands. No backward auxiliary strands were added to the initial reaction mixture. A graphical representation of all gates and auxiliary species is given in the SI S8.2. The kinetics data show that the minority species was converted into the buffer species B first, then into the majority species. The model prediction of the consensus network using the strand displacement-level model is shown as dashed lines. The prediction is based on a model parameterization obtained by fitting to the individual reactions (Section S8). d, Amplification levels. The end points (15 hours) of each reaction show that the DNA-based consensus network correctly amplifies the majority towards totality. Red trace: X/(X+Y) at 15 hours; green trace Y/(X+Y) at 15 hours.

The network consists of two autocatalytic and one non-catalytic bimolecular reaction (see Fig. 5b): A reaction between signals X and Y creates two copies of the buffer signal B while a reaction involving B and X (Y) creates two copies of X (Y). Intuitively, the minority and majority signals initially cancel each other producing the buffer signal, which is then converted back to the majority signal. For the threshold to be set at the point where concentrations of the two species are equal, the two autocatalytic reactions should occur at the same rate. To compensate for minor differences in the rates of the two autocatalytic reactions (SI Section 8.2) and make reaction rates similar, we adjusted gate and auxiliary species concentrations.

Fig. S21 shows the ndsDNA gates needed to implement this reaction network (sequences and other design considerations are listed in S2 and Table S6). Example data traces in Fig. 5c clearly show that the network correctly classifies the majority for all eight input combinations tested. Each panel shows the time evolution of the concentration of X (red), Y (green) and B (yellow) for given starting concentrations of X and Y. Fig. 5d shows the net amplification of the majority signal relative to the minority signal. The results for the DNA implementation and the expected dynamics of the formal CRN (see Fig. S20) are in qualitative agreement: we observe the gradual decrease of the minority, intermediate build-up of buffer and the initial decrease but long-term increase of the majority.

We also constructed a strand displacement model for each reaction of the consensus network using Visual DSD, and parameterized these models using experimental measurements for each reaction and for the individual fork and join gates (Figs. S21,S23,S24). By composing models of individual reactions into a model of the full consensus network, we were able to quantitatively predict the dynamics of the consensus network solely from the models of its constituent parts, up to a constant scaling factor (Fig. 5c, see Section S8 for further details).

Discussion

We developed a new systematic design strategy for non-living molecular systems with functional behaviours, paired with a technology for robust and efficient synthesis of the molecular components. Our scheme is built upon de novo designed interactions not known to occur in nature. Our components did not require (directed) evolution to achieve efficacy but were designed in their ultimate form by the authors. As such our work can be seen as a step in the larger human enterprise of recapitulating the mastery of biology over matter with de novo engineering.

As human engineering is driven inexorably toward molecular scale devices, we must be careful to avoid shoehorning theory developed for digital electronics (e.g. logic circuits) into the chemical context. For well over a century, CRNs have provided the mathematical language to describe and predict the dynamics of chemical experiments. Here, we leveraged this significant theoretical investment and demonstrated the prescriptive use of CRNs for programming molecular nano-controllers.

Although our devices are entirely synthetic, they are biocompatible and there is a natural path toward applications in sensing and smart drug delivery in vivo. Cell state is encoded in the sequences and concentrations of RNAs, and recent work showed that strand displacement logic gates can recognize miRNA profiles in living mammalian cells (34). Further, the demonstration of the power of strand displacement as a mechanism for building synthetic molecular circuits tempts the hypothesis that there are natural strand displacement-based cellular regulatory networks with interesting dynamics yet to be discovered.

Methods

Preparation of plasmid-derived ndsDNA gates

Double-stranded DNA templates were cloned into a high-copy-number plasmid and transformed into E. Coli. A single colony was picked from an Ampicillin selective plate and a 800 ml overnight culture was grown with Ampicillin at 100 µg/ml at 37°C with vigorous shaking. Plasmids were extracted using a QIAGEN Maxi-prep kit and inserts were sequenced to ensure that there was no sequence error or recombination in the ndsDNA gates. Cloned ndsDNA gates were first digested with a restriction enzyme (PvuII-HF) at 37°C for one hour to release the gates from the plasmid backbone. Reactions were run with 4 units of PvuII-HF per 1 µg of plasmid. The reaction mix then was ethanol precipitated in order to optimize reaction conditions for the next digestion step. Join gates were digested with the nicking enzyme Nb.BsrDI at 65°C for one hour using 4 units of enzyme per 1 µg of plasmid. Fork gates were digested with the nicking enzyme Nt.BstNBI at 55°C for one hour using 8 units of enzyme per 1 µg of plasmid (for enzyme amount optimization see SI Sections S3.2 and S3.4). All enzymes were purchased from New England Biolabs. For kinetics experiments, enzymes were dissociated from DNA by adding sodium dodecyl sulphate (SDS) to a final concentration of 0.15% (see SI Section S3.5). Gates were then used for experiments without further purification from enzymes or plasmid backbone.

Modelling and parameter inference

Computational models were constructed for each analysed circuit, using the DNA Strand Displacement (DSD) programming language and Visual DSD software (14, 48). The unknown kinetic parameters in the model were inferred from the experimental data using Markov Chain Monte Carlo methods, as implemented in the Filzbach software “see authors website: http://research.microsoft.com/science/tools”. Such methods require the definition of a likelihood function, which describes the probability of reproducing the observed data D, given a model hypothesis and corresponding parameter set θ, i.e. Pr(D|θ,H). We used ordinary differential equation simulations for each circuit. C# code was generated using the Visual DSD tool, then integrated numerically with adaptive step-size ODE integrators (http://mstlab.org/eng/projects/Pages/Solvers.aspx Microsoft Research Solvers library for .NET). For further details, SI S7.

Additional Materials and Methods can be found in SI Section S9.