Abstract
Particle rearrangements, compaction under pressure and in vitro dissolution have been evaluated after melt dispersion of ibuprofen, Avicel and Aerosil. The Cooper–Eaton and Kuno equations were utilized for the determination of particle rearrangement and compression behavior from tap density and compact data. Particle rearrangement could be divided into two stages as primary and secondary rearrangement. Transitional tapping between the stages was found to be 20–25 taps in ibuprofen crystalline powder, which was increased up to 45 taps with all formulated powders. Compaction in the rearrangement stages was increased in all the formulations with respect to pure ibuprofen. Significantly increased compaction of ibuprofen under pressure can be achieved using Avicel by melt dispersion technique, which could be beneficial in ibuprofen tablet manufacturing by direct compression. SEM, FTIR and DSC have been utilized for physicochemical characterization of the melt dispersion powder materials. Dissolution of ibuprofen from compacted tablet of physical mixture and melt dispersion particles has also been improved greatly in the following order: Ibc<Ibsmd1<Ibsmd2<Ibsmp10<Ibsmd5<Ibsmd10.
Keywords: Particle rearrangement, Compression behavior, Ibuprofen, Aerosil lubricated mcc, Melt dispersion, In vitro dissolution
1. Introduction
In die compaction of powders, materials are subjected to compressive forces, which lead to volume reduction and tablet is produced. The volume reduction process is generally divided into three different stages: (i) die filling, (ii) particle rearrangement and (iii) deformation and bonding of discrete particles [1,2]. Particle rearrangement is the particle motion without deformation or fracturing of the particles. It is a critical process for densification during the initial compression phase [2–6] at low applied pressures. Rearrangement of particles becomes insignificant with increasing pressure and the next phase proceeds by elastic deformation, plastic flow or fragmentation of the particles. The compression ability and the dissolution rate of ibuprofen are poor and several efforts have been made in past for their improvement. Crystal engineering [7] and also spherical agglomeration [8] were developed for producing directly compressible ibuprofen. There are many reports on solid matrix systems prepared by melting or fusion [9–11] for specific pharmaceutical processing and improvement of drug dissolution. Hot-melt granules of drug (BAY 12-9566)—Gelucire 50/13—Neusilin dispersion can be compressed easily into tablets with up to 30% w/w drug loading [12]. Many reports are already published on techniques of melt dispersion [13,14] and melt solidification [15,16] of ibuprofen. Melt granulation technique was also adopted in ibuprofen tablet formulations [17].
The present study has been explored to evaluate the particle rearrangement under tapping and compression under applied pressure of the hot-melt ibuprofen dispersion with Avicel containing Aerosil and in vitro dissolution of the compact. Melt dispersion powder mix has been tableted by direct compression, which is supposed to bring about improvement in both mechanical behavior and dissolution of drug. Cooper and Eaton [18] described the compaction process of powders under applied pressure and introduced a biexponential equation. This equation has also been applied here in describing the densification of powder under tapping process. Kuno [19] developed his equation under tapping only to describe the powder packing process. Kawakita and co-workers [20,21] have described the densification process both by tapping and applied pressure. Therefore, the Cooper–Eaton compaction parameters under tapping process could be of importance. Kuno described the powder packing process and developed the equation based on the relationships between the change in apparent density and the number of tappings. The early stage of compaction process as a function of pressure due to slippage of particles or rearrangement has been explained in different ways in the literature although it is difficult to characterize and quantify [1,2,6,18,22,23]. An attempt has been made here to characterize the early stages of compaction behavior by tapping process. Characterization of particle rearrangements before deformation and compression during deformation with increasing pressure has been studied applying two different mathematical models, namely Cooper–Eaton and Kuno. Physicochemical characterization of the melt dispersion powder materials has also been carried out by SEM, FTIR and DSC.
2. Materials and methods
2.1. Preparation of powder materials by melt dispersion method
Ibuprofen (native crystalline powder: IOL Chemicals and Pharmaceuticals Ltd., India), microcrystalline cellulose (Avicel PH 101, average particle size 50 μm, mess size 60/200: Lupin Pharmaceuticals, Mumbai, India) and colloidal silicone dioxide (Aerosil 200, average particle size 15 nm: Lupin Pharmaceuticals, Mumbai, India) were used in this study. Avicel has been lubricated with Aerosil (1%, 2%, 5% and 10%) by simple blending using mortar and spatula without triturating for 5 min and thereafter named as Smcc1, Smcc2, Smcc5 and Smcc10, respectively.
In this process 5 g of ibuprofen was placed in a beaker for 45 min at ∼80 °C in an incubator. Each silicified sample was incorporated into the completely melted ibuprofen and kneaded for few minutes to a homogeneous mass. The mass was cooled to laboratory ambient temperature and passed through mesh 30. In this way four powdered samples were prepared and named as Ibsmd1, Ibsmd2, Ibsmd5 and Ibsmd10 and preserved in screw cap bottles. The formulation detail of melt dispersion ibuprofen powder has been tabulated in Table 1.
Table 1.
Ibuprofen powder samples prepared by melt dispersion technique.
| Powder formulation | Aerosil added to Avicela (%) | Ibc:Smcc ratio | Technique used | Aerosil in final mix (%) |
|---|---|---|---|---|
| Ibc | – | Crystalline ibuprofen alone | – | – |
| Ibsmp10b | 10 (Smcc10) | 1:1 | Physical mixture | 5.0 |
| Ibsmd1c | 1 (Smcc1) | 1:1 | Melt dispersion | 0.5 |
| Ibsmd2c | 2 (Smcc2) | 1:1 | Melt dispersion | 1.0 |
| Ibsmd5c | 5 (Smcc5) | 1:1 | Melt dispersion | 2.5 |
| Ibsmd10c | 10 (Smcc10) | 1:1 | Melt dispersion | 5.0 |
Lubrication was done by physical mixing of Aerosil with Avicel (mcc) in a mortar with spatula before use and named as Smcc.
Prepared by blending crystalline ibuprofen and Smcc in a mortar with spatula and not crushed.
Kneaded mass was prepared after incorporating Smcc into the completely melted ibuprofen (Ibc) at ∼80 °C and cooled to laboratory ambient temperature and passed through mesh 30.
2.2. Density measurement
Bulk density is the ratio of weight of powder to its volume before tapping. The bulk density of powder is dependent on particle packing. The bulk density was measured by pouring powder sample into a graduated 50 ml cylinder (stoppered) and the volume of the powder sample was recorded directly from the cylinder. The measurement was repeated five times varying the amount (15–20 g) and the value was reported. The tapped volume was measured up to 200 taps using a bulk density measurement apparatus (Koshiash Instruments bulk India) and the height of the powder was determined visually. The true density was determined by helium pycnometer (Pycno 30, Smart Instruments, India) without replication.
2.3. Compaction of powder
Ibuprofen pure and other formulated powders were compacted on a hydraulic pellet press (Kimaya Engineers, India) over a compression pressure ranging from 245 to 2942 MPa, using a 10 mm diameter die and flat faced punches. Materials for each pellet were weighed accurately (400 mg) and poured manually into the die and pellets of each formulation were prepared. Maximum upper punch pressure at each load with a dwelling time of 60 s was recorded for compaction of each tablet in the laboratory ambient condition (∼27 °C, ∼60% RH). The thickness of each pellet was measured with a digital micrometer (Mitutoyo, Japan). This data was used for the calculation of apparent density, porosity and degree of volume reduction. Tablets were preserved in a wide mouth tightly closed container immediately after compression.
2.4. Characterization of particle rearrangement and compression behavior
2.4.1. Application of Cooper–Eaton equation
Cooper and Eaton developed a biexponential equation for describing the compaction of powders as a function of applied pressure and adopted from other fields of industry for research in pharmaceutical compression process. The equation is
| (1) |
where D0 and D are the relative density at zero pressure and at pressure P, respectively, a indicates the fraction of the theoretical maximal densification, which could be achieved in the first stage by filling large voids by interparticulate slippage and b indicates small voids by deformation or fragmentation at a higher pressure in the second stage of densification. Ka and Kb describe the magnitude of pressure at which the respective compaction process would occur with the greatest probability of density. Tablets were produced on a hydraulic pellet press and the parameters of the second stage due to particle deformation were determined from the graphical plot of Ln((1/D0)−(1/D))/(1/D0)−1 versus 1/P, where the slope of the linear region is Kb and the ordinate intercept of that linear region of the second stage compaction measures (a+b).
Rearrangement of discrete particles could be described by two major steps [24,25] based on cohesiveness of the powdered material as (i) primary rearrangements of fine discrete particles and (ii) secondary rearrangements. Replacing pressure, P, by the tapping number, N, in the Cooper–Eaton equation we get
| (2) |
where D0 and D are the relative density before tapping obtained by poured density divided by equilibrium tapped density and the relative density at Nth tapped obtained by apparent density of a powder column divided by equilibrium tapped density, respectively. The coefficient K1 represents the tapping required to induce densification by primary particle rearrangements, which has the greatest probability of density, whereas K2 represents the tapping required to induce densification through secondary particle rearrangements. a1 and a2 are the dimensionless constants that indicate the fraction of the theoretical maximum densification of tapping, which could be achieved by filling voids by primary rearrangements (a1) and secondary rearrangements (a2). Above parameters were determined from the graphical plot of Ln(1/D0)−(1/D)/((1/D0)−1) versus 1/N, where K1 and K2 were determined by the slopes of two linear regions, while a1 and (a1+a2) determined from the ordinate intercepts of the linear regions of initial and second stage of tapping, respectively.
2.4.2. Application of the Kuno equation
The relationship between the change in apparent density and the number of tappings described by Kuno is
| (3) |
where ρt is the apparent density at equilibrium, ρn the apparent density at Nth tapped state, ρo the apparent density at initial cascade state and K the rate of packing process under tapping.
Eq. (3) can be rewritten as
| (4) |
| (5) |
where ln d=D
As the constant D is related to the process of particles rearrangement by two major steps [24,25], the total rearrangement phenomena can be described by the following biexponential equation:
| (6) |
where d1=(ρp−ρo) is the density difference that indicates the primary rearrangements of fine discrete particles, d2=(ρt−ρp) the density difference due to secondary rearrangement process followed by primary rearrangement, d1+d2=ρt−ρo the density difference that describes the total rearrangement phenomenon that is the maximal compaction achieved after primary rearrangement of discrete particles and secondary rearrangement altogether and Kp and Ka are the constants that give a measure of the rate of packing during primary rearrangement and the rate of packing during secondary rearrangement, respectively. Hence, the packing of particle mass by primary rearrangement and secondary rearrangement could be expressed as
| (7) |
| (8) |
where ρp is the apparent density of powder column, which describes the extent of primary rearrangement of discrete particles. The above constants were determined by biphasic linear plots of ln(ρt−ρn) versus N, where Kp and Ka were determined from the slope of the first and second linear regions, respectively, and (d1+d2) and d2 were determined from ordinate intercepts of these two linear regions.
The consolidation phenomenon on applied pressure can be described by the same equation. After replacing the tapping number, N, by pressure, P, the Kuno equation can be expressed as
| (9) |
| (10) |
putting ln a=A
| (11) |
where ρT is the true density and ρ is the apparent density at the specific applied pressure P.
A is the constant obtained from ordinate intercept of the graphical representation ln(ρT−ρ) versus P. The slope, K, represents the rate of packing under pressure or consolidation under pressure. The intercept, A, is extrapolated from the linear part of the Kuno plot. The constant A could be related to the process of compaction by two major steps: (i) die filling and particle rearrangement and (ii) particle deformation and bond formation of discrete particles:
| (12) |
where a1=(ρT−ρr) is the density difference that indicates the theoretical maximal compaction, which could be achieved by die filling and particle rearrangement, a2=(ρr−ρo) the density difference due to plastic deformation and bond formation only and K1 and K2 are the constants that give a measure of the rate of packing during die filling and particle rearrangement and the rate of packing during plastic deformation, respectively.
The biphasic equation can be expressed as
| (13) |
(ρr−ρo) and K2 were determined from the graphical plot of dense compact of ln(ρT−ρ) versus P.
2.5. Characterization by differential scanning calorimetry (DSC), Fourier transformed infrared (FTIR) spectroscopy and scanning electron microscopy (SEM)
Differential scanning calorimetry (DSC) thermograms of the formulated powdered products were recorded on a differential scanning calorimeter (DSC Q10 V9.4 Build 287). Accurately weighed samples (2–5 mg) were placed in sealed aluminum pans, and scanned at a heating rate of 10 °C/min over the temperature range of 20–170 °C using a nitrogen gas purge at 50 ml/min. Fourier transformed infrared (FTIR) spectra of the powdered samples were recorded using FTIR spectrometer (FTIR-4100typeA, Jasco, Tokyo, Japan) employing the potassium bromide pellet method. The samples were scanned from 4000 to 400 cm−1. All spectra were collected through the scan of accumulations 80 at a resolution of 4 cm−1 and scanning speed of 2 mm/s. Spectral Manager for Windows software (Jasco, Tokyo, Japan) was used for data acquisition and holding. The morphology of the particulate samples was investigated using scanning electron microscopy (SEM) (Instrument JSM-6390 Jeol, Japan). Samples were mounted on carbon sticky tabs and sputtered with gold coating prior to observations.
2.6. In vitro dissolution testing
In vitro drug release of the compressed tablets of all formulations (Ibc, Ibsmp10, Ibsmd1, Ibsmd2, Ibsmd5 and Ibsmd10) was performed using the rotating paddle method (900 ml phosphate buffer of pH 7.2 as dissolution medium maintained at 37±0.5 °C and 50 rpm) with a Disso 2000 dissolution apparatus (Labindia, India) and the dissolution was continued for 120 min. At predetermined time intervals, 5-ml samples were collected and then replaced with an equal volume of dissolution medium. Collected samples were then filtered through a 0.45 μm membrane filter (WHATMAN Puradisc 25 Nylon, India) and absorbance data were recorded at 222 nm using UV–vis spectrophotometer (JASCO V-630 spectrophotometer, Software: Spectra Manager). The mean of four determinations was used to calculate the amount of drug released from the samples using standard calibration curve and the error expressed as standard deviation (mean±sd, n=4).
2.7. Statistics
The analysis of variance (ANOVA) is a powerful resource that can be used for analyzing the quality of the estimated regression line. The total variation in the dependent variable was subdivided into meaningful components that were then observed and treated in a systematic manner. We had n experimental data points in the usual form (xi, yi) and the regression line was estimated. In our estimation following formulation was utilized:
i.e. SST=SSR+SSE, where SST is the total corrected sum of squares, SSR the regression sum of squares and SSE the sum of squares of residuals.
SSR reflects the amount of variation in the y-values explained by the model, in this case the postulated straight line. The SSE component reflects variation about the regression line. To test the hypothesis, we computed
and accepted Ho at α-level of significance when f<fa (1, n−2). It is customary to refer to the various sums of squares divided by their respective degrees of freedom as mean squares. When the null hypothesis was accepted, that is when the computed F-statistic did not exceed the critical value f0.05 (1, n−2), we have concluded that there was an insignificant amount of variation in the response accounted for by the postulated model, the straight-line function. If the F-statistic exceeds the critical value data will not reflect sufficient evidence to support the model postulated.
3. Results and discussion
3.1. Characteristics of particle applying Cooper–Eaton equation
Fig. 1 shows the Cooper–Eaton plots of dense compacts of four representative melt dispersion powders (Ibsmd1, Ibsmd2, Ibsmd5 and Ibsmd10). The profiles of ibuprofen (Ibc) and physical mixture (Ibsmp10) were included in the figure to get a comparative view. The Cooper–Eaton model fitted well to the data (R2=0.911–0.969, and null hypothesis was accepted) to produce dense compact in the pressure range 245–2942 MPa. Values of the Cooper–Eaton parameters of the dense compact are depicted in Table 2. Kb determined from the slope improved in all the formulated melt dispersions [17.61(±1.890)–20.61(±1.989) MPa] than the pure drug (4.95±0.781 MPa). This means the pressure required to induce densification by deformation [26] is more in the formulated mixture than in ibuprofen alone.
Fig. 1.

Cooper–Eaton plots of dense compact consolidated under pressure for melt dispersion powders (Ibsmd1, Ibsmd2, Ibsmd5 and Ibsmd10). All the profiles maintained linearity (R2>0.91, and the null hypothesis was accepted). Profiles of ibuprofen (Ibc) and physical mixture (Ibsmp10) were included in the figure to get a comparative view.
Table 2.
Cooper–Eaton compression parameters of the dense compacts of melt dispersion of ibuprofen.
| Powder formulation | Compression pressure range (MPa) | (−)Kb (MPa) (mean±sd, n=4) | (a+b) (mean±sd, n=4) | R2 | Computed f=SSR/s2 | p Value |
|---|---|---|---|---|---|---|
| Ibc | 245–2942 | 4.95±0.781 | 0.978±0.089 | 0.921 | 0.2 | Insig |
| Ibsmp10 | 245–2942 | 11.44±1.076 | 0.975±0.058 | 0.931 | 36.4 | Insig |
| Ibsmd1 | 245–2942 | 18.36±1.161 | 0.950±0.097 | 0.965 | 135.0 | Insig |
| Ibsmd2 | 245–2942 | 17.61±1.890 | 0.944±0.057 | 0.911 | 4.6 | Insig |
| Ibsmd5 | 245–2942 | 20.61±1.989 | 0.944±0.078 | 0.949 | 1.8 | Insig |
| Ibsmd10 | 245–2942 | 18.45±1.155 | 0.951±0.068 | 0.969 | 154.4 | Insig |
Critical value f0.05 (1, n−2) is more than 224; Insig=insignificant; Kb=pressure at which the theoretical maximal densification achieved in the second stage by filling small voids by deformation or fragmentation at higher pressure; (a+b)=total fraction of theoretical densification.
Compaction can be completely explained by two separate processes when the sum of a and b is equal to unity (1) [18]. This occurs by particle rearrangement and plastic flow or fragmentation. If the sum of a and b is less than unity, other processes must become operative before complete compaction is achieved. The compaction process can be explained by the two aforementioned processes when the sum of a and b is equal to unity (1). Compaction cannot be explained exclusively by these two processes if the sum is less than unity, that is, there are other processes present. The summation (a+b) yielded a value closer to unity [from 0.947(±0.085) to 1.035(±0.095)] in all the cases, which indicated that an almost unity packing fraction (nonporous compact) could be obtained from all these powder mix of ibuprofen in combination with Avicel/Aerosil or alone at studied pressure.
Particle rearrangements were described based on tapping utilizing the Cooper–Eaton equation (2) in which the pressure, P, was replaced in the Cooper–Eaton equation (1) by the tapping number N. Fig. 2 exhibits the plot of Ln(1/D0)−(1/D)/((1/D0)−1) versus 1/N of all samples of Ibsmd. Each profile clearly depicted the two distinct linear regions and was also found to fit the biexponential Cooper–Eaton equation (R2 values ranging from 0.909 to 0.995; null hypothesis was accepted). Rearrangement parameters under tapping applying the Cooper–Eaton equation of all the samples are tabulated in Table 3.
Fig. 2.
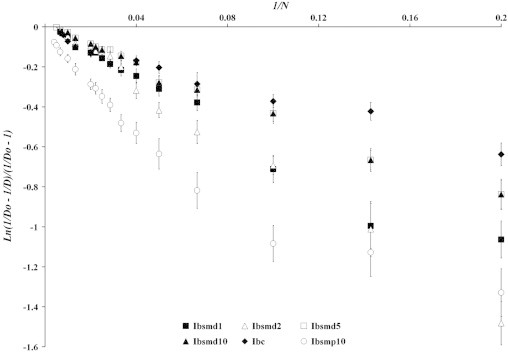
Plots of ln((1/D0)−(1/D))/((1/D0)−1) versus 1/N based on tapping for characterization of particle rearrangements of melt dispersion powders (Ibsmd1, Ibsmd2, Ibsmd5 and Ibsmd10). Two distinct linear regions (biexponential) (R2 values 0.925–0.994, and the null hypothesis was accepted) are identified in each profile, which indicate two major steps of particle rearrangement, namely (i) primary rearrangement of fine discrete particles and (ii) secondary rearrangement or agglomerate formation.
Table 3.
Particle rearrangements under tapping applying the Cooper–Eaton equation on the basis of equilibrium apparent density of ibuprofen samples of melt dispersion.
| Powder formulation | Preliminary rearrangement |
Secondary rearrangement |
(a1+a2) | Npc | Computed f=SSR/s2 (1st line) (2nd line) | p Value | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| (−) K1 (mean±sd, n=5) | a1 (mean±sd, n=5) | R2 | (−) K2 (mean±sd, n=5) | a2 (mean±sd, n=5) | R2 | |||||
| Ibc | 2.280±0.231 | 0.888±0.061 | 0.927 | 3.943±0.351 | 0.098±0.0083 | 0.922 | 0.986±0.068 (0.56)* | 20 | (150.7) (59.1) | Insig |
| Ibsmp10 | 3.480±0.353 | 0.524±0.043 | 0.909 | 11.696±1.031 | 0.423±0.0431 | 0.995 | 0.947±0.085 (0.50)* | 20–25 | (183.4) (5.5) | Insig |
| Ibsmd1 | 5.587±0.431 | 0.943±0.078 | 0.928 | 6.890±0.703 | 0.073±0.0061 | 0.976 | 1.016±0.086 (0.43)* | 20–30 | (52.1) (2.9) | Insig |
| Ibsmd2 | 7.054±0.338 | 0.965±0.083 | 0.994 | 6.189±0.440 | 0.056±0.0045 | 0.963 | 1.020±0.083 (0.48)* | 25–30 | (4.6) (3.6) | Insig |
| Ibsmd5 | 4.229±0.231 | 0.920±0.079 | 0.991 | 9.329±0.783 | 0.114±0.0201 | 0.964 | 1.035±0.095 (0.41)* | 40–45 | (223.4)* (2.9) | Insig |
| Ibsmd10 | 4.233±0.430 | 0.979±0.085 | 0.987 | 6.006±0.541 | 0.054±0.0028 | 0.986 | 1.034±0.090 (0.37)* | 35–40 | (223.4)* (1.8) | Insig |
Critical value f0.05 (1, n−2) is more than 215 and for * more than 224; Insig=insignificant; K1 represents the tapping required to induce densification by primary particle rearrangement and K2 is representative of the tapping required to induce densification by secondary particle rearrangement; a1, a2=dimensionless constants that indicate the fraction of the theoretical maximum densification achieved by filling voids by primary rearrangement (a1) and by secondary rearrangement (a2); Npc is the transitional tapping of primary rearrangement and secondary rearrangement as per Cooper–Eaton model; * value in the parentheses indicates total packing fraction calculated on the basis of particle true density by total rearrangements via tapping process.
The tappings required to induce densification by primary particle rearrangement (K1) and by secondary particle rearrangement (K2) are improved in all the samples of melt dispersion powders [3.480(±0.353)–7.054(±0.338) and 6.006(±0.541)–11.696(±1.031), respectively] than ibuprofen alone [2.280(±0.231) and 3.943(±0.351), respectively]. Maximum improvement has been observed in primary rearrangement with Ibsmd2 (7.054±0.338) and secondary rearrangement with Ibsmd5 (9.329±0.783). The physical mixture (Ibsmp10) exhibited K1 and K2 values as 3.480±0.353 and 11.696±1.031, respectively. The fraction of the theoretical maximum densification achieved by filling voids by primary rearrangement (a1) out of total rearrangements due to tapping varied 0.524(±0.043)–0.979(±0.085) and by secondary rearrangement (a2) due to tapping varied 0.054(±0.00280)–0.423(±0.0431) in the powder samples. Therefore, densification by particle rearrangement proceeds mainly by primary rearrangement process rather than the secondary one in all the ibuprofen powders. The summation (a1+a2) produced a value almost closer to unity [0.986(±0.068)–1.035(±0.095)] in all the melt dispersion samples, which indicated that the total rearrangements could be explained almost exclusively by these two steps (primary and secondary rearrangements) and other processes were absent. In the case of physical mixture (0.947±0.085 for Ibsmp10) other processes may become operative before complete rearrangement is achieved. Total packing fraction by total rearrangements via tapping process varied 0.37–0.56 calculated on the basis of particle true density. This means 37–56% densification could be possible by rearrangements of the particles only as understood by tapping process based on the Cooper–Eaton equation without applying pressure.
3.2. Characteristics of particle applying the Kuno equation
The Kuno plot of ln(ρt−ρn) verses N of the melt dispersion powders has been illustrated in Fig. 3 to describe the change in densification under tapping. Data of pure ibuprofen and physical mixture (Ibsmp10) have also been presented in this figure. Two distinct linear regions have been identified in each profile and found to fit the biexponential Kuno equation (R2 values 0.955–0.996, and null hypothesis was accepted). The rate of packing process of the Kuno equation could be described by the process of particle rearrangement under tapping. Two major steps of particle rearrangement, namely (i) primary rearrangements of fine discrete particles and (ii) secondary rearrangements, can be explained as the two rearrangement parameters. The rearrangement parameters of all the samples applying the Kuno equation are tabulated in Table 4. The rate of packing during primary rearrangement (Kp) and the rate of packing during secondary rearrangements (Ka) have been improved in all the samples of melt dispersion powders [from −3.793×10−2(±0.326) to −5.012×10−2(±0.269) and from −1.463×10−2(±0.152) to −2.333×10−2(±0.203), respectively] rather than that in pure ibuprofen [between −3.727×10−2(±0.311) and −1.425×10−2(±0.181), respectively]. The particle rearrangement was described by Kuno to occur in two steps: (i) primary rearrangement (ii) secondary rearrangement. Physical mixture (Ibsmp10) did not show any improvement in neither of the primary and secondary rearrangement processes [−2.017×10−2(±0.158) and −0.545×10−2(±0.029)]. Improvement is noticed in primary rearrangement in the order Ibsmp10<Ibc<Ibsmd5<Ibsmd1<Ibsmd2<Ibsmd10 and in secondary rearrangement in the order Ibsmp10<Ibc<Ibsmd2<Ibsmd1<Ibsmd10<Ibsmd5. Kawashima et al. [27] prepared microspheres of ibuprofen and have shown the increased rate of packing compared to that of original crystals of ibuprofen using the Kuno equation. Density difference due to primary rearrangements of fine discrete particles (ρp−ρo) and that due to secondary rearrangement (ρt−ρp) are more with the formulated powders than the ibuprofen alone. Melt dispersion particles became more compacted in the total rearrangement process (ρt−ρo) than that of pure drug and physical mixture. Highest difference in density of (ρt−ρo) was exhibited by Ibsmd1 (0.771 g/ml). Apparent density of powder column that describes the extent of primary rearrangement (ρp) of discrete particles of melt dispersion and physical mixture varied in a narrow range from 0.603 (±0.058) to 0.689 (±0.059) g/ml while pure drug has shown poor value (0.449±0.041 g/ml). Transitional tapping between primary rearrangement and secondary rearrangement of ibuprofen powder applying the Cooper–Eaton equation (Npc) and the Kuno equation (Npk) occurred within 20–25 taps. The same parameter increased with the formulated powders of melt dispersion and found up to 40/45 taps applying two equations. The values are reported in Tables 3 and 4.
Fig. 3.
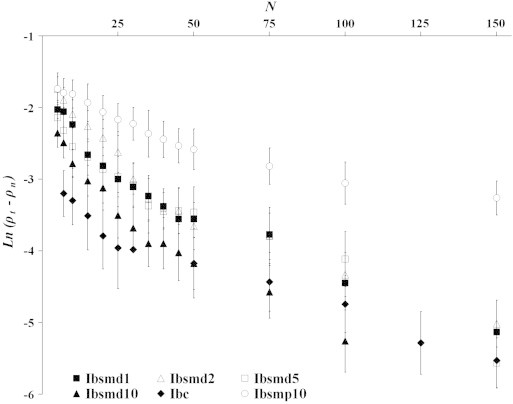
Kuno plots of ln(ρt−ρn) versus N of melt dispersion powders (Ibsmd1, Ibsmd2, Ibsmd5 and Ibsmd10). Two distinct linear regions (biexponential) have been identified in each profile with R2 values 0.903–0.996 and the null hypothesis was also accepted.
Table 4.
Particle rearrangements under tapping applying Kuno equation of melt dispersion of ibuprofen.
| Powder formulation | (−)Kp×102 (mean±sd, n=5) (R2) | (−)Ka×102 (mean±sd, n=5) (R2) | (ρp−ρo) | (ρt−ρo) | (ρt−ρp) | ρp | Npk | Computed f=SSR/s2 (1st line) (2nd line) | p Value |
|---|---|---|---|---|---|---|---|---|---|
| Ibc | 3.727±0.311 (0.959) | 1.425±0.181(0.983) | 0.019 | 0.103 | 0.084 | 0.449(±0.041) | 25 | (4.03) (1.52) | Insig |
| Ibsmp10 | 2.017±0.158 (0.996) | 0.545±0.029(0.971) | 0.103 | 0.150 | 0.047 | 0.640(±0.043) | 45 | (3.44) (2.08) | Insig |
| Ibsmd1 | 3.817±0.341 (0.962) | 1.580±0.0133(0.974) | 0.101 | 0.771 | 0.670 | 0.635(±0.052) | 40–45 | (3.93) (0.84) | Insig |
| Ibsmd2 | 4.772±0.456 (0.990) | 1.463±0.152(0.980) | 0.127 | 0.214 | 0.087 | 0.689(±0.059) | 40–45 | (3.45) (0.86) | Insig |
| Ibsmd5 | 3.793±0.326 (0.970) | 2.333±0.203(0.955) | 0.023 | 0.176 | 0.153 | 0.607(±0.045) | 35 | (5.79) (3.93) | Insig |
| Ibsmd10 | 5.012±0.269 (0.983) | 2.107±0.231(0.985) | 0.067 | 0.151 | 0.084 | 0.603(±0.058) | 35 | (4.16) (0.54) | Insig |
Critical value f0.05 (1, n−2) is more than 224; Insig=insignificant; Kp and Ka are the constants that give a measure of the rate of packing during primary rearrangement and the rate of packing during secondary rearrangement, respectively, where (ρp−ρo) indicates density difference due to primary rearrangements of fine discrete particles, (ρt−ρp) is the density difference due to agglomerate formation only after achieving primary rearrangement, (ρt−ρo) describes the density difference for total rearrangement phenomena that is the maximal compaction achieved after primary rearrangement of discrete particles and agglomerate formation altogether, ρp is the apparent density of powder column that describes the extent of primary rearrangement of discrete particles, (all in g/ml), Kp and Ka are the constants measuring the rate of packing during primary rearrangement and the rate of packing during secondary rearrangement, respectively, and Npk is the transitional tapping of primary rearrangement and secondary rearrangement or agglomerate formation as per the Kuno equation.
Consolidation phenomenon of the dense compact produced under pressure of all ibuprofen powder samples has also been explained by plotting Ln(ρT−ρ) versus P replacing the tapping number, N, by pressure, P, in the original Kuno equation and is illustrated in Fig. 4 for melt dispersion materials. For all the powder samples the graphs maintained practically linear and were found to fit to the linear relationship of the Kuno equation (R2 value 0.901–0.981, and null hypothesis was accepted) to produce dense compact in the pressure range of 245–2942 MPa. The value of the Kuno parameters of the dense compact are depicted in Table 5. The rate of packing or consolidation during plastic deformation (K2) was not changed significantly in the formulated powder compared to pure ibuprofen powder. The density difference (ρT−ρo) indicated by the process of compaction occurred (i.e. (i) die filling and particle rearrangement and (ii) particle deformation and bonding of discrete particles) has been increased in the formulation. Thus, by applying the Kuno equation under pressure it may be understood that increased compaction can be achieved both by lubrication with Aerosil and by melt dispersion. Density difference due to die filling and particle rearrangement (ρT−ρr) actually dominated over plastic deformation (ρr−ρo).
Fig. 4.
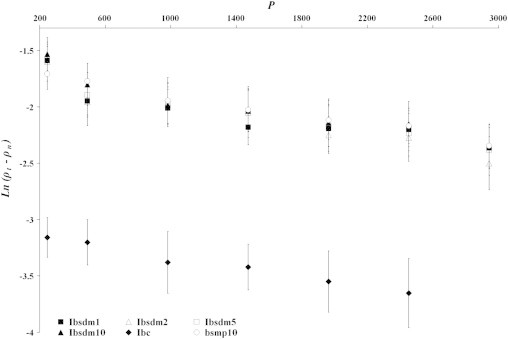
Plots of ln(ρT−ρ) versus P of the dense compact consolidated under pressure for melt dispersion powders (Ibsmd1, Ibsmd2, Ibsmd5 and Ibsmd10). All the powder samples in the graph show linear relationship (R2 values 0.901–0.982; the null hypothesis was also accepted) to produce dense compact in the pressure range.
Table 5.
Compression parameters of the dense compact applying the Kuno equation of melt dispersion of ibuprofen.
| Powder formulation | Compression pressure range (MPa) | (−) K2×103 (mean±sd, n=4) (R2) | (ρT−ρo) | (ρr−ρo) | ( ρT−ρr) | ρr (mean±sd, n=4) | Computed f=SSR/s2 | p Value |
|---|---|---|---|---|---|---|---|---|
| Ibc | 245–2942 | 0.224±0.018 (0.981) | 0.685 | 0.044 | 0.641 | 0.474±0.035 | 222.3 | Insig |
| Ibsmp10 | 245–2942 | 0.221±0.020 (0.977) | 1.043 | 0.187 | 0.856 | 0.528±0.041 | 193.7 | Insig |
| Ibsmd1 | 245–2942 | 0.154±0.011 (0.908) | 0.809 | 0.152 | 0.656 | 0.700±0.055 | 10.6 | Insig |
| Ibsmd2 | 245–2942 | 0.225±0.019 (0.907) | 0.797 | 0.170 | 0.627 | 0.732±0.051 | 28.6 | Insig |
| Ibsmd5 | 245–2942 | 0.247±0.015 (0.901) | 0.784 | 0.189 | 0.595 | 0.774±0.068 | 25.7 | Insig |
| Ibsmd10 | 245–2942 | 0.195±0.019 (0.940) | 0.848 | 0.175 | 0.673 | 0.711±0.049 | 22.5 | Insig |
Critical value f0.05 (1, n−2) is more than 224; Insig=insignificant; K2=rate of packing under pressure or consolidation during plastic deformation; (ρT−ρo)=density difference that indicates the theoretical maximal compaction which achieved by two major steps: (i) die filling and particle rearrangement and (ii) plastic deformation and bond formation of discrete particle; (ρT−ρr)=density difference due to die filling and particle rearrangement; (ρr−ρo)=density difference due to plastic deformation and bond formation only; ρr=apparent density of powder column describes the extent of die filling and particle rearrangement (density in g/ml).
3.3. Scanning electron microscopy studies
The crystalline drug (Ibc) has a distinct geometric shape (Fig. 5A). In the physical mixture (Ibsmp10) drug crystal surfaces are covered by the Avicel/Aerosil particles and the crystals are almost not affected (Fig. 5B). The melt dispersion particulate beads (Ibsmd10) are of irregular shape with rough/porous surface (Fig. 5C and D). It revealed that agglomerate has been produced during melt dispersion and size of the individual crystallite comprising the agglomerate was also significantly less than the individual crystal of pure drug. This transformation of individual crystal of pure drug into irregular porous/rough surfaced agglomerate of small crystallite is the possible indication of partial amorphization.
Fig. 5.

Scanning electron micrographs of samples of ibuprofen crystals, physical mixture and melt dispersion powders. (A) Ibc (distinctive geometric shape of crystalline ibuprofen, magnification 500×); (B) Ibsmp10 (ibuprofen crystals are identified in the physical mixture, magnification 500×); (C) Ibsmd10 (magnification 500×) and (D) Ibsmd10 (magnification 1000×) (in Ibsmd10 size of the individual crystallite comprising the agglomerate was significantly decreased than the individual crystal of pure drug).
3.4. FTIR studies
The FTIR spectrum of crystalline ibuprofen (Ibc) in Fig. 6 shows the characteristic absorbance peak at 1719 cm−1 with high intensity due to carbonyl stretching. The absence of major shift in the peak positions for melt agglomerate and physical mixture suggested the absence of major interactions in the solid state between Avicel/Aerosil and ibuprofen. Minor changes in shifting and intensity of peak may be related to the amorphous transformation [28].
Fig. 6.
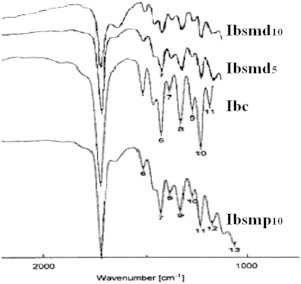
FTIR spectra of ibuprofen powder samples: Ibc shows characteristic peak of ibuprofen at 1719 cm−1 of high intensity due to carbonyl stretching. The absence of major shift in the peak positions for physical mixture and melt agglomerate (Ibsmp10, Ibsmd5 and Ibsmd10) suggested the absence of major interaction.
3.5. Differential scanning calorimetry studies
DSC thermograms of ibuprofen samples are presented in Fig. 7. The DSC thermogram of crystalline ibuprofen (Ibc) showed a melting endotherm at 76.6 °C with normalized energy of 121.9 J/g. The thermograms of Ibsmp10, Ibsmd5 and Ibsmd10 show a gradual decrease in melting endotherm at 75.6, 74.4 and 73.7 °C with energies 59.2, 49.9 and 48.5 J/g, respectively, attributing to gradual decrease in crystalline intensity of ibuprofen in the respective samples. The ibuprofen melting onset temperature (74.4 °C) also gradually decreased in the melt dispersion samples (73.7, 72.0 and 71.7 °C) due to the presence of drug in the matrix of Avicel/Aerosil. DSC results might be an indication of maximum amorphization of ibuprofen in Ibsmd10 [29].
Fig. 7.
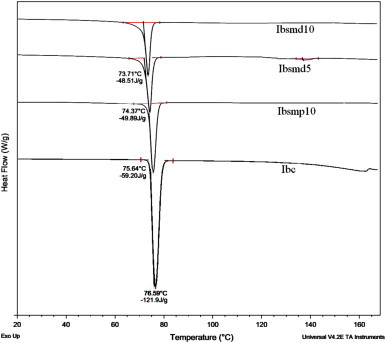
DSC thermograms of ibuprofen powder samples (Ibc, Ibsmp10, Ibsmd5 and Ibsmd10). Ibc melts at 76.59 °C. Gradual decrease in melting endotherm of Ibsmp10, Ibsmd5 and Ibsmd10 has been observed at 75.64, 74.37 and 73.71 °C, respectively.
3.6. In vitro dissolution studies
Fig. 8 shows dissolution patterns of ibuprofen from crystalline drug (Ibc), physical mixture (Ibsmp10,) and melt dispersion samples (Ibsmd1, Ibsmd2, Ibsmd5 and Ibsmd10). The dissolution rate of pure ibuprofen was very low (37.1±9.9% and 45.5±3.5% at 60 and 120 min, respectively). Poor dissolution of drug from crystalline ibuprofen has already been reported by several researchers earlier [30,31]. The dissolution rate was greatly improved both in physical mixture and melt dispersion samples. Presence of Avicel disintegrated the tablets very firstly. Moreover, improved dissolution may be due to increased wettability and increased amorphization of the drug. Presence of silicon dioxide increased hydrophilicity of the drug particle and facilitated access of water during dissolution. Maximum degree of wettability and amorphization might have brought about by maximum concentration of silicon dioxide in Ibsmd10 and improved dissolution [28] to the maximum extent at 120 min (98.1±1.8%). The dissolution of ibuprofen has been increased in the physical mixture (77.2±3.2% in Ibsmp10) rather than the melt dispersion samples of Ibsmd1 (70.2±3.2%) and Ibsmd2 (75.3±2.5%). Ibsmd5 has exhibited dissolution up to 89.1±1.98%. These improvements in dissolution have also been reported previously when ibuprofen was co-milled with silicon containing clay (kaolin) because of amorphization of the drug [32].
Fig. 8.
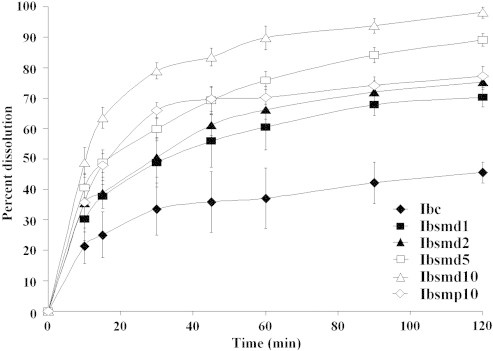
Dissolution profiles of ibuprofen tablets (Ibc, Ibsmd1, Ibsmd2, Ibsmd5, Ibsmd10 and Ibsmp10). Each data point represents the mean±sd of four repetitions.
4. Conclusions
An attempt has been made for evaluation of particle rearrangement under tapping and consolidation by deformation and fragmentation under applied pressure after melt dispersion of ibuprofen, Avicel and Aerosil. The Cooper–Eaton and Kuno equations were applied for determination of both rearrangement and compaction parameters under pressure from tap density and compact data, respectively. The compressibility to induce densification by primary particle rearrangement and by secondary particle rearrangement may be understood by tapping was improved in all the samples of melt dispersion powders than pure ibuprofen powder. Total packing fraction by particle rearrangement occurred up to 37–56%, calculated on the basis of particle density via tapping process, which was mainly by primary rearrangement process rather than the secondary one in all the ibuprofen powders based on the Cooper–Eaton equation. The rates of packing during both primary rearrangement and secondary rearrangement have been improved in all the samples of melt dispersion powders compared to ibuprofen crystals based on the biexponential Kuno equation. Transitional tapping between primary and secondary rearrangement was 20–25 taps with crystalline ibuprofen and the same increased up to 40–45 taps in the melt dispersion mixtures. Pressure required to achieve densification in the second stage by filling small voids by deformation or fragmentation at a higher pressure was also more in the formulated mixture than in ibuprofen alone. The densification achieved by filling large voids by interparticulate slippage and small voids by deformation or fragmentation at a higher pressure was operated simultaneously and an almost nonporous compact was obtained from all the melt dispersion powder samples of ibuprofen. The rate of packing process during die filling and particle rearrangement and the rate of packing or consolidation during plastic deformation did not change greatly in the melt dispersion powder compared to ibuprofen crystals. Increased compaction can be achieved after melt dispersion of ibuprofen and silicon dioxide lubricated microcrystalline cellulose than ibuprofen alone and could be utilized in the direct compression of ibuprofen tablet manufacturing. The dissolution of ibuprofen has been greatly improved in the physical mixture and melt dispersion particles than the crystalline drug. Increased degree of silicification improved both wettability and amorphization of the drug, which brought about increased dissolution. The degree of improvement in dissolution was found in the order of Ibc<Ibsmd1<Ibsmd2<Ibsmp10<Ibsmd5<Ibsmd10.
References
- 1.Heckel R.W. Density–pressure relationships in powder compaction. Trans Metall Soc AIME. 1961;221:671–675. [Google Scholar]
- 2.Heckel R.W. An analysis of powder compaction phenomena. Trans Metall Soc AIME. 1961;221:1001–1008. [Google Scholar]
- 3.Duberg M., Nystro M.C. Studies on direct compression of tablets XVIII. Porosity–pressure curves for the characterization of volume reduction mechanisms in powder compression. Powder Technol. 1986;46:67–75. [Google Scholar]
- 4.Sun C., Grant D.J.W. Influence of elastic deformation of particle on Heckel analysis. Pharm Dev Technol. 2001;6:193–200. doi: 10.1081/pdt-100000738. [DOI] [PubMed] [Google Scholar]
- 5.Walker E.E. The properties of powder—part VI. The compressibility of powders. Trans Faraday Soc. 1923;19:73–82. [Google Scholar]
- 6.Nordstrom J., Welch K., Frenning G., Alderborn G. On the physical interpretation of the Kawakita and Adams parameters derived from confined compression of granular solids. Powder Technol. 2008;182:424–435. [Google Scholar]
- 7.Rasenack N., Muller B.W. Crystal habit and tableting behavior. Int J Pharm. 2002;244:45–57. doi: 10.1016/s0378-5173(02)00296-x. [DOI] [PubMed] [Google Scholar]
- 8.Jbilou M., Ettabia A., Guyot-Hermann A.-M., Guyot J.C. Ibuprofen agglomerates preparation by phase separation. Drug Dev Ind Pharm. 1999;25:297–305. doi: 10.1081/ddc-100102174. [DOI] [PubMed] [Google Scholar]
- 9.Breitenbach J. Melt extrusion: from process to drug delivery technology. Eur J Pharm Biopharm. 2002;54:107–117. doi: 10.1016/s0939-6411(02)00061-9. [DOI] [PubMed] [Google Scholar]
- 10.Bashiri-Shahroodi A., Nassab P.R., Szabo-Revesz P., Rajko R. Preparation of a solid dispersion by a dropping method to improve the rate of dissolution of meloxicam. Drug Dev Ind Pharm. 2008;34:781–788. doi: 10.1080/03639040801925735. [DOI] [PubMed] [Google Scholar]
- 11.Flament M.N., Duport G., Leterme P., Farah N., Gayot A. Development of 400 μm pellets by extrusion-spheronization: application with gelucir 50/02 to produce a sprinkle form. Drug Dev Ind Pharm. 2004;30:43–51. doi: 10.1081/ddc-120027510. [DOI] [PubMed] [Google Scholar]
- 12.Gupta M.K., Goldman D.R., Bogner H., Tseng Y.C. Enhanced drug dissolution and bulk properties of solid dispersions granulated with a surface adsorbent. Pharm Dev Tech. 2001;6:563–572. doi: 10.1081/pdt-120000294. [DOI] [PubMed] [Google Scholar]
- 13.Adeyeye C.M., Price J.C. Development and evaluation of sustained release ibuprofen-wax microspheres. I. Effect of formulation variables on physical characteristics. Pharm Res. 1991;8:1377–1383. doi: 10.1023/a:1015845022112. [DOI] [PubMed] [Google Scholar]
- 14.Adeyeye C.M., Price J.C. Development and evaluation of sustained release ibuprofen-wax microspheres. II. In vitro dissolution studies. Pharm Res. 1994;11:575–579. doi: 10.1023/a:1018931002991. [DOI] [PubMed] [Google Scholar]
- 15.Paradkar A.R., Maheshwari M., Ketkar A.R., Chauhan B. Preparation and evaluation of ibuprofen beads by melt solidification technique. Int J Pharm. 2003;255:33–42. doi: 10.1016/s0378-5173(03)00081-4. [DOI] [PubMed] [Google Scholar]
- 16.Maheshwari M., Ketkar A.R., Chauhan B., Patil V.B., Paradkar A.R. Preparation and characterization of ibuprofen–cetyl alcohol beads by melt solidification technique: effect of variables. Int J Pharm. 2003;261:57–67. doi: 10.1016/s0378-5173(03)00292-8. [DOI] [PubMed] [Google Scholar]
- 17.Dhumal R.S., Shimpi S.L., Chauhan B., Mahadik K.R., Paradkar A. Evaluation of a drug with wax-like properties as a melt binder. Acta Pharm. 2006;56:451–461. [PubMed] [Google Scholar]
- 18.Cooper A.R., Eaton L.E. Compaction behaviour of some ceramic powders. J Am Ceram Soc. 1962;45:97–101. [Google Scholar]
- 19.Kuno H. In: Powder (Theory and Application) Kulo T., Jimbo G., Saito E., Takahashi H., Hayakawa S., editors. Maruzen; Tokyo: 1979. pp. 341–346. [Google Scholar]
- 20.Kawakita K., Lüdde K.H. Some considerations on powder compaction equations. Powder Technol. 1971;4:61–68. [Google Scholar]
- 21.Kawakita K., Tsutsumi Y. A comparison of equations for powder compression. Bull Chem Soc Japan. 1966;39:1364–1368. [Google Scholar]
- 22.Denny P.J. Compaction equations: a comparison of Heckel and Kawakita equations. Powder Technol. 2002;127:162–172. [Google Scholar]
- 23.Klevan I., Nordstrom J., Bauer-Brandl A., Alderborn G. On the physical interpretation of the initial bending of a Shapiro–Konopicky–Heckel compression profile. Eur J Pharm Biopharm. 2009;71:395–401. doi: 10.1016/j.ejpb.2008.09.014. [DOI] [PubMed] [Google Scholar]
- 24.Comoglu T. An overview of compaction equations. J Fac Pharm Ankara. 2007;36:123–133. [Google Scholar]
- 25.Carstensen JT. Advanced pharmaceutical solids, vol. 110. MD, Indian reprint; 2008.
- 26.Shivanand P., Sprockel O.L. Compaction behavior of cellulose polymers. Powder Technol. 1992;69:177–184. [Google Scholar]
- 27.Kawashima Y., Niwa T., Handa T., Takeuchi H., Iwamoto T., Itoh K. Preparation of controlled-release microspheres of ibuprofen with acrylic polymers by a novel quasi-emulsion solvent diffusion method. J Pharm Sci. 1989;78:68–72. doi: 10.1002/jps.2600780118. [DOI] [PubMed] [Google Scholar]
- 28.Shen S., Chow P.S., Chen F., Tan R.B.H. Submicron particles of sba-15 modified with MgO as carriers for controlled drug delivery. Chem Pharm Bull. 55, 2007:985–991. doi: 10.1248/cpb.55.985. [DOI] [PubMed] [Google Scholar]
- 29.Elkordy A.A., Essa E.A. Dissolution of ibuprofen from spray dried and spray chilled particles. Pak J Pharm Sci. 2010;23:284–290. [PubMed] [Google Scholar]
- 30.Maheshwari M., Jahagirdar H., Paradkar A. Melt sonocrystallization of ibuprofen: effect on crystal properties. Eur J Pharm Sci. 2005;25:41–48. doi: 10.1016/j.ejps.2005.01.013. [DOI] [PubMed] [Google Scholar]
- 31.Newa M., Bhandari K.H., Li D.X., Kwon T.H., Kim J.A., Yoo B.K. Preparation, characterization and in vivo evaluation of ibuprofen binary solid dispersions with poloxamer 188. Int J Pharm. 2007;343:228–237. doi: 10.1016/j.ijpharm.2007.05.031. [DOI] [PubMed] [Google Scholar]
- 32.Mallick S., Pattnaik S., Swain K., De P.K., Saha A., Ghoshal G. Formation of physically stable amorphous phase of ibuprofen by solid state milling with kaolin. Eur J Pharm Biopharm. 2008;68:346–351. doi: 10.1016/j.ejpb.2007.06.003. [DOI] [PubMed] [Google Scholar]


