Abstract
People can attend to and track multiple moving objects over time. Cognitive theories of this ability emphasize location information and differ on the importance of motion information. Results from several experiments have shown that increasing object speed impairs performance, although speed was confounded with other properties such as proximity of objects to one another. Here, we introduce a new paradigm to study multiple object tracking in which object speed and object proximity were manipulated independently. Like the motion of a planet and moon, each target–distractor pair rotated about both a common local point as well as the center of the screen. Tracking performance was strongly affected by object speed even when proximity was controlled. Additional results suggest that two different mechanisms are used in object tracking—one sensitive to speed and proximity and the other sensitive to the number of distractors. These observations support models of object tracking that include information about object motion and reject models that use location alone.
Keywords: Multiple object tracking (MOT), Additive factors logic, Proximity, Speed, Size
Introduction
In order to interact successfully with a dynamic and fluid visual environment, it is critically important that we are able to keep track of objects as they move through the world. Driving a car through traffic, navigating through a crowd, or even playing ball sports such as basketball, all demonstrate that people can successfully account for the movement of several objects in their environment. Even in the absence of defining characteristics, people are able to keep track of a limited number of moving targets amongst identical distractors. Previous research has identified several factors that appear to influence tracking, such as the location of targets in the visual field and their relationship with other moving objects (Alvarez & Cavanagh, 2005; Alvarez & Franconeri, 2007; Suganuma & Yokosawa, 2006).
In the laboratory, this ability has been studied almost exclusively using the multiple object tracking (MOT) paradigm (Pylyshyn & Storm, 1988). In the standard MOT paradigm, participants are presented with a set of identical objects of which a subset are cued as targets to be tracked. The display is then set in motion, with objects moving more or less randomly within a limited area. Following a tracking period of several seconds, participants are asked to identify the targets. Results from numerous experiments using this paradigm show that participants can track a limited number of objects, suggesting that tracking is a capacity-limited process (Alvarez & Cavanagh 2005; Alvarez & Franconeri, 2007; Pylyshyn & Storm, 1988). The precise number of objects that can be tracked simultaneously depends on the individual as well as on the display parameters adopted. For example, target–distractor proximity impacts performance (Pylyshyn, 2004; Tombu & Seiffert, 2008), as does the number of distractors in a display (Bettencourt & Somers, 2009; Sears & Pylyshyn, 2000). Liu and colleagues (2005) have also demonstrated that increasing object speed impairs tracking. Similarly, Alvarez and Franconeri (2007) have shown that object speed determines the number of objects that can be successfully tracked. Drastically reducing speed can increase tracking capacity twofold, whereas large increases in speed can reduce capacity to just one. Numerous other effects have been demonstrated using the MOT task, including effects of target arrangement (Scholl et al. 2001; Yantis, 1992), spatiotemporal properties (St. Clair, Huff, & Seiffert, 2010; Suganuma & Yokosawa, 2006; vanMarle & Scholl, 2003), and gaze position (Fehd & Seiffert, 2008, 2010; Zelinsky & Neider, 2008).
Cognitive theories that attempt to explain how object tracking is accomplished have emphasized the role of location information over speed information. Visual index theory (FINSTs; Pylyshyn, 2001) describes the tracking mechanism as a set of preattentive pointers used to identify and encode the locations of the targets. These do not encode visual features of objects, but do serve as a guide for directed attention to retrieve the features from the location indicated by a visual index. Although the theory does not specify directly whether motion information, such as speed or direction, is part of a visual index, the emphasis of the theory is on location information. Likewise, the multifocal attention account of object tracking (Cavanagh & Alvarez, 2005) also emphasizes the location of target objects and explains tracking with directed attention to the locations of target objects. Although a control mechanism is posited to help move attention along with moving items (Cavanagh & Alvarez, 2005), it remains to be specified how this mechanism works and whether it is sensitive to object speed. Both theories posit that the proximity of distractors plays a key role in tracking performance. Neither theory explicitly states that speed has no role in the tracking mechanism and both could be extended to account for speed effects.
However, the observation that object speed affects tracking performance does not necessarily indicate that speed has a direct effect on the tracking mechanism. Some evidence exists to support the notion that the tracking mechanism treats location as crucial, while speed and direction of motion are not. Keane and Pylyshyn (2006) provided evidence that people do not extrapolate the position of a moving object during a disappearance and suggested that only location information is used in the tracking process (though see also Fencsik, Klieger, & Horowitz, 2007). However, some researchers have suggested that the representations used for target recovery after a disappearance are not the same as those used for moment-to-moment tracking (Horowitz, Birnkrant, Fencsik, Tran, & Wolfe, 2006). If speed information is not crucial to the mechanism used in object tracking, then the decline in performance with increasing speed may be due to an indirect effect. In the typical MOT display, objects move randomly inside a confined space, so the parameters of object proximity and speed often vary continuously. Franconeri and colleagues (Franconeri, Lin, Pylyshyn, Fisher, & Enns, 2008) made the astute observation that increasing the speed of objects in this type of display also increases the frequency with which objects approach one another. If targets are more likely to be lost when they are crowded by nearby distractors, then crowding (e.g., Bouma, 1970)—and not object speed per se—may be responsible for reduced tracking performance as speed increases (Franconeri, Jonathan, & Scimeca, 2010). The effect of speed on tracking performance could be indirect, due to the increase in crowding that accompanies increases in speed using the typical MOT paradigm.
The nature of the typical MOT paradigm, in fact, confounds several important parameters. The paradigm was first introduced by Pylyshyn and Storm (1988) as a simple method to test whether people could track multiple, identical objects that moved independently. The specifics of the display were relatively unimportant provided that the objects were always visible and targets were only recognizable from their previous history. Indeed, much published work using the paradigm varies both temporal and spatial parameters widely, including possibly important details such as whether or not objects can occlude one another and whether objects move in straight paths. As the objects move about the box, their proximity to other objects, eccentricity, consistency of motion, and sometimes speed and acceleration, can change simultaneously. As such, the paradigm is not ideal for investigating what these types of visual attributes could reveal about the underlying mechanism. Object tracking as an ability, however, need not be measured using the MOT paradigm. Some previous work has employed other tasks to investigate object tracking, such as detection of trajectory deviation (Narasimhan, Tripathy, & Barrett, 2009; Tripathy & Barrett, 2004; Tripathy, Narasimhan, & Barrett, 2007), recovery of targets after disappearance (Horowitz et al., 2006), and target localization (Howard & Holcombe, 2008; Iordanescu, Grabowecky, & Suzuki, 2009). Here, we introduce a new paradigm to study object tracking in which proximity between objects, speed and eccentricity are controlled factors.
The goal of the present experiments was to examine how speed influences tracking performance. In the first experiment, we introduced a new paradigm, the Planets and Moons Tracking (PMT) paradigm, to study target–distractor proximity and speed effects independently. To anticipate, results show speed effects when proximity was controlled. Further analysis using additive factors logic demonstrated that the effects of both speed and proximity load on the same mechanism used for object tracking. The second experiment used the PMT paradigm to investigate the effect of the number of distractors to provide evidence that multiple mechanisms are used for object tracking. The current investigation was designed to provide evidence that the speed of objects influences the efficacy of object tracking independently of other factors and to give some insights into the mechanisms that underlie object tracking.
Experiment 1: speed and distractor proximity
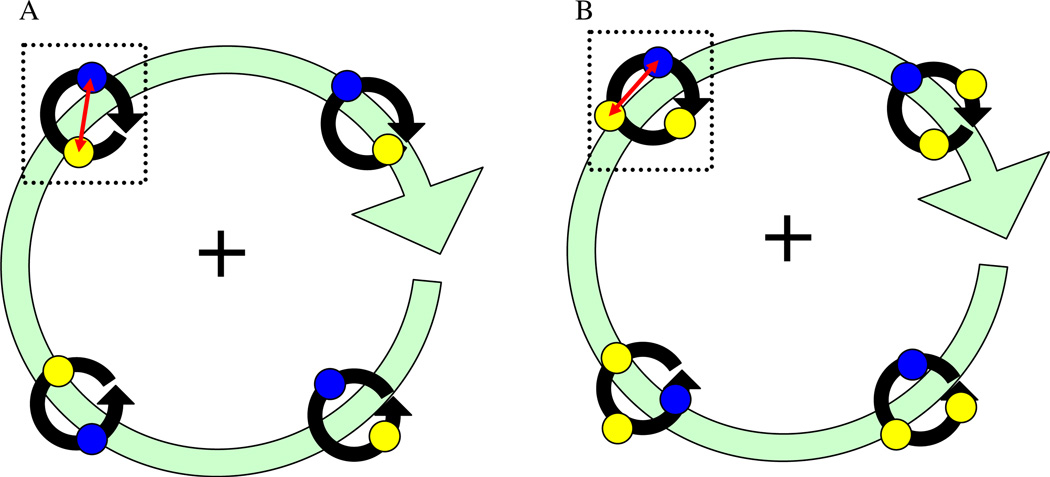
The goal of this work was to independently manipulate object speed and distractor proximity to determine whether each has independent—or interdependent—effects on tracking ability. This experiment used a modified version of the MOT paradigm, called the Planets and Moons Tracking (PMT) paradigm, in which target and distractor motion is constrained. In the PMT paradigm (Fig. 1a), dots are organized into pairs that rotate about a common local point as well as around a central fixation marker. In this way, the display is similar to a solar system, in which planets and moons rotate around a common center of mass that also rotates around the sun. The strength of this design is that factors such as proximity, speed (along both axes of rotation), eccentricity and number of distractors can be manipulated independently. Unlike the traditional MOT paradigm, in which manipulating any one of these factors has unintended effects on others, the PMT paradigm does not confound these factors. With this powerful paradigm, we examined the effects of speed and proximity to determine whether these characteristics influence tracking ability independently or coactively. Employing the PMT paradigm allows for both a convergent methodology to examine whether speed affects tracking independently of crowding (Franconeri et al., 2008) and a new avenue to investigate the role of likely contributing factors affecting tracking ability.
Fig. 1.
The planets and moons tracking (PMT) paradigm. a One target dot (blue/dark) and one distractor dot (yellow/light) were spaced evenly around an invisible circle. Color and shading is for illustration purposes only, as all dots in the experimental displays were white. Groups of dots (dotted boxes) were spaced evenly around a larger invisible circle centered on the fixation cross. Dots moved on two axes of rotation shown here with arrows. Each group moved around the central fixation cross at the same rate. Simultaneously, dots making up each group also rotated around their group centers. This design allowed target-distractor proximity and speed to be examined independently. b The PMT display for two distractors in each group (Experiment 2)
Method
Participants
Twenty-nine healthy adult members of the Vanderbilt University community, reporting normal or corrected-to-normal vision participated in this study in exchange for partial fulfillment of course credit or $10 (USD). Participants were tested in accordance with the Vanderbilt University Human Subjects Protection Policy and APA 2002 Code of Ethics.
Apparatus and stimuli
Testing was performed on a Mac PowerPC G4 computer with an OSX platform running Matlab 7 and the Psychophysics toolbox version 3.0.8 (Brainard, 1997; Pelli, 1997). The screen refresh rate was 89 Hz. Viewing distance was approximately 57 cm.
Visual Display
As shown in Fig. 1a, the visual display consisted of four groups of white dots, each of which consisted of a target and a distractor, on a black background. Each dot had a radius of 0.3°. For each group, dots were arranged equidistantly along a small imaginary circle whose perimeter passed through the center of each dot. Varying the radius of the small imaginary circle created the three conditions of proximity. Distance between the target and its neighboring distractor varied from 3.20° (near) to 3.52° (medium) to 3.84° (far) of visual angle, giving a magnitude of the manipulation of about 20%. The absolute difference in distance was 0.64°, which was just slightly more than one width of a dot (diameter = 0.60°). Proximity was fixed within trials, but was manipulated across trials. Similarly, groups were organized such that the center of each group of dots was located equidistantly on a large imaginary circle (radius = 8°) centered on a white fixation cross (0.8 × 0.8°) at screen center.
Dot Motion
On half the trials, dot groups rotated clockwise around the center of the display and rotated counter-clockwise in the other half of the trials. The angular speed of the dot groups was always 89°/s; therefore, a group made a complete display rotation roughly every four seconds. On every trial, half of the dot groups rotated clockwise around the center of their dot group, with the other half rotating counter-clockwise. Several factors affected the angular speed at which dots rotated about the center of their group, although within a group all dots rotated at the same angular speed at any point in time. As described below (Procedure), a separate staircase was used for each participant to determine an optimal initial dot speed. This initial speed was then adjusted to equate for distance traveled at each level of proximity. This was necessary because the linear length of an arc depends on two factors: its angular size, and the radius of the circle upon which it is constructed. Because the size of the circle used to create each group varied with proximity, angular speed needed to be adjusted to hold linear distance traveled constant across levels of proximity. Further, we added variability to dot speeds for each group within a trial so that the motion of one group did not predict the motion of another group. For each group independently, initial dot angular speeds were adjusted up or down by up to 25%. Temporal variability was added by adjusting, by up to ±40%, dot angular speeds for each group independently every 225 ms. Finally, dot angular speed was also manipulated across trials. The manipulation of dot speed was implemented by increasing the dot angular speeds by a factor of 1.5 on half the trials.
Dot speeds can be summarized mathematically using the two equations that follow. Each is calculated separately for each dot group:
| (1) |
Where GBS = group base speed, IS = initial speed (as determined using a separate staircase procedure described below), prox(trial) represents the proximity value for this trial [3.2, 3.52, 3.84°, for prox(near), prox(medium) and prox(far), respectively] and speed(trial) represents the speed value for this trial (1 or 1.5). Equation 2 adds temporal variability to dot speeds and is recalculated every 225 ms:
| (2) |
Where Sx represents speed at time x and GBS is the group base speed calculated in Eq. 1.
Procedure
Each trial consisted of three phases; target cues, tracking and response. During target cues, stationary dots were presented for 500 ms, after which the targets were outlined in red for 1,000 ms. The cues were then removed, leaving all dots stationary and appearing identical. The tracking phase began 500 ms later, as the display went into motion for a period of 6 s. Motion then ended and participants indicated the targets by using the mouse and keyboard to select one dot from each of the groups of dots. Therefore, chance performance at this task would result in 50% accuracy.
Pilot data and previous work suggested that there was a large degree of individual variability in terms of tracking ability (Green & Bavelier, 2006). Therefore, the experiment was divided into two phases. In the first phase, a staircase procedure was performed to determine the optimal dot angular speed for each participant. The optimal value for our purpose was a speed where participants were able to successfully track roughly 90% of targets in the easiest condition. This value was then used as the base speed in the second phase of the experiment where the experimental data was collected.
The staircase phase consisted of two blocks of trials. Trials were exactly the same as those from the main experiment, except that the largest value of proximity (far) was always employed. The first block consisted of two practice trials to familiarize participants with the task and was followed by a second block in which participants performed 40 staircase trials. Angular speeds of the dots within each group were initially set to 127°/s such that a full group rotation was completed roughly every three seconds. This value was then subjected to the procedure for determining angular speeds of groups as described in the section entitled ‘Dot Motion’ above. Across trials, this initial angular speed setting (which started at 127°/s) was adjusted up or down in 10.3°/s steps depending on performance. Speed adjustments were made based on tracking accuracy over the last two trials. If average performance was lower than three correct out of the four targets, the rotational speed was decreased, whereas if performance was higher, it was increased. The average angular speed over the last ten trials was used as the initial speed for that participant. The speed of the dot groups in the experimental trials was 80% of the individual’s base speed. The experimental phase, consisting of a practice block of 12 trials, and was followed by four experimental blocks of 36 trials.
Design
This experiment employed a 3 (proximity) × 2 (speed) within-subjects design. On fast trials, all group rotational speeds were increased by a factor of 1.5. Three levels of target-distractor proximity were employed. For all groups on a given trial, center-to-center dot distances were 3.84, 3.52 or 3.20° of visual angle (far, medium or near proximity). In the experimental phase, each combination of proximity and speed was presented six times per block, for a total of 36 trials per block.
Results and discussion
Accuracy results were first corrected for guessing. Because participants were instructed to choose only one dot from each pair, guessing accuracy was 50% and the correction was straightforward: corrected accuracy = accuracy − (100 − accuracy). As suggested in previous work, we assume chance performance is 50% because it is equivalent to pure guessing in which participants have no information about target locations (Hulleman, 2005). If subjects became completely flummoxed over the course of the trial and lost track of all targets, they could still respond by randomly selecting one dot per group as per the instructions. Thus, in the context of the PMT paradigm, pure guessing would produce 50% accuracy on average. Results are presented in Table 1. Scores corrected for guessing were submitted to a within-subjects repeated measures ANOVA with proximity (far, medium, near) and speed (slow, fast) as factors.
Table 1.
Percent correct after correcting for guessing (uncorrected in parentheses) – Experiment 1
| Proximity | Speed | |||
|---|---|---|---|---|
| Slow | Fast | Mean | ||
| All subjects | Far | 64.08 (82.04) | 48.78 (74.39) | 56.43 (78.22) |
| Medium | 57.54 (78.77) | 37.14 (68.57) | 47.34 (73.67) | |
| Near | 40.88 (70.44) | 24.86 (62.43) | 32.87 (66.43) | |
| Mean | 54.17 (77.08) | 36.93 (68.46) | 45.55 (72.77) | |
| n=17 Additive factors subset | Far | 73.53 (86.77) | 58.58 (79.29) | 66.05 (83.03) |
| Medium | 67.77 (83.89) | 53.92 (76.96) | 60.85 (80.42) | |
| Near | 56.00 (78.00) | 35.78 (67.89) | 45.89 (72.95) | |
| Mean | 65.77 (82.88) | 49.43 (74.71) | 57.60 (78.80) | |
Results revealed significant effects of both manipulations. In line with the results of Franconeri and colleagues (2008), a significant effect of proximity was observed [F(2, 56) = 64.6, p < .001]. As proximity increased from far to near, corrected accuracy fell by over 20%. Consistent with previous reports, we find that tracking ability is highly sensitive to the proximity of targets to distractors (Tombu & Seiffert, 2008). Distractor proximity may have a strong impact on tracking efficiency when distractors are close to targets because it may greatly increase the demand for a high-resolution representation of target locations. However, contrary to the observations of Franconeri and colleagues, a significant effect of speed was observed [F(1, 28) = 49.4, p < .001]. Increasing speed by a factor of 1.5 reduced accuracy (after correcting for guessing) by 17%. This result demonstrates that manipulating speed, even when not accompanied by a corresponding increase in crowding, is sufficient to affect tracking performance. No interaction between proximity and speed was observed on corrected accuracy (F < 1). Our results clearly show that both proximity and speed directly influence tracking performance when manipulated independently. Therefore, models of multiple object tracking must have a mechanism through which both proximity and speed separately can influence tracking performance.
Additive factors analysis
An added benefit of adopting an experimental design that allows for the independent manipulation of factors affecting a cognitive ability is that it permits the identification of independent processes involved in that ability through the use of additive factors logic (Schweickert, 1985; Sternberg, 1969). The idea is that the architecture of cognitive systems can be described by isolating mechanisms that are dependent upon different factors. According to additive factors logic, two factors that influence a common mechanism will interact with one another, whereas two factors that do not will have additive effects. For example, improving your aim and using a heavier hammer would interactively improve how far you can drive a nail into a piece of wood, whereas using a softer wood would have an independent effect. Additive factors logic has been applied mainly to reaction time data, but has also been adapted for use in paradigms where accuracy is the primary dependent measure (Schweickert, 1985), as is the case here. By applying additive factors logic to the results it was possible to determine whether proximity and speed affected tracking via a common mechanism.
In order to apply additive factors logic to the data, accuracy must first be corrected for guessing and then submitted to a logarithmic transform (see Schweickert, 1985). Correction for guessing allows the data to reflect the performance of the cognitive ability being assessed, here object tracking. In our analysis, we have assumed that, when the tracking mechanism fails, participants guess which item in each group is the target and which is the distractor. We consider alternate guessing hypotheses in the General discussion. The log transform (using a base of 10) rescales the data so that a manipulation that has the same proportional effect at various levels of performance will have the same absolute effect at all levels after the transformation. If two factors affect a common process, their effects measured after the transformation should interact; if they affect independent processes, their effects should not interact.
Due to the nature of the log scale, as performance approaches chance levels, the transformation required to apply additive factors logic becomes increasingly sensitive to slight variability in performance. Moreover, performance at or below chance cannot be transformed at all. As a result, only participants who performed significantly better than chance in all conditions were included in the additive factors analysis. To assess this, for each participant in each condition, we submitted the untransformed proportion of correctly selected targets on each trial to a t test. If accuracy in every condition was statistically better than chance, the participant’s data were included in the subsequent analysis. Seventeen of the 29 participants met our criterion for inclusion. Mean performance in each condition for this subset of the participants is included in the bottom half of Table 1.
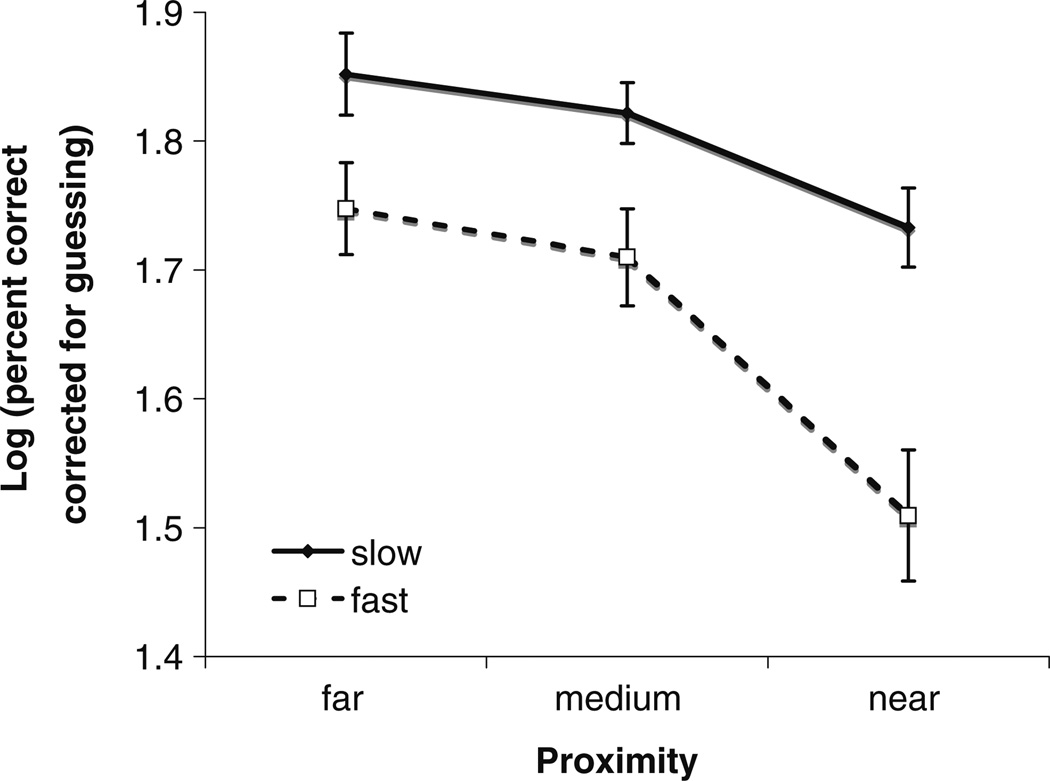
Following the correction for guessing and log transformation, accuracy results were submitted to a within-subjects repeated measure ANOVA with proximity (far, medium, near) and speed (slow, fast) as factors. Mean performance is plotted in Fig. 2. Confirming the results of the initial analysis, the main effects of both proximity and speed were significant [F(2, 32) = 33.2, p < .001 and F(1, 16) = 25.0, p < .001, respectively]. Performance declined with increasing proximity and speed. Proximity and speed also entered into a significant interaction [F(2, 32) = 5.0, p < .02]. The effect of speed roughly doubled when the dots were most proximal relative to other levels of proximity. In order to rule out a ceiling effect, a follow up 2 × 2 ANOVA was performed on just the medium and near proximity conditions across speed. Again, both the main effects of proximity and speed were significant [F(1, 16) = 35.6, p < .001 and F(1, 16) = 24.3, p < .001, respectively]. Most importantly, a significant interaction was again observed [F(1, 16) = 7.2, p < 0.02], reflecting the doubling of the effect of speed going from the medium to the near level of proximity.
Fig. 2.
Results from Experiment 1. Log transformed corrected accuracy as a function of proximity and speed. The purpose of the log transformation was to allow for the application of additive factors analysis. Untransformed accuracy is included in Table 1. Both proximity and speed influenced tracking performance when manipulated independently. In addition, these factors also interacted, indicating that they influence a common mechanism involved in tracking
By additive factors logic, the observation of a significant interaction between speed and proximity indicates that these manipulations affect a common processing mechanism. Tracking performance is limited by both the proximity of targets to distractors, as well as by the speed of the objects in the display. Furthermore, both of these effects load on the same mechanism required for object tracking, suggesting that speed is as integral to the tracking process as proximity. Does the conclusion that speed and proximity affect a common mechanism mean that proximity mediates the effect of speed? This argument stems from a theory of tracking in which spatial interactions between representations of targets and distractors are sufficient to explain tracking errors (Franconeri et al., 2008). Such a theory explains proximity effects directly, but explains speed effects indirectly through an increase in proximity. Our results show, however, that speed effects can be obtained when proximity is constant suggesting that these manipulations may each affect a tracking mechanism independently.
It is worthwhile considering exactly how our manipulation of speed influenced performance. One possibility was that increasing the speed of the dots created a target-target distance confound whereby targets were closer to other targets in the fast condition than in the slow condition. Previous research has demonstrated that target–target interference also impairs multiple object tracking (Shim, Alvarez, & Jiang, 2008). Increasing the speed of the dots in the PMT display also increased the frequency with which targets approached other targets, so perhaps the performance decrease with speed was due to the greater number of times that targets pass by targets. However, average target–target distance did not vary with speed in the current experiments and minimum target–target distances were always at least twice as large as the distance between target–distractor pairs. Increasing speed also decreased the duration targets spend near each other on each pass. Overall, targets spend the same amount of time close to other targets in the fast condition as they do in the slow condition. It is currently unclear whether tracking performance is limited by the number of target–target passes or the total time. Furthermore, our proximity manipulation increased target–distractor proximity and simultaneously decreased target–target proximity, yet performance impairments, not improvements were found. Together these findings suggest that target–target interference is unlikely to be a strong contributor to the effects observed in this experiment.
Another alternative confound to be addressed is the variability of the dot motion. Because the methods included temporal and group variability to dot speeds in a proportional manner (see Eqs. 1 and 2), the absolute variability of the dot speeds in the fast conditions was larger than it was in the slow conditions (in other words, the range of speeds is larger in the fast conditions than in the slow conditions). In the present experiment, we used independent dot speed variability at the group level to ensure that target positions could not be inferred from other target locations and chose to keep proportional dot speed variability constant across levels of speed. The alternative was to keep absolute dot speed variability constant, but then proportional dot speed variability would have been confounded with speed. Although we find the conclusion that increasing dot speed impaired tracking performance more likely, it is important to acknowledge that it may have resulted from the increase in absolute dot speed variability that accompanied the increase in speed. Additional experimentation focusing on dot speed and speed variability is required to determine the exact cause of the impairment due to speed observed. Regardless, speed, through either changes in displacement over time or in range, influences tracking.
Experiment 2: number of distractors and distractor proximity
The previous experiment used additive factors logic to identify a mechanism sensitive to both speed and proximity that is involved in tracking. Based on previous work, Pylyshyn (2006) has proposed a two-stage model where objects are parsed from the background in the first stage and targets are indexed in the second. In this experiment, using the PMT paradigm and additive factors logic, we test the hypothesis that MOT consists of two mechanisms. We manipulated both the number of distractors per group as well as target-distractor proximity. On half of the trials, each target was accompanied by a single distractor, while on the other half of the trials, two distractors accompanied each target. Proximity was manipulated as in Experiment 1. If the number of distractors and proximity influence different mechanisms, their effects should be additive when analyzed using additive factors logic.
Methods
With the following exceptions, the methods employed in this experiment were identical to those employed in Experiment 1. Twenty-eight participants participated. Experiment 2 was a 3 (proximity) × 2 (number of distractors per group) within-subjects design. Levels of proximity were the same as those used in Experiment 1 (3.84, 3.52 or 3.20°) and there were either one or two distractors per group. One of the consequences of manipulating the number of distractors, was to change the relationship between proximity and the diameter of the imaginary circle used to construct the dot groups. As shown in Fig. 1a by the red arrow, in the one-distractor condition, proximity is equal to the diameter of the circle used to construct target-distractor pairs. However, as shown in Fig. 1b, in the two-distractor condition, this was not the case. In order to equate proximity across levels of number of distractors, the diameter of the circle used to construct target–distractor triplets was increased by a factor of 1.155 (proximity values in Eq. 1 were also adjusted accordingly).
A second consequence of increasing the number of distractors was to increase the frequency with which targets pass by the starting positions of other dots within groups. Whereas in the one-distractor condition a target passes the starting position of a dot every 180° degrees, in the two-distractor condition, this occurs every 120°. Because the ability to track objects is linked to the frequency with which targets encounter locations previously occupied by distractors (as demonstrated by Verstraten, Cavanagh, & Labianca 2000), we simultaneously manipulated the speed of dot group rotation with the number of distractors. Group rotational speeds in the two-distractor condition were reduced by a factor of 1.5 relative to the one-distractor condition (in Eq. 1, GBS was divided by 1.5). Although this controls for the frequency with which targets encounter previously occupied locations, it does introduce a new confound whereby dots are traveling faster in the one-distractor condition relative to the two-distractor condition. However, because decreasing speed and increasing the number of distractors are anticipated to operate in opposite directions, any impairment in the two-distractor condition can be solely attributed to increasing the number of distractors, although it likely understates the effect of the manipulation.
Results and discussion
Accuracy results were first corrected for guessing and then submitted to a within-subjects repeated measure ANOVA with proximity (far, medium, near) and number of distractors (one, two) as factors. Because the number of distractors in each group varied by condition, the correction for guessing was weighted by the number of choice options. We defined corrected accuracy as accuracy − (100 − accuracy)/(number of distractors per group). Results are presented in Table 2. Replicating the results of Experiment 1, proximity significantly affected tracking performance [F(2, 54) = 69.8, p < .001]. As proximity increased, performance declined. As the number of distractors increased performance also suffered [F(1, 27) = 65.5, p < .001]. The addition of a second distractor per group decreased corrected accuracy in excess of 25%. The interaction between proximity and number of distractors did not approach significance (F < 1). Adding distractors, even when this addition did not result in an increase in target-distractor proximity, reduced tracking performance.
Table 2.
Percent correct after correcting for guessing (uncorrected in parentheses) – Experiment 2
| Proximity | Number of Distractors | |||
|---|---|---|---|---|
| One | Two | One | ||
| All subjects | Far | 66.13 (83.06) | 40.77 (60.52) | 53.45 (71.79) |
| Medium | 58.75 (79.37) | 32.83 (55.22) | 45.79 (67.30) | |
| Near | 46.97 (73.49) | 21.12 (47.42) | 34.05 (60.45) | |
| Mean | 57.28 (78.64) | 31.58 (54.38) | 44.43 (66.51) | |
| n=16 Additive factors subset | Far | 71.71 (85.86) | 49.43 (66.29) | 60.57 (76.07) |
| Medium | 66.55 (83.27) | 42.24 (61.49) | 54.39 (72.38) | |
| Near | 55.12 (77.56) | 31.05 (54.04) | 43.09 (65.80) | |
| Mean | 62.04 (82.23) | 40.91 (60.60) | 52.68 (71.42) | |
One possibility for the rather large impact of increasing the number of distractors in Experiment 2 may be related to the PMT paradigm itself. Whereas in the traditional MOT paradigm target and distractor motion is generally unrelated, in the PMT paradigm distractors are yoked to targets. In fact, all the objects are moving similarly because they were all in perfect rotation around two center points. As such distractors may have a larger effect in the PMT paradigm than they would in the traditional MOT paradigm. Additional empirical work is required to test this hypothesis.
Additive factors analysis
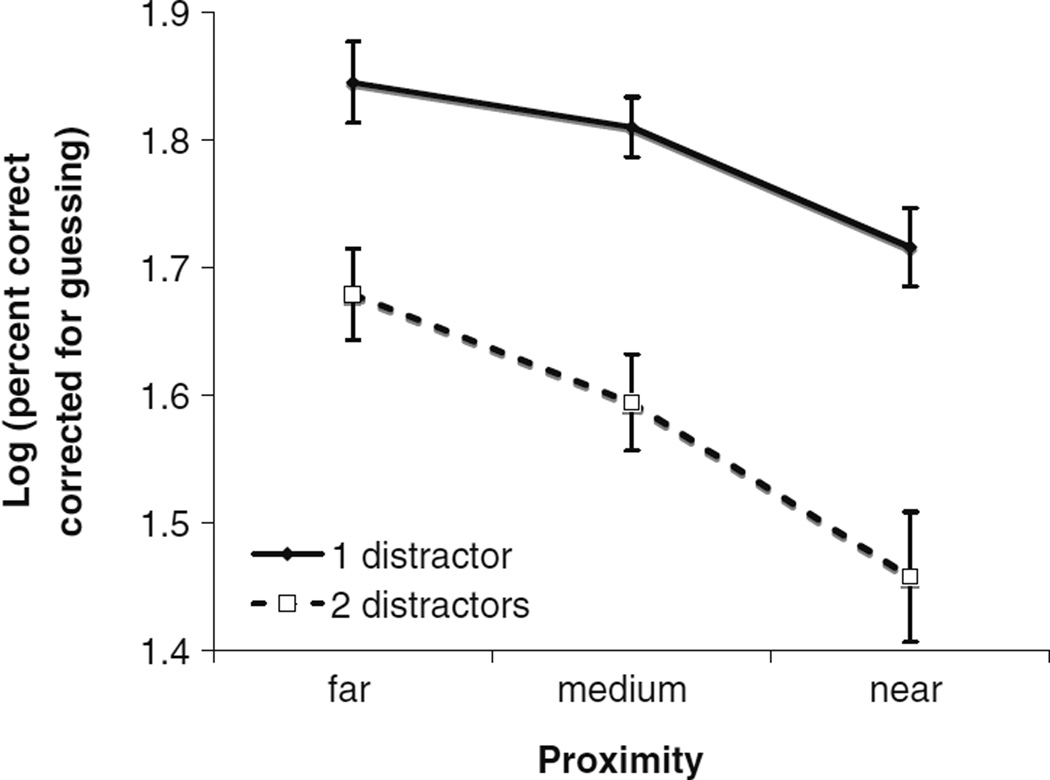
As in Experiment 1, participant data were excluded that did not meet the performance criterion, resulting in the inclusion of 16 out of 28 participants. Data were corrected for guessing and log transformed before being submitted to a 3 (proximity) × 2 (number of distractors) within-subjects repeated measures ANOVA. Mean performance is displayed in Fig. 3. Mean performance in each condition for this subset of the participants is included in the bottom half of Table 2. Confirming the results of the initial analysis, increasing either proximity or the number of distractors impaired tracking performance [F(2, 30) = 34.5, p < .001 and F(1,15) = 28.6, p < .001, respectively]. The interaction between proximity and number of distractors approached, but failed to achieve significance [F(2, 30) = 2.6, p > .08]. To address the possibility of a ceiling effect, a 2 × 2 ANOVA was performed excluding the far conditions. Again increases in either proximity or the number of distractors impaired performance [F(1, 15) = 27.9, p < .001 and F(1, 15) = 23.8, p < .001, respectively]. However, there was no indication that these factors interacted [F(1, 15) = 1.3, p > .26). Proximity and number of distractors were additive, indicating that they influence tracking via independent mechanisms. This finding supports the hypothesis that tracking is accomplished via two mechanisms. One mechanism is sensitive to the number of distractors in the display, whereas the other is sensitive to both the proximity of targets to distractors and the speed of the objects in the display.
Fig. 3.
Results from Experiment 2. Log transformed corrected accuracy as a function of proximity and number of distractors. The purpose of the log transformation was to allow for the application of additive factors analysis. Untransformed accuracy is included in Table 2. Both proximity and the number of distractors affected tracking performance. However, these factors did not interact indicating that proximity and number of distractors have their influence on tracking performance via independent mechanisms
General discussion
Two related yet distinct sets of conclusions can be drawn from this study. The first set of conclusions relates to the factors influencing tracking performance, whereas the second set relates to the process via which tracking is accomplished.
Factors influencing tracking performance
Using the PMT paradigm, which allows for the independent manipulation of factors influencing tracking, the results from these experiments clearly indicate that speed, proximity and the number of distractors in the display each influence tracking performance when the other factors are held constant. Making similar inferences using the traditional MOT paradigm would be problematic due to the fact that it is difficult to vary any one factor without also affecting another. Although similar to traditional MOT displays in many respects, because target dots move amongst identical distractors, several potentially important differences in the characteristics of MOT and PMT displays are immediately evident. For example, in the PMT paradigm, distractors are yoked to targets and target-distractor pairs follow the same overall trajectory. Also, distractors follow targets along similar paths, which has been shown to specifically impair tracking in MOT displays (Suganuma & Yokosawa, 2006). Finally, unlike other research using rotating pairs of objects (Franconeri et al., 2010; Intriligator & Cavanagh, 2001), here the object motions are hierarchical, with rotating pairs each rotating around a central point, which may add to the complexity of the motion that must be accounted for by a tracking process. As such, conclusions drawn from these results must be extended to traditional MOT paradigms with caution. However, this limitation does not diminish the strengths that this new paradigm offers. Furthermore, the PMT paradigm could be considered to resemble real world situations in which targets and distractors behave in a nonrandom fashion. Similar to the PMT paradigm, a quarterback looking to pass to a teammate in a man-to-man defense will often face a tracking task in which distractors (opposing team members) are yoked to targets (teammates). However, the real power of the paradigm is not its similarity to motion of real objects, but instead the ability to independently manipulate important factors. To summarize, the PMT paradigm has the distinct advantage over the traditional MOT paradigm, because it can isolate influential factors, such as speed, even if it has some limitations as well.
Notwithstanding the foregoing caveat, our finding from Experiment 1 that increasing speed impaired tracking performance stands in stark contrast to the conclusions drawn by Franconeri and colleagues (2008). By scaling the display, Franconeri and colleagues demonstrated that increasing the retinal speed of the objects while simultaneously increasing the size of the objects in the display produced no effect on tracking performance. It is possible that motion perception mechanisms sensitive to temporal frequency responded similarly across the scaling manipulation supporting similar tracking performance. However, there were also other factors, most notably object size and eccentricity, that likely contributed to performance. The scaling manipulation, then, did not manipulate speed independently of other factors. Using the PMT paradigm, the influence of object speed on tracking was demonstrated independent of crowding. This set of results conclusively shows that speed directly impacts tracking performance.
More recently, Franconeri et al. (2010) have provided additional evidence aimed at supporting the notion that object speed does not impact tracking performance directly. These authors concluded that the total cumulative distance was the most important factor determining performance and that speed effects were indirectly a result of distance covered. All the experiments reported here used a constant display duration, so that speed and cumulative distance were confounded. However, regardless of whether speed or duration are the important factors in determining results, these observations suggest that time is an important component to tracking performance. As discussed previously, it is currently unclear whether tracking performance is limited by the number of target–target passes or the total time. Because one of the two must be accounted for, a purely spatial mechanism is insufficient to account for these effects. Models of tracking behavior must include a component sensitive to time, as we elucidate below.
Our results also show that increasing the number of distractors in the display impairs tracking performance (Experiment 2). In traditional displays with objects moving independently within a box, increasing the number of distractors also resulted in an increase in the density of the display, and hence more occurrences of crowding (Sears & Pylyshyn, 2000). This confound has made it difficult to determine the independent impact of additional distractors. Recently, density and number of distractors has been dissociated using MOT and evidence favored a strong effect of the number of distractors (Bettencourt & Somers, 2009). Here, using the PMT paradigm, increasing the number of distractors resulted in no change in crowding, yet a dramatic impact on tracking performance was observed. This result converges with the previously published work by showing that adding distractors, even in the absence of confounding influences, also impairs tracking.
Correction for guessing
In our analysis, we have assumed that when the tracking system fails completely, participants lose all targets and are forced to resort to guessing. Responses reflect the general task demand, such that participants choose four dots at the end of each trial, but with no information about which dots are targets (as in Hulleman, 2005). We refer to this idea as the ‘pure-guessing’ theory. Alternatively, participants may be able to track one target using a mechanism independent from the multiple object tracking system. As such, when multiple object tracking fails completely, participants would still track one target correctly. We refer to this idea as the ‘one-free’ theory. Note that the two theories make different predictions about floor performance. When there are equal numbers of targets and distractors, pure-guessing predicts floor performance of 50%, because there is a 50% chance of choosing the target in each target–distractor pair. The one-free theory predicts a floor of 62.5% tracking performance, because it assumes perfect tracking for one target, plus a 50% chance of choosing the target in each of the remaining three target–distractor pairs. These two theories require different corrections for guessing, which has a large impact on the interpretation of the results in this study. For example, consider the results from the Near-Fast condition in Experiment 1. In this condition, participants accurately identified each target 62.43% of the time. Assuming pure-guessing, we concluded that participants were tracking about 37% of the targets and guessing at the rest. However, if one instead assumes one-free, one would conclude that participants were tracking the one-free target, but were little better than chance for the remaining targets. Given the importance of correcting for guessing in this study, especially in the additive factors analysis, it was important to attempt to better understand floor performance.
To examine performance with respect to the pure-guessing and one-free theories, we looked at trial-to-trial performance. On a given trial, participants can correctly identify 0–4 out of the 4 targets. The main difference between the predictions of the two models involves the number of trials where participants fail to identify any targets (0/4 performance). According to the one-free theory, this should never occur. The average number of trials (out of 144) in which participants failed to choose even one target was 2.90 (SE 0.52) in Experiment 1 and 6.00 (SE 1.00) in Experiment 2. Both values were significantly larger than zero [t(28) = 5.6, p < .0001, t(27) = 6.0, p < .0001, respectively]. As such, we conclude that pure-guessing is a better description of behavior and therefore the correction for guessing applied to the results of Experiments 1 and 2 was appropriate.
On a theoretical basis, it also seems appropriate to assume chance level is tracking zero targets. It seems entirely plausible that participants could attempt to track multiple objects and lose track of all of them at some point in the trial, ending with no information about the targets’ locations. Similar to a poor juggler tossing pins, if people attempt to keep too many objects in play, they could end up dropping all of them. One could argue that tracking one object is functionally different from multiple objects because smooth pursuit eye movements would be used. However, our previous work (Fehd & Seiffert, 2008) has demonstrated that both single and multiple object tracking sometimes involve smooth pursuit and fixating targets as they move, which suggests that tracking multiple objects employs the same eye movement mechanisms as tracking one object. If the tracking task is conceived as a method to investigate how people sustain representations of individuated objects, rather than only a way to investigate divided attention, then chance performance results from a complete breakdown of the system, resulting in zero targets tracked.
Impact on models of object tracking
Taken as a whole, these results suggest that models of object tracking need to include mechanisms that are sensitive to proximity, number of distractors and speed. Prominent models emphasize the role of location and object proximity in the tracking process, but have not specified a role for object speed (Pylyshyn, 2001; Cavanagh & Alvarez, 2005). Modifying these theories to include a sensitivity to object speed, however, could be accomplished by adding periodic updating of target representations. Stored target locations are compared to new visual input with a decision mechanism that updates a target location to match the object that best fits the target. We hypothesize that the rate of updating determines success at distinguishing targets from nearby distractors. As either speed of the targets or proximity of distractors increase, so too does the likelihood that a distractor will be closer to a target location stored in memory than the target that previously occupied it. Thus, speed and proximity impair tracking performance through the same mechanism; namely, a limit in the ability to make correct target correspondence matches given a limited updating rate of the representation of target locations.
Visual index theory proposes that targets are tracked with spatial pointers (Pylyshyn, 2006; Pylyshyn, 2001; Pylyshyn & Storm, 1988). Assuming that visual indexes need to be periodically updated to match the location of targets would produce the type of sensitivity to speed that has been observed here. The mechanism for binding visual indexes to object representations remains unclear and could potentially contain a component that is compromised at faster speeds, such as a periodic update of index links. Other modifications could account for a sensitivity to speed, such as a limit to the speed with which visual indexes can move or an impairment in the ability to link visual indexes to visual information at fast speeds.
Multifocal attention theory proposes that spatial attention divides to maintain representations of the multiple targets, and a central control process moves the attentional foci as the targets move (Cavanagh & Alvarez, 2005). Assuming that the control process works periodically is in line with this theory and could update attentional foci either serially (described further below), or in parallel at discrete time intervals. Periodicity of updating from the control process could come about if it were a limited capacity resource that took time to calculate the appropriate shifts. Such a limited capacity resource could also account for target set size effects, if fewer targets are updated faster, predicting the performance trade-off between number of targets tracked and object speed (Alvarez & Franconeri, 2007). Similarly, the total number of updates required would be a trade-off between object speed and the duration of the trial accounting for this trade-off in performance (Franconeri, Jonathan, & Scimeca, 2010). Although it is unclear at this time what the resource might be that limits the updating process, this description of visual attention as a limited capacity resource is consistent with conceptions of visual attention that have been forwarded elsewhere (Kahneman, 1973; Pashler, 1999; Pastukhov, Fischer, & Braun, 2009; Sperling & Dosher, 1986; Tombu & Jolicoeur, 2003; van der Heijden, 1975). With the addition of periodic updating, the multifocal attention theory accounts for the current results well.
A more specific model of object tracking, called the MOMIT model (Oksama & Hyönä, 2008), already includes a mechanism that is sensitive to object speed and is similar in structure to a serially updating multifocal attention theory. In the model, the efficacy of tracking depends on object speed because target locations are serially stored in memory at discrete intervals. Error in connecting memory of target location at time 1 with the newly perceived location of the target at time 2 is more likely if the target has moved farther in that interval. This is essentially the same mechanism described by Pylyshyn and Storm (1988) for a serial attentional tracking system and ruled out with evidence that people track multiple targets amongst identical distractors with better accuracy than this mechanism predicts. The MOMIT model accurately predicts human behavior in a tracking task that includes identification of objects, because all objects have unique identities (Oksama & Hyönä, 2008). It is identity matching that allows the MOMIT model to succeed. It remains an open question, then, how one could modify the MOMIT model to account for the current results demonstrating speed effects on tracking of targets that are identical to distractors.
A two-mechanism model of MOT
Through the employment of additive factors logic, our results can also be used to describe mechanisms of the process through which tracking takes place. Taken together, the results of these experiments suggest that there are at least two mechanisms at play in tracking. One mechanism is sensitive to the number of distractors in the display, while a second mechanism was identified that is sensitive to target–distractor proximity, as well as the speed of the objects in the display. Interestingly, our previous research (Tombu & Seiffert, 2008) identified both speed and proximity as factors that influence the attentional demands of tracking. Taken together with the results of the present study, this result suggests that (at least) the second mechanism requires the deployment of capacity-limited attentional resources. Additional research will be required to determine exactly what duties are being performed by the two mechanisms identified in the present work.
One hypothesis that we have considered is that tracking results from a two-mechanism system that includes both competitive and suppressive mechanisms. This idea is related to theories in the attention literature such as the Biased Competition theory (BCT; Desimone & Duncan, 1995) and the Selective Tuning Model (STM; Tsotsos et al., 1995). In the tracking context, a saliency map would be used to keep a representation of the locations of targets in space. Salience would be determined by bottom-up factors corresponding to target-defining features, top-down factors that bias competition toward locations previously containing targets, and fluctuations corresponding to representational noise. Because these influences may take time to be integrated, this saliency map requires periodic refreshing to update target locations as targets move. It is limitations in this updating process that produce the sensitivity to object speed that we have observed here.
In order to successfully track a subset of identical objects, top-down factors must bias competition in favor of target locations. This top-down influence may take the form of a suppressive surround. For each target independently, but in parallel, each target location is protected (or enhanced), while all other locations, including other targets, are suppressed. Surround inhibition could take different forms such as exclusively spatially based or including color, motion and space. Results from Pylyshyn (2004) provide evidence supporting the notion of surround inhibition and suggest that what is being inhibited may be only locations sharing target features. In this scheme, because each target inhibits all other targets as well as the distractors, once a certain number of targets is reached, target–target inhibition may reduce target salience to such a low value that targets become indistinguishable from distractors. This target–target mutual inhibition—and not a limit in the number of slots available for tracking—may be responsible for the apparent capacity limit in MOT (Franconeri et al., 2008; Shim et al., 2008).
This two-mechanism model can account for the results of the current experiments. As discussed above, we speculate that the frequency with which target locations require refreshing is determined by factors including target–distractor proximity and speed. Essentially, refreshing target locations involves the recalculation of the salience map and represents the mechanism identified in Experiment 1. Once bottom-up and top-down factors have been applied to the saliency map, new target locations must be determined by identifying the most salient locations on the map. This may occur via a winner-takes-all (WTA) competition modified so that the top locations are selected as the new target locations. As the number of distractors increases, there would be an increase in the likelihood that a selected location was not occupied by a target. This type of WTA mechanism could account for the effects of the number of distractors found in Experiment 2. While this model accounts for the results of the present experiments, further research is required to determine its suitability as a general model of MOT.
Conclusions
The present investigation introduced a new paradigm for investigating multiple object tracking that controls for confounds, thus allowing for the independent manipulation of factors thought to influence tracking. Using this paradigm, we convincingly demonstrate that speed, proximity and the number of distractors all directly influence tracking performance while ruling out potential confounds that often accompany the use of conventional MOT paradigms. Furthermore, this approach allowed for the use of additive factors logic, which permits the identification of independent factors influencing tracking performance. Through its application two mechanisms were identified that play a role in multiple object tracking. Further research is required to better understand the processing carried out by each mechanism.
Acknowledgments
The authors would like to thank Justin Ericson and Nicole Jardine for valuable assistance with testing participants, providing suggestions for the experimental designs and comments on the manuscript, and Jeremy Wolfe, Jonathan Flombaum and Steven Franconeri for their insightful comments. This work was funded by the National Institutes of Health grant EY014984 awarded to A.E.S.
References
- Alvarez G, Cavanagh P. Independent resources for attentional tracking in the left and right visual hemifields. Psychological Science. 2005;16:637–643. doi: 10.1111/j.1467-9280.2005.01587.x. [DOI] [PubMed] [Google Scholar]
- Alvarez G, Franconeri S. How many objects can you track?: Evidence for a resource-limited attentive tracking mechanism. Journal of Vision. 2007;7(13):1–10. doi: 10.1167/7.13.14. 14. [DOI] [PubMed] [Google Scholar]
- Bettencourt K, Somers D. Effects of target enhancement and distractor suppression on multiple object tracking capacity. Journal of Vision. 2009;9:7. doi: 10.1167/9.7.9. [DOI] [PubMed] [Google Scholar]
- Bouma H. Interaction effects in parafoveal letter recognition. Nature. 1970;226:177–178. doi: 10.1038/226177a0. [DOI] [PubMed] [Google Scholar]
- Brainard D. The psychophysics toolbox. Spatial Vision. 1997;10:433–436. [PubMed] [Google Scholar]
- Cavanagh P, Alvarez G. Tracking multiple objects with multifocal attention. Trends in Cognitive Sciences. 2005;9:349–354. doi: 10.1016/j.tics.2005.05.009. [DOI] [PubMed] [Google Scholar]
- Desimone R, Duncan J. Neural mechanisms of selective visual attention. Annual Review of Neuroscience. 1995;18:193–222. doi: 10.1146/annurev.ne.18.030195.001205. [DOI] [PubMed] [Google Scholar]
- Fehd H, Seiffert A. Looking at the center of targets helps multiple object tracking. Journal of vision. 2010;10(4):1–13. doi: 10.1167/10.4.19. 19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fehd H, Seiffert A. Eye movements during multiple object tracking: Where do participants look? Cognition. 2008;108:201–209. doi: 10.1016/j.cognition.2007.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fencsik DE, Klieger SB, Horowitz TS. The role of location and motion information in the tracking and recovery of moving objects. Perception & Psychophysics. 2007;69:567–577. doi: 10.3758/bf03193914. [DOI] [PubMed] [Google Scholar]
- Franconeri SL, Jonathan SV, Scimeca JM. Tracking multiple objects is limited only to object spacing, not by speed, time or capacity. Psychological Science. 2010 doi: 10.1177/0956797610373935. [DOI] [PubMed] [Google Scholar]
- Franconeri S, Lin J, Pylyshyn Z, Fisher B, Enns J. Evidence against a speed limit in multiple object tracking. Psychonomic Bulletin & Review. 2008;15(4):802–808. doi: 10.3758/pbr.15.4.802. [DOI] [PubMed] [Google Scholar]
- Green C, Bavelier D. Enumeration versus multiple object tracking: The case of action video game players. Cognition. 2006;101:217–245. doi: 10.1016/j.cognition.2005.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horowitz TS, Birnkrant RS, Fencsik DE, Tran L, Wolfe JM. How do we track invisible objects? Psychonomic Bulletin & Review. 2006;13:516–523. doi: 10.3758/bf03193879. [DOI] [PubMed] [Google Scholar]
- Hulleman The mathematics of multiple object tracking: From proportions correct to number of objects tracked. Vision Research. 2005;45(17):2298–2309. doi: 10.1016/j.visres.2005.02.016. [DOI] [PubMed] [Google Scholar]
- Intriligator J, Cavanagh P. The spatial resolution of visual attention. Cognitive Psychology. 2001;43(3):171–216. doi: 10.1006/cogp.2001.0755. [DOI] [PubMed] [Google Scholar]
- Iordanescu L, Grabowecky M, Suzuki S. Demand-based dynamic distribution of attention and monitoring of velocities during multiple-object tracking. Journal of Vision. 2009;9(4):1–12. doi: 10.1167/9.4.1. 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kahneman D. Attention and Effort. New York: Prentice-Hall; 1973. [Google Scholar]
- Keane BP, Pylyshyn ZW. Is motion extrapolation employed in multiple object tracking? Tracking as a low-level non-predictive function. Cognitive Psychology. 2006;52:346–368. doi: 10.1016/j.cogpsych.2005.12.001. [DOI] [PubMed] [Google Scholar]
- Liu G, Austen E, Booth K, Fisher B, Argue R, Rempel M, Enns J. Multiple-object tracking is based on scene, not retinal, coordinates. Journal of Experimental Psychology: Human Perception and Performance. 2005;31:235–247. doi: 10.1037/0096-1523.31.2.235. [DOI] [PubMed] [Google Scholar]
- Narasimhan S, Tripathy SP, Barrett BT. Loss of positional information when tracking multiple moving dots: The role of visual memory. Vision Research. 2009;49(1):10–27. doi: 10.1016/j.visres.2008.09.023. [DOI] [PubMed] [Google Scholar]
- Oksama L, Hyönä J. Dynamic binding of identity and location information: A serial model of multiple identity tracking. Cognitive Psychology. 2008;56:237–283. doi: 10.1016/j.cogpsych.2007.03.001. [DOI] [PubMed] [Google Scholar]
- Pashler HE. The psychology of attention. Cambridge: MIT Press; 1999. [Google Scholar]
- Pastukhov A, Fischer L, Braun J. Visual attention is a single, integrated resource. Vision Research. 2009;49:1166–1173. doi: 10.1016/j.visres.2008.04.011. [DOI] [PubMed] [Google Scholar]
- Pelli D. The videotoolbox software for visual psychophysics: Transforming numbers into movies. Spatial Vision. 1997;10:437–442. [PubMed] [Google Scholar]
- Pylyshyn Z. Some puzzling findings in multiple object tracking: I. Tracking without keeping track of object identities. Visual Cognition. 2004;7:801–822. [Google Scholar]
- Pylyshyn Z. Some puzzling findings in multiple object tracking (MOT): II. Inhibition of moving targets. Visual Cognition. 2006;14:175–198. [Google Scholar]
- Pylyshyn Z. Visual indexes, preconceptual objects, and situated vision. Cognition. 2001;80:127–158. doi: 10.1016/s0010-0277(00)00156-6. [DOI] [PubMed] [Google Scholar]
- Pylyshyn Z, Storm R. Tracking multiple independent targets: Evidence for a parallel tracking mechanism. Spatial Vision. 1988;3:179–197. doi: 10.1163/156856888x00122. [DOI] [PubMed] [Google Scholar]
- Scholl BJ, Pylyshyn ZW, Feldman J. What is a visual object? Evidence from target merging in multiple-object tracking. Cognition. 2001;80(1/2):159–177. doi: 10.1016/s0010-0277(00)00157-8. [DOI] [PubMed] [Google Scholar]
- Schweickert R. Separable effects of factors on speed and accuracy: Memory scanning, lexical decision, and choice tasks. Psychological Bulletin. 1985;97:530–546. [PubMed] [Google Scholar]
- Sears C, Pylyshyn Z. Multiple object tracking and attentional processing. Canadian Journal of Experimental Psychology. 2000;54:1–14. doi: 10.1037/h0087326. [DOI] [PubMed] [Google Scholar]
- Shim WM, Alvarez GA, Jiang YV. Spatial separation between targets constrains maintenance of attention on multiple objects. Psychonomic Bulletin & Review. 2008;15:390–397. doi: 10.3758/PBR.15.2.390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sperling G, Dosher BA. Strategy and optimization in human information processing. In: Boff LKK, Thomas J, editors. Handbook of perception and human performance. Vol. 1. New York: Wiley; 1986. pp. 2-1–2-65. [Google Scholar]
- St. Clair R, Huff M, Seiffert A. Conflicting motion information impairs multiple object tracking. Journal of Vision. 2010;10(4):1–13. doi: 10.1167/10.4.18. 18. [DOI] [PubMed] [Google Scholar]
- Sternberg S. The discovery of processing stages: Extensions of Donders’ method. Acta Psychologia. 1969;30:276–315. [Google Scholar]
- Suganuma M, Yokosawa K. Grouping and trajectory storage in multiple object tracking: Impairments due to common item motions. Perception. 2006;35:483–495. doi: 10.1068/p5487. [DOI] [PubMed] [Google Scholar]
- Tombu M, Jolicoeur P. A central capacity sharing model of dual-task performance. Journal of Experimental Psychology: Human Perception and Performance. 2003;29(1):3–18. doi: 10.1037//0096-1523.29.1.3. [DOI] [PubMed] [Google Scholar]
- Tombu M, Seiffert A. Attentional costs in multiple-object tracking. Cognition. 2008;108:1–25. doi: 10.1016/j.cognition.2007.12.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tripathy SP, Barrett BT. Severe loss of positional information when detecting deviations in multiple trajectories. Journal of Vision. 2004;4(12):1020–1043. doi: 10.1167/4.12.4. 4. [DOI] [PubMed] [Google Scholar]
- Tripathy S, Narasimhan S, Barrett B. On the effective number of tracked trajectories in normal human vision. Journal of Vision. 2007;7:1–18. doi: 10.1167/7.6.2. [DOI] [PubMed] [Google Scholar]
- Tsotsos J, Culhane S, Wai W, Lai Y, Davis N, Nuflo F. Modeling visual attention via selective tuning. Artificial Intelligence. 1995;78:507–545. [Google Scholar]
- van der Heijden AHC. Some evidence for a limited capacity parallel selfterminating process in simple visual search tasks. Acta Psychologica. 1975;39:21–41. doi: 10.1016/0001-6918(75)90019-0. [DOI] [PubMed] [Google Scholar]
- vanMarle K, Scholl BJ. Attentive tracking of objects vs. substances. Psychological Science. 2003;14:498–504. doi: 10.1111/1467-9280.03451. [DOI] [PubMed] [Google Scholar]
- Verstraten FA, Cavanagh P, Labianca AT. Limits of attentive tracking reveal temporal properties of attention. Vision Research. 2000;40(26):3651–3664. doi: 10.1016/s0042-6989(00)00213-3. [DOI] [PubMed] [Google Scholar]
- Yantis S. Multielement visual tracking: Attention and perceptual organization. Cognitive Psychology. 1992;24:295–340. doi: 10.1016/0010-0285(92)90010-y. [DOI] [PubMed] [Google Scholar]
- Zelinsky GJ, Neider M. An eye movement analysis of multiple object tracking in a realistic environment. Visual Cognition. 2008;16:553–566. [Google Scholar]