Modeling Task Control of Eye Movements

Abstract

In natural behavior, visual information is actively sampled from the environment by a sequence of gaze changes. The timing and choice of gaze targets and the accompanying attentional shifts are intimately linked with ongoing behavior. Nonetheless, modeling of the deployment these fixations has been very difficult because they depend on characterizing the underlying task structure. Recently, advances in eye tracking during natural vision, together with the development of probabilistic modeling techniques, have provided insight into how the cognitive agenda might be included in the specification of fixations. These techniques take advantage of the decomposition of complex behaviors into modular components. A particular subset of these models casts the role of fixation as that of providing task-relevant information that is rewarding to the agent, with fixation being selected on the basis of expected reward and uncertainty about environmental state. We review this work here and describe how specific examples can reveal general principles in gaze control.

Human vision gathers information in complex, noisy, dynamic environments to accomplish tasks in the world. In the context of everyday visually guided behavior, such as walking, humans must accomplish a variety of goals, such as controlling direction, avoiding obstacles, and taking note of their surroundings. They must manage competing demands for vision by selecting the necessary information from the environment at the appropriate time, through control of gaze. How is this done, apparently so effortlessly, yet so reliably? What kind of a control structure is robust in the face of the varying nature of the visual world, allowing us to achieve our goals? While the underlying oculomotor neural circuitry has been intensively studied and is quite well understood, we do not have much understanding of how something becomes a target in the first place [1].

It has long been recognized that the current behavioral goals of the observer play a central role in target selection [2, 3, 4]. However, obtaining a detailed understanding of exactly how gaze targets are chosen on the basis of cognitive state has proved very difficult. One reason was that, until recently, it has been difficult to measure eye movements in active behavior, so the experimental situations that were examined typically involved fixing the subject's head and measuring gaze on a computer monitor. Within this tradition it was natural to first consider how stimulus features such as high contrast or color might attract gaze. Formalizing this approach, Koch and Ullman introduced the concept of a saliency map [5] that defined possible gaze points as regions with visual features that differed from the local surround. For example, a red spot on a green background is highly salient and attracts gaze. It was quickly recognized that visual features alone are insufficient, and that stimulus-defined saliency or conspicuity is modulated by behavioral goals, or top-down factors, to determine the priority of potential gaze points. Consequently later models of salience (or priority) weight the stimulus saliency computations by factors that reflected likely gaze locations, such as sidewalks or horizontal surfaces, or introduce a specific task such as searching for a particular object [6, 7]. These models reflect the consensus that saccadic target selection is determined by activity in a neural priority map of some kind in areas such as the lateral intra-parietal cortex and frontal eye fields [8, 9, 10]. However, the critical limitation of this kind of modeling is that it applies to situations where the subject inspects a static image on a computer monitor, and this situation does not make the same demands on vision that are made in the context of active behavior, where visual information is used to inform ongoing actions [11]. While there have been successful attempts to model specific behaviors such as reading or visual search, we need to develop a general understanding of how the priority map actively transitions from one target to the next as behavior evolves in time.

The use of a computer monitor was typically imposed by the limitation of eye tracking methodology, which required that the subject's head be in a fixed position. This limitation was removed, however, when Land developed a simple head-mounted eye tracker that allowed observation of human gaze behavior in the context of everyday tasks [12]. This development provided a more fertile empirical base for understanding how gaze is used to gather information to guide behavior. In the subsequent decades, improvements in eye tracking methodology have allowed a wide variety of natural visually guided behavior to be explored [11, 13, 14]. While these observations have provided very clear evidence for the control of gaze by the current cognitive agenda, a second critical roadblock has been the difficulty in developing a deeper theoretical understanding of how this agenda determines changes of gaze from one target to the next, given the inherent complexity of interactions with the world in the course of natural behavior. It is these gaze transitions that are hard to capture in standard experimental paradigms, and the problem that we address here is how to capture the underlying principles that control them.

The challenge of modeling tasks is at first blush intractable, given the diversity and complexity of visually guided behavior. However, observations of gaze control in natural behavior suggest a potential simplifying assumption, namely, that complex behavior can be broken down into simpler sub-tasks, or modules, that operate independently of each other, and thus must be attended to separately. For example, in walking, heading towards a goal and avoiding obstacles might be two such sub-tasks. The gaze control problem then reduces to one of choosing which sub-task should be attended at any moment (e.g. look towards the goal versus look for obstacles). In both these cases, gaze is taken as an indicator of the current attentional focus for subtask computation. Gaze and attention are very tightly linked [15, 16] and there is now a significant body of work on natural gaze control suggesting that gaze is a good, although imperfect, indicator of the current attentional computation. Subjects sequentially interrogate the visual image for highly specific, task-relevant information, and use that information selectively to accomplish a particular sub-task [17, 18, 19]. In this conceptualization, vision is seen as fundamentally sequential. Thus gazing at a location on the path ahead might allow calculation of either the current walking direction or the location of an obstacle relative to the body, but it is assumed that these computations are sequential rather than simultaneous, given that both are attentionally demanding. While the assumption of independent sub-tasks is almost certainly an oversimplification, it is a useful first step, since it is consistent with a body of classic work on a central attentional bottleneck that limits simultaneous performance of multiple tasks e.g. [20, 21]. For the most part a new visual computation will involve a shift in gaze. This is not always true, for example when spatially global visual information is needed, or when peripheral acuity is good enough to provide the necessary information without a gaze shift. However, it is valid for many instances, and it is those cases we focus on here.

In this brief review we describe models of gaze control that use the simplification of modules in two different but closely related contexts. In the first situation we consider the problem of how to allocate attention, and hence gaze, to different but simultaneously active behavioral goals. In driving a car, simultaneously active goals might be to follow a lead car while obeying a speed limit and staying in the lane. Here the challenge for gaze is to be in the right place at the right time, when the environment is somewhat unpredictable. This setting deals with the problem of competition between potential actions and has been labeled “the scheduling problem” [22]. The second situation, tackles the problem of structuring elaborate behavioral sequences from elemental components. We consider a sequential task, such as making a sandwich, where gaze is used to provide information for an extended sequence of actions. The question asked is: Given gaze locationand hand movement information of a subject in the process of making a sandwich, can we determine the stage in the construction they are currently working on? It turns out that a probabilistic model, termed a dynamic Bayes network [23], provides sufficient information to identify each task stage. Thus the observed data are used to infer the internal state that generates the behavior.

Task modules, secondary reward and reinforcement learning

Multiple tasks that are ongoing simultaneously are a ubiquitous characteristic of general human behavior and consequently the brain has to be able to allocate resources between them. This scheduling problem can be addressed if there is a way of assigning value to the different tasks. It has been demonstrated that external reward, in the form of money or points in humans, and juice in monkeys, influences eye movements in a variety of experiments [1, 24, 25]. It remains to be established how to make the definitive link between the primary rewards used in experimental paradigms and the secondary rewards that operate in natural behavior, where eye movements are for the purpose of acquiring information [1, 11]. In principle, the neural reward machinery provides an evaluation mechanism by which gaze shifts can ultimately lead to primary reward, and thus potentially allow us to understand the role that gaze patterns play in achieving behavioral goals. A general consensus is that this accounting is done by a secondary reward estimate, and a huge amount of research implicates the neurotransmitter dopamine in this role. It is now well established that cells in many of the regions involved in saccade target selection and generation are sensitive to expectation of reward, in addition to coding the movement itself [26, 27, 28, 29, 30, 31]. The challenge is to distill this experimental data into a more formal explanation.

All natural tasks embody delayed rewards whereby decisions made in the moment must anticipate future consequences. The value of searching for searching for a type of food must include estimates of its nutritional value, as well as costs in obtaining it. Furthermore the value of a task at its initiation can only reflect the expected ultimate reward, since reward in the natural world is uncertain. Moreover, a consequence of this uncertainty is that the initial evaluation needs to be continually updated to reflect actual outcomes [32]. An important advance in this direction has been the development of reinforcement learning models. Recent research has shown that a large portion of the brain is involved in representing different computational elements of reinforcement learning models, and this provides a neural basis for the application of such models to understanding sensory-motor decisions [32, 33, 34]. Additionally, reinforcement learning has become increasingly important as a theory of how simple behaviors may be learned [33], particularly as it features a discounting mechanism that allows it to handle the problem of delayed rewards.

A central attraction of such reinforcement learning models for the study of eye movements is that they allow one to predict gaze choices by taking into account the learnt reward value of those choices for the organism, providing a formal basis for choosing fixations in terms of their expected value to the particular task that they serve. However reinforcement learning has a central difficulty in that it does not readily scale up to realistic natural behaviors. Fortunately this problem can be addressed by making the simplifying assumption that complex behaviors can be factored into subsets of tasks served by modules that can operate more or less independently [22]. Each independent module, which can be defined as a Markov decision process, computes a reward-weighted action recommendation for all the points in its own state space, which is the set of values the process can take. As the modules are all embedded within a single agent, the action space is shared among all modules and the best action is chosen depending on the relative reward weights of the modules. The modules provide separate representations for the information needed by individual tasks, and their actions influence state transitions and rewards individually and independently. The modular approach thus allows one to divide an impractically large state space into smaller state spaces that can be searched with conventional reinforcement learning algorithms[35]. The factorization can potentially introduce state combinations for which there is no consistent policy, but experience shows that these combinations, for all practical purposes, are very rare.

Expected reward as a module's fixation protocol

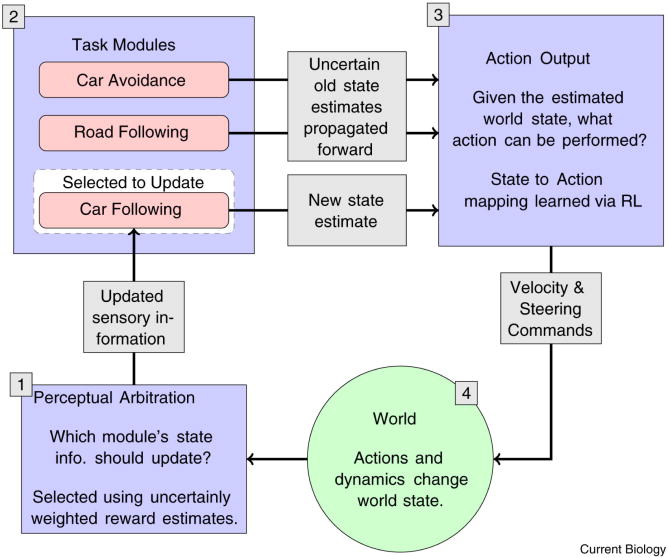
The module formulation directly addresses the scheduling problem in that it allows fixation choices be understood in terms of competing modules' demands for reward. In the driving scenario, where, separate modules might address subtasks such as such as avoiding other cars, following a leader car, staying in the lane, and so on, and specific information is gathered from the visual image to support the actions required for those tasks. The overall system is illustrated in Fig. 1. In any realistic situation the state estimates are subject to numerous sources of uncertainty, for example degraded peripheral vision or visual memory decay, which in turn confound reward estimates. At a given moment the subject acquires a particular piece of information for a module (e.g. locates the nearest car), takes an action (chooses avoidance path), and then decides what module should get gaze next. When a particular module is updated with information from gaze, as shown for Car following in the Figure, the new sensory information reduces uncertainty about the state of the environment relevant to that module (e.g. location of an obstacle). The next action is chosen on the basis of the mapping from states to actions, which may be learnt through reinforcement. As a consequence of the action (e.g. moving in a particular direction), the state of the world is changed and the agent must decide which module's state should be updated next by gaze (highlighted in the figure). The assumption is that fixation is serial process where one visual task accesses new information at each time step, and all other tasks must rely on noisy memory estimates.

Figure 1. Overall cognitive system model.

[1] While driving, multiple independent modules compete for gaze to improve their state estimates. [2] The winner, in this case Car Following, uses a fixation to improve its estimate of the followed car's location [3] The driver's action is selected according to the policy learned through RL. [4] The consequences of action selection are computed via the car simulator.

The central hypothesis is that gaze deployment depends on both reward and uncertainty. The gaze location chosen is the one that reduces a module's reward-weighted uncertainty the most. This reward uncertainty protocol was developed by Sprague et al [22] to simulate behavior in a walking environment and was shown to be superior to the common round-robin protocol used in robotics. Evidence that gaze allocation in a dynamic, noisy environment is in fact controlled by reduction of visual uncertainty weighted by subjective reward value was obtained by Sullivan et al [36]. This study tracked eye movements of participants in a simulated driving task where uncertainty and implicit reward (via task priority) were varied. Participants were instructed to follow a lead car at a specific distance and to drive at a specific speed. Implicit reward was varied by instructing participants to emphasize one task over the other, and uncertainty was varied by adding uniform noise to the car's velocity. Gaze measures, including look proportion, duration and interlook interval, showed that drivers more closely monitor the speedometer if it had a high level of uncertainty, but only if it was also associated with high task priority or implicit reward.

Modeling the growth of uncertainty

The data from Sullivan et al [36] was then modeled by Johnson et al [37] using an adaptation of the reward uncertainty protocol to estimate the best reward and noise values for each task directly from the gaze data. Because optimal behavior for driving consisted of staying at a fixed setpoints in distance and speed, they were able to use the simplification of a servo controller for choosing the action, an approximation that works well in this instance. The policy dictated by reinforcement and the policy dictated by error-reducing servo control are almost the same for these kinds of tropic behaviors. Thus for example, in both models, the driver should speed up if the distance is greater than desired.

The growth in state space uncertaintyin each module was estimated using a stochastic diffusion model (cf [38]). In this class of model, the growth of uncertainty about a particular kind of information, such as speed, is simulated as a particle executing a random walk until it exceeds some threshold value. In each of the modules, the threshold models relative task priority, with a lower threshold signifying greater importance or reward, and the drift rate represents the growth of noise or uncertainty. As the module's state estimate approaches the threshold, the probability of triggering a gaze change increases. The gaze change reduces the respective module's state variance, as would occur when a subject gathers sensory data. Thus lower thresholds and/or higher noise values were more likely to trigger saccades to update that module's state. As in the Sprague et al [22] formulation, each task module depends on its own set of world-state variables that are relevant to its specific task. The model included three modules: one for following a car, one for maintaining a constant speed and a third for staying in a lane. The relevant state variables were in the form of desired set points. The car-following task module used the car's deviation from a desired distance behind leader and the difference between the agent's heading and the angle of this goal. The constant speed maintenance module used the absolute speed of the car. Finally, the lane module used the car's angle to the nearest lane center. The driving commands were chosen to reduce a weighted sum of errors from each of these. The human subject's three–dimensional virtual driving world is simplified in the simulation as a two-dimensional plane. The simulated world contains a single road with two lanes similar to the one used by the human drivers.

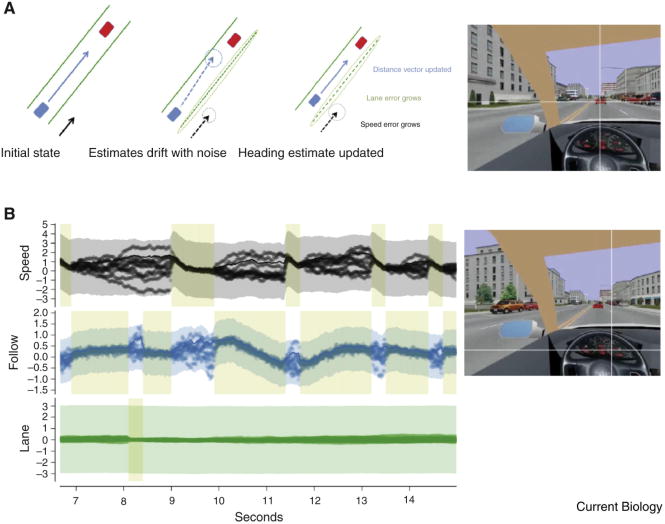
In a standard stochastic diffusion model, decisions are made when the drifting state crosses a boundary threshold. In contrast, in the ‘softmax’ version used in Johnson et al [37], the model selection is probabilistic. Rather than a deterministic decision, approaching a boundary increases the bias towards selecting high priority modules and not selecting low priority ones. However, the probabilistic nature of selection means that low priority modules still have a non-zero chance of selection, which provides needed flexibility in capturing the variability of human fixation behavior. Figure 2 summarizes features of the model simulations, including a caricature of a typical heading update as well as a typical segment of the performance of the three modules' boundary data and sensory update histories. The model can predict the frequency histograms for fixation durations on the lead car and the speedometer, and fits human data remarkably well.

Figure 2. Evolution of state variable and uncertainty information for three modules.

A Depiction of an update of the Follow module. Starting in the initial state, the necessary variables are known, but noise causes them to drift. According to the model reward uncertainty measurements, the Follow module is selected for a gaze update. This improves its state estimate while the other modules' state estimates drift further. B. A progression of state estimates for the three modules: constant speed maintenance, leader following and lane following. In each, the lines indicate state estimate vs. time for that module's relevant variable, in scaled units. Thus, for the speed module, the y-axis depicts the car's velocity, for the follow module it depicts the distance to a setpoint behind the lead car, and for the lane module it shows the angle to the closest lane center. If estimates overlap into a single line, the module has low uncertainty in its estimate. If estimates diverge, making a ‘cloud’, the module has high uncertainty. An update from the simulation for the Follow module can be seen at ten seconds. The fixation, indicated by pale shaded rectangle, lasts for 1.5 seconds. The figure shows how the individual state estimates drift between looks and how the state variables are updated during a look. The colored transparent region shows the noise estimate for each module. C. (top) Fixation on speedometer; (bottom) fixation on car.

The driving model is not unique. Within the study of behavior and eye movements in driving several control models have been suggested for particular behaviors, e.g. car following, lane following [39, 12]. Salvucci and Taatgen [40, 41] have also presented a 'multithreaded theory of cognition' that is similar to the Sprague et al scheduling model in that it uses a modular structure, however their simulation is more abstract than [37] and does not model fine-grained fixation intervals. The framework also requires many free parameters. The bottom line is that models that treating the deployment of gaze as a sensory-motor arbitration problem, embedded in a dynamic engagement with the environment, have considerably more traction conceptually than other approaches.

Bayesian models for interpreting sequential tasks

In the driving task, the modules were independent and competing while executing in parallel. We now turn to a different kind of situation, where modules are executed sequentially, such as making a cup of tea or a sandwich. This situation is more complex in that a more elaborate model of the task itself is required in order to understand the transition from one subtask to the next. For example, after picking up the knife when making a sandwich, the next step might be “take the lid off the jelly”, “put the bread on the plate”, or “pick up the knife.” We need a model of the underlying task order that keeps track of progress in order to predict the most likely transition, and to interpret the role of any given fixation. Land and colleagues make an attempt to understand the task structure in their seminal work on eye movements while making tea [42]. They postulated that tasks can be described hierarchically, where the overall goal such as “make tea” is the highest level, and this is divided into sub-goals at lower levels. At the lowest level they described “object related actions” such as “remove the lid” or “pick up the cup” and suggested that these were functional primitives. Accomplishing one of these primitives typically involved several eye movements, whose function Land et al classified into four types: locating, directing, guiding, and checking.

Although it is fairly easy for a human observer to infer the structure of the task by inspection of a subject's fixation data, as in the case of tea making, ideally one would like a more formal theoretical approach to understanding the underlying structure that would allow us to understand the variations from one time to the next as well as variations from one subject to the next. The central issue revolves around the fact that the brain has to organize the solution to the task and, as a way station to ferreting out a satisfactory theory, one would like to understand what kinds of information are at least sufficient to predict task performance.

One helpful way to think about the problem is to characterize the steps in the task, suchas the ones that Land et al posited, as part of a multidimensional probability distribution that includes all the momentary sensorimotor observations, as well as the steps that have been carried out so far. If this information is available, then the current subtask could be estimated as the most probable one after integrating over all the other variables' probability distributions. Done directly, this integration process would be very expensive, but it turns out that most the task variables are typically independent of each other and this allows the integration over the dependencies that do occur to be factored into inexpensive components.

Coding probabilities in Dynamic Bayes Networks

An elegant way to represent sparsely factored probabilities is to use a class of Markov models called dynamic Bayes networks [23]. Such networks can represent the probabilities of states, with likelihoods coded in transitions between the states. The structure is dynamic as the probabilistic bookkeeping extends in time. For example, in the case of making a sandwich, we might treat a subtask goal such as “bread on plate” as a state, and the subsequent state as “ lid off the peanut butter jar”, and the transition between these states as having some probability distribution depending on task features, task context and time. Sandwich making has much underlying regularity to its observed behavior [42, 44, 45], and it's possible to infer the underlying task structure very accurately by incorporating the observable data, such as the gaze location, hand position, hand orientation, and image features as well as the prior sequence of states of the task.

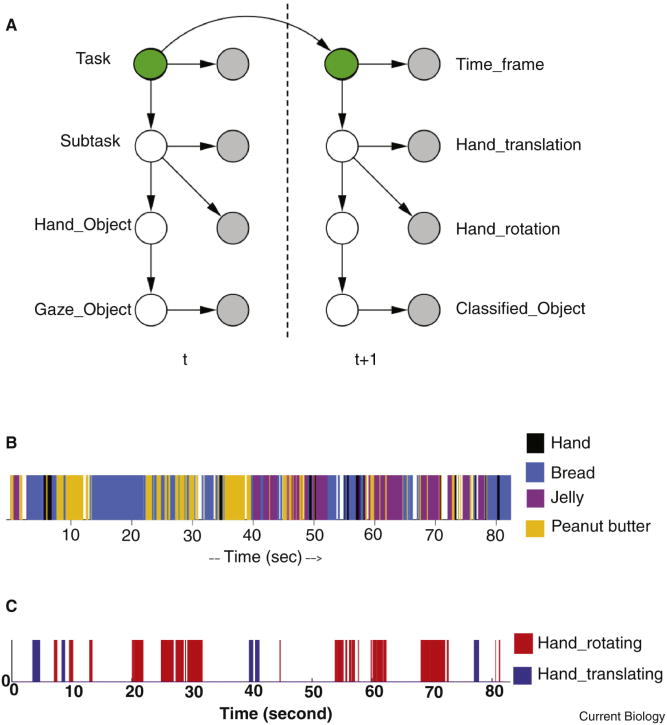
Yi and Ballard successfully applied dynamic Bayes networks to sandwich making [43]. In a preparatory step similar in spirit to Land's locating, directing, guiding, and checking classifications, they grouped the raw temporal data sequences into a low-level language of elemental operations by painstakingly annotating the videos of the sandwich makers. Thus picking up the knife (an object-related action in Land's terminology) could be coded as the sequence: fixate knife/extract knife_location/put_hand knife_location/pickup. This low-level annotation allowed the computer to automatically recognize common subsequences from different subjects and group them into the sub-tasks indicated in Fig.3, even though the sub-tasks were done indifferent orders by the different subjects. While there is some arbitrariness in the video annotation, it proves sufficiently robust for an algorithm to automatically recognize the task steps. If these steps can be reliably recognized given the data from the eye, and hand, and the state of the scene, then we can have confidence that this is a valid model of the task execution.

Figure 3. Recognized Steps in peanut butter and jelly sandwich making.

A computational model uses Bayesian evidence pooling to pinpoint steps in the task by observing the sandwich constructor's actions. The algorithm has access to the central one degree of visual input centered at the gaze point, which is delimited by the crosshairs. Also the position and orientation of each wrist is measured. The label in the upper left is the algorithm's estimate of the stage in the task.

The dynamic Bayes network requires the statistics of sub-task transitions, which can be gathered from subjects' sandwich making data. As mentioned, at each point in time the network factors the task probability function, exploiting useful constraints, for example, “spread the peanut butter” cannot occur prior to “pick up the knife.” Additional helpful sets of constraints are also exploited, and those elaborate the substructure of the task variables, such as subtask, gaze location, image state etc. The crucial dependencies between these variables turn out to be very sparse, providing great economies in the factorization of the overall probability distribution. For example, a fixation classification of “Jelly” all but rules out the task of “spreading peanut butter.”

Taking advantage of this sparseness of the interdependencies, Yi and Ballard's recognition model of sandwich making used fixation and hand movement data in combination with ongoing subtask identifications. The specific dynamic Bayes model used to analyze the data was hand engineered and is shown in Fig. 4A. The model uses ongoing measurements from a single subject in the course of making the sandwich and attempts to report the correct stages in the task. The conditional probabilities expressed in the model are based on the statistics of observations of human sandwich makers. To help understand how this works, let us elaborate a low level component of the model that relates the different possible gaze targets denoted “Gaze Object,” to the classifications made by the visual system, which are denoted “ClassifiedObject”and given by the set {Nothing, Peanut butter, Jelly, Bread, Hand}. The bottom two nodes and connecting arrow in the graph are the dynamic Bayes net notation for the probability factorization P(GazeOject)P(ClassifiedObject|GazeObject). Using Bayes rule, this is proportional to the product P(GazeObject|ClassifiedObject)P(ClassifiedObject), where the former can be estimated from studying human sandwich makers and the latter is unity for the result of the visual classifier. Once the probability estimate for the GazeObject is determined, it can be used to estimate the node above it in the network, by the same procedure. Continuing in this fashion allows the task label to be determined at each point in time

Figure 4. Dynamic Bayes Network details.

A. The dynamic Bayes network model of human gaze use factors the task variables and associated conditionally independent variables into a complex network. The network connectivity dictates how peripheral information can be propagated back to estimate the task variables. Although peripheral estimates can be very noisy, the task stages can be estimated very reliably. Filled circles denote measured data and open circles denote variables whose values must be computed. Bayes rule governs the propagation process. For example, the joint probability P(Gaze object, ClassifiedObject) can be factored as P(Gaze_object)P(ClassifiedObject| Gaze object). Bayes rule is then used to compute the probability of the gaze object given a measurement of the recognized object. Data recorded from previous sandwich makers is used to estimate the non-peripheral conditional probabilities. Successive time intervals are combined into a single ongoing task estimate, which results in the labels displayed in Fig. 3. B. The model classifies color information from the fixation point into one of the four classes of ClassifiedObject for each interval, but the results are very noisy C. The measurements for hand motion are classified into Hand Translating(eg reaching), Hand Rotating(eg screwing)for a fraction of the temporal intervals associated with stable gaze. Nonetheless, this information, when combined with the visual classifications and internal task priors, proves sufficient for task estimation.

Summarizing, dynamic Bayes networks are a way to model possible underlying consistencies in state transitions, and such a model can then be a repository for the performance data of different subjects. Once the network has been initialized in this way, it can use its probability estimates to track the performance of a new subject. Note that, as implemented here, one can think of the model as one held by an observer watching the sandwich construction, but that with relatively minor modifications, it could also be a model of the sandwich constructor's own mental process. Dynamic Bayes networks are fast becoming a general tool for task models. For example, the Itti laboratory [46, 47] have extended this approach to the more demanding pacing of video games.

The approach does not prove that dynamic Bayes formalisms are necessary, only that they are sufficient to account for a large number of of the data sets. Another limitation is that if the task is changed, then they have to be modified and re-trained. Another point make is that, unlike the driving example, the network model uses a more abstract descriptive level, and does not address the individual fixation statistics. However despite these caveats, the ability of these models to account for wide varieties of fixation data makes them quite compelling.

Conclusion

Our understanding of the use of fixations in natural behavior has undergone very rapid recent developments spurred on with the rapid advances in wearable eye trackers. However, the development of formal models has been difficult. The most fundamental difficulty is to describe dynamic interaction with the visual input. With the recent development of new technology and computational formalisms, has it been possible to resolve the issue of how generalizable the results from a particular task model might be. The work reviewed here shows how even such specific tasks as driving and sandwich-making can be understood in quite general terms. The critical feature of the approach is the decomposition into subtasks. In the example of driving a car, gaze patterns can be explained as competitions between these subtasks for updating each task's crucial state information. This scenario is representative of any situation that can be modeled as a small collection of simultaneously ongoing tasks whose sensory updating demands have to be multiplexed. To handle this, modular reinforcement learning seems to have the required additional structure because the individual tasks can be learned, and also they provide the necessary scaffolding for describing the competition for fixations. The simulations described here show that they can account for the dynamics of fixations in multiplexed situations and, to our knowledge this is the first time this has been done. Another aspect of the subtask decomposition occurs when the subtasks represent sequential steps in carrying out a complex task, such as making a sandwich. This example allows the application of classes of graphical models to represent the underlying task structure. Dynamic Bayes networks can provide very good accounts of the use of fixations in complicated dynamic scenarios that can be seen as a succession of stages in a single overriding task, and further the understanding of the role of specific fixations. These two examples were selected as representative of this new research avenue and are meant to show the considerable promise of extending the understanding of the use of fixations in complex natural behaviors. The focus of the review has been on endogenous attentional control of tasks, but a complete story has, in addition, to account for exogenous stimuli that can change the agent's agenda (11). As noted in the introduction, there is an extensive literature on exogenous attentional capture, but the task of satisfactorily integrating them into a complete system remains.