Skip to main content
PMC home page
Nucleic Acids Research logoLink to Nucleic Acids Research
. 2014 Aug 11;42(15):9753–9760. doi: 10.1093/nar/gku719

Quantitative models for accelerated protein dissociation from nucleosomal DNA

Cai Chen 1,3, Ralf Bundschuh 1,2,3,*
PMCID: PMC4150810  PMID: 25114052

Abstract

Binding of transcription factors to their binding sites in promoter regions is the fundamental event in transcriptional gene regulation. When a transcription factor binding site is located within a nucleosome, the DNA has to partially unwrap from the nucleosome to allow transcription factor binding. This reduces the rate of transcription factor binding and is a known mechanism for regulation of gene expression via chromatin structure. Recently a second mechanism has been reported where transcription factor off-rates are dramatically increased when binding to target sites within the nucleosome. There are two possible explanations for such an increase in off-rate short of an active role of the nucleosome in pushing the transcription factor off the DNA: (i) for dimeric transcription factors the nucleosome can change the equilibrium between monomeric and dimeric binding or (ii) the nucleosome can change the equilibrium between specific and non-specific binding to the DNA. We explicitly model both scenarios and find that dimeric binding can explain a large increase in off-rate while the non-specific binding model cannot be reconciled with the large, experimentally observed increase. Our results suggest a general mechanism how nucleosomes increase transcription factor dissociation to promote exchange of transcription factors and regulate gene expression.

INTRODUCTION

In eukaryotes, DNA is repeatedly wrapped around histone protein complexes to form nucleosomes. This process compacts long DNA molecules so they fit inside the cell nucleus (1). Wrapping DNA into nucleosomes prevents access for DNA-binding proteins (such as transcription factors, RNA and DNA polymerases and DNA repair enzymes) to their target sites (2,3). By controlling access to DNA, nucleosomes appear to regulate many biological processes including gene expression, DNA replication, and DNA repair (4).

In order to accommodate numerous DNA processing complexes, nucleosomes undergo dynamic changes where nucleosomal DNA transiently unwraps exposing it to DNA-binding proteins by thermal fluctuations (5,6). The equilibrium between partially wrapped and fully wrapped DNA is largest near the two DNA entry–exit regions of the nucleosome (5–7). These dynamics have been quantitatively described and modeled using a free energy landscape for DNA unwrapping from a nucleosome on the 601 positioning sequence (8).

Transcription factors (TFs) are essential molecules that regulate gene expression at the transcriptional level (9). Many of their target sites fall into the entry–exit regions of nucleosomes (10) and are thus wrapped around the histone octamer. In such cases, the transcription factor is sterically occluded from its target site, which reduces the rate of transcription factor binding (11). The resulting change in transcription factor binding site occupancy is well known as a mechanism for regulation of gene expression via chromatin structure (2,3). Interestingly, recent single molecule experiments (12) found that transcription factor dissociation rates from target sites within nucleosome entry–exit regions are enhanced by two to three orders of magnitude relative to naked DNA. However, the detailed physical mechanisms are unknown.

Here, we quantitatively model this process to understand potential mechanisms behind this nucleosomal increase in TF dissociation rate. In the experiments by Luo et al. (12), the TF binding site is located such that it faces the histone core, i.e. such that in the bound state the TF has to be located in between the unwrapped DNA and the histone core. Thus, steric or electrostatic interactions between the TF and the nucleosome occur far away from the DNA binding site of the TF and given the size of the TF would likely result in forces that are relatively tangential to the DNA. Also, the DNA bound by the TF has to be fully unwrapped from the histone core in this geometry and thus deformations of the DNA inflicted by the TF binding can influence the DNA–histone interactions at most through hydrodynamic effects. For any of these interactions, it is difficult to imagine that they affect dissociation of transcription factors by two to three orders of magnitude. However, even if the effects of these direct interactions between the TF and the histones are to be included, understanding the mechanisms in the absence of direct forces between the nucleosome and the TF provides an important baseline.

We propose two mechanisms behind the acceleration in TF dissociation and explicitly model both of them: (i) Both TFs studied in Luo et al. (12), LexA and Gal4, bind DNA as a homodimer and bind to their operator half-sites with 1000-fold lower affinity (13,14). Thus, the nucleosome can change the equilibrium between monomeric and dimeric binding, a process that has also recently been pointed out to increase off-rates of dimeric transcription factors due to high concentrations of transcription factors in solution (15). (ii) The nucleosome can change the equilibrium between binding at the specific binding site and non-specific binding to the surrounding DNA. We quantitatively model both scenarios. Since the exact value of the dissociation rate from naked DNA was too slow to be experimentally determined in Luo et al. (12), and the binding affinity for Gal4 monomer is also not known (both are required for our modeling), we focused on the LexA case. However, while the precise parameters are not known, we expect qualitatively similar results in the Gal4 case.

Our results indicate that the non-specific binding mechanism cannot be reconciled with experimental findings, but the dimer mechanism can account for increases in off-rate by a factor as high as 200. Overall, our results suggest a general mechanism how nucleosomes increase dimeric transcription factor dissociation to facilitate transcription factor exchange and regulate gene expression.

MATERIALS AND METHODS

We model the process that TFs dissociate from a single nucleosome since experimentally the presence of neighboring nucleosomes does not affect the association or dissociation rates (12). In both of our models, the dynamics are summarized by rate matrices, which satisfy the master equation:

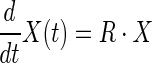graphic file with name M1.gif

where 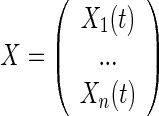Inline graphic and Xi(t) are the time-dependent concentrations of each state (n is the total number of states).

The solution to this master equation is

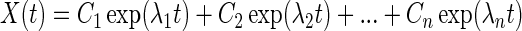graphic file with name M3.gif

where 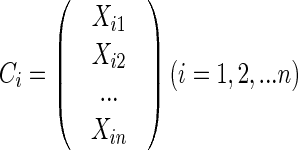Inline graphic are the eigenvectors of R, and 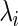Inline graphic are the eigenvalues of R (16).

For a rate matrix, the single eigenvalue corresponding to the steady state of the system is zero, while all the remaining eigenvalues are negative. If we thus set 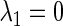Inline graphic, we get 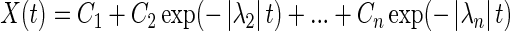Inline graphic, where C1 is the steady state of the system. Therefore, the largest non-zero eigenvalue yields the slowest exponential decay rate, which dominates the approach to the steady state for long times and thus corresponds to the experimentally measured off-rate.

In both models, we first model the case that the transcription factor dissociates from naked DNA (without a nucleosome). We fit these models of binding to naked DNA to experimental data (TF off rate from naked DNA) to determine the kinetic parameters of the TF-DNA interaction.

We then incorporate the nucleosome free energy landscape data from (8) to calculate the TF off-rate in the presence of a nucleosome using the nucleosome unwrapping and rewrapping rates. This calculated off-rate is compared with the experimental values. In general, the nucleosome unwrapping and rewrapping rates for the nth base pair of DNA are determined by:

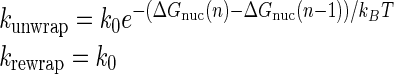graphic file with name M8.gif

where ΔG(n) is the Gibbs free energy landscape due to unwrapping n base pairs (8), kB is Boltzmann's constant and T is the temperature. We take k0 = 105 s−1 (the base rate for wrapping fluctuations) from (8). In the dimeric binding model, which includes a fully unwrapped, a partially unwrapped and a fully wrapped state of the nucleosome, these step-by-step unwrapping and rewrapping rates were combined into rates of changes of the number of wrapped base pairs by larger amounts at once as described in the Results section.

RESULTS

Dimeric binding

In the study of Luo et al. (12), two transcription factors were investigated: (i) Escherichia coli transcription repressor protein LexA, which has a very specific binding site of 16 bp and dissociation constant of Kd ∼ 0.1 nM (17), and forms a stable dimer where each monomer binds to a half site of the whole LexA binding site (13,18,19); (ii) A model eukaryotic transcription factor Gal4, which recognizes its 17 bp consensus binding site with an even smaller dissociation constant of Kd ∼ 10 pM (20) and also binds DNA as a homodimer (20,21). Since both TFs are homodimers and bind to two specific half sites, we propose that one of the two binding sites will dissociate first. In the presence of a nucleosome (Figure 1A), if the site that is closer to the nucleosome dyad dissociates first, the nucleosome can rewrap and prevent rebinding. Once the other site dissociates, the TF will completely detach. Therefore, when the nucleosome is present it can ‘rachet’ the protein off by blocking reassociation at the site proximal to it. However, in the absence of the nucleosome, when one of two binding sites dissociates, it would rapidly rebind again, meaning that both sites dissociating at once would be rare. This should increase the off-rate of the TF in the presence of a nucleosome relative to naked DNA, just as it does in the presence of multiple dimeric non-specific binding proteins saturating on a stretch of DNA (15).

Figure 1.

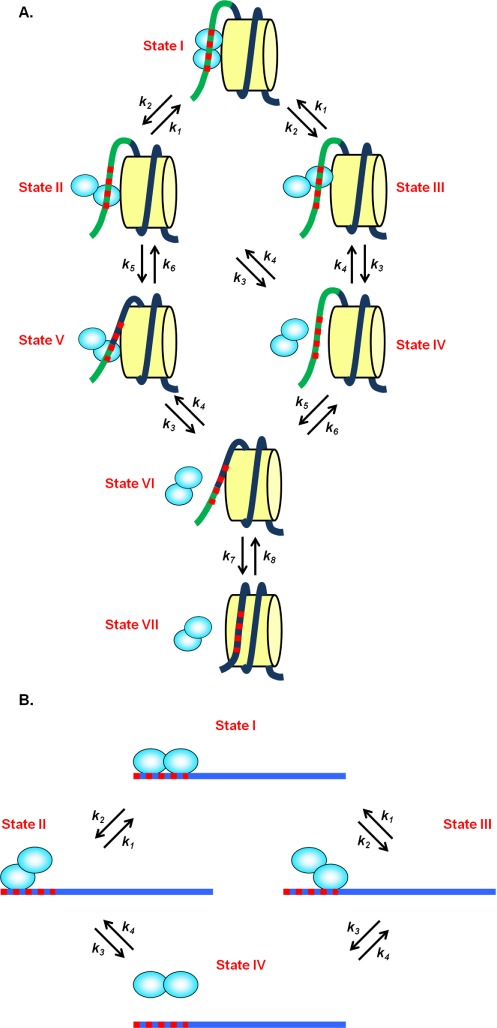
Figure 1.

Open in a new tab

Dimeric model of TF dissociation from (A) a nucleosome and (B) from naked DNA. (A) In the presence of a nucleosome (yellow cylinder), if the site which is closer to the nucleosome dyad dissociates first (State I to State II), the nucleosome can rewrap (State II to State V). Once the other site dissociates, the TF will fall off (State V to State VI) and the nucleosome will be completely wrapped (State VI to State VII). If the further site dissociates first (State I to State III), the nucleosome needs to wait for the closer site to dissociate and then be rewrapped (State III to VII). The dark blue line is the DNA that is wrapped around the histone core while the light green line is the DNA unwrapped from the nucleosome. The red dashed line is the TF binding site. (B) In the absence of the nucleosome, when one of two binding sites dissociates (State I to State II or III), it can rebind again (State II or III to State I) or completely dissociate (State II or III to State IV).

Here, we model this process quantitatively to test if this model can explain the experimental results of Luo et al. (12). To determine the rates of transition between the partially bound states in the presence of a nucleosome, we first build our model for the case that the TF binds to naked DNA. This model for naked DNA consists of four states (Figure 1B), namely, both TF half sites unbound, only one of the two half sites bound and both half sites bound.

To describe the transitions in this model, we introduce the rates k1, k2, k3 and k4: k1 is the transition rate from either of the partially bound states to the fully bound state (both half sites bound), while k2 is the rate from the fully bound state to either of the partially bound states. k3 is the transition rate from either partially bound state to the fully unbound state while k4 is the rate for the TF to bind to one of the half sites.

These dynamics can be summarized by the rate matrix

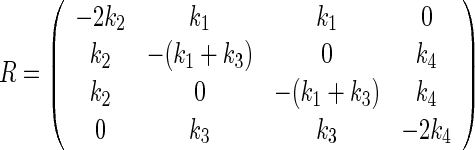graphic file with name M9.gif

We have to determine the values of k1, k2, k3 and k4 from experiment, at which point we have to limit ourselves to LexA as indicated in the introduction. Since experiments provide only a measurement of the overall dissociation rate of the TF, we first need to find additional relations between the rates. Based on the results in (13), when one of the two half sites is mutated (or when the dimerization domain of LexA is removed), LexA can still bind to the half site that is not mutated, but with ∼1000-fold lower affinity. If we call the dissociation constant of LexA fully bound Kd (LexA, full) and the dissociation constant of LexA partially bound (LexA only binds to a half site) Kd (LexA, partial), we thus have Kd (LexA, full) / Kd (LexA, partial) = 1/1000. Since Kd (LexA, full) / Kd (LexA, partial) = exp (-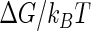Inline graphic) = k2 / k1, where 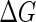Inline graphic is the free energy difference between a partially bound and the fully bound state, we get k1 / k2 = 1000. Moreover, since both k2 and k3 represent how fast one of the LexA monomers dissociates from the DNA, we treat these two rates to have the same numerical value (k2 = k3). Then, to calculate the overall off rate of LexA, we set k4 = 0 to designate the state, in which LexA is unbound, the steady state and solve for the largest non-zero eigenvalue of the rate matrix R. This eigenvalue can be calculated analytically to be

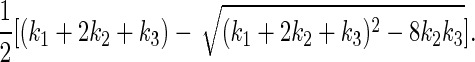graphic file with name M12.gif

By equating the absolute value of this overall off rate to the experimental value of 0.0034 s−1 (12) and using the relationships k2 = k3 and k1 / k2 = 1000 introduced above, we can solve for k1, k2 and k3 and obtain k1 = 1700 s−1 and k2 = k3 = 1.7 s−1. k4 can then be inferred from measurements of the overall Kd (LexA, full) (∼0.07 nM) which yields k4 = 0.025 s−1 nM−1 [LexA] where [LexA] denotes the concentration of LexA.

In the presence of a nucleosome, if the binding site closer to the nucleosome dyad dissociates first, the nucleosome can rewrap thus facilitating TF dissociation (Figure 1A). Keeping track of the nucleosome unwrapping state leads us to a model with seven states (Figure 1A). In this model, the transition rates k1, k2, k3 and k4 are only dependent on the TF and its binding target and are completely unrelated to the nucleosome; we thus use the same values for these four parameters as in the naked DNA case. We further introduce the rates k5, k6, k7 and k8, which reflect the nucleosome rewrapping and unwrapping. Since the TF will only affect the properties of the nucleosomal DNA that is already unwrapped for TF binding (not related to k5, k6, k7 and k8) but not the nucleosomal DNA still wrapped around the histone core (related to k5, k6, k7 and k8), the TF can affect the wrapping and rewrapping rates at most through changing the hydrodynamics of the unwrapped DNA (other than the obvious effect that the binding of the TF entirely prevents certain wrapping events, which we explicitly include here through the structure of our model). We thus assume that the rates k5, k6, k7 and k8 are not affected by the presence of the TF and take them from (8) as

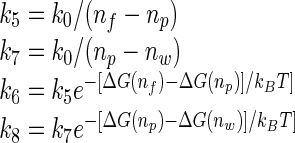graphic file with name M13.gif

where nf is the number of DNA base pairs unwrapped from the nucleosome that is required for the TF to fully bind (states I, II, III and IV in Figure 1A), np is the number of DNA base pairs unwrapped that is required for the TF to bind to the half site that is farther from the nucleosome core (states V and VI in Figure 1A), and nw is 0 which represents the number of unwrapped base pairs when the nucleosome is fully wrapped (state VII in Figure 1A). The rate k5 describes rewrapping from states that allow the TF to bind fully (states I, II, III and IV in Figure 1A) to states that allow only partial binding of the TF (states V and VI in Figure 1A). This rewrapping comprises (nf - np) independent and individual rewrapping steps in sequence. Thus, the rewrapping time of this entire event is (nf - np) times the rewrapping time of an individual base pair, resulting in the rewrapping rate to be 1/(nf - np) of the base rate of k0 = 105 s−1 for wrapping fluctuations from (8) (see Materials and Methods section). Analogous arguments yield the effective rewrapping rate k7.

Similar to the rate matrix in the absence of a nucleosome, the rate matrix for the seven state model with a nucleosome can be written as

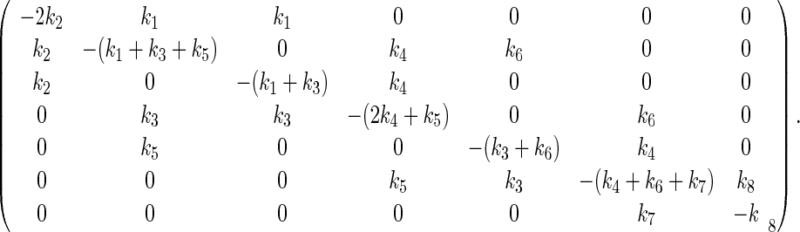graphic file with name M14.gif

For LexA, all its parameters are determined either by the naked DNA experiments or from (8). In the experiment, only the state in which LexA completely dissociates from the nucleosome and the nucleosome is fully wrapped (state VII in Figure 1A) is detected as the ‘off’ state based on its high FRET signal. Therefore, to calculate the overall off rate of LexA in the presence of a nucleosome, we set k8 = 0 to designate this high FRET state as the steady state (this also implies that ΔG(np)- ΔG(nw) is not relevant for the off-rate).

The overall off-rate of LexA in the presence of a nucleosome can be calculated as the largest non-zero eigenvalue of the rate matrix of the seven state model numerically (22). In our calculation, we found that the only parameter the overall off rate is sensitive to is the free energy difference ΔΔG ≡ ΔG(nf) - ΔG(np) between the two states when LexA is fully or partially bound (Supplementary Text). For example, the concentration of LexA affects the overall off rate (k4 is not equal to zero in the presence of a nucleosome); however, we tested a number of different LexA concentrations ranging from 0 to 50 000 nM as also tested in the experiment (12) and found that the overall off-rate only changes slightly (Supplementary Text). The value of the one important parameter ΔΔG depends on the exact amount of unwrapping (nf and np) of the nucleosome which is unknown. Thus, we tested several numerical values of ΔΔG (5 to 7 kBT) in the range of reasonable amounts of unwrapping. We found that koff (nucleosome) ranges from 0.2 to 0.65 per second (Figure 2 and Supplementary Text), which is an increase by 50- to 200-fold compared to the naked DNA case.

Figure 2.

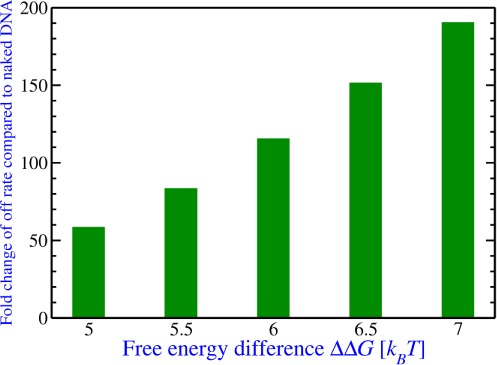
Figure 2.

Open in a new tab

The overall off-rate of LexA dissociation from the nucleosome compared to naked DNA for the dimeric model. Several numerical values of the nucleosome unwrapping free energy difference between State II and State IV of the model in Figure 1A are used to calculate the overall off rate of LexA in the presence of a nucleosome which is shown here as a fold change compared to the naked DNA case.

Non-specific binding

Transcription factors bind to their specific target site on DNA. However, at high concentrations, transcription factors also bind to non-specific DNA targets with much lower binding affinity. Moreover, in the process of searching for a specific target, it is inevitable that transcription factors encountering non-specific DNA scan along this non-specific DNA which affects the specific-DNA targeting rate of the protein. Studies on several DNA binding proteins including LacI revealed that proteins bind to their targets much faster than the 3D diffusion limit, which was explained by this facilitated-diffusion model (23–27). We propose that if TFs can also bind to non-specific binding sites, then the nucleosomes can rewrap and prevent rebinding of TFs to their specific binding site. Thus, nucleosomes can change the equilibrium between binding at the specific binding site and non-specific binding to the surrounding DNA; we propose that non-specific binding may contribute to the large increase of the overall off-rate of TFs in the presence of a nucleosome compared to naked DNA.

In our model, we assume that the TF can slide—diffusing in one dimension over the DNA molecule—and dissociate from any position. We model this diffusion as base-by-base diffusion along the DNA with multiple non-specific binding sites, in which the TF slides only one single base in one step.

Analogously to the dimeric binding model, we first build this model in the case that the TF binds to naked DNA. Here, the TF can slide along the DNA in two directions and can also dissociate from the DNA (Figure 3A). Among all the binding sites, only one site is the specific target for the TF and the others are non-specific binding sites for the TF.

Figure 3.

Figure 3.

Open in a new tab

Non-specific binding model of TF dissociation from (A) naked DNA and (B and C) from a nucleosome. (A) In the absence of the nucleosome, the TF can slide along the DNA in two directions (black arrows, k1) or dissociate from the DNA (Purple arrow, kns,off). (B) In the presence of a nucleosome, five possibilities for the next step of a certain state exist: (i) and (ii) the TF can slide along both directions in the unwrapped nucleosome (black arrows, k1); (iii) and (iv) the nucleosome can unwrap and rewrap (orange arrows, kunwrap, krewrap); or (v) the TF can dissociate from the unwrapped nucleosome (purple arrow, kns,off). The figure shows LexA binding to a non-specific site. Among all the binding sites, only one site is the specific target for the TF (red dashed line in (A) and (B)) and the others are non-specific binding sites for the TF. (C) Illustration of the minimum distance (d in bp) between the TF and the unwrapping position of the nucleosome. At this minimum distance when the TF binds to DNA, the nucleosome cannot rewrap anymore and the TF can only slide in one direction.

We introduce the sliding rates of the TF, k1 and k2: k1 is the sliding rate of the TF from a non-specific binding site to another site (both specific binding site and non-specific binding site), while k2 is the sliding rate of the TF from the specific binding site to a neighboring non-specific binding site. We define the ratio of k1 and k2 as K = k1 / k2. Similar to the dimeric binding model, this ratio is determined by how ‘tightly’ the TF binds to the sites, i.e. by the binding affinity difference between non-specific and specific binding sites, or the ratio of the dissociation constants between non-specific and specific binding, as

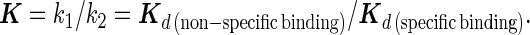graphic file with name M15.gif

Since the TF can dissociate from any binding site, we further introduce rate parameters for TF dissociation from the specific binding site (ks,off) and the non-specific binding sites (kns,off). Similarly, the ratio ks,off / kns,off is determined by the ratio of dissociation constants between non-specific and specific binding (K = kns,off / ks,off = Kd (non-specific binding) / Kd (specific binding)). We assume that the on rate for TF reassociation to the nucleosome is the same for specific and non-specific binding sites (kns,on = ks,on = kns,off / Kd (non-specific binding) · [TF] = ks,off / Kd (specific binding) · [TF]).

Again, we use the measured overall off rate of TF dissociation from naked DNA to determine the unknown parameters and thus have to limit ourselves to the case of LexA. Since several parameters are unknown, we vary their values within experimentally reasonable values. The parameters we vary are the ratio K = Kd (non-specific binding) /Kd (specific binding) and sliding rate k1 because all other parameters can be obtained based on these two. We varied K from 100 to 100,000 based on experimental estimates of this number (28), and varied k1 from 103 s−1 to 107 s−1 to cover the range of sliding rates of many known DNA-binding proteins (29). We investigated all combinations of K and k1 resulting in 35 different conditions (Figure 4).

Figure 4.

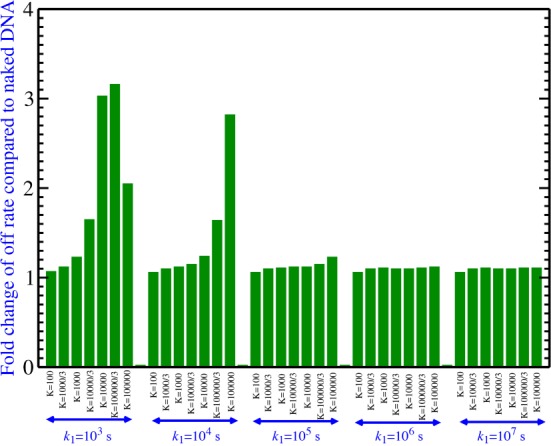
Figure 4.

Open in a new tab

The overall off rate of LexA dissociation from a nucleosome compared to naked DNA for the non-specific binding model. The overall off rate of LexA in the presence of a nucleosome for 35 combinations of the unknown parameters K and k1 covering the entire range of biologically plausible values is calculated and presented as a fold change compared to the naked DNA case.

For each value of K and k1 there is only one unspecified parameter (ks,off or kns,off, which are connected via kns,off = K * ks,off) that we fit by requiring that the largest non-zero eigenvalue of the rate matrix reproduce the experimentally measured overall LexA off rate from naked DNA of 0.0034 s−1.

These fitting parameters are then used to calculate the overall off-rate of LexA in the presence of a nucleosome for every combination of K and k1 explored. In the presence of a nucleosome (Figure 3B), LexA can (i) slide along both directions in the unwrapped nucleosome; or (ii) dissociate from or reassociate to the unwrapped nucleosome. In the meantime, the nucleosome can unwrap and rewrap and this can affect LexA binding and dissociation. Similar to the dimeric model we can calculate the base-by-base nucleosome rewrapping and unwrapping rates (Materials and Methods), which then specifies the rate matrix. Similar to the dimeric model only the state in which LexA dissociates from the nucleosome and the nucleosome is fully wrapped is considered as the ‘off’ state (high FRET state in the experiment).

Due to the unknown bulk size of the proteins, we further define a parameter d that is the minimum distance (in bp) between LexA and the unwrapping position of the nucleosome. At this minimum distance when LexA binds to DNA, the nucleosome cannot rewrap anymore and the LexA protein can only slide in one direction (Figure 3C). This parameter affects the off-rate of the TF because it determines which particular point in the nucleosome free energy landscape corresponds to the sliding of the TF onto and off of its specific binding site; since the nucleosome free energy landscape is not simply a straight line of constant slope (8), this position determines the unwrapping rate associated with the specific binding site and thus directly influences the dynamics of the system. For each K and k1, we tested d = 0, 1, …, 21 and picked the d with the largest off-rate among all 22 largest non-zero eigenvalues in order to obtain an upper bound for the increase of the overall off-rate in the presence of a nucleosome compared to the naked DNA. We found that in all the K and k1 we tested, we always got the largest off-rate when d = 7 (i.e. when the minimum distance between LexA and the unwrapping position of the nucleosome is 7 bp) (Supplementary Table S1). Similarly, we varied [LexA] and found the largest off-rates at [LexA] = 0 nM (Supplementary Table S2, note that we started with the state in which one LexA molecule is fully bound to the DNA even in the absence of LexA in solution). Nevertheless, in spite of choosing the maximizing values of d and [LexA], the off-rates for none of the reasonable choices of K and k1 differ significantly from the overall off-rate of LexA from naked DNA (0.0034 s−1) (Figure 4 and Supplementary Table S3).

In order to investigate the sensitivity of our finding on the specifics of the nucleosome unwrapping free energy landscape, we also tested the effect of changing the position of the LexA binding site from positions 8–27 within the 601 nucleosome positioning sequence (used in the experiment of Luo et al. (12)) to 1–20 and 18–37. However, even then we found increases in the overall off-rate of LexA by at most one order of magnitude compared to naked DNA (Supplementary Table S4).

Based on these results, we conclude that the non-specific binding model cannot explain the large increase of the overall off rate of LexA in the presence of a nucleosome compared to naked DNA as observed in the experiment (12). It might be true that LexA does not slide on DNA (29) as there is no such experimental evidence; however, even if it slides on DNA, it is not the sliding that can explain the large increase of its off-rate from a nucleosome compared to the naked DNA based on the non-specific model.

Predictions for future experiments

In addition to explaining the experimental results of Luo et al. (12), we can now use our dimeric binding model to make predictions that can be tested in future experiments.

First, we investigate the consequences of mutating away half of the LexA binding site, just as done for naked DNA in (13). This includes two cases: (i) mutating the half site near the nucleosome dyad; (ii) mutating the half site far from the nucleosome dyad. We model both cases following the dimeric binding model and using the same parameters choosing ΔΔG = 6 kBT. Here, the LexA fully bound state no longer exists and the seven states reduce to three as indicated for each case in Supplementary Figure S1. We find that in both cases the overall off-rate of LexA dissociation from the nucleosome is approximately equal to k3 (∼1.7 s−1). Unlike the non-mutated case, it is not sensitive to the free energy differences between the fully and partially unwrapped state of the nucleosome. While this value (∼1.7 s−1) is a 500-fold increase compared to the overall off-rate of LexA from naked DNA without a mutation and a 5-fold increase compared to the overall off rate of LexA from a nucleosome predicted from the dimeric binding model, it is indeed the same as the off rate k3 from naked DNA with one half site mutated. This indicates that the overall off-rate of LexA in the presence of the nucleosome should not be changed compared to naked DNA when half of its target is mutated—a result that also applies to a TF that binds as a monomer.

Furthermore, since many TFs bind close to the entry–exit region, we investigated the case when half of the LexA binding site is located outside of the nucleosome positioning sequence (from −10 to −1) such that the nucleosome cannot unwrap or rewrap in this region, while the other half is within the nucleosome positioning sequence (from 1 to 10) (Supplementary Figure S2). Similarly, we model this process with the dimeric binding model using the same parameters but changing nucleosome unwrapping and rewrapping states and rates based on (8). We find that the overall off-rate of LexA dissociation from the nucleosome is ∼1.45 s−1, a 400-fold increase compared to the overall off-rate of LexA from naked DNA and a 4-fold increase compared to the overall off-rate of LexA from within the nucleosome at the same parameters.

DISCUSSION

In this work, we quantitatively modeled the process of transcription factor dissociation from a nucleosome by investigating two possible mechanisms that could explain a recent single-molecule study. In the study of Luo et al. (12), they reported that the dissociation rates of two transcription factors, LexA and Gal4, from a target site within the nucleosome entry–exit region are enhanced by two to three orders of magnitude relative to naked DNA. We choose LexA as a model because some of the experimental data required for our modeling are not available for Gal4. However, the results should be very similar for Gal4 as the two TFs share similar properties, such as that both of them bind long and specific DNA binding sites (the LexA binding site is 16 bp long (18) while the Gal4 binding site is 17 bp long (21)) as homodimers. Since a large number of eukaryotic TFs can bind to their target sites in a dimeric form (in human, at least one quarter of the TFs bind to their target sites as dimers—the best studied TFs that can form dimers alone number at least 500 (30), while the upper bound on the number of TF-coding genes is 1700–1900 (31)), our dimeric binding model is applicable to a wide range of eukaryotic TFs and not just the two specific ones used in the experiments by Luo et al. (12).

We first modeled the case that LexA dissociates from naked DNA (without a nucleosome). We fit these models to experimental data to determine the kinetic parameters of transcription factor-DNA interaction. We then incorporated nucleosome free energy landscape data from (8) to calculate the LexA off-rate in the presence of a nucleosome. This calculated off-rate was then compared with the experimental values (12). Our results indicate that the non-specific binding mechanism cannot be reconciled with experimental findings but that the dimeric binding model can indeed explain increases in off-rate by a factor as high as 200. Finally, based on the dimeric binding model we made further predictions of other cases that are experimentally testable in the future, most specifically that the significant acceleration of dissociation should not occur if the half site is mutated away or for transcription factors that bind as monomers. Another interesting consequence of our calculations is that the off-rates of monomeric TFs should not show the dramatic increase observed for dimeric TFs, since monomeric TFs would be described by the non-specific binding model. It would be interesting to see this prediction tested in future experiments as well.

It is important to point out that the 601 nucleosome positioning sequence, which was used in the experiment and in the determination of the free energy landscape (8) on which our calculations are based, has an unusually high binding affinity to the histone much stronger than what occurs in vivo. Thus, the question arises if our calculations (and the experimental results they explain) are specific to the 601 sequence. In fact, since it is not known precisely which bases unwrap due to the binding of the TF, our calculations of the dimeric model never refer to specific positions in the free energy landscape, but employ the free energy landscape solely to determine reasonable values of the only relevant free energy difference ΔΔG (see Figure 2). The differences in overall free energy between the 601 nucleosome positioning sequence and other less stable positioning sequences found in vivo, e.g. the 5S positioning sequence, are several kBT compared to an overall free energy of 30–40 kBT (8). Thus, for these less stable nucleosome positioning sequences the overall slope of the free energy landscape will be smaller than the one for the 601 sequence but not significantly smaller. This implies that, while the ΔΔG for these other sequence may not reach to the upper bound of the range for the 601 sequence (∼6–7 kBT), the lower end of the range (∼5–6 kBT), which based on our calculations still yields a 50-fold increase in off-rate, is a reasonable assumption for these less stable nucleosome positioning sequences. Thus, our calculations and the experimental findings should still be applicable to weaker nucleosome positioning sequences found in vivo albeit with a somewhat reduced effect.

We note that although the dimeric binding model explains a large increase in the overall off-rate of LexA dissociation from a nucleosome compared to naked DNA, it still misses another 5- to 10-fold increase compared to the 1000-fold increase of the off-rate in the experimental data. This might indicate the presence of some direct steric or electrostatic force that the nucleosome exerts on LexA. Since direct nucleosome-TF interactions will be diminished if the TF is facing away from the histone, the importance of such direct interactions could in principle be tested by repeating the experiments with an outward facing TF, i.e. by moving the TF binding site 5 to 6 bp in either direction from the site in (12); however, such data are not currently available. One recent theoretical study (32) shows that nucleosomes can exert force on RNA polymerase and that this force can slow the polymerase transcribing down by about 10-fold. Another recent experimental study indicates that a neighboring nucleosome can affect the off-rate of a transcription factor from its binding site by ∼7-fold presumably through mechanical interactions (33). While this provides evidence that nucleosomes can indeed affect TF dissociation, the factor is far away from the 1000-fold changes in off-rate as observed in Luo et al. (12). However, these findings might give some explanation of the 5- to 10-fold increase in off-rate that our dimeric binding model is missing. In order to investigate this further, the effect of a largely tangential force on TF unbinding would have to be understood in more detail. Overall, our results suggest a general mechanism how transcription factors dissociate from nucleosomes to promote exchange of transcription factors and regulate gene expression.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

SUPPLEMENTARY DATA
supp_42_15_9753__index.html (976B, html)

Acknowledgments

We very gratefully acknowledge Dr. Michael Poirier for providing experimental data and numerous insightful discussions of this work and useful feedback for the manuscript.

FUNDING

National Science Foundation [DMR-01105458 to R.B.]. Source of open access funding: National Science Foundation [DMR-01105458].

Conflict of interest statement. None declared.

REFERENCES

  • 1.Luger K., Mader A.W., Richmond R.K., Sargent D.F., Richmond T.J. Crystal structure of the nucleosome core particle at 2.8 A resolution. Nature. 1997;389:251–260. doi: 10.1038/38444. [DOI] [PubMed] [Google Scholar]
  • 2.Harbison C.T., Gordon D.B., Lee T.I., Rinaldi N.J., Macisaac K.D., Danford T.W., Hannett N.M., Tagne J.B., Reynolds D.B., Yoo J., et al. Transcriptional regulatory code of a eukaryotic genome. Nature. 2004;431:99–104. doi: 10.1038/nature02800. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Jiang C., Pugh B.F. A compiled and systematic reference map of nucleosome positions across the Saccharomyces cerevisiae genome. Genome Biol. 2009;10:R109. doi: 10.1186/gb-2009-10-10-r109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Venters B.J., Pugh B.F. How eukaryotic genes are transcribed. Crit. Rev. Biochem. Mol. Biol. 2009;44:117–141. doi: 10.1080/10409230902858785. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Polach K.J., Widom J. Mechanism of protein access to specific DNA sequences in chromatin: a dynamic equilibrium model for gene regulation. J. Mol. Biol. 1995;254:130–149. doi: 10.1006/jmbi.1995.0606. [DOI] [PubMed] [Google Scholar]
  • 6.Li G., Widom J. Nucleosomes facilitate their own invasion. Nat. Struct. Mol. Biol. 2004;11:763–769. doi: 10.1038/nsmb801. [DOI] [PubMed] [Google Scholar]
  • 7.Simon M., North J.A., Shimko J.C., Forties R.A., Ferdinand M.B., Manohar M., Zhang M., Fishel R., Ottesen J.J., Poirier M.G. Histone fold modifications control nucleosome unwrapping and disassembly. Proc. Natl. Acad. Sci. U.S.A. 2011;108:12711–12716. doi: 10.1073/pnas.1106264108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Forties R.A., North J.A., Javaid S., Tabbaa O.P., Fishel R., Poirier M.G., Bundschuh R. A quantitative model of nucleosome dynamics. Nucleic Acids Res. 2011;39:8306–8313. doi: 10.1093/nar/gkr422. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Latchman D.S. Transcription factors: an overview. Int. J. Biochem. Cell Biol. 1997;29:1305–1312. doi: 10.1016/s1357-2725(97)00085-x. [DOI] [PubMed] [Google Scholar]
  • 10.North J.A., Shimko J.C., Javaid S., Mooney A.M., Shoffner M.A., Rose S.D., Bundschuh R., Fishel R., Ottesen J.J., Poirier M.G. Regulation of the nucleosome unwrapping rate controls DNA accessibility. Nucleic Acids Res. 2012;40:10215–10227. doi: 10.1093/nar/gks747. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Li G., Levitus M., Bustamante C., Widom J. Rapid spontaneous accessibility of nucleosomal DNA. Nat. Struct. Mol. Biol. 2005;12:46–53. doi: 10.1038/nsmb869. [DOI] [PubMed] [Google Scholar]
  • 12.Luo Y., North J.A., Rose S.D., Poirier M.G. Nucleosomes accelerate transcription factor dissociation. Nucleic Acids Res. 2014;42:3017–3027. doi: 10.1093/nar/gkt1319. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Kim B., Little J.W. Dimerization of a specific DNA-binding protein on the DNA. Science. 1992;255:203–206. doi: 10.1126/science.1553548. [DOI] [PubMed] [Google Scholar]
  • 14.Liang S.D., Marmorstein R., Harrison S.C., Ptashne M. DNA sequence preferences of GAL4 and PPR1: how a subset of Zn2 Cys6 binuclear cluster proteins recognizes DNA. Mol. Cell. Biol. 1996;16:3773–3780. doi: 10.1128/mcb.16.7.3773. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Sing C.E., Olvera de la Cruz M., Marko J.F. Multiple-binding-site mechanism explains concentration-dependent unbinding rates of DNA-binding proteins. Nucleic Acids Res. 2014;42:3783–3791. doi: 10.1093/nar/gkt1327. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Berberansantos M.N., Martinho J.M.G. The integration of kinetic rate-equations by matrix-methods. J. Chem. Educ. 1990;67:375–379. [Google Scholar]
  • 17.Lewis L.K., Harlow G.R., Gregg-Jolly L.A., Mount D.W. Identification of high affinity binding sites for LexA which define new DNA damage-inducible genes in Escherichia coli. J. Mol. Biol. 1994;241:507–523. doi: 10.1006/jmbi.1994.1528. [DOI] [PubMed] [Google Scholar]
  • 18.Butala M., Zgur-Bertok D., Busby S.J. The bacterial LexA transcriptional repressor. Cell. Mol. Life Sci. 2009;66:82–93. doi: 10.1007/s00018-008-8378-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Mohana-Borges R., Pacheco A.B., Sousa F.J., Foguel D., Almeida D.F., Silva J.L. LexA repressor forms stable dimers in solution. The role of specific dna in tightening protein-protein interactions. J. Biol. Chem. 2000;275:4708–4712. doi: 10.1074/jbc.275.7.4708. [DOI] [PubMed] [Google Scholar]
  • 20.Carey M., Kakidani H., Leatherwood J., Mostashari F., Ptashne M. An amino-terminal fragment of GAL4 binds DNA as a dimer. J. Mol. Biol. 1989;209:423–432. doi: 10.1016/0022-2836(89)90007-7. [DOI] [PubMed] [Google Scholar]
  • 21.Marmorstein R., Carey M., Ptashne M., Harrison S.C. DNA recognition by GAL4: structure of a protein-DNA complex. Nature. 1992;356:408–414. doi: 10.1038/356408a0. [DOI] [PubMed] [Google Scholar]
  • 22.Eaton J.W., Bateman D., Hauberg S. GNU Octave version 3.0.1 manual : a high-level interactive language for numerical computations. Charleston: SoHo Books; 2010. Edition 3 for Octave 3.0.1. ed. [Google Scholar]
  • 23.Berg O.G., Winter R.B., von Hippel P.H. Diffusion-driven mechanisms of protein translocation on nucleic acids. 1. Models and theory. Biochemistry. 1981;20:6929–6948. doi: 10.1021/bi00527a028. [DOI] [PubMed] [Google Scholar]
  • 24.Winter R.B., von Hippel P.H. Diffusion-driven mechanisms of protein translocation on nucleic acids. 2. The Escherichia coli repressor–operator interaction: equilibrium measurements. Biochemistry. 1981;20:6948–6960. doi: 10.1021/bi00527a029. [DOI] [PubMed] [Google Scholar]
  • 25.Winter R.B., Berg O.G., von Hippel P.H. Diffusion-driven mechanisms of protein translocation on nucleic acids. 3. The Escherichia coli lac repressor–operator interaction: kinetic measurements and conclusions. Biochemistry. 1981;20:6961–6977. doi: 10.1021/bi00527a030. [DOI] [PubMed] [Google Scholar]
  • 26.Slutsky M., Mirny L.A. Kinetics of protein-DNA interaction: facilitated target location in sequence-dependent potential. Biophys. J. 2004;87:4021–4035. doi: 10.1529/biophysj.104.050765. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Halford S.E., Marko J.F. How do site-specific DNA-binding proteins find their targets? Nucleic Acids Res. 2004;32:3040–3052. doi: 10.1093/nar/gkh624. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Poirier M.G., Oh E., Tims H.S., Widom J. Dynamics and function of compact nucleosome arrays. Nat. Struct. Mol. Biol. 2009;16:938–944. doi: 10.1038/nsmb.1650. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Barsky D., Laurence T.A., Venclovas C. How Proteins Slide on DNA. In: Williams M.C., Maher L.J., editors. Biophysics of DNA-Protein Interactions from Single Molecules to Biological Systems. New York: Springer; 2011. pp. 39–68. [Google Scholar]
  • 30.Amoutzias G.D., Robertson D.L., Van de Peer Y., Oliver S.G. Choose your partners: dimerization in eukaryotic transcription factors. Trends Biochem. Sci. 2008;33:220–229. doi: 10.1016/j.tibs.2008.02.002. [DOI] [PubMed] [Google Scholar]
  • 31.Vaquerizas J.M., Kummerfeld S.K., Teichmann S.A., Luscombe N.M. A census of human transcription factors: function, expression and evolution. Nat. Rev. Genet. 2009;10:252–263. doi: 10.1038/nrg2538. [DOI] [PubMed] [Google Scholar]
  • 32.Koslover E.F., Spakowitz A.J. Force fluctuations impact kinetics of biomolecular systems. Phys. Rev. E, Stat. Nonlinear Soft Matter Phys. 2012;86:011906. doi: 10.1103/PhysRevE.86.011906. [DOI] [PubMed] [Google Scholar]
  • 33.Kim S., Brostromer E., Xing D., Jin J., Chong S., Ge H., Wang S., Gu C., Yang L., Gao Y.Q., et al. Probing allostery through DNA. Science. 2013;339:816–819. doi: 10.1126/science.1229223. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

SUPPLEMENTARY DATA
supp_42_15_9753__index.html (976B, html)
supp_gku719_nar-00618-z-2014-File006.pdf (1.1MB, pdf)

Articles from Nucleic Acids Research are provided here courtesy of Oxford University Press

RESOURCES