Abstract
All numerate humans have access to two systems of number representation: an exact system that is argued to be based on language and that supports formal mathematics, and an Approximate Number System (ANS) that is present at birth and appears independent of language. Here we examine the interaction between these two systems by comparing the profiles of people with Williams Syndrome (WS) with those of typically developing children between ages 4 and 9 years. WS is a rare genetic deficit marked by fluent and well-structured language together with severe spatial deficits, deficits in formal math, and abnormalities of the parietal cortex, which is thought to subserve the ANS. One of our tasks, requiring approximate number comparison but no number words, revealed that the ANS precision of adolescents with WS was in the range of typically developing 2- to 4-year-olds. Their precision improved with age but never reached the level of typically developing 6- or 9-year-olds. The second task, requiring verbal number estimation using number words, revealed that the estimates produced by adolescents with WS were comparable to those of typically developing 6- and 9-year-olds, i.e., were more advanced than their ANS precision. These results suggest that ANS precision is somewhat separable from the mapping between approximate numerosities and number words, as the former can be severely damaged in a genetic disorder without commensurate impairment in the latter.
Keywords: Approximate Number System (ANS), Williams syndrome, non-symbolic number comparison, verbal number estimation
Introduction
Educated humans have access to two different types of numerical representation: an exact representation that is argued to be based on language and that enables us to perform formal mathematics, and an approximate representation that is present in many other species and in human neonates and therefore must begin independent of language (Feigenson, Dehaene, & Spelke, 2004; Izard, Sann, Spelke, & Streri, 2009). The exact system of number is thought to rely on left-lateralized areas of the temporal cortex, including the left angular gyrus (Ansari, 2008; Dehaene, Molko, Cohen, & Wilson, 2004), that are also implicated in other language-mediated processes such as reading and verbal short-term memory (Fiez & Petersen, 1998; Paulesu, Frith, & Frackowiak, 1993; Price, 1998). Most children acquire these exact number representations slowly over the course of the preschool years, and evidence suggests that learning number words (i.e., the memorized count sequence) may play an important role in this process (Carey, 2009; Wynn, 1992). In contrast, approximate numerical representations are thought to rely on the Approximate Number System (ANS), which produces rapid numerical estimates independently of language or sensory modality, and which supports basic comparison and arithmetic operations over these approximate representations (Barth, La Mont, Lipton, & Spelke, 2005; Gilmore, McCarthy, & Spelke, 2007; McCrink & Spelke, 2010; McCrink & Wynn, 2004). The ANS is thought to activate the horizontal segment of the intraparietal sulcus and adjacent areas of parietal cortex (Ansari, 2008; Dehaene et al., 2004), which are also implicated in spatial attention and the processing of spatial relationships (Hubbard, Piazza, Pinel, & Dehaene, 2005).
Although this developmental and neural separation suggests a certain degree of independence between the exact and the approximate number systems, several lines of research provide evidence for a link between the two. Studies in adults reveal greater activation of the left angular gyrus for trained (i.e., well-learned) multiplication problems and greater activation of the intraparietal sulcus for untrained multiplication problems (Delazer et al., 2003; Ischebeck, Zamarian, Egger, Schocke, & Delazer, 2007; Ischebeck et al., 2006), suggesting that as numerical computations become more well-learned, they come to rely less on approximate representations and more on verbally-mediated ones. In addition, recent evidence suggests that the precision of individuals’ ANS is associated with math abilities throughout the lifespan (Feigenson, Libertus, & Halberda, 2013; Halberda, Ly, Willmer, Naiman, & Germine, 2012; Halberda, Mazzocco, & Feigenson, 2008; Libertus, Feigenson, & Halberda, 2011; Libertus, Odic, & Halberda, 2012) (cf., Inglis, Attridge, Batchelor, & Gilmore, 2011; Price, Palmer, Battista, & Ansari, 2012) and that ANS precision in infants and children between 3 and 5 years of age predicts later math ability (Libertus, Feigenson, & Halberda, 2013; Mazzocco, Feigenson, & Halberda, 2011b; Starr, Libertus, & Brannon, in press).
Furthermore, ANS representations must be linked to exact number words because such a mapping is required in order to communicate about approximate number. Imagine a viewer seeing an array of 20 dots and generating an ANS representation of ABOUT-20. For the viewer to convey this experience to others, the representation of ABOUT-20 (thought to be a noisy distribution of activity on a mental number line, with a peak at the mental representation of 20) must be mapped to an exact verbal (“twenty”) or written (“20”) number symbol.
The creation of a mapping between noisy ANS representations to number symbols unfolds over the preschool and early school years in typically developing numerate children (Le Corre & Carey, 2007; Lipton & Spelke, 2005; Mundy & Gilmore, 2009; Wagner & Johnson, 2011). However, the nature of this mapping is not well understood. As others have pointed out (Carey, 2009), mapping between these two systems seems trivial when both sets of representations are mature and typically developed. For example, adults learning a second language can easily acquire a link between a new number word in their second language and their approximate number representations. For an adult learner of French, the ability to say “cinquante” upon seeing an array of e.g., 47 dots would be expected to emerge quickly once “cinquante” has been added to the lexicon.
However, additional insight about the mapping between ANS representations and number words may be gained by asking what happens when one of the two mapping components is underdeveloped or impaired. Preschool-aged children offer a case in which approximate number representations are typically developing, but in which language skills are still emerging. By the time they are 3 to 5 years old, children have ANS representations that are precise enough to support discriminations of quantities differing by a 3:4 or 4:5 ratio (Halberda & Feigenson, 2008). Around this same time, they learn the ordered list of number words in their language. Some evidence suggests that it is not until well after children know the exact meanings of these number words that they also learn the words’ approximate meaning—i.e., that they map number words to ANS representations (Le Corre & Carey, 2007). Although other findings contend that children do acquire the mapping before learning number words’ exact meanings (Wagner & Johnson, 2011), there is general agreement that the mapping is not observed until late in the preschool years. However, it remains unclear why children take so long to map between the two types of representations. One possible explanation is that children’s ANS representations are still too noisy to be reliably mapped to particular number words, although currently there is no evidence directly supporting this explanation.
In the present work, we sought to gain more purchase on the mapping between number words and the ANS by examining two different groups of individuals. We examined typically developing preschool-aged children (who have intact ANS representations, but are still becoming proficient language users) and individuals with Williams syndrome (WS) (who are thought to have impaired ANS representations, but whose language system is relatively strong). Williams syndrome (WS) is a genetic deficit that presents with clear impairments in spatial and numerical abilities but significant strength in language. Comparing these two groups can allow us to assess the contributions of children’s ANS precision, versus their knowledge of the numerical content of number words, in determining the proficiency of mapping between these two representations. That is, we can ask whether individuals with WS exhibit an ANS-number word mapping that is constrained by their ANS precision (which we hypothesize to be deficient), or whether their proficient language abilities support a typical mapping.
WS is a relatively rare genetic disorder occurring in 1 out of 7500 births, caused by a sub-microscopic deletion of about 25 genes on chromosome 7q11.23 (Stromme, Bjornstad, & Ramstad, 2002). Over 20 years of research have verified that the WS cognitive profile includes severe impairments in a range of spatial abilities including visual-spatial construction tasks (Mervis, Morris, Bertrand, & Robinson, 1999), mental imagery and mental rotation (Farran, Jarrold, & Gathercole, 2001; Stinton, Farran, & Courbois, 2008), some aspects of navigation (Farran, Blades, Boucher, & Tranter, 2010; Farran, Courbois, Van Herwegen, & Blades, 2012; Lakusta, Dessalegn, & Landau, 2010; Nardini, Atkinson, Braddick, & Burgess, 2008), recognition of objects from unusual viewpoints (Landau, Hoffman, & Kurz, 2006), and somatosensory localization (Yoshioka, Dillon, Beck, Rapp, & Landau, 2013). Moreover, there is evidence for brain abnormalities in areas of the intraparietal sulcus (IPS) and hippocampus (Meyer-Lindenberg et al., 2004; Meyer-Lindenberg, Mervis, & Berman, 2006), which are known to support a range of spatial-cognitive functions as well as non-verbal numerical processing (Hubbard et al., 2005).
The profile of WS performance in the domain of number is complex (O’Hearn & Luna, 2009). First, several sources of evidence suggest that WS involves impairment to mathematical competence. Adults with WS have been described as having persistent difficulty with mathematics (Udwin, Davies, & Howlin, 1996), performing at the level of typical 6- to 8-year-olds on a standardized test of math abilities (the Test of Early Mathematics Ability: TEMA-2; Ginsburg & Baroody, 1990; O’Hearn & Landau, 2007). Less complex math abilities also appear to be impaired: Ansari and colleagues (2003) assessed the counting abilities of children with WS, specifically asking whether these children observed the cardinality principle (i.e., that the last number in the count sequence denotes the number of items in the set). Seven-year old children with WS were on par with typically developing 3- to 4-year-old children who were matched on their visual-spatial abilities.
A more specific claim about the nature of numerical impairment in WS has come from reports suggesting that people with WS show relative strength in number tasks that rely on language, and relative weakness in tasks that tap magnitude representation and do not rely on language. For example, Krajcsi and colleagues (2009) found that children with WS had longer reaction times than typically developing 2nd, 3rd, and 10th graders when comparing which of two Arabic numerals represented the greater quantity, but not when retrieving addition and multiplication facts. Krajcsi and colleagues posited that the relative weakness of children with WS in the comparison task points to an impaired ANS system, whereas their relative strength in retrieving number facts points to language boosting verbally mediated number skills. Consistent with this, O’Hearn and Landau (2007) found that adolescents with WS who were tested on the TEMA-2 performed relatively poorly on items that likely engaged the mental number line – for example, judging which of two numbers was closer to a third (cf., Ansari et al., 2003; Paterson, Girelli, Butterworth, & Karmiloff-Smith, 2006) – but performed on par with mental age-matched children on verbally mediated items involving counting, reading, and writing Arabic numerals.
More direct evidence for deficient ANS representations in individuals with WS comes from Paterson and colleagues (2006), who tested children and adults with WS on an approximate number comparison task using sets of dots with fewer than ten dots per set. They found that people with WS did not exhibit the usual pattern of faster responding to sets that were numerically further apart than sets that were numerically closer in value. And in a recent study by Rousselle, Dembour, and Noel (2013) children and adults with WS were found to have significantly lower ANS precision compared to verbally matched controls. Furthermore, Ansari and colleagues (2007) asked 9-year-old children and adults with WS to estimate the number of dots presented in groups of 5, 7, 9, and 11. They found that the “mean approximate accuracy” (i.e., being accurate within +/− 1 items) of participants with WS between ages 9 years and adulthood did not exceed the developmental improvements observed between ages 4–5 years and 6–7 years in typically developing children. van Herwegen and colleagues (2008) found that children with WS between 15 and 58 months failed to discriminate 8 dots from 16, an ability demonstrated by typically developing infants by 6 months of age (Xu & Spelke, 2000). Finally, Opfer and Martens (2012) found that the ability of adults with WS to place an Arabic numeral in its appropriate position on a written number line was atypical for their chronological age; their performance did not show the shift from logarithmic to linear organization that is typically seen during the elementary school years.
This apparent impairment to approximate number in WS, coupled with the relative sparing of language, provides us with an opportunity to better understand the mapping between ANS representations and exact, linguistically-mediated number representations. Here we assessed ANS representations and their mapping to number words in two samples of adolescents and adults with WS, and in several samples of typically developing children. Critically (and differently from previous investigations), we used tightly matched tasks to measure both the precision of the ANS representations themselves, and the accuracy of the mapping of these representations to number words. That is, we used a Numerical Comparison task in which participants simply indicated which of two dot collections was more numerous, and a Verbal Estimation task in which participants verbally estimated the number of dots in one of two dot collections.
We had three goals: First, we sought to confirm that individuals with WS have decreased ANS precision. As most previous studies have measured numerical approximation in WS using tasks requiring the use of number words (Ansari et al., 2007; O’Hearn & Landau, 2007), it is important to assess abilities using a task in which no number words are needed. Second, for both individuals with WS and typically developing children, we sought to compare the precision of their ANS representations to the accuracy of their mapping of these representations to number words. If having poor (i.e., less precise) ANS representations limits the successful creation of a mapping between the ANS and exact number words, then we expect to observe that participants with WS have both poor ANS representations and a poor mapping between these representations and the number words. An alternative hypothesis is that the mapping between ANS representations and number words emerges from an understanding of the numerical content of the exact number words themselves.. In this case, we may find that individuals with WS have poor ANS precision, but a normal mapping between ANS representations and the number words.
Experiment 1
Methods
Participants
Eighteen participants with Williams syndrome (WS; 10 females, mean age = 15 years, 5 months; range 7 to 32 years), thirteen typically developing 4-year-old children (3 females, mean age = 4 years, 6 months), thirteen typically developing 6-year-olds (5 females, mean age = 6 years, 6 months), and twelve typically developing 9-year-olds (7 females, mean age = 9 years, 4 months) participated. Participants with WS were recruited through the Williams Syndrome Association (WSA), and were tested either in the laboratory or in a quiet room at the site of the biennial conference of the WSA. All participants with WS had a positive diagnosis of WS via the fluorescent in situ hybridization (FISH) test, and had an average composite IQ score of 77.92 (SD = 13.21) on the (KBIT-2; Kaufman & Kaufman, 2004), which is within the typical range reported for this population (Mervis & Becerra, 2007; Mervis et al., 1999; Volterra, Capirci, Pezzini, Sabbadini, & Vicari, 1996). All typically developing children were recruited via local schools and were tested in the laboratory. Adult participants and parents of all children tested provided informed written consent prior to their participation. Three participants with WS and one typically developing 4-year-old were unable to complete either task. One 4-year-old was unable to complete the Verbal Estimation task. Data from both tasks for two 6-year-old children and two 9-year-old children were lost due to experimenter error.
Materials
Numerical Comparison task (“Which has more?”)
Participants were told that they would see briefly flashed displays of blue and yellow dots on a computer screen and that they would have to indicate which collection had more dots by saying “blue” or “yellow.” The task required no naming of numerals. The experimenter initiated each trial when the participant appeared to be attentive, and recorded participants’ response by pushing one of two buttons on a keyboard. Two different sounds provided feedback throughout the experiment. A high-pitched tone indicated a correct answer; a low-pitched tone indicated an incorrect answer. Participants were familiarized to these sounds on eight practice trials during which the experimenter provided additional verbal feedback to ensure that the participants understood the task and were motivated to participate.
Each collection contained between 5 and 16 dots. On half of the trials the correct answer was yellow; on the other half the correct answer was blue. On half of the trials the numerically larger collection also was larger in cumulative surface area (area-correlated trials), and on the other half the numerically larger collection was smaller in cumulative surface area (area anti-correlated trials). The spatial arrangement of the dots and their sizes varied in each array (average radius = 32 pixels, SD = 7 pixels). Each stimulus array was presented for 1000 milliseconds. Three different numerical ratios were presented: 1.33, 1.67, and 2.4, with 32 trials for each ratio (96 trials in total). In half of the trials for each ratio, the blue and yellow dot collections were spatially intermixed at the center of the screen; in the other half, the two collections were separated on either side of the screen. Spatially intermixed and separated trials were blocked, with block order counterbalanced between participants.
Verbal Estimation task (“How many?”)
Participants were told that they would see briefly flashed displays of dots on a computer screen and that they had to say how many yellow dots they saw. Thus this task required participants to produce a number word on each trial. No feedback about the correctness of the answers was provided. Displays were identical to the Numerical Estimation Task in that each stimulus array contained between 5 and 16 yellow and blue dots each and was presented for 1000 ms. Again, on half of the trials blue and yellow dot collections were spatially intermixed at the center of the screen; on the other half, the two collections were separated on either side of the screen. Half of the trials were area-correlated and half were area anti-correlated. Spatially intermixed and separated trials were blocked, with block order counterbalanced between participants. Participants received 4 practice trials and 48 test trials.
Procedure
Order of the Numerical Comparison and the Verbal Estimation task was counterbalanced between participants. Participants received monetary compensation or a small toy after they completed the tasks.
Results
Numerical Comparison task (“Which has more?”)
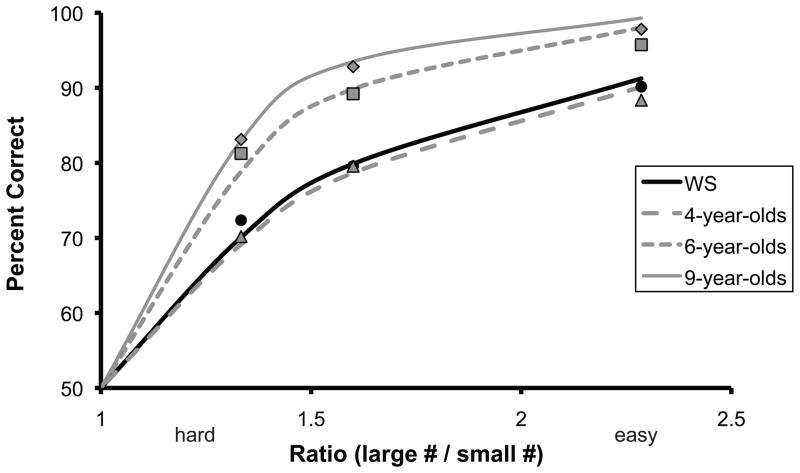
Participants’ accuracy decreased as the numerical ratio between the blue and yellow dots approached equality, (i.e., as the ratio approached 1), in a manner that was consistent with Weber’s law. As can be seen in Figure 1, individuals with WS performed more similarly to typically developing (TD) 4-year-olds than to 6- or 9-year-olds. We explored these group differences with ANOVA and planned t-tests.
Figure 1.
Experiment 1: Accuracy (percent correct) on the Numerical Comparison task is plotted as a function of the ratio between numerical values for participants with Williams syndrome (WS, circles), as well as typically developing 4-year-olds (triangles), 6-year-olds (squares), and 9-year-olds (diamonds).
To identify each individual participant’s Weber fraction (w), an estimate of their ANS precision, we fit each participant’s responses across all trials with a commonly used psychophysical model (1) (Green & Swets, 1966; Halberda & Feigenson, 2008; Halberda et al., 2008; Pica, Lemer, Izard, & Dehaene, 2004).
| (1) |
In this model, n1 is the numerosity of the larger set, n2 is the numerosity of the smaller set, and erfc is the complementary error function. The model assumes that the underlying representations are distributed along a continuum of Gaussian random variables. An important implication of this model is that the two different numerosities presented on each trial will often activate similar and overlapping representations. As the ratio of the two quantities becomes increasingly similar (i.e., approach a ratio of 1), their Gaussian representations will tend to overlap more and participants should have greater difficulty determining which collection of dots is more numerous, resulting in decreasing accuracy.
This model has only a single free parameter w, which indexes the amount of imprecision in the underlying Gaussian representations (i.e., the standard deviation of the Gaussian number representations such that SDn = n * w). Larger w values indicate larger standard deviations and thereby poorer discrimination across all ratios and numerosities. The best fitting w value was determined for each participant using the least-squares method. We were unable to obtain w estimates for two participants with WS due to a high degree of variability in their responses. Thus, data from these participants were excluded from the final analyses yielding a final sample size of 13 participants with WS, 12 TD 4-year-olds, 11 TD 6-year-olds, and 10 TD 9-year-olds.
We did not observe any significant differences in w estimates for spatially overlapping versus separated trials (F(1,40) = 0.5, p = .48), nor any significant interaction between this factor and participant group (WS, TD 4-, 6-, or 9-year-olds) (F(3,40) = 0.82, p = .49). Thus, we collapsed across trial types (spatially intermixed versus separated collections) to compute our final w estimates.
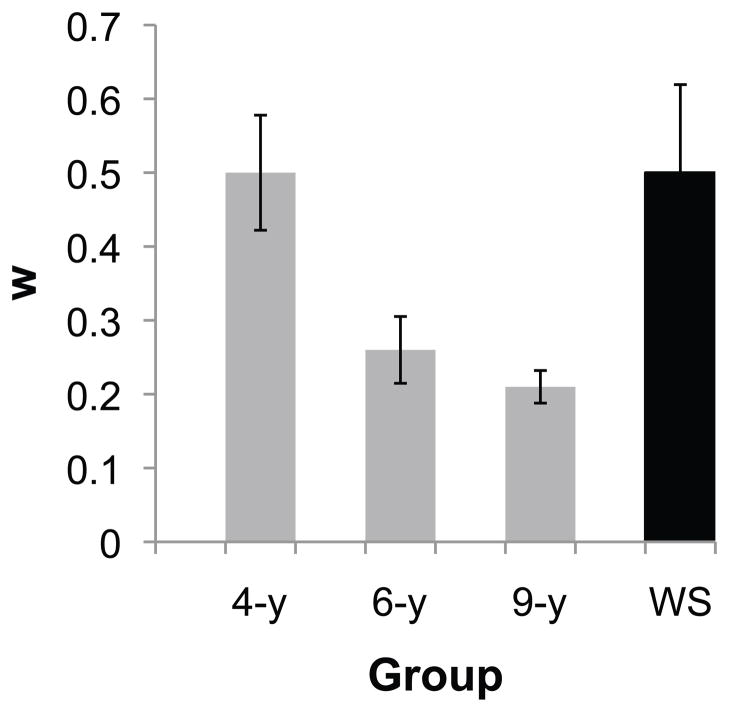
An ANOVA with group as between-subject factor and w estimates as dependent measure revealed a significant main effect of group (F(3,42) = 3.35, p = .03) (Figure 2). Planned pair-wise comparisons (t-tests) revealed significant differences in the w estimates of participants with WS and 6-year-olds (p = .05) and participants with WS and 9-year-olds (p = .02), but not between participants with WS and 4-year-olds (p = .95). For the TD children, we observed significant differences between the w estimates of 4-year-olds and 6-year-olds (p = .05) and 4-year-olds and 9-year-olds (p = .02), but not between 6-year-olds and 9-year-olds (p = .67). These results suggest that the ANS precision of participants with WS was lower than that of TD 6- and 9-year-old children, and was indistinguishable from the level of TD 4-year-olds (Figure 2).
Figure 2.
Average Weber fraction estimate w on the Number Comparison task for 4-year-old (4-y), 6-year-old (6-y), and 9-year-old (9-y) TD children as well as participants with Williams syndrome (WS).
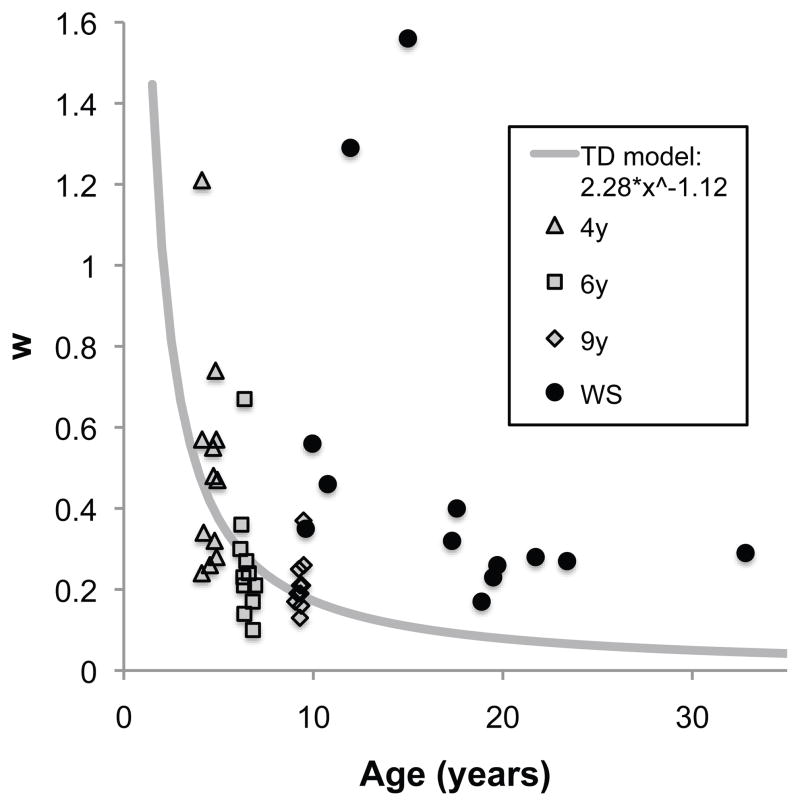
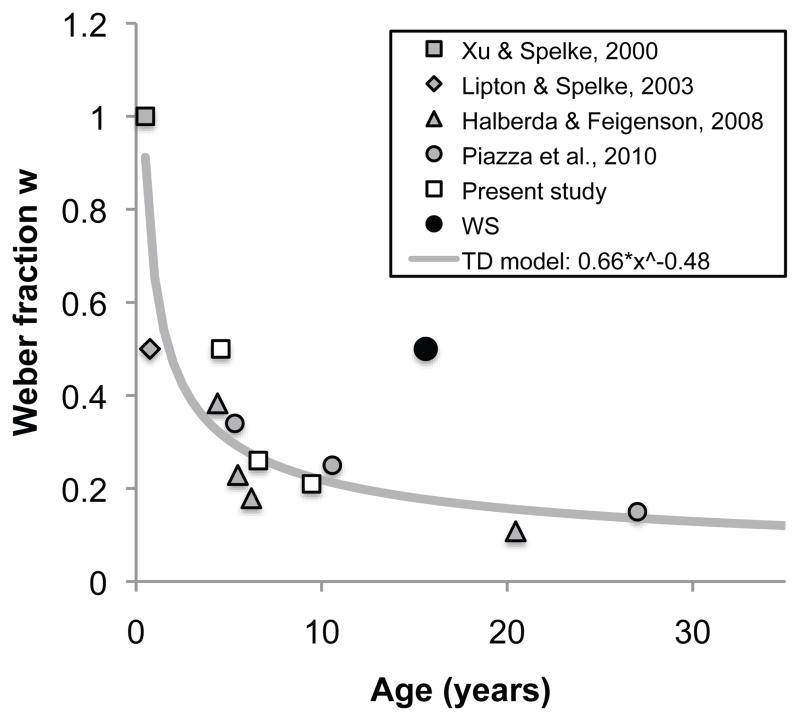
Figure 3 presents a scatterplot in which the Weber fraction (w) of each child is presented as a function of their age at time of testing. Whereas TD 4-year-olds and participants with WS showed high variability across individuals, 6-year-olds and especially 9-year-olds showed decreased variability in performance consistent with developmental improvements in ANS precision (w). Placing these estimates in the context of the literature on ANS precision (w), we found developmental improvements in ANS precision from 4 to 9 years of age, and significantly impaired precision in individuals with WS (Figure 4). Given that our task involved no verbal labels and assessed performance with brief flashes of large numbers of items (cf Ansari et al., 2007), it appears that individuals with WS do indeed have abnormally low ANS precision, i.e., high Weber fractions.
Figure 3.
Typical developmental trajectory of Weber fraction estimate w on the Number Comparison task based on data from typically developing children in Experiment 1. Participants with Williams syndrome (circles) are superimposed on the graph.
Figure 4.
Typical developmental trajectory of Weber fraction estimate w based on the literature and the present study
Verbal Estimation task (“How many”?)
In order to examine the mapping between participants’ ANS representations and their number words, we used a dot estimation task in which participants saw collections of dots that were presented too quickly to count, then provided a verbal estimate of the number of dots in each flash (Ansari et al., 2007; Halberda, Sires, & Feigenson, 2006; Le Corre & Carey, 2007; Whalen, Gallistel, & Gelman, 1999). The accuracy and precision of this mapping between ANS representations and number words can be described by several factors including: the slope and intercept of a linear regression function relating the actual number of dots presented to the participants’ verbal estimates, and the coefficient of variation (CV), or variability, of their numerical responses (Whalen et al., 1999). A perfect mapping between the ANS and the number words would result in a slope of one, an intercept of zero, and a CV that is – theoretically – identical to w (as both CV and w are estimates of the standard deviations of the internal Gaussian approximate number representations).
To calculate these three parameters, we regressed the true number of presented dots onto each participant’s response on a trial-by-trial basis. This generated an estimate of slope and intercept for each participant. We then calculated the difference between each estimate and the regression line and normalized these errors by the predicted value to obtain a normalized error across all numerosities. We have recently demonstrated that the SD of this normalized error is equivalent to CV (see Odic et al., in preparation). Outlier estimates (1.56% of trials) were eliminated using a non-recursive technique described by Van Selst and Jolicoeur (1994). Data from one participant with WS and one 4-year-old were excluded from the final analyses due to linear slope and/or intercept estimates that were more than 3 SDs above or below their respective group means, resulting in a final sample of 14 participants with WS, and 10 TD children in each age group for all analyses involving slope and intercept. Additionally, data from one participant with WS were excluded from the final analyses due to a CV estimate that was more than 3 SD above the mean of the WS group resulting in a final sample of 14 participants with WS, 11 4-year-old TD children, 10 6-year-old TD children, and 10 9-year-old TD children for all analyses involving CV.
Recall that performance on the non-verbal numerical comparison task revealed that individuals with WS have ANS precision (w) on par with TD 4-year-old children. If low levels of precision of the ANS are a limiting factor for creating an accurate mapping between the ANS and the number words, then individuals with WS should be similarly impaired on this Verbal Estimation task (i.e., they should perform similar to 4-year-olds). If, instead, the learning of a mapping between the number words and their meaning emerges from an understanding of the numerical content of the number words, then individuals with WS may perform better than TD 4-year-olds on this Verbal Estimation task (e.g., they should perform similar or superior to 6- or 9-year-olds).
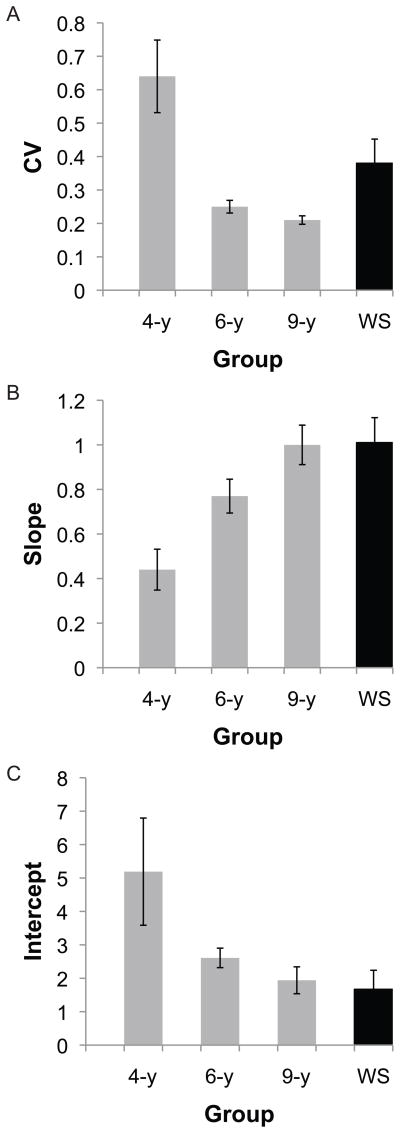
As can be seen in Figure 5, participants with WS performed more similarly to TD 9-year-olds on the Verbal Estimation task. We explored these differences with ANOVAs and planned t-tests for each of the three measures (slope, intercept, and CV).
Figure 5.
Average slope (A), intercept (B), and CV (C) estimates on the Verbal Estimation task for 4-year-old (4-y), 6-year-old (6-y), and 9-year-old (9-y) typically developing children as well as participants with Williams Syndrome (WS).
For linear slope estimates, an ANOVA with group as between-subject factor revealed a significant main effect of group (F(3,39) = 7.36, p = .001) (Figure 5a). Planned pair-wise comparisons revealed significant differences between 4-year-olds and all other groups (all ps < .03), but neither between participants with WS and 9-year-olds (p = .94) nor between 6- and 9-year-olds (p = .12). There was a trend towards a significant difference between participants with WS and TD 6-year-olds (p = .08), with individuals with WS tending to perform better than 6-year-olds.
For intercept estimates, an ANOVA with group as between-subject factor revealed a significant main effect of group (F(3,39) = 3.44, p = .03) (Figure 5b). Planned pair-wise comparisons (t-tests) revealed significant differences between 4-year-olds and all other groups (all ps < .05). There were neither significant differences between participants with WS and 6-year-olds (p = .44) nor between participants with WS and 9-year-olds (p = .82). Finally, there were no significant differences between 6- and 9-year-olds (p = .60).
For CV estimates, an ANOVA with group as between-subject factor revealed a significant main effect of group (F(3,41) = 7.12, p = .001) (Figure 5c). Planned pair-wise comparisons (t-tests) revealed significant differences between 4-year-olds and all other groups (all ps < .01), but neither between participants with WS and 6-year-olds (p = .20), nor between participants with WS and 9-year-olds (p = .10). Typically developing 6- and 9-year-olds also did not differ from each other (p = .71).
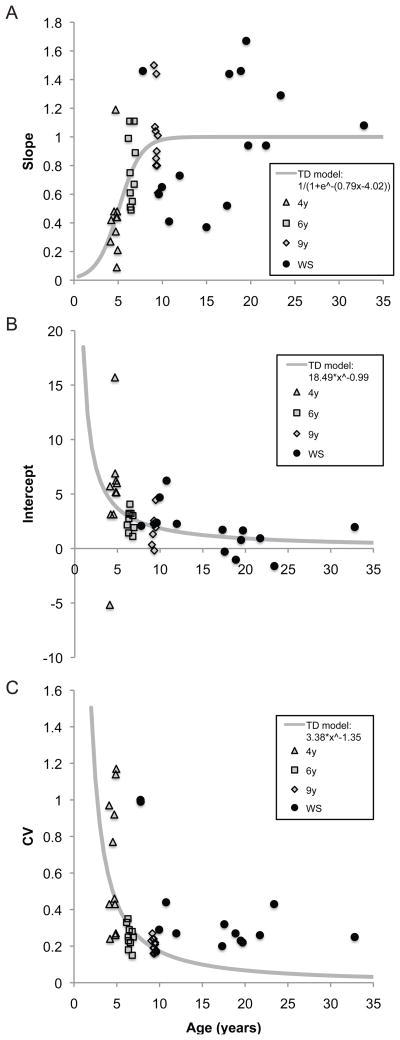
Figure 6 presents scatterplots and developmental trajectories, with each child’s performance depicted as a function of age at the time of testing. Although individuals with WS showed variability in their performance, the estimates of the mapping between their ANS representations and their verbal number words suggests a more fully-formed mapping than that of TD 4-year-olds for slope (Figure 6a), intercept (Figure 6b), and CV (Figure 6c).
Figure 6.
Typical developmental trajectory of slope (A), intercept (B), and CV (C) estimates on the Verbal Estimation task based on data from typically developing children in Experiment 1. Participants with Williams syndrome (circles) are superimposed on the graph.
Discussion
Experiment 1 reveals that people with Williams syndrome (WS) have a significantly decreased ability to rapidly compare the numerosities of two visually presented collections, relative to typically developing children aged 6 years and older. The Approximate Number System (ANS) precision of our group with WS, with a mean age of 15 years, was indistinguishable from the precision of typically developing 4-year-olds in our study, and significantly lower than that of typically developing 6- and 9-year-olds. When compared to the ANS precision of typically developing populations across a wider age range – based on studies in the published literature and the data obtained in the present study – the ANS precision of people with WS in the present study was estimated to be below even the level of typically developing 2-year-olds (Figure 4). It is important to note that individuals with WS do appear to have an operational ANS – as evidenced by the observation that their discrimination performance accorded with Weber’s law (Figure 1) – albeit with greatly reduced precision.
In spite of having a level of ANS precision commensurate with that of typically developing 4-year-olds, the individuals with WS in Experiment 1 appear to have mastered a mapping between their noisy ANS representations and number words (e.g., “seven”) that was on par with the typically developing 9-year-olds. The three metrics that index the accuracy and precision of the mapping between the ANS and number words (i.e., linear slope, intercept, and CV) all showed developmental improvements between 4 and 9 years of age, with 9-year-olds performing near ceiling (with optimal performance being a linear slope = 1 and an intercept = 0). Further studies are needed to map the full developmental trajectory beyond 9 years of age, and could also assess whether participants with WS perform at an appropriate level given their chronological age. In sum, our findings suggest that people with WS use the ANS to make verbal number estimations, and that their ability to map these nonverbal numerical representations to their verbal number words is more accurate than would be expected from their impaired ANS precision (w).
Studies with typically developing children and adults show developmental improvements in ANS precision until the age of 30 years (Halberda & Feigenson, 2008; Halberda et al., 2012). Thus, in our second experiment we sought to examine whether ANS precision and the mapping between ANS representations and number words also improve with age in people with WS. To this end, we tested a separate group of people with WS on abbreviated versions of the Numerical Comparison and Verbal Estimation tasks used in Experiment 1—this afforded us a wider range of ages and allowed us to examine the effects of age on the ANS precision and ANS-number word mappings in people with WS. To shorten overall testing time and to keep in line with the experimental parameters used in previous studies with participants around this age (Halberda & Feigenson, 2008; Halberda et al., 2012), we only used spatially intermixed displays of blue and yellow dots and presented stimuli for 300 ms.
Experiment 2
Method
Participants
Twelve people with Williams syndrome (WS; 7 females, mean age = 19 years, 9 months; range = 12 to 29 years) participated who had not previously participated in Experiment 1. They were recruited through the Williams Syndrome Association (WSA), and were tested either in the laboratory or in a quiet room at the site of the biennial conference of the WSA. All participants had a positive diagnosis of WS via the fluorescent in situ hybridization (FISH) test and an average composite IQ score of 72.75 (SD = 14.55) on the Kaufman Brief Intelligence Test, Second edition (KBIT-2; Kaufman & Kaufman, 2004). Adult participants and parents of children tested provided informed written consent prior to their participation, and participants received monetary compensation after they completed the task. Two participants were unable to complete the Verbal Estimation task.
Materials
Numerical Comparison task (“Which has more?”)
All aspects of the task were as in Experiment 1 except for the following changes: Each stimulus array was presented for 300 ms. The four different numerical ratios presented were: 1.16 (e.g. 6 blue dots vs. 7 yellow dots), 1.33, 2.0, and 3.0, with 12 trials for each ratio (48 trials in total). All trials presented the blue and yellow dots intermixed at the center of the screen.
Verbal Estimation task (“How many?”)
All aspects of the task were as in Experiment 1 except that each stimulus array contained 7, 10, or 13 yellow dots in a random spatial configuration, and was presented for 300 ms (note that because of the inherent variability of the ANS, participants were unlikely to recognize the fact that the same 3 numerosities were shown repeatedly and no feedback was given). Participants received 7 practice trials and 12 trials for each numerosity (i.e., 36 test trials in total).
Participants always completed the Numerical Comparison task before the Verbal Estimation task and the tasks were administered as part of a larger battery of tests examining a range of spatial competencies in people with WS.
Results
All data were analyzed as described for Experiment 1. We were unable to obtain Weber fraction estimates for three participants on the Numerical Comparison task due to high variability in their responses. The average w for the remaining participants was 0.58 (SD = 0.30), indicating that, on average, the most difficult ratio participants with WS could reliably discriminate was 5:8 (e.g., 10 versus 16 dots). The average CV was 0.27 (SD = 0.06), the average linear slope estimate was 0.99 (SD = 0.67), and the average intercept was 1.67 (SD = 2.13).
Developmental change in participants with Williams Syndrome
The w estimates obtained in the Numerical Comparison task did not differ between Experiment 1 and Experiment 2 (t(20) = 0.54, p = .59). CV, linear slope, and intercept estimates obtained in the Verbal Estimation task also did not differ by experiment (CV: t(22) = −1.21, p = .24; slope: t(21) = −0.93, p = .93; intercept: t(20) = −0.24, p = .81). Therefore, we combined the data from both versions of the tasks in order to assess with greater power whether there were any developmental effects within our participants with Williams syndrome.
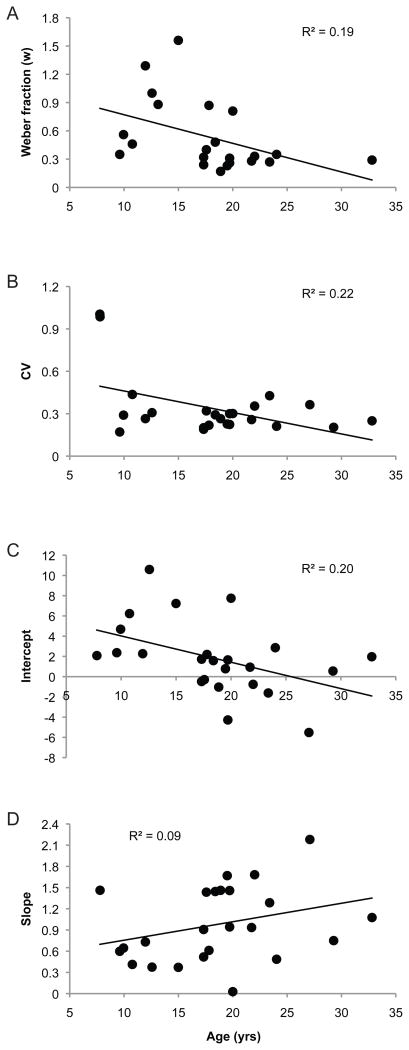
Within the combined WS group, age was significantly correlated with w (R2 = 0.19, p < .05; Figure 7a), suggesting that, despite their overall lower ANS precision compared to typically developing children, participants with WS showed improvements in ANS precision with age. Age was also correlated with CV (R2 = 0.22, p = .02; Figure 7b) and intercept estimates (R2 = 0.21, p = .03; Figure 7c), suggesting that participants with WS also improve in verbally estimating numerosities with age. Age was not correlated with linear slope estimates (R2 = 0.08, p = .18; Figure 7d).
Figure 7.
Correlations between age and ANS precision (Weber fraction, A) on the Numerical Comparison task, coefficient of variation (CV, B), intercept (C), and slope (D) estimates on the Verbal Estimation task in participants with Williams syndrome.
General Discussion
We had several goals in this series of experiments. The first was to characterize the precision of the Approximate Number System (ANS) in people with WS and to compare it to that of typically developing children. The second was to characterize the mapping between the non-verbal ANS representations and exact number words. The third was to examine the developmental trajectory of ANS precision and the mapping between ANS representations and number words in individuals with WS.
To address the first goal, we presented participants with two briefly flashed displays containing different numbers of blue and yellow dots, and asked them to judge which collection was more numerous. In Experiment 1, we found that the ANS precision of participants with WS, with an average age of 15 years, was indistinguishable from that of typically developing 4-year-olds and was significantly lower than that of typically developing 6- and 9-year-olds. Given the developmental trajectory established in the literature, we found the ANS precision of the participants with WS to be in the range of typically developing 2- to 4-year-old children. Despite the imprecision in their ANS representations, our results suggest that participants with WS do have a functioning ANS: their performance on the Numerical Comparison task was well fit by a standard model of Weber’s law.
To address the second goal, we tested participants’ ability to verbally estimate the number of items in a visual array. We found that the performance of individuals with WS in Experiment 1 was significantly better than that of typically developing 4-year-old children and did not differ from the level of 6- and 9-year-old typically developing children. The developmental trajectories we observed suggest only moderate improvement of verbal estimation abilities between 6 and 9 years of age in typically developing children, perhaps, nearing ceiling performance as judged by the metrics of linear slope and intercept. Further studies will be needed to map out the complete developmental trajectory of the mapping between nonverbal ANS representations and number words beyond the ages tested here, and can also assess whether participants with WS perform at an appropriate level given their chronological age.
The central puzzle of the current results is that individuals with WS present with ANS precision on par with typically developing 4-year-olds, but they have mastered a mapping between their number words and the ANS that is as accurate as typically developing 9-year-olds. These findings bear on the open question of how the mapping between the ANS and the number words is formed in the first place, and how it is maintained.
Although typically developing children have ANS representations from birth (Izard et al., 2009) and usually learn a subset of the count words in their language by the early preschool years (Wynn, 1992), they do not successfully map between these two systems until approximately 5 years of age (Le Corre & Carey, 2007). Our results suggest that the relative lateness of this achievement in typically developing children is unlikely to be due to children having to wait until their ANS representations are precise enough to support a mapping to the number words. Participants with WS had ANS representations with precision in the range of typically developing 2- to 4-year old children. Yet the robustness of their mappings of ANS representations to number words was equivalent to typically developing 6- to 9-year-olds. In contrast, 4-year-old children exhibited poor mappings (i.e., high coefficients of variation and high intercepts, and slopes closer to zero on the Verbal Estimation task) but had a mapping function with a slope near 0.2 and an intercept near 5, which was indistinguishable from random responding. These results suggest that having relatively imprecise ANS representations does not preclude the creation of a fairly accurate mapping between these noisy representations and the number words.
The superior performance of individuals with WS in the Verbal Estimation task compared to their performance in the Numerical Comparison task is consistent with suggestions from other authors that people with WS have relative strength in number tasks that engage the language system. For example, Ansari and colleagues (2003) found that children with WS are highly accurate at reciting the count list, but that they do not demonstrate a commensurate understanding of the cardinality principle.
Our estimates of the accuracy of the mapping between the number words and ANS representations focused on the slope and intercept of the regression line, as well as CV. While CV and w are, in theory, convergent estimates of the precision of the ANS representations, and should therefore be identical, task differences between our Verbal Estimation task and Number Comparison task may have enabled individuals with WS to show a more typical CV relative to w. For example, the Verbal Estimation task required participants to quickly approximate the number of items in one collection, and then apply a verbal label to this estimate. The Number Comparison task required participants to approximate two collections, mentally compare these, and then generate a response (“blue” or “yellow”) to indicate which collection was more numerous. Thus a major difference between the tasks is the need to represent one collection (Verbal Estimation task) versus two (Number Comparison task). This difference makes it hard to conclude that approximate number tasks that engage language have an absolute advantage for participants with WS. However, our findings raise interesting questions about whether having access to specific verbal number labels somehow sharpens estimation performance. Adolescents with WS, for example, show excellent performance when verbally counting up to 21 (and possibly higher) (O’Hearn & Landau, 2007). They may have severely impaired ANS precision, as measured by approximate number comparisons, but it may be possible that they have had enough experience with counting sets of objects that they are able to verbally estimate numerosity reasonably well and attach well-known verbal labels in a way that matches the performance of typically developing 9-year-olds, despite their much poorer ANS precision.
A third goal was to examine the developmental trajectory of ANS precision and the mapping between ANS representations and number words in individuals with WS. Despite showing that individuals with WS successfully mapped ANS representations to number words, the developmental profile revealed by our study suggests a severely protracted growth trajectory, with final truncation at a level similar to that of typically developing children of a much younger age. People with WS did show an improvement in ANS precision with age, but this relationship was a modest one, since by adolescence the ANS precision level had only reached that of typically developing preschool-aged children. We also found improvements in the mapping between ANS representations and number words with age, but these effects were less consistent across measures in that they were only reliable for CV and intercept estimates but not linear slope. To fully elucidate the trajectory of ANS development in people with WS will require longitudinal work, an expansion of the upper age range of participants beyond the ages tested here, and a closer examination of the functional importance of the different measures on the Verbal Estimation task. In addition, other cognitive skills such as general processing speed and attention should be tested in order to investigate whether growth in these skills might explain improvements in ANS precision with age. Although our results suggest that the upper limit in ANS precision is on average equivalent to typically developing 4-year-olds, we now know that typically developing individuals continue to experience improvements in ANS precision through at least age 30 years (Halberda et al., 2012). Thus, it is possible that people with WS also experience ANS growth past adolescence, in which case the ANS precision we have reported here would underestimate their mature potential.
Importantly, we note that the pattern we observed here for ANS precision – performance in adolescents and young adults with WS that is in the range of normally developing 2- to 4-year-olds – is consistent with a recent proposal about the WS developmental profile for a wide range of other foundational cognitive domains. Based on evidence from spatial and linguistic development, Landau and Hoffman (2012) suggested that people with WS may undergo very slow but otherwise normal development followed by plateauing some time during adolescence. The consequence is that aspects of cognitive structure that are normally acquired early in life develop slowly but normally in people with WS, reaching maturity at later ages than in the normal population. In contrast, those cognitive functions that normally undergo protracted developmental timelines also develop slowly, but never reach maturity due to plateauing of all learning during adolescence. By this hypothesis, WS does not lead to the targeted impairment of specific cognitive systems over others, except insofar as the cognitive system in question is one that normally emerges early versus on a more protracted timeframe. Although speculative, this proposal predicts that the same should be true for basic numerical representations. The empirical finding of a severely limited ANS could be explained by extremely slow growth – up to the precision of a typical 4-year-old – followed by developmental arrest in adulthood, resulting in a final mature level considerably lower than that normally attained in adolescence or adulthood.
Finally, our findings support a recent finding by Rousselle and colleages (2013) that some of the math deficits found in people with WS may be due to underlying deficits in basic numerical approximation and the arithmetic or ordinal intuitions that the ANS supports. This appears to be similar to previous findings that non-WS individuals with developmental dyscalculia have poor ANS precision (Mazzocco, Feigenson, & Halberda, 2011a; Piazza et al., 2010). Future studies are needed to elucidate which aspects of mathematics are particularly affected by decreases in ANS precision. Such findings might be widely applicable to other disorders that are also associated with low math ability, such as Turner syndrome and Fragile X syndrome (Mazzocco, 1998, 2001; Mazzocco & McCloskey, 2005; Rovet, 1993; Temple & Marriott, 1998). For all of these cases, a key question for the future is whether basic cognitive functions – including ANS representations – can be improved by early training.
To summarize, our goals were to characterize the precision of the Approximate Number System (ANS) in people with WS compared to that of typically developing children, and to characterize the mapping between the non-verbal ANS representations and exact number words. Our results reveal that people with WS have severely limited numerical approximation abilities, commensurate with those of typically developing 2- to 4-year-old children. In contrast, people with WS showed relative strength in producing mappings between numerical approximations and number words, but this relative difference was modest, amounting to a several-year advantage. These results suggest that even very imprecise ANS representations can support a mapping with exact number words, and that a robust understanding of counting and the numerical content of these words – rather than more precise ANS representations – may be a key component in the mastery of this mapping.
Acknowledgments
This research was supported by NIH R01 HD057258 to LF and JH and R01 NS050876 to BL.
References
- Ansari D. Effects of development and enculturation on number representation in the brain. Nature Reviews Neuroscience. 2008;9:278–291. doi: 10.1038/nrn2334. [DOI] [PubMed] [Google Scholar]
- Ansari D, Donlan C, Karmiloff-Smith A. Typical and atypical development of visual estimation abilities. Cortex. 2007;43(6):758–768. doi: 10.1016/s0010-9452(08)70504-5. [DOI] [PubMed] [Google Scholar]
- Ansari D, Donlan C, Thomas MS, Ewing SA, Peen T, Karmiloff-Smith A. What makes counting count? Verbal and visuo-spatial contributions to typical and atypical number development. J Exp Child Psychol. 2003;85(1):50–62. doi: 10.1016/s0022-0965(03)00026-2. [DOI] [PubMed] [Google Scholar]
- Barth H, La Mont K, Lipton J, Spelke ES. Abstract number and arithmetic in preschool children. Proc Natl Acad Sci U S A. 2005;102(39):14116–14121. doi: 10.1073/pnas.0505512102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carey S. The Origin of Concepts. Oxford: Oxford University Press; 2009. [Google Scholar]
- Dehaene S, Molko N, Cohen L, Wilson AJ. Arithmetic and the brain. Current Opinition in Neurobiology. 2004;14(2):218–224. doi: 10.1016/j.conb.2004.03.008. [DOI] [PubMed] [Google Scholar]
- Delazer M, Domahs F, Bartha L, Brenneis C, Lochy A, Trieb T, et al. Learning complex arithmetic: an fMRI study. Cognitive Brain Research. 2003;18(1):76–88. doi: 10.1016/j.cogbrainres.2003.09.005. [DOI] [PubMed] [Google Scholar]
- Farran EK, Blades M, Boucher J, Tranter LJ. How do individuals with Williams syndrome learn a route in a real-world environment? Developmental Science. 2010;13(3):454–468. doi: 10.1111/j.1467-7687.2009.00894.x. [DOI] [PubMed] [Google Scholar]
- Farran EK, Courbois Y, Van Herwegen J, Blades M. How useful are landmarks when learning a route in a virtual environment? Evidence from typical development and Williams syndrome. Journal of Experimental Child Psychology. 2012;111(4):571–585. doi: 10.1016/j.jecp.2011.10.009. [DOI] [PubMed] [Google Scholar]
- Farran EK, Jarrold C, Gathercole SE. Block Design Performance in the Williams Syndrome Phenotype: A Problem with Mental Imagery? Journal of Child Psychology and Psychiatry. 2001;42(6):719–728. doi: 10.1111/1469-7610.00768. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Dehaene S, Spelke E. Core systems of number. Trends in Cognitive Sciences. 2004;8(7):307–314. doi: 10.1016/j.tics.2004.05.002. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Libertus ME, Halberda J. Links between the intuitive sense of number and formal mathematics ability. Child Development Perspectives. 2013;7(2):74–79. doi: 10.1111/cdep.12019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fiez JA, Petersen SE. Neuroimaging studies of word reading. Proceedings of the National Academy of Sciences. 1998;95(3):914–921. doi: 10.1073/pnas.95.3.914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilmore CK, McCarthy SE, Spelke ES. Symbolic arithmetic knowledge without instruction. Nature. 2007;447(7144):589–591. doi: 10.1038/nature05850. [DOI] [PubMed] [Google Scholar]
- Ginsburg HP, Baroody AJ. Test of Early Mathematics Ability. 2. Austin, Texas: Pro Ed; 1990. [Google Scholar]
- Green D, Swets JA. Signal detection theory and psychophysics. New York: John Wiley & Sons, Inc; 1966. [Google Scholar]
- Halberda J, Feigenson L. Developmental change in the acuity of the ‘number sense’: The approximate number system in 3-, 4-, 5-, and 6-year-olds and adults. Developmental Psychology. 2008;44(5):1457–1465. doi: 10.1037/a0012682. [DOI] [PubMed] [Google Scholar]
- Halberda J, Ly R, Willmer J, Naiman D, Germine L. Number sense across the lifespan as revealed by a massive Internet-based sample. Proceedings of the National Academy of Sciences, Early Edition; 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halberda J, Mazzocco MM, Feigenson L. Individual differences in non-verbal number acuity correlate with maths achievement. Nature. 2008;455(7213):665–668. doi: 10.1038/nature07246. [DOI] [PubMed] [Google Scholar]
- Halberda J, Sires SF, Feigenson L. Multiple spatially overlapping sets can be enumerated in parallel. Psychol Sci. 2006;17(7):572–576. doi: 10.1111/j.1467-9280.2006.01746.x. [DOI] [PubMed] [Google Scholar]
- Hubbard EM, Piazza M, Pinel P, Dehaene S. Interactions between number and space in parietal cortex. Nat Rev Neurosci. 2005;6(6):435–448. doi: 10.1038/nrn1684. [DOI] [PubMed] [Google Scholar]
- Inglis M, Attridge N, Batchelor S, Gilmore C. Non-verbal number acuity correlates with symbolic mathematics achievement: But only in children. Psychonomic Bulletin & Review. 2011 doi: 10.3758/s13423-011-0154-1. [DOI] [PubMed] [Google Scholar]
- Ischebeck A, Zamarian L, Egger K, Schocke M, Delazer M. Imaging early practice effects in arithmetic. Neuroimage. 2007;36(3):993–1003. doi: 10.1016/j.neuroimage.2007.03.051. [DOI] [PubMed] [Google Scholar]
- Ischebeck A, Zamarian L, Siedentopf C, Koppelstaetter F, Benke T, Felber S, et al. How specifically do we learn? Imaging the learning of multiplication and subtraction. Neuroimage. 2006;30(4):1365–1375. doi: 10.1016/j.neuroimage.2005.11.016. [DOI] [PubMed] [Google Scholar]
- Izard V, Sann C, Spelke ES, Streri A. Newborn infants perceive abstract numbers. Proc Natl Acad Sci U S A. 2009;106(25):10382–10385. doi: 10.1073/pnas.0812142106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufman AS, Kaufman NL. Kaufman Brief Intelligence Test. 2. San Antonio, TX: Pearson; 2004. [Google Scholar]
- Krajcsi A, Lukacs A, Igacs J, Racsmany M, Pleh C. Numerical abilities in Williams syndrome: Dissociating the analogue magnitude system and verbal retrieval. Journal of Clinical and Experimental Neuropsychology. 2009;31(4):439–446. doi: 10.1080/13803390802244126. [DOI] [PubMed] [Google Scholar]
- Lakusta L, Dessalegn B, Landau B. Impaired geometric reorientation caused by genetic defect. Proceedings of the National Academy of Sciences. 2010;107(7):2813–2817. doi: 10.1073/pnas.0909155107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landau B, Hoffman JE. Spatial representation: From gene to mind. New York, NY: Oxford University Press; 2012. [Google Scholar]
- Landau B, Hoffman JE, Kurz N. Object recognition with severe spatial deficits in Williams syndrome: sparing and breakdown. Cognition. 2006;100(3):483–510. doi: 10.1016/j.cognition.2005.06.005. [DOI] [PubMed] [Google Scholar]
- Le Corre M, Carey S. One, two, three, four, nothing more: An investigation of the conceptual sources of the verbal counting principles. Cognition. 2007;105(2):395–438. doi: 10.1016/j.cognition.2006.10.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Libertus ME, Feigenson L, Halberda J. Preschool Acuity of the Approximate Number System Correlates with School Math Ability. Developmental Science. 2011;14(6):1292–1300. doi: 10.1111/j.1467-7687.2011.01080.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Libertus ME, Feigenson L, Halberda J. Is Approximate Number Precision a Stable Predictor of Math Ability? Learning and Individual Differences. 2013;25:126–133. doi: 10.1016/j.lindif.2013.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Libertus ME, Odic D, Halberda J. Intuitive sense of number correlates with math scores on college-entrance examination. Acta Psychologica. 2012;141:373–379. doi: 10.1016/j.actpsy.2012.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipton JS, Spelke ES. Preschool Children’s Mapping of Number Words to Nonsymbolic Numerosities. Child Development. 2005;76(5):978–988. doi: 10.1111/j.1467-8624.2005.00891.x. [DOI] [PubMed] [Google Scholar]
- Mazzocco MM. A process approach to describing mathematics difficulties in girls with Turner syndrome. Pediatrics. 1998;102(2 Pt 3):492–496. [PubMed] [Google Scholar]
- Mazzocco MM. Math learning disability and math LD subtypes: evidence from studies of Turner syndrome, fragile X syndrome, and neurofibromatosis type 1. Journal of Learning Disabilities. 2001;34(6):520–533. doi: 10.1177/002221940103400605. [DOI] [PubMed] [Google Scholar]
- Mazzocco MM, Feigenson L, Halberda J. Impaired acuity of the approximate number system underlies mathematical learning disability. Child Development. 2011a;82(4):1224–1237. doi: 10.1111/j.1467-8624.2011.01608.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazzocco MM, Feigenson L, Halberda J. Preschoolers’ precision of the approximate number system predicts later school mathematics performance. PLoS One. 2011b;6(9):e23749. doi: 10.1371/journal.pone.0023749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazzocco MM, McCloskey M. Math Performance in Girls with Turner or Fragile X Syndrome. In: Campbell JI, editor. Handbook of Mathematical Cognition. New York, NY: Psychology Press; 2005. [Google Scholar]
- McCrink K, Spelke ES. Core multiplication in childhood. Cognition. 2010;116(2):204–216. doi: 10.1016/j.cognition.2010.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCrink K, Wynn K. Large-number addition and subtraction by 9-month-old infants. Psychological Science. 2004;15(11):776–781. doi: 10.1111/j.0956-7976.2004.00755.x. [DOI] [PubMed] [Google Scholar]
- Mervis CB, Becerra AM. Language and communicative development in Williams syndrome. Mental Retardation and Developmental Disabilities Research Reviews. 2007;13(1):3–15. doi: 10.1002/mrdd.20140. [DOI] [PubMed] [Google Scholar]
- Mervis CB, Morris CA, Bertrand J, Robinson BF. Williams Syndrome: Findings from an Integrated Program of Research. In: Tager-Flusberg H, editor. Neurodevelopmantal Disorders. Cambridge, MA: MIT Press; 1999. [Google Scholar]
- Meyer-Lindenberg A, Kohn P, Mervis CB, Kippenhan JS, Olsen RK, Morris CA, et al. Neural Basis of Genetically Determined Visuospatial Construction Deficit in Williams Syndrome. Neuron. 2004;43:623–631. doi: 10.1016/j.neuron.2004.08.014. [DOI] [PubMed] [Google Scholar]
- Meyer-Lindenberg A, Mervis CB, Berman KF. Neural mechanisms in Williams syndrome: a unique window to genetic influences on cognition and behaviour. Nature Reviews Neuroscience. 2006;7:380–393. doi: 10.1038/nrn1906. [DOI] [PubMed] [Google Scholar]
- Mundy E, Gilmore CK. Children’s mapping between symbolic and nonsymbolic representations of number. J Exp Child Psychol. 2009;103(4):490–502. doi: 10.1016/j.jecp.2009.02.003. [DOI] [PubMed] [Google Scholar]
- Nardini M, Atkinson J, Braddick O, Burgess N. Developmental trajectories for spatial frames of reference in Williams syndrome. Developmental Science. 2008;11(4):583–595. doi: 10.1111/j.1467-7687.2007.00662.x. [DOI] [PubMed] [Google Scholar]
- O’Hearn K, Landau B. Mathematical skill in individuals with Williams Syndrome: Evidence from a standardized mathematics battery. Brain and Cognition. 2007;64(3):238–246. doi: 10.1016/j.bandc.2007.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Hearn K, Luna B. Mathematical skills in Williams syndrome: insight into the importance of underlying representations. Dev Disabil Res Rev. 2009;15(1):11–20. doi: 10.1002/ddrr.47. [DOI] [PubMed] [Google Scholar]
- Opfer JE, Martens MA. Learning without representational change: development of numerical estimation in individuals with Williams syndrome. Developmental Science. 2012;15(6):863–875. doi: 10.1111/j.1467-7687.2012.01187.x. [DOI] [PubMed] [Google Scholar]
- Paterson SJ, Girelli L, Butterworth B, Karmiloff-Smith A. Are numerical impairments syndrome specific? Evidence from Williams syndrome and Down’s syndrome. Journal of Child Psychology and Psychiatry. 2006;47(2):190–204. doi: 10.1111/j.1469-7610.2005.01460.x. [DOI] [PubMed] [Google Scholar]
- Paulesu E, Frith CD, Frackowiak RSJ. The neural correlates of the verbal component of working memory. Nature. 1993;362:342– 345. doi: 10.1038/362342a0. [DOI] [PubMed] [Google Scholar]
- Piazza M, Facoetti A, Trussardi AN, Berteletti I, Conte S, Lucangeli D, et al. Developmental trajectory of number acuity reveals a severe impairment in developmental dyscalculia. Cognition. 2010;116(1):33–41. doi: 10.1016/j.cognition.2010.03.012. [DOI] [PubMed] [Google Scholar]
- Pica P, Lemer C, Izard V, Dehaene S. Exact and approximate arithmetic in an Amazonian indigene group. Science. 2004;306(5695):499–503. doi: 10.1126/science.1102085. [DOI] [PubMed] [Google Scholar]
- Price CJ. The functional anatomy of word comprehension and production. Trends Cogn Sci. 1998;2(8):281–288. doi: 10.1016/s1364-6613(98)01201-7. [DOI] [PubMed] [Google Scholar]
- Price GR, Palmer D, Battista C, Ansari D. Nonsymbolic numerical magnitude comparison: Reliability and validity of different task variants and outcome measures, and their relationship to arithmetic achievement in adults. Acta Psychologica. 2012;140:50–57. doi: 10.1016/j.actpsy.2012.02.008. [DOI] [PubMed] [Google Scholar]
- Rousselle L, Dembour G, Noel MP. Magnitude Representations in Williams Syndrome: Differential Acuity in Time, Space and Number Processing. PLoS One. 2013;8(8):e72621. doi: 10.1371/journal.pone.0072621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rovet JF. The psychoeducational characteristics of children with Turner syndrome. Journal of Learning Disabilities. 1993;26(5):333–341. doi: 10.1177/002221949302600506. [DOI] [PubMed] [Google Scholar]
- Starr AB, Libertus ME, Brannon EM. Number sense in infancy predicts mathematical abilities in childhood. Proceedings of the National Academy of Sciences; (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stinton C, Farran EK, Courbois Y. Mental Rotation in Williams Syndrome: An Impaired Ability. Developmental Neuropsychology. 2008;33(5):565–583. doi: 10.1080/87565640802254323. [DOI] [PubMed] [Google Scholar]
- Stromme P, Bjornstad PG, Ramstad K. Prevalence estimation of Williams syndrome. Journal of Child Neurology. 2002;17(4):269–271. doi: 10.1177/088307380201700406. [DOI] [PubMed] [Google Scholar]
- Temple CM, Marriott AJ. Arithmetical ability and disability in Turner’s Syndrome: A cognitive neuropsychological analysis. Developmental Neuropsychology. 1998;41:47–67. [Google Scholar]
- Udwin O, Davies M, Howlin P. A longitudinal study of cognitive abilities and educational attainment in Williams syndrome. Develomental Medicine and Child Neurology. 1996;38:1020–1029. doi: 10.1111/j.1469-8749.1996.tb15062.x. [DOI] [PubMed] [Google Scholar]
- Van Herwegen J, Ansari D, Xu F, Karmiloff-Smith A. Small and large number processing in infants and toddlers with Williams syndrome. Developmental Science. 2008;11(5):637–643. doi: 10.1111/j.1467-7687.2008.00711.x. [DOI] [PubMed] [Google Scholar]
- Van Selst M, Jolicoeur P. A Solution to the Effect of Sample Size on Outlier Elimination. Quarterly Journal of Experimental Psychology. 1994;47A(3):631–650. [Google Scholar]
- Volterra V, Capirci O, Pezzini G, Sabbadini L, Vicari S. Linguistic Abilities in Italian Children with Williams Syndrome. Cortex. 1996;32:663–677. doi: 10.1016/s0010-9452(96)80037-2. [DOI] [PubMed] [Google Scholar]
- Wagner JB, Johnson SC. An association between understanding cardinality and analog magnitude representations in preschoolers. Cognition. 2011;119(1):10–22. doi: 10.1016/j.cognition.2010.11.014. [DOI] [PubMed] [Google Scholar]
- Whalen J, Gallistel CR, Gelman R. Nonverbal counting in humans: The psychophysics of number representation. Psychological Science. 1999;10(2):130–137. [Google Scholar]
- Wynn K. Children’s Acquisition of the Number Words and the Counting System. Cognitive Psychology. 1992;24:220–251. [Google Scholar]
- Xu F, Spelke ES. Large number discrimination in 6-month-old infants. Cognition. 2000;74(1):B1–B11. doi: 10.1016/s0010-0277(99)00066-9. [DOI] [PubMed] [Google Scholar]
- Yoshioka T, Dillon MR, Beck GC, Rapp B, Landau B. Tactile localization on digits and hand: Structure and development. Psychological Science. 2013;24(9):1653–1663. doi: 10.1177/0956797613478617. [DOI] [PMC free article] [PubMed] [Google Scholar]