Summary
Increases in cytosolic Ca2+ concentration ([Ca2+]i) mediated by NMDA-sensitive glutamate receptors (NMDARs) are important for synaptic plasticity. We studied a wide variety of dendritic spines on rat CA1 pyramidal neurons in acute hippocampal slices. Two-photon uncaging and Ca2+ imaging revealed that NMDAR-mediated currents increased with spine-head volume and that even the smallest spines contained a significant number of NMDARs. The fate of Ca2+ that entered spine heads through NMDARs was governed by the shape (length and radius) of the spine neck. Larger spines had necks that permitted greater efflux of Ca2+ into the dendritic shaft, whereas smaller spines manifested a larger increase in [Ca2+]i within the spine compartment as a result of a smaller Ca2+ flux through the neck. Spine-neck geometry is thus an important determinant of spine Ca2+ signaling, allowing small spines to be the preferential sites for isolated induction of long-term potentiation.
Introduction
Glutamate receptors sensitive to N-methyl-D-aspartate (NMDA) mediate increases in the intracellular free Ca2+ concentration ([Ca2+]i) of neurons that lead to bidirectional regulation of synaptic plasticity ( Lisman, 1989 and Shouval et al., 2002), which supports self-organization of neuronal networks in the central nervous system ( Lisman, 2003, Mori and Mishina, 2003 and Nakazawa et al., 2004). Synaptic functions and plasticity have been proposed to be dependent on synaptic structure ( Bonhoeffer and Yuste, 2002, Harris et al., 2003 and Kasai et al., 2003). With the use of two-photon photolysis of caged glutamate, we previously showed that spine-head volume is an important determinant of the expression of α-amino-3-hydroxy-5-methyl-4-isoxazolepropionate (AMPA)-sensitive glutamate receptors ( Matsuzaki et al., 2001), which mediate fast glutamatergic synaptic transmission. We recently applied the same approach to induce NMDA receptor (NMDAR)-dependent long-term plasticity at visually selected single spines; this plasticity was dependent on spine-head volume and was induced more efficiently in smaller spines than in larger ones ( Matsuzaki et al., 2004). However, the dependence of NMDAR-mediated Ca2+ signaling on spine structure has not been clarified, given that selective stimulation of the single presynaptic fibers that innervate identified spines has been difficult to achieve electrically because of the spread of the electric current.
The role of diverse spine-neck structures in the regulation of neuronal signaling is also unclear (Rall, 1970, Svoboda et al., 1996 and Shepherd, 1996). In particular, it remains unknown whether spine necks allow outflow of Ca2+ into the dendritic shaft (Helmchen, 2002). Although some studies have predicted outflow of Ca2+ from spine heads into the dendritic shaft (Majewska et al., 2000a, Holthoff et al., 2002 and Korkotian et al., 2004), it has been claimed that such outflow is attributable mostly to the buffering action of the large concentrations of the Ca2+ indicator dyes used for Ca2+ measurement in these studies (Sabatini et al., 2002).
We have now used two-photon photolysis of a caged-glutamate compound (MNI-glutamate) (Matsuzaki et al., 2001) to achieve three-dimensionally confined application of glutamate at single spine heads or across the dendritic surface of CA1 pyramidal neurons in acute hippocampal slices. We combined this approach with two-photon Ca2+ imaging and whole-cell patch-clamp recording to monitor the activation of NMDARs in these neurons with a high spatial resolution. A low-affinity Ca2+ indicator was used to minimize the perturbation of endogenous Ca2+-buffering capacity. We investigated NMDAR-mediated Ca2+ signaling in various types of spines and found that spine-head volume was negatively correlated with spine [Ca2+]i but positively correlated with [Ca2+]i of the dendritic shaft at the base of the spine neck. These data suggest that the spine neck is a critical determinant of spine Ca2+ signaling and enables small spines to be the preferential sites of induction and consolidation of long-term structural plasticity. We provide a simple, quantitative model of spine Ca2+ signaling to account for the function of spine necks.
Results
Ca2+ Imaging with a Dual-Scanning Two-Photon Microscope
We imaged CA1 pyramidal neurons clamped in the whole-cell mode with a solution containing the low-affinity Ca2+ indicator Oregon Green-BAPTA-5N (OGB-5N, 500 μM) and the Ca2+-insensitive dye Alexa Fluor 594 (40 μM) (Figure 1A). These two dyes emit green and red fluorescence, respectively, but have broad two-photon absorption spectra that allow their simultaneous excitation at 830 nm (Sabatini et al., 2002). The [Ca2+]i was determined ratiometrically from the fluorescence of both dyes (Figure 1B) in the presence of the AMPA receptor (AMPAR) blocker CNQX (10 μM), the metabotropic glutamate receptor blocker MCPG (200 μM), and Mg2+ (50 μM). Given that OGB-5N has a low affinity for Ca2+ (dissociation constant, 32 μM) (DiGregorio and Vergara, 1997) and its Ca2+ binding ratio (κ) is <15.6 (Neher and Augustine, 1992), it affects the intrinsic Ca2+ buffers of neurons only minimally. This value of κ is smaller than those for previous Ca2+-imaging studies in pyramidal neurons (Helmchen et al., 1996, Majewska et al., 2000a and Sabatini et al., 2002) and therefore would be expected to have the least effect on the spatiotemporal pattern of Ca2+ signaling; we estimated the binding ratio of the intrinsic Ca2+ buffer to be 86 (see below). For simplicity, we assumed the resting [Ca2+]i to be zero in the present study, given that OGB-5N does not allow precise measurement of [Ca2+]i at values of <0.3 μM. The line for scanning was aligned with the axis of individual spines to monitor [Ca2+]i in the spine head and at the base of the spine simultaneously (Figure 1A). Alexa Fluor 594 fluorescence was also used for structural measurements.
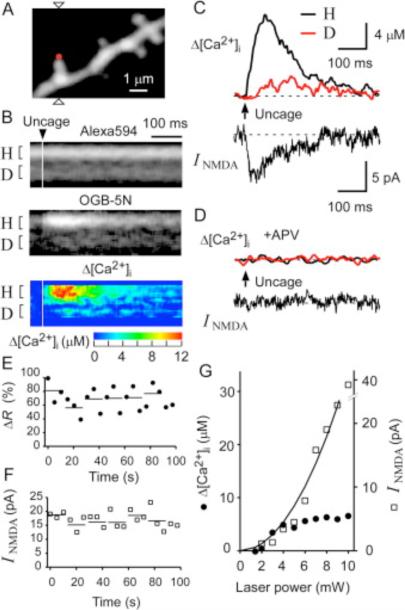
Figure 1. NMDAR-Mediated Ca2+ Signaling in Single Spines of CA1 Pyramidal Neurons in Response to Two-Photon Uncaging of MNI-Glutamate.
(A) A three-dimensionally stacked two-photon fluorescence image of a region of a dendrite labeled with Alexa Fluor 594. Arrowheads indicate the line of laser scanning at 830 nm for fluorescence imaging, and the red dot represents the point of uncaging of MNI-glutamate.
(B) Line-scan images of the spine shown in (A) for Alexa Fluor 594 (top), OGB-5N (middle), and Δ[Ca2+]i obtained from the ratio of OGB-5N to Alexa Fluor 594 (bottom). The time of uncaging of MNI-glutamate is indicated by the arrowhead. The magnitude of Δ[Ca2+]i is pseudocolor coded as indicated.
(C) Δ[Ca2+]i in the spine head (“H”) and at the base of the spine (“D”) shown in (A) as well as NMDAR-mediated current (INMDA) recorded in the whole-cell patch-clamp mode. Regions of averaging of fluorescence to estimate Δ[Ca2+]i are indicated as “H” and “D” in (B).
(D) Elimination by APV (100 μM) of the [Ca2+]i and INMDA responses to uncaging of MNI-glutamate in the neuron shown in (A).
(E and F) Stability of the maximal increase in the fluorescence ratio (ΔR) between OGB-5N and Alexa Fluor 594(E) and of the maximal INMDA (F) in a spine head subjected to uncaging of MNI-glutamate for >20 times. Horizontal lines indicate averages of three consecutive amplitudes.
(G) Dependence of Δ[Ca2+]i and NMDAR-mediated current on the laser power for uncaging in a spine head with a volume of 0.12 μm3.
Two-photon uncaging of MNI-glutamate (10 mM) was induced at the distal pole of a dendritic spine with a mode-locked Ti:sapphire laser (720 nm, 3 mW, 5 ms). This uncaging protocol was expected to induce currents with amplitudes about two to three times as large as those of miniature excitatory postsynaptic currents (EPSCs) (Matsuzaki et al., 2001). The NMDAR blocker APV (100 μM) eliminated both the increase in [Ca2+]i (Δ[Ca2+]i) and the whole-cell current induced by photolysis of MNI-glutamate (Figures 1C and 1D), indicating that the response was primarily mediated by NMDARs (Koester and Sakmann, 1998 and Kovalchuk et al., 2000). The amplitude of Δ[Ca2+]i in the spine head often exceeded 10 μM (see Figure 3C), consistent with previous observations (Petrozzino et al., 1995). There was little delay between the onset of the NMDAR-mediated current and that of Δ[Ca2+]i in the spine head (Figure 1C), indicating that the NMDARs were present in the spines. The Ca2+ signals also indicated the absence of a large concentration of high-affinity Ca2+ buffers in pyramidal neurons, in contrast to cerebellar Purkinje neurons (Maeda et al., 1999).
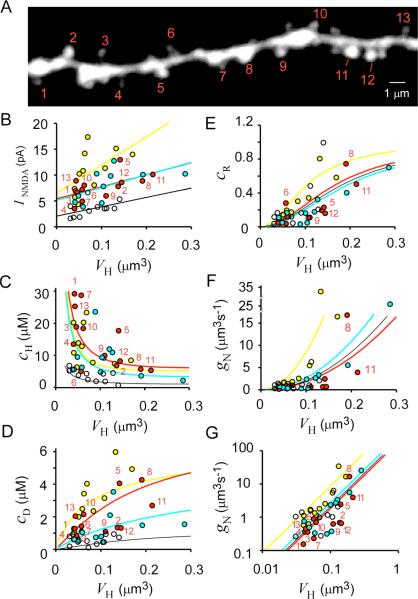
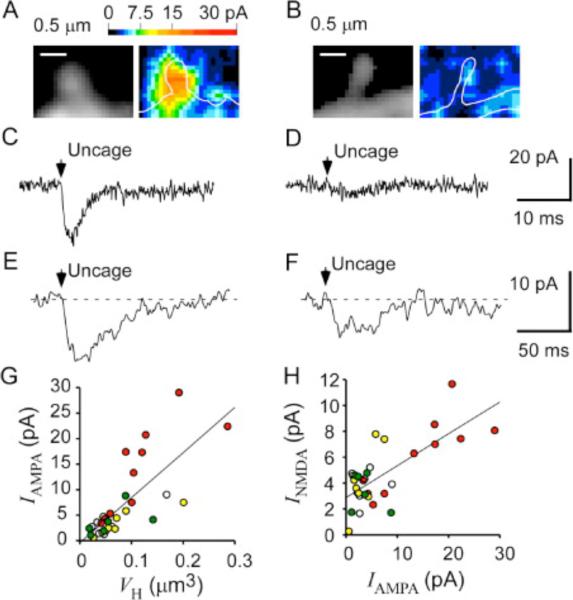
Figure 3. Dependence of NMDAR-Mediated Current and Ca2+ Signaling on Spine-Head Volume.
(A) Stacked Alexa Fluor 594 image of a dendritic region in which uncaging of MNI-glutamate was induced at the numbered spines and line-scan imaging was performed along the axis of each spine. Original xy images are shown in Figure S5.
(B–D) VH dependence of NMDAR-mediated current (INMDA) (B) as well as of Δ[Ca2+]i in the spine head (cH) (C) and in the dendritic shaft at the base of the spine (cD) (D). Straight lines in (B) are linear regression lines. Uncaging was induced at the spines (red circles) indicated in (A) and at spines in three other dendrites (yellow, blue, and white circles). The amplitude of currents was measured at their peak, and Δ[Ca2+]i was measured at the time of the maximal value in spine heads.
(E) VH dependence of the coupling ratio (cR = cD/cH) for each spine.
(F and G) VH dependence of Ca2+ conductance of the spine neck (gN) and its double logarithmic plot, respectively. Smooth curves in (C)–(G) were drawn according to (24), (25), (26), (27) and (28) with four different sets of dendritic parameters as described in “Spine Ca2+ Model.”
The peak amplitudes of Δ[Ca2+]i and current varied markedly, with a coefficient of variation (CV) of ~0.3, as a result of the noise of recording and of channel gating (Figures 1E and 1F). The variability could be reduced to 0.11–0.21 by the averaging of three consecutive traces (Figures 1E and 1F), and we performed such averaging in all subsequent experiments. The peak Δ[Ca2+]i in the spine head and the peak NMDAR-mediated current (INMDA) showed similar nonlinear dependence on the laser power at power values of <5 mW ( Figure 1G), consistent with two-photon excitation of MNI-glutamate. The values of Δ[Ca2+]i tended to saturate at laser powers of >5 mW, probably as a result of saturation of the activation of NMDARs in the single spines; the peak Δ[Ca2+]i was in the range of 4 to 20 μM, which is less than the affinity of OGB-5N for Ca2+ (32 μM). In contrast, INMDA showed no apparent saturation ( Figure 1G), probably as a result of the spillover of glutamate to surrounding dendritic structures ( Rusakov and Kullmann, 1998). We therefore set the laser power to ~3 mW to minimize the spillover effect in all subsequent experiments. Such power was necessary to obtain an adequate signal-to-noise ratio for the NMDARs.
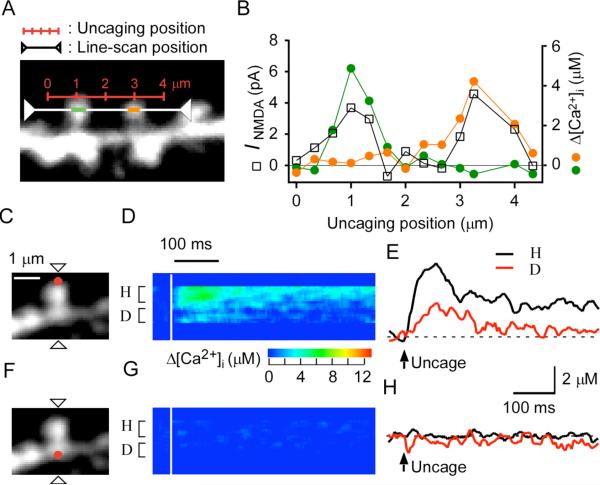
The spatial spread of activation of NMDARs was estimated by inducing sequential uncaging of MNI-glutamate at several points along the line connecting the distal tips of two neighboring spines separated by a distance of 2 μm (Figure 2A). The peaks of the maximal amplitudes of INMDA for the two spines were well separated ( Figure 2B), and each peak was highly correlated with the Δ[Ca2+]i for the respective spine. This result confirmed that NMDARs were selectively activated in single, isolated spines when uncaging was induced at the spine tip under our experimental conditions. The full-width at half-maximal (FWHM) resolution of INMDA thus estimated was ~1.4 μm, consistent with the prediction made from the established slow gating of NMDARs ( Rusakov and Kullmann, 1998) (see Experimental Procedures).
Figure 2. Spatial Spread of NMDAR Activation and of Δ[Ca2+]i in CA1 Pyramidal Neurons.
(A) A stacked Alexa Fluor 594 image of a dendritic region. The red scale indicates the line along which uncaging of MNI-glutamate was sequentially induced, and the white line represents the scanning line for acquisition of fluorescence images.
(B) NMDAR-mediated current as well as Δ[Ca2+]i in the left (green circles) and right (orange circles) spines elicited by uncaging of MNI-glutamate at points along the red line in (A).
(C) Stacked Alexa Fluor 594 image of a spine for which line scanning was applied at the line indicated by the arrowheads and uncaging of MNI-glutamate was induced at the red spot.
(D and E) Line-scan images for Δ[Ca2+]i (D) and averaged traces of Δ[Ca2+]i (E) obtained from the spine shown in (C) during uncaging of MNI-glutamate at the red spot. Regions of averaging of fluorescence for Δ[Ca2+]i are indicated as “H” and “D” in (D).
(F–H) Panels corresponding to (C)–(E), respectively, for uncaging of MNI-glutamate at the position on the dendritic shaft indicated by the red dot in (F).
We found that the NMDAR-dependent increase in [Ca2+]i in the dendritic shaft occurred with a delay of 5–30 ms for 90% of spines (n = 41) (Figure 1C), suggesting that Ca2+ that entered through NMDARs in the spine head spread into the dendritic shaft via the spine neck. Photolysis of MNI-glutamate at the dendritic shaft (Figure 2F) induced only small increases in [Ca2+]i (n = 7) (Figures 2G and 2H) compared with those that were apparent with uncaging at the spine tip (Figures 2C–2E). Increases in [Ca2+]i were often undetectable (0.5 ± 0.5 μM, mean ± SD) when uncaging was effected at arbitrary points along the dendritic shaft at a distance of >2 μm from a neighboring spine, indicating that NMDARs were present in relatively small numbers on the dendritic shaft compared with the spine head and that the Δ[Ca2+]i in shafts induced by two-photon uncaging of MNI-glutamate at isolated spine heads was attributable solely to Ca2+ efflux from those spine heads. The outflow of Ca2+ from spine to dendrite was considered physiological because it was similarly recorded at a temperature (32°C) higher than that (23°C–25°C) routinely used (n = 5, data not shown).
Dependence of the NMDAR-Mediated Response on Spine Structure
We induced uncaging of MNI-glutamate at spine heads that were separated from neighboring spines by >1.2 μm (unless the neighboring spines were much smaller than the selected spine) in order to record NMDAR-mediated currents that were attributable only to the identified spine (Figure 3A). Under these conditions, we were able to minimize the spillover effect on neighboring spines to <10% (Figure 2B). We measured the peak amplitude of INMDA ( Figure 3B) as well as Δ[Ca2+]i in the spine head (cH) ( Figure 3C) and in the dendritic shaft at the base of the spine (cD) ( Figure 3D) at the time when Δ[Ca2+i in the head was maximal (see Figure 8E). Data from four dendrites from different animals (41 spines in total) are summarized in Figures 3B–3D. Our conclusions were also supported by data (not shown) from an additional 17 dendrites (213 spines in total). We found that the amplitude of INMDA correlated with spine-head volume (VH), and this relation was most pronounced for spines on the same dendrite ( Figure 3B), with the mean value (r−) of correlation coefficients being 0.48 for the four dendrites. A substantial INMDA was detected even in small spines, in contrast to the situation for AMPAR-mediated currents (see Figure 7G) ( Matsuzaki et al., 2001). This observation was confirmed by the fact that a marked Δ[Ca2+]i was detected in the head of most small spines ( Figure 3C). In Figure 3, we were mainly concerned with the diversity of spine parameters in each dendrite, since there was parametric variability among the dendrites to a certain degree (see “Spine Ca2+ Model” in Experimental Procedures).
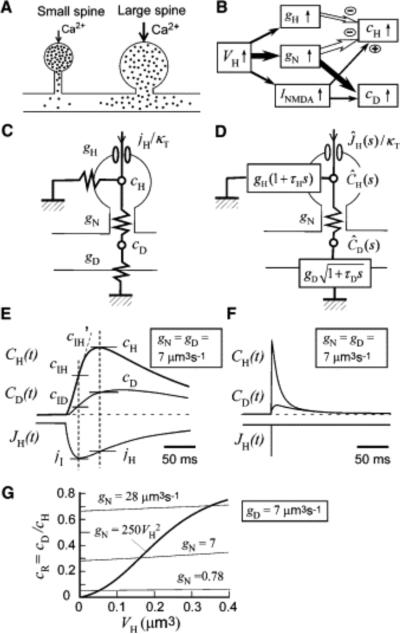
Figure 8. Spine Ca2+ Signals.
(A) NMDAR-mediated influx of Ca2+ (dots) in small and large spines. The narrow neck of small spines results in larger and more confined increases in [Ca2+]i in the spine head, allowing induction of LTP at the level of the single spine. The thick neck of large spines gives rise to smaller increases in spine [Ca2+]i and greater outflow of Ca2+ into the dendritic shaft.
(B) Diagram showing the relative effects of spine-head volume (VH) on spine-neck Ca2+ conductance (gN), spine-head Ca2+ conductance (gH), and INMDA, as well as of the latter parameters on spine-head [Ca2+]i (cH) and [Ca2+]i in the dendritic shaft adjacent to the spine (cD).
(C) Stationary model of Ca2+ signaling in a spine, where gD, jH, and κ T represent Ca2+ conductance of the dendritic shaft, Ca2+ influx, and the total Ca2+ binding ratio, respectively.
(D) Time-dependent model, where τH and τD represent the time constants of [Ca2+]i in the spine head and dendritic shaft, respectively.ĴH(s), ĈH(s), and ĈD(s) are the Laplace transforms of JH (t), CH (t), and CD (t), respectively, which represent the time courses of Ca2+ influx and of [Ca2+]i in the spine head and in the dendritic shaft adjacent to the spine, respectively.
(E and F) Simulation of CH(t) and CD(t) based on the model in (D) and (29) and (30), where JH(t) is either EPSC-like (E) or impulsive (F), and gN, gD , and gH are all set to 7.0 μm3 s−1 . As indicated in (E), cH, cD, and jH are obtained at the time when CH(t) is maximal, and cIH, cIH′, cID, and jI are obtained at the time when JH(t) is maximal.
(G) VH dependence of cR (equal to cD/cH) in the time-dependent model in (D), where cD and cH are obtained as indicated in (E). The value of gN is either fixed (thin lines) or VH dependent (thick line). The values of gD, τD, τH are set at 7 μm3 s−1 , 0.2 s, 0.05 s, respectively, and gH is altered according to VH/τH.
Figure 7. Functional Expression of AMPARs and NMDARs in the Same Spines.
(A and B) Fluorescence images (left) of spines and their maps of AMPAR-mediated current (right). Current amplitude is pseudocolor coded as indicated.
(C and D) Maximal AMPAR-mediated currents in the spines shown in (A) and (B), respectively.
(E and F) NMDAR-mediated currents evoked by uncaging of MNI-glutamate at the tips of the spines show in (A) and (B), respectively.
(G) VH dependence of the maximal AMPAR-mediated currents for 31 spines on four dendrites represented by different colors.
(H) Relation between the maximal amplitudes of NMDAR-mediated and AMPAR-mediated currents recorded from the same spines. Data in (G) and (H) were obtained from preparations different from those shown in Figure 3.
We found that cH tended to be largest in spines with a small VH (r− = –0.50) (Figure 3C). A similar VH dependence was previously observed for EPSCs evoked in CA1 pyramidal neurons by stimulation of presynaptic fibers ( Nimchinsky et al., 2004). This inverse relation might be expected to be a direct consequence of a large spine volume giving rise to an increased rate of Ca2+ pumping or to increased dilution due to the reduced surface-to-volume ratio. However, several observations demonstrated that these explanations were not predominantly responsible for the inverse relation. First, if they were, cD would be expected to show a VH dependence similar to that of cH , because Ca2+ efflux into the shaft would be proportional to cH. We found, however, that cD was actually greater for spines with a larger VH (r− = 0.48) ( Figure 3D). Furthermore, a plot of the coupling ratio (cR = cD/cH) between cD and cH for each spine ( Figure 3E) revealed that cR was markedly dependent on VH, with all values being <1, consistent with the notion that cD reflects the outflow of Ca2+ from the spine head to the shaft (a cR of >1 would imply the presence of a substantial number of extrasynaptic NMDARs). Similar VH dependencies of cH and cR were found in the presence of a blocker of the Ca2+ pump in the internal Ca2+ stores, cyclopiazonic acid (CPA, 30 μM) ( Figure S1 in the Supplemental Data available with this article online), indicating that the VH dependencies were due neither to Ca2+-induced Ca2+ release ( Emptage et al., 1999) nor to Ca2+ uptake into the internal Ca2+ stores ( Majewska et al., 2000a).
The coupling ratio represents the efficiency of Ca2+ spread into the dendritic shaft, the major determinant of which would be expected to be the structure of the spine neck. We considered an equivalent circuit model of spine Ca2+ signaling under stationary conditions (see Figure 8C), given that [Ca2+]i remained increased for >100 ms in response to uncaging of MNI-glutamate (see Discussion for time-dependent condition). The model predicts apparent flow of Ca2+ through the spine neck as
| (1) |
where gN and gD are Ca conductances of the spine neck and dendritic shaft, respectively (see “Spine Ca2+ Model” in Experimental Procedures). It then follows that cR relates directly to gN as
| (2) |
Indeed, we found that the coupling ratio was related to the structure of the spine neck as revealed by fluorescence images (see Figure 5A), with spines having shorter and thicker necks exhibiting larger coupling ratios. This observation implies that large spines tend to couple efficiently to the dendritic shaft as a result of a large neck conductance (gN) and that clearance of Ca2+ along the dendritic shaft may result in a smaller cH (see Figure 8A). In contrast, large and confined increases in [Ca2+]i in small spines may be attributable to a small gN. Spine-neck geometry may therefore regulate the spread of spine Ca2+ signals, as was originally proposed for electrical signals in spines ( Rall, 1970). To test this idea (see Figures 8A and 8B), we characterized the three major mechanisms of Ca2+ clearance from spine heads as reflected by gD, gN, and the Ca2+ conductance of the spine head (gH).
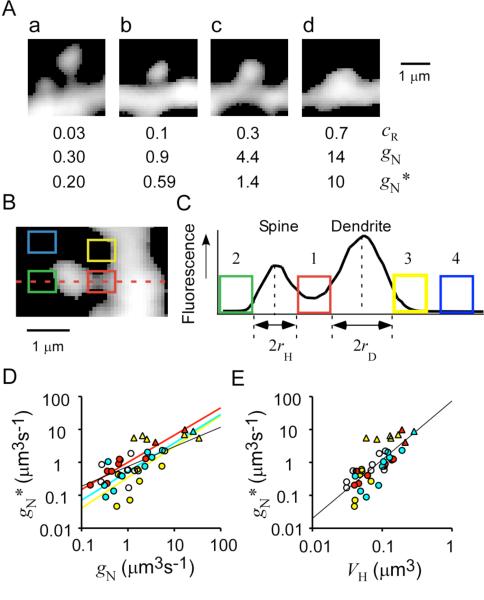
Figure 5. Spine-Neck Geometries.
(A) Stacked Alexa Fluor 594 fluorescence images of dendritic spines with different cR values. Necks appear to be shorter and thicker for spines with a larger cR. Two values of spine-neck Ca2+ conductance, gN and gN*, were estimated from cR and from fluorescence analysis as described below, respectively.
(B) Stacked Alexa Fluor 594 fluorescence image of a spine subjected to analysis of neck geometry.
(C) Fluorescence profile along the dashed line for the spine shown in (B). Four regions were selected for fluorescence measurement. The neck region (1) is flanked by the edges of the spine head and dendritic shaft, which are determined by curve fitting (see Experimental Procedures). For those stubby spines whose neck structures were not well resolved, we assumed lN as 0.05 μm and obtained rN at the base of the spine. Regions of background fluorescence for the spine head (2) and the dendritic shaft (3) are placed at the predicted edge of a spherical spine and cylindrical shaft. A region of nonspecific background fluorescence (4) was positioned between 2 and 5 μm from the shaft.
(D) Relation between gN* and gN. Data obtained from the same dendrites are represented by the same colors as in Figure 3. We estimated gN* from neck fluorescence according to Equation 4 and assuming Dapp = 12 μm2 s−1 (see Experimental Procedures).
(E) Double logarithmic plot of the VH dependence of gN*. Straight lines in (D) and (E) are linear regression lines. Triangles in (D) and (E) indicate those stubby spines whose values of gN* were obtained by assuming lN = 0.05 μm.
Ca2+ Conductance of the Dendritic Shaft
To quantify gD, we measured Ca2+ diffusion along a dendritic shaft by line scanning along the axis of the dendrite after stimulation of NMDARs of one spine by two-photon uncaging of MNI-glutamate ( Figure 4A). Dendritic [Ca2+]i remained at the plateau level for >100 ms ( Figure 1 and Figure 4), suggesting that the distribution of Ca2+ along the dendrite was virtually stationary from 50 to 150 ms after uncaging. Indeed, the spatial distribution of Ca2+ along the shaft obtained at two different time points ( Figure 4B, boxes 1 and 2) could be fitted by a single exponential function ( Figure 4C) with similar length constants (λ = 1.6–1.9 μm). The dendritic λ ranged between 1.2 and 1.9 μm, with a mean value of 1.6 μm (n = 6). The input Ca2+ conductance of the dendritic shaft (μm3 s−1) can be obtained in a manner analogous to that for the derivation of the input electrical conductance of axons ( Johnston and Wu, 1995 and Nicholls et al., 2001) as
| (3) |
where τD and rD are the time constant of [Ca2+]i for and radius of the dendritic shaft, respectively (see Equation 15).
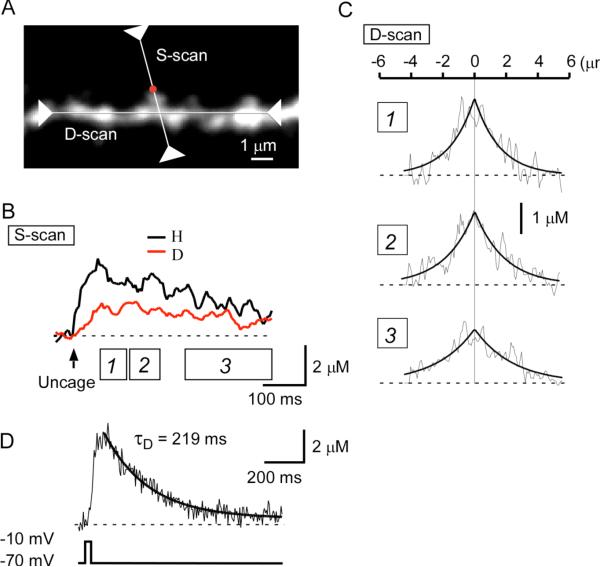
Figure 4. Spread of Ca2+ along the Axis of a Dendritic Shaft.
(A) Stacked Alexa Fluor 594 fluorescence image of a dendritic region subjected to line scanning along both the axis of a spine (S-scan) and that of the parent dendritic shaft (D-scan). Uncaging of MNI-glutamate was performed at the position indicated by the red dot.
(B) Averaged Δ[Ca2+]i in the spine head (H) and at the base of the spine (D).
(C) Spatial gradient of Δ[Ca2+]i at three different time periods (boxes 1, 2, 3) depicted in (B). Smooth curves are exponential functions with length constants of 1.6 μm, 1.9 μm, and 2.4 μm for the periods 1, 2, and 3, respectively. (D) Time course of Δ[Ca2+]i in a dendritic shaft whose soma was depolarized to −10 mV for 40 ms. The decay of Δ[Ca2+]i was fitted with an exponential curve with a time constant (τD) of 219 ms.
The value of τD was obtained from the decay of [Ca2+]i after a sustained depolarization of neurons to −10 mV for 40 ms (Figure 4D). The decay was fitted by a single exponential function with a time constant ranging between 129 and 262 ms and with a mean value of 210 ms (n = 7). This mean value gave an estimate for gD, defined by Equation 3, of 48rD2 μm3 s−1. The mean ± SD diameter of dendrites in our preparations was 0.79 ± 0.15 μm (0.38–1.05 μm, n = 41), giving a mean gD of ~7 μm3 s−1. These data yield an estimate for the apparent diffusion constant of Ca2+ in dendrites (Dapp = λ2/τD) of 12 μm2 s−1 (see Equation 14). This value is similar to the estimates of Dapp for intrinsic buffers ( Allbritton et al., 1992, Gabso et al., 1997 and Maeda et al., 1999), supporting that Ca2+ diffusion in the cytosol was not significantly affected by the usage of the Ca2+ indicator in our experimental conditions, where the Ca2+ binding ratio was raised only by 15.6 relative to the intrinsic binding ratio of 86 (see below). Also, diffusion of Ca2+ indicators might be retarded in the cytosol ( Kurebayashi et al., 1993, Gabso et al., 1997 and Majewska et al., 2000a). It has recently been reported that CA1 pyramidal neurons show signfiicant expression of a diffusible high-affinity Ca2+ buffer, calbindin - D28K ( Muller et al., 2005), and Dapp may be greater in the cells that are not whole-cell dialyzed.
Ca2+ Conductance of the Spine Neck
We next estimated gN based on Equation 2 with the use of the value of gD estimated for a small region of the dendrite at the base of a spine (see “Spine Geometries” in Experimental Procedures). We found that gN was highly related to VH ( Figure 3F). Neck conductance was small (<2 μm3 s−1) when the spine-head volume was <0.1 μm3 ( Figure 3F), but it increased markedly in spines with head volumes of >0.1 μm3. A double logarithmic plot ( Figure 3G) revealed that gN was roughly proportional to the second power of VH. The values of gN were similar to those of gD, supporting the notion that Ca2+ diffusion through the spine neck can substantially affect [Ca2+]i in the spine head.
The head-neck relation was confirmed by values of gN (gN*) estimated from fluorescence images of Alexa Fluor 594-labeled neurons according to the equation
| (4) |
where rN and lN represent the radius and length of the spine neck, respectively ( Hille, 2001). Necks appeared dim and masked by the fluorescence of dendritic shafts and spine heads ( Figure 5A), and we therefore corrected for background fluorescence as shown in Figures 5B and 5C (see Experimental Procedures). For those stubby spines whose neck structures were not well resolved ( Figure 5Ad), we assumed lN as 0.05 μm and obtained rN at the base of the spine. We found that the values of gN were well correlated with those of gN*, especially for spines on the same dendrite (r− = 0.75) (r = 0.74, p < 0.0001, n = 39) ( Figure 5D), despite the inherent imprecision in the estimates of gN*. These data confirmed that gN estimated from Ca2+ imaging did in fact reflect spine-neck geometry.
We found that gN* also depended on the second power of VH ( Figure 5E) and that this relation was due to the correlation of VH with both neck diameter (r = 0.7, p < 0.001, n = 32) and neck length (r = –0.54, p < 0.0011) ( Figure S2). The ranges of neck diameter and length were similar to those determined by a previous analysis based on serial reconstruction of electron-microscopic images ( Harris et al., 1992). It has been difficult to analyze both spine-head volume and neck dimensions by electron microscopy, however, and the head-neck relation has not been previously demonstrated. In contrast, both the head volume and neck dimensions were readily determined both in our Ca2+-imaging experiments and by our Alexa Fluor 594 fluorescence measurements. Estimation of gN by Ca2+ imaging is likely to be especially reliable because it does not depend on the angle of spines with respect to the focal plane.
The head-neck relation was also maintained during structural plasticity associated with long-term potentiation (LTP) induced by repetitive uncaging of MNI-glutamate (Matsuzaki et al., 2004). We reexamined imaging data from our previous study and found that increases in gN* were induced approximately in proportion to spine-head enlargement (r = 0.51, p < 0.0013) ( Figure S3A). Indeed, the increase in gN* was attributable predominantly to an increase in neck radius (r = 0.56, p < 0.0004, n = 35) ( Figure S3B) rather than to a decrease in neck length (r = –0.22, p = 0.21) ( Figure S3C), in contrast to previous proposals ( Fifkova and Anderson, 1981 and Crick, 1982).
Ca2+ Conductance of the Spine Head
Clearance of Ca2+ from the spine head is mediated both by Ca2+ diffusion through the spine neck (gN) and by Ca2+ pumps in the spine head. We quantified the rate of Ca2+ pumping in terms of spine-head conductance (gH) (see Figure 8C). For simplicity, we combined the effects of Ca2+ pumps in the Ca2+ stores and those in the plasma membrane, and we assumed that the capacity of pumping was proportional to both VH and [Ca2+]i. The apparent Ca2+ clearance by Ca2+ pumps in the presence of Ca2+ buffers is then given by equation
| (5) |
where γH and κT represent pump rate (s−1) and total Ca2+ binding ratio ( Neher and Augustine, 1992 and Neher, 1995), respectively, and τH represents the time constant of the Ca2+ signal in the spine head (τH = γH/κT = VH/gH). According to the definition of the Ca2+ binding ratio, κT can be estimated from
| (6) |
where jI and cIH′ represent molar Ca2+ flux at the peak of INMDA and the rate of increase in [Ca2+]i, respectively (see Figure 8E) (see Equation 20). In the actual modeling, we corrected for the effect of Ca2+ pumping (gH) and Ca2+ diffusion through the neck (gN) with (18) and (19). The values of κT thus obtained varied among spines ( Figure 6A) because of errors in their estimation, but they were independent of VH (r = –0.24, p = 0.22, n = 27) and the mean ± SD value was 102 ± 73. We thus estimated the intrinsic Ca2+ binding ratio of the spine head (κ) to be 86 (equal to 102 – 16) in the whole-cell clamped neurons. The estimated value of κ is consistent with those (40–120) determined for many other cell types ( Zhou and Neher, 1993, Helmchen et al., 1996 and Maeda et al., 1999). In the same preparations, Sabatini et al. (2002) estimated κ to be 20; however, these researchers relied on population behavior of Ca2+-decay kinetics among spines, and they did not measure Ca2+ influx directly.
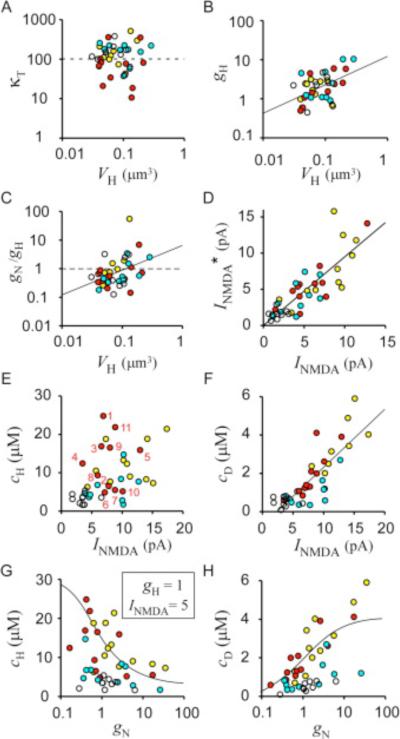
Figure 6. Determinants of Spine Ca2+ Signaling.
(A and B) VH dependence of κT and gH, respectively, among spines.
(C) VH dependence of the gN/gH ratio.
(D) Predicted values of NMDAR-mediated current (INMDA*) from Equation 8 plotted against actual INMDA for each spine. Values of INMDA were obtained at the peak of spine [Ca2+]i as shown in Figure 8E.
(E and F) INMDA dependence of cH and cD, respectively, among spines. Straight lines in (A)–(D) and (F) are linear regression lines.
(G and H) gN dependence of cH and cD, respectively, among spines. Data obtained from the same dendrites are represented by the same colors as those in Figure 3. The smooth lines in (G) and (H) were obtained from (21) and (22), respectively, assuming gH = 1 μm3 s−1, gD = 7 μm3 s−1, INMDA = 5 pA, κT = 102, and gN = 250 VH2.
The value of gH was then obtained from cH, cD, jH (see Figure 8E), and κT according to our model (see Figure 8C):
| (7) |
where jH represents Ca2+ influx at the peak of Δ[Ca2+]i in the spine head (see Equation 19). We found that gH was weakly proportional to VH (r = 0.49, p = 0.002, n = 38) ( Figure 6B), as expected from the relation gH = VH/τH. The time constant of spine-head [Ca2+]i estimated from τH =VH/gH was 0.05 ± 0.06 s (mean ± SD). This value is similar to a previous estimate of 0.014 s obtained from the time constant of decay of Ca2+ transients ( Sabatini et al., 2002), taking into account the fact that we performed our experiments at room temperature (23°C–25°C) as opposed to 34°C in the previous study.
We found that gN was as significant as gH in determining the spine Ca2+ signal, because values of gN and gH varied in a similar range and the ratio between gN and gH was scattered around a value of 1 ( Figure 6C). This ratio was positively correlated with VH (r = 0.39, p < 0.015, n = 38) ( Figure 6C), reflecting the steeper V H dependence of gN (equal to αNV 2H) ( Figure 3G) relative to that of gH (equal to V H/τH). The smaller gN of small spines thus contributes to a greater extent than does the lower rate of Ca2+ pumping (gH) to the larger cH ( Figure 3C) and smaller c D ( Figure 3D) of these spines compared with those of larger spines. Consequently, Ca2+ pumping (gH) is the major mechanism of Ca2+ clearance in certain spines with a small gN, as was previously proposed ( Sabatini et al., 2002). Such isolation of Ca2+ signals by the spine neck, however, was only partial in many spines ( Figure 3E).
Prediction of NMDAR-Mediated Current from Ca2+ Imaging
To test the validity of our equivalent circuit model (see Figure 8C), we predicted NMDAR-mediated current from Ca2+-imaging data and compared the predicted value with the actual whole-cell measurement of INMDA. Based on the model, we can predict the amplitude of NMDAR-mediated current (INMDA*) from measurement of cH and cD and the use of κT, gH, and gD as follows:
| (8) |
where ∈ and F are the fractional Ca2+ current ( Schneggenburger et al., 1993) mediated by the NMDAR and the Faraday constant, respectively (see Equation 23). The predicted values (INMDA*) matched reasonably well with the actual values at the peak of spine [Ca2+]i, even with a fixed value (0.05 s) of τH (equal to VH/gH) (r = 0.83, p < 0.0001, n = 41) ( Figure 6D). Remaining errors could be eliminated by adjusting τH between 0.01 and 0.2 s at each spine (data not shown). This analysis shows that our model accounts well for NMDAR-dependent Ca2+ signaling in dendrites.
Expression of AMPARs versus NMDARs
Finally, we analyzed the coexpression of NMDARs and AMPARs in the same spines. We first obtained a three-dimensional map of AMPAR-mediated current as described previously (Matsuzaki et al., 2001) by measurement of current in the presence of APV and in the absence of CNQX (Figures 7A–7D). We then removed APV and measured NMDAR-mediated current evoked at the distal tip of spines in the presence of CNQX (Figures 7E and 7F). The level of AMPAR expression increased with spine size (r = 0.75, n = 31) ( Figure 7G), consistent with our previous results ( Matsuzaki et al., 2001). The spines that showed a higher level of expression of AMPARs also expressed a larger number of NMDARs (r = 0.73, n =31) ( Figure 7H). As the spine-head volume increased, the AMPAR/NMDAR ratio also increased. Furthermore, a substantial number of NMDARs was present even in spines with a low level of AMPAR expression ( Figure 7H).
Discussion
We have systematically investigated the dependence of NMDAR-mediated Ca2+ signaling on spine geometry in hippocampal CA1 pyramidal neurons. Two-photon uncaging of MNI-glutamate allowed us to apply glutamate at any selected spine or dendritic surface and revealed a marked dependence of NMDAR-mediated Ca2+ signaling on spine geometry. The role of the spine neck in determining the fate of the Ca2+ signal, which we have clarified in the present study, is similar to the one originally proposed for attenuation of electrical signals by this structure (Rall, 1970); the spine neck was thus suggested to function physiologically to adjust the relative weights of synaptic inputs. Our data instead suggest that the spine neck determines the relative occurrence of Ca2+- dependent synaptic plasticity at each spine.
Expression of NMDARs
We have found that all small spines manifest a substantial NMDAR-mediated current (INMDA). The extent of IAMPA in small spines was less than that of INMDA, whereas the ratio of these currents changed markedly as the spine-head volume increased. Given that small spines have small postsynaptic densities (PSDs) ( Harris and Stevens, 1989), our data suggest that NMDARs are anchored to small PSDs more effectively than are AMPARs, possibly as a result of direct binding of NMDARs to many PSD proteins—such as PSD95, α-actinin, Ca2+- and calmodulin-dependent protein kinase II, and S-SCAM—that do not bind with high affinity to AMPARs ( Sheng and Kim, 2002 and Kasai et al., 2003). In addition, AMPARs may require a larger amount of F-actin for their efficient expression in PSDs ( Kim and Lisman, 1999 and Krucker et al., 2000). Thus, small spines might fulfill some of the criteria for “silent synapses” ( Liao et al., 1995, Isaac et al., 1995 and Durand et al., 1996). We detected small AMPAR-mediated currents even in small spines, however, suggesting that there are no strictly silent synapses, although we cannot exclude the possibility that such small currents were mediated by extrasynaptic receptors.
Our results provide a direct demonstration that expression of functional NMDARs (INMDA) is correlated with spine-head volume (VH). This finding is consistent with ultrastructural observations indicating that the amount of NMDAR immunoreactivity is correlated with the size of PSDs ( Nusser et al., 1998), which is also correlated with VH ( Harris and Stevens, 1989). However, it has been difficult with traditional serial reconstruction techniques based on electron microscopy to demonstrate a direct positive correlation between spine-head volume and NMDAR density. We also found that INMDA was correlated with IAMPA at the level of single spines, consistent with the electrophysiological demonstration that the amplitudes of AMPAR and NMDAR components of EPSCs are often highly correlated ( Tyzio et al., 1999 and Groc et al., 2002). The amplitudes of NMDAR-mediated currents were more variable than predicted, even though we averaged three current traces to reduce channel noise to a CV of 0.11, suggesting the operation of additional regulatory mechanisms of NMDAR expression other than that dependent on VH.
The amplitude of INMDA showed only a weak correlation with spine-head [Ca2+]i within each dendrite (cH, r− = 0.18) ( Figure 6E). This apparent paradox is explained by the fact that the expected correlation between INMDA and cH was canceled out by the positive correlation of INMDA with VH and the negative correlation between VH and cH ( Figure 8B). Large variability in cH, even among spines with a similar INMDA, were explained by the diversity of spine structures: spines 1, 7, and 9 in Figure 6E showed similar INMDA values, but their structures as reflected by VH and gN (especially gN) were highly divergent ( Figure 3G) in a manner that can account for the differences in cH ( Figure 8B). Thus, spine structure is as critical as INMDA itself in determining cH. It is possible that the expression of NMDARs is minimized in small spines to reduce cD ( Figure 6F), whereas spine structure determines the amplitude of cH as necessary ( Figures 8A and 8B).
Spine Head-Neck Relations
Our measurement of Ca2+ diffusion demonstrated that the Ca2+ conductance of the spine neck was highly dependent on spine-head volume (VH), roughly in proportion to the second power of VH. We have found that the spine neck is dynamically altered during the spine-head enlargement that underlies LTP ( Matsuzaki et al., 2004), suggesting that the same mechanisms that sculpt the spine head also affect spine-neck conductance. Such spine head-neck relations appear to be preserved in individuals with mental retardation ( Purpura, 1974 and Fiala et al., 2002), particularly in those with fragile X syndrome ( Hinton et al., 1991), in whom spines tend to have smaller heads and longer necks than in control individuals.
A similar tendency is present in the data of a study based on serial electron-microscopic reconstruction, in spite of a large variability in the measurements (Harris et al., 1992). A weak positive correlation between spine-head volume and neck diameter as well as a negative correlation between neck length and neck diameter are thus apparent (Harris et al., 1992). In Golgi-stained preparations, spines with a large head (mushroom spines) also tend to have thicker necks than do thin spines (Peters and Kaiserman-Abramof, 1970). In contrast with morphological measurements, our functional measurement of neck Ca2+ conductance (gN) provides an integrated index of the entire neck structure and has established the correlation between neck structure and head volume.
It should be noted, however, that the neck Ca2+ conductance was highly variable, differing by a factor of >10 even in spines with similar head volumes and that VH and gN can be independently controlled to some extent. This finding is consistent with the existence of stubby and mushroom spines, although we could not determine a clear threshold value of gN that delineates these two types of spine. Moreover, most spines could be grouped into one of three classes—thin, mushroom, and stubby—on the basis of both VH and gN* ( Figure S3E), although there was no clear boundary between these designations. The three types of spine may thus simply reflect three extremes of one continuous population of spines. We detected more typical mushroom spines with long narrow necks and large heads (filled stars in Figure S3E) in slice culture preparations, in which cells were allowed to recover fully from the injury inflicted by sectioning than we did in acute hippocampal slices. Although such spines diverged more markedly from the power relation gN = αNV 2H, they were relatively rare (3.5%, 4 out of 115 spines), and, on the whole, the correlation between VH and gN* in cultured slice preparations was steep and significant (r = 0.55, p < 0.0001, Figure S3E). It remains to be determined whether the same rule applies to other neurons and brain regions. It is possible that distinct relations between gN and VH contribute to neuron-specific regulation of spine structural plasticity.
Influence of the Spine Neck on Dendritic Ca2+ Signaling
The neck Ca2+ conductance (gN) and head Ca2+ pumping (gH) both play a role in isolation of spine Ca2+ signaling from the dendritic shaft and show a positive correlation with spine-head volume (VH). However, we found that gN is much more important than gH in the control of cH ( Figure 8B). We thus showed that the VH dependence and dynamic range of gN were greater than those of gH. Furthermore, the dependence of cH and cD on spine structure can be explained to a large extent by gN, even assuming a constant gH, in our model ( Figures 6G and 6H). In contrast, if gN is maintained constant, cR would remain constant as VH increases ( Figure 8G). Finally, our model predicts that shaft [Ca2+]i (cD) approaches zero at VH = 0 ( Figure 3D) (see Equation 27) as a result of the steep (second power) VH dependence of gN. Thus, the dependence of gN on V 2H plays a pivotal role in isolation of the Ca2+ signal in small spines.
In the foregoing analysis, we have assumed NMDAR-mediated Ca2+ influx to be stationary (Figure 8C), although it is actually time dependent (Figure 1C), as is the case with EPSCs. In the time-dependent condition, direct dilution of Ca2+ by the volumes of the spine head and dendritic shaft comes into play (Figure 8D). Our simulation, however, reveals that spine-neck geometry is also the pivotal factor for spine Ca2+ signaling in the time-dependent condition. First, the coupling ratio (cR) does not depend markedly on VH when gN is held constant ( Figure 8G), even in the EPSC-like model ( (29) and (30)). This finding indicates that the steep V H dependence of cR in the EPSC-like condition also must be due to the VH dependence of gN . Second, shaft [Ca2+]i (cD) is reduced when Ca2+ influx is time dependent ( Figures 8E and 8F). As far as the time integrals of increases in [Ca2+]i are concerned, however, Equation 32 shows that the ratio between the time integral of the increase in head [Ca2+] and that of the increase in shaft [Ca2+]i is exactly the same as cR in the stationary condition. Third, the time integral of CH(t) depends on gN in the same manner ( Equation 33), as is apparent in the stationary condition ( Equation 21), although the peak value of CH(t) is dependent only on VH , not on gN, in impulsive Ca2+ influx ( Equation 34).
A rapid decay time constant (14 ms) for the Ca2+ signal in the spine head obtained in a previous study was attributed mostly to Ca2+ pumping (gH) in the spine head, not to Ca2+ outflow (gN) into the dendritic shaft ( Sabatini et al., 2002). We calculate from this estimate that the head Ca2+ conductance (gH = VH/τH) of a typical spine with a VH of 0.05 μm3 would be 3.6 μm3 s−1. If we assume a spine neck with typical dimensions of rN = 0.1 μm and lN = 0.2 μm, we can estimate, from Equation 4, that gN is as large as 1.1 μm3 s−1, even assuming a moderate value of Dapp of 12 μm2 s−1 derived from our data. These calculations indicate that Ca2+ diffusion along the spine neck plays a substantial role in Ca2+ clearance in most spines, even assuming the large gH found by Sabatini et al. (2002). Indeed, we detected a marked increase in shaft [Ca2+]i for most spines under our experimental conditions, in which the Ca2+ binding ratio of the Ca2+ indicator was only 15.6, whereas the intrinsic Ca2+ binding ratio was estimated as 86. Sabatini et al. (2002) detected relatively small increases in the variance of shaft [Ca2+]i (~20% of the variance of spine [Ca2+] in their Figures 4C and 4D) during back-propagating action potential-induced Ca2+ transients, and these were considered as evidence against diffusion of Ca2+ through the spine neck. The small increases in shaft noise, however, can be attributed to a large dilution effect of the dendritic shaft on impulsive Ca2+ influx ( Figure 8F). It has been proposed using high-affinity Ca2+ indicators that there was a diffusional coupling between the spine head and dendritic shaft ( Majewska et al., 2000a and Holthoff et al., 2002) and that spine elongation resulted in a better isolation of the spine Ca2+ signal ( Majewska et al., 2000b and Korkotian et al., 2004).
The role of the spine neck in determination of Ca2+ signaling is similar to the one originally proposed for attenuation of electrical signals (Rall, 1970 and Coss and Perkel, 1985). This latter notion was subsequently dismissed because of the diffusion of small molecules through the spine neck (Svoboda et al., 1996). We believe that our present data indicate that Rall's original idea deserves further consideration, given that we detected substantial expression of NMDARs even in small spines, which have a small neck conductance. The electrical conductance of the spine neck can be estimated from Equation 4 by replacing Dapp with 1/ρ, where ρ represents the specific resistance of the cytoplasm in the spine neck. If we assume ρ = 100 Ω cm, the equation gives a value of 963 pS for the narrowest possible spine neck with a diameter of 0.05 μm and a length of 2 μm ( Harris et al., 1992). The current flow into the dendrite would thus have been reduced by half assuming the opening of 50 channels with a single-channel conductance of 20 pS. This effect is predicted to be small for AMPARs, because they are expressed at a minimal level in small spines with a small gN ( Figure 7G). In contrast, expression of NMDARs is substantial in small spines, and NMDAR-mediated currents might indeed be electrically attenuated by narrow spine necks ( Rall, 1970 and Johnston and Wu, 1995). This attenuation might limit the infinitely large head [Ca2+]i (cH) at small VH that is predicted by Equation 26.
Spine Necks and Structural Plasticity
Small spines have been found to be less stable than large spines in vivo (Grutzendler et al., 2002 and Trachtenberg et al., 2002), and we have previously shown that small spines in slice preparations are the preferential sites for induction of long-term structural plasticity (Matsuzaki et al., 2004). We have now established that small spines tend to have narrow necks, which impede the efflux of Ca2+ into the dendritic shaft, and that this structural feature is the major contributing factor to the large, isolated increases in [Ca2+]i in small spine heads (Figure 8A). Their necks thus allow individual expression of LTP in small spines (Matsuzaki et al., 2004). Synaptic Ca2+ signaling in small spines appears to be optimized for selective induction of plasticity. In contrast, Ca2+ signaling in large spines appears to be optimized for smaller increases in head [Ca2+]i and larger increase in shaft [Ca2+]i (Figure 8A). Such Ca2+ efflux may contribute to synaptic plasticity, although its precise role remains to be determined. Spines actually exhibit a continuous structural distribution (Figure 3G; Figure S3E). Given that spine necks quantitatively regulate dendritic Ca2+ signals, they are likely important determinants of synaptic plasticity, which is bidirectionally regulated by Ca2+ signals (Lisman, 1989 and Shouval et al., 2002).
The spine neck may also play a role in consolidation of spine structural plasticity. We have shown that large spines undergo marked enlargement during photochemical tetanus but that this morphological effect is not permanent (Matsuzaki et al., 2004), indicating that the consolidation of structural plasticity is impaired in large spines. This impairment cannot be attributed only to the smaller increases in [Ca2+]i in such spines because many small spines showed similar increases (Figure 3C) yet their enlargement was long lasting (Supplemental Figure 2b of Matsuzaki et al., 2004). We have now shown that spine-neck structure (gN) is highly dependent on VH. The impaired consolidation of enlargement of large spines can thus now be explained either by their large head volume or thick neck geometry ( Figure S3D).
In summary, we propose that spine-head and spine-neck geometries play distinct roles in synaptic transmission and its plasticity, respectively. We have shown that the spine neck is the most important determinant of NMDAR-dependent Ca2+ signaling and Ca2+-dependent synaptic plasticity, whereas the spine head determines synaptic transmission per se, given that spine-head volume is critical for expression of NMDARs (present study) and of AMPARs (Matsuzaki et al., 2001 and Matsuzaki et al., 2004) both in the steady state and during plasticity.
Experimental Procedures
Preparations
Hippocampal slices with a thickness of 350 μm were prepared from 15- to 22-day-old Sprague-Dawley rats (Matsuzaki et al., 2001). All physiological experiments were performed at room temperature (23°C–25°C), unless otherwise noted. For a detailed description, see the Supplemental Data.
Two-Photon Excitation Imaging and Uncaging of MNI-Glutamate
Time-lapse two-photon imaging of dendritic spines was performed with an upright microscope (BX50WI; Olympus, Tokyo, Japan) equipped with a water-immersion objective lens (LUMPlanFI/IR 60×, numerical aperture of 0.9) and with a self-made program based on LabView (National Instruments, Austin, TX). For a further description of uncaging and Ca2+ imaging, see the Supplemental Data.
Ca2+ Imaging
Calcium imaging was based on the OGB-5N/Alexa Fluor 594 fluorescence ratio (R). Fluorescence emission was acquired at 400–570 nm (green channel) and 590–650 nm (red channel) for OGB-5N and Alexa Fluor 594, respectively. Fluorescence of OGB-5N and Alexa Fluor 594 contributed less than 1% to the total fluorescence of the red and green channels, respectively, in our recording conditions. Background levels of Alexa Fluor 594 and OGB-5N fluorescence were obtained from the same image and were subtracted from specific signals. We performed in situ calibration of R by whole-cell perfusion with internal solutions containing 10 mM EGTA or 10 mM Ca2+, which provided estimates of R min and Rmax as 0.112 and 1.176. Given that R before stimulation (R0) was similar to Rmin, we used the relation ΔR = R – R0 to estimate [Ca2+]i in micromolar as 32 × ΔR/(1.1 – ΔR) = KCa(R – Rmin)/(Rmax – R), assuming the affinity (KCa) of OGB-5N for Ca2+ to be 32 μM ( DiGregorio and Vergara, 1997). We started imaging roughly 30 min after whole-cell perfusion, when the fluorescence intensity had reached its plateau value. Throughout the recording period for more than 1 hr, we detected neither significant change in the resting [Ca2+]i nor increase in the decay time constants of NMDAR-mediated Ca2+ transients in spine heads (30–220 ms).
Electrophysiology
Neurons were voltage clamped at −70 mV, and the currents were low-pass filtered at 2 kHz and sampled at 50 kHz. Series resistance was 15.4 ± 4.0 MΩ (mean ± SD). Three-dimensional mapping of AMPARs was performed as described in the Supplemental Data.
Spine Geometries
We first calibrated the fluorescence of Alexa Fluor 594 in a volume of cytosol with the use of the largest spine in a dendritic region as described (Matsuzaki et al., 2004), assuming that Alexa Fluor 594 homogeneously filled the volume of dendrites and σx and σz to be 0.18 and 0.78 μm, respectively. For more details, see the Supplemental Data.
Spine Ca2+ Model
We consider a single-compartment model of the dendritic spine in which Ca2+ enters through NMDARs and exits both through the action of Ca2+ pumps and by diffusion through a spine neck into a dendritic shaft of infinite length (Figure 8C). With the rapid buffer approximation (Neher, 1998 and Maeda et al., 1999), the spatiotemporal distribution of [Ca2+]i along the dendritic shaft [CD(x,t)] with a uniform radius (rD) can be described by
| (9) |
where
| (10) |
and
| (11) |
DCa represents the diffusion constant of Ca2+, Di and κi the diffusion constants and Ca2+ binding ratios of existing Ca2+ buffer molecules, and τD the time constant of [Ca2+]i in the dendritic shaft. For simplicity, we assume [Ca2+]i = 0 in the resting state. The spine is at x = 0, and we assume that Ca2+ flux is proportional to the difference between [Ca2+]i in the spine head [CH(t)] and that in the dendritic shaft [CD(0,t)] and to the Ca2+ conductance of the spine neck (gN, Equation 4). We then have
| (12) |
| (13) |
with a length constant (μm) of
| (14) |
If we define dendritic-shaft conductance (μm3 s−1) as
| (15) |
Equation 12 yields Equation 1 and
| (16) |
Amplitudes of NMDAR currents (INMDA) were converted to influx of Ca2+ into a volume of 1 μm3 by
where F is the Faraday constant and ∈ the fractional Ca2+ current of NMDARs. In pyramidal neurons, ∈ was estimated as 0.107 ( Garaschuk et al., 1996), which gives
For [Ca2+]i in the spine head, CH(t), we have
| (17) |
The values of κT and gH were estimated from the following two simultaneous equations derived from Equation 17:
| (18) |
and
| (19) |
where cIH′, cIH, cID, and jI were obtained from traces at the peak of JH(t), whereas c H, cD, and jH were obtained at the peak of CH(t) ( Figure 8E). In the actual setting of the parameters,
| (20) |
When Ca2+ influx is stationary and c = jH/κT, (1) and (19) yield
| (21) |
and
| (22) |
Using (16) and (21), we also have
| (23) |
We found that spine-head volume (VH) was related to the expression of NMDARs ( Figure 3B) and spine-neck Ca2+ conductance ( Figure 3G) as
| (24) |
| (25) |
respectively. With the use of these relations, the VH dependence of cH, cD, and cR was obtained from (21), (22) and (16), as
| (26) |
| (27) |
and
| (28) |
(24), (25), (26), (27) and (28) fit well the actual data in Figures 3B–3G, assuming a set of values (gD, τH, α0, α1, αN) as (5.02, 0.036, 17, 153, 206), (8.22, 0.066, 12, 93, 281), (8.03, 0.064, 28, 186, 883), and (7.5, 0.039, 8.8, 11.6, 219) for red, blue, yellow, and white dendrites, respectively. The negative VH dependence of cH ( Figure 3C) ( Equation 26) could be attributed predominantly to the positive VH dependence of gN ( Figure 3G) ( Equation 25, αN) and gH ( Equation 5) as well as to the presence of NMDARs even in small spines ( Figure 3B) ( Equation 24, α0). The positive VH dependence of cD ( Figure 3D) ( Equation 27) could be attributed to the positive VH dependence of gN ( Equation 25, αN) and of INMDA ( Figure 3B) ( Equation 24, α1). If gN depends on a power of VH of <2, cD shows a nonzero positive value at VH close to 0, indicating that the V 2H dependence of gN helps isolate the Ca2+ signal in small spines.
When Ca2+ influx is time dependent, the Laplace transformation of (9), (12) and (17) yields the transforms of CH(t) and CD(t) as
| (29) |
and
| (30) |
respectively, where Ĉ(s) is the transform of JH(t)/κT, and
| (31) |
Given that ĈD(0) = ĈR(0)ĈH(0) and ,
| (32) |
showing that the integrated CD(t) and CH(t) depend on spine structure exactly as in the stationary condition ( Equation 16). Similarly, Equation 29 gives
| (33) |
indicating that integrated CH(t) depends on gN as does the stationary cH ( Equation 21). The peak amplitude of CH(t) for impulsive Ca2+ influx is determined by dilution due to spine-head volume (VH), as Equation 29 gives
| (34) |
To obtain time-dependent solutions, we analytically derived inverse Laplace transforms of ĈH(s)Ĉ(s) or ĈD(s)Ĉ(s) with Mathematica 5.0 software. Numerical solutions were then calculated for an impulse response [Ĉ(s) = 1] (Figure 8F) and for an EPSC-like Ca2+ influx
(Figures 8E and 8G). The factor 1.4 serves to adjust the peak amplitude of the influx as c. The value of gN was either set constant, as indicated, or varied as gN = 250 V 2H, whereas τH = 0.05 s and gD = 7 μm3 s−. The time-dependent simulation revealed that values of CR and gN 2+ obtained from EPSC-like Ca2+ influx (Figure 8E) were less than the actual values by ~40% (Figure 8G), but we do not attempt to correct for this because it does not affect the conclusions of the present work.
Acknowledgments
We thank N. Takahashi and T. Kise for technical assistance, as well as K. Hama and H. Hirase for helpful discussion. This work was supported by Grants-in-Aid from the Ministry of Education, Culture, Sports, Science, and Technology of Japan (H.K. and M.M.) as well as by grants from the Human Frontier Science Program (G.C.R.E.-D. and H.K.), NIH (G.C.R.E.-D. and H.K.), NSF (G.C.R.E.-D), the Takeda Science Foundation (H.K.), and the McKnight Endowment Fund for Neuroscience (G.C.R.E.-D.).
References
- Allbritton NL, Meyer T, Stryer L. Range of messenger action of calcium ion and inositol 1,4,5-trisphosphate. Science. 1992;258:1812–1815. doi: 10.1126/science.1465619. [DOI] [PubMed] [Google Scholar]
- Bonhoeffer T, Yuste R. Spine motility. Phenomenology, mechanisms, and function. Neuron. 2002;35:1019–1027. doi: 10.1016/s0896-6273(02)00906-6. [DOI] [PubMed] [Google Scholar]
- Coss RG, Perkel DH. The function of dendritic spines: a review of theoretical issues. Behav. Neural Biol. 1985;44:151–185. doi: 10.1016/s0163-1047(85)90170-0. [DOI] [PubMed] [Google Scholar]
- Crick F. Do dendritic spines twitch? Trends Neurosci. 1982;5:44–46. [Google Scholar]
- DiGregorio DA, Vergara JL. Localized detection of action potential-induced presynaptic calcium transients at a Xenopus neuromuscular junction. J. Physiol. 1997;505:585–592. doi: 10.1111/j.1469-7793.1997.585ba.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durand GM, Kovalchuk Y, Konnerth A. Long-term potentiation and functional synapse induction in developing hippocampus. Nature. 1996;381:71–75. doi: 10.1038/381071a0. [DOI] [PubMed] [Google Scholar]
- Emptage N, Bliss TV, Fine A. Single synaptic events evoke NMDA receptor-mediated release of calcium from internal stores in hippocampal dendritic spines. Neuron. 1999;22:115–124. doi: 10.1016/s0896-6273(00)80683-2. [DOI] [PubMed] [Google Scholar]
- Fiala JC, Spacek J, Harris KM. Dendritic spine pathology: cause or consequence of neurological disorders? Brain Res. Brain Res. Rev. 2002;39:29–54. doi: 10.1016/s0165-0173(02)00158-3. [DOI] [PubMed] [Google Scholar]
- Fifkova E, Anderson CL. Stimulation-induced changes in dimensions of stalks of dendritic spines in the dentate molecular layer. Exp. Neurol. 1981;74:621–627. doi: 10.1016/0014-4886(81)90197-7. [DOI] [PubMed] [Google Scholar]
- Gabso M, Neher E, Spira ME. Low mobility of the Ca2+ buffers in axons of cultured Aplysia neurons. Neuron. 1997;18:473–481. doi: 10.1016/s0896-6273(00)81247-7. [DOI] [PubMed] [Google Scholar]
- Garaschuk O, Schneggenburger R, Schirra C, Tempia F, Konnerth A. Fractional Ca2+ currents through somatic and dendritic glutamate receptor channels of rat hippocampal CA1 pyramidal neurones. J. Physiol. 1996;491:757–772. doi: 10.1113/jphysiol.1996.sp021255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Groc L, Gustafsson B, Hanse E. Spontaneous unitary synaptic activity in CA1 pyramidal neurons during early postnatal development: constant contribution of AMPA and NMDA receptors. J. Neurosci. 2002;22:5552–5562. doi: 10.1523/JNEUROSCI.22-13-05552.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grutzendler J, Kasthuri N, Gan WB. Long-term dendritic spine stability in the adult cortex. Nature. 2002;420:812–816. doi: 10.1038/nature01276. [DOI] [PubMed] [Google Scholar]
- Harris KM, Stevens JK. Dendritic spines of CA 1 pyramidal cells in the rat hippocampus: serial electron microscopy with reference to their biophysical characteristics. J. Neurosci. 1989;9:2982–2997. doi: 10.1523/JNEUROSCI.09-08-02982.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris KM, Jensen FE, Tsao B. Three-dimensional structure of dendritic spines and synapses in rat hippocampus (CA1) at postnatal day 15 and adult ages: implications for the maturation of synaptic physiology and long-term potentiation. J. Neurosci. 1992;12:2685–2705. doi: 10.1523/JNEUROSCI.12-07-02685.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris KM, Fiala JC, Ostroff L. Structural changes at dendritic spine synapses during long-term potentiation. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2003;358:745–748. doi: 10.1098/rstb.2002.1254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Helmchen F. Raising the speed limit—fast Ca(2+) handling in dendritic spines. Trends Neurosci. 2002;25:438–441. doi: 10.1016/s0166-2236(02)02232-4. [DOI] [PubMed] [Google Scholar]
- Helmchen F, Imoto K, Sakmann B. Ca2+ buffering and action potential-evoked Ca2+ signaling in dendrites of pyramidal neurons. Biophys. J. 1996;70:1069–1081. doi: 10.1016/S0006-3495(96)79653-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hille B. Ion Channels of Excitable Membranes. Sinauer Associates; Sunderland, UK: 2001. [Google Scholar]
- Hinton VJ, Brown WT, Wisniewski K, Rudelli RD. Analysis of neocortex in three males with the fragile X syndrome. Am. J. Med. Genet. 1991;41:289–294. doi: 10.1002/ajmg.1320410306. [DOI] [PubMed] [Google Scholar]
- Holthoff K, Tsay D, Yuste R. Calcium dynamics of spines depend on their dendritic location. Neuron. 2002;33:425–437. doi: 10.1016/s0896-6273(02)00576-7. [DOI] [PubMed] [Google Scholar]
- Isaac JT, Nicoll RA, Malenka RC. Evidence for silent synapses: implications for the expression of LTP. Neuron. 1995;15:427–434. doi: 10.1016/0896-6273(95)90046-2. [DOI] [PubMed] [Google Scholar]
- Johnston D, Wu SM-S. Foundations of Cellular Neurophysiology. MIT Press; Boston, MA: 1995. [Google Scholar]
- Kasai H, Matsuzaki M, Noguchi J, Yasumatsu N, Nakahara H. Structure-stability-function relationships of dendritic spines. Trends Neurosci. 2003;26:360–368. doi: 10.1016/S0166-2236(03)00162-0. [DOI] [PubMed] [Google Scholar]
- Kim CH, Lisman JE. A role of actin filament in synaptic transmission and long-term potentiation. J. Neurosci. 1999;19:4314–4324. doi: 10.1523/JNEUROSCI.19-11-04314.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koester HJ, Sakmann B. Calcium dynamics in single spines during coincident pre- and postsynaptic activity depend on relative timing of back-propagating action potentials and sub-threshold excitatory postsynaptic potentials. Proc. Natl. Acad. Sci. USA. 1998;95:9596–9601. doi: 10.1073/pnas.95.16.9596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korkotian E, Holcman D, Segal M. Dynamic regulation of spine-dendrite coupling in cultured hippocampal neurons. Eur. J. Neurosci. 2004;20:2649–2663. doi: 10.1111/j.1460-9568.2004.03691.x. [DOI] [PubMed] [Google Scholar]
- Kovalchuk Y, Eilers J, Lisman J, Konnerth A. NMDA receptor-mediated subthreshold Ca(2+) signals in spines of hippo-campal neurons. J. Neurosci. 2000;20:1791–1799. doi: 10.1523/JNEUROSCI.20-05-01791.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krucker T, Siggins GR, Halpain S. Dynamic actin filaments are required for stable long-term potentiation (LTP) in area CA1 of the hippocampus. Proc. Natl. Acad. Sci. USA. 2000;97:6856–6861. doi: 10.1073/pnas.100139797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurebayashi N, Harkins AB, Baylor SM. Use of fura red as an intracellular calcium indicator in frog skeletal muscle fibers. Biophys. J. 1993;64:1934–1960. doi: 10.1016/S0006-3495(93)81564-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao D, Hessler NA, Malinow R. Activation of post-synaptically silent synapses during pairing-induced LTP in CA1 region of hippocampal slice. Nature. 1995;375:400–404. doi: 10.1038/375400a0. [DOI] [PubMed] [Google Scholar]
- Lisman J. A mechanism for the Hebb and the anti-Hebb processes underlying learning and memory. Proc. Natl. Acad. Sci. USA. 1989;86:9574–9578. doi: 10.1073/pnas.86.23.9574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lisman J. Long-term potentiation: outstanding questions and attempted synthesis. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2003;358:829–842. doi: 10.1098/rstb.2002.1242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maeda H, Ellis-Davies GC, Ito K, Miyashita Y, Kasai H. Supralinear Ca2+ signaling by cooperative and mobile Ca2+ buffering in Purkinje neurons. Neuron. 1999;24:989–1002. doi: 10.1016/s0896-6273(00)81045-4. [DOI] [PubMed] [Google Scholar]
- Majewska A, Brown E, Ross J, Yuste R. Mechanisms of calcium decay kinetics in hippocampal spines: role of spine calcium pumps and calcium diffusion through the spine neck in biochemical compartmentalization. J. Neurosci. 2000a;20:1722–1734. doi: 10.1523/JNEUROSCI.20-05-01722.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Majewska A, Tashiro A, Yuste R. Regulation of spine calcium dynamics by rapid spine motility. J. Neurosci. 2000b;20:8262–8268. doi: 10.1523/JNEUROSCI.20-22-08262.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuzaki M, Ellis-Davies GCR, Nemoto T, Miyashita Y, Iino M, Kasai H. Dendritic spine geometry is critical for AMPA receptor expression in hippocampal CA1 pyramidal neurons. Nat. Neurosci. 2001;4:1086–1092. doi: 10.1038/nn736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuzaki M, Honkura N, Ellis-Davies GC, Kasai H. Structural basis of long-term potentiation in single dendritic spines. Nature. 2004;429:761–766. doi: 10.1038/nature02617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mori H, Mishina M. Roles of diverse glutamate receptors in brain functions elucidated by subunit-specific and region-specific gene targeting. Life Sci. 2003;74:329–336. doi: 10.1016/j.lfs.2003.09.020. [DOI] [PubMed] [Google Scholar]
- Muller A, Kukley M, Stausberg P, Beck H, Muller W, Dietrich D. Endogenous Ca2+ buffer concentration and Ca2+ microdomains in hippocampal neurons. J. Neurosci. 2005;25:558–565. doi: 10.1523/JNEUROSCI.3799-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakazawa K, McHugh TJ, Wilson MA, Tonegawa S. NMDA receptors, place cells and hippocampal spatial memory. Nat. Rev. Neurosci. 2004;5:361–372. doi: 10.1038/nrn1385. [DOI] [PubMed] [Google Scholar]
- Neher E. The use of fura-2 for estimating Ca buffers and Ca fluxes. Neuropharmacology. 1995;34:1423–1442. doi: 10.1016/0028-3908(95)00144-u. [DOI] [PubMed] [Google Scholar]
- Neher E. Usefulness and limitations of linear approximations to the understanding of Ca++ signals. Cell Calcium. 1998;24:345–357. doi: 10.1016/s0143-4160(98)90058-6. [DOI] [PubMed] [Google Scholar]
- Neher E, Augustine GJ. Calcium gradients and buffers in bovine chromaffin cells. J. Physiol. 1992;450:273–301. doi: 10.1113/jphysiol.1992.sp019127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicholls JG, Martin AR, Wallace BG, Fuchs PA. From Neuron to Brain. Sinauer Associates; Sunderland, UK: 2001. [Google Scholar]
- Nimchinsky EA, Yasuda R, Oertner TG, Svoboda K. The number of glutamate receptors opened by synaptic stimulation in single hippocampal spines. J. Neurosci. 2004;24:2054–2064. doi: 10.1523/JNEUROSCI.5066-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nusser Z, Lujan R, Laube G, Roberts JD, Molnar E, Somogyi P. Cell type and pathway dependence of synaptic AMPA receptor number and variability in the hippocampus. Neuron. 1998;21:545–559. doi: 10.1016/s0896-6273(00)80565-6. [DOI] [PubMed] [Google Scholar]
- Peters A, Kaiserman-Abramof IR. The small pyramidal neuron of the rat cerebral cortex. The perikaryon, dendrites and spines. Am. J. Anat. 1970;127:321–355. doi: 10.1002/aja.1001270402. [DOI] [PubMed] [Google Scholar]
- Petrozzino JJ, Miller LDP, Connor JA. Micromolar Ca2+ transients in dendritic spines of hippocampal pyramidal neurons in brain slice. Neuron. 1995;14:1223–1231. doi: 10.1016/0896-6273(95)90269-4. [DOI] [PubMed] [Google Scholar]
- Purpura DP. Dendritic spine “dysgenesis” and mental retardation. Science. 1974;186:1126–1128. doi: 10.1126/science.186.4169.1126. [DOI] [PubMed] [Google Scholar]
- Rall W. Cable properties of dendrites and effects of synaptic location. In: Andersen P, Jansen JKS, editors. Excitatory Synapic Mechanisms. Universitetsforlaget; Oslo: 1970. pp. 175–187. [Google Scholar]
- Rusakov DA, Kullmann DM. Extrasynaptic glutamate diffusion in the hippocampus: ultrastructural constraints, uptake, and receptor activation. J. Neurosci. 1998;18:3158–3170. doi: 10.1523/JNEUROSCI.18-09-03158.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabatini BL, Oertner TG, Svoboda K. The life cycle of Ca(2+) ions in dendritic spines. Neuron. 2002;33:439–452. doi: 10.1016/s0896-6273(02)00573-1. [DOI] [PubMed] [Google Scholar]
- Schneggenburger R, Zhou Z, Konnerth A, Neher E. Fractional contribution of calcium to the cation current through glutamate receptor channels. Neuron. 1993;11:133–143. doi: 10.1016/0896-6273(93)90277-x. [DOI] [PubMed] [Google Scholar]
- Sheng M, Kim MJ. Postsynaptic signaling and plasticity mechanisms. Science. 2002;298:776–780. doi: 10.1126/science.1075333. [DOI] [PubMed] [Google Scholar]
- Shepherd GM. The dendritic spine: a multifunctional integrative unit. J. Neurophysiol. 1996;75:2197–2210. doi: 10.1152/jn.1996.75.6.2197. [DOI] [PubMed] [Google Scholar]
- Shouval HZ, Castellani GC, Blais BS, Yeung LC, Cooper LN. Converging evidence for a simplified biophysical model of synaptic plasticity. Biol. Cybern. 2002;87:383–391. doi: 10.1007/s00422-002-0362-x. [DOI] [PubMed] [Google Scholar]
- Svoboda K, Tank DW, Denk W. Direct measurement of coupling between dendritic spines and shafts. Science. 1996;272:716–719. doi: 10.1126/science.272.5262.716. [DOI] [PubMed] [Google Scholar]
- Trachtenberg JT, Chen BE, Knott GW, Feng G, Sanes JR, Welker E, Svoboda K. Long-term in vivo imaging of experience-dependent synaptic plasticity in adult cortex. Nature. 2002;420:788–794. doi: 10.1038/nature01273. [DOI] [PubMed] [Google Scholar]
- Tyzio R, Represa A, Jorquera I, Ben Ari Y, Gozlan H, Aniksztejn L. The establishment of GABAergic and glutamatergic synapses on CA1 pyramidal neurons is sequential and correlates with the development of the apical dendrite. J. Neurosci. 1999;19:10372–10382. doi: 10.1523/JNEUROSCI.19-23-10372.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou Z, Neher E. Mobile and immobile calcium buffers in bovine adrenal chromaffin cells. J. Physiol. 1993;469:245–273. doi: 10.1113/jphysiol.1993.sp019813. [DOI] [PMC free article] [PubMed] [Google Scholar]