AUTOMATING THE ANALYSIS OF EEG RECORDINGS FROM PREMATURELY-BORN INFANTS: A BAYESIAN APPROACH

Abstract

Ojective

To implement an automated analysis of EEG recordings from prematurely-born infants and thus provide objective, reproducible results.

Methods

Bayesian probability theory is employed to compute the posterior probability for developmental features of interest in EEG recordings. Currently, these features include smooth delta waves (0.5-1.5 Hz, >100 μV), delta brushes (delta portion: 0.5-1.5Hz, >100 μV; “brush” portion: 8-22 Hz, <75 μV), and interburst intervals (<10 μV), though the approach taken can be generalized to identify other EEG features of interest.

Results

When compared with experienced electroencephalographers, the algorithm had a true positive rate between 72% and 79% for the identification of delta waves (smooth or “brush”) and interburst intervals, which is comparable to the inter-rater reliability. When distinguishing between smooth delta waves and delta brushes, the algorithm's true positive rate was between 53% and 88%, which is slightly less than the inter-rater reliability.

Conclusions

Bayesian probability theory can be employed to consistently identify features of EEG recordings from premature infants.

Significance

The identification of features in EEG recordings provides a first step towards the automated analysis of EEG recordings from premature infants.

1. Introduction

Premature infants undergo extensive cerebral maturation in the neonatal intensive care unit (NICU), but they are also vulnerable to brain injury that can result in later motor and cognitive disability (Hack et al., 2002; Wood et al., 2000). Because of the risks to the infant, it is crucial that physicians be able to identify and provide treatment for brain insults as early as possible. When available, electroencephalographic (EEG) recordings play an important role in identifying alterations in cerebral function and they can be obtained continuously at the bedside.

One impediment to the widespread adoption of EEG within the NICU is that it must be interpreted by a skilled electroencephalographer, but access to an electroencephalographer is not available in all NICUs. Additionally, there are numerous subtleties involved in the interpretation of EEG recordings such that even experts may disagree, making EEG analysis somewhat subjective. Furthermore, even when an expert is available, the process of reading an EEG is often time-consuming, resulting in delays of a day or more between recording and diagnosis. Each of these limitations could be addressed by an automated approach to EEG analysis. An algorithm designed to aid in the analysis of EEG would increase access to this vital tool by making EEG practical in NICUs without an elecroencephalographer, eliminate subjectivity in the diagnosis, and provide real-time information to physicians. For a further explanation of the value of a quantitative approach, see Niemarkt et al. (2008).

Many attempts to automate the analysis of EEG recordings have dealt with seizure detection (Gotman et al., 1997; Liu et al., 1992; Roessgen et al., 1998; Wilson, 2005; Deburchgraeve et al., 2008; Navakatikyan et al., 2006; Altenburg et al., 2003; Temko et al., 2011; Faust et al., 2010). However, there is a growing body of literature attempting to obtain quantitative measures of the non-seizure EEG. A number of automated techniques have emerged for the classification of background activity either through the detection of the burst-suppression pattern (Löfhede et al., 2010; Palmu et al., 2010a,b) or the detection of interburst intervals (Niemarkt et al., 2010a). Others have used quantitative analysis to identify normative patterns of development. These analyses have used aEEG analysis (Niemarkt et al., 2010b), interburst interval detection (Niemarkt et al., 2010a), frequency analysis (Victor et al., 2005; West et al., 2006; Scher, 1995), amplitude analysis (West et al., 2006), or a combination of many measures including spectral entropy (Korotchikova, 2009). The use of quantitative analyses has led to several interesting findings. Inder et al. (2003) found a correlation between decreased spectral edge frequency and increased severity of white matter injury. Eiselt et al. (1997) compared the spectra between the two hemispheres of the brain and found that the spectral power was higher in the right hemisphere than the left, indicating functional differences between the two sides are present even in the neonate. Korotchikova (2011) found that grades of hypoxic ischaemic encephalopathy could be predicted using a combination of several quantitative EEG measures.

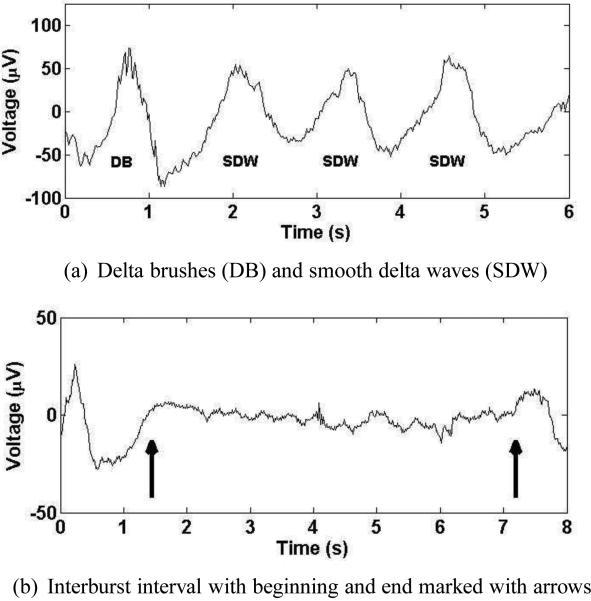
While many automated analyses of EEG recordings have been successful in their attempt to agree with a visual analysis of the EEG provided by electroencephalgraphers, no automated analyses have been widely adopted to date, meaning more work is needed to bring this valuable tool into the NICU. The primary focus of this study is identifying developmental landmarks. The landmarks of interest are interburst intervals and delta waves, with delta waves being further subdivided into smooth delta waves and delta brushes. Delta waves are defined as large amplitude (≥ 100μV) waves having frequencies between 0.5 and 1.5 Hz. Delta brushes are delta waves that contain superimposed high-frequency “brush” waves, which are typically located near the top of the delta wave and can range anywhere between 8 and 22 Hz in frequency and have amplitudes of 10 to 75 μV. Delta brushes have also been referred to as “beta-delta complexes” or “spindle-like fast waves” (Mizrahi et al., 2004). Smooth delta waves are any delta waves not containing brush activity. Examples of delta waves and delta brushes can be seen in Fig. 1(a), where smooth delta waves are marked “SDW” and the delta brush is marked “DB”. Note that not all smooth delta waves are perfectly smooth, but simply lack brush activity. Delta brushes typically appear around 28 weeks postmenstrual age (PMA) and continue through 39 weeks with a gradual progression from the central regions to the occipital and temporal areas. Their absence from these regions during this period is indicative of abnormal development. However, the presence of delta waves can be a sign of pathology; sustained rhythmic delta activity in the bifrontal or bioccipital regions both represent an abnormal EEG finding (Mizrahi et al., 2004).

Figure 1.

Examples of delta brushes, smooth delta waves, and interburst intervals

Another developmental landmark of interest is the interburst interval, which is a period of low-voltage (< 10μV) signal during which brain activity is minimal. Figure 1(b) contains an example of an interburst interval, with the arrows marking the beginning and end of the interburst interval. In general, the EEG should become more continuous as PMA increases in the healthy neonate, meaning maturation can be tracked by identifying interburst intervals.

The goal of this project is to provide a first step towards the automation of EEG analysis in premature infants. The algorithm is designed to mimic electroencephalographers by identifying developmental landmarks known to correlate with normal or abnormal neurological development in premature infants within the NICU environment. The landmarks of interest in this project are delta brushes, smooth delta waves, and interburst intervals, though the method of identification can be expanded to identify nearly any wave of interest. The implementation of this algorithm has the potential to offer objective, real-time information to clinicians at the bedside without requiring a specialist to interpret the EEG.

2. Methods

2.1. Bayesian Probability

Bayesian probability theory, a mathematical theory of inference in which probabilities represent degrees of plausibility or a state of knowledge regarding a particular hypothesis, is employed to identify the EEG features of interest. Jaynes (1956, 2003), building on the works of many previous authors such as Cox (1946) and Jeffreys (1939), worked to fully develop the theory. He put forth three basic desiderata, which form the basis for Bayesian probability theory:

1. Degrees of plausibility are represented by real numbers

2. The theory must have qualitative correspondence with common sense

3. The theory must be consistent.

From these three desiderata, the rules of probability theory, known as the sum rule and the product rule, can be derived. Given two hypotheses A and B and some information I, the sum rule tells one how to compute the probability for A OR B given that information I, which is represented by p(A + B|I). Note that the “+” symbol inside the parentheses represents an OR operator. The sum rule takes the form

$$p(A+B\mid I)=p(A\mid I)+p(B\mid I)-p(AB\mid I).$$ (1)

It stipulates that the probability for A OR B given I is equal to the probability for A given only the information I, plus the probability for B given I, less the joint probability for A AND B given I. The product rule tells one how to form the probability for A AND B given the information I, which is represented by p(AB|I). The product rule,

$$p(AB\mid I)=p(A\mid BI)p(B\mid I),$$ (2)

indicates that the probability for A AND B given I is equal to the probability for A given both B and I times the probability for B given only I. However, this factorization is not unique; the probability for B and A is the same as the probability for A and B, so one could also choose the factorization

$$p(AB\mid I)=p(B\mid AI)p(A\mid I).$$ (3)

Equating Eq. (2) and Eq. (3) gives

$$p(A\mid BI)p(B\mid I)=p(B\mid AI)p(A\mid I),$$ (4)

and dividing by p(B|I) yields

$$p(A\mid BI)=\frac{p(B\mid AI)p(A\mid I)}{p(B\mid I)},$$ (5)

which is Bayes’ theorem. Bayes’ theorem represents learning from experience; if one knows the probability for A given some information I, and subsequently acquires some new information B, then Bayes’ theorem dictates how the new information should be incorporated to determine the probability for A given both B and I. Bayes’ theorem becomes more intuitive with a change of notation. If the symbol A is replaced by some hypothesis H and B is replaced by some data D, then Bayes’ theorem can be written

$$p(H\mid DI)=\frac{p(D\mid HI)p(H\mid I)}{p(D\mid I)}.$$ (6)

In this form, it can be seen that Bayes’ theorem dictates how data should be incorporated to update one's existing knowledge regarding a hypothesis.

Each term in Bayes’ theorem has a name. The term p(H|DI) is called a posterior probability. It is the probability for a hypothesis when the data and all relevant background information have been taken into account. The term p(D|HI) is the direct probability for the data, and in some cases is proportional to a likelihood function. The term p(H|I) is called the prior probabality for the hypothesis. It allows the researcher to incorporate any information known about the hypothesis before data collection. The term in the denominator, p(D|I), is called the evidence or the global likelihood, and it often serves as a normalization constant.

2.2. Structure of the Algorithm

The Bayesian calculations discussed below have been implemented in a computer program that identifies features in the EEG. The algorithm has been designed to identify smooth delta waves, delta brushes, interburst intervals, and general activity. It is divided into two steps, each requiring its own calculation for the posterior probability (see Appendixes A, B for details on obtaining the full calculations). The first step identifies delta waves, interburst intervals, and periods of general activity, where general activity is any section of the EEG recording not containing an interburst interval or delta wave. The second step takes the delta waves identified _in the first step and attempts to further subdivide them by classifying them as either smooth delta waves or delta brushes. The algorithm was implemented in real-time using Fortran 95 running in parallel on an eight processor Linux PC.

2.3. Step One: Delta Waves, Interburst Intervals, and General Activity

The first step in the algorithm is to identify interburst intervals and delta waves. To achieve this identification, the algorithm must allocate the EEG data {d₁, d₂, ....d_m} = D to one of three classes: interburst interval, delta wave, and general activity. The goal then is to calculate the posterior probability for each class p(M|DI), where the classes are represented symbolically by M, and M = 1 designates the interburst interval class, M = 2 designates the delta wave class, and M = 3 designates the general activity class. Once the posterior probabilities for each class have been computed, the algorithm categorizes the data based on which class has the highest posterior probability.

To calculate the posterior probability for each class, the data must be related to the classes. Each class is comprised of one or more patterns, and each pattern is represented symbolically by a function which is designated by ${\mathcal{P}}_{jM}$, where ${\mathcal{P}}_{jM}$ is the jth pattern in class M. So, the equation that relates the data to the classes is of the form

$$d_t={\mathcal{P}}_{jM}\left(t\right)+n_t,$$ (7)

where n_t is additive noise. Each pattern ${\mathcal{P}}_{jM}$ consists of a vector of N_m amplitudes, A_jM, as well as the prior information related to those amplitudes. For simplicity, the notation

$${\mathcal{P}}_{jM}\left(t\right)=A_{tjM}$$ (8)

is adopted with the understanding that the prior for the amplitude A_tjM is assigned using the prior information about the pattern ${\mathcal{P}}_{jM}\left(t\right)$. The prior information for each pattern in each class is unique. In particular, for an amplitude at time t, the prior information about the pattern specifies the most probable value of the amplitude, the low and high range of the amplitude, and the variability of the amplitude in a given pattern.

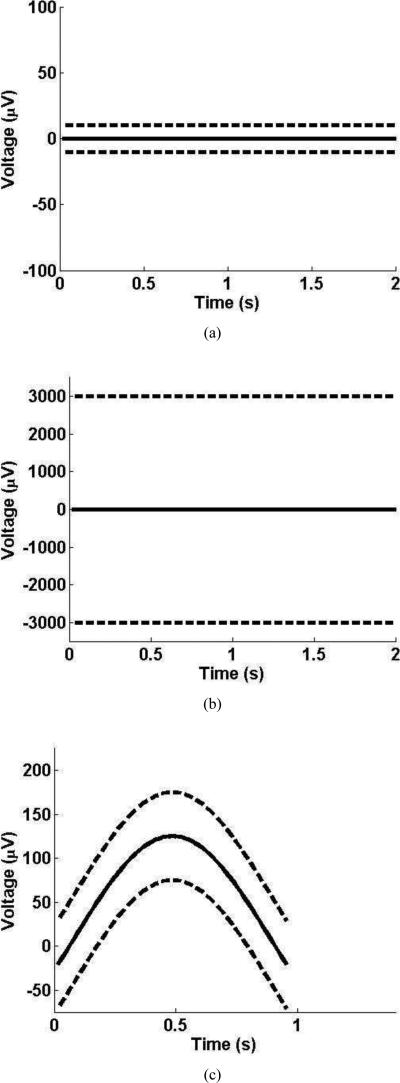
In the case of the interburst interval class, only one pattern is required, and the prior information about the interburst interval restricts the amplitudes to low values. More specifically, the prior information dictates that the most probable value of an amplitude in the interburst interval class is zero μV for the duration of the interval, and that the bounds on the amplitudes are –10μV and 10μV. The interburst interval pattern is shown in Fig. 2(a), with the solid line representing the most probable values of the amplitudes and the dotted lines representing the bounds on the amplitudes.

Figure 2.

Examples of patterns from different classes. In each subfigure, the solid line indicates the most probable value of the amplitude and the dashed line indicates the bounds on the amplitude. Figure 2(a) contains the pattern for the interbust interval class. Figure 2(b) contains the pattern for the general activity class. Figure 2(c) contains one example pattern from the delta wave class.

The general activity class also contains only one pattern, which is shown in Fig. 2(b). This pattern is similar to the interburst interval pattern, but the bounds used in this pattern are much larger than those used in the interburst interval pattern.

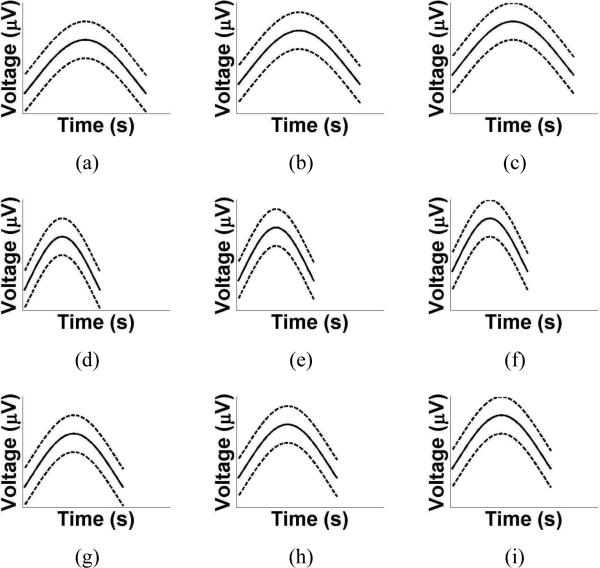
Finally, in the case of the delta wave class, multiple patterns are required to describe the various morphologies of delta waves. An example of a delta wave pattern is shown in Fig. 2(c). One can see that the solid line, which is the most probable value of the amplitudes, varies to reflect the shape of the delta wave. Additionally, the high and low bounds are ±50μV from the most probable value to allow for variations in the shape of the delta waves. To demonstrate how the delta wave patterns differ from each other, several are plotted in Fig. 3.

Figure 3.

Examples of patterns from the delta wave class. In each subfigure, the solid line indicates the most probable value of the amplitude and the dashed line indicates the bounds on the amplitude. The patterns differ in their width and vertical offset to model the various morphologies of delta waves.

2.4. Step Two: Delta Brushes and Smooth Delta Waves

After having identified delta waves, the algorithm must distinguish between smooth delta waves and delta brushes, and a separate calculation is required to do this. The smooth delta wave patterns and the delta brush patterns are identical in shape to the delta wave patterns used in the first step of the algorithm (see Fig. 3). However, the prior information regarding the amplitudes differs. First, the bounds on the amplitudes are eliminated because the feature in question has already been identified as a delta wave. Second, in order to distinguish between smooth delta waves and delta brushes, a smoothness constraint is placed on the amplitudes for a smooth delta wave pattern. For delta brush patterns, there is no such constraint.

2.5. EEG data

EEG recordings were obtained on 233 neonates at Royal Women's Hospital and Royal Children's Hospital in Melbourne, Australia between April 2001 and December 2003. The recordings were taken using a 2-channel BrainZ BRM2 monitor with a 0.1 Hz high-pass filter. Of the 233, 14 infants were selected for further study. These infants had no intraventricular hemorrhage and no abnormal cranial ultrasound studies throughout their course in the NICU, as well as normal mental (Mental Development Index > 85) and psychomotor development (Psychomotor Developmental Index > 85) at two years of age. The average gestational age of the 14 infants was 28.1 (27-29.6) weeks, and the average PMA at the time of recording was 29.4 (28-31.6) weeks. For each infant, a 10 minute epoch was selected for further study. These epochs were chosen based on their high number of delta brushes, smooth delta waves, and interburst intervals. The selected EEG epochs were required to have a maximum impedance of 10kΩ, but otherwise no artifact rejection was performed.

Two experienced electroencephalographers, both of whom were blinded to the results of the algoirthm, were given the 14 recordings (140 minutes of data) and asked to independently identify interburst intervals, smooth delta waves, and delta brushes. In order to have consistent definitions of these waves, the electroencephalographers were asked to identify positive delta waves that were at least 100μV in amplitude and between 0.5 Hz and 1.5 Hz; for interburst intervals, they were asked to consider only those sections in which the amplitude remained under 10μV and exceeded 5 seconds. For consistency, only the left channel was studied for each infant. Two of the 14 recordings were used by the algorithm designer to modify the patterns to give the best agreement between the algorithm and the electroencephalographers. The remaining 12 recordings were used to compare the algorithm and the electroencephalographers, leaving a total of 2 hours for comparison.

3. Results

The results for the identification of delta waves and inter-burst intervals is shown in Tables 1-3. Table 1 offers a general comparison between the algorithm and both readers. From this table, it can be seen that the algorithm is conservative in its classification, identifying fewer delta waves and interburst intervals than either Reader 1 or Reader 2.

Table 1.

Comparison of the total number of delta waves and interburst intervals identified by both readers and the algorithm. The algorithm, designed to be conservative in its classification, identified fewer delta waves and interburst intervals than either reader.

	Delta Waves	Interburst Intervals
Reader 1	709	65
Reader 2	754	62
Algorithm	686	59

Table 3.

Comparison of the performance of the algorithm to Reader 1 and Reader 2 when identifying interburst intervals. The algorithm had a lower true positive and false positive rate when compared to either reader.

(a) Reader 1 as gold standard
	True Positives	False Positives
Algorithm	47/65 (72%)	12/59 (20%)
Reader 2	48/65 (74%)	14/62 (23%)

(b) Reader 2 as gold standard
	True Positives	False Positives
Algorithm	47/62 (76%)	12/59 (20%)
Reader 1	48/62 (77%)	17/65 (26%)

Table 2 offers a more direct comparison between the algorithm and both readers when identifying delta waves. In Table 2(a), Reader 1 is taken as the gold standard and both the algorithm and Reader 2 are compared with Reader 1. The algorithm correctly identified 557 of the 709 delta waves identified by Reader 1, yielding a true positive rate of 79%. However, of the 686 delta waves identified by the algorithm, 129 were not identified by Reader 1, giving a false positive rate of 19% for the algorithm. In order to accurately judge the algorithm's performance, these numbers must be compared with Reader 2's performance. From Table 2(a), Reader 2 had a true positive rate of 82% with a false positive rate of 23%, meaning that the algorithm has both a slightly lower true positive rate and slightly lower false positive rate when compared with Reader 2. This trend continues when Reader 2 is taken as the gold standard for identifying delta waves, which is shown in Table 2(b).

Table 2.

Comparison of the performance of the algorithm to Reader 1 and Reader 2 when identifying delta waves. The algorithm had a lower true and false positive rate when compared to either reader.

(a) Reader 1 as gold standard
	True Positives	False Positives
Algorithm	557/709 (79%)	129/686 (19%)
Reader 2	579/709 (82%)	174/754 (23%)

(b) Reader 2 as gold standard
	True Positives	False Positives
Algorithm	574/754 (76%)	112/686 (16%)
Reader 1	579/754 (77%)	129/709 (18%)

Table 3 displays the results of the algorithm's performance when identifying interburst intervals. When Reader 1 is taken as the gold standard, Table 3(a), the algorithm correctly identified 72% of interburst intervals while having a false positive rate of 20%. For comparison, Reader 2 identified 74% interburst intervals correctly with 23% of the interburst intervals identified by Reader 2 being false positives. Similar results are found in Table 3(b), in which Reader 2 is taken as the gold standard. Just as in the selection of delta waves, the algorithm consistently identified interburst intervals at a lower true positive rate than the electroencephalographers, but also maintained a lower false positive rate.

Table 4 contains the results of the classification of delta waves into smooth delta waves and delta brushes. Only delta waves identified by both readers and the algorithm were used for this comparison. The algorithm did not perform as well at distinguishing between smooth delta waves and delta brushes as it did when identifying the delta waves, which can be seen in table 4(a), where Reader 1 was taken as the gold standard. In this case, the algorithm identified 87% of smooth delta waves identified by Reader 1, while correctly identifying 53% of the delta brushes identified by Reader 1. Reader 2 identified 89% of smooth delta waves identified by Reader 1 while correctly identifying 67% of delta brushes. The algorithm also had lower true positive rates when Reader 2 was taken as the gold standard (see Table 4(b)).

Table 4.

Comparison of the performance of the algorithm to Reader 1 and Reader 2 when distinguishing between smooth delta waves and delta brushes. The algorithm did not perform as well as the readers, with smooth delta wave and delta brush true positive rates lower than both readers.

(a) Reader 1 as gold standard
	SDW True Pos.	DB True Pos.
Algorithm	375/432 (87%)	35/66 (53%)
Reader 2	386/432 (89%)	44/66 (67%)

(b) Reader 2 as gold standard
	SDW True Pos.	DB True Pos.
Algorithm	358/408 (88%)	42/90 (47%)
Reader 1	386/408 (95%)	44/90 (49%)

The algorithm can also be evaluated by focusing on the classifications in which both electroencephalographersare in agreement (Table 5). In those instances, the algorithm performs well when identifying interburst intervals, delta waves, and smooth delta waves; for these features, the true positive rates are all at 86% or higher with false positive rates at 12% or lower. For the identification of delta brushes, however, the true positive rate is substantially lower at 61% with a higher false positive rate of 46%.

Table 5.

The performance of the algorithm when Reader 1 and Reader 2 are in agreement.

	True Positives	False Positives
Interburst Intervals	42/48 (88%)	7/59 (12%)
Delta Waves	498/579 (86%)	53/686 (8%)
Smooth Delta Waves	344/386 (89%)	17/406 (4%)
Delta Brashes	27/44 (61%)	42/92 (46%)

4. Discussion

The performance of the algorithm must be evaluated relative to the inter-rater reliability. In the case of the identification of delta waves and interburst intervals, the algorithm was in agreement with the two electroencephalographers nearly as much as they were in agreement with each other. The algorithm was designed to maximize the true positive rate while maintaining a low false positive rate; because the true positive detection rates were only a few percent lower than the readers’, the algorithm's performance was comparable to the readers.

When distinguishing between smooth delta waves and delta brushes, the agreement between the electroencephalographers and the algorithm was not as strong. In this case, the readers were in better agreement with each other than the algorithm was with either of them. Of particular concern is that 46% of the delta brushes identified by the algorithm were classified as smooth delta waves by both Reader 1 and Reader 2 (see Table 5). While this number is high, it should be noted that 34% of the delta brushes identified by Reader 2 were classified as smooth delta waves by both Reader 1 and the algorithm. A similar cause for concern, as shown in Table 4(a), is that the algorithm identified more false positive delta brushes (432-375=57) than it did true positives (35). However, this result is simply the result of the data containing an order of magnitude more smooth delta waves than delta brushes. Indeed, Table 4(a) similarly shows that Reader 2 also identified more false positive delta brushes at 46 than true positive delta brushes at 44. These results underscore the difficulty in identifying delta brushes. There exists a continuum of waves between perfectly smooth delta waves and “classic” delta brushes, so forcing them to be classified into one of two categories will inevitably lead to disagreements, even between experienced electroencephalographers. Ultimately, the results of these markings indicate that while the algorithm does not perform as well as the expert readers, its performance is reasonable given the level of disagreement that exists between the expert readers themselves.

Having demonstrated that the algorithm can identify developmental landmarks nearly as consistently as experienced electroencephalographers, there are two main advantages to its use. The first advantage is consistency. While the algorithm may not always agree with the electroencephalographers, it will make its classifications consistently, and having consistent measures may prove useful in correlating EEG development with outcome. Second, the algorithm has been designed to run in real-time, thus providing the physician with immediate feedback regarding the state of the infant.

Despite these advantages, there algorithm has a number of weaknesses as currently implemented. First, because the algorithm is focused on identifying specific developmental landmarks and these landmarks represent a small percentage of the EEG recording, the algorithm presently ignores much of the EEG recording. If these portions of the recording contain waves indicative of abnormal neurologic development, the algorithm will be ignorant of this. This shortcoming can be overcome to some extent with the addition of more developmental landmarks, but because much of the typical premature EEG recording contains waves of nonspecific morphology, much of the recording will remain unclassified by the algorithm. Second, the algorithm has no method for automatic artifact detection. If it is to be implemented in the NICU, it will have to rely on its users to identify portions of the EEG recording that have been compromised. Third, as with any automated technique, the algorithm's results will be complicated by the use of sedatives.

The current algorithm is a simple proof of principle, and for this reason its focus has been the identification of a limited number of developmental landmarks. However, the algorithm has the potential to be more powerful than its current implementation. It can be expanded to identify other developmental landmarks of interest through the creation of additional patterns. Furthermore, if implemented on a multiple-channel EEG recording, the algorithm will be capable of offering quantitative measures of synchrony of synchrony by comparing the results from different channels.

5. Conclusions

EEG offers a noninvasive and continuous method for monitoring the premature brain, but its potential has yet to be fully realized because of the subjectivity associated with its interpretation, a lack of standardized measures, a lack of EEG readers, and the delay between recording and diagnosis. These shortcomings can be addressed with an automated approach to EEG analysis that provides real-time, objective information to clinicians. This project has used Bayesian probability theory to consistently identify developmental landmarks in the EEG recording, and thus provide a first step towards such an approach. Its flexibility allows for additional develomental landmarks to be identified, which leaves open the possibility to gain further insight into the developing brain with future work.

Highlights.

1. Developmental features of interest in the EEG recordings from prematurely-born infants can be detected automatically.

2. The automated detection of certain features is as consistent as the inter-rater reliability of experienced electroencephalographers.

3. The method of detection, which uses Bayesian probability theory, can be generalized to identify additional EEG features of interest.

7. Appendix

The software is available for others. For inquiries regarding the use of the algorithm, contact the corresponding author. The full Bayesian calculations associated with this article can be found below in Appendixes A, B.

Appendix A. Step One Calculation

The goal, when given an EEG recording containing a sequence of data values {d₁, d₂, ....d_m} = D, is to determine whether the data contain a delta wave, interburst interval, or general activity. If M represents either the delta wave, interburst interval, or general activity class, then to identify the class present in the data, one computes the posterior probability for each class given the data and the prior information, p(M|DI). This posterior probabability is given by Bayes’ theorem

$$p(M\mid DI)=\frac{p(D\mid MI)p(M\mid I)}{p(D\mid I)},$$ (A.1)

where p(D|MI) is the direct probability for the data given the class, p(D|I) is the direct probability for the data given only the prior information, and p(M|I) is the probability for the class given only the prior information, which is sometimes called a prior probability. The denominator in this equation is a normalization constant. To see this, one reintroduces the class M into p(D|I), which yields

$$p(M\mid DI)=\frac{p(D\mid MI)p(M\mid I)}{{\sum }_{M=1}^{3}p(DM\mid I)},$$ (A.2)

where there are 3 classes to be summed over in the denominator. Applying the product rule to the denominator yields

$$p(M\mid DI)=\frac{p(D\mid MI)p(M\mid I)}{{\sum }_{M=1}^{3}p(D\mid MI)p(M\mid I)}.$$ (A.3)

In this form, it is easily seen that the denominator is simply a normalization constant, and so it is omitted with the understanding that the posterior probability must be normalized at the end of calculation. The posterior probability for the class M then becomes

$$p(M\mid DI)\propto p(D\mid MI)p(M\mid I).$$ (A.4)

In this calculation it is assumed that each class is equally probable, so a uniform prior probability is assigned to p(M|I), and this constant can be included in the proportionality to obtain

$$p(M\mid DI)\propto p(D\mid MI).$$ (A.5)

In general, the class M contains multiple patterns, and these patterns are introduced through the sum rule

$$p(M\mid DI)\propto \sum _{j=1}^{N_M}p(D{\mathcal{P}}_{jM}\mid MI),$$ (A.6)

where there are N_M patterns in class M and ${\mathcal{P}}_{jM}$ is the jth pattern contained in class M. Applying the product rule to factor $p(D{\mathcal{P}}_{jM}\mid MI)$ yields

$$p(M\mid DI)\propto \sum _{j=1}^{N_M}p(D\mid {\mathcal{P}}_{jM}MI)p({\mathcal{P}}_{jM}\mid MI).$$ (A.7)

Like the prior probability for the class, a uniform prior prior probability is assigned to the patterns. The equation for the posterior probability for class M then simplifies to

$$p(M\mid DI)\propto \frac{1}{N_M}\sum _{j=1}^{N_M}p(D\mid {\mathcal{P}}_{jM}MI).$$ (A.8)

Unlike the denominator p(D|I) and the prior probablity for the models p(M|I), the 1|/N_M term that comes from $p({\mathcal{P}}_{jM}\mid MI)$ can not be included in the proportionality constant because the number of patterns in a class is class-dependent.

The probability for a particular class M is equal to a summation of the direct probabilities for the data given the patterns contained in that class. However, the calculation for the direct probability for the data given any pattern is identical, so for notational simplicity, the calculation is done using a single generic pattern with the understanding that the notaton must be revised to include things like the pattern number and the class at its completion. In the calculation that follows, this generic pattern will be represented by $\mathcal{P}$, and the amplitudes associated with this pattern are designated as {A₁, A₂, ...A_m} = A. To proceed with the calculation of the direct probability for the data given a generic pattern, $p(D\mid \mathcal{P}I)$, the amplitudes A of the pattern $\mathcal{P}$ are introduced by application of the sum rule

$$p(D\mid \mathcal{P}I)=\int p(D\mathbf{A}\mid \mathcal{P}I)d\mathbf{A}.$$ (A.9)

This is an m-dimensional integral, where m is the total number of amplitudes. Using the product rule to factor $p(D\mathbf{A}\mid \mathcal{P}I)$, Eq. (A.9) becomes

$$p(D\mid \mathcal{P}I)=\int p(D\mid \mathbf{A}\mathcal{P}I)p(\mathbf{A}\mid \mathcal{P}I)d\mathbf{A}.$$ (A.10)

The product rule can be used to factor the prior probabilities for the amplitudes. Applying the product rule to the right-hand term in Eq. (A.10), one obtains

$$p(\mathbf{A}\mid \mathcal{P}I)=p(A_2\dots A_m\mid A_1\mathcal{P}I)p(A_1\mid \mathcal{P}I).$$ (A.11)

If the prior probabilities for the amplitudes are assumed to be logically independent, Eq. (A.11) simplifies to

$$p(\mathbf{A}\mid \mathcal{P}I)=p(A_2\dots A_m\mid \mathcal{P}I)p(A_1\mid \mathcal{P}I),$$ (A.12)

and repeated application of the product rule yields

$$p(D\mid \mathcal{P}I)=\int p(D\mid \mathbf{A}\mathcal{P}I)\prod _{t=1}^m\left[p(A_t\mid \mathcal{P}I)\right]d\mathbf{A}.$$ (A.13)

At this point the likelihood and the prior probabilities for the amplitudes must be assigned. A Gaussian is assigned to the likelihood, which takes the form

$$p(D\mid \mathbf{A}\mathcal{P}I)=\prod _{t=1}^m\frac{1}{\sqrt{2\pi {\sigma }^2}}\text{exp}\left\{-\frac{{(d_t-A_t)}^2}{2{\sigma }^2}\right\},$$ (A.14)

where σ is the standard deviation of the noise prior probability. The patterns are used to construct the prior probabilities for the amplitudes, which are represented by bounded Gaussians

$$p(A_t\mid \mathcal{P}I)\approx \{\begin{array}{cc}\hfill \frac{1}{\sqrt{2\pi {\beta }_t^2}}\text{exp}\left\{-\frac{{(A_t-u_t)}^2}{2{\beta }_t^2}\right\}\hfill & \text{if}{L}_t\le A_t\le H_t\hfill \\ \hfill 0\hfill & \text{otherwise},\hfill \end{array}\phantom{\}}$$ (A.15)

where u_t is the most probable value of the amplitude A_t, β_t is the standard deviation of the Gaussian prior probability, and L_t and H_t represent the low and high bounds at time t. Equation (A.15) is an approximation because the Gaussian is bounded by L_t and H_t. For this approximation to be valid, the bounds must not significantly truncate the Gaussian prior. In this study, the approximation is good to within one part in 10⁴.

Taking Eq. (A.15) as an equality and substituting it and the likelihood from Eq. (A.14) into Eq. (A.10), the direct probability for the data becomes

$$p(D\mid \mathcal{P}I)=\prod _{t=1}^m{\int }_{L_t}^{H_t}{\left(2\pi {\beta }_t\sigma \right)}^{-1}\text{exp}\left\{-\frac{{(A_t-d_t)}^2}{2{\sigma }^2}\right\}\times \text{exp}\left\{-\frac{{(A_t-u_t)}^2}{2{\beta }_t^2}\right\}d{A}_t.$$ (A.16)

When evaluating this integral, it is helpful both notationally and conceptually to introduce the term Â_t, which is the expected value of the amplitude A_t and defined as

$${\widehat{A}}_t\equiv \frac{{\beta }_t^2{d}_t+{\sigma }^2{u}_t}{{\beta }_t^2+{\sigma }^2}.$$ (A.17)

Rewriting Eq. (A.16) in terms of the expected amplitudes Â_t, the direct probability for the data becomes

$$p(D\mid \mathcal{P}I)=\prod _{t=1}^m{\left(2\pi {\beta }_t\sigma \right)}^{-1}\text{exp}\left\{\frac{-[{\beta }_t^2{d}_t^2+{\sigma }^2{u}_t^2]}{2{\beta }_t^2{\sigma }^2}\right\}\times {\int }_{L_t}^{H_t}\text{exp}\left\{\frac{-({\beta }_t^2+{\sigma }^2)}{2{\beta }_t^2{\sigma }^2}(A_t^2-2A_t{\widehat{A}}_t)\right\}d{A}_t.$$ (A.18)

Completing the square

$$p(D\mid \mathcal{P}I)=\prod _{k=1}^m{\left(2\pi {\beta }_t\sigma \right)}^{-1}\text{exp}\left\{\frac{-[{\beta }_t^2{d}_t^2+{\sigma }^2{u}_t^2]}{2{\beta }_t^2{\sigma }^2}\right\}\times \text{exp}\left\{\frac{+({\beta }_t^2+{\sigma }^2)}{2{\beta }_t^2{\sigma }^2}{\widehat{A}}_t^2\right\}\times {\int }_{L_t}^{H_t}\text{exp}\left\{\frac{-({\beta }_t^2+{\sigma }^2)}{2{\beta }_t^2{\sigma }^2}{(A_t-{\widehat{A}}_t)}^2\right\}d{A}_t$$ (A.19)

and changing variables

$${\lambda }_t^2\equiv \frac{{\beta }_t^2+{\sigma }^2}{2{\beta }_t^2{\sigma }^2}{(A_t-{\widehat{A}}_t)}^2$$ (A.20)

so that

$$d{A}_t=\sqrt{\frac{2{\beta }_t^2{\sigma }^2}{{\beta }_t^2+{\sigma }^2}}d{\lambda }_t,$$ (A.21)

gives

$${\int }_{L_t^{\prime }}^{H_t^{\prime }}{e}^{-{\lambda }_t^2}d{\lambda }_t=\frac{\sqrt{\pi }}{2}\left\{\text{erfc}\left(L_t^{\prime }\right)-\text{erfc}\left(H_t^{\prime }\right)\right\},$$ (A.22)

where

$$L_t^{\prime }\equiv \frac{\sqrt{{\beta }_t^2+{\sigma }^2}}{\sqrt{2}{\beta }_t\sigma }[L_t-{\widehat{A}}_t]$$ (A.23)

and

$$H_t^{\prime }\equiv \frac{\sqrt{{\beta }_t^2+{\sigma }^2}}{\sqrt{2}{\beta }_t\sigma }[H_t-{\widehat{A}}_t].$$ (A.24)

Combining Eqs. (A.17) and (A.19-A.22) and simplifying the result yields

$$p(D\mid \mathcal{P}I)=\prod _{t=1}^m\frac{[\text{erfc}\left(L_t^{\prime }\right)-\text{erfc}\left(H_t^{\prime }\right)]}{2\sqrt{2\pi ({\beta }_t^2+{\sigma }^2)}}\text{exp}\left\{\frac{-{(d_t-u_t)}^2}{2({\beta }_t^2+{\sigma }^2)}\right\}.$$ (A.25)

This is the final result for the direct probability of the data given a generic pattern.

To obtain the posterior probability for a class, Eq. (A.25) must be substituted into Eq. (A.8). With a change in notation to represent a specific pattern rather than the generic pattern, the posterior probability for a class becomes

$$p(M\mid DI)\propto \frac{1}{N_M}\sum _{j=1}^{N_M}\prod _{t=1}^m\frac{[\text{erfc}\left(L_{tjM}^{\prime }\right)-\text{erfc}\left(H_{tjM}^{\prime }\right)]}{2\sqrt{2\pi ({\beta }_{tjM}^2+{\sigma }^2)}}\times \text{exp}\left\{\frac{-{(d_t-u_{tjM})}^2}{2({\beta }_{tjM}^2+{\sigma }^2)}\right\},$$ (A.26)

where the subscripts tjM designate the time, the pattern, and the class respectively. Additionally, $L_{tjM}^{\prime }$, $H_{tjM}^{\prime }$, and Â_tjM are given by

$$L_{tjM}^{\prime }\equiv \frac{\sqrt{{\beta }_{tjM}^2+{\sigma }^2}}{\sqrt{2}{\beta }_{tjM}\sigma }[L_{tjM}-{\widehat{A}}_{tjM}],$$ (A.27)

$$H_{tjM}^{\prime }\equiv \frac{\sqrt{{\beta }_{tjM}^2}+{\sigma }^2}{\sqrt{2}{\beta }_{tjM}\sigma }[H_{tjM}-{\widehat{A}}_{tjM}]$$ (A.28)

and

$${\widehat{A}}_{tjM}\equiv \frac{{\beta }_{tjM}^2{d}_t+{\sigma }^2{u}_{tjM}}{{\sigma }^2+{\beta }_{tjM}^2}.$$ (A.29)

Appendix B. Step Two Calculation

The method for classifying smooth delta waves and delta brushes is similar to the method taken in Appendix A. When given a sequence of data {d₁, d₂, ....d_m} = D from an EEG recording, the goal is to evaluate the posterior probability p(M|DI) for the classes of interest M. However, in this portion of the algorithm, the data must be classified as either a smooth delta wave or a delta brush, so M = 1 will designate the smooth delta wave class and M = 2 will designate the delta brush class. Each class contains multiple patterns, which are represented symbolically by ${\mathcal{P}}_{jM}$, where ${\mathcal{P}}_{jM}$ is the jth pattern in class M. The equation relating the data to each class is given by

$$d_t={\mathcal{P}}_{jM}\left(t\right)+n_t,$$ (B.1)

where n_t is an additive noise. Again, the shorthand notation

$${\mathcal{P}}_{jM}\left(t\right)=A_{tjM}$$ (B.2)

is adopted with the understanding that the prior for the amplitude A_tjM is given by ${\mathcal{P}}_{jM}\left(t\right)$.

The posterior probability for a class, p(M|DI), is given by Bayes’ theorem

$$p(M\mid DI)=\frac{p(D\mid MI)p(M\mid I)}{p(D\mid I)}.$$ (B.3)

The calculation follows the same steps as shown in Eqs. (A.1-A.9), so that the equation for the direct probability for the data, given a generic pattern, is given by

$$p(D\mid \mathcal{P}I)=\int p(D\mathbf{A}\mid \mathcal{P}I)d\mathbf{A}.$$ (B.4)

This is an m-dimensional integral, where m represents the total time of the pattern. Note that there are no bounds on the amplitudes, so the limits of the integration extend to infinite. Additionally, unlike the previous calculation, there is prior information regarding the numerical values of adjacent amplitudes. Consequently, the prior probabilities for the amplitudes are not logically independent, and care must be taken to factor the priors correctly. The product rule is used to factor A₁, A₂, and A₃

$$\begin{array}{cc}\hfill p(D\mid \mathcal{P}I)& =\int p(D{A}_2\dots A_m\mid A_1\mathcal{P}I)p(A_1\mid \mathcal{P}I)d\mathbf{A}.\hfill \\ \hfill & =\int p(D{A}_3\dots A_m\mid A_1{A}_2\mathcal{P}I)p(A_1\mid \mathcal{P}I)p(A_2\mid A_1\mathcal{P}I)d\mathbf{A}.\hfill \\ \hfill & =\int p(D{A}_4\dots A_m\mid A_1{A}_2{A}_3\mathcal{P}I)p(A_1\mid \mathcal{P}I)p(A_2\mid A_1\mathcal{P}I)\times p(A_3\mid A_1{A}_2\mathcal{P}I)d\mathbf{A}.\hfill \end{array}$$ (B.5)

At this point the pattern can be seen, and factoring all amplitudes yields

$$p(D\mid \mathcal{P}I)=\int p(D\mid \mathbf{A}\mathcal{P}I)p(A_1\mid \mathcal{P}I)\times \prod _{t=2}^{m}p(A_t\mid A_{t-1}\dots A_1\mathcal{P}I)d\mathbf{A},$$ (B.6)

where the prior probability for A₁ has been written separately because it does not have a dependence on any other amplitudes. The probabilities are then

$$p(D\mid A_1\dots A_m\mathcal{P}I)=\prod _{t=1}^m\frac{1}{\sqrt{2\pi {\sigma }^2}}\text{exp}\left\{\frac{-{(A_t-d_t)}^2}{2{\sigma }^2}\right\}$$ (B.7)

for the likelihood,

$$p(A_1\mid \mathcal{P}I)=k_1\text{exp}\left\{\frac{-{(A_1-u_1)}^2}{2{\beta }_1^2}\right\}$$ (B.8)

for the prior probability for A₁, and

$$p(A_t\mid A_{t-1}\dots A_1\mathcal{P}I)=k_2\text{exp}\left\{\frac{-{(A_t-u_t)}^2}{2{\beta }_t^2}\right\}\times \text{exp}\left\{\frac{-{(A_t-A_{t-1})}^2}{2{\gamma }_t^2}\right\}$$ (B.9)

for the prior probability for A_t given amplitudes A₁ through A_t–1. Equation (B.9) contains a hyperparameter γ_t, which imposes the smoothness constraint. For delta wave patterns, a small value of γ_t requires that consecutive amplitudes be close in magnitude (smooth). However, for delta brush patterns, a large value of γ_t imposes no smoothness constraint and leaves the delta brush patterns free to model brushes when they are present. The constants k₁ and k₂ are required to ensure the probabilities are properly normalized, but the normalization is complicated and is computed in Appendix B.1. For now, the calculation will continue with k = k₁k₂ representing the normalization constant. Substituting Eqs. (B.7-B.9) into Eq. (B.6) gives

$$p(D\mid \mathcal{P}I)=k\int \prod _{t=1}^m\left[{\left(2\pi {\sigma }^2\right)}^{-1∕2}\text{exp}\left\{\frac{-{(A_t-d_t)}^2}{2{\sigma }^2}\right\}\right]\times \text{exp}\left\{\frac{-{(A_1-u_1)}^2}{2{\beta }_1^2}\right\}\times \prod _{t=2}^m\left[\text{exp}\left\{\frac{-{(A_t-u_t)}^2}{2{\beta }_t^2}\right\}\text{exp}\left\{\frac{-{(A_t-A_{t-1})}^2}{2{\gamma }_t^2}\right\}\right]d\mathbf{A},$$ (B.10)

as the direct probability for the data. Separating out t = 1 from the product and rearranging yields

$$p(D\mid \mathcal{P}I)=k\left[{\left(2\pi {\sigma }^2\right)}^{-m∕2}\right]\times \int \text{exp}\left\{\frac{-{(A_1-u_1)}^2}{2{\beta }_1^2}+\frac{-{(A_1-d_1)}^2}{2{\sigma }^2}\right\}\times \text{exp}\left\{\sum _{t=2}^m\left[\frac{-{(A_t-d_t)}^2}{2{\sigma }^2}+\right]\right\}\times \text{exp}\left\{\sum _{t=2}^m\left[\frac{-{(A_t-u_t)}^2}{2{\beta }_t^2}+\frac{-{(A_t-A_{t-1})}^2}{2{\gamma }_t^2}\right]\right\}d\mathbf{A}$$ (B.11)

for the direct probability. Gathering like terms, Eq. (B.11) can be rewritten in the form

$$p(D\mid \mathcal{P}I)=k\left[{\left(2\pi {\sigma }^2\right)}^{-m∕2}\right]\text{exp}\left\{-\frac{1}{2}\sum _{t=1}^m\left[\frac{d_t^2}{{\sigma }^2}+\frac{u_t^2}{{\beta }_t^2}\right]\right\}\times \int \text{exp}\left\{-\frac{1}{2}\left[\sum _{j=1}^m\sum _{k=1}^m{A}_j{R}_{jk}{A}_k-2\sum _j{A}_j{S}_j\right]\right\}d\mathbf{A},$$ (B.12)

where the elements of the R-matrix are given by

$$\left\{\begin{array}{cc}{R}_{11}={\sigma }^{-2}+{\beta }_1^{-2}+{\gamma }_1^{-2}\hfill & \hfill \\ R_{mm}={\sigma }^{-2}+{\beta }_m^{-2}+{\gamma }_m^{-2}\hfill & \hfill \\ R_{jj}={\sigma }^{-2}+{\beta }_j^{-2}+2{\gamma }_j^{-2}\hfill & 1<j<m\hfill \\ R_{j-1,j}=-{\gamma }_j^{-2}\hfill & 1<j\le m\hfill \\ R_{j,j-1}=-{\gamma }_j^{-2}\hfill & 1<j\le m\hfill \\ R_{jk}=0\hfill & \text{otherwise}\hfill \end{array}\right\}$$ (B.13)

and the elements of the S-vector are given by

$$S_j=d_j{\sigma }^{-2}+u_j{\beta }_j^{-2}1\le j\le m.$$ (B.14)

Defining a function f(A),

$$f\left(\mathbf{A}\right)\equiv \frac{1}{2}{\mathbf{A}}^T\mathbf{RA}-\mathbf{AS},$$ (B.15)

and Taylor expanding about the amplitudes  that maximize f(A), one obtains

$$f\left(\mathbf{A}\right)\approx f\left(\widehat{\mathbf{A}}\right)+\frac{1}{2}{(\mathbf{A}-\widehat{\mathbf{A}})}^T\frac{{\partial }^2}{\partial {\mathbf{A}}^2}f\left(\mathbf{A}\right)(\mathbf{A}-\widehat{\mathbf{A}}),$$ (B.16)

where

$$f\left(\widehat{\mathbf{A}}\right)=\frac{1}{2}{\widehat{\mathbf{A}}}^T\mathbf{R}\widehat{\mathbf{A}}-\widehat{\mathbf{A}}\mathbf{S}$$ (B.17)

and

$$\frac{{\partial }^2}{\partial {\mathbf{A}}^2}f\left(\mathbf{A}\right)=\mathbf{R}.$$ (B.18)

Substituting Eqs. (B.17) and (B.18) into Eq. (B.16) yields

$$f\left(\mathbf{A}\right)=\frac{1}{2}{\widehat{\mathbf{A}}}^T\mathbf{R}\widehat{\mathbf{A}}-\widehat{\mathbf{A}}\mathbf{S}+\frac{1}{2}{(\mathbf{A}-\widehat{\mathbf{A}})}^T\mathbf{R}(\mathbf{A}-\widehat{\mathbf{A}}).$$ (B.19)

where the peak amplitudes  are given by

$$\widehat{\mathbf{A}}={\mathbf{R}}^{-1}\mathbf{S}.$$ (B.20)

Note that the approximation in Eq. (B.15) has been replaced with an equality in Eq. (B.19) because f(A) is quadratic in A. Substituting Eqs. (B.15) and (B.19) into Eq. (B.12) gives

$$p(D\mid \mathcal{P}I)=k\left[{\left(2\pi {\sigma }^2\right)}^{-m∕2}\right]\text{exp}\left\{-\frac{1}{2}\sum _{t=1}^m\left[\frac{d_t^2}{{\sigma }^2}+\frac{u_t^2}{{\beta }_t^2}\right]\right\}\times \text{exp}\left\{-\frac{1}{2}{\widehat{\mathbf{A}}}^T\mathbf{R}\widehat{\mathbf{A}}+\widehat{\mathbf{A}}\mathbf{S}\right\}\times \int \text{exp}\left\{-\frac{1}{2}{(\mathbf{A}-\widehat{\mathbf{A}})}^T\mathbf{R}(\mathbf{A}-\widehat{\mathbf{A}})\right\}d\mathbf{A}$$ (B.21)

for the direct probability for the data. The integral in Eq. (B.21) is a multivariate Gaussian quadrature integral, which can be easily evaluated. See Sivia and Skilling [2], and Bretthorst [1] for details. Evaluating the integrals gives

$$\int \text{exp}\left\{-\frac{1}{2}{(\mathbf{A}-\widehat{\mathbf{A}})}^T\mathbf{R}(\mathbf{A}-\widehat{\mathbf{A}})\right\}d\mathbf{A}=\frac{{\left(2\pi \right)}^{m∕2}}{\sqrt{\text{det}\left(\mathbf{R}\right)}},$$ (B.22)

and substituting Eq. (B.22) into Eq. (B.21) yields

$$p(D\mid \mathcal{P}I)=\frac{k}{{\sigma }^{m∕2}\sqrt{\text{det}\left(\mathbf{R}\right)}}\text{exp}\left\{-\frac{1}{2}\sum _{t=1}^m\left[\frac{d_t^2}{{\sigma }^2}+\frac{u_t^2}{{\beta }_t^2}\right]\right\}\times \text{exp}\left\{-\frac{1}{2}{\widehat{\mathbf{A}}}^T\mathbf{R}\widehat{\mathbf{A}}+\widehat{\mathbf{A}}\mathbf{S}\right\}.$$ (B.23)

Equation (B.23) can be rewritten in summation notation, and takes a form similar to Eq. (B.11), where the integral has been evaluated. This change of notation gives

$$p(D\mid \mathcal{P}I)=\frac{k}{{\sigma }^{m∕2}\sqrt{\text{det}\left(\mathbf{R}\right)}}\times \text{exp}\left\{\frac{-{({\widehat{A}}_1-u_1)}^2}{2{\beta }_1^2}+\frac{-{({\widehat{A}}_1-d_1)}^2}{2{\sigma }^2}\right\}\times \text{exp}\left\{\sum _{t=2}^m\left[\frac{-{({\widehat{A}}_t-d_t)}^2}{2{\sigma }^2}+\frac{-{({\widehat{A}}_t-u_t)}^2}{2{\beta }_t^2}+\frac{-{({\widehat{A}}_t-{\widehat{A}}_{t-1})}^2}{2{\gamma }_t^2}\right]\right\},$$ (B.24)

which is the direct probability for the data given a pattern. However, the normalization constant still needs to be evaluated, and this is the subject of the next subsection.

Appendix B.1. The Normalization Constant

To properly normalize the prior probabilities for the amplitudes from Eq. (B.6), the condition

$$1=\int p(A_1\mid \mathcal{P}I)\prod _{t=2}^{m}p(A_t\mid A_{t-1}\dots A_1\mathcal{P}I)d\mathbf{A}$$ (B.25)

must be satisfied. Substituting Eqs. (B.8) and (B.9), and writing the product of exponentials as the exponential of a sum gives

$$k^{-1}=\int \text{exp}\left\{\frac{-{(A_1-u_1)}^2}{2{\beta }_1^2}\right\}\times \text{exp}\left\{\sum _{t=2}^m\left[\frac{-{(A_t-u_t)}^2}{2{\beta }_t^2}+\frac{-{(A_t-A_{t-1})}^2}{2{\gamma }_t^2}\right]\right\}d\mathbf{A},$$ (B.26)

where k = k₁k₂. Equation (B.26) is of the same form as Eq. (B.11), so the same steps are taken to evaluate the integral. Equation (B.26) is then rewritten in matrix form

$$k^{-1}=\text{exp}\left\{-\frac{1}{2}\sum _{t=1}^m\left[\frac{u_t^2}{{\beta }_t^2}\right]\right\}\int \text{exp}\left\{-\frac{1}{2}\left[\sum _{j=1}^m\sum _{k=1}^m{A}_j{Z}_{jk}{A}_k-2\sum _j{A}_j{Y}_j\right]\right\}d\mathbf{A},$$ (B.27)

where the elements of the Z matrix are given by

$$\left\{\begin{array}{cc}{Z}_{11}={\beta }_1^{-2}+{\gamma }_1^{-2}\hfill & \hfill \\ Z_{mm}={\beta }_m^{-2}+{\gamma }_m^{-2}\hfill & \hfill \\ Z_{jj}={\beta }_j^{-2}+2{\gamma }_j^{-2}\hfill & 1<j<m\hfill \\ Z_{j-1,j}=-{\gamma }_j^{-2}\hfill & 1<j\le m\hfill \\ Z_{j,j-1}=-{\gamma }_j^{-2}\hfill & 1<j\le m\hfill \\ Z_{jk}=0\hfill & \text{otherwise}\hfill \end{array}\right\}$$ (B.28)

and the elements of the Y vector are

$$Y_j=u_j{\beta }_j^{-2}1\le j\le m.$$ (B.29)

In this calculation, the Z matrix is analogous to the R matrix defined in Eq. (B.13), and the Y vector is analogous to the S vector defined in Eq. (B.14). Though the details are omitted here, the previous calculation can be repeated using these new quantities, which yields

$$k=\frac{\sqrt{\text{det}\left(\mathbf{Z}\right)}}{{\left(2\pi \right)}^{m∕2}}\text{exp}\left\{\frac{{({\widehat{A}}_1^{\prime }-u_1)}^2}{2{\beta }_1^2}\right\}\times \text{exp}\left\{\sum _{t=2}^m\left[\frac{{({\widehat{A}}_t^{\prime }-u_t)}^2}{2{\beta }_t^2}+\frac{{({\widehat{A}}_t^{\prime }-{\widehat{A}}_{t-1}^{\prime })}^2}{2{\gamma }_t^2}\right]\right\}$$ (B.30)

for the normalization constant, where Â′ is the vector of peak amplitudes given by the equation Â′ = Z^–1Y. Combining Eqs. (B.24) and (B.30) yields the direct probability for the data given a general pattern

$$p(D\mid \mathcal{P}I)=\frac{1}{{\left(2\pi {\sigma }^2\right)}^{m∕2}}\frac{\sqrt{\text{det}\left(\mathbf{Z}\right)}}{\sqrt{\text{det}\left(\mathbf{R}\right)}}\times \text{exp}\left\{\frac{-{({\widehat{A}}_1-u_1)}^2}{2{\beta }_1^2}+\frac{-{({\widehat{A}}_1-d_1)}^2}{2{\sigma }^2}+\frac{{({\widehat{A}}_1^{\prime }-u_1)}^2}{2{\beta }_1^2}\right\}\times \text{exp}\left\{\sum _{t=2}^m\left[\frac{-{({\widehat{A}}_t-d_t)}^2}{2{\sigma }^2}+\frac{-{({\widehat{A}}_t-u_t)}^2}{2{\beta }_t^2}+\frac{-{({\widehat{A}}_t-{\widehat{A}}_{t-1})}^2}{2{\gamma }_t^2}\right]\right\}\times \text{exp}\left\{\sum _{t=2}^m\left[\frac{{({\widehat{A}}_t^{\prime }-u_t)}^2}{2{\beta }_t^2}+\frac{{({\widehat{A}}_t^{\prime }-{\widehat{A}}_{t-1}^{\prime })}^2}{2{\gamma }_t^2}\right]\right\}.$$ (B.31)

To obtain the probability for a class given the data and background information, Eq. (B.31) is substituted into Eq. (A.8), yielding

$$p(M\mid DI)\propto \sum _{j=1}^N\frac{1}{{\left(2\pi {\sigma }^2\right)}^{m∕2}}\frac{\sqrt{\text{det}\left(\mathbf{Z}\right)}}{\sqrt{\text{det}\left(\mathbf{R}\right)}}\times \text{exp}\left\{\frac{-{({\widehat{A}}_{1jM}-u_{1jM})}^2}{2{\beta }_{1jM}^2}+\frac{-{({\widehat{A}}_{1jM}-d_1)}^2}{2{\sigma }^2}\right\}\times \text{exp}\left\{\frac{{({\widehat{A}}_{1jM}^{\prime }-u_{1jM})}^2}{2{\beta }_{1jM}^2}\right\}\times \text{exp}\left\{\sum _{t=2}^m\left[\frac{-{({\widehat{A}}_{tjM}-d_t)}^2}{2{\sigma }^2}+\frac{-{({\widehat{A}}_{tjM}-u_{tjM})}^2}{2{\beta }_{tjM}^2}\right]\right\}\times \text{exp}\left\{\sum _{t=2}^m\left[\frac{-{({\widehat{A}}_{tjM}-{\widehat{A}}_{t-1jM})}^2}{2{\gamma }_{tjM}^2}\right]\right\}\times \text{exp}\left\{\sum _{t=2}^m\left[\frac{{({\widehat{A}}_{tjM}^{\prime }-u_{tjM})}^2}{2{\beta }_{tjM}^2}+\frac{{({\widehat{A}}_{tjM}^{\prime }-{\widehat{A}}_{t-1jM}^{\prime })}^2}{2{\gamma }_{tjM}^2}\right]\right\},$$ (B.32)

which is the posterior probability for a class M given the EEG data D and background information I, and is the equation implemented in the algorithm to determine if a delta wave is a smooth delta wave or a delta brush.