Minimum Requirements for Accurate and Efficient Real-Time On-Chip Spike Sorting

Abstract

Background

Extracellular recordings are performed by inserting electrodes in the brain, relaying the signals to external power-demanding devices, where spikes are detected and sorted in order to identify the firing activity of different putative neurons. A main caveat of these recordings is the necessity of wires passing through the scalp and skin in order to connect intracortical electrodes to external amplifiers. The aim of this paper is to evaluate the feasibility of an implantable platform (i.e. a chip) with the capability to wirelessly transmit the neural signals and perform real-time on-site spike sorting.

New Method

We computationally modelled a two-stage implementation for online, robust, and efficient spike sorting. In the first stage, spikes are detected on-chip and streamed to an external computer where mean templates are created and sent back to the chip. In the second stage, spikes are sorted in real-time through template matching.

Results

We evaluated this procedure using realistic simulations of extracellular recordings and describe a set of specifications that optimise performance while keeping to a minimum the signal requirements and the complexity of the calculations.

Comparison with Existing Methods

A key bottleneck for the development of long-term BMIs is to find an inexpensive method for real-time spike sorting. Here, we simulated a solution to this problem that uses both offline and online processing of the data.

Conclusions

Hardware implementations of this method therefore enable low-power long-term wireless transmission of multiple site extracellular recordings, with application to wireless BMIs or closed-loop stimulation designs.

1. Introduction

For more than half a century neuroscientists have recorded extracellular action potentials, namely spikes, generated by neurons in order to understand how information is represented and transmitted through the nervous system (Hubel., 1957). Until recently, these experiments involved sampling small numbers of neurons over short sessions of a few hours, but with advances in chronic electrode arrays it has become possible to record spikes from large numbers of neurons over several months (Harris et al., 2003, Buzsaki., 2004, Quian Quiroga and Panzeri., 2009). These techniques inspired translational efforts to develop Brain-Machine Interfaces (BMIs) that communicate directly with the nervous system for therapeutic benefit (Donoghue., 2002, Carmena et al., 2003, Chapin., 2004, Musallam et al., 2004, Velliste et al., 2008, Nicolelis and Lebedev., 2009). For example, neural signals from the motor cortex of paralysed patients have been recently used to operate assistive devices such as computers and robotic prostheses (Hochberg et al., 2006).

The first step for invasive BMI systems (i.e. those involving the use of intracranial electrodes), as for any extracellular recording, is to detect the spikes and then identify which spike corresponds to which neuron in a process called ‘spike sorting’ (Letelier and Weber., 2000, Pouzat et al., 2002, Quian Quiroga et al., 2004, Zhang et al., 2004, Rutishauser et al., 2006, Vargas-Irwin and Donoghue., 2007). For this, spikes are classified according to their shapes, assuming that, in principle, each neuron fires spikes with a stereotyped waveform (Buzsaki et al., 2012, Quian Quiroga., 2012). Data is then relayed to an external computer where the motor commands are decoded based on the activity of several individual neurons (Quian Quiroga and Panzeri., 2009). A main caveat of current invasive BMI systems, and of any setup for extracellular recordings, is the need of wires passing through the scalp and skin in order to connect intracortical electrodes to external amplifiers. Ideally, to avoid risks of infections, among other things, one would like to implant a low-power device with a wireless link transmitting the signal to an external receiver (Aghagolzadeh and Oweiss., 2011, Harrison., 2008, Rapoport et al., 2012). A first strategy to do this is to stream all the recorded data wirelessly for processing in an external computer. However, to perform spike detection and sorting, neural signals are typically sampled at very high rates – around 25 kHz per channel or more – thus producing an immense amount of data to be transmitted (approx. 500 Kbit/s per channel). Bandwidth limitations severely restrict the number of channels that can be transmitted, as well as power requirements and consequently battery lifetime. Another alternative is to perform spike sorting directly in the implanted device (Mavoori et al., 2005, Zhang et al., 2012, Zumsteg et al., 2005, Zviagintsev et al., 2005). By doing so, the amount of data to be transmitted is reduced to just binary events signalling the firing of spikes (typically occurring at the order of Hz, compared to the kHz time resolution needed to transmit the raw data). However, given the computational complexity of spike sorting, these methods compromise either performance or hardware practicability.

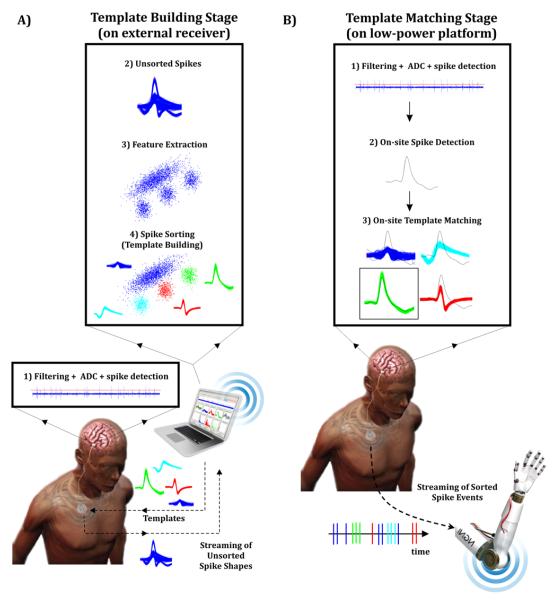
The goal of this paper is to computationally test the feasibility of a hybrid, two-stage strategy for a real-time, hardware-efficient and robust spike sorting implementation. In the first ‘template building’ stage, the implanted device automatically detects and wirelessly streams spikes to an external computer performing the heavy processing steps of spike sorting (i.e. template definition by feature extraction and clustering). The mean spike templates for each channel are then sent back to the implanted device and, in the second ‘template matching’ stage, spikes detected in real time are compared with these mean templates and assigned to the one with the least distance. Given the low complexity and robustness of template matching, this approach enables low-power processing while preserving the quality of the signal.

To the best of our knowledge, there is only one previous study that proposed the idea of doing real-time spike sorting using downloaded templates from a training session (Rizk et al., 2009). In that study, Rizk and collaborators presented a 96-channel implantable platform with the capability to wirelessly stream detected spikes and perform real-time template matching in an external device. However, one caveat of the implementation proposed in that study –as argued by the authors- is that the power consumption of the chip is far from ideal, and therefore the device does not have enough resources to perform template matching inside the body. Here, we study the extent to which we can reduce the specifications of a hypothetical chip similar to the one described in Rizk et al (2009) without significantly impoverishing performance. Using a set of synthetic data mimicking real extracellular recordings (Martinez et al., 2009, Camunas-Mesa and Quian Quiroga., 2013), we systematically investigated the minimum data and processing requirements – in terms of filtering, sampling frequency, signal resolution, etc. – that still allows reliable spike detection and sorting, but reducing hardware resource (energy and complexity) requirements. We report that typical specifications of extracellular recordings (e.g. 28 kHz of sampling rate and 16-bit resolution) can be largely reduced without considerably dropping performance. Finally, we validate the choice of these minimum requirements using real data.

2. Methods

2. 1. Synthetic Extracellular Recordings

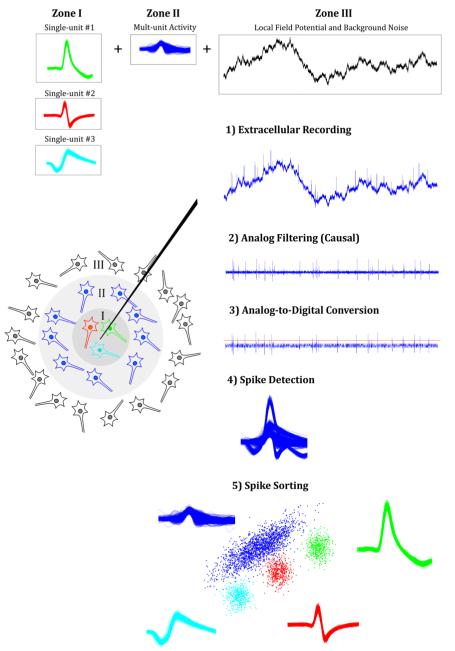
Simulated extracellular recordings were generated by modelling the contribution of the local field potentials (LFPs), background noise, multi-unit activity and single-unit activity (Fig. 1).

Figure 1. Simulation and processing of extracellular recordings.

Recordings were created considering three zones. Zone 1 models the neurons located close to the tip of the electrode, generating single-unit activity. In Zone 2, neurons produce spikes that cannot be clustered due to their small amplitude, leading to multi-unit activity. Zone 3 represents the activity of further away neurons that give rise to the background noise. Extracellular recordings were generated by adding the activity in these three zones (step 1). Signals were then filtered using different specifications (step 2). Virtual Analog-to-digital conversion (ADC) was simulated by downsampling the data and quantizing the signal to a lower resolution (step 3). Spikes were then detected and sorted (steps 4 and 5).

To simulate the LFPs and the background noise, we used surrogates of one real extracellular recording from the human medial temporal lobe (MTL). The subject was a patient with pharmacologically intractable epilepsy who was implanted with intracranial electrodes for clinical reasons (Fried et al., 1997). To record single-neuron activity, the intracranial probe had a total of 9 micro-wires at its end, with 8 active recording channels and 1 reference. The differential signal from the micro-wires was amplified, sampled at 28 kHz and 16-bit resolution with a signal input range of ±1mV. The size of the electrodes used in this recording was 40 μm, and the signal bandwidth was (0.1-9000) Hz. The recording was performed with a Neuralynx “Cheetah-32” system, which works in conjunction with “Lynx-8” amplifiers. These amplifiers have an input noise of 15 μV p-p and an output noise of 10 mV p-p. A full list of specifications about the “Lynx-8” amplifier can be found in http://neuralynx.com/manuals/Lynx-8_Manual.pdf

The channel used to create the surrogates did not exhibit single-unit nor multi-unit activity, but had the same power spectrum and amplitude characteristics of neighbouring channels that had both types of activity. Surrogates were constructed applying the Fourier transform, shuffling the phases, and then applying the inverse transform. Here, we used the implementation proposed by (Schreiber and Schmitz., 2000), which uses a constrained randomisation, thus preserving not only the power spectrum but also the amplitude distribution. Each simulation was built using a different surrogate.

Synthetic multi-unit and single-unit activity were added to the LFP and background noise with the implementation described in (Martinez et al., 2009). The simulations were created using a database with 594 different average spike shapes, taken from real recordings from the monkey neocortex and basal ganglia. Multi-unit activity –i.e. spikes that can be detected but cannot be clustered into different single units due to their relatively small amplitude– was created by mixing the activity of the whole database of 594 spikes shapes, leading to multi-unit amplitude uniformly distributed between 20 μV and 40 μV. The multi-unit firing rate was set at 20 Hz. Single-unit activity was generated by adding spike shapes with varying amplitudes (as specified below) to the background noise and LFP. The spike shapes added to the signal were 92 samples long and had a smooth decay to zero in order to avoid introducing edge artifacts. The spike train of each single-unit followed a Poisson process, with a mean firing rate of 5 Hz. Spikes that fell within a 2 ms window following another spike were removed to introduce a refractory period and delete overlapping spikes.

We created 90 different simulations, each two-minute long and containing three single units apart from the multi-unit activity. From these 90 simulations, 30 were used for the spike detection test (Section 3.1), 30 were used for the spike sorting (template building) test (Section 3.2) and also as training set for the real-time spike sorting test (Section 3.3). The remaining 30 simulations were used as testing set for the real-time spike sorting test (Section 3.3). Each of these sets of 30 simulations consisted in 10 simulations at each SNR (low, medium, high). The three spike shapes used for each of these sets of 10 simulations were randomly selected, but kept constant across SNRs (in order to solely vary the SNR). Different SNR values were obtained by adding spikes with different amplitudes (i.e. changing the signal and keeping the noise constant). In this study, we used single-unit amplitudes between 50 μV and 200 μV, consistently with single-unit spikes observed in real recordings (e.g. Quian Quiroga et al., 2008).

For the spike detection test (Section 3.1), we used spike amplitudes of 50 μV (low SNR simulations), 75 μV (medium SNR simulations), and 100 μV (high SNR simulations). Supp. Fig. 1 shows a simulated dataset with the three different SNRs. This approach gave SNR values of: 7.1 (low SNR), 10.7 (medium SNR), and 14.3 (high SNR). Simulations with spike amplitudes larger than 100 μV were not included here because they yielded a spike detection performance of 100% for all tested specifications.

For the spike sorting (template building) test (Section 3.2), we used spike amplitudes between 100 μV and 200 μV for the simulations with highest SNR. Simulations with medium and low SNR were created by lowering the amplitude of the spikes by 25% (medium SNR), or 50% (high SNR). Overall, this approach yielded SNR values of: 10.7 (low SNR), 16.0 (medium SNR), and 21.4 (high SNR). The use of different SNRs for the spike detection and spike sorting tests is due to the fact that these two different problems have different breakpoints (i.e. spike sorting is more difficult than spike detection).

For the template building test (Section 3.3), we used the simulations of Section 3.2 as training set (i.e. for template building), and then we created a separate set of simulations with identical parameters to use as a testing set.

2.2. Filtering and Virtual Analog-to-Digital Conversion (ADC)

Following the approach used by many hardware-efficient platforms previously proposed (e.g. (Mavoori et al., 2005, Gosselin and Sawan., 2010)), simulated extracellular recordings were filtered prior to data conversion. Filters were created using the Analogue Filter Design library in Matlab. Signals were filtered using three standard filter types: Elliptic, Butterworth, or Bessel. The high-pass cut-off frequency was set to {100,200,…,900} Hz, and the low-pass cut-off frequency to {1,2,…,9} kHz, while the number of poles of the filter was {1,2,…,6}. To simulate real-time on-chip filtering, we causally filtered the data with the Matlab function filter. For comparison to offline analysis, signals were also filtered using a non-causal implementation with zero-phase response, using the function filtfilt in Matlab.

Virtual ADC with different sampling rates and resolutions was simulated by downsampling and quantising the filtered data. Sampling frequencies were set to 28 kHz, 14 kHz, 7 kHz, 4 kHz, and 2 kHz. The resolution was set to {4,6,…,16} bits with a fixed dynamic range of ±500 μV. In those cases in which we downsampled the data below the Nyquist frequency (sampling frequencies of 4, 2 and 1KHz), we added an additional second order low-pass elliptic filter to avoid aliasing.

2.3. Spike Detection

Spikes were detected by amplitude thresholding, using the unsupervised method proposed by (Quian Quiroga et al., 2004) for each different filter specification, sampling frequency, and resolution listed above. The threshold (Thr) was automatically set to:

$$\mathit{Thr}=4{\sigma }_n\text{where}{\sigma }_n=\text{median}\left(\frac{\mid x\mid }{\mathrm{0.6745}}\right)$$ [1]

Slightly lower or higher thresholds (from 3 to 5 times σ_n) yielded similar results (see Section 3.1). Given a simulation with Nsu single-unit spikes, spike detection performance was calculated by computing:

$$\text{performance}=P_d\times \theta \left(P_d\right)\times 100\%$$ [2]

with

$$P_d=\left(1-\frac{\mathit{Ne}}{\mathit{Nsu}}\right)$$ [3]

where Ne is the number of errors defined as the number of missed single-unit spikes plus the number of false positives, and θ(x) is the unit step function. Intuitively, this definition ensures that performance will be 100% if and only if the number of errors is zero, and 0% if the number of errors is equal or higher than Nsu.

2.4. Spike Sorting and Template Building

Spike sorting was performed using “Wave_Clus”, an unsupervised method described in (Quian Quiroga et al., 2004). In order to prevent biases introduced by user subjectivity, we used the completely unsupervised solution provided by this method. For each detected spike, 64 samples were stored and aligned to the peak for further processing. After spike storage, features of the spike shapes were extracted by using the wavelet transform. The coefficients that best separated the spike shapes were selected using a Kolmogorov–Smirnoff test of Normality, choosing the ten coefficients with the least Normal distribution (i.e. those most likely to represent more than one cluster of spike shapes). In the last step, spikes were classified using superparamagnetic clustering (Quian Quiroga et al., 2004, Blatt et al., 1996, Domany., 1999). The code for spike detection and sorting implemented here is available at http://www.le.ac.uk/csn.

To evaluate spike sorting performance, we assumed perfect spike detection. We then computed the number of hits, misses and false positives using the same criterion described in (Pedreira et al., 2012):

• Hits: A cluster is identified as a hit if it fulfills two conditions: (1) at least 50% of the spikes correspond to the same neuron; and (2) the number of detected spikes are, at least, 50% of the total number of spikes generated for this particular neuron.

• Misses: The number of misses is quantified as the total number of generated neurons (i.e. three for all the simulations in this study) minus the number of hits.

• False Positives: All detected clusters that are not hits are considered as false positives.

Spike sorting performance was defined as:

$$\text{performance}=P_s\times \theta \left(P_s\right)\times 100\%$$ [4]

with

$$P_s=\left(1-\frac{\mathit{Ne}}{\text{Nunits}}\right)$$ [5]

where Ne is the number of errors defined as the number misses plus the number of false positives, Nunits is the number of single-units present in the recording (i.e. 3 for all simulations in this study), and θ(x) is the unit step function. This definition yields a 100% performance if neither misses nor false positives are present in the classification results. A performance of 0% means that the number of errors (either misses or false positives) is equal or greater than the number of neurons simulated in the recordings.

2.5. Real-Time Template Matching

We then explored the use of template matching for real-time classification of spikes. Given a spike defined by $\overrightarrow{y}$ and a mean template defined by $\overrightarrow{T}$ (both column vectors of length n), we evaluated the following 5 metrics:

• Squared Euclidean Distance: $d={\sum }_{i=1}^n{(y_i-T_i)}^2$

• Norm 1: $d={\sum }_{i=1}^n\mid y_i-T_i\mid$

• Norm Infinite: $d=\underset{i}{\max }(\mid y_i-T_i\mid )$

• Mahalanobis: $d={(\overrightarrow{y}-\overrightarrow{T})}^t{S}^{-1}(\overrightarrow{y}-\overrightarrow{T})$ where S is the covariance matrix (size n×n) of a given template, defined as:

  $$S=\frac{1}{m-1}\sum _{j=1}^m(T^j-\overrightarrow{T}){(T^j-\overrightarrow{T})}^t$$ [6]

  Where T^j is a column vector of length n representing the j^th out of the m observations made to create the mean template $\overrightarrow{T}$. In other words, T^j is the j^th out of the m spikes in the training set for this particular cluster (mean template $\overrightarrow{T}$ is created with spikes coming from a training set, see last paragraph of Section 2.1).

• Nearest Neighbours: Given a spike detected in the testing set, we compute its Squared Distance to all spikes detected in the training set. The 5 training spikes with closest distance (i.e., the 5 nearest neighbours) provided one vote, and the test spike was assigned to the most common class among those 5 votes. Because we had 4 clusters per simulation (i.e. 4 candidates: 3 single-units and 1 multi-unit) and 5 neighbours (i.e. 5 votes), it is therefore possible that 2 different clusters have the same number of votes (i.e. 2 votes each, and the remaining vote to a third cluster). In that situation, the new spike was randomly assigned to one of the two clusters with 2 votes.

Template matching performance was assessed by calculating the proportion of spikes that were correctly classified. To solely quantify template matching performance, we assumed perfect template building. The complexity of each metric was estimated by measuring the machine time needed to classify all spikes in a dataset using implementations in Matlab with a PC with a 3.47 GHz clock and 48 Gb RAM. Given that the absolute value of this time depends on the computer specifications where the simulations were run, here we only report relative times that are informative of the relative complexity of the different metrics. Note also that the time taken by the Matlab implementations may slightly differ from the actual implementations used on-chip, so these results should be taken as first order approximations.

2.6. Validation of the Method Using Real Data

To validate the minimum requirements found in this study, we tested our method with real data coming from the human MTL. Extracellular recordings were obtained from 10 different electrodes implanted for clinical reasons in 5 different patients with pharmacologically intractable epilepsy (Fried et al, 1997). The equipment used and the signal characteristics are the same as the ones described in Section 2.1. From each of these 10 electrodes, we obtained one trace (length: 2 min) to test spike detection (as in Section 3.1) and template building (as in Section 3.2), and another equally long trace for template matching (as in Section 3.3). Data contained two single units apart from the multi-unit activity. The mean single-unit firing rate was (4.2 ± 0.9) Hz.

We first performed spike detection, spike sorting (template building), and template matching using the highest sampling specifications (28 kHz of sampling rate and 16-bit resolution) and offline processing of the data (i.e. non-causal filtering). Following a procedure identical to the one described in Section 2.2, we then set the sampling rate to be 7 kHz, decimated the data to 10-bit resolution, and implemented a causal second order elliptic filter between 300 and 3000 Hz. Taking as “ground truth” the results obtained with highest specifications, spike detection performance was quantified as in Equation 3, and spike sorting performance as in Equation 5. For template matching we used the Squared Euclidean Distance, and performance was computed as explained in Section 2.5.

3. Results

3.1. Effect of Basic Signal Features on Spike Detection

First, we tested the effect of basic signal features on spike detection performance. We used a positive threshold on amplitude as in Quian Quiroga et al. (2004) and Equation 1. Setting the threshold to values slightly higher or lower did not affect our results. In particular, we found that threshold values between 3 to 5 times σ_n led to very similar results (see Supp. Fig. 2).

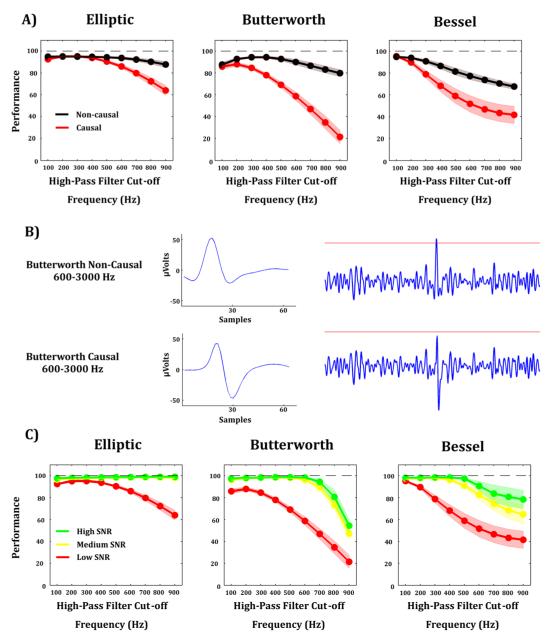
The simulated data were filtered using different specifications before passing through virtual ADC. In order to mimic real-time processing, we used causal filters, and compared these results with the ones obtained using non-causal filters (see Methods). Fig. 2-A shows the spike detection performance (for the simulations with lowest SNR) yielded by different filter types with different high-pass cut-off frequencies, both causal and non-causal. In order to investigate the effect of the high-pass cut-off frequency, the low-pass cut-off frequency was kept constant and set to a value of 3 kHz with the number of poles (i.e. the order of the filter) set to 2. Spike detection performance was clearly better for non-causal filters (Fig 2-A). Previous research has shown that the phase distortions introduced by causal filters create a spurious distortion in the spike shapes (Quian Quiroga., 2009). In line, we found that such distortions also impair spike detection (see Fig 2-B for an example). We also observed that performance became worse as we increased the high-pass cut-off frequency (Fig 2-C). This observation was true for the three SNRs and for the Butterworth, Bessel, and to a lesser degree, Elliptic filters.

Figure 2. Effect of filtering on spike detection.

A) For different high-pass cut-off frequencies, non-causal filters (black line) lead to better spike detection performance than causal filters (red line) for the Elliptic (left panel), Butterworth (center panel), and Bessel (right panel) filters. These results are based on the simulations with low SNR. B) Illustration of phase distortion effects introduced by causal filters. For a given threshold value, the spike obtained with the non-causal filter is detected (top-right panel) whereas the spike obtained with the causal filter is not (low-right panel). C) For different SNRs, higher cut-off frequencies of the high-pass filter lead to worse spike detection for the Elliptic (left panel), Butterworth (center panel), and Bessel (right panel) filters.

In order to examine the effect of the low-pass cut-off frequency, we kept constant the high-pass cut-off frequency and set it to the value that yielded best performance for each type of filter (i.e. 300 Hz for the Elliptic filter, 200 Hz for the Butterworth filter, and 100 Hz for the Bessel filter). The number of poles was also kept constant and set to a value of 2. We observed that all filters with a low-pass cut-off frequency equal or larger than 3 kHz led to nearly optimal performance for all SNRs (Supp. Fig. 3-A). We then pursued a similar approach but setting the low-pass cut-off frequency to a constant value of 3 kHz and varying the number of poles. We found that spike detection performance decreased as we progressively increased the order of the filter (Supp. Fig 3-B). This observation is explained by the fact that causal filters with higher order produce larger ‘ringing’ effects (Quian Quiroga, 2009), accentuating the artificial rebound observed in Fig 2-B, and thus lowering more the amplitude of the spike shape.

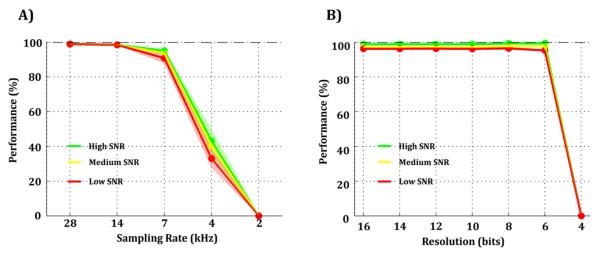
We then studied how different sampling conditions affect spike detection performance. In order to do so, we used a 2^nd order Elliptic filter between 300 Hz and 3 kHz which led to 100% performance using a sampling rate of 28 kHz and 16-bit resolution. Original data were downsampled to a lower sampling rate, and also decimated to a lower amplitude resolution (see Methods). We found that the minimum sampling rate in which spike detection performance is not significantly affected for all SNRs was 7 kHz (Fig. 3-A). Similarly, the minimum number of bits that allow correct spike detection was 6 bits which is equivalent to a signal resolution of 15.6 μV/bit (Fig. 3-B). This finding was not explained by the fact of setting the threshold using high-precision calculations in Matlab, given that implementing the same approach but with limited precision yielded exactly the same results.

Figure 3. Effect of sampling rate and signal resolution on spike detection.

A-B) Spike detection performance for different sampling rates (A) or signal resolutions (B) for high (green), medium (yellow), and low (red) SNRs.

3.2. Effect of Basic Signal Features on Spike Sorting and Template Building

Spike sorting is the process of clustering spikes coming from different neurons according to their shape (Quian Quiroga., 2012). The most complex steps of any spike sorting algorithm are first, to estimate how many neurons are present in the recording (Pedreira et al., 2012) and second, to define the proper templates to search for. We tested the performance of a widely used spike sorting method (Quian Quiroga et al., 2004) under different sampling conditions of the signal. This allowed assessing the minimum requirements -in terms of power consumption- that a neural recorder must have to perform high-quality spike sorting.

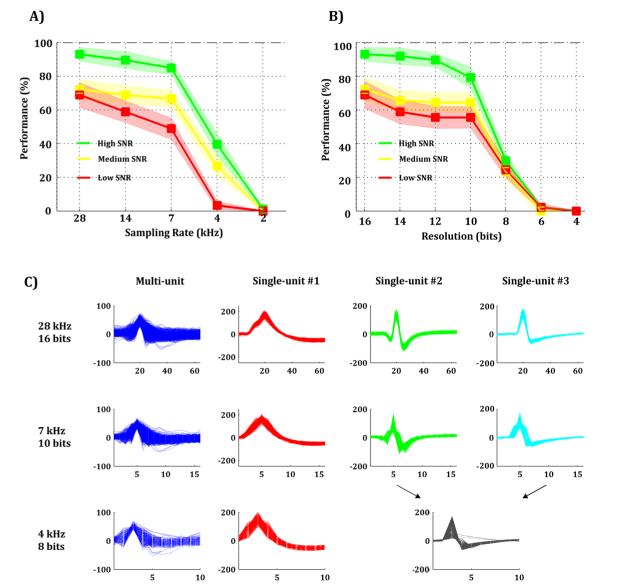
Signals were filtered using a 2^nd order Elliptic filter between 300 Hz and 3 kHz. Different filter specifications led to identical results. Fig. 4-A and 4-B show the spike sorting performance (see Methods) for different sampling rates and for different resolutions, respectively. Even though, in general, performance strongly depended on the SNR of the signal, all performance curves show the same pattern. With sampling rates higher than 7 kHz all performances were qualitatively similar, whereas sampling rates below 7 kHz showed a strong decrease in performance (Fig. 4-A). Likewise, spike sorting performance shows a clear decay for signal resolutions lower than 0.97 μV/bit (i.e. 10 bits spread over ±500μV), while higher values lead to a practically unaltered performance (Fig. 4-B). Fig. 4-C shows an example of how spike shapes belonging to different neurons end up being mixed due to sampling limitations (see Supp. Fig. 4 for more details).

Figure 4. Effect of sampling rate and signal resolution on spike sorting and template building.

A-B) Spike sorting performance for different sampling rates (A) and signal resolutions (B) for high (green), medium (yellow), and low (red) SNRs. C) Illustration of how different clusters (single-unit #2 and #3) are mixed up due to sampling limitations. For this example, a sampling rate of 7 kHz and a signal resolution of 10 bits allow correct identification of the three clusters.

In general, signals sampled with 7 kHz and with a 10-bit resolution (in a signal input range of ±500 μV) can lead to a spike sorting performance almost as good as the one obtained with signals with much higher (and commonly used) power-demanding specifications. For example, the proportion of misclassified spikes using signals with 28 kHz and 16-bit resolution (typically 6 out of 3797 for the highest SNR, see Supp. Table 1) was very similar to the ones obtained using 7 kHz and 10-bit resolution (typically 20 out of 3797). Supp. Table 1 shows the median of the distribution of misclassified spikes for different values of sampling rate, signal resolution and SNR.

3.3. A Hybrid Strategy for Real-Time Spike Sorting

To perform real-time on-chip spike sorting we modelled a hybrid approach consisting in two parts (Fig. 5). In the first stage (i.e. Template Building Stage, see Fig 5-A), a low-power implantable platform filters the data, performs ADC, and detects the spikes in real-time. The detected spikes are wirelessly streamed to an external receiver performing all the heavy calculations, i.e. extracting spike features and doing the sorting to build the spike templates. Those templates are then wirelessly sent back to the low-power platform. In the second stage (i.e. Template Matching Stage, see Fig. 5-B) spike shapes are classified in real time. As in the first part, the low-power implantable platform filters the data, performs ADC, and detects the spikes in real-time. Each detected spike is then compared to the templates of the corresponding channel, and assigned to most similar one via template matching.

Figure 5. Hybrid strategy for real-time spike sorting.

A) In the Template Building Stage, spikes are detected in real time after filtering and ADC of the signal. Unsorted spike events are streamed to a power-demanding computer where templates are built and sent to the low-power platform. B) In the Template Matching Stage, spikes are detected in real time after filtering and ADC. Detected spikes are then compared to the templates via template matching. This method allows streaming only binary spike events with a label indicating which neuron fired at each time.

In order to computationally test the feasibility of this approach, we assessed the performance and complexity of different template matching metrics under different sampling conditions (Fig. 6). Templates were built using the 2-min long signals described in Section 2.4 (training set), and template matching performance –calculated as the fraction of correctly classified spikes in a given dataset– was assessed using another set of simulations with identical parameters (testing set, see Methods).

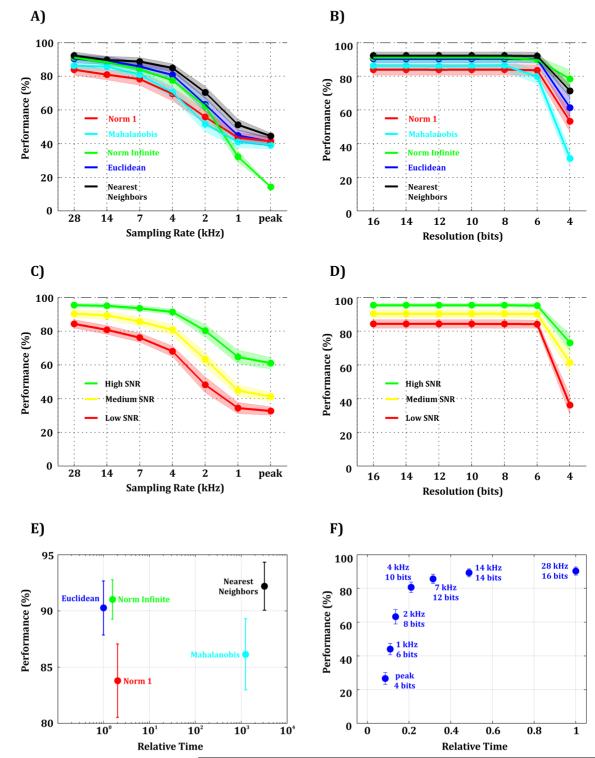
Figure 6. Effect of sampling rate and signal resolution on real-time template matching for different metrics.

A-B) For simulations with Medium SNR, template matching performance for different sampling rates (A), signal resolutions (B) and different metrics: Norm 1 (red), Mahalanobis (cyan), Norm Infinite (green), Squared Euclidean (blue), and Nearest Neighbors (black). C-D) Template matching performance for different sampling rates (C) and signal resolutions (D) for the Squared Euclidean distance and for high (green), medium (yellow), and low (red) SNRs. E) Relative complexity of each metric for signals with 28 kHz and 16-bit resolution. Values are normalized to the metric with least complexity (Squared Euclidean distance). F) Relative complexity of the Squared Euclidean distance for different sampling rates and signal resolutions. Values are normalized to the condition with highest complexity (28 kHz and 16-bit resolution).

We first studied the effect of sampling rate on different template matching metrics. Fig. 6-A shows the template matching performance yielded by all tested metrics using simulations with Medium SNR. As the sampling rate decreased, we observed a smooth decay in template matching performance for all metrics. In particular, we found that 7 kHz -the minimum sampling frequency giving a good performance for spike detection and spike sorting- yielded a performance equal or larger than 80% for all metrics. We then implemented a similar analysis to study the effect of signal resolution. Fig. 6-B shows, for simulations with Medium SNR, that 6 or more bits lead to almost identical template matching results. This is equivalent to a signal resolution equal or better than 15.6 μV/bit. The same behaviour was observed for the three levels of noise both for the different sampling rates and resolutions (see Fig. 6-C, D for Squared Euclidean Distance, and Supp. Fig. 5, 6 for other metrics).

Some of the metrics used in this study are clearly more difficult to implement on hardware. For example, to compute the Mahalanobis distance, it is necessary to invert a matrix whose size scales with the number of spikes in the training set (i.e. the number of templates, see Equation 6). To give an estimate of the compromise between relative complexity (see Methods) and performance, we plotted these two variables against each other for different metrics (Fig. 6-E) and simulations with highest specifications (28 kHz of sampling rate and 16-bit resolution). We observed that all metrics led to a very similar performance, while the Mahalanobis and Nearest Neighbours distances were at least 3 orders of magnitude more complex than the others. We then estimated the complexity of different metrics in terms of computation time for signals with different sampling conditions (Fig. 6y, Supp. Fig. 7). We found that by selecting optimal sampling parameters, the complexity of the calculation can be reduced by at least 5 times compared to the most power-demanding specifications (i.e., 16-bit resolution and 28 kHz of sampling rate) without a noticeable reduction in performance.

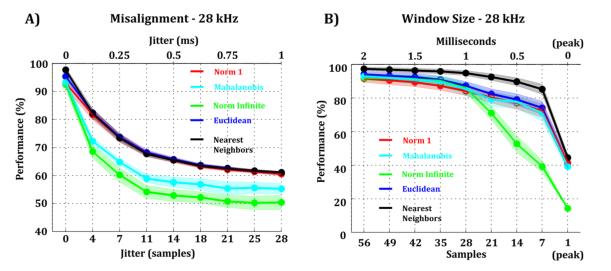
One key step before template matching is to align the spikes (e.g. to their peak) for an accurate point-wise comparison with the templates. Given that the proposed method was inspired by its possible application to low-power architectures, it is then plausible that the alignment method might elicit a certain degree of error. Therefore, we studied the robustness of our approach to different levels of spike-template peak misalignment. In order to do so, we artificially shifted the spikes by a number of samples coming from a uniform distribution U(-s, s), introducing a jitter of s in the peak alignment. For example, a jitter value of 4 indicates that individual spikes were shifted -either left or right- by a number of samples lower or equal than 4, taken from a uniform distribution. This is equivalent to have a peak-alignment method having an error of no more than 4 samples. We found that template matching performance was very sensitive to peak misalignment, especially for the Mahalanobis and Norm Infinite metrics (Fig. 7-A). For the remaining metrics, a small (~0.125 ms) error in the alignment could still yield a fairly reasonable performance (80%), but larger misalignments gave a considerable loss of performance (30% or more). In particular, a 4 sample-error at 28 kHz (Fig. 7-A), a 2-sample error at 14 kHz (Supp. Fig. 8-A), or a 1-sample error at 7 kHz (Supp. Fig. 8-C) decreased the performance in approximately 20%. This finding implies that a good method for peak alignment is crucial for on-line spike sorting through template matching.

Figure 7. Effect of misalignment and window size on template matching.

A) Template matching performance for different metrics and different jitter values in the peak alignment of the spikes. B) Template matching performance for different metrics and for spikes with different window sizes. For both cases, data was sampled at 28 kHz with a 16-bit resolution.

Finally, we investigated the optimal window size that allows correct template matching. In order to do so, we reduced the number of considered data points. Spike shapes were symmetrically cropped, shortening the time window, and then we calculated the template matching performance for each time window. Fig. 7-B shows the performance of different metrics for progressively smaller window sizes. We observed that for all metrics except the Norm Infinite, a window size of only 0.5 ms gave a performance drop of typically 20% (10% for Nearest Neighbours) while it reduced the amount of data needed to be stored by at least 4 times. This is equivalent to selecting a window size of 14 samples at a sampling rate of 28 kHz (Fig. 7-B), 7 samples at 14 kHz (Supp. Fig. 8-B), or 4 samples at 7 kHz (Supp. Fig. 8-D). These results, together with the misalignment analysis (Fig, 7-A), suggest that the Norm Infinite metric is less reliable than the Squared Euclidean metric, even though they both lead to a very similar performance under perfect sampling conditions (Fig. 6-E). Real-time template matching was simulated using high-precision mathematics in Matlab. However, in a low-power device, all calculations would presumably have the same limited resolution as the data. We tested the impact of limited-precision calculations in real-time template matching for the Squared Euclidean, Norm 1, and Norm Infinite metrics, which are the only ones that are simple enough to be implemented in a low-power device (Fig. 6-E). We found that the performance of limited-precision template matching was similar to the one obtained with high-precision calculations, leading to the same breakpoint in performance (6 bits).

3.4. Assessing the Feasibility of the Method using Real Data

We then sought to validate our method using real extracellular recordings, obtained from the human MTL (see Section 2.6). To do so, we obtained ten datasets to test spike detection (as in Section 3.1) and template building (training set, as in Section 3.2). A separate set of ten traces (obtained from different times in the same recordings) was used for testing real-time template matching (testing set, as in Section 3.3).

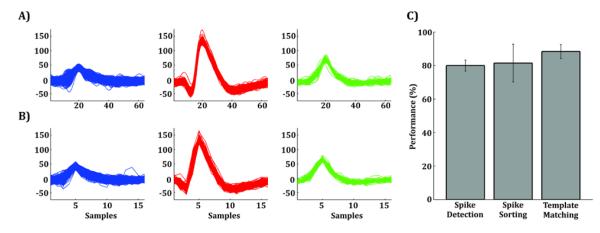
Fig. 8-A shows an example with the clusters obtained in one of the ten datasets using highest specifications (28 kHz of sampling rate and 16-bit resolution) and offline data processing (i.e. non-causal filtering). Fig. 8-B shows the same but using the minimum signal requirements derived from the computational analysis presented in this study (7 kHz and 10-bit resolution). Real-time processing was simulated by the use of a causal filter (i.e. second order elliptic filter between 300 and 3000 Hz). To quantify the performance of the method proposed in Fig. 5, we assumed that the results obtained with highest specifications were correct, and compared them with the ones obtained using our minimum requirements. We found that spike detection performance was (80±3)%, spike sorting performance was (81±11)%, and template matching performance was (88±4)% the one obtained using optimal values (Fig. 8-C). This ~20% drop in performance is at the benefit of reducing the data needed to be processed in ~85% (64 data-points × 16 bits = 1024 bits per spike, vs. 16 data-points × 10 bits = 160 bits per spike).

Figure 8. Validating minimum requirements with real data.

A) Clusters detected in one real extracellular recording, obtained from the human medial temporal lobe, using highest specifications (28 kHz and 16-bit resolution) and offline data processing (i.e. non-causal filters). The blue cluster represents multi-unit activity whereas the red and green clusters represent two different single units. B) Same as A) but using the minimum signal requirements found in this study (7 kHz and 10-bit resolution) and real-time data processing (i.e. causal filters). C) Spike detection, spike sorting, and template matching performance obtained with real extracellular recordings.

3.5. Power Consumption

Actual applicability of this strategy depends of course on the fact that the overall power requirements of this hypothetical chip are reduced compared to existing devices. For example, if a real-time spike sorting method reduces the amount of data needed to be streamed at the cost of performing computationally expensive calculations (therefore increasing the overall power consumption of the chip), then such a method will very likely fail leading to a real hardware implementation.

In the case of the spike sorting approach simulated here, the simplicity of the on-chip calculations indicates that the decrease in power consumption due to data reduction overcomes the power needs to perform those calculations. Based on the power requirements reported in low-power neural interfaces(Lopez et al., 2012, Gibson et al., 2013, Karkare et al., 2013, Wattanapanitch and Sarpeshkar., 2011, Rush and Troyk., 2012), we can estimate the power consumption of this hypothetical chip and assess its feasibility. Assuming an analog front-end (AFE) performing amplification, filtering, and ADC at 7 kHz and 10-bit resolution we estimate a spending of approximately 10 μW per channel only for this step (Wattanapanitch and Sarpeshkar., 2011). If the device has 10 Mbit/s maximum channel capacity, the communication energy is therefore 1 nJ/bit (Rush and Troyk., 2012). Considering 100 channels and 100 neurons firing at 1 Hz, we estimate that a device streaming the raw signal without any data reduction spends ~8 mW. This is because Power = AFE Power + Communication Power = (10 μW × 100 channels) + (10bits × 7 kHz × 100 channels) × 1 nJ/bit = 1 mW + 7 mW = 8mW. This value is obtained using the minimum signal requirements derived in this study (i.e. 7 kHz and 10-bit resolution); however, using typical specifications (i.e. 28 kHz and 16-bit resolution) the power requirements would be larger than 45 mW.

This number is decreased to ~4.6 mW if we include spike detection by amplitude thresholding (thus only streaming the unsorted spikes) spending an extra 2 μW per channel for data processing (Karkare et al., 2013), i.e., Power = AFE Power + Spike Detection Power + Communication Power = (10 μW × 100 channels) + (2 μW × 100 channels) + [(10bits × 16 samples/spike + 8 bits/channel id. + 16 bits/spike timestamp) × 100 neurons × 1 Hz] × 1 nJ/bit = 1 mW + 0.2 mW + 1.8 mW = 3 mW.

Adding the final step described in this paper, i.e. spike sorting via template matching -for which we estimate an extra 8 μW per channel (Karkare et al., 2013)-, the overall power consumption of the device can be estimated to be Power = AFE Power + Spike Detection Power + Spike Sorting Power + Communication Power = (10 μW × 100 channels) + (2 μW × 100 channels) + (8 μW × 100 channels) + [(8 bits/channel id. + 16 bits/spike timestamp) × 100 neurons × 1 Hz] × 1 nJ/bit = 1 mW + 0.2 mW + 0.8 mW + 0.24 mW = 2.24 mW. Hence, in principle, real-time template matching reduces the power requirements by a factor of ~4 compared to sending raw data with optimal specifications (7 kHz and 10-bit resolution), whereas it leads to a decrease by at least a factor of 20 if we compare with the most power-demanding -yet typically used- specifications (28 kHz and 16-bit resolution).

4. Discussion

4.1. Minimum Signal Requirements for Spike Detection and Sorting

In the last several years, different unsupervised spike sorting algorithms have become available to identify the activity of individual neurons with hardly any user intervention (Letelier and Weber., 2000, Pouzat et al., 2002, Quian Quiroga et al., 2004, Zhang et al., 2004, Rutishauser et al., 2006, Vargas-Irwin and Donoghue., 2007). To date, most of these algorithms are computationally expensive and run in power-demanding systems. Recent efforts have sought to develop hardware-efficient spike sorting methods for application to low-power chips (Mavoori et al., 2005, Zhang et al., 2012, Zumsteg et al., 2005, Zviagintsev et al., 2005). Here, we studied how basic signal features (in terms of filtering, sampling rate, and resolution) affect the quality of real-time spike sorting.

Firstly, we observed that causal filters introduce phase distortions that might impair spike detection using an amplitude threshold. This finding is consistent with a previous work showing that phase distortions change the waveform of extracellular spikes, artificially leading to a bi-phasic shape (Quian Quiroga., 2009). The same study also shows that the use of non-causal filters with zero-phase response eliminates such distortions. However, non-causal filters are not always an option, especially for portable on-chip, real-time applications. One alternative would be to implement a transform function that cancels the non-linear phase response of the filter. However, the drawback of this approach is that it would increase the computational load of the low-power device. Instead, here we show that the drop in performance for causal (compared to non-causal) filters can be reduced by carefully selecting their main parameters. In particular, low values of high-pass cut-off frequency, together with the use of a second order filter, minimised the distortions and hence the decrease in performance.

We also found that a sampling rate of 7 kHz and a signal resolution of 10 bits (in a fixed signal input range of ±500μV) can lead to acceptable spike detection and sorting performance (≥80% for high SNRs). Current data acquisition systems use sampling and resolution parameters that exceed by far the minimum requirements found in this study. This is probably explained by the fact that computational power was not considered a bottleneck until very recently.

Extracellular action potentials have been typically recorded over sessions lasting no more than a few hours, but novel improvements in chronic electrode arrays allow performing recordings over days, or even months (Jackson et al., 2006, Jackson et al., 2007). This development, together with the possibility of recording from hundreds of channels, enormously increased the amount of data needed to be stored. For instance, a one-day recording from 100 channels at a sampling rate 28 kHz and 16-bit resolution produce approximately 500 GB of data. In this study, we provide evidence that this number could in principle be reduced by a factor of 6.4 (e.g. sampling at 7 kHz with 10 bits) without a noticeable loss of information about the spiking activity of individual neurons (Fig. 4).

4.2. Real-Time Hardware-Efficient Spike Sorting

To date, most of the experiments involving long-lasting recordings imply relaying the neural signals to an external receiver via wires passing through the scalp and skin. In order to decrease risks of infections, several groups started developing implantable devices with the capability of wirelessly streaming the data (Mavoori et al., 2005). However, bandwidth limitations restrict the battery lifetime and/or the available number of channels to a point below what would be practical. Hence, there is a clear need to find the optimal specifications of current extracellular recordings that minimise power consumption. Here, we showed that the sampling requirements of these signals can be largely reduced, consequently increasing the number of channels that can be processed and the battery lifetime.

One critical point to minimise hardware requirements is to filter the data analogically (i.e. prior to ADC) to the optimal bandwidth for spike detection and sorting. This allows reducing the dynamic range of the signal (hence decreasing power needs) at the cost of eliminating the information carried by low-frequency LFPs. As an alternative, digital filtering for band separation could be implemented after ADC. This would increase the dynamic range but would allow the recording and potential transmission of LFP signals.

Previous works have described the use of low-power neural platforms (i.e., chips) that reduce the amount of transmitted data by detecting the spikes in real-time (Gosselin and Sawan., 2010), and extracting relevant features prior to transmission (Oweiss et al., 2007). More ambitious approaches proposed to perform on-chip spike sorting to wirelessly stream binary spike events (Mavoori et al., 2005, Abu-Nimeh et al., 2009, Aghagolzadeh et al., 2010). For example, (Mavoori et al., 2005) presented an implantable chip that performs (i) amplification and analog filtering, (ii) ADC at 12 kHz, (iii) spike detection with a programmable micro-controller, and (iv) spike sorting with a window discriminator before data streaming or closed-loop stimulation. This type of neural interfaces, although supervised and based on a single channel, has been shown to induce long-term plasticity in the motor cortex of freely behaving non-human primates (Jackson et al., 2006). Here, we computationally tested a method that has the capability to record from multiple channels, using an unsupervised and high-performance spike sorting algorithm (Quian Quiroga et al., 2004). In particular, we evaluated the possibility of implementing a hybrid on-chip spike sorting approach based in two steps. First, in a template-building stage, spikes are detected in real-time and sent to an external receiver where mean templates are created offline, using Wave_Clus. In the second stage, spikes are sorted in real-time through template matching. The key point of the proposed strategy is that all the heavy calculations are performed outside the chip in a power-demanding computer, whereas real-time processing consists in performing template matching, using the information created in the first step (i.e. the mean templates corresponding to each unit). Given that template matching is computationally inexpensive in comparison to template definition, this mixed approach exploits the advantages of combining offline and online processing.

Using realistic simulations of extracellular recordings (Martinez et al., 2009, Camunas-Mesa and Quian Quiroga., 2013), we computationally modelled this hypothetical chip, and estimated its complexity and performance under different specifications. We repeated this analysis for different template-matching metrics, and found that the Squared Euclidean distance provided the best relationship of performance versus complexity. Other metrics tested in this study were either too complex for hardware implementation (i.e. Mahalanobis and Nearest Neighbors, see Fig. 6-E), less robust to noise level (i.e. Norm 1, see Supp. Fig. 4-A,B), or less robust to the selection of small window sizes (i.e. Norm Infinite, see Fig. 7-B). Moreover, we investigated the extent to which this approach was robust to misalignment in the spikes, and observed that a good peak alignment was necessary before template matching. This is because template matching is a point-wise comparison between the detected spike and the mean template. As a consequence, this result suggests that for on-chip implementations it is worth allocating power to performing an accurate peak alignment.

4.3. Hardware Implementation

As argued in Section 3.5, hardware applicability of this approach depends on the development of an integrated circuit with less power requirements than existing ones. However, it also depends on facing a set of issues that normally arise in real recordings. For example, microscopic electrode shifts can lead to large changes in spike waveforms, or even to sudden disappearances of entire clusters (Mavoori et al., 2005, Jackson et al., 2006, Jackson et al., 2007). In the case of our implementation, this would imply the necessity to perform a re-calibration (as in Fig. 5-A) in order to adjust the templates (Fig. 5-B). This drawback is nevertheless a common feature to most implantable systems developed to date (Karkare et al., 2013, Kamboh and Mason., 2013, Kamboh and Mason., 2013, Chen et al., 2012, Saeed and Kamboh., 2013), but see Karkare et al. (2013) for one exception.

One possible way to overcome this issue is to track online the stability of the recording using one or more indicators of performance drop. For example, in BMI applications the most straightforward indicator can be decoding performance (Lebedev and Nicolelis., 2006). However, for exploratory neuroscience and other applications such as basic research in freely-behaving animals(Jackson et al., 2006, Chestek et al., 2009b, Harrison et al., 2011), indicators of performance drop should be independent on the existence of a decoder. In this case, we propose to use a threshold on template matching distance set in a way that if the distance between a spike and all templates is larger than such value, then the spike should be considered as misclassified. With this, it would be possible to follow the temporal evolution of the proportion of misclassified spikes and request a re-calibration after it exceeds a certain number. Exact values for these thresholds will certainly depend on the stability of the recording and the specific application.

To allow accurate and efficient real-time template matching, we showed that a good alignment method is crucial (Fig. 7-A). Previous spike sorting methods dealing with this problem have proposed to upsample the spike shapes after detection in order to improve peak alignment (Quian Quiroga et al., 2004). However, upsampling increases complexity and power requirements of the chip, and therefore, alternative approaches were sought in the past (Horiuchi et al., 2004, Paraskevopoulou and Constandinou., 2011). For example, Paraskevopoulou and Constandinou presented a low-power (< 1μW) integrated neural circuit that outperforms typical digital solutions for spike alignment (Paraskevopoulou and Constandinou., 2011). Hardware application of the method described in this study will therefore require the implementation of this type of low-power circuits.

The minimum requirements found in this study for spike detection are extendable to other systems performing spike detection by amplitude thresholding, which is by far the most used technique (Harrison., 2008, Koustos et al., 2013, Obeid and Wolf., 2004, Rizk et al., 2007). Also, for template matching, we showed that our results are robust to the selection of several widely-used metrics (Fig 7-A and 7-B), regardless their different relative complexities (Fig. 7-E). In the case of template building, we believe that our results would be similar to the ones obtained with other algorithms but a systematic comparison with other methods is outside the scope of the current study.

Among its possible applications, the method introduced here can be applied, for example, to closed-loop stimulation designs (Gorzelic et al., 2013, Mueller et al., 2013). Moreover, the hardware implementation of this method is extremely appealing for animal research given that it would allow long-lasting recordings without the necessity of wires passing through the scalp, reducing the risk of infections(Mavoori et al., 2005, Jackson et al., 2006, Chestek et al., 2009b, Harrison et al., 2011). Similarly, current research towards next-generation BMIs is focused on the implementation of implantable low-power chips with the capability to stream the neural signals wirelessly (Harrison., 2008, Rapoport et al., 2012, Aghagolzadeh et al., 2010). Besides all possible applications to clinical and basic neuroscience, this method is also applicable to all low-power systems performing template matching (Erten and Salam., 1994, Ranganathan and Venugopal., 1994), such as electro-cardiogram implantable systems (Ota et al., 2013) .

We showed that using hardware specifications that are 4 times less power-demanding than typical ones, performance is reduced in only ~20% (see Section 3.5). However, depending on the particular implementation of this method, this decay in performance might or not be acceptable. For example, in neuroscience experiments with non-human primates (Jackson et al, 2006; Jackson et al, 2007) it may be reasonable to prioritize performance over power reduction, whereas for other applications, like decoding approaches for BMIs (Lebedev and Nicolelis, 2006), it might be more important to prioritize a low power implementation to allow, for example, larger number of channels. Moreover, in the latter case, the acceptable decay in spike sorting performance will depend on the design of the particular decoding algorithm used. In any case, in this study we reported how performance decays along with critical hardware parameters, so that when designing the actual hardware implementation it may be possible to find out a compromise that would be suitable for different applications or alternatively, to develop different designs that would optimize performance for each application.

4.4. Conclusions

Finding a spike sorting algorithm that allows real-time communication from a low-power platform has become in the latest years the key signal-processing bottleneck for next-generation BMIs (Lebedev and Nicolelis., 2006, Chestek et al., 2009a). In this paper, we simulated a solution to this problem that uses both offline and real-time processing of the data. Using realistic simulations of extracellular recordings (Martinez et al., 2009, Camunas-Mesa and Quian Quiroga., 2013), we computationally tested its practicability and found the specifications that optimise performance while minimising the signal requirements - and thus the power consumption for future hardware implementation.

Previous attempts to study the effect of different hardware compromises analysed the impact of dimensionality reduction (i.e. number of coefficients) for spike sorting (Gibson et al., 2013, Gibson et al., 2010), and the number of errors in a wireless protocol versus packet length (Aghagolzadeh and Oweiss., 2011). In line, Zhang and collaborators studied how sampling rate and resolution affect the reconstruction error after wireless data transmission (Zhang et al., 2012), whereas Thorbergsson and colleagues studied the effect of these parameters on offline processing outside the body (Thorbergsson et al., 2012). Here, building up on the results of these studies, we extended this analysis to a real-time spike sorting algorithm that is suitable to be implemented on chip, similar to the one described by Rizk and colleagues (Rizk et al., 2009). In particular, we studied the effect of sampling rate, resolution, and filtering on spike detection and sorting performance. Moreover, we compared the performance yielded by five widely-used template matching metrics under different sampling constrains, and provided quantitative evidence about the drop in performance given by misalignment. Finally, we showed that typical window sizes (e.g. 64 points) can be reduced by more than 50% without a significant drop in performance, implying an important reduction in power requirements. To summarize, this computational analysis documents the specifications that minimise complexity and hardware resources allowing accurate spike sorting for real-time on-chip applications.