Abstract
Linking structural neuroimaging data from multiple modalities to cognitive performance is an important challenge for cognitive neuroscience. In this study we examined the relationship between verbal fluency performance and neuroanatomy in 54 patients with frontotemporal degeneration (FTD) and 15 age-matched controls, all of whom had T1- and diffusion-weighted imaging. Our goal was to incorporate measures of both gray matter (voxel-based cortical thickness) and white matter (fractional anisotropy) into a single statistical model that relates to behavioral performance. We first used eigenanatomy to define data-driven regions of interest (DD-ROIs) for both gray matter and white matter. Eigenanatomy is a multivariate dimensionality reduction approach that identifies spatially smooth, unsigned principal components that explain the maximal amount of variance across subjects. We then used a statistical model selection procedure to see which of these DD-ROIs best modeled performance on verbal fluency tasks hypothesized to rely on distinct components of a large-scale neural network that support language: category fluency requires a semantic-guided search and is hypothesized to rely primarily on temporal cortices that support lexical-semantic representations; letter-guided fluency requires a strategic mental search and is hypothesized to require executive resources to support a more demanding search process, which depends on prefrontal cortex in addition to temporal network components that support lexical representations. We observed that both types of verbal fluency performance are best described by a network that includes a combination of gray matter and white matter. For category fluency, the identified regions included bilateral temporal cortex and a white matter region including left inferior longitudinal fasciculus and frontal–occipital fasciculus. For letter fluency, a left temporal lobe region was also selected, and also regions of frontal cortex. These results are consistent with our hypothesized neuroanatomical models of language processing and its breakdown in FTD. We conclude that clustering the data with eigenanatomy before performing linear regression is a promising tool for multimodal data analysis.
Keywords: Language, Verbal fluency, Multimodal, FTD
Introduction
One of the fundamental challenges of cognitive neuroscience is relating brain anatomy to cognitive processes. Most neuroimaging studies linking brain structure to behavior use mass univariate approaches, relying on a whole-brain regression framework in which the relationship between a dependent variable (e.g. gray matter density or fractional anisotropy; FA) and a behavioral measure is assessed at every voxel in the brain.1 An advantage of this traditional approach is that it makes few a priori assumptions about the location of the relationship, or the spatial extent of the brain region(s) relating to behavior. However, there are also some challenges. An obvious limitation is that, without some sort of prior narrowing of focus, voxelwise methods result in a large number of statistical tests that need correction for multiple comparisons. A common strategy to address multiple comparisons is to accumulate voxel data into larger regions of interest (ROIs). However, ROIs are often difficult and labor-intensive to define for each application. For example, the cytoarchitectonic boundaries of Broca's area involved in language are both structurally (Amunts et al., 1999) and functionally (Clos et al., 2013) heterogeneous across individuals. The anatomical boundaries of a particular label set may not align with functionally relevant areas or the concentration of pathological change in a disease under study. These issues motivate the use of data-driven ROIs (DD-ROIs) that can be defined automatically on different populations of images, have soft boundaries instead of the hard labeling of most manual label sets, and can be optimized based on criteria other than visual anatomical boundaries. Such approaches have been used for automated diagnosis of Alzheimer's disease (Klöppel et al., 2008) and the classification of primary progressive aphasia variants (Wilson et al., 2009). Variability of white matter across individuals has also been suggested to impact language performance (Berthier et al., 2012; Flöel et al., 2009). Another important issue with ROI studies of white matter is the lack of available labels: while there are several dense parcellations of cortical gray matter available to researchers, there are few white matter atlases and those that are available focus on major tracts that can be delineated using diffusion tensor imaging.
In this report, we use a multivariate approach that aims to integrate neuroimaging measures of gray matter and white matter in order to define a large-scale neural network that accounts for linguistic performance. This approach relies on “eigenanatomy” (Avants et al., 2012a; McMillan et al., 2013b, 2014), which is a recently proposed algorithm for generating DD-ROIs. These soft ROIs are defined automatically by maximizing the covariance of voxel-wise measurements normalized to template space and collected into a matrix representation. There is no need for prior manual labeling of the subject images and one only needs to define an anatomical domain of interest in the template, for example cortical gray matter for cortical thickness and white matter for diffusion-tensor statistics. Eigenanatomy also addresses the need to take into account spatial smoothness in the ROIs. Voxelwise approaches do this in a post-hoc manner by considering clusters of contiguous results. More recent multivariate approaches take spatial dependency as a given, and seek to capitalize on this from the outset. We view this as a sensible assumption, given the continuous nature of the neural tissue, and the fact that processes such as neural development, age-related cortical thinning, and gray matter loss due to neurodegenerative disease all show a significant degree of spatial localization. By capitalizing on these dependencies, we should be able to better characterize variations in brain shape and tissue structure. Further, theoretical arguments suggest that exploiting prior knowledge when solving challenging optimization problems fundamentally improves results in terms of performance, stability and interpretability (Wolpert and Macready, 1997).
In combination with eigenanatomy dimensionality reduction, we apply a model selection procedure to determine which DD-ROIs in gray matter and white matter form the most efficient regression models of behavioral measures. This approach combines information from multiple imaging modalities in a principled manner within a single regression framework while maintaining the interpretability of classic regression models. Although in theory researchers certainly appreciate the joint contribution of gray matter and white matter integrity to behavioral performance, in practice it has proven difficult to study these at the same time in the same set of subjects. In particular, it has been challenging to quantitatively evaluate the relative contribution of gray matter and white matter to behavior: if a patient has damage to both, which is the better predictor of performance?
To demonstrate the utility of our multivariate approach, we focus on the neural basis of language limitations in patients with frontotemporal degeneration (FTD). The two most common forms of FTD yield either a language disorder, primary progressive aphasia (PPA) (Gorno-Tempini et al., 2011), or a disorder of personality, social comportment, and executive dysfunction, behavioral-variant FTD (bvFTD) (Rascovsky et al., 2011). Within PPA there is a semantic variant (svPPA) that is characterized by difficulty with naming, word meaning, and object knowledge. This variant has been associated with considerable atrophy in the anterior and ventral temporal lobe, more prominently on the left than the right, as well as disease in uncinate and inferior longitudinal fasciculi projections (Mahoney et al., 2013; Whitwell et al., 2010). There is also a non-fluent/agrammatic variant (naPPA), involving slowed, effortful speech with grammatical difficulty and this has been associated with left-lateralized frontal and anterior-superior temporal cortical regions and prominent white matter disease in corpus callosum and inferior frontal-occipital fasciculus (Grossman, 2012; Grossman et al., 2012; Mahoney et al., 2013). bvFTD is not associated with an obvious aphasia, though executive-social limitations can have consequences on language processing (McMillan et al., 2013a), and these patients have gray matter frontal atrophy that is most prominent in ventral and medial frontal regions and extends into dorsolateral frontal areas, with associated disease in white matter projections from these areas (Lillo et al., 2012; Zhang et al., 2013).
Given the distributed localization of disease within the FTD variants we hypothesize that distinct large-scale neural networks contribute to patients' language limitations. Specifically, we focus on verbal fluency. This is a complex task that involves mental search through the lexicon of words that meet the criteria of a category. This process requires conceptual knowledge of word meanings, lexical retrieval, and executive resources involving a flexible mental search strategy. Verbal fluency tasks are common neuropsychological measures that can be adjusted to stress different cognitive processes and thus place different demands on a large-scale neuroanatomical network. For example, a category fluency task (“Name as many animals as you can”) emphasizes knowledge of lexical and conceptual information. By contrast, a letter fluency task (“Name as many words as you can that begin with the letter F”) requires lexical information and additionally requires an advanced executive search strategy to search through all words that begin with a specific letter. In the context of FTD patients, svPPA patients have more difficulty with category fluency than letter fluency and this has been associated with temporal cortex disease (Libon et al., 2009a). However, letter fluency appears to be more associated with frontal cortex disease in FTD and is compromised in bvFTD and nvPPA (Libon et al., 2009a). Assessments of gray matter regions contributing to verbal fluency tasks have been performed using a priori regions of interest (Amunts et al., 2004) or regression analyses using voxel-based morphometry (Libon et al., 2009b). We are unaware of investigations evaluating the relative contributions of gray matter and white matter disease to verbal fluency deficits in FTD.
Together, we hypothesize that our novel multivariate approach and model selection procedure will reveal a large-scale neural network that supports verbal fluency, including fronto-temporal gray matter regions as well as white matter projections between these brain regions, and that the cortical-white matter network implicated in performance will be tailored to the specific task. We test this in a multimodal imaging study of FTD. These observations would provide proof-of-concept evidence for utilizing this approach to better understand the relative contributions of gray matter and white matter in the context of cognitive neuroscience, and would improve our understanding of brain-behavior relationships in neurodegenerative conditions like FTD.
Materials and methods
Participants
We recruited 54 patients from the Penn Frontotemporal Degeneration Center and Hospital of the University of Pennsylvania Cognitive Neurology Clinic who were native-English speakers and clinically-diagnosed with FTD by a board-certified neurologist using published criteria of either PPA (Gorno-Tempini et al., 2011) or bvFTD (Rascovsky et al., 2011). Other causes of dementia were excluded by clinical exam, blood and neuroimaging tests. Exclusion criteria included other neurologic, psychiatric or medical conditions that can result in cognitive change. Some patients may have been on a small, stable dose of a non-sedating neuroleptic or anti-depressant medication. We also recruited 15 healthy older adults who were demographically comparable in age and education relative to the patient cohort. All subjects had T1-and diffusion-weighted structural MRI scans. Thirty-eight subjects performed cognitive testing on the same day as image acquisition, a further 20 were tested within 90 days of imaging, and the remaining 11 subjects had testing within 6 months of MRI. All participants and, if necessary, their caregivers, participated in an informed consent process approved by the University of Pennsylvania Institutional Review Board.
The demographics and dementia diagnoses of the subjects are summarized in Table 1. The subgroups are demographically matched but are diverse in terms of cognitive performance on the verbal fluency tasks. The control subgroup has a negative history of neurological or psychiatric diagnoses, and has the highest average fluency scores. The PPA subgroups (split in Table 1 into a non-fluent/agrammatic aphasic naPPA and semantic-variant svPPA) have the lowest average scores. The bvFTD subgroup has the largest range of scores, overlapping with both the control and PPA subgroup. Including all of these groups gives us data points spanning a wide range of the verbal fluency scores, which is important for building regression models in which they are the dependent variables. The differences in subgroup verbal fluency are discussed further in the Results section and illustrated in Figs. 6 and 7.
Table 1.
Subject demographics, including sample size n for seniors and subjects with each FTD phenotype, presented as mean ± standard deviation. The last column is the p-value from a one-way ANOVA with the null hypothesis that there is no difference in age, years of education or right-handedness between the four groups. For disease duration and the cognitive scores, the ANOVA is performed within the 3 FTD groups only. The p-value is greater than 0.05 for MMSE and category fluency, but not letter fluency. A post-hoc test (Tukey Honest Significant Difference) on letter fluency suggests a significant difference between bvFTD and naPPA (p < 0.02) but not between other FTD groups (p < 0.35).
| Seniors | bvFTD | naPPA | svPPA | Total | ANOVA (p) | |
|---|---|---|---|---|---|---|
| n | 15 | 33 | 9 | 12 | 69 | NA |
| Sex (F, M) | 9,6 | 12,21 | 3,6 | 8,4 | 32,37 | 0.17 |
| Age(yr) | 62 ± 6 | 62 ± 7 | 68 ± 11 | 63 ± 8 | 63 ± 8 | 0.16 |
| Education (yr) | 16 ± 3 | 16 ± 3 | 14 ± 3 | 16 ± 3 | 16 ± 3 | 0.50 |
| Disease duration | NA | 5 ± 3 | 3 ± 2 | 3 ± 2 | 4 ± 3 | 0.15 |
| MMSE | 29 ± 1 | 24 ± 6 | 20 ± 8 | 24 ± 5 | 25 ± 6 | 0.26 |
| Category fluency | 20 ± 6 | 11 ± 5 | 8 ± 5 | 8 ± 5 | 12 ± 7 | 0.07 |
| Letter fluency | 49 ± 11 | 26 ± 15 | 12 ± 9 | 20 ± 10 | 28 ± 17 | 0.01 |
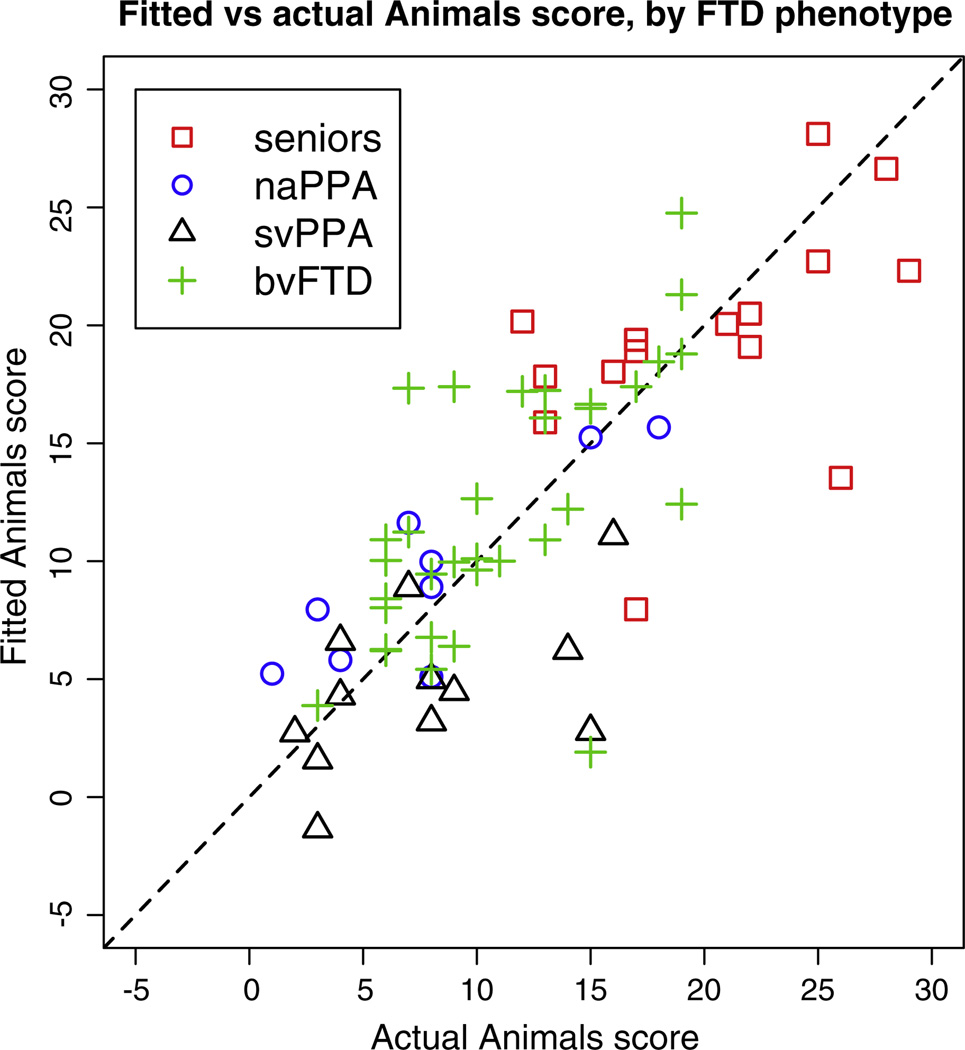
Fig. 6.
Category fluency score vs predicted score from the regression model with 4 predictors, R2 = 0.59. The dashed line indicates y = x.
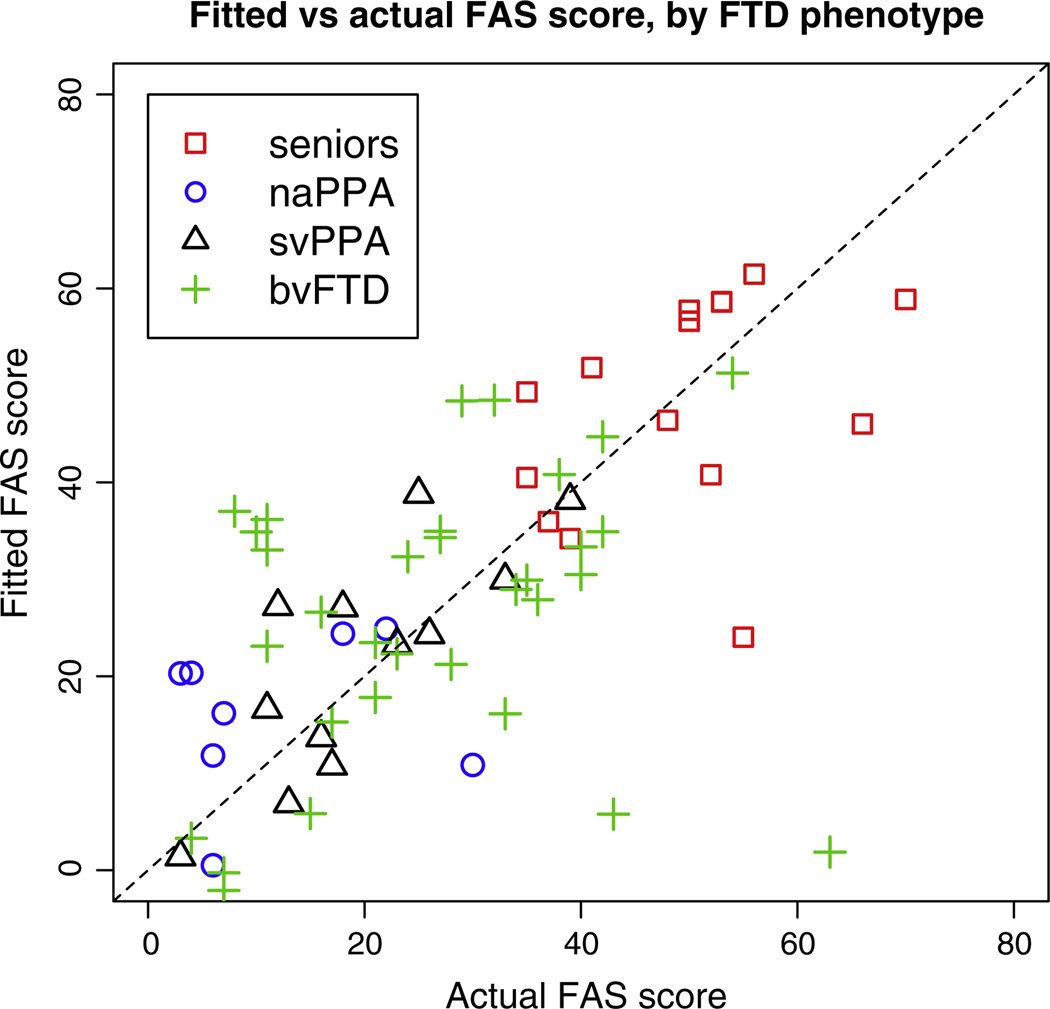
Fig. 7.
Letter fluency score vs predicted score from the regression model with 3 predictors, R2 = 0.43. The dashed line indicates y = x.
Cognitive testing
We administered 2 verbal fluency measures to patients, letter fluency (FAS) and category fluency (animals). For letter fluency, participants are required to name as many words as possible that begin with the letters F, A, or S. Participants are given 1 min per letter and we report the mean words per minute. For category fluency, participants are required to produce as many animal names as possible in 1 min. We report the total names produced.
Magnetic resonance imaging
Images were acquired on a 3 T Siemens scanner. AT1 structural acquisition was acquired with TR (repetition time) 1620 ms, TE (echo time) 3 s, 192 slices of thickness 1 mm, field of view (FOV) 256 × 256 mm, reconstructed to 0.9766 × 0.9766 mm2 in-plane resolution. The diffusion tensor imaging acquisition was a single-shot, spin-echo, diffusion-weighted echo-planar imaging sequence with GRAPPA acceleration factor of 3. The diffusion sampling scheme consists of four images with b = 0 s/mm2, followed by measurements with 30 non-collinear/non-coplanar directions isotropically distributed in angular space (b = 1000 s/mm2), TR 6700 ms, TE 85 ms, slice thickness 2.2 mm, and FOV 245 × 245 mm2, reconstructed to 2.19 × 2.19 mm2 in-plane resolution.
Image pre-processing
The MRI images were processed with the PipeDream neuroimaging toolkit http://sourceforge.net/projects/neuropipedream, which implements multi-modal spatial normalization pipelines powered by ANTs (Avants et al., 2014). To compute cortical thickness, the T1 brain image is first segmented into three tissues using the Atropos tool in ANTs (Avants et al., 2011). The gray matter and white matter probability maps are then input to the Diffeomorphic Registration-Based Cortical Thickness (DiReCT) algorithm (Das et al., 2009). The diffusion images are skull-stripped and diffusion tensors are calculated using a weighted linear least squares algorithm (Salvador et al., 2005) implemented in Camino (Cook et al., 2006). Both the diffusion and the T1 images are normalized to a common template space using ANTs. A regularized intra-subject registration corrects for the distortion between the diffusion image and the T1 image, this is then combined with the warp between the T1 image and the T1 template. After warping, the anatomical alignment of diffusion tensors is restored by applying the Preservation of Principal Directions algorithm (Alexander etal., 2001).
Gray matter and white matter parcellation using eigenanatomy
Given the set of spatially aligned images, we used eigenanatomy to parcellate the data into coherent regions based upon the variation in the subject population (Avants et al., 2012a). Like Principal Component Analysis (PCA), eigenanatomy finds a low-dimensional representation of the very high-dimensional data matrix containing all voxel data for all subjects, specifically by computing a sparse singular value decomposition of the input data matrix (either cortical thickness or FA). Further details of the algorithm are given in Avants et al. (2012b). We use the eigenvectors as DD-ROIs to compute weighted-average gray matter and white matter values for use in regression modeling of verbal fluency. Eigenanatomy has additional constraints compared to traditional PCA, which are relevant to neuroimaging data. The decomposition is sparse, meaning that the principal components are constrained to have nonzero weights in a small fraction of the brain. The eigenvectors are unsigned, meaning they can be straightforwardly used to compute linear weighted averages in a similar manner to standard ROIs based on anatomical labeling. Unsigned eigenvectors avoid the difficulties of interpreting statistics computed on components containing a combination of positive and negative weights (Todd et al., 2013). The decomposition is spatially clustered, meaning that although we do not force the components to be a single contiguous region, we prefer components that retain spatial smoothness and specificity, compared to traditional PCA eigenvectors, which can be distributed widely throughout the brain.
We produced gray matter and white matter eigenanatomy separately. For gray matter, cortical thickness images were aligned to the template space and averaged. A mask was defined by thresholding in voxels where the average thickness is greater than 0.1 mm, then multiplying this image by a pre-defined binary cortical mask in the template space. The binary cortical mask was defined by warping the Non-rigid Image Registration Evaluation Project (N1REP) cortical labels (Christensen et al., 2006) to the template space. A Gaussian smoothing was applied to the normalized subject images with kernel standard deviation 1 mm. The data were then transcribed into an n × pt matrix where pt = 504471 is the number of voxels in the thickness mask and there are n = 69 subjects. The procedure for white matter is similar, the average FA image was masked at a value of 0.25, including pf = 392248 voxels, and subject images were smoothed and converted to an n × pf matrix format in the same way. We defined the mask to include cerebral tissue only, excluding cerebellum and brainstem.
The eigenanatomy algorithm requires the user to define the number of eigenvectors to be output and their sparsity, which controls the maximum spatial extent of each eigenvector. With N eigenvectors, sparsity of 1/N will produce a set of eigenvectors that approximately cover the whole brain. We set the number of eigenvectors to 32, which yielded the same number of cortical DD-ROIs as there are labels in the NIREP parcellation (Christensen et al., 2006) that we used to generate the cortical mask. We used the same settings for white matter. Gray matter and white matter images were parcellated independently using the same parameters in sccan: 20 iterations, L1 penalty with gradient step size 0.5, manifold smoothing kernel of 1 voxel, and a minimum cluster size of 1000 voxels within each eigenvector. In each case, eigenanatomy is computed by maximizing the variance in the original data that is captured by the decomposition. Using this process, we reduced our input data of approximately 1 million voxels to 64 DD-ROIs that capture most of the variance in the data set. We compute the eigenanatomy on the complete data set, yielding a decomposition determined only by the input images, without reference to disease diagnosis or cognitive test scores.
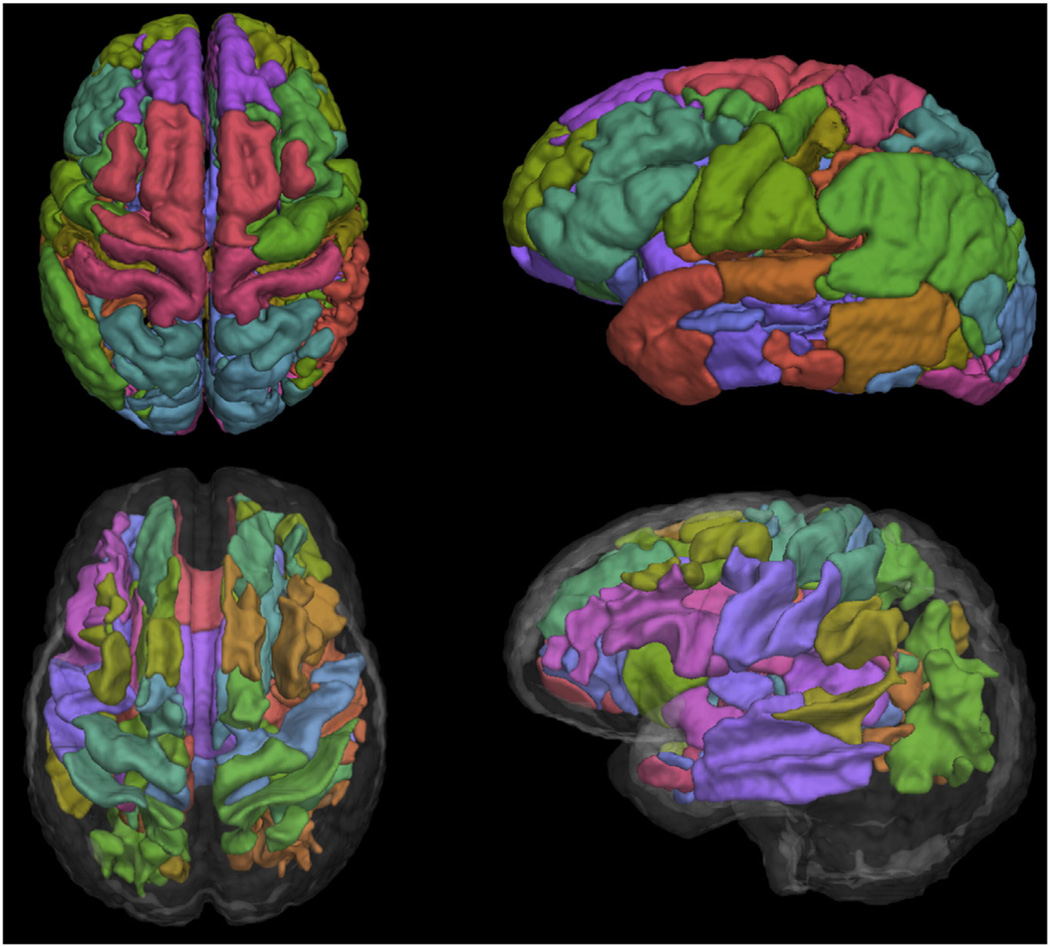
Surface renderings of the DD-ROIs are shown in Fig. 2. They are thresholded and rendered as hard labels for easier visualization, however we use the original soft DD-ROIs for correlation with cognitive performance.
Fig. 2.
Surface rendering of the 32 eigenanatomy regions for gray matter (top row) and white matter (bottom row).
Model selection for correlation with cognition
Our hypothesis is that both gray matter integrity and white matter integrity make important contributions to cognitive performance, and hence we predict a stronger correlation between the MRI measures and cognition when we include relevant gray matter and white matter predictors. Mathematically, if we have a matrix of voxel data Pt for thickness or Pf for FA, eigenanatomy outputs principal component eigenvectors qi, 1 ≤ i ≤ 32. We normalized the eigenvectors, q̂i = qi/|qi| to unity, so that the projections are the weighted mean of the thickness or FA. We arrange the eigenvectors into a matrix Q = [q̂1, …, q̂32]. Concatenating the projections Xt = Pt Qt and Xf = Pf Qf, we have a matrix X containing the 64 projections for each of the 69 subjects.
We applied model selection techniques to search for an efficient model of category-guided and letter-guided fluency scores using a subset of predictors within X. A variety of techniques exist for model selection in linear regression. It is usually not feasible to examine all possible models, so a strategy is required for exploring the space of possible models and ranking them using some metric that can reliably separate better from worse models. The Aikake Information Criterion (AIC) (Akaike, 1974) favors models that fit the data better, but penalizes more complex models, it thus quantifies a trade-off between the competing goals of improving fit to the data and avoiding extraneous predictors that fit to noise. Related information theoretic techniques include correction for small sample sizes (AICc) (Sugiura, 1978) or penalize larger models in a different way (Schwarz, 1978). These techniques provide a relative ordering of models but do not assess the goodness of fit to the data in an absolute sense or whether the correlations generalize to unseen data. The latter can only be truly tested with unseen validation data, but cross-validation within the sample can offer some insight to the ability of a model to predict left out data.
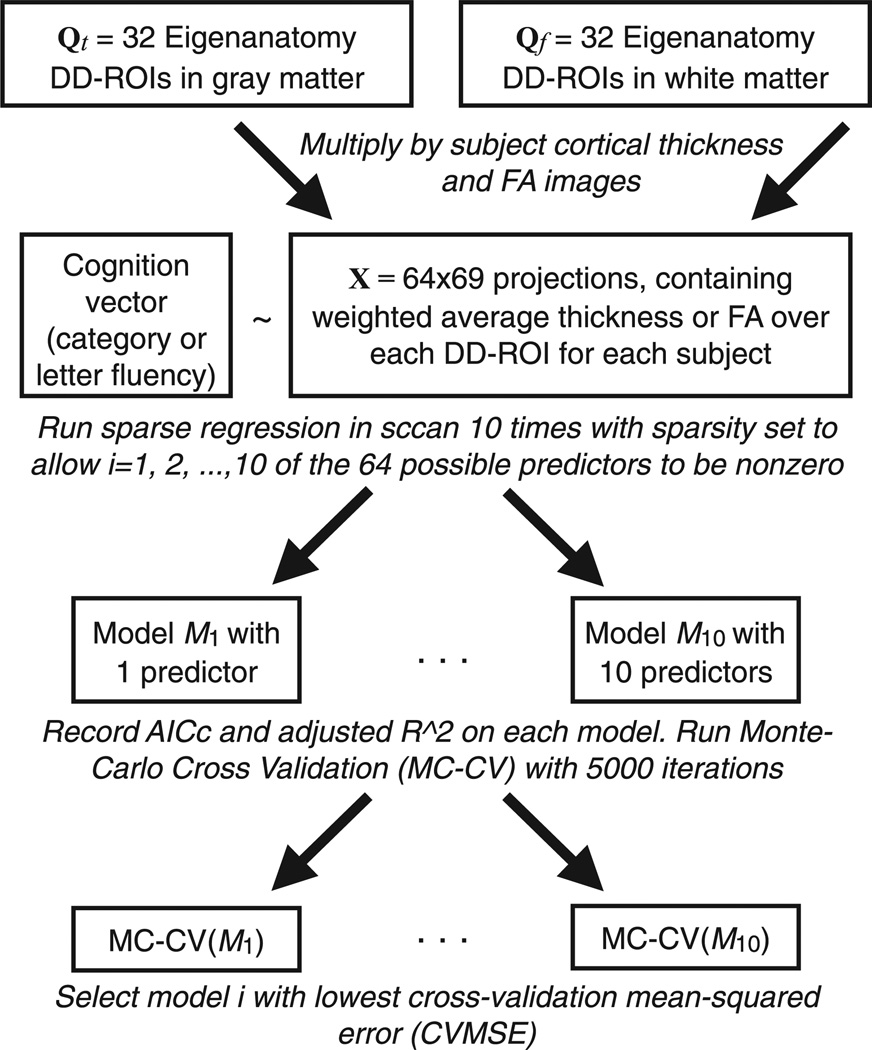
Fig. 1 outlines the process we used to generate and test candidatV models. We generated candidate models using sparse L1 regularized linear regression implemented in the sccan tool (Kandel et al., 2013). We ran the regression 10 times on the full data set, varying sparsity to allow i predictors in X to be non-zero, where 1 ≤ i ≤ 10. We also performed the same regressions using Xt and Xf, so that we could compare multi-modality models to models with the same number of predictors drawn from a single modality.
Fig. 1.
Outline of the model selection algorithm. The eigenanatomy projections are combined into a single matrix, yielding 64 potential predictors of cognition in the sparse regression. We produce models with different numbers of predictors by varying the sparseness parameter; these are then tested independently via cross-validation. The same procedure is used to test models from each modality separately, in that case we have 32 potential predictors for the sparse regression step.
We used cross-validation to test the 10 candidate models from the sparse regression. Each candidate model Mi uses a specific set of i predictors and is tested separately. We used the bestglm package in R to perform Monte-Carlo cross-validation. One quarter of the data (18 subjects) are chosen at random and assigned to a test data set, the remaining data (51 subjects) are used as training data. Ordinary least squares linear regression is performed on the training data using the predictors in Mi. The model fit to the training data is then used to predict the test data, and the errors are recorded. This procedure was repeated for 5000 random partitions of the data into training and testing sets. We used the same procedure to do cross-validation on the models that were restricted to using only gray matter (cortical thickness) or only white matter (FA) predictors.
Results
Regression models of category-guided and letter-guided verbal fluency
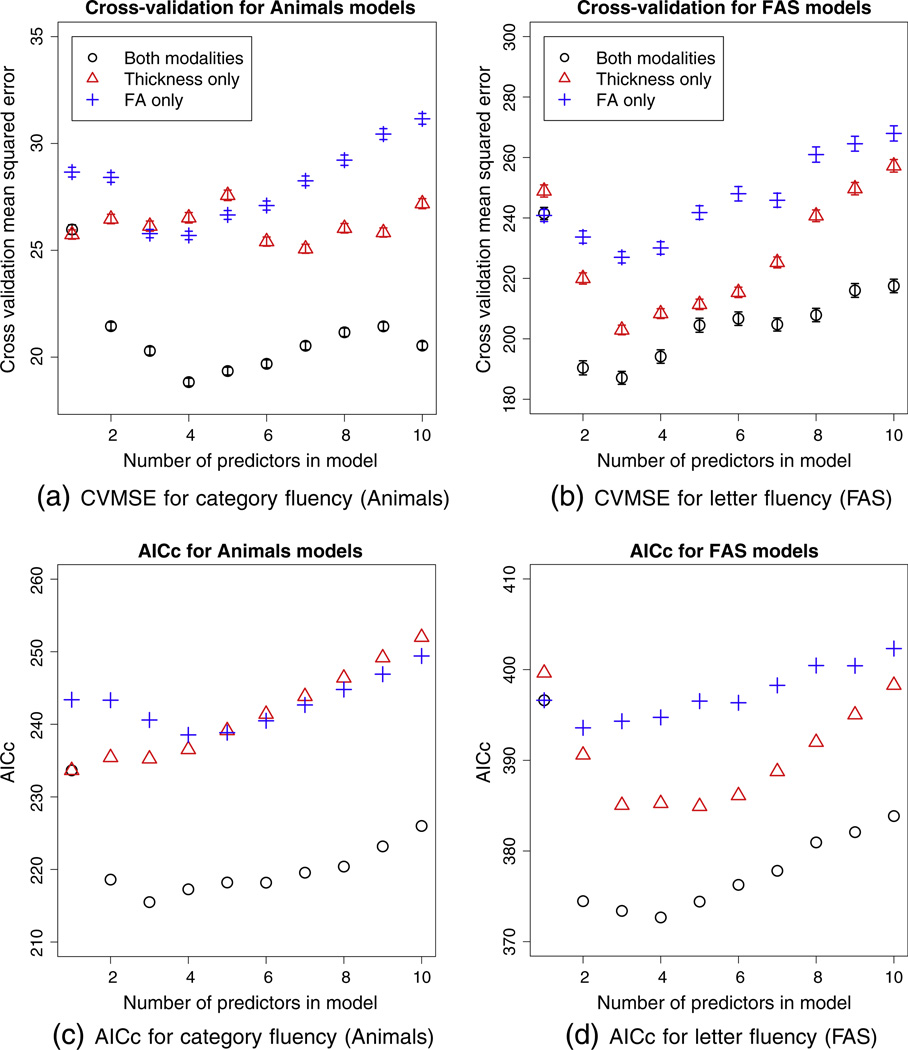
The cross-validation mean squared errors (CVMSE) are shown in the top row of Fig. 3. Models that use predictors from both modalities have lower CVMSE than those that are restricted to a single modality. The models with minimum CVMSE had 4 predictors for category fluency and 3 predictors for letter fluency. The predictor regions in these models are shown in Figs. 4 and 5.
Fig. 3.
Top row: mean squared error for Monte Carlo cross-validation of the sparse regression models, with 18 subjects left out Points are the average mean squared error over 5000 folds, vertical bars are 95% confidence intervals on the mean values. Bottom row: AICc scores for the same regression models. The legend follows that of the top row.
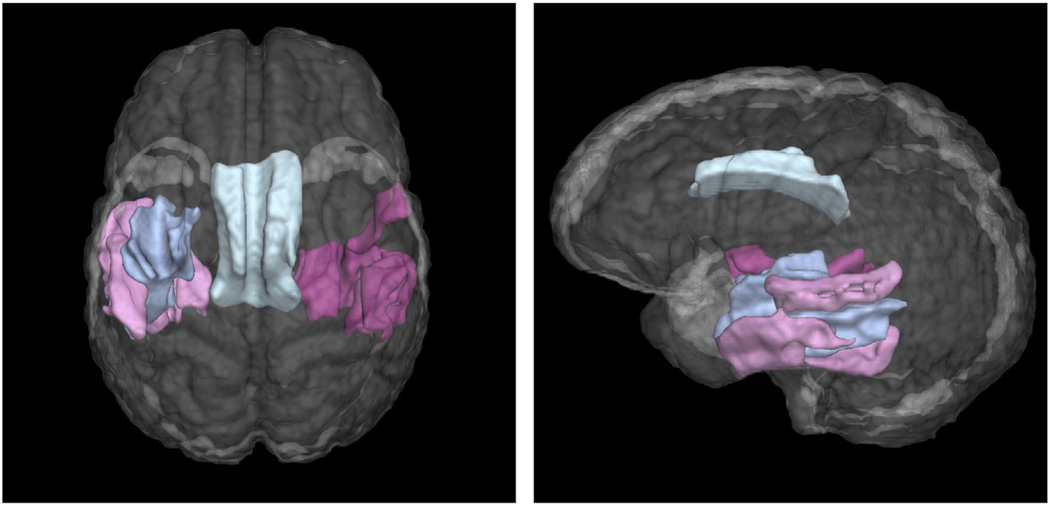
Fig. 4.
Four eigenanatomy regions used in the sparse regression model of category fluency with minimum cross-validation error. Gray matter predictors are pink, white matter predictors are blue.
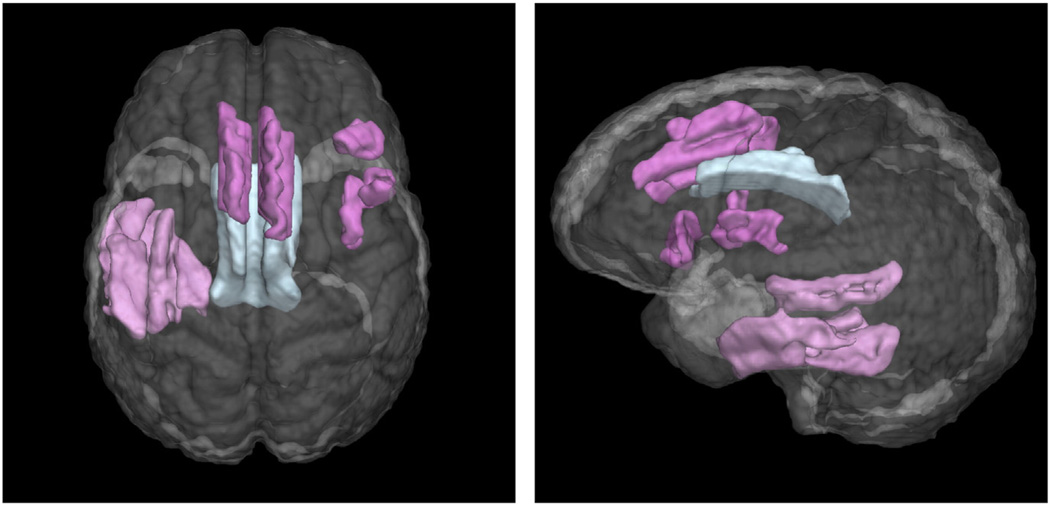
Fig. 5.
Three eigenanatomy regions used in the sparse regression model of letter fluency with minimum cross-validation error. Gray matter predictors are pink, white matter predictors are blue.
The large-scale network identified by cross-validation for category fluency shown in Fig. 4 implicated regions of left temporal cortex, including posterior–lateral middle and inferior temporal gyri. Comparable regions in right temporal lobe were also implicated. In addition to these gray matter regions, a white matter region including the left inferior longitudinal fasciculus and the left frontal-occipital fasciculus was implicated. The model with 5 predictors has very similar cross-validation performance, the regions are shown in supplementary Fig. S1. This model uses the same regions as the 4-predictor model plus an additional region of the left temporal lobe, anterior to the light pink region in Fig. 4.
The network identified for letter fluency is shown in Fig. 5. This model included a region in left temporal cortex also found in the category fluency task, covering middle and inferior left temporal cortex. However, for letter fluency, a different set of frontal regions was also selected, including superior frontal gyrus/SMA, and right inferior frontal cortex. The same white matter region as for the animal fluency task was also selected.
Different candidate models would be selected using selection criteria other than CVMSE. Cross-validation is our preferred approach because it estimates over-fitting empirically rather than imposing a fixed penalty for extra parameters. For comparison, we show the AICc scores for the candidate models on the bottom row of Fig. 3. These plots show similar trends, suggesting that three or four predictors would yield the best model, and showing that the multi-modality models outperform single-modality models as they do in the cross-validation experiments. However, the optimal models according to AICc differ by one predictor from the cross-validation experiments. Ranked by AICc, the model with 3 predictors is optimal for category (animals) fluency and the model with 4 predictors is optimal for letter (FAS) fluency. An additional ranking of the models by the adjusted R2 metric is shown in supplementary Fig. S2. Adjusted R2 selects a larger model (8 predictors) for category fluency, but agrees with AICc for letter fluency. The eigenanatomy regions selected by AICc and R2 are shown in supplementary Figs. S4, S3 and S5.
Figs. 6 and 7 show the predicted scores from the selected sparse regression model plotted against actual scores. Regression statistics relating to these plots are listed in Table 2. The R2 is higher for the category than for letter fluency, indicating better correlation between the model predictions and the observed category scores. Part of this difference is due to a single data point – letter fluency was underestimated in one subject with bvFTD by more than three times the residual standard error (RSE). Removal of this point increases the R2 from 0.43 to 0.53. AIthough the models are not sufficient for prediction of individual scores, the results suggest that we have accomplished our goal of identifying gray matter and white matter structures that play an important role in verbal fluency performance.
Table 2.
Test and prediction results, including the range of scores in the data set, the median score over all subjects and the standard deviation about the mean score. The last two columns refer to the selected regression models. The actual scores are plotted against those predicted by regression in Figs. 6 and 7; the category results have higher R2 and are thus more tightly clustered around the diagonal. RSE is the residual standard error for the models with four and three predictors for category and letter fluency respectively, as shown in Figs. 4 and 5.
| Verbal fluency test | Sample range of score | Median | Std. dev. | R2 | RSE |
|---|---|---|---|---|---|
| Category (animals) | 1–29 | 11 | 6.7 | 0.59 | 4.7 |
| Letter (FAS) | 3–70 | 27 | 17.4 | 0.43 | 14.7 |
Performance of selected models across FTD phenotypes
For category-guided naming fluency, Fig. 6 suggests that the anatomic model underlying svPPA performance overlaps less with the model associated with naPPA and bvFTD performance. This would be consistent with the degraded lexical-semantic representations that are relatively unique to svPPA. By comparison, for the anatomic model underlying performance on the letter fluency task, there appears to be greater overlap in the distribution of all three groups. This would be consistent with the claim that the lexical representation component of letter fluency is less prominent.
Discussion
In this study we provide proof-of-concept evidence that DD-ROIs and linear regression can provide insight into the structural brain networks that support verbal fluency. First, we used eigenanatomy to reduce the dimensionality in an unsupervised manner from almost a million voxels to 64 DD-ROIs chosen to capture the variance of the data set in both cortical thickness and white matter FA. Next, we applied sparse regression and cross-validation to find a subset of DD-ROIs whose weighted average thickness or FA formed the best model of category-guided and letter-guided fluency. The selected models for both tasks include white matter and gray matter predictors, suggesting an important role for the combined contribution of both white matter imaging and gray matter imaging in the underlying networks. Specifically, we observed that category fluency was related to left temporal cortex, including posterior-lateral middle and inferior temporal gyri, along with white matter in left inferior longitudinal fasciculus and the left frontal-occipital fasciculus. Letter fluency was related to similar temporal cortex regions and white matter regions as category fluency but additionally included superior frontal gyrus. In the sections below we discuss our results and approach in greater detail.
Dimensionality reduction using eigenanatomy
We used eigenanatomy for data reduction and this approach provided us with DD-ROIs chosen to capture the variation in the data set. By reducing dimensionality, we were able to minimize multiple comparisons problems inherent in voxelwise statistical tests and apply cross-validation to select regression models. The eigenanatomy algorithm computes unsigned DD-ROIs, which we use to compute regional weighted averages of cortical thickness or FA. This approach retains the interpretability of classical regions of interest, while allowing DD-ROIs to be generated automatically for a specific data set and across multiple modalities.
Multimodal data fusion using model selection
The fusion of gray matter and white matter in cognitive neuroscience models is essential to understand large-scale neural networks that account for behavior. In this study we demonstrated that the combination of gray matter and white matter outperformed either modality alone in accounting for verbal fluency performance. This approach builds on previous work that emphasized only gray matter components of the brain networks that contribute to verbal fluency deficits in FTD (Libon et al., 2009a). Libon et al. demonstrated that left temporal cortex contributed to both letter fluency and category fluency but that additional frontal cortex was related to letter fluency, to support the additional executive demands associated with mental search strategy. Moreover, Libon et al. demonstrated differences between category fluency and letter fluency, where the former appears to depend more on lexical representations while the latter appears to involve executive resources more heavily. This kind of difference should distinguish patients with svPPA from those with other FTD phenotypes, and indeed we found that patients with svPPA were somewhat segregated from the other groups in the brain network contributing to semantically-guided category naming performance.
At a broad level, converging evidence from both patient and functional imaging work provides a coherent picture regarding the brain networks involved in category fluency tasks. As noted previously, depending on the category being accessed, these tasks can rely on a combination of lexical, phonological, and semantic information, as well as executive search processes involved in retrieving the relevant information. Anatomically, there is good agreement that lexical information relies heavily on posterior portions of left middle temporal gyrus (Grossman et al., 2004). Visual semantic information is represented in part in fusiform gyrus and other ventral temporal structures (Martin, 2007) with additional reliance on heteromodal regions (Binder and Desai, 2011; Bonner et al., 2013). These regions devoted to language content are complemented by regions of frontal cortex more heavily involved in retrieval and search strategy. Some of these frontal regions appear to play a more domain-general role in cognitive processes (Duncan, 2010; Woolgar et al., 2011).
The regression algorithm and model selection procedures were unaware of which predictors came from which modality but they consistently returned predictors from both modalities in models of both letter fluency and category fluency. These models outperformed single-modality models in the cross-validation experiments, suggesting that the use of two modalities is not redundant and both gray matter and white matter features contribute to the prediction of verbal performance.
Potential caveats and alternative approaches
Several issues must be kept in mind when considering our observations. The potential number of predictors is large, necessitating dimensionality reduction and sparse modeling. Even with dimensionality reduction through methods like eigenanatomy, we still have a relatively large number of potential predictors, nearly equaling the number of subjects. The model selection in this work was limited in scope: we used a fixed eigenanatomy decomposition and sparse regression to generate candidate models with 1 to 10 predictors, and then used within-sample cross-validation to choose between the candidate models. The definition of the DD-ROIs themselves may also influence the results. We decided to use 32 regions for both gray matter eigenanatomy and white matter eigenanatomy, which yielded 64 DD-ROIs in total. The optimal number of DD-ROIs is not obvious a priori, and may not be the same for gray matter and white matter, however the choice to use an equal number allowed us to compare gray matter and white matter models with the same number of potential predictors and similar spatial extent of each, which would be difficult to accomplish with currently available anatomical label sets.
In this work we used eigenanatomy to perform unsupervised feature selection, blind to the subsequent regression against cognition, in order to minimize over-fitting. However, independent validation with unseen data is required to test the generalizability of the selected regions and the associated regression models. Related future work with independent training and testing data would be to optimize the eigenanatomy decomposition itself for prediction of cognition, and to compare our approach of eigenanatomy plus sparse regression with alternative dimensionality reduction and model selection techniques. Even without modifying the eigenanatomy procedure, we could explore a larger space of candidate models, beyond the 10 models we tested for each fluency task. For example, McMillan et al. (2014) trained and tested a classification model of AD vs FTD pathology. They used a fixed eigenanatomy decomposition and tested a large number of candidate regression models, which were then validated on unseen data.
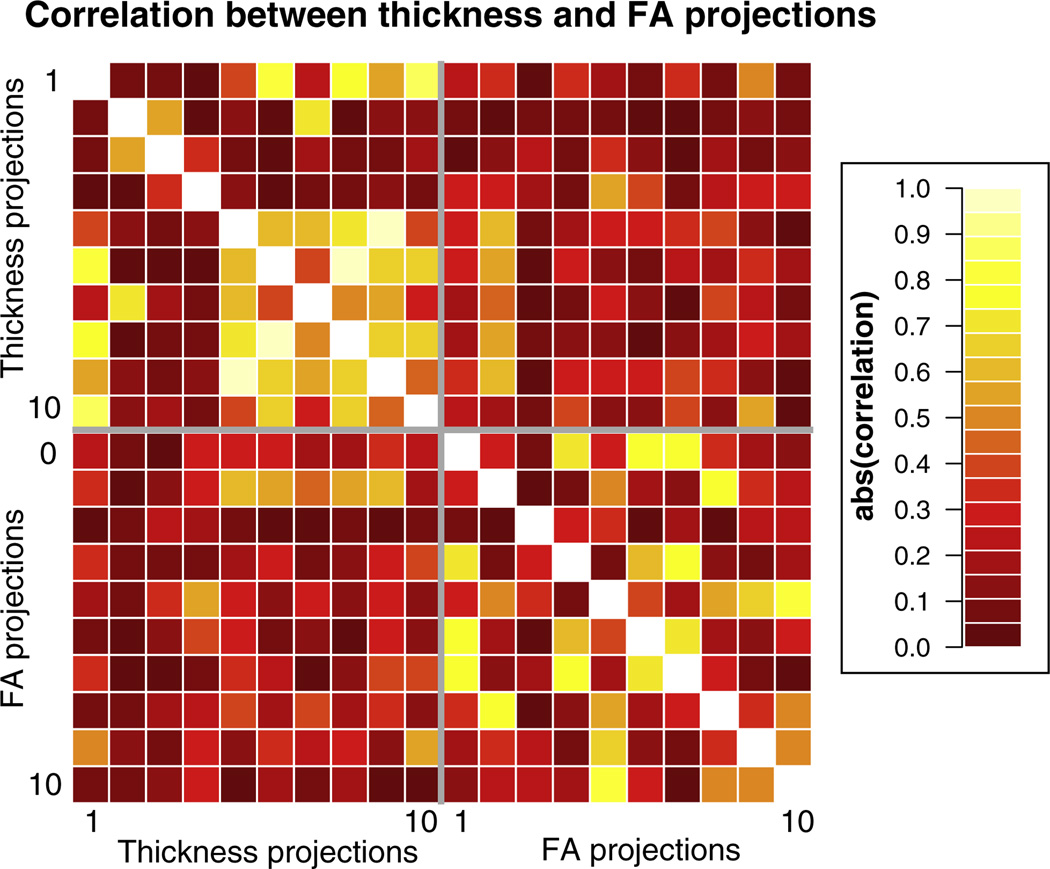
Model selection is also complicated by correlation between predictors across distinct regions that naturally form structural networks or that are affected in similar ways by pathology. While the eigenanatomy DD-ROIs are spatially distinct, the resulting projections (i.e., the weighted-average thickness or FA over the DD-ROI) can be correlated. The correlation matrix between the first 10 thickness and FA projections is shown in Fig. 8.
Fig. 8.
Matrix of the absolute value of the correlations between the first 10 thickness and FA projections. There is a higher correlation between pairs of thickness projections (median 0.28) than between pairs of FA projections (median 0.25), or projections from mixed modalities (median 0.14).
In order to discourage over-fitting to the data, we selected models containing relatively few brain regions. While these are efficient from a regression perspective in that they minimize cross-validation error, they will not form a complete description of the structural brain networks supporting verbal fluency. Our choice of sparsity constraints will tend to exclude predictors based on DD-ROIs where the FA or cortical thickness is highly correlated with predictors already in the model, since correlated predictors may not improve the regression model substantially even if the underlying anatomy is equally relevant to the integrity of the structural network.
The DD-ROIs provided by an eigenanatomy decomposition are optimized to explain variance in the data and not to fit a particular regression model. This allowed us to use a common set of DD-ROIs to explore models of different fluency tasks. Training a prediction model on the brain data without a separate dimensionality reduction, for example by using partial least squares (Krishnan et al., 2011) or a penalized regression approach (Kandel et al., 2013), has potential to build more predictive models, if carefully trained and tested to avoid over-fitting.
In this work, the multimodal data fusion was done implicitly by combining independently derived eigenanatomy projections from both modalities into a single sparse regression model. It is not necessary in principle to separate the gray matter and white matter data sets in this way, an approach such as Sparse Canonical Correlation Analysis could be used to define DD-ROIs containing both modalities (Avants et al., 2010). Separating the DD-ROIs by modality allowed us to test the relative performance of models containing gray matter, white matter, and multimodal predictors.
Conclusions
We have shown that, using eigenanatomy, it is possible to reduce gray matter and white matter neuroimaging data into DD-ROIs and to fuse both modalities to best account for verbal fluency performance. Using a small number of predictors, we are able to model category and letter fluency with R2 of around 0.5 in our data set. The sparse regression models include white matter and gray matter predictors, suggesting an important role for both white matter imaging and gray matter imaging in understanding verbal fluency. Together, these techniques provide a promising framework within which to explore multimodal fusion of neuroimaging data and the linking of these data with cognitive performance.
Supplementary Material
Acknowledgments
This work was supported by grants AG043503, AG017586, AG032953, AG038490, NS044266, and NS053488 from the National Institutes of Health, and by funding from the Wyncote Foundation.
Abbreviations
- AIC
Aikake Information Criterion
- AICc
corrected AIC
- bvFTD
behavioral-variant FTD
- CVMSE
cross-validation mean squared error
- FTD
frontotemporal degeneration
- naPPA
non–fluent/agrammatic variant PPA
- PPA
primary progressive aphasia
- svPPA
semantic variant PPA
Footnotes
For parsimony we refer to “voxelwise” analyses, but this also applies to mass-univariate surface-based analyses.
Uncited reference
Appendix A. Supplementary data
Supplementary data to this article can be found online at http://dx.doi.org/10.1016/j.neuroimage.2014.05.008.
References
- Akaike H. A new look at the statistical model identification. IEEE Trans. Autom. Control. 1974;19(6):716–723. [Google Scholar]
- Alexander DC, Pierpaoli C, Basser PJ, Gee JC. Spatial transformations of diffusion tensor magnetic resonance images. IEEE Trans. Med. Imaging. 2001 Nov;20(11):1131–1139. doi: 10.1109/42.963816. http://dx.doi.org/10.1109/42.963816. [DOI] [PubMed] [Google Scholar]
- Amunts K, Schleicher A, B rgel U, Mohlberg H, Uylings HBM, Zilles K. Broca's region revisited: cytoarchitecture and intersubject variability. J. Comp. Neurol. 1999 Sep;412(2):319–341. doi: 10.1002/(sici)1096-9861(19990920)412:2<319::aid-cne10>3.0.co;2-7. http://dx.doi.org/10.1002/%28SICI%291096–9861%2819990920%29412%3A2%3C319%3A%3AAID-CNE10%3E3.0.CO%3B2–7. [DOI] [PubMed] [Google Scholar]
- Amunts K, Weiss PH, Mohlberg H, Pieperhoff P, Eickhoff S, Gurd JM, Marshall JC, Shah NJ, Fink GR, Zilles K. Analysis of neural mechanisms underlying verbal fluency in cytoarchitectonically defined stereotaxic space — the roles of Brodmann areas 44 and 45. NeuroImage. 2004 May;22(1):42–56. doi: 10.1016/j.neuroimage.2003.12.031. http://dx.doi.Org/10.1016/j.neuroimage.2003.12.031. [DOI] [PubMed] [Google Scholar]
- Avants BB, Cook PA, Ungar L, Gee JC, Grossman M. Dementia induces correlated reductions in white matter integrity and cortical thickness: a multivariate neuroimaging study with sparse canonical correlation analysis. Neurolmage. 2010;50(3):1004–1016. doi: 10.1016/j.neuroimage.2010.01.041. http://dx.doi.org/10.1016/j.neuroimage.2010.01.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avants BB, Tustison NJ, Wu J, Cook PA, Gee JC. An open source multivariate framework for n-tissue segmentation with evaluation on public data. Neuroinformatics. 2011 Dec;9(4):381–400. doi: 10.1007/s12021-011-9109-y. http://dx.doi.org/10.1007/sl2021-011-9109-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avants B, Dhillon P, Kandel BM, Cook PA, McMillan CT, Grossman M, Gee JC. Eigenanatomy improves detection power for longitudinal cortical change. Medical Image Computing and Computer-assisted Intervention. MICCAI; 2012a. pp. 206–213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avants B, Dhillon P, Kandel BM, Cook PA, McMillan CT, Grossman M, Gee JC. Eigenanatomy improves detection power for longitudinal cortical change. Med. Image Comput. Comput Assist Interv. 2012b:206–213. doi: 10.1007/978-3-642-33454-2_26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avants B, Tustison NJ, Stauffer M, Song G, Wu B, Gee J. The Insight ToolKit image registration framework. Front Neuroinformatics. 2014;8(44) doi: 10.3389/fninf.2014.00044. http://dx.doi.org/10.3389/fninf.2014.00044/abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berthier ML, Lambon Ralph MA, Pujol J, Green C. Arcuate fasciculus variability and repetition: the left sometimes can be right. Cortex. 2012 Feb;48(2):133–143. doi: 10.1016/j.cortex.2011.06.014. (URL http://eutils.ncbi.nlm.nih.gov/entrez/eutils/elink.fcgi?dbfrom=pubmed&id=21802076&retmode=ref&cmd=prlinks) [DOI] [PubMed] [Google Scholar]
- Binder JR, Desai RH. The neurobiology of semantic memory. Trends Cogn. Sci. 2011 Nov;15(11):527–536. doi: 10.1016/j.tics.2011.10.001. http://dx.doi.Org/10.1016/j.tics.2011.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonner MF, Peelle JE, Cook PA, Grossman M. Heteromodal conceptual processing in the angular gyrus. Neurolmage. 2013 May;71:175–186. doi: 10.1016/j.neuroimage.2013.01.006. http://dx.doi.org/10.1016/j.neuroimage.2013.01.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christensen GE, Geng X, KuhI JG, Bruss J, Grabowski TJ, Pirwani IA, Vannier MW, Allen JS, Damasio H. Biomedical Image Registration. Springer; 2006. Introduction to the non-rigid image registration evaluation project (NIREP) pp. 128–135. http://dx.doi.org/10.1007/11784012_16. [Google Scholar]
- Clos M, Amunts K, Laird AR, Fox PT, Eickhoff SB. Taclding the multifunctional nature of Broca's region meta-analytically: co-activation-based parcellation of area 44. Neurolmage. 2013 Jun;83C:174–188. doi: 10.1016/j.neuroimage.2013.06.041. (URL http://eutils.ncbi.nlm.nih.gov/entrez/eutils/elink.fcgi?dbfrom=pubmed&id=23791915&retmode=ref&cmd=prlinks) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cook PA, Bai Y, Nedjati-Gilani S, Seunarine KK, Hall MG, Parker GJM, Aexander DC. Camino: open-source diffusion-MRI reconstruction and processing; Berkeley. International Society for Magnetic Resonance in Medicine 14th Scientific Meeting. ISMRM.2006. p. 2759. [Google Scholar]
- Das SR, Avants BB, Grossman M, Gee JC. Registration based cortical thickness measurement. Neurolmage. 2009 Apr;45(3):867–879. doi: 10.1016/j.neuroimage.2008.12.016. http://dx.doi.0rg/lO.lOl6/j.neuroimage.2008.12.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duncan J. The multiple-demand (MD) system of the primate brain: mental programs for intelligent behaviour. Trends Cogn. Sci. 2010 Apr;14(4):172–179. doi: 10.1016/j.tics.2010.01.004. http://dx.doi.org/10.1016/j.tics.2010.01.004. [DOI] [PubMed] [Google Scholar]
- Faraway JJ. Linear Models with R. Vol. 63. Chapman and Hall/CRC; 2004. [Google Scholar]
- Flöel A, de Vries MH, Scholz J, Breitenstein C, Johansen-Berg H. White matter integrity in the vicinity of Broca's area predicts grammar learning success. Neurolmage. 2009 Oct;47(4):1974–1981. doi: 10.1016/j.neuroimage.2009.05.046. (URL http://eutils.ncbi.nlm.nih.gov/entrez/eutils/elinkfcgi?dbfrom=pubmed&id=19477281&retmode=ref&cmd=prlinlks) [DOI] [PubMed] [Google Scholar]
- Gorno-Tempini ML, Hillis AE, Weintraub S, Kertesz A, Mendez M, Cappa SF, Ogar JM, Rohrer JD, Black S, Boeve BF, Manes F, Dronkers NF, Vandenberghe R, Rascovsky K, Patterson K, Miller BL, Knopman DS, Hodges JR, Mesulam MM, Grossman M. Classification of primary progressive aphasia and its variants. Neurology. Memory and Aging Center, Department of Neurology, UCSF, 350 Parnassus Avenue, Suite 905, San Francisco, CA 94143–1207, USA. 2011 Mar;:1006–1014. doi: 10.1212/WNL.0b013e31821103e6. (marilu@memory.ucsf.edu, URL http://eutils.ncbi.nlm.nih.gov/entrez/eutils/elinkfcgi?dbfrom=pubmed&id=21325651&retmode=ref&cmd=prlinks) [DOI] [PMC free article] [PubMed]
- Grossman M. The non-fluent/agrammatic variant of primary progressive aphasia. Lancet Neurol. 2012 Jun;11(6):545–555. doi: 10.1016/S1474-4422(12)70099-6. (URL http://eutils.ncbi.nlm.nih.gov/entrez/eutils/elinkfcgi?dbfrom=pubmed&id=22608668&retmode=ref&cmd=prlinlks) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grossman M, McMillan C, Moore P, Ding L, Glosser G, Work M, Gee J. What's in a name: voxel-based morphometric analyses of MRI and naming difficulty in Alzheimer's disease, frontotemporal dementia and corticobasal degeneration. Brain. 2004 Mar;127(Pt 3):628–649. doi: 10.1093/brain/awh075. http://dx.doi.org/10.1093/brain/awh075. [DOI] [PubMed] [Google Scholar]
- Grossman M, Powers J, Ash S, McMillan C, Burkholder L, Irwin D, Trojanowski JQ. Disruption of large-scale neural networks in non-fluent/agrammatic variant primary progressive aphasia associated with frontotemporal degeneration pathology. Brain Lang. 2012 Dec; doi: 10.1016/j.bandl.2012.10.005. (URL http://eutils.ncbi.nlm.nih.gov/entrez/eutils/elink.fcgi?dbfrom=pubmed&id=23218686&retmode=ref&cmd=prlinlks) [DOI] [PMC free article] [PubMed]
- Kandel BM, Wolk DA, Gee JC, Avants B. Information Processing in Medical Imaging. Berlin Heidelberg: Springer; 2013. Predicting cognitive data from medical images using sparse linear regression; pp. 86–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klöppel S, Stonnington CM, Chu C, Draganski B, Scahill RI, Rohrer JD, Fox NC, Jack CR, Jr., Ashburner J, Frackowiak RSJ. Automatic classification of MR scans in Alzheimer's disease. Brain. 2008 Mar;131(Pt 3):681–689. doi: 10.1093/brain/awm319. http://dx.doi.org/10.1093/brain/awm319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishnan A, Williams LJ, Mcintosh AR, Abdi H. Partial Least Squares (PLS) methods for neuroimaging: a tutorial and review. Neurolmage. 2011 May;56(2):455–475. doi: 10.1016/j.neuroimage.2010.07.034. http://dx.doi.Org/10.1016/j.neuroimage.2010.07.034. [DOI] [PubMed] [Google Scholar]
- Libon DJ, McMillan C, Gunawardena D, Powers C, Massimo L, Khan A, Morgan B, Farag C, Richmond L, Weinstein J, Moore P, Coslett HB, Chatterjee A, Aguirre G, Grossman M. Neurocognitive contributions to verbal fluency deficits in frontotemporal lobar degeneration. Neurology. 2009a Aug;73(7):535–542. doi: 10.1212/WNL.0b013e3181b2a4f5. (URL http://eutils.ncbi.nlm.nih.gov/entrez/eutils/elink.fcgi?dbfrom=pubmed&id=19687454&retmode=ref&cmd=prlinks) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Libon DJ, McMillan C, Gunawardena D, Powers C, Massimo L, Khan A, Morgan B, Farag C, Richmond L, Weinstein J, Moore P, Coslett HB, Chatterjee A, Aguirre G, Grossman M. Neurocognitive contributions to verbal fluency deficits in frontotemporal lobar degeneration. Neurology. 2009b Aug;73(7):535–542. doi: 10.1212/WNL.0b013e3181b2a4f5. http://dx.doi.org/10.1212/WNL0b013e3181b2a4f5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lillo P, Mioshi E, Burrell JR, Kiernan MC, Hodges JR, Hornberger M. Grey and white matter changes across the amyotrophic lateral sclerosis-frontotemporal dementia continuum. PLoS ONE. 2012;7(8):e43993. doi: 10.1371/journal.pone.0043993. (URL http://eutils.ncbi.nlm.nih.gov/entrez/eutils/elink.fcgi?dbfrom=pubmed&id=22952843&retmode=ref&cmd=prlinks) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahoney CJ, Malone LB, Ridgway GR, Bucldey AH, Downey LE, Golden HL, Ryan NS, Ourselin S, Schorr JM, Rossor MN, Fox NC, Warren JD. White matter tract signatures of the progressive aphasias. NeurobioL Aging. 2013 Jan; doi: 10.1016/j.neurobiolaging.2012.12.002. (URL http://eutils.ncbinlmnih.gov/entrez/eutils/elikfcgi?dbfrom=pubmed&id=23312804&retmode=ref&cmd=prlinlks) [DOI] [PMC free article] [PubMed]
- Martin A. The representation of object concepts in the brain. Annu. Rev. Psychol. 2007;58:25–45. doi: 10.1146/annurev.psych.57.102904.190143. http://dx.doi.org/10.1146/annurev.psych.57.102904.190143. [DOI] [PubMed] [Google Scholar]
- McMillan CT, Coleman D, Clark R, Liang TW, Gross RG, Grossman M. Converging evidence for the processing costs associated with ambiguous quantifier comprehension. Front. Psychol. 2013a;4(153):1–10. doi: 10.3389/fpsyg.2013.00153. http://dx.doi.org/10.3389/fpsgy.2013.00153/abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMillan CT, Irwin DJ, Avants B, Powers J, Cook P, Toledo JB, Wood EM, Van Deerlin VM, Lee CMY, Trojanowski JQ, Grossman M. White matter imaging helps dissociate tau from TDP-43 in frontotemporal lobar degeneration. J. Neurol. Neurosurg. Psychiatry. 2013b doi: 10.1136/jnnp-2012-304418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMillan CT, Avants BB, Cook P, Ungar L, Trojanowski JQ, Grossman M. The power of neuroimaging biomarkers for screening frontotemporal dementia Hum Brain Mapp. 2014 Mar; doi: 10.1002/hbm.22515. http://dx.doi.org/10.1002/hbm.22515. [DOI] [PMC free article] [PubMed]
- Rascovsky K, Hodges JR, Knopman D, Mendez MF, Kramer JH, Neuhaus J, van Swieten JC, Seelaar H, Dopper EGP, Onyike CU, Hillis AE, Josephs KA, Boeve BF, Kertesz A, Seeley WW, Rankin KP, Johnson JK, Gorno-Tempini ML, Rosen H, Prioleau-Latham CE, Lee A, Kipps CM, Lillo P, Piguet 0, Rohrer JD, Rossor MN, Warren JD, Fox NC, Galasko D, Salmon DP, Black SE, Mesulam M, Weintraub S, Dickerson BC, Diehl-Schmid J, Pasquier F, Deramecourt V, Lebert F, Pijnenburg Y, Chow TW, Manes F, Grafman J, Cappa SF, Freedman M, Grossman M, Miller BL. Sensitivity of revised diagnostic criteria for the behavioural variant of frontotemporal dementia. Brain. 2011 Sep;134(Pt 9):2456–2477. doi: 10.1093/brain/awr179. (URL http://eutils.ncbi.nlm.nih.gov/entrez/eutils/elink.fcgi?dbfrom=pubmed&id=23218686&retmode=ref&cmd=prlinkspubmed&id=pubmed&id=23218686&retmode=ref&cmd=prlinks21810890&retmode=pubmed&id=23218686&retmode=ref&cmd=prlinksref&cmd=pubmed&id=23218686&retmode=ref&cmd=prlinksprlinks) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salvador R, Pea A, Menon DK, Carpenter TA, Pickard JD, Bullmore ET. Formal characterization and extension of the linearized diffusion tensor model. Hum Brain Mapp. 2005 Feb;24(2):144–155. doi: 10.1002/hbm.20076. http://dx.doi.org/10.1002/hbm.20076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwarz G. Estimating the dimension of a model. Ann. Stat. 1978;6(2):461–464. (URL http://www.jstor.org/stable/2958889) [Google Scholar]
- Sugiura N. Further analysis of the data by Akaikes information criterion and the finite corrections. Commun. Stat Theory Methods. 1978;7(1):13–26. http://dx.doi.org/10.1080/03610927808827599. [Google Scholar]
- Todd MT, Nystrom LE, Cohen JD. Confounds in multivariate pattern analysis: theory and rule representation case study. Neurolmage. 2013 Aug;77:157–165. doi: 10.1016/j.neuroimage.2013.03.039. http://dx.doi.org/10.1016/j.neuroimage.2013.03.039. [DOI] [PubMed] [Google Scholar]
- Whitwell JL, Avula R, Senjem ML, Kantarci K, Weigand SD, Samikoglu A, Edmonson HA, Vemuri P, Knopman DS, Boeve BF, Petersen RC, Josephs KA, Jack CR. Gray and white matter water diffusion in the syndromic variants of frontotemporal dementia. Neurology. 2010 Apr;74(16):1279–1287. doi: 10.1212/WNL.0b013e3181d9edde. (URL http://eutils.ncbi.nlm.nih.gov/entrez/euhls/elink.fcgi?dbfrom=pubmed&id=20404309&retmode=ref&cmd=prlink) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson SM, Ogar JM, Laluz V, Growdon M, Jang J, Glenn S, Miller BL, Weiner MW, Gorno-Tempini ML. Automated MRI-based classification of primary progressive aphasia variants. Neurolmage. 2009 Oct;47(4):1558–1567. doi: 10.1016/j.neuroimage.2009.05.085. http://dx.doi.org/10.1016/j.neuroimage.2009.05.085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolpert DH, Macready WG. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997;1(1):67–82. (URL http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=585893) [Google Scholar]
- Woolgar A, Hampshire A, Thompson R, Duncan J. Adaptive coding of task-relevant information in human frontoparietal cortex. J. Neurosci. 2011 Oct;31(41):14592–14599. doi: 10.1523/JNEUROSCI.2616-11.2011. http://dx.doi.org/10.1523/JNEUROSCI.2616-ll.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Tartaglia MC, Schuff N, Chiang GC, Ching C, Rosen HJ, Gorno-Tempini ML, Miller BL, Weiner MW. MRI signatures of brain macro-structural atrophy and microstructural degradation in frontotemporal lobar degeneration subtypes. J. Alzheimers Dis. 2013;33(2):431–444. doi: 10.3233/JAD-2012-121156. (URL http://eutils.ncbi.nlm.nih.gov/entrez/eutils/elink.fcgi?dbfrom=pubmed&id=22976075&retmode=ref&cmd=prlinks) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.