Fractal Tempo Fluctuation and Pulse Prediction

Abstract

WE INVESTIGATED PEOPLES’ ABILITY TO ADAPT TO THE fluctuating tempi of music performance. In Experiment 1, four pieces from different musical styles were chosen, and performances were recorded from a skilled pianist who was instructed to play with natural expression. Spectral and rescaled range analyses on interbeat interval time-series revealed long-range (1/f type) serial correlations and fractal scaling in each piece. Stimuli for Experiment 2 included two of the performances from Experiment 1, with mechanical versions serving as controls. Participants tapped the beat at ¼- and ⅛-note metrical levels, successfully adapting to large tempo fluctuations in both performances. Participants predicted the structured tempo fluctuations, with superior performance at the ¼-note level. Thus, listeners may exploit long-range correlations and fractal scaling to predict tempo changes in music.

Fractal Tempo Fluctuation and Pulse Prediction

A piece of music is never performed precisely as notated. Musicians produce intentional and unintentional tempo changes in performance (Palmer, 1997) that highlight important aspects of musical structure (Shaffer & Todd, 1987; Sloboda, 1985; Todd, 1985) and convey affect and emotion (Bhatara, Duan, Tirovolas, & Levitin, 2009; Chapin, Large, Jantzen, Kelso, & Steinberg, 2009; Sloboda & Juslin, 2001). Despite such fluctuations in tempo, listeners perceive temporal regularity, including pulse and meter (Epstein, 1995; Large & Palmer, 2002). Pulse and meter embody expectancies for future events, and deviations from temporal expectancies are thought to be instrumental in musical communication (Large & Palmer, 2002).

One theoretical framework explains pulse and meter as neural resonance to rhythmic stimuli (Large, 2008). Neural resonance predicts spontaneous oscillations, entrainment to complex rhythms, and higher order resonances at small integer ratios, leading to the perception of meter. Phase entrainment alone does not provide sufficient temporal flexibility to accommodate large changes in tempo. Therefore, several oscillator models have included tempo adaptation as a parameter dynamics (e.g., Large & Kolen, 1994; McAuley, 1995). Such models predict that people track tempo fluctuations; thus, adaptation of oscillator frequency happens in response to changes in stimulus tempo. The empirical literature supports the case for nonlinear resonance (see Large, 2008), and a number of findings support tempo tracking (e.g., Dixon, Goebl, & Cambouropoulos, 2006). However, recent results have called into question the intrinsic periodicity of pulse, and the notion that people follow, or track, changes in tempo.

As measured by continuation tapping (e.g., Stevens, 1886) spontaneous oscillations are pseudoperiodic. When hundreds of successive intervals are collected and a spectral analysis is applied to the resultant time-series, one typically finds that the spectrum is characterized by a linear negative slope of log-power vs. log-frequency (e.g., Lemoine, Torre, & Delignières, 2006; Madison, 2004). Fractal, or 1/f structure also has been reported in synchronization with periodic sequences (Chen, Ding, & Kelso, 1997; Pressing & Jolley-Rogers, 1997). Thus, longer term temporal fluctuations in endogenous oscillation and entrainment exhibit 1/f structure, a common feature in biological systems (West & Shlesinger, 1989, 1990) and psychological time-series (Gilden, 2001; Van Orden, Holden, & Turvey, 2003). Pulse in music performance is not purely periodic either, and research has revealed important relationships between music structure and patterns of temporal fluctuation (for a review, see Palmer, 1997). For example, rubato marks group boundaries, especially phrases, with decreases in tempo and dynamics and amount of slowing at a boundary reflecting the depth of embedding (Shaffer & Todd, 1987; Todd, 1985). Patterns of temporal fluctuation have further been shown to reflect metrical structure (Sloboda, 1985). However, it has not been established whether pulse in music performance exhibits 1/f structure.

Numerous studies have probed the coordination of periodic behavior with periodic auditory sequences (for a review, see Repp, 2005). Between 250 ms and 2000 ms, variability in interval perception and production increases with interval duration, following Weber's law (Michon, 1967); at intervals larger than 2000 ms or smaller than 250 ms, variability increases disproportionately. Asynchronies are less variable in 1:n synchronization; this has been termed the subdivision benefit. Additionally, one typically observes an anticipation tendency, such that participants’ taps consistently precede the stimulus. Anticipation tendency is significantly decreased or absent in entrainment to complex rhythms such as music (see Repp, 2005).

People adapt to phase and tempo perturbations of periodic sequences (Large, Fink, & Kelso, 2002; Repp & Keller, 2004). For randomly perturbed and sinusoidally modulated sequences, participants’ intertap intervals (ITIs) echo tempo fluctuations at a lag of one (Michon, 1967; Thaut, Tian, & Azimi-Sadjadi, 1998); this behavior is referred to as tracking. Drake, Penel, and Bigand (2000) confirmed that people are readily able to coordinate with temporally fluctuating music performances. Dixon et al. (2006) asked listeners to rate the correspondence of click tracks to temporally fluctuating music excerpts and to tap along with the excerpts. Smoothed click tracks were preferred over unsmoothed, and tapped IBIs were smoother than the veridical IBI curves. This observation is consistent with the hypothesis of tempo tracking dynamics for nonlinear oscillators (Large & Kolen, 1994). However, in an expressive performance of a Chopin Etude, Repp (2002) found strong lag-0 crosscorrelation between listeners’ ITIs and the interbeat intervals (IBIs), showing that participants predict tempo changes. Prediction performance increased across trials for music but not for the series of clicks that mimicked the expressive timing pattern, suggesting that musical information provided a structural framework that facilitated pattern learning.

Meter may be another factor in temporal prediction. In a mechanical excerpt of the Chopin Etude, both perception and synchronization measures exhibited consistent patterns of fluctuation across trials and participants, reflecting not only phrase structure but also metrical structure (Repp, 2002, 2005). In entrainment with complex rhythms containing embedded phase and tempo perturbations, adaptation at one tapping level reflected information from another metrical level (Large et al., 2002). In another study, phase perturbations at subdivisions perturbed tapping responses despite the fact that both task instructions and stimulus design encouraged listeners to ignore the perturbations (Repp, 2008). Such findings are consistent with the hypothesis of a network of oscillators of different frequencies, coupled together in the perception of a complex rhythm (cf. Large, 2000; Large & Jones, 1999; Large & Palmer, 2002).

The current research considered pseudoperiodicity of pulse, coordination of pulse with temporally fluctuating rhythms, and the role of meter in these phenomena. Experiment 1 assessed whether patterns of temporal fluctuation in music performances exhibit long-range correlation and fractal scaling. Experiment 2 used two of these performances as stimuli, and mechanical versions were included as controls, in a synchronization task. Participants were asked to tap the beat at ¼-note and ⅛-note metrical levels on different trials for both versions of both pieces. We asked whether listeners would track or predict tempo fluctuations.

Experiment 1: Fractal Structure in Piano Performance

Experiment 1 investigated whether long-range correlation and fractal scaling were evident in the tempo fluctuations of expressive music performance. Long-range correlation and fractal scaling are two properties that are characteristic of fractal temporal processes (Mandelbrot, 1977), and have been observed in many natural systems (Chen et al., 1997; Dunlap, 1910; Hurst, 1951; Mandelbrot & Wallis, 1969; van Hateren, 1997; Yu, Romero, & Lee, 2005). Long-term correlations of a persistent nature, or memory, can be seen in a time series if the adjacent values of the stochastic component are positively correlated. Long-range correlation implies fractal structure. Scaling means that measured properties of the time series depend upon the resolution of the measurements, and can be seen in a scaling function, which describes how the values change with the resolution at which the measurement is done. Both long-range correlation and fractal scaling imply self-similarity: the future resembles the past and the parts resemble the whole.

We measured tempo fluctuations by comparing the performance with the music score and extracting beat times. We then performed fractal analyses (Bassingthwaighte, Liebovitch, & West, 1994; Feder, 1988) on the IBIs to look for long-range correlation. Such analyses require long time-series, so we recorded and analyzed entire performances including hundreds of beats (Delignières et al., 2006), and assessed structure at different time scales (i.e., different metrical levels). To assess whether such structures would be found across music styles, we collected performances of four pieces of music from different styles that contain different rhythmic and structural characteristics.

Method

STIMULI

The stimuli consisted of four music pieces: (1) Aria from Goldberg Variations, by J. S. Bach; (2) Piano Sonata No. 8 in C minor Op. 13, Mvt. 1, by Ludwig van Beethoven (measures 11-182); (3) Etude in E major, Op. 10, No. 3 by Frédéric Chopin; (4) “I got rhythm” by George Gershwin. The pieces were chosen as exemplars of different music styles: baroque (Bach), classical (Beethoven), romantic (Chopin), and jazz (Gershwin). These styles differ in meaningful ways, including rhythmic characteristics, level of syncopation, absolute tempo, and amount of tempo fluctuation. Chopin's Etude in E major (the first 5 measures) has been studied extensively by Repp (1998).

TASK

A piano performance major from The Harid Conservatory was paid $100 to prepare all four pieces as if for a concert, including natural tempo fluctuations. The pianist was instructed not to use any ornamentation or add notes beyond what was written in the score. The pieces were recorded on a Kawai CA 950 digital piano that records the timing, key velocity, and pedal position via MIDI technology. The pianist was allowed to record each piece until she was satisfied with a performance, and then chose her best performance, which was analyzed as described next.

ANALYSIS

Each performance was matched to its score using a custom dynamic programming algorithm (Large, 1992; Large & Rankin, 2007). Chords were grouped by the same algorithm and onset time was defined to be the average of all note onset times in the chord. We extracted beat times as the times of performed events that matched events in the score. Beats to which no event corresponded were interpolated using local tempo. Beat times were extracted at three metrical levels ($\frac{1}{16}$-note, ⅛-note, ¼-note¹), and IBIs were calculated by subtracting successive beat times, providing an IBI time-series for each performance at each of the three levels. We measured entire music performances and assessed structure at different time scales, which in our case means different levels of metrical structure.

Mean and variance do not accurately characterize self-similar temporal processes because they do not take into account the sequential aspects of fluctuations or the presence of memory in a process. We considered sequential aspects of temporal fluctuations in performance with the goal of determining whether these fluctuations are random and independent or if they have memory, which would imply that the underlying process exhibits fractal structure. Long-range correlations in the IBI time-series were assessed with both a power spectral density analysis and a rescaled range analysis (Bassingthwaighte et al., 1994; Feder, 1988; Rangarajan & Ding, 2000). For the spectral density analysis, power was plotted against frequency on a log-log plot, and a linear correlation was used to find the slope, –α of the best-fit line. A straight line on a log-log plot suggests that the spectral density, S(f), scales with frequency, f, as a power law with S(f) ~ f^–α. The time-series is considered to have long-range correlation when α is different from zero (Malamud & Turcotte, 1999). A second, theoretically equivalent analysis was performed using Hurst's rescaled range (R/S) analysis (Mandelbrot & Wallis, 1969). The R/S analysis yields a parameter, H, as a measure of fractal dimension. H is theoretically related to α by the identity α = 2H – 1. H can assume any value between 0 and 1. When H = .5 the points in the time-series are uncorrelated, H > .5 indicates persistence (i.e., deviations are positively correlated between time steps), and H < .5 indicates antipersistence (i.e., deviations are negatively correlated between consecutive time steps). Statistical significance of the parameter H was obtained by performing the analysis on 1000 runs of the shuffled data (randomly ordered versions of the same data set) and comparing the results. Shuffling the data eliminates correlational structure and yields a result near H = .5. Both the spectral method and the R/S method can be susceptible to artifacts (e.g., in estimation of the spectral slope), such that reliance on either method in isolation can lead to faulty conclusions. Therefore, we use both methods and require convergence to establish long-range correlation (Rangarajan & Ding, 2000).

Results

Results of the beat extraction process are shown in Table 1 for each of three metrical levels along with tempo. The shortest time-series yielded 143 events (Gershwin, ¼-note level) while the longest time-series yielded 1945 events (Beethoven, $\frac{1}{16}$-note level). Thus, each time-series had a sufficient number of data points for fractal analysis (Delignières et al., 2006). Most beats corresponded to note onsets and others were inserted in the time-series as described above. At the ⅛-note level, a total of 20 beats (5.2%) were added to the Bach, 2 beats (0.7%) to the Chopin, 10 beats (1.5%) to the Beethoven, and 15 beats (5.2%) to the Gershwin.² More events were added at the $\frac{1}{16}$-note level, while fewer were added at the ¼-note level. At the ⅛- and ¼-note levels, the IBI time-series for the first 5 measures of the Chopin was significantly correlated with Repp's typical timing profile (1998) for this piece, r(16) = .86, p < .001 (⅛-note), r(7) = .54, p = .13 (¼-note).

TABLE 1.

Mean Fractal Statistics—Performance Data.

	# Events			H			Tempo IBI / ¼-note
Piece	$\frac{1}{16}$	⅛	¼	$\frac{1}{16}$	⅛	¼
Bach	767	384	192	.68*	.73**	.76**	1259 ms
Beethoven	1945	973	487	.69**	.71**	.72**	487 ms
Chopin	611	306	153	.90**	.92**	.94**	1383 ms
Gershwin	572	286	143	.75**	.75**	.76**	626 ms

Note. Number of events and mean H for the interbeat intervals (IBIs) of each performance at three metrical levels. The mean tempo for each piece is listed in the last column.

^*p < .01

^**p < .001

Spectral density plots for the ⅛-note level IBI time-series are shown in Figure 1 (A-D). For each piece, log power decreased with log frequency in a manner consistent with a 1/f power-law distribution. Using linear regression, all slopes were estimated to be different from zero, which implies long-range memory processes. The results for the R/S analysis are shown in Figure 1 (E-H). All Hurst coefficients were significantly greater than the shuffled data (p < .001), which is indicative of persistent (nonrandom) processes that can be characterized as fractal. Thus, the spectral and R/S analyses revealed long-range memory processes.

FIGURE 1.

Spectral density (A-D) and rescaled range (E-H) analyses of the interbeat intervals (IBIs) at the ⅛-note level of the performances for Bach (A, E), Beethoven (B, F), Chopin (C, G), and Gershwin (D, H).

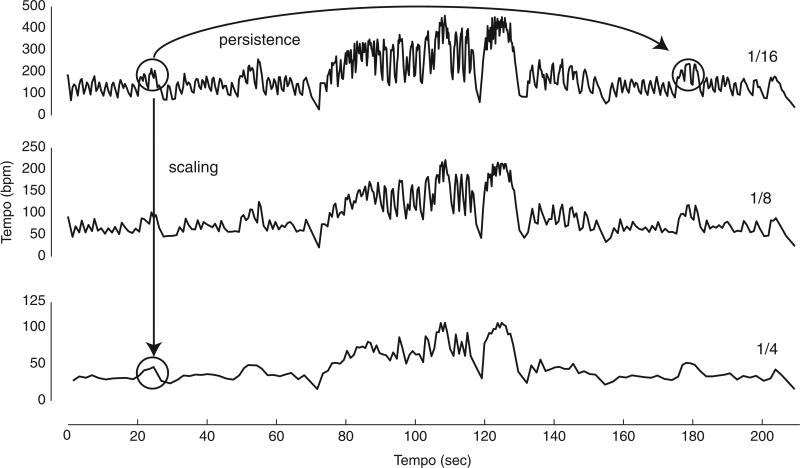
Next, we considered fractal scaling, applying spectral analyses and R/S analyses at each of the three metrical levels. Table 1 provides H values at $\frac{1}{16}$-, ⅛-, and ¼-note levels for each piece. The R/S analysis exhibits a slightly increasing H value at each level. This is expected, and it indicates that the amount of structure in the temporal fluctuations does not change with metrical level. This result is considered to be a clear indication of fractal scaling (Malamud & Turcotte, 1999). The meaning of this result is underscored in Figure 4 below, which shows tempo maps for the Chopin at each of the three metrical levels for visual comparison. The same structure is apparent, regardless of the time scale at which the process is measured.

FIGURE 4.

The tempo map (bpm = 60/IBI) for 3 different metrical levels ($\frac{1}{16}$-note, ⅛-note, ¼-note) of Chopin's Etude in E major, Op. 10, No. 3, illustrating fractal scaling of tempo fluctuations. Fractal scaling implies that changes at fast time scales could facilitate prediction of changes at slow time scales (downward arrows), persistence implies that changes early in the sequence could facilitate prediction of changes later in the sequence (arched arrow).

Discussion

Our analysis of IBIs revealed both long-term correlation and fractal scaling. Long-term correlation (persistence) means that fluctuations are systematic, such that increases in the tempo tend to be followed by further increases, and decreases followed by further decreases. Moreover, IBIs early in the time-series are correlated with IBIs found much later in the time-series, implying structure in the performer's dynamic expression of tempo. Although differences between the music styles were apparent, all were significantly fractal, suggesting that this finding generalizes across musical and rhythmic styles. We found similar H values at each metrical level (Table 1), showing similar fluctuations at each time scale. The finding of fractal structure is considered evidence against a central time-keeper mechanism (cf. Madison, 2004), a functional clock that produces near-isochronous intervals with stationary, random variability (e.g.,Vorberg & Wing, 1996). Admittedly, our pianist did not intend to produce isochronous intervals. However, if the intention was to play the same pieces without tempo fluctuation, the timing profiles would likely correlate with those of the expressive performances (Penel & Drake, 1998; Repp, 1999), and if so, they would display similar fractal structure. Chen, Ding, & Kelso (2001) proposed that long-range correlated timing fluctuations are likely the outcome of distributed neural processes acting on multiple time scales.

As discussed above, there are important relationships between music structure (such as phrasing patterns) and patterns of temporal fluctuation (see Palmer, 1997). Fractal structures also include embedded regularities (i.e., scaling), so the types of regularities we observe here are not different from previously observed patterns; rather, they represent a different approach to measuring music structure. This approach facilitates the analysis of long performances, and does not require measurement of—or correlation with—other aspects of music structure. However, such correlations may be assumed to exist based on previous studies. Additionally, we found correlation with Repp's typical timing profile for the Chopin, so we know that they exist in these data as well. Moreover, 1/f distributions have been shown along other musical dimensions, including frequency fluctuation (related to melody) for a wide variety of musical styles including classical, jazz, blues, and rock (Voss & Clarke, 1975). Thus, the measurement of structure along one dimension may reflect structure along other dimensions. It also is possible that there would be individual differences in the amount of fractal structure produced by different performers; this issue is currently under investigation. In Experiment 2 we consider the implications of 1/f structure of performance tempo for temporal coordination with expressively performed rhythms.

Experiment 2: Synchronizing with Performances

The aim of Experiment 2 was to understand how people adapt to naturally fluctuating tempi in music performance. Specifically, we asked to what extent people track and/or predict tempo changes.

Method

STIMULI

Two of the four pieces analyzed in Experiment 1, Goldberg Variations, Aria by J. S. Bach and Etude in E major, Op. 10, No. 3 by Frédéric Chopin, were chosen as stimuli for Experiment 2 because they had similar mean tempi but different rhythmic characterizations and levels of tempo fluctuations. The expressive performances recorded in Experiment 1 were used as one set of stimuli, and controls (mechanical performances) were created from the score using Cubase, running on a Macintosh G3 450 MHz computer. No timing or dynamic changes/fluctuations were contained in the mechanical versions; each note value was produced as it appeared in the score. The tempo was set to the mean tempo of the corresponding expressive version (Bach ¼-note IBI = 1259 ms; Chopin ¼-note IBI = 1383 ms).

PARTICIPANTS

Seven right-handed volunteers from the FAU community participated (1 female, 6 male). Music training ranged from zero to eight years. Each participant signed an informed consent form that was approved by the Institutional Review Board of FAU. One of the participants was excluded from the analysis due to incomplete data.

PROCEDURE

Participants were seated in an IAC sound-attenuated experimental chamber wearing Sennheiser HD250 linear II headphones. The music was presented by a custom Max/MSP program running on a Macintosh G3 computer. Sounds were generated using the “Piano 1” patch on a Kawai digital CA 950 piano. Participants tapped on a Roland Handsonic HPD-15 drumpad that sent the time and velocity of the taps to the Max/MSP program. An induction sequence of 8 beats was provided to illustrate the correct phase and period (¼- or ⅛-note) at which to tap. Continuing from the induction sequence, participants tapped the beat with their index finger on the drumpad for the entire duration of the piece. Six trials were collected for the mechanical and expressive versions at both the ¼- and ⅛-note level. To minimize learning effects trials were blocked by piece, performance, and metrical level. Data for different pieces were collected on different days within one week, and the order of pieces was randomized. On each day, tapping with mechanical performances was recorded first, and ⅛–note trials were followed by ¼-note trials. This procedure was intended to maximize learning of each piece during the mechanical trials and minimize learning while tapping to expressive performances (cf. Repp, 2002).

ANALYSIS

Phase, ϕ_n, of each tap relative to the local beat was calculated as

$${\varphi }_n=\frac{T_n-B_m}{B_m-B_{m-1}}$$

where T_n is the time of the tap, B_m is the time of the closest beat in the musical piece, and B_m–1 is the preceding beat, and ϕ_n is the relative phase of tap n. The resulting variable is circular on the interval (0, 1), and was reset to the interval (–.5, .5) by subtracting 1 from all values greater than 0.5. Although past research often has used mean and standard deviation of timing errors, those methods ignore the circular nature of relative phase and treat –.5 and .5 as describing different values. Instead, circular statistics (Batschelet, 1981; Beran, 2004) were used to calculate the mean and angular deviation (analogous to standard deviation of a linear variable) of relative phase. In addition to the mean and angular deviation of relative phase, ITI (defined as the time between successive taps) and relative phase were analyzed using the spectral density and R/S analyses used in Experiment 1.

Finally, a prediction index and a tracking index (Repp, 2002) were used to describe how participants adapted to changes in tempo. These measures are based on crosscorrelation between the ITIs and the IBIs of the expressive performance. The prediction index (r₀*) is a (normalized) lag-0 crosscorrelation of ITIs with IBIs; it therefore, indicates how well participants predict when the next beat will occur.

$${r_0}^{\star }=\frac{(r_0-a{c}_1)}{(1-a{c}_1)}$$

Where r₀ is the lag-0 crosscorrelation between ITI and IBI, and ac₁ is the lag-1 autocorrelation of the IBIs. Perfect anticipation of tempo changes results in r₀* = 1.

The tracking index (r₁*) is a (normalized) lag-1 crosscorrelation of ITI with IBI; and therefore, indicates the extent that participants track tempo change.

$${r_1}^{\star }=\frac{(r_1-a{c}_1)}{(1-a{c}_1)}$$

Where r₁ is the lag-1 correlation between ITI and IBI, and ac₁ is the lag-1 autocorrelation of the IBIs. If the participants are responding to the tempo fluctuations by matching the previous IBI, they will lag the expressive performance by one beat (e.g., Michon, 1967), thus, r₁* = 1.

Results

MEAN AND ANGULAR DEVIATION OF RELATIVE PHASE

Four-way ANOVAs, with factors Performance Type (mechanical, expressive), Metrical Level (¼-, ⅛-note), Piece (Bach, Chopin), and Trial (× 6) were used to analyze the mean and angular deviation of relative phase. Pairwise t-tests were used for posthoc comparisons. Because no significant effects of Trial or interactions containing Trial were found, implying that no learning had taken place, the ANOVAs were rerun without the factor Trial, as three-way ANOVAs. Mean relative phases, shown in Figure 2 (A, B), were relatively small—less than 3% of the IBI—indicating that participants were able to do the task. We did not observe an anticipation tendency; on average, taps fell slightly after the beat, regardless of performance type. Statistical testing revealed that mean relative phase was greater for Chopin than for Bach, F(1, 5) = 17.00, p < .01. Significant two-way interactions were also found for Piece and Performance Type, F(1, 5) = 31.75, p < .01, and Performance Type and Metrical Level, F(1, 5) = 5.42, p < .05. These interactions arose because mean relative phase was greater in expressive performances for Chopin (p < .001), and mean relative phase was significantly greater for the ⅛-note level in the expressive performances (p < .02). No other significant effects were found.

FIGURE 2.

Mean (A, B) and angular deviation (C, D) of relative phase, averaged across the entire performance, as a function of performance type for each piece (A, C) and tapping level (B, D). Error bars represent one standard error.

For angular deviation of relative phase, shown in Figure 2 (C, D), the ANOVA revealed significant main effects of Performance Type, F(1, 5) = 214.26, p < .001, Piece, F(1, 5) = 18.18, p < .01, and Metrical Level, F(1, 5) = 137.79, p < .001. Mechanical was less variable than expressive; Bach was less variable than Chopin, and the ¼-note level was less variable than the ⅛-note level. A significant two-way interaction was found between Performance Type and Piece, F(1, 5) = 38.64, p < .01. Both pieces were more variable for the expressive performance (p < .001), and the Chopin expressive was significantly more variable than the Bach expressive performance (p < .001). Also, a significant two-way interaction was found between Performance Type and Metrical Level, F(1, 5) = 81.56, p < .001; the expressive performances were much more variable than the mechanical at both the ¼- and ⅛-note levels (p < .001), and the ⅛-note variability for the expressive performance was significantly greater than the ¼-note variability for the expressive (p < .001). The results for the mean and angular deviation of relative phase indicate that overall, participants were able to entrain. For the expressive performances, participants were more accurate and more precise at the ¼-note level. Moreover, participants were less accurate and more variable for the Chopin expressive performance, whose IBIs showed greater variability than the Bach. No other significant main effects or interactions were found.

PREDICTION AND TRACKING

Four-way ANOVAs, with factors Index (prediction, tracking), Metrical Level (¼-, ⅛-note), Piece (Bach, Chopin), and Trial (× 6) were used to analyze the prediction and tracking indices. Because no significant effects of trial or interactions containing trial were found, implying that no learning had taken place, the ANOVAs were rerun without the factor trial, as three-way ANOVAs. Pairwise t-tests were used for posthoc comparisons. Prediction and tracking indices, shown in Figure 3, were used to identify patterns of anticipation and reaction to changes in tempo. Because changes in tempo are required for the calculation of these measures, they were only calculated for the expressive performances. Significant main effects of Piece, F(1, 5) = 70.95, p < .001, and Index, F(1, 5) = 50.18, p < .001, were found, and their interaction was significant, F(1, 5) = 19.76, p < .01. In general, participants predicted tempo changes and prediction was more efficient for the Chopin than for the Bach. No other two-way interactions were significant. However, the three-way interaction between, Index, Level, and Piece was significant F(1, 5) = 10.69, p < .02. For the Chopin, prediction was significantly stronger than tracking at both metrical levels (p < .01). For the Bach, prediction was significantly greater than tracking at the ¼-note level (p < .05), but at the ⅛-note level prediction was not significantly different from tracking (p = .80). In the Bach performances, temporal intervals were highly variable so that the ⅛-note level was not consistently subdivided; whereas, from the point of view of a ¼-note referent, more subdivisions were available. The Chopin performances contained running $\frac{1}{16}$-notes throughout the piece; thus, subdivisions were present at both tapping levels. Overall, this suggests that the presence of subdivisions may aid or be partially responsible for the prediction effect.

FIGURE 3.

Prediction and tracking indices for the expressive versions of Bach and Chopin at the ⅛- and ¼-note levels. Error bars represent one standard error.

SPECTRAL DENSITY AND RESCALED RANGE ANALYSIS

We also performed spectral and R/S analyses on the ITIs and the relative phases for each trial. In general, the H and α values agreed according to the equation α = 2H – 1. Note that a significance measure is available for each trial using the R/S analysis; the results for the R/S analysis (H) are reported in Table 2. Repp (2002) found phrase structure modulations in the ITIs of people tapping to music without tempo fluctuations. Therefore, it might be expected that tapping to mechanical performances would show some rudiments of fractal structure. However, for ITIs to the mechanical performances, 77-97% of trials were antipersistent (p < .05; H < .5, which implies negative long-range correlation); a result that is comparable to synchronization with a metronome (Chen et al., 1997). Chen et al. (1997) attributed this to the nature of the ITI calculation, suggesting that ITI is not an appropriate variable for fractal analysis in synchronization tasks. However, our results indicate a clear difference when compared to the expressive performances, in which 100% of the ITIs were significantly persistent (p < .05; H > .5, which implies positive long-range correlation). Moreover, mean H values for the expressive trials matched H values for the respective performances, suggesting that ITIs for the expressive performances reflected the fractal structure of the performances, as might be expected.

TABLE 2.

Mean Fractal Statistics—Tapping Data.

				Relative Phase
Intertap Interval	H	% Persistent	% Antipersistent	H	% Persistent	% Antipersistent
Bach Mechanical ⅛	.408	0	94	.692	72	0
Bach Mechanical ¼	.466	0	77	.633	22	0
Bach Expressive ⅛	.725	100	0	.654	36	0
Bach Expressive ¼	.72	100	0	.671	36	0
Chopin Mechanical ⅛	.428	0	80	.696	63	0
Chopin Mechanical ¼	.402	0	97	.666	27	0
Chopin Expressive ⅛	.86	100	0	.679	47	0
Chopin Expressive ¼	.898	100	0	.682	30	0

Note. Mean H for the intertap intervals (ITIs) and relative phase, averaged across participants and trials. Percentage of significant trials (persistent or antipersistent, p < .05) based on the R/S analysis, are shown.

The H values for the relative phases also told an interesting story. For relative phases to the mechanical performances, 63-72% of the trials were significantly persistent (p < .05) at the ⅛-note level. While this is less than the 100% expected from the literature (Chen et al., 1997; Chen et al., 2001), it is still a large percentage of trials. However, when tapping to mechanical performances at the ¼-note level, only 22-27% of the trials were significantly persistent (p < .05). Thus, at the ¼-note level, relative phase time-series were less fractal for mechanical performances. We found an even more surprising result for relative phase in the expressive performances. Overall, only about 1/3 of the trials were significantly persistent. While that number is far greater than chance, it is far fewer than would be expected based on synchronization with periodic sequences (Chen et al., 1997; Chen et al., 2001). Note that these are the trials in which the ITIs were 100% persistent, suggesting that the fractal structure somehow migrates from the asynchrony measure to the ITI when tapping to expressive performances with fractal structure. An ANOVA on the relative phase H values revealed an interaction between Performance Type and Metrical Level, F(1, 5) = 9.29, p < .05, confirming our findings.

Discussion

Our results show that people successfully entrain to complex musical rhythms, and their performance can be comparable for mechanical and expressive versions even when tempo fluctuations are large. For mechanical versions, there was no difference in accuracy (i.e., mean relative phase) between ⅛- and ¼-note levels, but there was a small, significant advantage in terms of precision (i.e., low variability) at the ¼-note level, a subdivision benefit. The large drop in number of persistent trials for relative phase at the ⅛- vs. ¼-note levels suggests a related effect of time scale. For the expressive performances there was a large improvement in both mean relative phase and angular deviation time-series between ⅛- and ¼-note levels. Participants were equally accurate for expressive and mechanical performances at the ¼-note level, and nearly as precise.

Crosscorrelational measures yielded significantly higher prediction than tracking indices; thus, people tend to anticipate, rather than react to, tempo fluctuations. For the expressive performances, 100% of the trials (ITIs) showed significant persistence–with fractal coefficients matching their respective performances, whereas fractal analysis on relative phase time-series showed far fewer persistent trials than would be expected from the synchronization literature. This suggests—albeit in a nonspecific way—that fractal structure is related to the prediction of tempo fluctuations. Moreover, for the expressive Bach performance, prediction increased at the ¼-note level. The same increase was not observed in the Chopin, however, indicating that it was not an artifact of the blocked design. The rhythm of the Bach consisted of highly varied temporal intervals, such that subdivisions were more often available at the ¼-note level, whereas for the Chopin, subdivisions were always present at both levels. Thus, prediction may have been partially due to the existence of subdivisions of the beat, providing information about the length of the IBI in progress. This interpretation is supported by the finding that accuracy and precision were superior at the ¼-note level for the Bach and Chopin.

General Discussion

How are the two main findings of the current study—fractal structuring of temporal fluctuations in piano performance and prediction of temporal fluctuations by listeners—related? Two of the properties implied by our results are fractal scaling and long-range correlation. Fractal scaling implies that fluctuation at lower levels of metrical structure (e.g., $\frac{1}{16}$-note) provides information about fluctuation at higher levels of metrical structure (e.g., ¼-note). Thus, the fact that tempo fluctuations scale implies that small time scale fluctuations are useful in predicting larger time scale fluctuations. Perturbations of subdivisions have been shown to produce positively correlated perturbations in on-beat synchronization responses, even when participants attempt to ignore the perturbations (Repp, 2008), and sensitivity to multiple metrical levels occurs in adapting to both phase and tempo perturbations (Large et al., 2002). Such responses would automatically exploit fractal scaling properties, enabling short-term prediction of tempo fluctuations. These observations could be explained by the Large and Jones (1999) model in which tempo tracking takes place at multiple time scales simultaneously via neural oscillations of different frequencies that entrain to stimuli and communicate with one another. This model successfully tracked temporal fluctuations in expressive performances, and systematic temporal structure characteristic of human performances improved tracking but randomly generated temporal irregularities did not (Large & Palmer, 2002).

Scaling does not tell the whole story, however. Tempo tracking would imply smoothed IBIs as found by Dixon et al. (2006) because tempo adaptations within a stable parameter range (cf. Large & Palmer, 2002) would effectively low-pass filter the fluctuations. But if participants’ ITIs were smoothed versions of the veridical IBIs, we would expect greater fractal magnitudes because smoothing means removing higher frequencies, which results in steeper slopes. However, the H values for ITIs were approximately equal to the H values of the IBIs themselves. Tempo tracking appears to be ruled out by this finding. Figure 4 illustrates how fractal structure may enable prediction in two related ways. Scaling (downward arrow) enables prediction if oscillations adapting to tempo changes at multiple time scales communicate with one another. Persistence (arched arrow) enables prediction within a given time scale, because it implies long-range correlation. To date, we are aware of no specific models that have been proposed to take advantage of this latter type of predictability.

In general, many natural signals have 1/f characteristics, and some authors hypothesize that neural systems have evolved to encode these signals more efficiently than others (Yu et al., 2005). Additionally, humans prefer stochastic compositions in which frequency and duration are determined by a 1/f noise source (Voss & Clarke, 1975). Thus, fractal temporal structuring of performance fluctuations may be well matched with human perceptual mechanisms. Moreover, several researchers have suggested a deep relationship between musical and other biological rhythms (Fraisse, 1984; Iyer, 1998). Other biological rhythms, such as heart rate, exhibit 1/f type temporal dependencies (for a review, see Glass, 2001); thus, if musical rhythm owes its structure, in part, to other biological rhythms, 1/f fluctuations would be heard as more natural than mechanical, or isochronous, rhythms. Indeed, fractal structure may not only enable prediction of temporal fluctuations, but may enhance affective or aesthetic judgments for music performances (cf. Bhatara et al., 2009; Chapin et al., 2009).

There is a continuous interaction between endogenous control mechanisms and environmental stimuli (Gibson, 1966); usually, these are impossible to separate when it comes to physiological rhythms (Glass, 2001). Our study shows that in music there is structure, in both the exogenous and endogenous processes, that persists throughout the interaction. Like many physiological rhythms, fluctuations in periodic tapping are structured in the absence of external stimuli, in the presence of periodic stimuli, and when there is long-term structure in the external stimulus (i.e., music). Moreover, fractal structure in stimuli may enhance interaction, such that endogenous processes are better able to lock on, perceive structure, and adapt to changes. Such processes may enable more successful interaction with the environment and between individuals.