Quasi-resonant circulation regimes and hemispheric synchronization of extreme weather in boreal summer

Significance

The recent decade has seen an exceptional number of boreal summer weather extremes, some causing massive damage to society. There is a strong scientific debate about the underlying causes of these events. We show that high-amplitude quasi-stationary Rossby waves, associated with resonance circulation regimes, lead to persistent surface weather conditions and therefore to midlatitude synchronization of extreme heat and rainfall events. Since the onset of rapid Arctic amplification around 2000, a cluster of resonance circulation regimes is observed involving wave numbers 7 and 8. This has resulted in a statistically significant increase in the frequency of high-amplitude quasi-stationary waves with these wave numbers. Our findings provide important insights regarding the link between Arctic changes and midlatitude extremes.

Abstract

The recent decade has seen an exceptional number of high-impact summer extremes in the Northern Hemisphere midlatitudes. Many of these events were associated with anomalous jet stream circulation patterns characterized by persistent high-amplitude quasi-stationary Rossby waves. Two mechanisms have recently been proposed that could provoke such patterns: (i) a weakening of the zonal mean jets and (ii) an amplification of quasi-stationary waves by resonance between free and forced waves in midlatitude waveguides. Based upon spectral analysis of the midtroposphere wind field, we show that the persistent jet stream patterns were, in the first place, due to an amplification of quasi-stationary waves with zonal wave numbers 6–8. However, we also detect a weakening of the zonal mean jet during these events; thus both mechanisms appear to be important. Furthermore, we demonstrate that the anomalous circulation regimes lead to persistent surface weather conditions and therefore to midlatitude synchronization of extreme heat and rainfall events on monthly timescales. The recent cluster of resonance events has resulted in a statistically significant increase in the frequency of high-amplitude quasi-stationary waves of wave numbers 7 and 8 in July and August. We show that this is a robust finding that holds for different pressure levels and reanalysis products. We argue that recent rapid warming in the Arctic and associated changes in the zonal mean zonal wind have created favorable conditions for double jet formation in the extratropics, which promotes the development of resonant flow regimes.

Climatic warming over the 20th century has increased the frequency of extreme heat and heavy rainfall events (1–7). On a global scale, the magnitude of this gradual increase can largely be explained by a slowly warming atmosphere, i.e., by thermodynamic arguments only. Thus, the rise in the number of heat extremes can largely be explained by a shift in the mean to warmer values (4, 5, 8). Likewise, upward trends in annual maximum daily rainfall are consistent with the increase in atmospheric moisture associated with warmer air (1, 2).

Global warming is also likely to affect large-scale atmospheric circulation patterns, which potentially could alter the frequency of heat and precipitation extremes on seasonal to subseasonal timescales (9–11). In principle, changes in atmospheric dynamics could cause a disproportionate change in the number and/or intensity of extreme weather events (12–14), beyond what is expected from thermodynamics. Moreover, the magnitude of several recent summer extreme weather events in the Northern Hemisphere midlatitudes cannot be explained by a simple shift in the mean (12, 15, 16). These events, which include high-impact extremes like the European heat wave of 2003 (15), the Russian heat wave and the Pakistan flooding in 2010 (17), and heat waves in the United States in recent years (18), were associated with anomalous circulation patterns characterized by persistent, blocking weather conditions (10, 19–22).

Atmosphere Dynamical Mechanisms

To explain the persistent weather conditions during recent extreme summers, several atmosphere dynamics mechanisms have been proposed (10, 14, 16, 23). Francis and Vavrus (23) suggested that a possible weakening of the zonal mean wind, caused by a reduced equator-to-pole thermal gradient due to Arctic amplification, would slow the eastward propagation of free-traveling planetary waves. This mechanism follows directly from Rossby wave theory. Starting from the linearized nondivergent barotropic vorticity equation (24) without any thermal or orographic forcing (i.e., an equation describing adiabatic free atmospheric waves), it is straightforward to derive an equation for the phase speed c:

$$c=U\mathrm{-}\frac{\beta }{\left(k^2+l^2\right)}$$ [1]

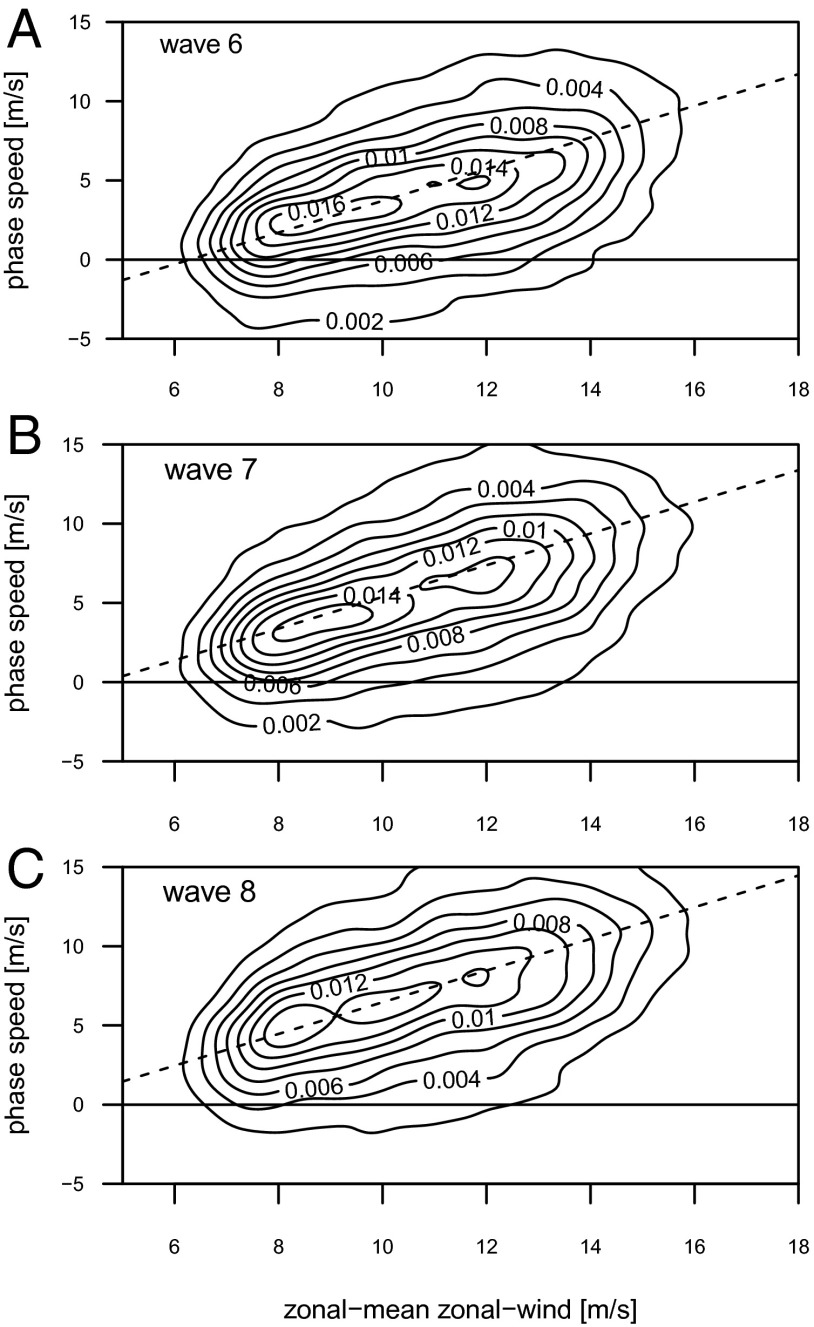
where U denotes the zonal mean zonal wind, β is the Rossby parameter, and k and l, respectively, are the zonal and meridional wave numbers. Thus, Eq. 1 shows that the speed of a free-traveling wave for any wave number scales linearly with the magnitude of the zonal mean zonal wind. Spectral analyses of observed wind fields show that, to a first order, synoptic waves with k equal to 6–8 (for which the stationary component is usually small) indeed follow the linear relationship given by Eq. 1. Here we used wind fields from ERA-Interim data (25) which combines observations with a meteorological forecast model to generate global gridded data. Fig. 1 plots probability density distributions (see SI Appendix, Methods) for daily values of the zonal mean zonal wind (U) and phase speed (c) for waves 6–8 at 500 millibars (mb) in the midlatitudes (averaged from 35°N to 65°N). The phase speed is determined by tracking the waves’ phase using spectral analysis of the meridional wind field for each individual day of the year (see SI Appendix, Methods). Clearly, at most times, synoptic waves travel eastward (positive c due to a positive U that is larger than the second term), with smaller waves, i.e., higher wave numbers, traveling faster. The spread in the zonal mean zonal wind reflects, in the first place, the seasonal cycle with weaker jets and hence slower wave propagation in summertime. Therefore, in boreal summer, a significant fraction of synoptic waves, notably with k = 6, have a phase speed close to zero (quasi-stationary) or are even traveling westward.

Fig. 1.

The 2D probability density distributions for daily values of the zonal mean zonal wind (U) and wave phase speed (c) at 500 mb aggregated from 35°N to 65°N for the 1979–2012 period for (A) wave 6, (B) wave 7, and (C) wave 8 for all calendar days. The dashed line shows the linear relationship given by Eq. 1.

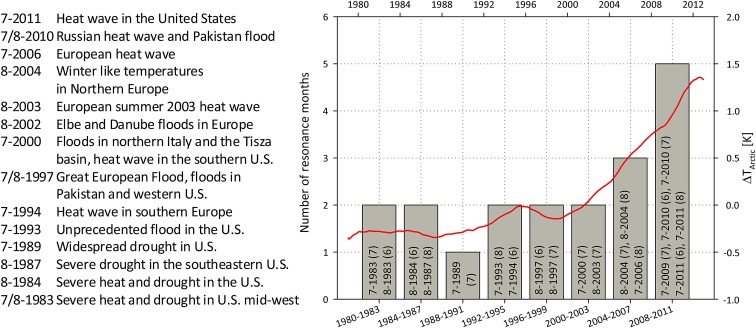
Petoukhov et al. (16) proposed a different mechanism that, rather than establishing a slowdown of free-traveling waves, amplifies the quasi-stationary component of waves with k equal to 6–8, also leading to more persistent weather conditions in summer. Thermally and orographically forced waves are quasi-stationary [as discussed in Petoukhov et al. (16)] and thus do not follow Eq. 1. Under normal conditions, the quasi-stationary component of both free and forced waves with zonal wave numbers 6–8 is weak because their energy is effectively dispersed toward the poles and the equator (26, 27). However, under specific conditions, their wave energy can be trapped in midlatitudinal waveguides, with only weak dispersion at the lateral boundaries. A key condition for the formation of waveguides is a double-peak configuration of the zonal mean zonal wind (or “double jet”), with maxima near 45°N and 70°N, respectively and a minimum in between. From the thermal wind equation it follows that this implies a sharp poleward temperature gradient at 45°N and 70°N and weak gradients in between. When the wave number of the trapped free wave is close to that of the thermally and orographically forced wave, then resonance between them can strongly magnify their amplitude. Thus, in addition to a wave guide, also the right forcing pattern is critical for resonance to occur. Therefore, in contrast to the linear slowdown in eastward propagation due to weakening of the zonal mean wind, resonance is a threshold process occurring only under specific double jet conditions. In principle it can occur throughout the year but the weaker circulation in spring and summer seems to favor resonance conditions. Starting from the quasi-linear nondivergent barotropic vorticity equation (24), Petoukhov et al. (16) derived a set of specific criteria needed for resonance to occur. Their paper focused only on the months July and August, and based on these criteria, it identified a total of 19 of these months since 1980 in which resonance conditions were fulfilled, almost all associated with memorable extreme weather events (Fig. 2). In recent years, a cluster of resonance events occurred coinciding with the onset of rapid Arctic amplification (Fig. 2). Before we discuss this recent cluster of events in more detail, we will first analyze the hemispheric-scale upper-level flows and quantify surface weather extremes during resonance periods.

Fig. 2.

Number of July and August resonance months identified by Petoukhov et al. (16) for eight 4-y periods from 1980 to 2011. Text in the gray bars indicates the actual months with, in brackets, the wave number involved in resonance, and the table on the left lists the associated extreme weather events (adapted from ref. 16). The red line plots the difference of surface warming in the Arctic (north of 65°N) and in the rest of the Northern Hemisphere (south of 65°N), illustrating the much more rapid surface warming in the Arctic since 2000.

Upper-Level Wind Field Analysis

Fig. 3 shows the frequency density of midlatitudinal Rossby waves, identified by wave number, phase speed, and amplitude, during July−August resonance periods compared with July−August climatology. The wave quantities were extracted from the 500-mb meridional wind field over a midlatitudinal belt stretching from 35°N to 65°N using daily ERA-Interim reanalysis (see SI Appendix, Methods). Amplitudes thus reflect the actual meridional wind speed over this latitudinal belt and therefore have units of meters per second. The climatological mean pdfs (solid curves in Fig. 3 A−D) show that the spectrum is dominated by eastward-traveling waves with the speed increasing with wave number, as also seen in Fig. 1 and predicted by linear Rossby wave theory. Nevertheless, a sizeable fraction of waves in July−August can be considered quasi-stationary (with an absolute phase speed c less than ∼2m/s) or even propagate westward, but these waves generally have low amplitudes. During resonance months, a distinct increase (red) in occurrence frequency of high-amplitude quasi-stationary waves is observed. This effect is strong for waves 6 and 7 (Fig. 3 A and B) but only weak for wave 8 (Fig. 3C). At the same time, the frequency density of fast-moving waves (i.e., faster than the July−August climatological mean phase speed) is reduced (blue). The mean phase speed during resonance months is reduced by more than a factor of 2 for wave 7 (from 2.85 m/s to 1.35 m/s) and by more than a factor 3 for wave 6 (from 1.50 m/s to 0.48 m/s). For wave 8, the reduction in the mean is smaller but still substantial, i.e., more than 20%. Fig. 3D plots the power density for different wave number and phase speed combinations (see SI Appendix, Methods) confirming this redistribution of kinetic energy during resonance periods: a reduction (blue) in the power of fast-moving waves and an amplification (red) of quasi-stationary waves 6, 7, and 8. Quasi-stationary waves with lower wave numbers are unaffected (waves 1–4) or actually see a reduction in amplitude (wave 5).

Fig. 3.

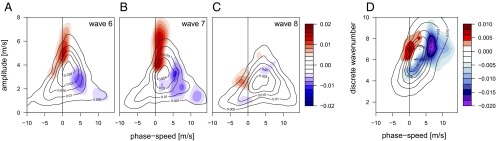
The 2D probability density distributions for daily values of the wave phase speed c and wave amplitude at 500 mb aggregated from 35°N to 65°N for days in July−August for the 1979–2012 period (solid lines) for (A) wave 6, (B) wave 7, and (C) wave 8. (D) The 2D power density plot (see SI Appendix, Methods) of wave number against phase speed. Color contours in all panels plot the anomaly during resonance months, showing an increase (red) in quasi-stationary waves and a decrease (blue) in transient waves.

As shown in Fig. 4, resonance periods are also characterized by a reduction in the zonal mean zonal wind (U), but the change is too small to fully account for the strong reduction in phase speed observed (Fig. 3). The strongest reduction in zonal mean zonal wind is seen during resonance periods of wave 7 (Fig. 4B), with a roughly 5% weakening of the mean flow (from 7.95 m/s to 7.61 m/s). Based on Eq. 1, this weakening can thus only explain a slowdown in phase speed by less than 0.5 m/s and not the 1.5 m/s reduction observed. This is true for waves 6 and 8 as well. Thus, slowing down of free-traveling waves due to weakening of the zonal mean flow can only explain a relatively small portion of the observed increase in high-amplitude quasi-stationary waves during resonance periods. Therefore, an amplification of quasi-stationary waves themselves, as predicted by resonance theory (16), is required in addition.

Fig. 4.

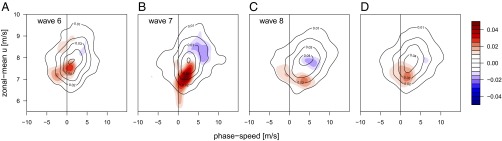
The 2D probability density distributions for daily values of the wave phase speed c and the zonal mean zonal wind (U) at 500 mb aggregated from 35°N to 65°N for days in July−August during 1979–2012 (solid lines) for (A) wave 6, (B) wave 7, (C) wave 8, and (D) the mean distribution for these three waves. Color contours plot the anomaly during resonance months, showing an increase in quasi-stationary flow patterns with reduced zonal mean winds.

Surface Extremes Analysis

Thus, midlatitude upper-level wind fields during resonance periods were characterized by high-amplitude quasi-stationary waves with k = 6–8 and a somewhat weaker zonal mean jet. However, were surface weather conditions more extreme due to these persistent circulation regimes? To quantify this, we define a simple midlatitude extreme (MEX) index (see SI Appendix, Methods):

$$\mathrm{MEX}\left(x,t\right)=\left(\frac{1}{N}{\displaystyle \sum _i^N{\left(\frac{\mathrm{\Delta }{x}_i\left(t\right)}{\sigma \left(x_i\right)}\right)}^2-{\mu }_{\mathrm{MEX}}}\right)/{\sigma }_{\mathrm{MEX}}.$$ [2]

Here x refers to any meteorological variable defined on a midlatitudinal grid consisting of N individual grid points at timestep t. Δx_i(t) is the anomaly of x, at timestep t and at grid point i, from its long-term, nonlinear trend and σ(x_i) is the SD of x at grid point i. The MEX index is normalized by subtraction of its time-averaged mean (μ_MEX) and division by its SD (σ_MEX) such that the climatological pdf centers around 0 and is defined in units of SD. High positive index values indicate extremes occurring simultaneously in many locations throughout the midlatitudes, i.e., hemispheric synchronization of extreme weather events.

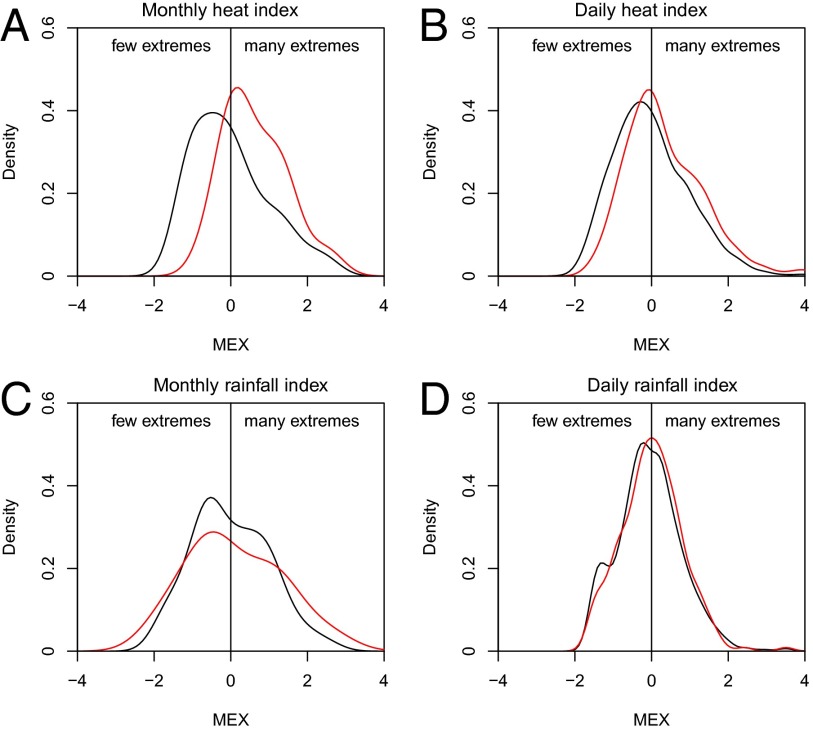
We calculate the MEX index for temperature and precipitation extremes for individual days and months (i.e., distinct July and August months) and compare resonance periods with July−August climatology (Fig. 5). Probability density distributions for daily heat and rainfall indices during resonance periods show only small differences compared with the climatological pdfs. The distribution of the daily rainfall index (Fig. 5D) shows no discernible differences (P value > 0.05), whereas that of the daily heat index (Fig. 5B) shows a small but statistically significant shift (P value < 0.05) to more extremes during resonance periods. The pdfs of monthly heat and rainfall indices show more pronounced differences between resonance months and climatology. The pdf of the monthly heat index primarily shifts toward more extremes (P value < 0.05), whereas the monthly rainfall index broadens (P value > 0.05), resulting in an increase of both few and many extremes. Thus, the temperature and precipitation patterns on any individual day during resonance periods were not particularly extreme. Instead, it was the persistence in these patterns that led to extreme heat and heavy rainfall on longer, i.e., monthly, timescales. However, only the changes in heat extremes are statistically significant at the 95% confidence level using the Kolmogorov−Smirnov statistical test.

Fig. 5.

Midlatitudinal extreme index (MEX) in units of SD for (A) monthly heat extremes, (B) daily heat extremes, (C) monthly rainfall extremes, and (D) daily rainfall extremes for 1979–2012 July−August climatology (black) and resonance months (red).

Recent Cluster of Resonance Events

Since 2000, an apparent cluster of resonance events is observed, with the frequency now almost twice that of the pre-2000 period (Fig. 2). This increase occurred, in the first place, due to increased wave 7 resonance (by a factor 2.8) and, in the second place, due to increased wave 8 resonance (by a factor 2.5), whereas the frequency of wave 6 resonance declined somewhat (by a factor 0.8). In the analysis presented above, we have shown that resonance events result in high-amplitude quasi-stationary waves (Fig. 3) and extreme weather conditions at the surface (Fig. 5). Here we ask the question whether the recent cluster of resonance events constitutes a statistically significant increase in the frequency of high-amplitude quasi-stationary waves. To address this, we estimate the amplitude probability density distribution for quasi-stationary waves, i.e., for those waves with a low phase speed c of less than 2 m/s, by applying a nonparametric kernel density estimation to daily wind field data for both the 1979–1999 and 2000–2012 period. We do this analysis for both the 500-mb and 300-mb pressure levels and both for the ERA-Interim and National Centers for Environmental Prediction (NCEP)-National Center for Atmospheric Research (NCAR) reanalysis. We test whether changes in distribution are significant using both the Kolmogorov−Smirnov and Mann−Whitney statistical tests.

Fig. 6 shows daily wave amplitude distributions for quasi-stationary waves 6–8 for the ERA-Interim reanalysis at 500 mb. For wave 7, the distribution has shifted to higher amplitudes with an especially pronounced increase of very high amplitudes (>5 m/s). This shift is statistically significant at the 95% confidence level as shown by the Kolmogorov−Smirnov and Mann−Whitney statistical tests (SI Appendix, Table S1). The number of days with a quasi-stationary wave 7 with amplitudes larger than 3 m/s increased by 30%, and, with amplitudes larger than 5 m/s, more than doubled. Likewise, for wave 8, the distribution has changed in favor of quasi-stationary waves with amplitudes in the range 2–4 m/s, i.e., the range that gets amplified during resonant flow regimes (Fig. 3C). However, this shift in the distribution is not statistically significant, just as the changes in amplitude of wave 6 (SI Appendix, Table S1). The combined distribution of amplitudes of quasi-stationary waves 7 and 8 also has seen a statistically significant shift at 95% confidence toward more high-amplitude waves and fewer low-amplitude waves (SI Appendix, Table S1 and Fig. S4). These detected changes in the amplitude distribution of quasi-stationary waves are robust and seen at higher altitudes (300 mb) as well as in other reanalysis products (NCEP-NCAR). Notably, the observed shift in the distribution toward higher amplitude quasi-stationary waves 7 and 8 is very similar at 300 mb (compare Fig. 6 with SI Appendix, Fig. S1) and in NCEP-NCAR (compare Fig. 6 with SI Appendix, Figs. S2 and S3). Moreover, the statistical significance of the observed changes is generally higher in the NCEP-NCAR reanalysis and at higher altitude (SI Appendix, Table S1). Finally, SI Appendix, Figs. S8−S11, show that the amplitude distribution of transient waves, with phase speed c > 4 m/s, has not changed from the 1979–1999 to 2000–2012 period. This again is seen at both altitudes and in both reanalysis products. We thus conclude that the recent cluster of resonance events has led to a detectable increase in the overall frequency of high-amplitude quasi-stationary waves with k = 7 and 8 since 2000, but it did not affect the amplitude distribution of transient waves. These observed statistical changes are thus in full agreement with those expected from resonance theory.

Fig. 6.

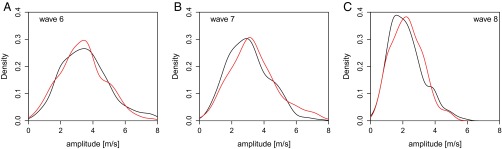
Probability density distributions of quasi-stationary waves (|c| < 2 m/s) at 500 mb for days in July−August during 1979–1999 (black) and 2000–2012 (red) for (A) wave 6, (B) wave 7, and (C) wave 8 in the Era Interim reanalysis. The shift in the distribution of wave 7 to higher amplitudes is statistically significant (see SI Appendix, Table S1).

Discussion

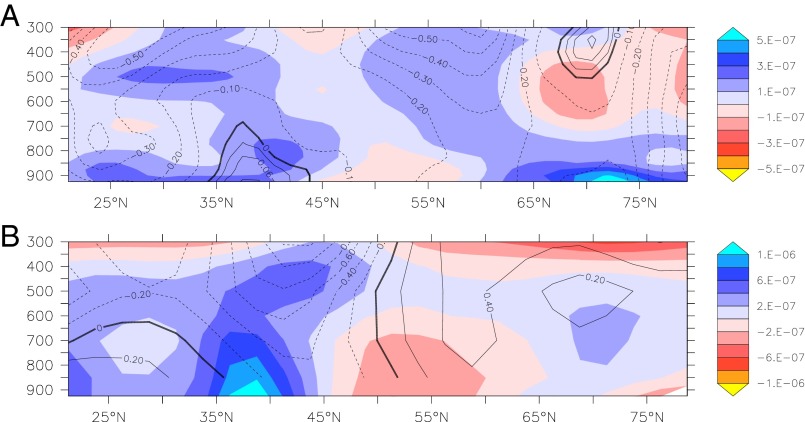
The recent cluster of boreal summer resonance events coincided with a period of rapid Arctic amplification. The rate of surface warming in the Arctic (north of 65°N) has been close to that of the rest of the Northern Hemisphere (south of 65°N) up until roughly the year 2000 (red line, Fig. 2). From that year onward, the Arctic has warmed at a substantially faster rate, and therefore the surface temperature difference between the Arctic and the region south of that has now been reduced by about 1.5 °C (Fig. 2). This has reduced the equator-to-pole thermal gradient at the surface, which is expected to weaken the zonal mean zonal wind. This weakening is indeed observed, but the vertical profile of zonal mean changes (Fig. 7) shows that the picture is more complex regionally. Fig. 7A shows zonal mean anomalies in thermal gradient (colors) and zonal wind (black contours) of the post-2000 period compared with 1979–1999 for the Northern Hemisphere troposphere in July and August. Over most latitudes and heights, the thermal gradient has weakened (blue), with the most pronounced weakening taking place in the near-surface subpolar region (900 mb, 70°N), as expected from Arctic amplification. However, there are two exceptions: (i) In the midlatitudes, the thermal gradient has remained essentially unchanged over all heights, and (ii) in the midtroposphere subpolar region (700−400 mb, 65°N–75°N), it has actually strengthened (red shading in Fig. 7). The latter causes an amplification of the subpolar jet (solid contours). In the midlatitudes, the thermal changes have led to a narrowing of the jet due to weakening at its southern (30°N−40°N) and northern (50°N−65°N) edges (dashed contours), but essentially no change in its core (40°N−50°N). These dynamical changes, with a more narrow subtropical jet and a stronger subpolar jet, in addition to the overall weakening of the zonal wind, are favorable for double jet formation. In particular, changes in the 500-mb air temperature have resulted in weaker gradients at 30°N and 60°N and sharper gradients at 45°N and 70°N, exactly as observed during resonance circulation regimes [see figure 5 of Petoukhov et al. (16)].

Fig. 7.

(A) Anomaly in poleward thermal gradient (color contours) in degrees Centrigrade per meter and zonal mean zonal wind (contour lines) in meters per second for July−August in 2000–2012 compared with 1979–1999. Negative anomalies (red) strengthen the magnitude and positive anomalies (blue) weaken the magnitude of the thermal gradient. Solid contours indicate an amplification of the zonal mean zonal wind and dashed contours indicate a weakening. (B) Same as in A but showing anomalies for 2081–2100 compared with 1981–2000 of the multimodel mean of the CMIP5 set of climate projections under scenario RCP8.5.

Our findings are consistent with Overland et al. (28), who showed that boreal summers in the last decade have been dominated by a negative Arctic Oscillation (AO) index. The summer AO index (i.e., the pressure difference between midlatitudes and high latitudes) and also the Arctic Dipole (AD) index (i.e., the pressure difference between the North American and the Siberian side of the Arctic) have both been anomalously negative over the last decade (28). The 6-y run (2007−2012) of near 1 SD negative excursions of the AO and AD index is estimated to have a likelihood of less than 1 in 1,000 (28). Although this should be considered a rough estimate, it is clear that the observed patterns of boreal summer circulation in recent years have been highly anomalous. Due to the smaller poleward pressure gradients, negative AO summers see weaker zonal mean jets and stronger meandering of the jet, just as during resonance periods.

The patterns of future zonal mean changes in the multimodel mean of the CMIP5 set of climate models show some similarities with the recently observed anomalies (compare Fig. 7 A and B). Under a high-emission scenario (RCP8.5), by the end of the 21st century, the July−August thermal gradients are generally projected to increase northward of 50°N (red) and decrease southward of 50°N (blue), leading to strengthening of the subpolar jet (solid contours) and weakening of the subtropical jet (dashed contours). Thus, these projected zonal mean changes seem favorable for a double jet flow regime. Moreover, the similarity between the recently observed changes and future climate model projections seems to suggest that changes in the Arctic, which become pronounced in the models only by midcentury (29), are driving the dynamical shifts. Arctic amplification, at least in July−August, does not manifest itself as a simple hemisphere-wide weakening of thermal gradients and hence zonal mean flow. Instead, the changes in thermal gradient seem consistent with areas of earlier spring snow loss over high-latitude (northward of 50°N) land areas (30). Also, upper-troposphere thermal gradients in the subpolar regions increase, and the reason for this is not fully understood. Nevertheless, the vertical profile of the observed changes in the poleward thermal gradient in subpolar regions (i.e., a reduction at low altitudes and increase at high altitudes; Fig. 7A) is consistent with reported warming trends, which show that recent Arctic amplification has been surface-based (31–33).

Much more detailed analysis would be needed, including numerical modeling experiments, to unravel the direction of causality: Is Arctic amplification really the driver behind dynamic changes or do dynamical changes have a strong effect on Arctic warming? This will be challenging since current general circulation models appear to be deficient in reproducing aspects of the summer jet climatology, which likely limits their ability to accurately simulate the development of Rossby waves (10). Also, future work should focus on the exact conditions that favor the occurrence of resonance flow regimes. Here we have taken a hemispheric approach, limiting our analysis to the Northern Hemisphere and to wave numbers 6–8. Possibly the phenomenon is important in the Southern Hemisphere or for other wave numbers as well; further analysis will be needed to investigate this.

Conclusions

In this study, we have shown that the daily upper-level wind field during months that satisfy resonance conditions for the planetary wave equations was characterized by anomalous high-amplitude quasi-stationary waves with wave numbers 6, 7, and 8. We thus demonstrate the link between the occurrence of resonance conditions and observed high-amplitude waves with a low phase speed. This finding supports resonant amplification of planetary waves as an important mechanism causing large-amplitude, slowly propagating waves. Weakening of the zonal mean zonal wind also moderately contributed to a slower eastward propagation of free-traveling synoptic-scale planetary waves during resonance events. We further find that these high-amplitude, quasi-stationary waves resulted in persistent weather conditions at the surface and therefore in a strong increase in heat extremes and rainfall extremes, especially on monthly timescales. We thus provide evidence that many of the persistent weather extremes in recent summers were caused by resonant circulation regimes. Our findings underscore the importance of double jet flow regimes, as suggested in previous studies (14, 22, 34, 35), both for explaining observed extremes and with respect to projected future changes.

Our study illustrates that shifts in upper-level atmospheric circulation regimes can strongly alter the occurrence of weather extremes at the surface. Such regime shifts occur irregularly and do not necessarily affect the time-averaged mean of specific flow quantities (9). Recent studies focused on long-term trends of mean flow quantities, like wave amplitude or phase speed, and typically failed to detect any significant trends (36, 37). Here we show that only specific sectors of the July/August wave spectrum have seen significant changes since the onset of rapid Arctic warming in 2000. That is, the amplitude of the quasi-stationary component of waves 7 and 8 has increased, consistent with the recent cluster of resonant flow regimes and extreme events involving these particular wave numbers. We argue that the changes in the zonal mean temperature profile, associated with rapid warming in the Arctic, have created favorable conditions for double jet formation and hence resonant flow regimes. This study thus adds to the growing body of evidence (23, 38–41) that rapid changes in the Arctic affect the large-scale circulation and thereby extreme weather in the midlatitudes.