TOXICITY PROFILING OF ENGINEERED NANOMATERIALS VIA MULTIVARIATE DOSE-RESPONSE SURFACE MODELING

Abstract

New generation in vitro high-throughput screening (HTS) assays for the assessment of engineered nanomaterials provide an opportunity to learn how these particles interact at the cellular level, particularly in relation to injury pathways. These types of assays are often characterized by small sample sizes, high measurement error and high dimensionality, as multiple cytotoxicity outcomes are measured across an array of doses and durations of exposure. In this paper we propose a probability model for the toxicity profiling of engineered nanomaterials. A hierarchical structure is used to account for the multivariate nature of the data by modeling dependence between outcomes and thereby combining information across cytotoxicity pathways. In this framework we are able to provide a flexible surface-response model that provides inference and generalizations of various classical risk assessment parameters. We discuss applications of this model to data on eight nanoparticles evaluated in relation to four cytotoxicity parameters.

1. Introduction

Nanotechnology is rapidly growing and currently used in various industries such as food, agriculture, electronics, textiles and health care. The widespread use of engineered nanomaterials (ENM) in over 800 consumer products increases the likelihood that these materials will come into contact with humans and the environment [Maynard et al. (2006), Kahru and Dubourguier (2009)]. Many biological processes take place at the nanoscale level, and the introduction of ENMs into living organisms could lead to interference in the molecular and cellular processes that are critical to life [Nel et al. (2009)]. This potential for human and environmental hazard has spurred recent interest in early identification of potentially hazardous nanomaterials. Knowledge about the potential hazard of nanomaterials is still lacking and a lot of study is required to understand how ENM properties such as size, shape, agglomeration state, solubility and surface properties could lead to hazard generation at the nano-bio interface [Stern and McNeil (2008), Nel et al. (2006)].

Current research in nano-toxicology includes new generation high-throughput screening (HTS) assays, which enable the simultaneous observation of multiple cellular injury pathways across an array of doses and times of exposure. In this article, for example, we analyze data on eight metal and metal oxide nanoparticles, monitored in relation to four cellular injury responses, derived from the hierarchical oxidative stress model of Nel et al. (2006) and Xia et al. (2006). All four outcomes are measured contemporaneously over a grid of ten doses and seven hours of exposure (see Figure 1). The four measured responses include mitochondrial superoxide formation, loss of mitochondrial membrane potential, elevated intracellular calcium and membrane damage [George et al. (2009)]. For increasing dosage and duration of exposure, we observe typical dose-response kinetics, with outcomes possibly depending on one another.

Fig. 1.

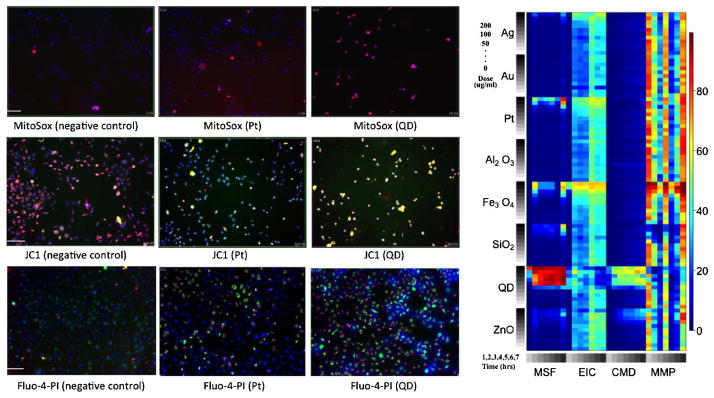
Fluorescence images and heat map of raw data. On the left are fluorescence images of RAW cells treated with various nanomaterials (quantum dot, platinum and a negative control) and dyed with compatible dye combinations including MitoSox, JC1, PI and Fluo-4. The subsequence fluorescence read-out, measured at varying wavelengths, provides a measure of the number of cells positive for the response. On the left is a heat map of the raw data for each particle and outcome. Colder colors indicate a smaller percentage of cells positive for the response and warmer colors indicate a larger percentage of cells positive for the response.

These assays provide an opportunity to help define biological relationships and may suggest which nanoparticles are likely to have an in vivo effect. While HTS assays cannot replace traditional animal studies, they are less costly, less labor intensive and can be used to explore the large number of potential nanomaterial variables that can influence human health hazards [Meng et al. (2010), Stanley et al. (2008), Maynard et al. (2006)]. The feasibility and utility of HTS assays have been illustrated in various fields such as functional genomics, with the use of microarray technology, as well as in pharmacology for the rapid screening of potential drug targets [Hoheisel (2006), White (2000)]. In toxicology, risk assessment involves the characterization of hazard as well as the potential for exposure while accounting for all assumptions and uncertainties. The HTS framework provides a wealth of information about cellular injury pathways but proves a challenge for the classic risk assessment paradigm. In fact, there is still disagreement in the HTS setting on how to define and how appropriate are classical risk assessment parameters such as no observable adverse effect level (NOAEL), the lowest observable adverse effect level (LOAEL) and the dose that produces 50% of the maximum response (EC50), among others.

Parametric functions such as families of sigmoidal curves are frequently used to fit dose-response data. Some commonly used sigmoidal models include log-logistic models, log-normal models and Weibull models [see Ritz (2010) for a recent review of these models]. The log-logistic functions are the most frequently used for modeling dose-response data in toxicology. The four parameter log-logistic model can be expressed as follows:

$$f(x;b,c,d,h)=c+\frac{d-c}{1+exp[b\{log(x)-log(h)\}]}.$$ (1)

Here h, the inflection point in the curve, provides a convenient risk assessment parameter, since it can be interpreted as the 50% effective or inhibitory dose (EC50, IC50) [Emmens (1940)]. Other special cases of this model include the 3 parameter log-logistic model which leads to the famous Hill equation [Hill (1910)] and special cases of the Michaelis–Menton kinetics. Further extensions of these models include the five parameter log-logistic function, which provides a bit more flexibility by allowing the function to be asymmetric [Finney (1979)], and the Brain-Cousens model, which includes an extra parameter to account for a possible favorable response to a toxin at low concentrations [Calabrese and Baldwin (2003)]. In general, these models assume that the dose-response function is completely known apart from the few parameters to be estimated, usually by determining which values of the parameters result in the best fit to the dose-response function.

Several other methods have been proposed to model nonlinear dose-response relationships relaxing strictly parametric assumptions. Ramsay (1988) proposed the use of monotone regression splines to model a dose-response function. In this case, piecewise polynomials or splines can allow greater flexibility while achieving monotonicity by imposing constraints on the estimated function. Li and Hunt (2004) proposed the use of linear B-splines with one random interior knot to model a nonlinear dose-response curve. In this context, the random interior knot provides inference on the dose at which the toxin begins to take effect and thereby provides a useful parameter for risk assessment. Kong and Eubank (2006) suggested the use of functions that combine smoothing spline techniques and the nonnegativity properties of cubic B-splines to estimate the dose-response curve. The use of nonparametric techniques to estimate dose-response curves often provides a more realistic representation of the data generating process. At the same time, however, some of these techniques make it more difficult to interpret the model in terms of classical risk assessment.

Recent literature advocates the simultaneous use of multiple outcomes to assess risk. Regan and Catalano (1999) proposed a bivariate dose-response model that accounts for the dependence among outcomes of developmental toxicity using generalized estimating equations. Geys et al. (2001) proposed a similar model for risk assessment of developmental toxicity, but approached the problem using latent variables. Yu and Catalano (2005) suggested a model for quantitative risk assessment of bivariate continuous measures of neurotoxicity using percentile regression. These methods are often aimed at the analysis of one potentially toxic agent as it relates to adverse events or continuous outcomes observed in association with exposure over a range of doses. Their direct applicability to the general HTS setting described earlier is therefore limited.

From a statistical perspective, cellular interrogation data based on high-throughput platforms can be characterized as multivariate dependent observations. Each nanoparticle is indeed associated with a multiple set of cellular outcomes recorded both longitudinally, in relation to different exposure durations, and cross-sectionally, in relation to a dose escalation design. This particular design structure suggests that valid statistical inference must account for potentially complex patterns of dependence between different observations. A reasonable dependence scheme might, for example, assume data to be dependent within outcome and particle, as well as between outcomes for the same particle.

In conjunction with considerations related to the joint sampling distribution of these data structures, appropriate statistical treatment must account for nonlinearities in the mean response associated with dose and duration dynamics. While, in principle, one can choose to define a random response surface in a completely nonparametric fashion, it is important to maintain a certain degree of interpretability, especially in relation to standard hazard assessment quantities of interest to substantive scientists. In summary, perhaps reductively, the overall modeling challenge lies in the definition of a flexible and interpretable probabilistic representation for a family of dependent dose-response random surfaces.

In this paper we propose a hierarchical dose-response model for the analysis of HTS data from nanotoxicology. Our model builds on earlier work [Hastie and Tibshirani (1986), Li and Hunt (2004)], expanding on them to account for the multivariate nature of the data and to address the estimation of a series of two-dimensional dose-response surfaces. We provide a flexible framework for modeling dose and duration response kinetics jointly, while providing inference on several risk assessment parameters of interest. We utilize a hierarchical structure to define dependence between outcomes and thereby borrow strength across injury pathways, providing the basis for a comprehensive risk assessment paradigm in HTS studies. We account for outlying observations via a T -distributed error model and describe how to carry out inference for the model parameters and their functions on the basis of simulated draws from their posterior distribution. To our knowledge, we are the first to propose a principled statistical methodology for the joint analysis of this new generation of in vitro data.

The remainder of the article is organized as follows. In Section 2 we introduce the proposed model. In Section 3 we discuss parameter estimation and associated inferential details. Section 4 employs the proposed model for the analysis of 8 metal oxide nanomaterials and describes inference for various risk assessment parameters of interest. We conclude with a critical discussion of the limitations and possible extensions of our method in Section 5.

2. Model formulation

2.1. Model description

In this section we describe a dose-response model for a general HTS study, where we monitor a multivariate continuous outcome y, corresponding to J cytotoxicity parameters, in association with the exposure of a number of cells to I different ENMs. More precisely, let y_ijk(d, t) denote a multivariate response corresponding to ENM i (i = 1, …, I), cytotoxicity parameter j (j = 1, …, J) and replicate k (k = 1, …, K) at dose d ∈ [0, D] and time t ∈ [0, T]. In typical applications one observes y over a discrete set of doses d̃ = (d₁, …, d_m1)′ and exposure times t̃ = (t₁,...., t_m2)′. However, for clarity of exposition, we simplify our notation and without loss of generality refer to a general dose d ∈ [0, D] and time t ∈ [0, T]. We introduce the following 4-stage hierarchical model.

Stage 1: Sampling model

The observed response of particle i, cytotoxicity parameter j and replicate k is modeled as

$$y_{\mathit{ijk}}(d,t)=m_{ij}(d,t)+{\epsilon }_{\mathit{ijk}}(d,t),$$ (2)

where ${\epsilon }_{\mathit{ijk}}(d,t)~N(0,{\sigma }_{{\epsilon }_j}^2/{\tau }_i)$. Here m_ij (d, t) denotes the response surface for particle i and outcome j. The proposed response surface describes dose and duration kinetics for all d ∈ [0, D] and t ∈ [0, T] and is expected to exhibit a nonlinear dynamic over these domains. The distribution of y_ijk is modeled in terms of the error term ε_ijk as a scaled mixture of normal random variables to account for outlying observations. The error variance is defined in terms of the measurement error variance ${\sigma }_{{\epsilon }_j}^2$, specific to cytotoxicity parameter j, and on ENM-specific variance inflation parameter τ_i. If we define the joint distribution of ε_ijk(d, t) and τ_i as P(ε_ijk(d, t), τ_i) = P(ε_ijk (d, t) | τ_i, σ_εj)P(τ_i|ν), choosing ${\epsilon }_{\mathit{ijk}}(d,t)\mid {\tau }_i,{\sigma }_{{\epsilon }_j}~N(0,{\sigma }_{{\epsilon }_j}^2/{\tau }_i)$ and τ_i|ν ~ Gamma(ν/2, ν/2), it can be shown that the marginal density of ${\epsilon }_{\mathit{ijk}}(d,t)\mid {\sigma }_{{\epsilon }_j}^2$ is distributed as a $T({\sigma }_{{\epsilon }_j}^2,\nu )$[West (1984)]. Under this framework, we can borrow strength across all ENMs by assuming the error variance is the same, but retain robustness in the model by allowing ENM-specific departures from normality. We allow the measurement error σ_εj to vary between cytotoxicity parameters due to heterogeneity in the cytotoxicity outcomes.

Stage 2: Response model at the ENM by cytotoxicity parameter level

The dose-response surface m_ij (d, t) spans two dimensions (dose and time), and is modeled in an additive fashion as described by Hastie and Tibshirani (1986). If we let (α_ij, ${\mathit{\beta }}_{ij}^{\prime },{\mathit{\varphi }}_{ij}^{\prime },{\mathit{\gamma }}_{ij}^{\prime },{\mathit{\psi }}_{ij}^{\prime },{\mathit{\delta }}_{ij}^{\prime },{\mathit{\chi }}_{ij}^{\prime }$)′ be a parameter vector indexing the dose-response surface m_ij (d, t), we can then define

$$m_{ij}(d,t)={\alpha }_{ij}+f_{ij}(d;{\mathit{\varphi }}_{ij},{\mathit{\beta }}_{ij})+g_{ij}(t;{\mathit{\psi }}_{ij},{\mathit{\gamma }}_{ij})+h_{ij}(d,t;{\mathit{\chi }}_{ij},{\mathit{\delta }}_{ij}).$$ (3)

Here f_ij (d; ϕ_ij, β_ij) is a function modeling the effect of dose d on response j for ENM i. Similarly, g_ij (t; ψ_ij, γ_ij) is the function modeling the effect of time t and h_ij (d, t; χ_ij, δ_ij) is the function modeling the interactive effect of dose and time. More specifically, we model the interaction of dose and time in a semi-parametric fashion as h_ij (dt; χ_ij, δ_ij). This parameterization allows us to retain direct interpretation of the model parameters, while avoiding over-fitting of sparse data. To ensure likelihood identifiability, we require, without loss of generality, that f_ij (d = 0; ϕ_ij, β_ij) = 0, g_ij (t = 0; ψ_ij, γ_ij) = 0, and h_ij (dt = 0; χ_ij, δ_ij) = 0. The parameters α_ij can therefore be interpreted as the background response level for each particle and outcome.

We model dose-response curves f_ij (d; ϕ_ij, β_ij), duration-response curves g_ij (t; ψ_ij, γ_ij) and dose-time response curves h_ij (dt; χ_ij, δ_ij) as linear combinations of basis functions. Specifically, we use linear B-splines with two random interior knots as points where the slope changes in a piecewise linear fashion. Let (x, η) denote a 4-dimensional B-spline basis with interior knots η= (η₁, η₂)′. Also, let β_ij = (β_ij1, …, β_{ij 4})′, γ_ij = (γ_{ij 1}, …, γ_{ij 4})′ and δ_ij = (δ_{ij 1}, …, δ_{ij 4})′ be 4-dimensional vectors of spline coefficients. The functions f_ij (d; ϕ_ij, β_ij), g_ij (t; ψ_ij, γ_ij) and h_ij (dt; χ_ij, δ_ij) can then be represented as follows:

$$\begin{array}{l}{f}_{ij}(d;{\mathit{\varphi }}_{ij},{\mathit{\beta }}_{ij})=\mathcal{B}{(d,{\mathit{\varphi }}_{ij})}^{\prime }{\mathit{\beta }}_{ij},\\ g_{ij}(t;{\mathit{\psi }}_{ij},{\mathit{\gamma }}_{ij})=\mathcal{B}{(t,{\mathit{\psi }}_{ij})}^{\prime }{\mathit{\gamma }}_{ij},\\ h_{ij}(dt;{\mathit{\chi }}_{ij},{\mathit{\delta }}_{ij})=\mathcal{B}{(dt,{\mathit{\chi }}_{ij})}^{\prime }{\mathit{\delta }}_{ij}.\end{array}$$ (4)

Identifiability restrictions f_ij (d = 0; ϕ_ij, β_ij) = 0, g_ij (t = 0; ψ_ij, γ_ij) = 0 and h_ij (dt = 0; χ_ij, δ_ij) = 0 are implemented by fixing β_{ij 1} = 0, γ_{ij 1} = 0 and δ_{ij 1} = 0, for all particles and outcomes (see Figure 2 for an illustration).

Fig. 2.

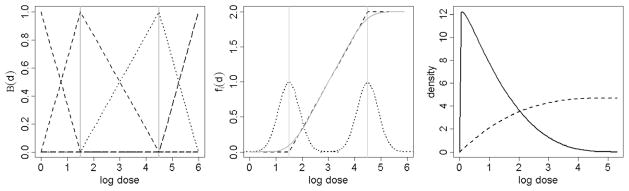
Dose-response as a change-point model. (left) B-spline basis function of degree 1, corresponding to change points (interior knots) at log doses of 1.5 and 4.5. (Middle) Example dose-response curve. The basis function on the left corresponds to a spline function with 2 change points. Each random change point has a corresponding distribution, resulting in a smooth dose-response curve. (Right) Example of a marginal prior distribution on the change points corresponding to the dose-response curve on the left. This formulation favors (a priori) the choice of conservative values for the location of the first change point (solid line), and a relatively diffuse prior for our second change point (dotted line).

Modeling dose and duration-response curves as piecewise linear functions allows for considerable flexibility while maintaining direct interpretability of the model parameters. Recall that in our formulation the interior knots are estimated as random quantities. This allows, marginally, for a smooth dose-response trajectory that is automatically adjusted to fit the data. The main advantage of the proposed functional representation is that, in the absence of a dose-time interaction, one can interpret the first interior knot ϕ_{ij 1} as the dose at which ENM i becomes toxic in relation to cytotoxicity parameter j (Maximal Safe Dose—similar to the classical NOAEL concept). A similar interpretation can be given to ψ_{ij 1}, in relation to duration-response. Note that the foregoing interpretation is contingent on fixing β_ij2 = 0, γ_ij2 = 0 and χ_ij2 = 0 when assuming no effect before the first change-point, and β_ij2 ≤ 0, γ_ij2 ≤ 0 and χ_ij2 ≤ 0 when assuming a tonic effect before the first change point. In the presence of a dose-time interaction, interpretation changes slightly and we instead consider the idea of safe exposure regions, which represent doses and time exposure combinations that do not induce cyto-toxicity. Finally, in the absence of an interaction, the parameters ϕ_{ij 2} and ψ_{ij 2} are respectively interpreted as the dose and time at which the response stabilizes, or cells start a possible recovery process.

We can expand the model further to allow for the exclusion of interaction functions where not needed. To do that, we include a latent indicator variable ρ_ij, so that for each particle i and outcome j

$$m_{ij}(d,t)=\{\begin{array}{ll}{\alpha }_{ij}+f_{ij}(d;{\mathit{\varphi }}_{ij},{\mathit{\beta }}_{ij})+g_{ij}(t;{\mathit{\psi }}_{ij},{\mathit{\gamma }}_{ij}),\hfill & \text{if}{\rho }_{ij}=0,\hfill \\ {\alpha }_{ij}+f_{ij}(d;{\mathit{\varphi }}_{ij},{\mathit{\beta }}_{ij})+g_{ij}(t;{\mathit{\psi }}_{ij},{\mathit{\gamma }}_{ij})+h_{ij}(dt;{\mathit{\chi }}_{ij},{\mathit{\delta }}_{ij}),\hfill & \text{if}{\rho }_{ij}=1,\hfill \end{array}$$ (5)

where ρ_ij ~ Bern(π) and π ~ U (0, 1). We require that if ρ_ij = 0, h_ij (dt; χ_ij, δ_ij) > 0, to ensure identifiability. The indicator variable ρ_ij can then be used to test explicitly for the dose-time interactions. The exchangeable Bernoulli trials prior on ρ_ij is designed to account for multiplicities [Scott and Berger (2006)]. This trans-dimensional parameterization is key to avoid overfitting, to facilitate parameter interpretation, and to allow for testing of specific scientific hypotheses related to the biological interference of nanomaterials.

For each ENM i and response j, we define the following prior distributions for α_ij, β_ij, γ_ij, and δ_ij:

$$\begin{array}{l}{\alpha }_{ij}~N\left({\alpha }_{o_i},{\sigma }_{{\alpha }_i}^2\right),\\ {\mathit{\beta }}_{ij}~N_4({\mathit{\beta }}_{o_i},{\mathbf{\sum }}_{{\mathit{\beta }}_i})I\{{\beta }_{ij1}=0;{\beta }_{ij2}\le 0;({\beta }_{ij3},{\beta }_{ij4})\ge 0\},\\ {\mathit{\gamma }}_{ij}~N_4({\mathit{\gamma }}_{o_i},{\mathbf{\sum }}_{{\mathit{\gamma }}_i})I\{{\gamma }_{ij1}=0;{\gamma }_{ij2}\le 0;({\gamma }_{ij3},{\gamma }_{ij4})\ge 0\},\\ {\mathit{\delta }}_{ij}\mid {\rho }_{ij}=1~N_4({\mathbf{m}}_{{\mathit{\delta }}_{ij}},{\mathbf{v}}_{{\mathit{\delta }}_{ij}})I\{{\delta }_{ij1}=0;{\delta }_{ij2}\le 0;({\delta }_{ij3},{\delta }_{ij4})>0\}.\end{array}$$ (6)

The truncated support for β_ij, γ_ij and δ_ij imposes functional constraints on f (·), g(·) and h(·), which are consistent with the expected behavior of canonical dose and duration kinetics. At the same time, however, it allows for the system to recover by permitting a decreasing slope after the second change point. The covariance matrix Σ_βi has diagonal elements σ_βiℓ, ℓ = 1, …, 4, and off diagonal elements equal to 0; similarly for Σ_γi.

Prior distributions for ϕ_ij, ψ_ij and χ_ij are defined to satisfy the following constraints: (0 < ϕ_ij1 < ϕ_ij2 < D), (0 < ψ_ij1 < ψ_ij2 < T) and (0 < χ_ij1 < χ_ij2 < DT). More precisely, we assume that the joint distribution of the interior dose and duration knots follows a generalized bivariate Beta density function, so that

$$\begin{array}{l}{\varphi }_{ij}~B_2(a_{{\varphi }_1},b_{{\varphi }_1},a_{{\varphi }_2},b_{{\varphi }_2},D),\\ {\psi }_{ij}~B_2(a_{{\psi }_1},b_{{\psi }_1},a_{{\psi }_2},b_{{\psi }_2},T),\\ {\chi }_{ij}~B_2(a_{{\chi }_1},b_{{\chi }_1},a_{{\chi }_2},b_{{\chi }_2},DT).\end{array}$$ (7)

Here we assume that a random vector x = (x₁, x₂)′ is distributed according to a generalized bivariate Beta distribution function (x ~ B₂(a₁, b₁, a₂, b₂, m)), with support (x) = {(x₁, x₂): 0 < x₁ < x₂ < m} if and only if

$$\begin{array}{l}p(\mathbf{x}\mid a_1,b_1,a_2,b_2,m)=p(x_1\mid a_1,b_1,m)p(x_2\mid x_1,a_2,b_2,m)\\ =\frac{1}{B(a_1,b_1)}\frac{x_1^{a_1-1}{(m-x_1)}^{b_1-1}}{m^{a_1+b_1-1}}\frac{1}{B(a_2,b_2)}\frac{{(x_2-x_1)}^{a_2-1}{(m-x_2)}^{b_2-1}}{{(m-x_1)}^{a_2+b_2-1}}.\end{array}$$ (8)

The foregoing formulation can be seen as a generalization of the Dirichlet distribution over a two-dimensional simplex. This general formulation can be simplified further, in order to achieve a right-skewed marginal distribution for x₁ and a uniform conditional distribution for x₂ given x₁. This is achieved by assuming b₁ > a₁ > 1 and a₂ = b₂ = 1.

Making use of this construction, we simplify the prior distribution in (7) as follows:

$$\begin{array}{l}{\varphi }_{ij}~B_2(1,{\lambda }_{{\varphi }_{i1}},{\lambda }_{{\varphi }_{i2}},1,1,D)I\{{\lambda }_{{\varphi }_{i2}}>{\lambda }_{{\varphi }_{i1}}>1\},\\ {\psi }_{ij}~B_2(1,{\lambda }_{{\psi }_{i1}},{\lambda }_{{\psi }_{i2}},1,1,T)I\{{\lambda }_{{\psi }_{i2}}>{\lambda }_{{\psi }_{i1}}>1\},\\ {\chi }_{ij}~B_2(1,l_{{\chi }_{i1}},l_{{\chi }_{i2}},1,1,T)I\{l_{{\chi }_{i2}}>l_{{\chi }_{i1}}>1\}.\end{array}$$ (9)

From a regulatory standpoint, this formulation favors (a priori) the choice of conservative values for the location of the first change point and a relatively diffuse prior distribution for our second change point (see Figure 2).

Stage 3: Response model at the ENM level

For each ENM i, we exploit conditional conjugacy to define the following prior distributions for population level parameters:

$${\alpha }_{o_i}~N(m_{{\alpha }_i},v_{{\alpha }_i}),{\mathit{\beta }}_{o_i}~N_4({\mathbf{m}}_{{\mathit{\beta }}_i},{\mathbf{v}}_{{\mathit{\beta }}_i}),{\mathit{\gamma }}_{o_i}~N_4({\mathbf{m}}_{{\mathit{\gamma }}_i},{\mathbf{v}}_{{\mathit{\gamma }}_i}).$$ (10)

In the absence of an interaction, the parameters β_oi and γ_oi represent summaries of the dose and duration-response trajectories across all outcomes and the α_oi parameters represent a summary of the baseline response across all outcomes. In the presence of an interaction, we may construct these summaries conditionally on specific doses and durations of exposure.

Finally, considering the distribution introduced in (9), we define a prior model for population level parameters λ_ϕi = (λ_ϕi1, λ_ϕi2) and λ_ψi = (λ_ψi1, λ_ψi2) as follows:

$${\lambda }_{{\varphi }_{i\ell }}~\text{Gamma}(a_{{\lambda }_{\varphi i\ell }},b_{{\lambda }_{\varphi i\ell }}),{\lambda }_{{\psi }_{i\ell }}~\text{Gamma}(a_{{\lambda }_{\psi i\ell }},b_{{\lambda }_{\psi i\ell }}),$$ (11)

where ℓ = 1, 2. The parameters λ_ϕi and λ_ψi can be used to construct summaries of dose and duration-response change points across all outcomes. Shape hyperparameters (a_λϕiℓ, b_λϕiℓ) and (a_λψiℓ, b_λψiℓ) can be tuned to favor more or less conservative values for the change-point locations at the particle level.

Stage 4: Hyperpriors

We complete the model by specifying prior distributions on our hyperparameters as follows:

$$\begin{array}{ll}1/{\sigma }_{{\epsilon }_j}^2~\text{Gamma}(a_{{\epsilon }_j},b_{{\epsilon }_j}),\hfill & 1/{\sigma }_{{\alpha }_i}^2~\text{Gamma}(a_{{\alpha }_i},b_{{\alpha }_i}),\hfill \\ 1/{\sigma }_{{\beta }_i}^2~\text{Gamma}(a_{{\beta }_i},b_{{\beta }_i}),\hfill & 1/{\sigma }_{{\gamma }_i}^2~\text{Gamma}(a_{{\gamma }_i},b_{{\gamma }_i}).\hfill \end{array}$$ (12)

We model our precision parameters as gamma distributions, exploiting conditional conjugacy. Again, prior parameters can be tuned to define more or less informative distributions consistent with the scale of the outcomes [Gelman (2006)]. Note that in our formulation, x ~ Gamma(a, b) denotes a Gamma distributed random quantity with shape a and rate b, such that E(x) = a/b.

3. Estimation and inference

3.1. Posterior simulation via MCMC

Using the B-spline representation introduced in Section 2.1, we can write the expected j th response level associated with ENM i, at dose d and exposure time t as

$$m_{ij}(d,t;{\alpha }_{ij},{\mathit{\beta }}_{ij},\dots )=\{\begin{array}{ll}{\alpha }_{ij}+\mathcal{B}{(d,{\mathit{\varphi }}_{ij})}^{\prime }{\mathit{\beta }}_{ij}+\mathcal{B}{(t,{\mathit{\psi }}_{ij})}^{\prime }{\mathit{\gamma }}_{ij},\hfill & \text{if}{\rho }_{ij}=0,\hfill \\ {\alpha }_{ij}+\mathcal{B}{(d,{\mathit{\varphi }}_{ij})}^{\prime }{\mathit{\beta }}_{ij}+\mathcal{B}{(t,{\mathit{\psi }}_{ij})}^{\prime }{\mathit{\gamma }}_{ij}+\mathcal{B}{(dt,{\mathit{\chi }}_{ij})}^{\prime }{\mathit{\delta }}_{ij},\hfill & \text{if}{\rho }_{ij}=1.\hfill \end{array}$$

Let β = {β_ij: i = 1, …, I, j = 1, …, J} and define γ and δ in a similar fashion. These parameters denote the full set of spline coefficients. Furthermore, consider knot parameters ϕ = {ϕ_ij: i = 1, …, I, j = 1, …, J}, with ψ and χ similarly defined, and background response parameters α = {α_ij: i = 1, …, I, j = 1, …, J}. Finally, let ${\mathit{\sigma }}_{\epsilon }^2={({\sigma }_{{\epsilon }_1}^2,\dots ,{\sigma }_{{\epsilon }_J}^2)}^{\prime }$ and τ = (τ₁, …, τ_I)′. If we denote with Y the complete set of response values for all particles and cytotoxicity outcomes, the likelihood function can be written as follows:

$$L(\mathit{\beta },\mathit{\gamma },\mathit{\delta },\mathit{\varphi },\mathit{\psi },\mathit{\chi },\mathit{\alpha },{\mathit{\sigma }}_{\epsilon }^2,\mathit{\tau },\mathit{\rho }\mid \mathbf{Y})\propto \prod _{i,j,k,d,t}\left[{\left(\frac{{\sigma }_{{\epsilon }_j}^2}{{\tau }_i}\right)}^{-1/2}exp\left\{-\frac{{(y_{\mathit{ijk}}(d,t)-m_{ij}(d,t;\dots ))}^2}{2{\sigma }_{{\epsilon }_j}^2/{\tau }_i}\right\}\right],$$ (13)

where the product is taken over all replicates k, particles i, outcomes j, doses d and times t. We are interested in the posterior distribution

$$P(\mathit{\beta },\mathit{\gamma },\mathit{\delta },\mathit{\varphi },\mathit{\psi },\mathit{\chi },\mathit{\alpha },{\mathit{\sigma }}_{\epsilon }^2,\mathit{\tau },\mathit{\rho }\mid \mathbf{Y})\propto L(\mathit{\beta },\mathit{\gamma },\mathit{\delta },\mathit{\varphi },\mathit{\psi },\mathit{\chi },\mathit{\alpha },{\mathit{\sigma }}_{\epsilon }^2,\mathit{\tau },\mathit{\rho }\mid \mathbf{Y})\times P(\mathit{\beta },\mathit{\gamma },\mathit{\delta },\mathit{\varphi },\mathit{\psi },\mathit{\chi },\mathit{\alpha },{\mathit{\sigma }}_{\epsilon }^2,\mathit{\tau },\mathit{\rho }),$$ (14)

where the prior model P (β, γ, δ, ϕ, ψ, χ, α, ${\mathit{\sigma }}_{\epsilon }^2$, τ, ρ) is fully described in Section 2.1. This quantity is, however, unavailable in closed analytic form, therefore, we base our inference on Markov Chain Monte Carlo (MCMC) simulations.

The proposed posterior simulation algorithm combines Gibbs steps within Metropolis–Hastings steps in a hybrid sampler, where we update parameters component-wise [Tierney (1994)]. We directly sample components when closed-form full conditional distributions are available using a Gibbs sampling algorithm [Geman and Geman (1984), Gelfand and Smith (1990)]; otherwise, we use the Metropolis–Hastings (MH) approach [Metropolis et al. (1953)]. Available full conditional distributions are given in the supplemental article, Appendix A [Patel et al. (2012)]. As we are considering selection of interaction functions in a trans-dimensional setting, we implement a reversible jumps algorithm to move between models with and without the dose-time interaction function h_ij (dt; χ_ij, δ_ij) [Green (1995)]. The model indicator ρ_ij and corresponding model parameters δ_ij and χ_ij are updated jointly using reversible jump MCMC steps. After the model structure has been specified, the model parameters are updated from their corresponding conditional posterior distributions. The proposed sampling scheme can be summarized as follows.

1. Fixed dimensional updates

Given the current state of the latent interaction indicators _ij, response surfaces are uniquely defined as in (5). Posterior sampling is standard here and proceeds by updating spline coefficients β, γ and δ from their conditional posterior via direct simulation [Patel et al. (2012)]. Knot parameters ϕ, ψ and χ are updated via a MH step. For example, when sampling the interior knot parameters ϕ we use an appropriate proposal kernel $q({\varphi }_{ij\ell }^0,{\varphi }_{ij\ell }^1)$ to efficiently construct Markov chains with the desired stationary distribution. While accounting for the fact that ϕ_ij1 < ϕ_ij2, we consider uniform proposal densities of the form

$$q({\varphi }_{ij\ell }^1\mid {\varphi }_{ij\ell }^0)=U({\varphi }_{ij\ell }^0-w_{\varphi ij\ell },{\varphi }_{ij\ell }^0+w_{\varphi ij\ell })I(S_{\varphi }),$$ (15)

where ℓ = 1, 2. Here S_ϕ denotes the appropriate support and must satisfy the constraints 0 < ϕ_{ij 1} < ϕ_{ij 2} < D. Proposed values of ϕ_ijℓ are accepted with the following probabilities:

$$min\left\{1;\frac{p({\varphi }_{ij\ell }^1\mid y_{\mathit{ijk}},{\mathit{\theta }}_{\backslash \varphi })}{p({\varphi }_{ij\ell }^0\mid y_{\mathit{ijk}},{\mathit{\theta }}_{\backslash \varphi })}\frac{q({\varphi }_{ij\ell }^0\mid {\varphi }_{ij\ell }^1)}{q({\varphi }_{ij\ell }^1\mid {\varphi }_{ij\ell }^0)}\right\},\ell =1,2.$$ (16)

To tune proposal kernels, each ϕ_ijℓ was sampled using an initial value of w that was re-calibrated throughout the burn-in period to achieve an acceptance rate between 30% and 70% [Roberts and Rosenthal (2001)]. Specifically, the acceptance rate of ϕ_ijℓ was monitored every 200 iterations throughout the burn-in period with w_ϕijℓ adjusted appropriately if the acceptance rate did not fall within the desired range. A similar Metropolis–Hastings scheme was adapted for sampling the duration-response parameters ψ, dose-time interaction parameters χ_ij | ρ_ij = 1, as well as for population level knot parameters.

2. Trans-dimensional updates

We sample the model space by randomly proposing the birth or death of dose-time interaction functions h_ij (·). This is accomplished by selecting a particle i and outcome j at random and by jointly updating ρ_ij, δ_ij and χ_ij. In detail,

1. For uniformly random i ∈ (1, …, I) and j ∈ (1, …, J), propose a systematic change ${\rho }_{ij}^0\to {\rho }_{ij}^1=1-{\rho }_{ij}^0$. We assume for the moment that we propose moving from ${\rho }_{ij}^0=0$ to ${\rho }_{ij}^1=1$, implying the birth of a new interaction function h_ij (·).

2. Propose new knots and spline coefficients ${\mathit{\delta }}_{ij}^1~q({\mathit{\delta }}_{ij}^1)$ and ${\mathit{\chi }}_{ij}^1~q({\mathit{\chi }}_{ij}^1)$.

3. Accept the proposed move with probability τ_b = min(1, R_b), where

   $$R_b=\frac{p(y_{\mathit{ijk}}\mid {\mathit{\delta }}_{ij}^1,{\mathit{\chi }}_{ij}^1,{\rho }_{ij}^1,{\mathit{\theta }}_{\backslash {\mathit{\delta }}_{ij},{\mathit{\chi }}_{ij},{\rho }_{ij}})}{p(y_{\mathit{ijk}}\mid {\rho }_{ij}^0,{\mathit{\theta }}_{\backslash {\mathit{\delta }}_{ij},{\mathit{\chi }}_{ij},{\rho }_{ij}})}\frac{p({\mathit{\delta }}_{ij}^1\mid {\rho }_{ij}^1)p({\mathit{\chi }}_{ij}^1\mid {\rho }_{ij}^1)}{q({\mathit{\delta }}_{ij}^1)q({\mathit{\chi }}_{ij}^1)}\frac{p({\rho }_{ij}^1)}{p({\rho }_{ij}^0)},$$ (17)

   where we use θ_\ω to denote all model parameters, with the exception of ω.

In the case where the proposed move would imply a death of an interaction function ${\rho }_{ij}^0=1\to {\rho }_{ij}^1=0$, the acceptance probability would simply be τ_d = 1/τ_b.

While the proposal densities q(δ_ij) q(χ_ij) in (17) can in theory be defined almost arbitrarily, to guarantee efficient exploration of the model space, we consider truncated multivariate normal proposals for δ_ij and χ_ij centered around regions of high posterior probability. Efficient optimization within the MCMC iterations is achieved using standard profile likelihood ideas [Severini and Staniswalis (1994)].

3.2. Posterior inference

In this section we discuss inference on ENM-specific risk assessment parameters, based on draws from the posterior distribution described in Section 3.1. Table 1 summarizes several quantities of interest including the maximal safe dose, maximal safe exposure time and the maximal response. This list is not exhaustive. However, other risk assessment parameters of interest, such as benchmark doses (BMD) or effective concentrations (ECα), are easily obtained from our model output in a numerical fashion. In the case of a dose-time interaction, these quantities are defined conditionally on specific doses and durations of exposure.

Table 1.

Risk assessment parameters. ENM level risk assessment parameters associated with the hierarchical model introduced in 2.1. For each parameter we summarize its function in the model and the related interpretation as a cytotoxicity risk factor

Parameter	Model function	Parameter interpretation
${\beta }_{3ij}^{\ast }$	Dose-response slope from ϕij 1 to ϕij 2	Overall dose effect
${\gamma }_{3ij}^{\ast }$	Duration-response slope from ϕij 1 to ϕij 2	Overall exposure time effect
ϕ1ij	Dose-response change point 1	Maximal safe dose
ψ1ij	Duration-response change point 1	Maximal safe exposure time
$m_{ij}^{\ast }$	Evaluated numerically	Maximal response

Let ${\mathit{\varphi }}_{ij}^{(n)},{\mathit{\psi }}_{ij}^{(n)},{\mathit{\chi }}_{ij}^{(n)},{\mathit{\beta }}_{ij}^{(n)},{\mathit{\gamma }}_{ij}^{(n)},{\mathit{\delta }}_{ij}^{(n)},{\alpha }_{ij}^{(n)}$ and ${\rho }_{ij}^{(n)}$, n = 1, …, N, denote N MCMC draws from the posterior distribution of ϕ_ij, ψ_ij, χ_ij, β_ij, γ_ij, α_ij and ρ_ij. In the absence of an interaction term, posterior samples ${\varphi }_{ij1}^{(n)}$ and ${\psi }_{ij1}^{(n)}$ directly provide us with an approximation of the posterior distribution for the maximal safe dose and maximal safe exposure time. We can also obtain the posterior samples for the overall dose effect, ${\beta }_{ij3}^{\ast (n)}={\beta }_{ij3}^{(n)}/({\varphi }_{ij2}^{(n)}-{\varphi }_{ij1}^{(n)})$, which is the slope of the dose-response curve between ϕ_{ij 1} and ϕ_{ij 2}. Similarly, we can obtain the posterior distribution for the overall time effect using posterior samples ${\gamma }_{ij3}^{\ast (n)}={\gamma }_{ij3}^{(n)}/({\psi }_{ij2}^{(n)}-{\psi }_{ij1}^{(n)})$. In the presence of a dose-time interaction, we can define any of the summaries described above conditionally on a given dose and time. For example, the maximal safe dose conditional on exposure time can be defined as min{ϕ_{ij 1}, χ_{ij 1}/t}, and posterior samples can be obtained from $min\{{\varphi }_{ij1}^{(n)},{\chi }_{ij1}^{(n)}/t\}$. Given posterior draws, one can proceed with the straightforward construction of standard posterior summaries, such as means, maxima a posteriori, modes, quantiles and credible regions. We may also be interested in testing for a dose-time interaction. The expected inclusion probability of the dose-time interaction function can be estimated using posterior draws ${\rho }_{ij}^{(n)}$ as ${\widehat{p}}_{ij}={\sum }_n{\rho }_{ij}^{(n)}/N$. Given the prior distribution described in (5), this posterior probability is known to adjust for multiplicities and can be used to test for a dose-time interaction. Scott and Berger (2006), for example, recommend selecting the median model, that is, including all interactions for which p̂_ij > 0.5. Also of interest is an estimate of the dose-response surface, m_ij (d, t), for particle i and outcome j. This surface is, of course, defined in an infinite-dimensional space. However, given the basis-function representation introduced in Section 2.1, we only need finite draws from the parameter set of interest. More precisely, draws from the marginal posterior distribution of the dose-response surface for any dose d ∈ [0, D] and time t ∈ [0, T] are given by

$$m_{ij}^{(n)}(d,t)=\{\begin{array}{ll}{\alpha }_{ij}^{(n)}+\mathcal{B}{(d,{\mathit{\varphi }}_{ij}^{(n)})}^{\prime }{\mathit{\beta }}_{ij}^{(n)}+\mathcal{B}{(t,{\mathit{\psi }}_{ij}^{(n)})}^{\prime }{\mathit{\gamma }}_{ij}^{(n)},\hfill & \text{if}{\rho }_{ij}^{(n)}=0,\hfill \\ {\alpha }_{ij}^{(n)}+\mathcal{B}{(d,{\mathit{\varphi }}_{ij}^{(n)})}^{\prime }{\mathit{\beta }}_{ij}^{(n)}+\mathcal{B}{(t,{\mathit{\psi }}_{ij}^{(n)})}^{\prime }{\mathit{\gamma }}_{ij}^{(n)}+\mathcal{B}{(dt,{\mathit{\chi }}_{ij}^{(n)})}^{\prime }{\mathit{\delta }}_{ij}^{(n)},\hfill & \text{if}{\rho }_{ij}^{(n)}=1.\hfill \end{array}$$ (18)

For each ${\mathit{\varphi }}_{ij}^{(n)},{\mathit{\psi }}_{ij}^{(n)},{\mathit{\beta }}_{ij}^{(n)},{\mathit{\varphi }}_{ij}^{(n)}$ and ${\alpha }_{ij}^{(n)}$, n = 1, …, N, we evaluate the dose-response function given in (18) over a grid of values D̃ = (d₁, …, d_n)′ and T̃ = (t₁, …, t_n)′. The posterior mean of the samples $m_{ij}^{(n)}$, n = 1, …, N, at each value of D̃ and T̃ can be used to summarize the fit of the dose-response surface, as shown in Figures 3 to 4. Other quantities of interest include the posterior distribution of the dose-response function f_ij (d; ϕ_ij, β_ij), duration-response function g_ij (t; ψ_ij, γ_ij) and dose-time interaction function h_ij (dt; χ_ij, δ_ij). Draws from the marginal posterior distribution of these functions for any dose d ∈ [0, D] and time t ∈ [0, T] are given by

Fig. 3.

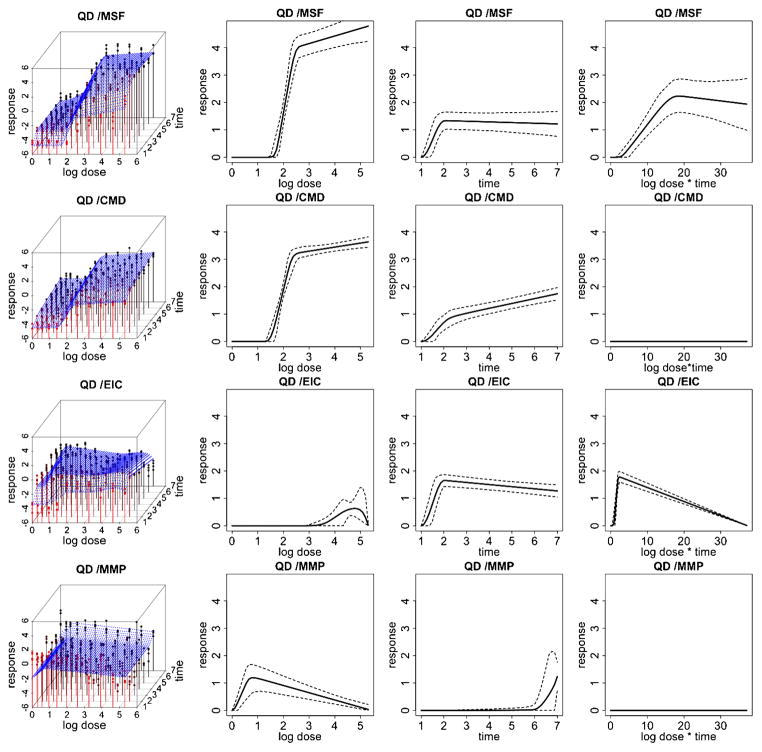
Fitted response curves for the quantum dot (QD) ENM. (left) Fitted response surfaces (column 1), dose-response function, f_ij (d) (column 2), duration-response function, g_ij (t) (column 3), dose/duration interaction function, h_ij (dt) (column 4) and associated 95% posterior intervals. In (column 1), the color red represents response values corresponding to lower time points and the color black represents response values corresponding to higher time points.

Fig. 4.

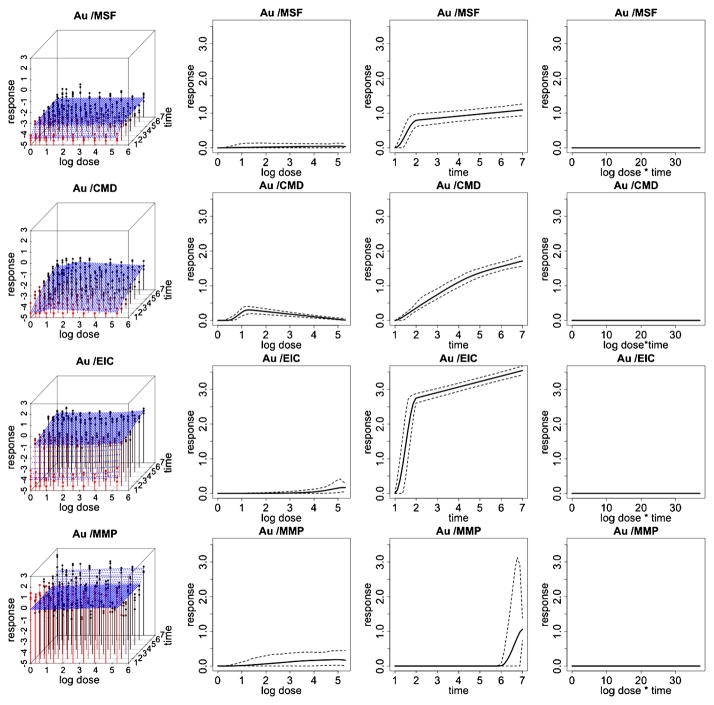
Fitted response curves for the gold (Au) ENM. Fitted response surfaces (column 1), dose-response function, f_ij (d) (column 2), duration-response function, g_ij (t) (column 3), dose/duration interaction function, h_ij (dt) (column 4) and associated 95% posterior intervals. In (column 1), the color red represents response values corresponding to lower time points and the color black represents response values corresponding to higher time points.

$$\begin{array}{l}{f}_{ij}^{(n)}(d;{\mathit{\varphi }}_{ij},{\mathit{\beta }}_{ij})=\mathcal{B}{(d,{\varphi }_{ij}^{(n)})}^{\prime }{\mathit{\beta }}_{ij}^{(n)},\\ g_{ij}^{(n)}(t;{\mathit{\psi }}_{ij},{\mathit{\gamma }}_{ij})=\mathcal{B}{(t,{\psi }_{ij}^{(n)})}^{\prime }{\mathit{\gamma }}_{ij}^{(n)},\\ h_{ij}^{(n)}(dt;{\mathit{\chi }}_{ij},{\mathit{\delta }}_{ij})=\mathcal{B}{(dt,{\chi }_{ij}^{(n)})}^{\prime }{\mathit{\delta }}_{ij}^{(n)}.\end{array}$$ (19)

For each draw, we evaluate the dose-response functions over a grid of values d ∈ D̃ and the duration-response functions over a grid of values t ∈ T̃. As described before, standard pointwise posterior summaries can be obtained in a straightforward fashion. Simultaneous confidence bands for the functional effect of interest can be constructed following the Monte Carlo approximation suggested by Baladandayuthapani, Mallick and Carroll (2005).

Additional summaries of interest can be obtained in a numerical fashion. For example, the posterior distribution for the maximal response value $m_{ij}^{\ast }=max\{m_{ij}(d,t);d\in [0,D],t\in [0,T]\}$; d ∈ [0, D], t ∈ [0, T]}, may be obtained evaluating $m_{ij}^{(n)}(d,t)$ over a fine grid of doses D̃ and times T̃. An approximate posterior draw from $m_{ij}^{\ast }$ can be defined as $m_{ij}^{\ast (n)}=max\{m_{ij}^{(n)}(d,t);d\in \stackrel{\sim }{D},t\in \stackrel{\sim }{T}\}$. Given smoothness constraints on m_ij (d, t), defined in Section 2.1, the foregoing procedure is likely to provide a good approximation to the posterior distribution of the maximal response value, provided D̃ and T̃ define a sufficiently detailed evaluation grid. Similar procedures may be adopted to obtain inference on other risk assessment parameters like ECαs or BMDs.

4. Applications

4.1. Synthetic data

To assess estimation of the model presented in Section 2, we present a simulation study in the supplemental article, Appendix B [Patel et al. (2012)]. The dose and time kinetics were simulated in an additive fashion, from various parametric functions, including both canonical and noncanonical profiles that are still reasonably interpretable under a toxicity framework. We also placed increasingly conservative priors on the population level parameters λ_ϕi and λ_ϕi in order to assess the sensitivity of the model results to our choice of prior parameters. In the supplemental article, Appendix C, we provide an additional sensitivity analysis assessing model results to our choice of prior model for the change-point parameters [Patel et al. (2012)]. We compare our prior model results to both a truncated normal prior and a parameterization of the bivariate beta prior that results in a uniform prior on the simplex.

Simulation results indicate that our model is robust to model misspecification and is not very sensitive to our choice of prior. We do, however, maintain that using the bivariate beta prior defined in (8) is likely to be more appropriate in data analytic frameworks, as the implied stochastic behavior of the response surface, a priori, reflects more closely the usual biological mechanisms of toxicity. More specifically, it assigns zero probability of toxicity to zero dose and time, where toxicity is indeed not expected to occur. Furthermore, this prior accounts for issues such as dosimetry, in which the administered doses are confounded by different particle bioavailability. Therefore, in some particles toxicity is not expected to occur for doses and times greater than zero.

4.2. Case study background

We illustrate the proposed methodology by analyzing data on macrophage cells (RAW cells) exposed to eight different metal and metal-oxide nanoparticles, monitored in relation to four cytotoxicity parameters. All four outcomes are measured over a grid of ten doses and seven times (hours) of exposure (see Figures 3 to 4). Cytotoxicity screening is based on the hierarchical oxidative stress model [George et al. (2009)]. More specifically, a multi-parametric assay that utilizes four compatible dye combinations and the subsequent change in fluorescence read-outs was used to measure four responses relating to the highest tier of oxidative stress (toxic oxidative stress). The four measured responses include mitochondrial superoxide formation (MSF), loss of mitochondrial membrane potential (MMP), elevated intracellular calcium (EIC) and cellular membrane damage (CMD). Figure 1 provides fluorescence images of cells exposed to various nanomaterials (50 μg/ml and 3 hours), including quantum dot, platinum and a negative control consisting of no nanomaterials. Row 1 includes images of cells treated with a dye combination including MitoSox, which permeates the mitochondria and fluoresces red when oxidized by superoxide. Red fluorescence measured in cells treated with MitoSox is therefore a measure of mitochondrial superoxide formation. Similarly, in Row 2 cells are treated with a dye combination including JC1, which stains the cytoplasm red in healthy cells, but forms a monomer in cells with decreased membrane potential and consequently stains the cytoplasm green. Finally, in Row 3 cells are strained with a dye combination including Fluo-4 and Propidium Iodide (PI). In cells with damaged membranes, PI is able to permeate the cell and bind to DNA where it causes the nucleus to emit a red florescence. Fluo-4 is a dye that emits a green fluorescence in the cytoplasm in cells with elevated intracellular calcium. Each sample was also stained with a Hoechst dye which causes all cell nuclei to emit a blue florescence, allowing for a count of the total number of cells. An analysis of the fluorescence readout, monitored at varying wavelengths, results in a measure of the percentage of cells positive for each response. Figure 1 also provides a heat map of the raw responses for each particle and outcome, where colder colors (blues and greens) indicate a smaller percentages of cells positive for the response and warmer colors (oranges and reds) indicate a higher percentage of cells positive for the response. The final data was normalized using a logit transformation to unconstrain the support so that it can take on values between −∞ and ∞. Our inferences are based on 20,000 MCMC samples from the posterior distribution in (14), after discarding a conservative 60,000 iterations for burn-in. MCMC sampling was performed in R version 2.10.0, and convergence diagnostics were performed using the package CODA (Convergence Diagnostics and Output Analysis), [Plummerm et al. (2006)].

4.3. Case study analysis and results

We fit the model described in Section 2.1 to the metal-oxide data set described in the previous section. The prior on the interior knot parameters was modeled using the simplified density described in (9). A set of relatively noninformative Gamma(2, 1) and Gamma(3, 1) priors were considered for the components of both λ_ϕi and λ_ψi, along with a vague B₂(2, 3, 1, 1, DT) prior for our dose-time interaction change-point parameter χ_ij. We also fixed β_{ij 2} = 0 and γ_{ij 2} = 0, assuming no effect before ϕ_{ij 1} and ψ_{ij 1}, thereby allowing, in the absence of a dose-time interaction, the interpretation of ϕ_{ij 1} as the maximal safe dose and ψ_{ij 1} as the maximal safe exposure time. Similarly, when ρ_ij = 1, we fixed δ_{ij 2} = 0. We placed Gamma(0.01, 0.01) priors on the 1/σ_εj parameters, Gamma(1, 0.1) priors on all remaining precision parameters and N(0, 10) priors on the α_oi parameters. The parameters β_oi and γ_oi are modeled as truncated multivariate normals with mean 1 and a covariance matrix with diagonal elements 10 and off-diagonal elements 0. Finally, we placed a prior distribution on the degrees of freedom parameter, for the T -distributed error described in Section 2.1. We specified the prior to be uniform on 1, 2, 4, 8, 16 and 32 degrees of freedom [Besag and Higdon (1999)]. In concordance with our synthetic data experiments, a sensitivity analysis on the case study data set proved robust to reasonable variations in the prior specification.

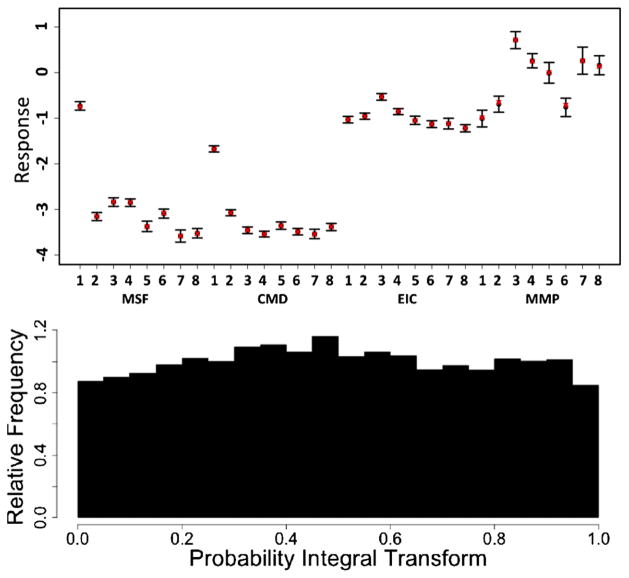
We provide graphical summaries of goodness of fit and posterior predictive performance in Figure 5. The top panel shows the mean and 95% posterior intervals of the posterior predictive mean response across all doses and times of exposure (black), along with the empirical mean response (red), for each particle and outcome. In all cases the empirical mean response is contained within the 95% posterior intervals of the posterior predictive mean distribution, indicating good average posterior coverage across doses and times of exposure. The bottom panel provides a plot of the probability integral transform histogram for the entire model [Gneiting, Balabdaoui and Raftery (2007)]. Visual assessment of the plot indicates that it is close to uniformity, suggesting relatively good posterior predictive calibration. Additional summaries and diagnostic tools are detailed in the supplemental article, Appendix E [Patel et al. (2012)].

Fig. 5.

Graphical model diagnostics. (Bottom) Probability Integral Transform assessing empirical calibration of the posterior predictive distribution. (Top) Mean and 95% posterior intervals of the posterior predictive mean response across all doses and times of exposure, for all outcomes and particles 1 through 8 (QD, ZnO, Fe₃O₄, Pt, Ag, SiO₂, Al₂O₃, Au). Also included are the empirical mean responses across all doses and times of exposure (red).

Figures 3 and 4 illustrate data and results associated with two of the particles examined in this HTS study. Particularly, we report inference for platinum and quantum dot nanomaterials for each of the 4 cytotoxicity outcomes. Inference for the remaining 6 particles is reported in the supplemental article, Appendix D [Patel et al. (2012)]. In these two figures, column 1 shows expected posterior dose-response surfaces across dose and time for all outcomes. As the posterior expectation marginalizes over the interior knots, smooth surfaces reflect the uncertainty about the location of these change points and provide an illustration of how the proposed technique will adjust for smoothness in an unsupervised fashion. Also included are functional posterior expectations associated with dose-response curves f_ij (d) (column 2), which represent the effect due to dose, duration response curves g_ij (t) (column 3), which represent the effect due to exposure time, and the expected dose-time interaction function h_ij (t) (column 4).

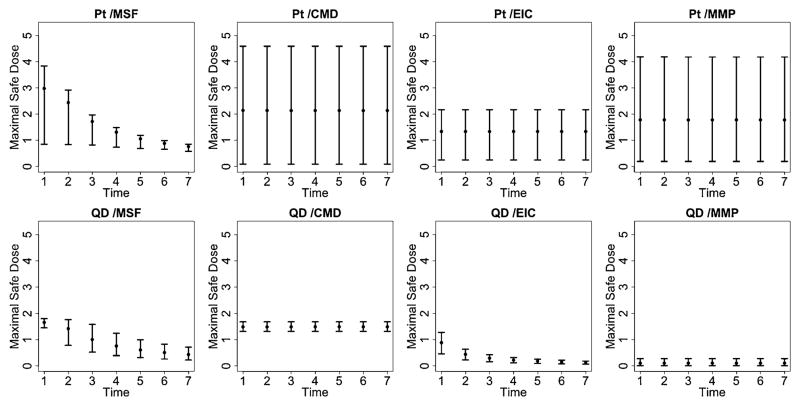
Figure 6 provides a plot of the estimated median response, relative to the background, for different doses and times of exposure. Blue colors indicate safety regions or areas of reduced risk to the cells, while red colored regions indicate increased risk of cytotoxicity. Finally, Figure 7 provides posterior summary estimates including mean and 95% posterior intervals for the maximal safe dose, conditional on the duration of exposure. Note that in the absence of a dose-time interaction, the maximal safe dose is the same across all exposure times.

Fig. 6.

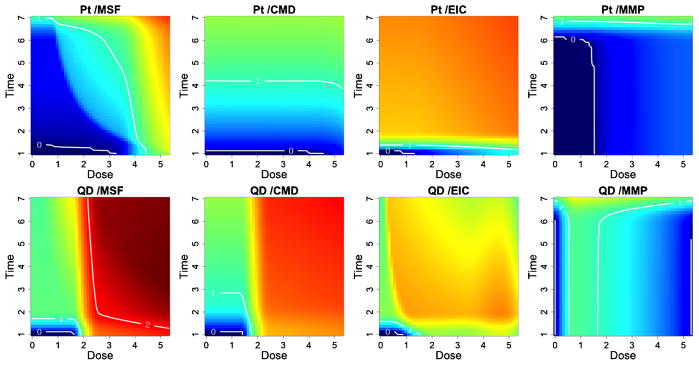
Safe exposure regions for the quantum dot (QD) and platinum (Pt) nanomaterials. For each particle and outcome we can define dose and time exposure regions which do not induce cytotoxicity. Red colored regions indicate greater cytotoxicity to the cells, whereas blue colored regions indicate reduced risk. Contour lines quantitate the median estimated response, relative to the background, where zero response areas can be interpreted as safe exposure regions.

Fig. 7.

Maximal Safe Dose for the quantum dot (QD) and platinum (Pt) nanomaterials. Posterior summary estimates of the maximal safe dose, conditional on exposure time, including the posterior mean and associated 95% posterior intervals. In the case of no interaction, the maximal safe dose is the same across all times.

Quantum dot (QD) shows a relatively high toxic response for plasma membrane damage and mitochondrial superoxide formation. In particular, we see a more pronounced dose effect for membrane damage and both a time, dose and significant dose-time interaction (ρ̂ = 0.99) effect for mitochondrial superoxide formation. This supports what has previously been demonstrated in conventional assays that QD nanoparticles stabilized by toluene are capable of inducing tiers 2 and 3 oxidative stress responses induced by the toluene [George et al. (2011)]. Platinum (Pt) shows a high dose and time response for mitochondrial superoxide formation, including a significant dose-time interaction effect (ρ̂ = 0.99), and a pronounced time effect for elevated calcium but not for mitochondrial depolarization or membrane damage, indicating that the particle induced sublethal effects to the cell without cytotoxicity. The Zinc oxide nanoparticle (ZnO), reported in the supplemental article, Appendix D, shows a relatively high toxic response for plasma membrane damage, elevated calcium and mitochondrial depolarization [Patel et al. (2012)]. In particular, we see a more pronounced time effect for the elevated calcium and both a time and dose-response for membrane damage and mitochondrial depolarization. This again verifies what has previously been demonstrated in conventional assays, since ZnO nanoparticles are capable of inducing tiers 2 and 3 oxidative stress responses through ${\text{Zn}}_2^{+}$ release [George et al. (2009)]. In contrast, the gold nanoparticle (Al), also reported in the supplemental article, Appendix D, shows very little response for all outcomes, indicating that, compared to the other particles, it has small risk of inducing a sublethal or lethal cytotoxic response [Patel et al. (2012)].

5. Discussion

In this article we propose a statistical framework for modeling dependent dose-response surfaces over multivariate outcomes. The proposed methodology accounts for dose and duration kinetics jointly using a flexible model which does not compromise interpretability. We account for the multivariate nature of the data using the hierarchical framework and thereby efficiently combine information and borrow strength across cellular injury patterns. We account for the nonrobust nature of the data by allowing for particle specific variance inflation, resulting in a T -distributed model for the error structure.

The main challenge associated with the class of models proposed in this manuscript is finding the right balance between model complexity and model interpretability. An alternative formulation of the dose-response surface would seek inference for a general smooth surface m_ij (d, t). However, our simplified approach, based on the assumptions of additivity and linearity, maintains a very appealing level of interpretability, allowing for the definition of specific risk assessment parameters while maintaining an adequate level of flexibility. A related generalization of the proposed additive framework would include a more general class of functional interactions to account for a possible synergistic effect between dose and duration of exposure. This would come at the cost of reduced interpretability, but, at the same time, could be of clear scientific interest in some contexts. In this initial modeling effort, we choose to work with a T -distributed error structure and therefore normalize our response to unconstrain the support so that it can take on values between −∞ and ∞. An alternative formulation could retain the original scale of the data, but rather define a generalized multivariate model such that the outcome distribution can be described using binomial or beta random quantities. This extension would require a substantial increase in computational complexity, with the possible need to consider numerical or analytical approximations, but it is clearly worthy of further methodological exploration.

The hierarchical formulation introduced in this article is easily adapted to the case where multiple cell lines are used to test for cytotoxicity. A natural integration strategy would perhaps find motivation in the meta analytic framework, with information shared between experiments via the structuring of one extra level in the hierarchy.

Finally, the proposed model can also be expanded by the inclusion of covariates. This is naturally defined as an extension to stage 3 of the model introduced in Section 2. The addition of covariates is especially important for relating specific ENM properties to toxicity, and is therefore an important area for future work.