Mathematical Model Formulation And Validation Of Water And Solute Transport In Whole Hamster Pancreatic Islets

Abstract

Optimization of cryopreservation protocols for cells and tissues requires accurate models of heat and mass transport. Model selection often depends on the configuration of the tissue. Here, a mathematical and conceptual model of water and solute transport for whole hamster pancreatic islets has been developed and experimentally validated incorporating fundamental biophysical data from previous studies on individual hamster islet cells while retaining whole-islet structural information. It describes coupled transport of water and solutes through the islet by three methods: intracellularly, intercellularly, and in combination. In particular we use domain decomposition techniques to couple a transmembrane flux model with an interstitial mass transfer model. The only significant undetermined variable is the cellular surface area which is in contact with the intercellularly transported solutes, A_is. The model was validated and A_is determined using a 3 × 3 factorial experimental design blocked for experimental day. Whole islet physical experiments were compared with model predictions at three temperatures, three perfusing solutions, and three islet size groups. A mean of 4.4 islets were compared at each of the 27 experimental conditions and found to correlate with a coefficient of determination of 0.87 ± 0.06 (mean ± S.D.). Only the treatment variable of perfusing solution was found to be significant (p < 0.05). We have devised a model that retains much of the intrinsic geometric configuration of the system, and thus fewer laboratory experiments are needed to determine model parameters and thus to develop new optimized cryopreservation protocols. Additionally, extensions to ovarian follicles and other concentric tissue structures may be made.

1. Introduction

Cryopreservation of cells and tissues is better understood when account is made of the heat and mass transfer that occurs during each stage of the process. This understanding of what occurs on a cellular level may lead to increased survival through optimization of each cryopreservation step [1, 2, 3]. Although these processes have been well characterized for single cell suspensions [4, 5], published work on modeling these processes in multicellular tissues is relatively scarce. This modeling is critical because the successful cryopreservation of cells nearly universally requires the equilibration of cells and tissues with multimolal concentrations of permeating cryoprotectant agents (CPAs) such as dimethyl sulfoxide, glycerol, or 1,2 propanediol.

For tissues, model selection is still an issue. For example, models have been constructed that describe water transport through a linear array of cells while neglecting transport through extracellular pathways [6], while Fidelman et al. [7] designed a model of isotonic solute-coupled volume flow in leaky epithelia using network thermodynamics to show how the Kedem and Ketchalsky mass transport parameters must behave in this system. Diller et al. [8] utilized bond graphs and network thermodynamics to show that, depending on the transport resistance of the interstitium, the interior cell volume lags significantly behind the exterior cells. Subsequently Schreuders et al. [9] again used pseudo bond graph and network thermodynamics to model diffusion through a tissue and show that the effects of coupling on the multiple species present in the model is significant. Later, de Frietas et al. expanded a network thermodynamics model of transport in islet cells to model solute and solvent transport in islets of Langerhans [10].

Alternatively, cell-to-cell interactions are ignored and a model based on a diffusion equation with a phenomenological solute diffusivity [11, 12, 13, 14]. These diffusion models may be appropriate for larger and denser tissues with a considerable number of cell layers, and many alternate diffusion-based models have been proposed. For example, Xu et al [15] use a one dimensional porous media model to simulate solute transport in tissues, and Abazari et al. [16] construct a thermodynamically accurate triphasic model for articular cartilage. Another related set models are Krogh cylinder models [17] used primarily in organ perfusion systems [18, 19]. The Krogh cylinder model describes a cylindrical unit of tissue of fixed dimensions perfused by a capillary with a radius which varies with capillary volume. The solution behavior in diffusion models is well understood and usually simple to implement. However, phenomenological diffusion constants depend on both the solute and the tissue structure, and thus applications are often restricted to experimental conditions in which measurements have been made.

Because islets are tissues with less than ten layers that have more or less a unifying, radially symmetric structure, it is computationally and mathematically advantageous to retain this geometrical information. This approach has been used in other tissue types in various ways. For example Mollee and Bracken describe a model that encompasses cell-to-cell transport along with transverse diffusion in the Stratum Corneum [20]. Their model uses a particular “solute capture and release” function to model the transverse diffusion through the lipids contained between corneocyte layers.

Using this idea, the present work builds upon these existing models, with the primary goal to model the mass transfer of solutes and solvents inside islets of Langerhans while retaining as much geometric information as possible. Note that the geometry of this model has clinically important analogues in other smaller tissues, such as ovarian follicles, a subject of current cryobiological research [21, 22, 23]. In this manuscript we derive a new model accounting for both diffusion through the interstitium of the spherical array of layers and cell-to-cell osmosis. This allows solute and water transport into and out of the deeper layers of the sphere by one of two methods: serially through each of the overlying layers and across that portion of the cell membrane that is exposed to the intercellular transport driven by diffusion.

The proposed model is in some respects similar to that proposed by Huang, Wylie and Miura [24] which is an extension of an approach of Tanner [25] where transport is compartimentalized a way that recognizes that cell-to-intersitium transport influences local envirionments which is connected by some diffusive process to other cells. Huang et al consider a model where there is no cell-to-cell transport, something we consider important here. Additional recent work to couple cell and interstitial transport has been done by, among others, Layton and Layton [26] where a model was constructed to account for the morphology of the outer medulla of the kidney.

In our model previously published data for hamster islets of Langerhans [27, 28] supply many of the biophysical parameters. Here we show that the only previously undetermined variable that significantly affects the model is the cellular surface area that is in contact with the intercellularly transported membrane permeable solutes (A_is). The model is validated and A_is determined using a 3 × 3 factorial experimental design blocked for experimental day. Whole islet experiments are compared with model predictions at three temperatures (8, 22, 37 °C), using three perfusing solutions (Dimethyl Sulfoxide (DMSO), Ethylene Glycol (EG), 3×Phosphate Buffered Saline (PBS)), and three islet size groups (< 80 μm, 80 μm to 110 μm, > 110 μm radii). Using coefficient of determination (R²) as our statistical measure, we show that our model provides an accurate description of volume excursion for whole islets in response to osmotic challenges.

2. Mathematical Model

2.1. Assumptions

The intra- and extracellular media are assumed to be ideal, hydrated, dilute multicomponent solutions and the membranes of the cells are simple and homogeneous. The equations which we use to analyze non-equilibrium fluxes of water and solute are based on the work of Kedem and Katchalsky (K/K) [31] which describe equations based on the assumptions of ideal and dilute solutions.

We will neglect concentration polarization and the effect of unstirred layers on the permeability of the cells. An identical assumption was made in Levin et. al. [6] where they drew upon the work of Levin et al. [32] to demonstrate that little solute polarization occurs within the small volume of aqueous solution separating closely packed cells. We assume that adjacent membranes can be modeled as two independent membranes in series, resulting in a halving of effective hydraulic conductivity and solute permeability.

We assume that both the cell surface area in contact with other cells (A_c) and in contact with intercellular media (A_is) are constant. The accuracy of this assumption is debatable (e.g. [33, 34]), however in general many investigators maintain constant surface area to avoid the problem of an increase in membrane surface area when the tissue expands past its isotonic volume [18, 19]. And we ignore intracellular diffusion effects, assuming solute entering a cell (layer) is distributed evenly throughout the cell. This assumption may be justified by the diffusion length given by $L_D=2\sqrt{{Dt}_c}$, where D is the diffusivity, and t_c is a characteristic time. In particular, we have D ≈ 1100 μm²/s (the approximate diffusivity of DMSO or EG), and t_c = 10 s (the approximate intracellular concentration equilibration time of an individual islet cell [27]). Thus $L_D=2\sqrt{1100\ast 10}\approx 210\mu \mathrm{m}$, which is significantly longer than the approximate islet cell radius of 6 μm, though perhaps not sufficiently long to discard for an entire islet of diameter approximately 100 to 200 μm.

2.2. Cell membrane mass transport model

Because parameter data for individual islets have already been published, we use the same formalism described by Kedem and Katchalsky, which gives the total volumetric mass flow J_v as well as the permeable non-electrolyte (e.g. DMSO or EG) mass flow J_s across a membrane in terms of the phenomenological coefficients L_p, ω, and σ [31]:

$$\begin{array}{l}\frac{dV}{dt}=J_v(c,C,k,K)A=-L_{p}A\overline{\mathrm{R}}T(k-K+\sigma (c-C)),\\ \frac{dS}{dt}=J_{s}A=(1-\sigma )\overline{C}{J}_v+\omega (c-C),\end{array}$$ (1)

where all parameters are defined in Table 1, and C̄ is the average of extracellular and intracellular CPA concentrations (osmolality) defined by Kedem and Ketchalsky,

Table 1.

Parameter list, their units and values if known. All CPA specific and cell and system parameters are determined from previous studies. In particular, all cell specific parameter values are from Benson et al. [27] and Liu et al. [28] and the solute diffusivity values, their activation energies, and the tortuosity value are from Maroudas et al. [29] and Page et al.[30]. Note that the fitting parameters are all functionally related (see Section 2.3), and $\overline{A_{\text{is}}}$ is the sole fitting parameter of the model.

CPA specific Parameter	Parameter Name	Value (EG)	Value (DMSO)	Units
Lp	Hydraulic Conductivity at 22 °C	0.00375	0.00375	μm s−1 atm−1
Ps	Solute Permeability	0.105	0.132	μm s−1
$E_{\mathrm{a}}^{L_p}$	Activation energy of water permeability	11.69	12.43	kCal/mol
$E_{\mathrm{a}}^{P_s}$	Activation energy of Solute Mobility	20.35	18.34	kCal/mol
σ	Reflection coefficient	0.75	0.55	unitless
ω	Solute mobility (temperature dependent calculated value)	—		Ps = ωR̄T

Cell and system Parameter	Parameter Name	Value	Units
V	Cell volume (individual islet cell)	970	μm3
Vb	Osmotically inactive fraction of the cell	0.40	unitless
A	Surface area of cell (assumed constant)	408	μm2
λ	Tortuosity	1.44	unitless
D	Diffusivity of CPA in water at 22 °C	1100	μm/s2
D	Diffusivity of NaCl in water at 22 °C	1075	μm/s2
D̄	Diffusivity of solute in tissue	D̄= Dλ−2	μm/s2
$E_{\mathrm{a}}^D$	Activation energy of diffusivity	5.46	kCal/mol
R	Gas constant	0.0821	L atm K−1 mol−1

Fitting Parameters	Parameter Name	Units
δ	Effective channel radius	μm
Ac	Surface area of cell in contact with other cells	μm2
Ais	Surface area of cell in contact with intracellular media	μm2
$\overline{A_{\text{is}}}$	Normalized surface area of cell in contact with intracellular media	μm2

State Variables	Variable Name	Units
T	Temperature	K
S	Intracellular moles of permeating solute	mol
C	Intracellular CPA Concentration	mol/kg
K	Intracellular salt concentration	mol/kg
c	Extracellular CPA Concentration	mol/kg
k	Extracellular salt concentration	mol/kg
C̄	Mean CPA concentration	mol/kg
Js	Solute mole flux	mol/μm2/s
Jv	Volume flux 6	μm/s
t	Time	s
R	Radius of whole islet	μm
r	Radius from center of whole islet	μm

$$\overline{C}=(c-C)/[ln(c/C)]\approx (c+C)/2.$$

The intracellular concentrations of salt and CPA during anisosmotic conditions were determined from the Boyle van’t Hoff relation applied to the osmotic responses of cells [28, 35], and active ionic transport of Na⁺ and K⁺ are assumed to have negligible effects on gross cellular volume, a fact supported by the results of our previous work, where the volumes of individual islet cells were tracked following exposure to high osmolality (540, 800, and 1355 mOsm/kg) saline solutions. Upon equilibration, no rectification was observed up to a minute post exposure. Moreover, in the present experiments, upon exposure to 1200 mOsm/kg saline solutions, there are no discernable volume effects of ion transport as volumes, once they reach their osmotic equilibrium appear to remain constant (see, e.g. Fig. 4).

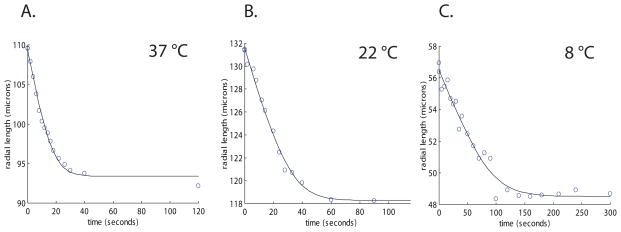
Figure 4.

Plots of islets with various radii perfused with 3× PBS at 37, 22, and 8 °C. The solid line is model predictions under the same experimental conditions. The best fits for channel radius (corresponding to A_is) were 1.79, 2.08, 1.21 μm and correlation coefficients (R²) were 0.99, 0.99, 0.97, respectively.

Finally, it will be convenient later to note that in the dilute approximation used here, C := S/V, and system (1) may be rewritten as follows, with J_v and J_s defined as above

$$\begin{array}{c}\frac{dV}{dt}=J_{v}A,\\ \frac{dC}{dt}=\frac{d(S/V)}{dt}=\frac{J_{s}AV-J_{v}AS}{V^2}.\end{array}$$ (2)

2.3. Geometry

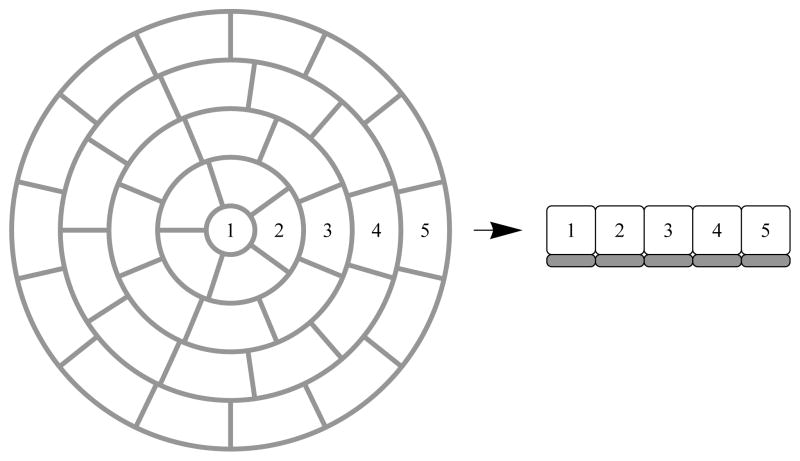
The mass transport model (1) was applied to the geometry shown in Fig. 1 and Fig. 2. This model is a series of concentric spheres and is built by assuming that the innermost sphere (sphere 1) is of the dimensions and volume of a single hamster islet cell (approximately 12.2 μm in diameter and 960 μm³ in volume). Each surrounding layer is the thickness of the diameter of one islet cell. All layers have water and solute permeabilities equal to L_p/2 and P_s/2 except for the outermost layer, with permeabilities equal to L_p and P_s. We then set L_p and E_a of L_p, P_s and E_a of P_s, and σ equal to values found for hamster islet membranes for DMSO and EG [27], where the temperature dependence of the permeability parameters L_p and P_s is given by the Arrhenius equation

Figure 1.

Geometric model of the whole islet of Langerhans made up of concentric shells of individual islet cells. Numbers indicate layer number where in each layer we assume radial symmetry. Grey boxes indicate the intersitium where concentration is modeled by a system of reaction diffusion equations dependent on the local concentration gradients across cell membranes at that layer.

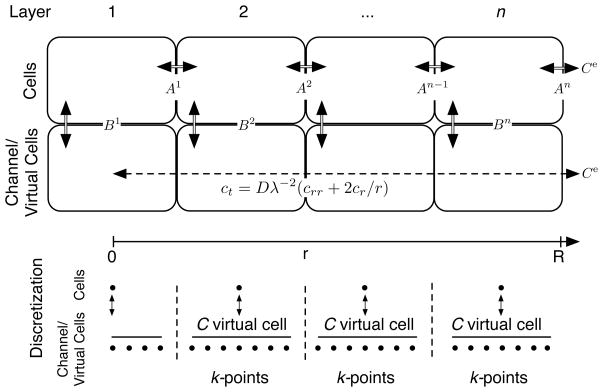
Figure 2.

Conceptual model of the combination of diffusion and cell-to-cell transport. Double lines indicate mass transport governed by the Kedem and Katchalsky (K/K) model, whereas the dashed line indicates mass transport governed by the diffusion equation in a sphere with tortuosity factor λ. At membrane interfaces A_i, i = 1, …, n − 1, we model transport as two membranes in series, resulting in a halved effective cell-to-cell permeability. At membrane interfaces B_i, i = 1, …, n, the exterior local concentration governing mass transport at the ith cell depth is given by the mean concentration in the “virtual cell.” Spatial discretization is also shown.

$$P(t)=P(T_{\text{ref}})exp\left(-\frac{E_a}{R}(T^{-1}-T_{\text{ref}}^{-1})\right),$$ (3)

where P is either L_p, P_s or the solute diffusivity D defined below, and T_ref = 295.15. The nonosmotically active portion V_b of the cells (layers) was also set to be 0.40 from previous experiments [28]. We assume that cylindrical channels are evenly distributed throughout the tissue.

In this model we assume that the extracellular (interstitial) volume of the islet remains fixed at 20% of the overall islet volume throughout the experimental perfusion, a value published by several authors [30, 36, 37]. The assumption that the ratio of intra- and extra- cellular space is fixed is supported by the experiments conducted in Benson et al. [27] and Liu et al. [28] which demonstrated that the V_b of individual islet cells is approximately 40% and the apparent V_b of the whole islet is also approximately 40%. These data lead to the conclusion that since the respective Boyle Van’t Hoff plots (normalized volume vs. 1/Osmolality) for individual islets and whole islets are identical, the extracellular volume of the islet must remain in direct proportion to the overall islet volume.

Here we model the extracellular space within the islet as a series of cylindrical channels penetrating the spherical model. The surface area of each concentric layer (boundaries A¹, …, Aⁿ in Fig. 2) is calculated from the cell-to-cell transport model with the cross-sectional area of the channels removed. First, to calculate the number of channels, we have the volume of one channel, V_channel = πδ²R, which, in turn allows us to calculate the number p of channels comprising 20% of the total islet volume p = 0.2V_islet/V_channel, and thus the constant total channel area A_is = p(2πδ). It is convenient to define the normalized A_is by dividing by the total cellular surface area

$$\overline{A_{\text{is}}}:=A_{\text{is}}\frac{V_{\mathit{cell}}}{0.8V_{\mathit{islet}}{A}_{\mathit{cell}}}.$$

This ratio is fixed for all cells and all time.

Finally, we note that the total cellular surface area is based on the calculated surface area of an individual spherical islet cell in suspension. Because this cell has a minimal surface area to volume ratio, we expect that because cells in tissues are aspherical and their physiologic volume is the same, the effective surface area of cells in a tissue construct should be higher. This implies that, though based in a theoretical framework, the above quantity is phenomenological and values should not indicate the “true” ratio of interstitial surface area to intercellular surface area.

2.4. Interstitial mass transport

Using the assumption of independent flow, isothermal conditions, and with concentration independent diffusivity, we may use the radially symmetric linear diffusion equation (see, e.g. [38]), coupled with initial and boundary conditions:

$$\begin{array}{l}\frac{\partial c}{\partial t}=\overline{D}\left(\frac{{\partial }^{2}c}{\partial r^2}+\frac{2}{r}\frac{\partial c}{\partial r}\right),\\ c(r,0)=c_0(r),\\ \frac{\partial }{\partial r}c(0,t)=0\\ c(R,t)=c^e(t).\end{array}$$ (4)

Here c is the concentration of extracellular solute (mol/kg), D is the diffusion coefficient (μm²/s), r is radius (μm), and t is time (s).

The solution of the solute diffusion equations was approximated using the method of lines where the spatial dimension was discretised leaving a system of ordinary differential equations. Essentially this is achieved by discretizing the spatial variable on a uniform grid, and applying 2nd order centered difference formulas to calculate approximate spatial derivatives, resulting in a system of linear ordinary differential equations, which were then solved using MatLab’s built-in ode15s solver. This technique facilitates the simultaneous solution of the combination of the linear diffusion equations from this section and the nonlinear ordinary differential equations in the following section.

The diffusion coefficient D for a freely diffusing solute in water and that for a solute in the tissue interstitium should be different, however the choice of an appropriate model is unclear. In particular, one must account for not only the effects of path constraints but solute-structure interaction. For example, a porous media model may be appropriate [15], or more complicated relationships between chemical potential and strain may be developed [16]. We ignore these complications and use the linear diffusion model (4) with a constant diffusion coefficient because we wish to capture a “first order” level of detail: more explicit models may be implemented later if applications warrant the detail.

We account for the specific geometry of islets by employing a tortuosity factor λ that scales the diffusivity constant. Specifically, the tortuosity factor is the actual length of the diffusion path per unit of length of diffusion, D̄ = λ⁻²D, moreover this factor is a function of tissue geometry and therefore is relatively solute independent. Maroudas et al. [29] and have shown that for a range of solutes, diffusion through articular cartilage yields a tortuosity factor of 1.35 to 1.44. Page et al. [30] conducted experiments on cat heart muscle which, arguably, has a histology more similar to islets than cartilage and found a tortuosity of 1.44. Additionally, Marudas et al. found that the temperature dependence of the diffusivity followed the Arrhenius model (see equation (3)) with an activation energy E_a of 5.46 Kcal/mole [29].

We therefore modified the diffusion coefficient D to account for diffusion through an islet by using D̄. Based on the molecular weight of DMSO (78.13 daltons) and EG (62.07 daltons) we assume free diffusivity of 1100 μm²/s and a tortuosity of λ = 1.4 [29, 30] yielding respective diffusion coefficients for EG and DMSO of D̄ = 530 μm²/s. For PBS we assume the free diffusion coefficient to be dominated by the major component NaCl (58.4 Daltons) and the diffusion coefficient by D̄ = 510 μm²/s [39]. We assume all diffusivities have an activation energy E_a = 5.46 Kcal/mole [29].

Because we assume uniform intracellular concentrations, the transmembrane volume flux at Bⁱ is governed by a mean concentration along this membrane. However we wished to include the effects of solute and solvent mass transfer on the local channel concentration. Though a piecewise defined Robin (Type 3) boundary condition would account for the flux along boundary $B={\cup }_{i=1}^n{B}^i$—requiring the solution of the diffusion equation in a two dimensional channel—at this length scale the diffusion normal to the cell membrane and across the channel is nearly instantaneous and the local concentration would be influenced only by the radial diffusion and the normal boundary conditions defined by the K/K model.

In practice, this should be identical to the application of so called “virtual” cells (see Fig. 2). We assume that the transmembrane flux across any boundary Bⁱ is governed by the mean local concentration governed by diffusion. This flux then affects the local concentration independent of diffusion. Numerically, this is achieved by performing a domain decomposition in r [40] in the channel with each layer constituting a new domain and coupling these layered domains to their associated cell layers using the K/K model by assuming that the concentration of a virtual cell associated with this domain is equal to the average of the concentrations of the nodes adjacent to an islet layer (see discretization in Fig. 2), and the volume of a virtual cell equal to 20% of the associated cell-layer volumes.

Finally, it is important to rule out the possibility of advective transport. In this case, the unitless parameter to describe the influence of advective transport in a model is the ratio of the advection to diffusion, often called the Péclet number, Pe = LV̄D⁻¹, where L, D and V̄ are characteristic length, diffusivity and fluid velocity, respectively. If Pe < 0.1 advective transport is usually negligible. In our case the characteristic diffusivity is D = 1100 μm²/s² use, the characteristic length is L = 50 μm and the characteristic fluid velocity is on the order of

$$\overline{V}=\underset{t}{sup}\frac{d}{dt}\frac{V_{\text{islet}}}{A_{\text{islet}}}=\underset{t}{sup}{r}^{\prime }(t)/3,$$

assuming that the change in islet volume is attributable to water volume flux, which has an experimentally determined value of V̄ ≈ 0.05 μm/s, yielding

$$\text{Pe}=L\overline{V}{D}^{-1}<0.1$$

indicating that advective transport is not likely to be a major component of the model.

We now can define the complete model. Suppose that we have the configuration in Fig. 2. Let Ω = [0, R], and partition Ω into disjoint subdomains Ω_i such that $\mathrm{\Omega }={\cup }_{i=1}^n{\mathrm{\Omega }}_i$. Let c_i : Ω_i × [0, ∞) → [0, ∞) be the concentration in the channel in the ith domain and W_i, C_i : [0, ∞) → [0, ∞) be the water volume and concentration in the ith cell layer, be defined by the system of coupled reaction-diffusion and ordinary differential equations (note that we use capital and lowercase variables for intra and extracellular quantities, respectively):

$$\begin{array}{l}\frac{\partial c_i}{\partial t}=D_i\left(\frac{{\partial }^2{c}_i}{\partial r^2}+2\frac{\partial c_i}{\partial r}\right)+f_c^i({\overline{c}}_i,C_i,W_i)\text{in}{\mathrm{\Omega }}_i\times (0,\infty ),\\ \frac{{dW}_i}{dt}=f_w^i({\overline{c}}_i,C_i,C_{i-1},C_{i+1},W_i),\\ \frac{{dC}_i}{dt}=f_C^i({\overline{c}}_i,C_i,,C_{i-1},C_{i+1},W_i),\end{array}$$

where c_i models both permeating solute c and nonpermeating solute k, supplemented with initial and boundary conditions (with Γ_i := ∂Ω_i−1 ∩ ∂Ω_i):

$$\begin{array}{ll}\hfill c_i=c_0& \text{in}{\mathrm{\Omega }}_i\times \{0\},\hfill \\ \hfill c_i=c_{i-1}& \text{in}{\mathrm{\Gamma }}_i\times [0,\infty ),i>1,\hfill \\ \hfill \frac{\partial c_i}{\partial r}=\frac{\partial c_i-1}{\partial r}& \text{in}{\mathrm{\Gamma }}_i\times [0,\infty ),i>1,\hfill \\ \hfill \frac{\partial c_i}{\partial r}=0& \text{in}\{0\}\times [0,\infty ),\hfill \\ \hfill c_n=c^e(t)& \text{in}\{R\}\times [0,\infty ),\hfill \\ \hfill W_i(0)=W_i^0,& \hfill \\ \hfill C_i(0)=C_i^0,& \hfill \end{array}$$

where ${\overline{c}}_i:=\frac{1}{\mid {\mathrm{\Omega }}_i\mid }{\int }_{{\mathrm{\Omega }}_i}{c}_{i}dx$ is the mean extracellular concentration at the ith level, and c^e : [0, ∞) → [0, ∞) is the extra-islet concentration.

We define the reaction terms fⁱ : ℝ^k → ℝ which stem from the K/K formalism. From system (2), we may define the reaction terms and ODEs

$$f_c^i=J_s(c_i,C_i)\frac{A_{is}}{0.2V_i}+J_v(c_i,C_i,k_i,K_i)\frac{c_i{A}_{is}}{0.2V_i},$$ (5)

$$f_w^i=J_v(C_i,c_i)A_{is}+J_v(C_i,C_{i-1},K_i,K_{i-1})\frac{A}{2}+J_v(C_i,C_{i+1},K_i,K_{i-1})\frac{A}{2},$$ (6)

$$f_C^i=J_s(C_i,c_i)\frac{A_{is}}{V_i}+J_v(C_i,c_i,K_i,k_i)\frac{C_i{A}_{is}}{V_i}+J_s(C_i,C_{i-1})\frac{A}{V_i}+J_v(C_i,C_{i-1},K_i,K_{i-1})\frac{C_{i}A}{2V_i}+J_s(C_i,C_{i+1})\frac{A}{V_i}+J_v(C_i,C_{i+1},K_i,K_{i+1})\frac{C_{i}A}{2V_i},$$ (7)

where J_v(c, C, k, K) and J_s(c, C) are defined in display (1), and we note that in the case of nonpermeating solute flux J_s = 0, and we assume that k^e(t) = 0.29 mol/L, isotonic dissociated molality of 1 x PBS.

Finally, the above model accounts for the movement of water and solutes across cell membranes. In the case where we model the diffusion of only the nonpermeating solutes in PBS, there is no permeating solute (c = C = 0), and the governing equations are simplified. In particular system (1) reduces to

$$\frac{dV}{dt}=J_v(0,0,K,k)A=-L_{p}A\overline{\mathrm{R}}T(k-K)$$ (8)

and J_s = 0. We also replace c and C with k and K respectively in system (4) as the diffusing solute.

3. Materials and Methods

3.1. Reagents

Unless stated otherwise, all chemical reagents were obtained from Sigma (St. Louis, MO). Collagenase P was purchased from Boehringer Mannheim (Indianapolis, IN). Cell culture reagents, including Hanks’ balanced salt solution, Medium 199, fetal bovine serum (FBS) and 0.25% trypsin-EDTA, were purchased from Gibco (Gaithersburg, MD)

3.2. Isolation of Islets From Hamsters

Hamster pancreatic islets were isolated as previously described by Gotoh et al. [41]. Briefly, 6–8 wk old golden hamsters (Harlan Sprague Dawley, Indianapolis, IN) were anesthetized via inhalation of Forane (Isoflourane; Ohmeda Caribe inc.; Guayama PR). The common bile duct was cannulated under a stereomicro-scope with a polyethylene catheter through which approximately 8 mL to 10 mL of cold (1 °C to 4 °C) M-199 medium containing 0.5 mg/mL of collagenase P was injected slowly until whole pancreas was swollen. The pancreas was excised and digested at 37 °C for approximately 50 min in M-199 medium containing 100 mg/mL of penicillin G and 100 mg/mL of streptomycin (no additional collagenase). The digest was washed three times in cold M-199 medium and passed through a sterile 500 mm stainless steel mesh. Islets were purified by centrifugation through a Ficoll density gradient (1037 kg/m³, 1096 kg/m³ and 1108 kg/m³) at 800×g for 20 min.

3.3. Perfusion of Islets and measurement of resulting volume excursions

The design and structure of the microperfusion chamber system is similar to that described elsewhere [42]. Briefly, the experiments were conducted by introducing 2 to 10 islets into the chamber cavity (height: 1 mm, diameter: 2 mm, volume: 3.14 μL) using the Hamilton syringe. With application of negative pressure from below, the solution moved out of the chamber, but the islets remained on the transparent porous membrane at the bottom of the cavity (polycarbonate screen membrane; Poretics Co., Livermore, CA; membrane thickness: 10 μm, pore diameter: 5 μm, pore density: 4 × 10⁵ pores/cm²). Next, 700 μL of a perfusion medium was loaded in the reservoir at the solution inlet and approximately 400 μL was perfused through the chamber by aspiration via a 1 mL syringe. The reservoir (with 300 μL of remaining solution) was then sealed via application of a glass cover slip, ensuring no evaporative effects. The entire perfusion took place in less than eight seconds and the original isotonic solution in the perfusion chamber cavity (3.14 μL) was quickly replaced over 100 times by the new perfusion medium, ensuring that none of the original isotonic solution remained in the chamber and that back diffusion of original solution into the chamber was impossible. Cells were immobilized by the downward flow of the perfusion medium during the perfusion process facilitating the recording of cell volume changes by a video camera.

The perfusion chamber and cell suspension cavity were cooled/heated with a temperature controller to reach an equilibrium. The prepared perfusion media was precooled or heated in a temperature-controlled methanol bath (Digital Temperature Controller, Model 9601, Polyscience Co., Niles, IL) to the same temperature as the perfusion chamber. Precooled/heated media was then perfused into the chamber and around the cell(s). During the experiment, the temperature variation of the perfusion medium and of the microperfusion chamber were monitored and the range of temperature difference between the perfusion medium and the chamber was ±0.2 °C during experiments (data not shown).

Individual video frames were imported into SigmaScan/Image (Jandel Corporation, San Rafael, CA). Islets were then outlined and area was measured by filling this outline. All islets used in this study were roughly spherical (unpublished data). A radius was then computed using this assumption of a spherical shape. Images were calibrated by measurement of spherical polyethylene beads (92.12 μm diameter, Coulter corporation, Epic division, Hialeah, FL).

The coupled system of partial and ordinary differential equations were discretized spatially as shown in Fig. 2, and the resulting ordinary differential equations were simultaneously solved using MATLAB (The MathWorks, Natick, MA) function “ode15s.” The best fit for A_is was found using the MATLAB function “fminsearch” which uses a modified simplex search method.

Model predictions were compared to experimental data using coefficient of determination (R²) calculations, and ANOVA was performed using the General Linear Models (GLM) computational procedure of the Statistical Analysis System (SAS; SAS Institute, Inc., Cary, NC). The model was validated and A_is determined using a 3×3 factorial experimental design blocked for experimental day. In this design the treatment structure consists of all possible combinations of all levels of all factors under investigation [43]. For our analysis, we chose to block (group) the experiments that were performed on the same day (from the same isolation of islets). This grouping was included in the SAS GLM model as a day effect which allowed model to remove (and test) the variability due to day to day variation. Significance of main effect was tested using the appropriate mean squares (Temperature effect tested by Temperature × Day interaction as the error term, etc.). This procedure partitioned the variance of the three main treatment effects: temperature, islet size, and perfusing solution as well as the two way interaction effects.

4. Results

A model was developed to describe the behavior of islets of Langerhans in the golden hamster when they are exposed to anisosmotic conditions. The model was validated and A_is determined using a 3 × 3 factorial experimental design which was blocked for experimental day. Whole islet in vitro experiments were compared with model predictions at three temperatures, using three perfusing solutions and three islet sizes.

4.1. Correlation of model with experimental data

Typical results for correlation of several of the experimental protocols are shown in Figs. 3 and 4. These figures include data from in vitro perfusion experiments using the three perfusion media (1.5 mol/kg DMSO, 1.5 mol/kg EG, and 3×PBS) and hamster islets of Langerhans. Superimposed on this data is the prediction of the mathematical model described above. Table 2 contains the combined data from all of the 27 experiments performed for this study.

Figure 3.

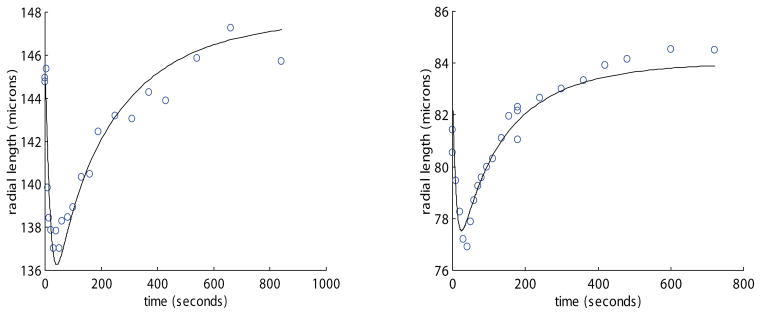
Representative plots of radius vs. time for two whole hamster islets of different sizes perfused with 1.5mol/kg DMSO at 22 °C. The solid line is model predictions under the same experimental conditions. The best fit channel radius (corresponding to A_is) for the left plot was 2.92 μm and correlation coefficient (R²) was .91. The A_is for the right plot is 1.84 μm with correlation coefficient 0.93. Note the effect of size on equilibration time.

Table 2.

Data from the 3×3 factorial experiment is shown where whole islets were compared with model predictions at three tempreatures (7 °C, 22 °C, 37 °C) using three perfusing solutions (DMSO, EG, and 3 × PBS) and three islet size groups (<80 μm, 80 μm to 110 μm, >110 μm radii).

CPA	Temp. (°C)	radius (μm)	# of islets	initial radius (μm)		Normalized Ais		coeff. of det.
				mean	S.D.	mean	S.D.	mean	S.D.
DMSO	37	< 80	3	69.98	7.56	0.34	0.07	0.77	0.10
DMSO	37	80 – 110	4	95.94	9.85	0.28	0.13	0.78	0.10
DMSO	37	> 110	3	120.07	6.49	0.39	0.14	0.81	0.16
EG	37	< 80	3	75.58	14.36	0.34	0.02	0.88	0.04
EG	37	80 – 110	4	91.74	3.28	0.20	0.04	0.90	0.02
EG	37	> 110	3	121.53	23.72	0.24	0.11	0.62	0.27
PBS	37	< 80	3	70.12	7.81	0.41	0.31	0.96	0.03
PBS	37	80 – 110	3	100.79	8.19	0.50	0.16	0.99	0.00
PBS	37	> 110	2	122.80	9.48	0.48	0.09	0.96	0.03
DMSO	22	< 80	2	76.64	6.82	0.22	0.13	0.76	0.15
DMSO	22	80 – 110	3	92.71	11.03	0.30	0.12	0.89	0.03
DMSO	22	> 110	3	123.27	17.97	0.22	0.14	0.89	0.12
EG	22	< 80	4	66.54	2.37	0.59	0.19	0.82	0.02
EG	22	80 – 110	3	86.58	10.62	0.42	0.08	0.85	0.00
EG	22	> 110	2	111.85	0.78	0.42	0.22	0.72	0.04
PBS	22	< 80	8	56.21	15.31	1.12	0.87	0.92	0.05
PBS	22	80 – 110	8	88.78	10.58	1.01	0.25	0.96	0.02
PBS	22	> 110	5	120.80	10.29	0.43	0.25	0.97	0.02
DMSO	8	< 80	6	53.48	14.44	0.48	0.10	0.86	0.07
DMSO	8	80 – 110	5	93.16	7.16	0.41	0.01	0.87	0.07
DMSO	8	> 110	4	125.03	23.67	0.42	0.05	0.93	0.04
EG	8	< 80	4	65.13	14.02	0.45	0.11	0.80	0.08
EG	8	80 – 110	5	91.21	8.66	0.42	0.03	0.88	0.05
EG	8	> 110	4	117.38	12.40	0.39	0.01	0.79	0.07
PBS	8	< 80	10	59.30	8.36	1.44	0.56	0.96	0.02
PBS	8	80 – 110	9	88.77	10.61	1.40	0.37	0.98	0.01
PBS	8	> 110	6	121.77	16.10	0.93	0.29	0.99	0.01
		Mean	4.41	92.86	10.81	0.54	0.18	0.87	0.06
		St. Dev	2.15			0.34		0.09

A mean of 4.4 islets were compared at each of the 27 experimental conditions and found to correlate with a coefficient of determination (R²) of 0.87 ± 0.06 (mean ± S.D.). This excellent value for R² demonstrates that, even with only one fitting variable, the model predicts the experimental data with a high degree of accuracy. The remaining 13% of the variability could possibly be explained by error in measurement.

4.2. Day Effect

The 3×3 factorial design was blocked for day and when using analysis of variance (ANOVA) for A_is, it was found that this day effect was significant (p < .05). This indicates that there is significant day to day variability of A_is for hamster islets. This variability may be explained by hamster to hamster variability, or by day to day isolation variability. Hamster to hamster variability was seen for hamster oocyte water permeability and activation energy [44]. However, it is more likely that even slight differences in digestion of the islets in collagenase from day to day could affect the A_is significantly. Visually, increased digestion renders some islets “looser” (Dr. Raymond Rajotte, personal communication) which could hypothetically increase A_is.

4.3. Interstitial surface area (A_is)

The $\overline{A_{\text{is}}}$ from 119 islets (10 hamsters over 5 experimental days) was found to have a mean of 0.54 ± 0.34 (mean ± S.D.) across all treatments. Values greater than one may seem at first to be counter-intuitive. However, we normalized our value of A_is to spherical internal individual islet cells, which have a minimal surface area to volume ratio. Therefore, non-spherical cells inside the islet would increase the overall surface area to volume ratio and increase the total membrane surface area of the islet, thus decreasing our normalized A_is.

We also compared A_is over experimental conditions using ANOVA and found the treatment variable of perfusing solution to be significant (p < .05). Furthermore, ANOVA with multiple comparisons demonstrated that A_is for PBS is greater than for DMSO or EG exposure (p < .05).

5. Discussion

In this manuscript we have proposed a model that accounts for multiple modes of solute and solvent transport in small tissues. This model utilizes a priori known cellular biophysical and physical chemical parameters, and makes some simple geometrical assumptions, most notably that each cell is equally available to the interstitium. This assumption is accounted for by the single fitting parameter, A_is, that provides tissue specific geometrical information about this surface area availability independent of solute.

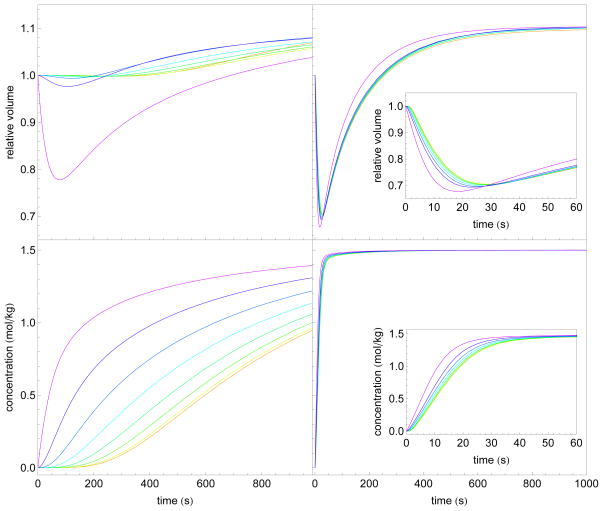
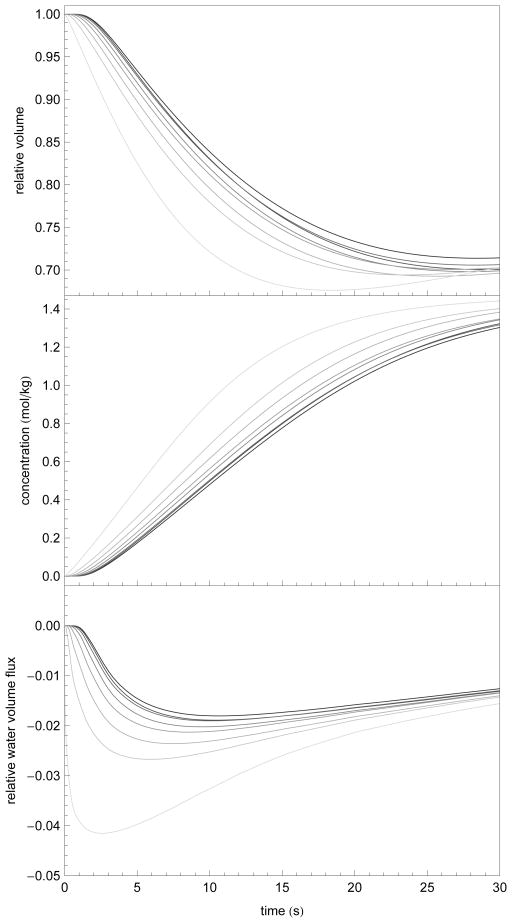
The present model combines elements of other previously proposed models. In particular cell-to-cell transport models have been previously proposed. This model captures similar effects to those of Levin et al. [6] as well as Diller et al. [8] in that transport is delayed in interior layers and thus whole islet equilibration takes over 1000 s. We applied our model in the absence of interstitial mass transport, and found similar results as Levin et al. and Diller et al. In particular, Fig. 5 shows the results of modeling of an eight layer intracellular transport model in the absence of interstitial diffusion (approximately 180 μm in total diameter) where the extra-islet concentration was fixed at 1.5 mol/kg EG in 1 x PBS.

Figure 5.

Comparison of the results of an eight layer model of approximately 180 μm diameter without interstitial diffusion (left column) and with interstitial diffusion (i.e. the full model; right column), subjected to perfusion with 1.5 mol/kg EG. Layers are indicated by the color spectrum with purple on the outside and red on the inside of the islet. In the left column, the model assumes that solute and water transport take place exclusively across layer membranes. In the right column is the full model. Inset in the right column is a shorter time-scale to illustrate the layer differences in the full model. The volumes indicated (top row) are normalized to each initial layer volume. Importantly, note that the great majority of the total volume is taken up by the outer layers and is not illustrated here.

The model defined by Schreuders et al. [9] focused mainly on the derivation of thermodynamically consistent flux equations in the case where the assumption of local homogeneity is invalid. Their derivation of this admittedly more complex model is justified by the argument that in the case of multiple mobile species, the independent flow assumption is invalid. In the present study the independent flow assumption is made because under our experimental conditions we expect minimal interaction between diffusing species, namely DMSO or EG and the major components of PBS. Moreover, our study, in contrast with the Schreuders study focuses on gains that can be made using the inherent geometry of the system—there is no reason why the pseudo-bond graph approach presented by Schreuders et al. could not be implemented in our model, allowing a more thermodynamically appropriate approach if we wish to model multiple component diffusion where we might expect solute-solute interactions.

Moreover, the network thermodynamic models described first by Schreuders et al. [9] and used to model whole pancreatic islets by de Freitas et al. [10, 45] are considerably simplified in the sense that they use compartmentalized flux models to reduce the spatial dependence to a system of coupled ordinary differential equations where spatial scales are ignored. This approach has the benefit of being considerably easier to solve numerically, but loses generality in the application of diffusion models, such as the simple porous media model used here. In fact, our model may be generalized quite easily to more appropriate porous media models, models where the spatial dependence of the diffusivity is realistic (e.g. in ovarian tissue where the epithelium tissue is different than the cortex tissue which is morphologically different from the medulla). Moreover, our approach is considerably more in line with that of present hybrid individual cell based modeling [46].

Alternatively, diffusion based models have been proposed for tissue mass transport. These models assume that the local contribution of cell-cell and cell-interstitium transport can be approximated by a phenomenological diffusivity parameter in a contiuum model such as the diffusion equation or its porous media analogues. For example, Han et al [14] use the same radially symmetric linear diffusion equation to model mass transport in rat ovaries. However, Levin [6] used diffusion length arguments to show that if cells do not interact and are treated as a “bunch of grapes” for small tissues, equilibration should be solely dependent on the mass transport of single cells in suspension. To wit, if the islet could truly be modeled as a “bunch of grapes,” with each cell completely exposed to interstitial diffusion, the behavior would be dependent on the diffusion characteristics of a sphere. Since the sphere would be equilibrated in a relatively small time (regardless of the diffusion coefficient and tortuosity factor), whole islets should equilibrate on the same time scale as individual islet cell. Further, if an islet was truly a “bunch of grapes” its behavior would be reasonably independent of the size of the islet, for the same reasons outlined above.

Benson et al. [27] showed that an individual cell perfused with 1.5 mol/kg DMSO at 22 °C would equilibrate in less than 150 seconds. Therefore under a pure diffusion model using CPA in water self-diffusion parameters, the whole islet would follow a similar time course as an individual islet cell. In fact, physical experiments below show that when an islet of approximately 150 μm diameter is exposed to 1.5 mol/kg DMSO the equilibration takes about 600 seconds (see Fig. 3). Furthermore, the size of the islet does affect the equilibration time. Therefore, the behavior of the hamster islet must be a combination of the two extremes. It must have some intercellular (interstitial) transport, but not all cells are completely exposed to this intercellular solute.

If, however, one keeps the non-interating model but discards the known self-diffusion parameter in lieu of a phenomenological diffusion coefficient (as in Han et al. [14]), the challenge here is that the wide range of application conditions needed in cryopreservation protocols, including up to 10 mol/kg CPA concentrations and a nearly 200 °C temperature change in a tissue type that varies greatly in diameter suggests that it is unlikely that a model with a non-geometrically based fitting parameter would be valid in the necessarily wide range of applications. This was the motivation for our approach: that existing physical data for cells and tissues in these widely varying conditions could be adapted to a hybrid model of transport with minimal phenomenological fitting parameters.

When we modeled permeating and nonpermeating solute transport simultaneously, we found that there were very limited nonpermeating concentration gradients generated by the cell-to-interstitium water transport (data not shown). With our assumption that water lost to the interstitium is not stored, these effects are likely mitigated by the inward diffusion of solutes from the exterior of the islet. Combined with the temporal delay and limited relative water flux values (see Figure 7), we believe that this limited nonpermeating solute gradient is reasonable.

Figure 7.

Numerical simulation of normalized individual islet volumes, intracellular solute concentration, and normalized water flux (w(0)⁻¹dw/dt) at each of eight layers (light to dark indicates exterior to interior layers) after exposure to 1.532 mol/kg EG 1 x PBS at 22 °C. These data demonstrate the predicted intraislet delay in response, the reduced total volume response, and the time to quasiequilibrium as a function of cell depth. The initial radius was the mean radius from Table 2 (r = 94 μm) and A_is was set to the mean interstitial area (A_is= 0.54).

One significant assumption in our model is that the ratio of interstitial volume to cellular volume remains fixed throughout. The overlap between the Boyle van’t Hoff relationships of isolated individual islet cells and their whole islet counterparts [27, 28] along with published work in other tissues [30, 36, 37], suggests that for tissues in osmotic equilibrium this assumption holds. The question remains whether the fixed volume ratio assumption holds in the non-equilibrium case and the potential impact of this assumption. In short, does the intracellular water lost to the interstitium get “stored”, and how big is this effect? To fully answer this question, we would need to examine the elasticity the intracellular structure as a function of packing, placement, and pressure which is difficult to validate experimentally and well beyond the scope of this manuscript.

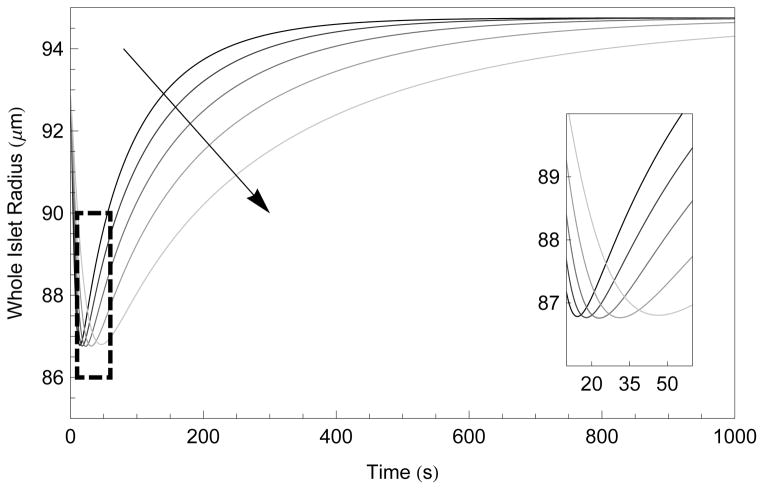
To attempt to address this assumption from within our theory, we first explore this possibility in a rough sense in Figure 6, where we note that increasing or decreasing the percentage of interstitial space by 50% results in fairly minor changes in total islet response, including nearly identical minimal radii. In fact, Figure 6 demonstrates that the change in interstitial space corresponds to changes in the number of pathways available for the diffusive transport that is considerably faster than the cell-to-cell transport alternative. This figure should represent the maximal error as it assumes a fixed error in this ratio.

Figure 6.

Numerical simulation of whole islet radius after exposure to 1.5 mol/kg EG in 1 x PBS at 22 °C as a function of time and percentage of interstitial volume, ranging from 30% to 10% in 5% increments, indicated by the arrow. The inset shows the time and minimal volume the same data. The initial radius was the mean radius from Table 2 (r = 94 μm) and A_is was set to the mean interstitial area (A_is= 0.54).

The transient error is limited by two factors. First, the time to quasi-equilibrium (where the chemical potential of water is in equilibrium and thus the flux of water is is an order of magnitude smaller) in individual islets cells exposed directly to 1.5 mol/kg DMSO or EG is approximately 20 seconds [47]. This is the largest time scale for quasi-equilibrium possible in our model as only the exterior layer will directly experience such a large osmotic gradient. Second, the outer layer will lose approximately 50% of its water volume to the exterior of the islet, and the remainder to the interstitium (depending on conformation). In interior layers, the extra-cellular gradient is considerably smaller, with resulting shorter quasi-equlibrium times. This can be seen clearly in Figure 7 where the normalized volume response and relative water volume flux $W^i{(0)}^{-1}\frac{{dW}_i}{dt}$ at each layer is given.

Another significant assumption in our model is that the contribution of fluid velocity on the solute transport is negligible. During the construction of the model, we use simplifying assumptions to argue that the Péclet number was sufficiently small to argue that advection is negligible (see [48] for a discussion of Péclet numbers in porous media models). Using the mean islet radius (r = 94 μm) and A_is = 0.54, we show the calculated of the Péclet number during the active first 30 seconds of exposure to 1.5 mol/kg EG at 22 °C in Figure 8. Here the fluid velocity was calculated by summing dW_i/dt for each interior layer (i = 1,…, 7 here) plus 0.5dW_n/dt for the exterior layer (n = 8 here), as approximately 50% of dW_n/dt will be lost to the extracellular media), divided by 0.2A_islet to account for transport only out of “interstitial channels”. Note that If we instead more conservatively assume dW_n/dt contributes entirely to the channel water velocity, the maximal Péclet number is still 0.08.

Figure 8.

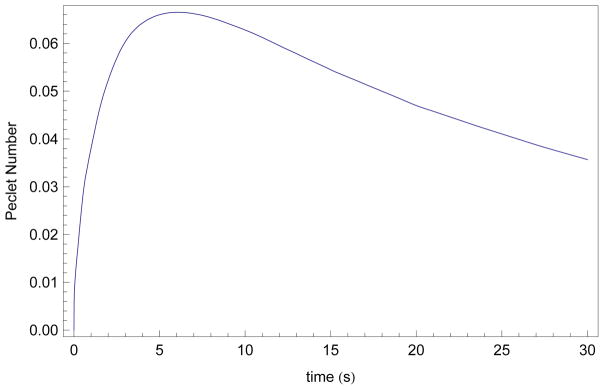
Numerical simulation of Péclet number as a function of time after exposure to 1.5 mol/kg EG in 1 x PBS at 22 °C, assuming an initial radius set to the mean radius from Table 2 (r = 94 μm) and A_is was set to the mean interstitial area (A_is= 0.54). Péclet numbers Pe = LVD⁻¹ were calculated using L = 50, D = 1100, and $V=\left({\sum }_{i=1}^7\frac{{dW}_i}{dt}+\frac{1}{2}\frac{{dW}_8}{dt}\right){(\text{Volume}\text{of}\text{channels}/\text{Volume}\text{of}\text{whole}\text{islet}\times 4\pi r^2)}^{-1}$.

In this manuscript we also experimentally validated the proposed model in hamster islets of Langerhans. Our results showed that, despite several simplifying assumptions, the model was in good agreement with experiments. In particular, there was no significant effect of permeating CPA on the fitted parameter A_is, but the use of a concentrated salt solution did significantly affect A_is. In the context of our model, this may suggest that the islets, when exposed to 3×PBS, have more surface area exposed to the interstitial diffusional transport than when they are exposed to DMSO or EG. A possible hypothesis is that there are areas of the islet which water is able to diffuse out of (in the case of hypertonic PBS perfusion) but larger molecules such as DMSO and EG are excluded from. This hypothesis is supported by the work of Barr et al. [49] who showed that the apparent extracellular spaces of smooth muscle decreased with increasing molecular size. Further, Bunch et al. [50] found that only 60% of total water to be available to DMSO in barnacle muscle. A second explanation may be that the two CPAs affect the histology of the islet in such a way as to “tighten” it and make it less susceptible to diffusional effects. Further exploration of this area may be warranted, and a straightforward follow up experiment would be to fit for A_is in the presence of other nonpermeating solutes of varying molecular diameter, ionic and non-ionic. An additional potential explanation is that our model assumes mutual diffusivity of all ionic components of PBS, where there may be a 50% difference in diffusivity of Na vs Cl ions [39]. Finally, we have ignored potential large effects of the electrical conductivity of the islet in high concentrations of PBS that may influence the movement of ionic solutes differentially and affect the model independely of the geometrical considerations mentioned above.

However, the lack of significant differences in A_is in the CPA groups (EG and DMSO from all islet sizes and temperatures) points to the conclusion that A_is is a parameter defined by the system geometry and, potentially, the type of diffusing solute. In short, from the results of these experiments, we expect that A_is will be the same for other similar non-ionic, CPA-type, solutes such as propylene glycol and glycerol. Because our model was intended for use in the prediction of the movement of these types of solutes, the present model and its resulting parameter A_is should be an extremely useful tool for the prediction of cryobiological protocols. This conclusion would indicate that our model has captured more information than a strictly phenomenological diffusion based model. Because of this, predictions based on knowledge of this parameter and knowledge of the diffusivities for other CPAs may be made without experimental measurements.

A specific advantage of our approach is that we have developed a model almost entirely independent of phenomenological parameters, facilitating a wide range of applications. We wish to use this model in the prediction of optimal cryopreservation protocols, which encompasses several interrelated steps for which an understanding of the cellular state is critical. One important aspect of modeling in cryopreservation is the temperature dependence of processes. It is expected that fluxes generally follow an Arrhenius law, but at Celsius temperatures below zero, mass-transport is challenging to measure accurately. Because the subzero temperature dependence of any phenomenological parameter such as a lumped “diffusion” term must be measured for each new combination of solutes and geometries, a phenomenological approach either must sacrifice accuracy or require multiple difficult biophysical measurements. On the other hand, our approach only depends on parameters with established temperature dependence such as the diffusivity of solutes in water. The geometry—and thus tortuosity factor, A_is, etc—is likely to be temperature independent. The only temperature dependent parameters required, then, are the hydraulic conductivity and solute permeability (L_p and P_s, respectively), for which the temperature dependence is well established [51].

It is well accepted that cells and tissues must be pre-equilibrated with a multimolal concentration of CPA before cooling to facilitate post-thaw survival [52, 53, 54]. This equlibration process has been shown to be deleterious from two perspectives. First, as shown in Fig. 3, exposure to high concentrations of extracellular (or extratissue) permeating CPA drives the rapid exosmosis of intracellular water, followed by the gradual recovery of this water as the slower permeating solutes cross the cell membrane. This large volume flux has been associated with cell damage in multiple cell types from multiple species [55, 56, 57, 58, 59, 60]. On the other hand, it has been shown that cells and tissues are sensitive to high concentrations of CPAs, necessitating rapid equlibration protocols [61, 62, 63]. There have been many studies with single cell suspensions to predict heuristically [64, 65, 66, 67, 68] or mathematically optimal [69, 70] protocols to mitigate these effects. The present model allows for the extension of these optimal control problems to small tissues. In particular the numerical approach of Benson et al. [71] should allow for the easy extension of single cell optimized CPA addition and removal protocols to the present model.

Second, combined with equations published for solute/solvent dynamics at low temperatures [18, 8, 19, 72] both the concentration of CPA within each layer at the time of freezing, and the concentration of water within the cells at the time of ice nucleation may be predicted. These values have also been shown to be of great importance to the overall outcome of the cryopreservation procedure [73, 4, 5]. There also has been recent discussion on the ice propagation in concentrically oriented tissues, where solute and solvent transport have been neglected [74, 75]. It would be of considerable interest to apply the intracellular ice and propagation theory discussed in these papers in combination with the model described and validated in this manuscript. A step towards this in pancreatic islets was made by de Freitas and Diller [76] but, though they used a network thermodynamic in their previous work [10, 45], they did not use this as a transport model in the prediction of intracellular ice formation at individual levels.

Because the present model geometry is radially symmetric with independent layers, this model could be applied to similar small tissue systems. A critically and clinically relevant tissue with this geometry is the ovarian follicle, which may be roughly described as a large center sphere (the oocyte) surrounded by layers of granulosa cells [77]. There has been much recent attention paid to cryopreservation of ovarian tissue with the hoped outcome of preservation of mature (beyond primordial stage) follicles [21, 78]. An understanding of the mass transport in ovarian follicles may provide insight into optimal cryopreservation protocols, even when these follicles are embedded within ovarian tissue.

6. Conclusions

A model has been constructed that accurately predicts volume excursion in response to osmotic and CPA challenges for whole islets while maintaining geometric information about the behavior of the entire islet. This model incorporates data describing fundamental biophysical characteristics from previous studies on individual hamster islet cells and describes transport through the islet by three methods: intracellularly, intercellularly, and a combination of these. Development of optimal cryopreservation protocols using this information remains to be accomplished.

Research Highlights.

• A solute-solvent mass transport PDE-ODE model for concentric layer tissues is derived.

• Known biophysical parameters for individual cells are coupled to a porous media model.

• Hamster islet of Langerhans responses to three solutes and temperatures are measured

• The model is fit to the data with only one free parameter: interstitial surface area.

• Nonpermeating solutes yield the only significant effect on interstitial surface area.