Abstract
In terms of making genes expression data more interpretable and comprehensible, there exists a significant superiority on sparse methods. Many sparse methods, such as penalized matrix decomposition (PMD) and sparse principal component analysis (SPCA), have been applied to extract plants core genes. Supervised algorithms, especially the support vector machine-recursive feature elimination (SVM-RFE) method, always have good performance in gene selection. In this paper, we draw into class information via the total scatter matrix and put forward a class-information-based penalized matrix decomposition (CIPMD) method to improve the gene identification performance of PMD-based method. Firstly, the total scatter matrix is obtained based on different samples of the gene expression data. Secondly, a new data matrix is constructed by decomposing the total scatter matrix. Thirdly, the new data matrix is decomposed by PMD to obtain the sparse eigensamples. Finally, the core genes are identified according to the nonzero entries in eigensamples. The results on simulation data show that CIPMD method can reach higher identification accuracies than the conventional gene identification methods. Moreover, the results on real gene expression data demonstrate that CIPMD method can identify more core genes closely related to the abiotic stresses than the other methods.
Introduction
The changing environmental conditions have a significant impact on the survival and growth of plants. A series of various abiotic stresses can bring about the overproduction of reactive oxygen species in plants, which may damage carbohydrates, proteins, lipids and DNA resulting in oxidative stress [1]. In order to cope with these abiotic stresses, including cold, drought, heat, osmotic press, salt, UV-B light stresses, etc., plants have their own defense mechanisms to adapt the complex and changeful environment [2], [3]. In other words, a particular set of interacting plants genes which are always called core genes exist in responding to each abiotic stress. Hence, how to extract these core genes is becoming a very meaningful issue in plant science.
With the development of science and technology, the emergence of gene microarray technology [4], [5] makes it possible for researchers to monitor gene expression levels on a genomic scale [6], [7]. This not only brings us more opportunities but also more challenges to study the gene expression data. Although the DNA microarray technology allows researchers to measure the expression levels of thousands (even more than 10,000) of genes in an experiment simultaneously, the gene expression data also have the problem: the characteristic genes which biologists are interested in occupy a very small part of the whole genes. It is difficult for us to catch the small but important part of the whole genes due to the complexity and multidimensionality of the gene expression data. Therefore, it becomes an urgent issue how to identify the characteristic genes from gene expression data in an effective way.
Among a variety of methods, feature selection is demonstrated to be a simple and effective method. To obtain the features of gene expression data, feature selection methods firstly calculate a score for each feature, then choose the features which gain high scores [8]. These methods can achieve a satisfactory performance and have a significant superiority on explaining the gene expression data more intuitive. But there exists a shortcoming that feature selection methods neglect the dependencies among features since they only calculate the score for each feature respectively. The appearance of feature extraction methods can overcome the shortcoming in an effective way [9]. As a tool to reduce the dimension, feature extraction methods take all the gene expression information simultaneously into consideration to extract the genes instead of feature selection methods. Until now, singular value decomposition (SVD) and principal component analysis (PCA) are commonly used methods of feature extraction. For example Kumar et al. applied SVD on Tuberculosis and Hypertension datasets to mine association in health care data [10]. Aradhya et al. used SVD for biclustering gene expression data [11]. PCA was used to cluster gene expression data by Yeung et al. [12]. PCA was used to select genes for microarray data analysis by Wang et al. [13]. Ma et al. applied PCA for identifying differential gene pathways [14].
Although SVD and PCA have already been used to analyze the gene expression data successfully, they still have some defects. For instance, SVD's left singular vectors and right singular vectors are always dense. In the same way, this drawback exists in the principal components (PCs) of PCA. Thus, it is difficult to explain these singular vectors and PCs objectively. Researchers have proposed a variety of mathematical methods to reduce the complexity of the data and make them more intelligible and interpretable. For example Liu et al. proposed robust PCA for discovering differentially expressed genes [15]. Wang et al. used non-negative matrix factorization (NMF) on cancer clustering [16]. Among these methods, sparse methods have distinct advantages and catch the attention of more and more people. Until now, a large number of sparse methods were proposed. For instance, Wang et al. raised robust sparse PCA (SPCA) by using weighted elastic net [17]. A sparse PCA via low-rank approximations was proposed by Papailiopoulos et al. [18]. Witten et al. proposed a penalized matrix decomposition [19], which was used for differential expression analysis [20], [21]. In addition, many sparse methods have already been chosen to deal with the gene expression data. Liu et al. used the first principal component (PC) of SPCA for extracting plants core genes [22]. Yin et al. identified differential gene pathways with SPCA [23]. Zheng et al. discovered molecular pattern [24] based on PMD.
The sparse methods mentioned above were proverbially applied on gene expression data analysis and have made many remarkable achievements. But these methods are usually unsupervised while the category label of each sample in gene expression data has been already known. That is, the class information is neglected by these sparse methods when processing gene expression data. For example PMD was used to extract plants core genes by Liu et al. [20]. However, the category labels of samples are quite important for gene identification that many excellent gene selection algorithms were achieved by using the class information. For instance Guyon et al. proposed the Support Vector Machine-Recursive Feature Elimination (SVM-RFE) method to select genes for cancer classification [25]. SVM-RFE is a classic gene selection algorithm that it eliminate genes one by one by using Recursive Feature Elimination (RFE) and achieve a very good performance. Many extensions on SVM-RFE algorithm were proposed by scholars. Tang et al. developed a new two-stage SVM-RFE algorithm to gene selection for microarray expression data analysis [26]. Ding et al. improved the computational performance of SVM-RFE by eliminating chunks of features at a time with little effect on the quality of reduced feature set [27]. Since SVM-RFE was designed to handle the binary feature selection problems, it is not suitable for multiclass feature selection problems. In order to solve this issue, Zhou et al. proposed a family of four extensions to SVM-RFE to solve these problems [28]. Duan et al. computed the feature ranking score from a statistical analysis of weight vectors of multiple linear SVMs trained on subsamples of the original training data at each step [29].
Therefore, we bring in the class information by the total scatter matrix and put forward a novel method to improve the performance of PMD-based gene extraction method for identifying plants core genes responding to abiotic stresses. We called it a Class-Information-based Penalized Matrix Decomposition (CIPMD). The scheme of CIPMD is as follows. Firstly, the total scatter matrix is obtained based on samples of the gene expression data. Secondly, we decompose the total scatter matrix by using SVD, and construct a new data matrix via multiplying the left singular vectors by the singular values. Thirdly, the new data matrix is decomposed to get the sparse eigensamples by PMD. Finally, the core genes are identified according to the nonzero entries in eigensamples.
Our main contributions of this paper are as follows. On one hand, it is the first time that it puts forward the CIPMD method via integrating the class information into penalized matrix decomposition. On the other hand, to identify plants core genes responding to abiotic stresses, it provides plenty of experiments on simulation and real gene expression data.
The remainder of the paper is organized as follows. Section 2 describes the methodology of CIPMD. Section 3 presents the numerical experiments and discusses the results. The conclusion is shown in Section 4.
Methodology
In this section, the class-information-based penalized matrix decomposition (CIPMD) method is introduced. Then, it is used to identify the core genes responding to the abiotic stresses.
2.1 The definition of CIPMD
In this subsection, we take the class information of samples into account and propose the CIPMD method to gain a better performance than PMD. At first, we bring in the class information via the total scatter matrix  . Then, a new data matrix is constructed by decomposing
. Then, a new data matrix is constructed by decomposing  . Finally, the new data matrix is decomposed by PMD. The following is our specific idea.
. Finally, the new data matrix is decomposed by PMD. The following is our specific idea.
2.1.1 The definition of scatter matrices
There exist many samples which contain different class labels in gene expression data. We take advantage of the class labels of samples via the total scatter matrix. For all the samples of all classes, we define three measures from the mathematical point of view. The first measure is named as a between-class scatter matrix (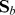 ) that is written as follows:
) that is written as follows:
| (1) |
where
 : the number of classes;
: the number of classes;
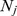 : the number of samples in class
: the number of samples in class 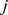 ;
;
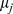 : the average value of class
: the average value of class 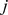 ;
;
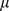 : the average value of all classes.
: the average value of all classes.
The second measure is named as a within-class scatter matrix (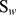 ) that is defined by
) that is defined by
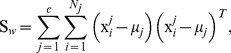 |
(2) |
where 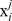 represents the
represents the  -th sample of class
-th sample of class 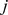 .
.
The third measure is named as the total scatter matrix (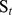 ) which is defined based on
) which is defined based on 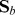 and
and 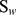 . In order to minimize the within-class distance and maximize the between-class distance, the formula of
. In order to minimize the within-class distance and maximize the between-class distance, the formula of 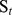 is given as follows:
is given as follows:
| (3) |
where 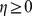 represents an adjustable parameter and gives a compromise between
represents an adjustable parameter and gives a compromise between 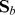 and
and 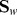 .
.
The between-class and the within-class distances can be calculated by the trace of corresponding scatter matrices. In detail, the formulas are as follows:
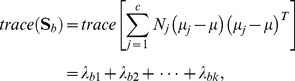 |
(4) |
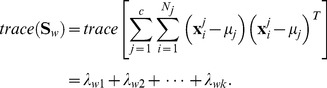 |
(5) |
In the two formulas above, the separation of the samples between classes can be measured by the 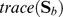 while the closeness of the samples within classes can be measured by the
while the closeness of the samples within classes can be measured by the 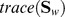 . The parameter
. The parameter 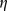 in eq. (3) is defined by [30]
in eq. (3) is defined by [30]
| (6) |
2.1.2 Constructing the new data matrix 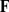
Due to the total scatter matrix 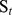 should be processed by PMD in a convenient way, so
should be processed by PMD in a convenient way, so 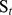 is preprocessed by matrix decomposition methods.
is preprocessed by matrix decomposition methods.
Firstly, the total scatter matrix 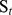 is decomposed by SVD, which can be written as follows:
is decomposed by SVD, which can be written as follows:
| (7) |
where 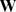 and
and 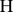 are orthogonal matrices,
are orthogonal matrices, 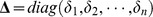 is the diagonal matrix which contains singular values,
is the diagonal matrix which contains singular values,  is the rank of the total scatter matrix
is the rank of the total scatter matrix 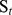 .
.
Secondly, a new data matrix 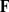 is constructed by
is constructed by
| (8) |
where  is the power of
is the power of 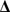 . The suitable value of
. The suitable value of  can be determined in Subsection 3.1.2 by using the simulation data.
can be determined in Subsection 3.1.2 by using the simulation data.
Finally, the new data matrix 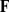 is decomposed by PMD.
is decomposed by PMD.
In this way, the total scatter matrix 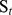 which contains large amounts of complex data is converted to the new data matrix
which contains large amounts of complex data is converted to the new data matrix 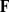 which is simple and easy to be processed.
which is simple and easy to be processed.
2.1.3 Penalized matrix decomposition (PMD)
In this subsection, we briefly introduce the PMD method proposed by Witten et al. [19]. Gene expression data always consist of 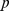 genes in
genes in  samples, in general,
samples, in general, 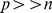 . According to subsection 2.1.1 and subsection 2.1.2, the new data matrix
. According to subsection 2.1.1 and subsection 2.1.2, the new data matrix 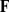 is obtained by calculating the original gene expression data. Therefore, we denote the gene expression data by the matrix
is obtained by calculating the original gene expression data. Therefore, we denote the gene expression data by the matrix 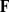 with size
with size 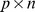 . Without loss of generality, we let the row mean of
. Without loss of generality, we let the row mean of 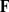 be zero. The matrix
be zero. The matrix 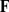 can be decomposed by SVD as follows:
can be decomposed by SVD as follows:
| (9) |
where 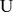 is a
is a 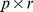 orthogonal matrix,
orthogonal matrix, 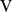 is an
is an 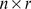 orthogonal matrix and
orthogonal matrix and 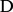 is a diagonal matrix. PMD can generalize this decomposition by imposing constraints on
is a diagonal matrix. PMD can generalize this decomposition by imposing constraints on 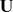 and/or
and/or 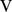 . PMD can be represented as the following optimization problem:
. PMD can be represented as the following optimization problem:
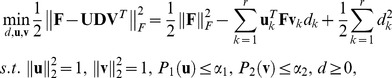 |
(10) |
where
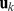 : the column
: the column 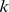 of
of 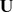 ;
;
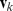 : the column
: the column 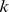 of
of 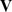 ;
;
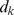 : the
: the 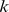 -th diagonal element of
-th diagonal element of 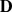 ;
;
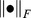 : the Frobenius norm;
: the Frobenius norm;
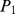 and
and 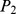 : convex penalty functions that can adopt a various of forms [19].
: convex penalty functions that can adopt a various of forms [19].
When 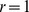 ,
,  and
and  satisfying eq.(10) can also satisfy the optimization problem as follows [19]:
satisfying eq.(10) can also satisfy the optimization problem as follows [19]:
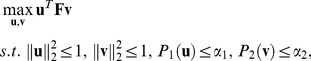 |
(11) |
and the 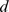 satisfying eq.(10) is
satisfying eq.(10) is 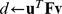 . The objection function
. The objection function  in eq.(11) is bilinear on
in eq.(11) is bilinear on  and
and  , that is to say, when
, that is to say, when  fixed, it is linear in
fixed, it is linear in  , and vice versa. By choosing the appropriate
, and vice versa. By choosing the appropriate 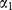 and
and 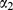 , the solution to eq.(11) which is named as rank-one PMD satisfies eq.(10) [19].
, the solution to eq.(11) which is named as rank-one PMD satisfies eq.(10) [19].
The iterative algorithm for rank-one PMD is summarized as follows:
Step1. Initialize  to have unit
to have unit 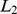 -norm.
-norm.
Step2. Iterate until convergence:
(a) 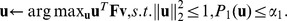
(b) 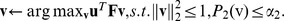
Step3. 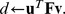
In order to obtain the rank- PMD, each time we use the residuals obtained by subtracting
PMD, each time we use the residuals obtained by subtracting 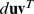 from
from 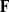 to maximize the eq.(11) repeatedly, i.e.,
to maximize the eq.(11) repeatedly, i.e., 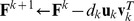 . The specific algorithm of rank-
. The specific algorithm of rank- PMD can be found in [19]. In this research, we only impose the penalty on
PMD can be found in [19]. In this research, we only impose the penalty on  , i.e.
, i.e. 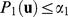 , and do not consider
, and do not consider  since core genes are identified according to
since core genes are identified according to  . PMD can produce sparse vectors
. PMD can produce sparse vectors  by choosing a suitable parameters
by choosing a suitable parameters 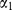 .
.
2.2 Identifying core genes by CIPMD
The gene expression data are stocked as the matrix 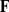 with size
with size 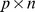 , in which each row of
, in which each row of 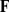 represents the transcriptional responses of a gene in all
represents the transcriptional responses of a gene in all  samples and each column of
samples and each column of 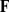 represents the expression level of a sample in all
represents the expression level of a sample in all 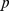 genes.
genes.
According to subsection 2.1.3, the matrix 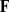 is decomposed into three matrices
is decomposed into three matrices 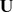 ,
, 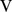 and
and 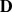 by PMD. The graphical depiction of CIPMD is shown in Figure 1. Following the convention in [31], we define
by PMD. The graphical depiction of CIPMD is shown in Figure 1. Following the convention in [31], we define 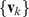 (columns of
(columns of 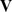 ) as eigenpatterns,
) as eigenpatterns, 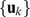 (columns of
(columns of 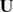 ) as eigensamples and
) as eigensamples and 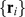 (rows of
(rows of 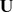 ) as eigengenes. As Figure 1 shows, the space of sample expression profiles
) as eigengenes. As Figure 1 shows, the space of sample expression profiles 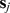 (a column of
(a column of 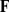 ) is spanned by
) is spanned by 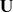 and the space of gene transcriptional responses
and the space of gene transcriptional responses 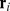 (a row of
(a row of 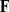 ) is spanned by
) is spanned by 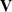 .
.
Figure 1. The graphical depiction of CIPMD.
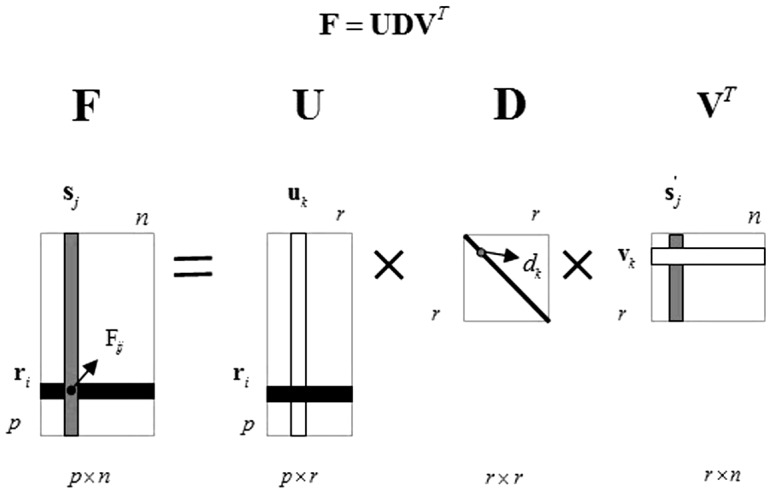
In this figure, the matrix 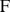 is decomposed into two bases matrices
is decomposed into two bases matrices 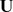 ,
, 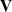 and a diagonal matrix
and a diagonal matrix 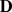 .
.
Our goal is to identify the core genes from the gene expression data. Generally speaking, due to the complexity of 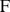 , it is difficult to identify the core genes from
, it is difficult to identify the core genes from 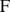 directly. So we must take measures to reduce the dimensionality of the gene expression data. As mentioned above, the space of sample expression profiles
directly. So we must take measures to reduce the dimensionality of the gene expression data. As mentioned above, the space of sample expression profiles 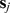 is spanned by
is spanned by 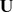 and
and 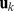 is a column of
is a column of 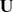 , so we can select a subset of
, so we can select a subset of 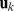 to represent
to represent 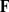 . Then the eigengenes are identified from the eigensamples which have the features of gene expression data. These eigengenes are regarded as core genes responding to the abiotic stresses. The detail of how to identify the core genes from the sample expression profiles is shown in the following.
. Then the eigengenes are identified from the eigensamples which have the features of gene expression data. These eigengenes are regarded as core genes responding to the abiotic stresses. The detail of how to identify the core genes from the sample expression profiles is shown in the following.
Firstly, the number of variables used to denote the sample expression profiles can be reduced by CIPMD. According to eq.(9), 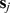 can be formulated as
can be formulated as 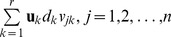 , where
, where 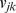 is the
is the 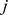 -th element in
-th element in 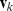 . It shows that
. It shows that 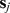 is a linear combination of
is a linear combination of 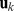 . In Figure 1,
. In Figure 1, 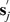 is the
is the 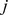 -th column of
-th column of 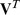 , which includes the positional information of the
, which includes the positional information of the 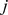 -th sample. By using
-th sample. By using 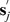 , the expression profiles of samples can be acquired by
, the expression profiles of samples can be acquired by  variables. However, the number of variables in sample expression profiles
variables. However, the number of variables in sample expression profiles 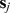 is
is 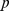 which is much larger than
which is much larger than  . Therefore, the number of variables used to denote the sample expression profiles can generally be reduced by CIPMD.
. Therefore, the number of variables used to denote the sample expression profiles can generally be reduced by CIPMD.
Secondly, since the eigensamples 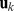 are used to reconstruct
are used to reconstruct 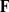 , the sample expression profiles
, the sample expression profiles 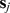 which contain the important information can be represented by the eigensamples
which contain the important information can be represented by the eigensamples 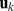 .
.
Thirdly, the sparse 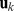 can be obtained by choosing the penalty function appropriately. According to the subsection 2.1.3, we can take penalty function
can be obtained by choosing the penalty function appropriately. According to the subsection 2.1.3, we can take penalty function 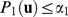 . By choosing a suitable parameters
. By choosing a suitable parameters 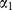 , the sparse
, the sparse 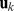 can be obtained.
can be obtained.
Finally, the core genes responding to abiotic stresses are identified via the sparse 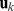 . The features of samples in gene expression data can be represented by the nonzero entries in the sparse
. The features of samples in gene expression data can be represented by the nonzero entries in the sparse 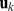 . Therefore, the nonzero entries can be denoted as the core genes responding to abiotic stresses.
. Therefore, the nonzero entries can be denoted as the core genes responding to abiotic stresses.
The whole scheme to identify the core genes can be summarized in the following:
Firstly, the total scatter matrix 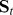 is obtained bases on the gene expression data
is obtained bases on the gene expression data  .
.
Secondly, 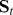 is decomposed into left singular vectors
is decomposed into left singular vectors 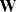 , right singular vectors
, right singular vectors  and a diagonal matrix
and a diagonal matrix 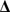 by using SVD, and a new data matrix
by using SVD, and a new data matrix 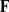 is constructed by multiplying
is constructed by multiplying 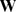 by
by 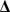 .
.
Thirdly, PMD decomposes the data matrix 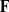 to obtain the sparse eigensamples
to obtain the sparse eigensamples 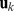 .
.
Fourthly, the genes corresponding to nonzero entries in 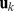 are identified as the core ones.
are identified as the core ones.
Finally, the core genes are checked by using Gene Ontology (GO) tool.
Results and Discussion
In this section, we evaluate the CIPMD method by applying it to identify the core genes responding to abiotic stresses. Subsection 3.1 and 3.2 provide the results on simulation and real gene expression data sets, respectively. For comparison, the sparse principal component analysis (SPCA) [32], penalized matrix decomposition (PMD) [19] and support vector machine-recursive feature elimination (SVM-RFE) [25] methods are used to identify the features on simulation and real gene expression data sets. The LIBSVM that Chang et al. proposed [33] is used to implement SVM-RFE algorithm.
3.1 Results on simulation data
In this subsection, the simulation data are firstly introduced. Then, the parameters of SPCA, PMD and CIPMD are chosen appropriately. Since SVM-RFE method eliminate genes one by one by using Recursive Feature Elimination (RFE) and have no control-sparsity parameters, so we do not consider it in this subsection. Finally, the results on simulation data are shown.
3.1.1 Data source
The simulation data are generated with 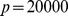 genes (roughly equal to the number of genes in real gene expression data) and
genes (roughly equal to the number of genes in real gene expression data) and 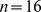 samples. In the two-class case, we assign 8 samples and
samples. In the two-class case, we assign 8 samples and 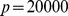 genes for each class. In the multi-class case, the 16 samples are divided equally into 4 classes.
genes for each class. In the multi-class case, the 16 samples are divided equally into 4 classes.
The simulation data are in 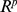 with
with 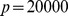 and generated as
and generated as 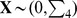 . Let
. Let 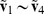 be four 20000-dimensional vectors, such that
be four 20000-dimensional vectors, such that 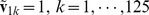 , and
, and 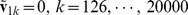 ;
; 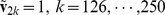 , and
, and 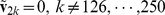 ;
; 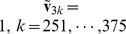 , and
, and 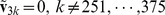 ;
; 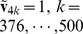 , and
, and 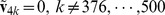 . Let
. Let 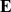 be a 20000-dimensional noise matrix, and
be a 20000-dimensional noise matrix, and 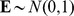 . Then we add
. Then we add 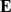 into
into 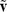 with different Signal-to-Noise Ratios (SNR). The preceding four eigenvectors of
with different Signal-to-Noise Ratios (SNR). The preceding four eigenvectors of 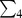 are normalized to be
are normalized to be 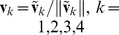 . And in order to make the first four eigenvectors dominate, we let the eigenvalues be
. And in order to make the first four eigenvectors dominate, we let the eigenvalues be 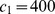 ,
, 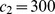 ,
, 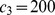 ,
, 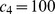 and
and 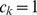 for
for  . In this way, the simulation idea in [34] is applied to generate the simulation data.
. In this way, the simulation idea in [34] is applied to generate the simulation data.
3.1.2 Parameters selection
In this subsection, the parameter  in eq.(8) is determined by the simulation experiment. Then the control-sparsity parameters of the three methods are selected appropriately.
in eq.(8) is determined by the simulation experiment. Then the control-sparsity parameters of the three methods are selected appropriately.
The determination of parameter
 : For CIPMD, we need to determine the appropriate parameter
: For CIPMD, we need to determine the appropriate parameter  in eq.(8) to make our method optimal. We randomly generate the simulation data by iterating 100 times to test the performance of CIPMD with different values of
in eq.(8) to make our method optimal. We randomly generate the simulation data by iterating 100 times to test the performance of CIPMD with different values of  . Figure 2 displays the performance of CIPMD with
. Figure 2 displays the performance of CIPMD with  varying from 0.5 to 5. From this figure it can be seen that all the values of
varying from 0.5 to 5. From this figure it can be seen that all the values of  can get very high identification accuracies. The best result is achieved when
can get very high identification accuracies. The best result is achieved when 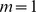 , so we take
, so we take 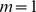 for CIPMD in the following experiments.
for CIPMD in the following experiments.The selection of control-sparsity parameters: Except for SVM-RFE, all the other three methods are sparse, whose control-sparsity parameters have a great influence on identification accuracy. The SPCA proposed by Journee et al. has an excellent performance both in computational speed and quality [32]. The parameter
 in SPCA is used to adjust the sparsity of PCs. According to the algorithm of CIPMD, the
in SPCA is used to adjust the sparsity of PCs. According to the algorithm of CIPMD, the 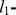 norm of
norm of  is taken as the penalty function, i.e.
is taken as the penalty function, i.e. 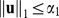 . Since
. Since 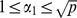 , let
, let 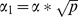 , where
, where 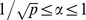 . So we can obtain a sparse
. So we can obtain a sparse  by choosing an appropriate
by choosing an appropriate 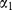 . For simplicity, only one factor is used, that is, let
. For simplicity, only one factor is used, that is, let 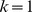 .
.
Figure 2. Accuracies of the CIPMD on simulation data set with different values of  .
.
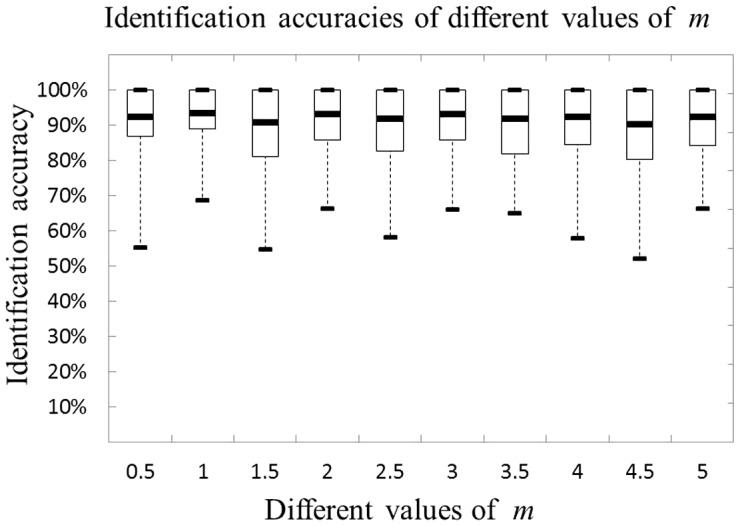
For fair comparison, 500 genes are identified by using these methods with their own appropriate parameters. And the Signal-to-Noise Ratio (SNR) is set to be 0.1 when the simulation data are generated.
3.1.3 Simulation results
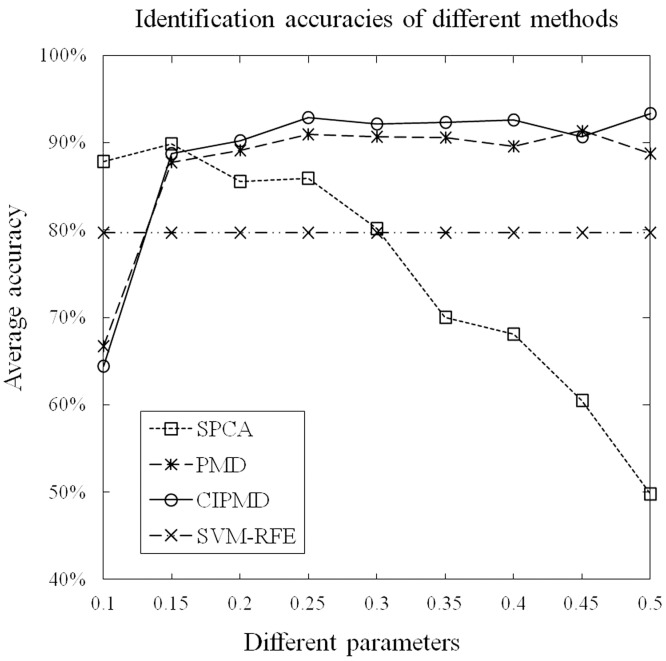
We randomly generate the simulation data by iterating 100 times to evaluate the performances of the four methods. The specific numerical values of identification accuracies of the four methods with different parameters are shown in supplementary file (Table S1). For the two-class case, the graphical depiction of the identification accuracies of these methods with different parameters is shown in Figure 3. From this figure, it can be seen that except for SVM-RFE, all the other three methods are sensitive to the control-sparsity parameters. The identification accuracies of SPCA are monotonically decreasing with the control-sparsity parameter when its value is greater than 0.15. On the contrary, the identification accuracies of PMD and CIPMD are monotonically increasing with the parameters when their values are smaller than 0.25. The identification accuracies of PMD and CIPMD are stabilized when the parameters are greater than 0.25. Moreover, all the four methods can obtain very high identification accuracies. Finally, our CIPMD has the highest accuracies among the four methods.
Figure 3. Accuracies of the four methods on simulation data with different paramaters in the case of two-class.
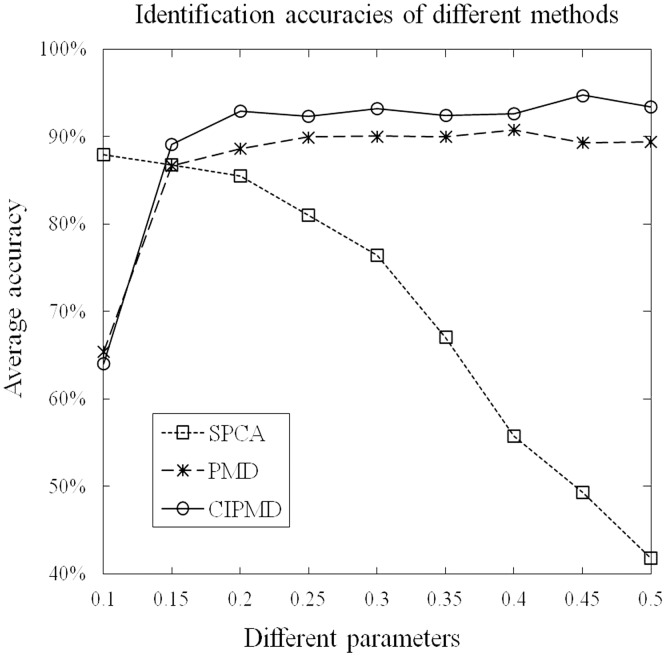
For the multi-class case, the graphical depiction of the identification accuracies of these methods with different parameters is shown in Figure 4. Since SVM-RFE was designed to deal with the binary gene selection problem, accordingly, it is not included in this part. From this figure, we can see that the identification accuracies of all the three methods can reach higher values. Similar to the two-class case, the identification accuracies of SPCA are monotonically decreasing with the increasing of control-sparsity parameter. When the parameters are greater than 0.2, the identification accuracies of CIPMD can reach the highest point and becomes stable. While the parameters are greater than 0.25, PMD reaches a plateau in terms of identification accuracy. Among the three methods, only the identification accuracies of CIPMD can reach more than 90%. Furthermore, except for the parameter is 0.1, CIPMD outperforms the other methods on identification accuracies with all parameters.
Figure 4. Accuracies of these methods on simulation data with different paramaters in the case of multi-class.
3.2 Results on gene expression data
The real gene expression data are introduced in subsection 3.2.1. Then, the gene ontology (GO) analysis is adopted to evaluate the performances of the four methods.
3.2.1 Data source
The raw gene expression data include two classes: shoots and roots in each stress. The Affymetix CEL files are downloaded from NASCArrays [http://affy.arabidopsis.info/] [35], reference numbers are: control, NASCArrays-137; cold stress, NASCArrays-138; osmotic stress, NASCArrays-139; salt stress, NASCArrays-140; drought stress, NASCArrays-141; UV-B light stress, NASCArrays-144; and heat stress, NASCArrays-146. The number of samples in each stress type is listed in Table 1. There are 22810 genes in each sample. The arrays are adjusted by using the GC-RMA software by Wu et al. [36] to avoid the background of optional noise and normalized by using quantile normalization. The GC-RMA results are gathered in a matrix to be processed by SPCA, PMD, SVM-RFE and CIPMD.
Table 1. The number of each stress types in the raw data.
| Stress Type | control | cold | drought | heat | osmotic | salt | UV-B |
| Number | 8 | 6 | 7 | 8 | 6 | 6 | 7 |
Our method brings in the class information of samples based on the total scatter matrix. Therefore, in our experiments, two stress types of gene expression data are processed simultaneously.
3.2.2 Gene Ontology (GO) analysis
Gene Ontology (GO) Term Enrichment tools can be used to describe genes in the input or query set and to help discover what functions the genes may have in common [37]. As a web-based tool, GOTermFinder can find the significant GO terms among a list of genes. Therefore, it offers some significant informations for the biological explanation of high-throughput experiments. The core genes responding to abiotic stresses identified by SPCA, PMD, SVM-RFE and CIPMD are checked by GOTermFinder which is publicly available at http://go.princeton.edu/cgi-bin/GOTermFinder [38]. Its threshold parameters are set as following: maximum P-value = 0.01 and minimum number of gene products = 2. Here, only the main results of GO Term Enrichment are shown.
Terms responding to stimulus: The numbers of genes responding to stimulus (GO:0050896), which is the ancestor of all the abiotic stresses, are identified by the four methods in shoot and root samples are listed in Table 2 and Table 3, respectively. The superior results are marked in bold type. From the two tables we can see that all these methods can identify genes with very high sample frequency and very low P-value.
Table 2. Response to stimulus (GO:0050896) in shoot samples.
| Stress Type | SPCA | PMD | CIPMD | SVM-RFE | ||||
| SF | PV | SF | PV | SF | PV | SF | PV | |
| Cold | 283 56.8% | 1.33E-62 | 294 58.9% | 3.89E-70 | 329 65.9% | 7.52E-98 | 259 51.9% | 8.6E-47 |
| Drought | 273 54.8% | 7.04E-56 | 303 60.7% | 8.84E-77 | 338 67.7% | 9.08E-106 | 251 50.3% | 4.07E-42 |
| Heat | 267 53.6% | 5.00E-52 | 220 44.0% | 5.84E-26 | 330 66.0% | 2.39E-98 | 271 54.3% | 2.93E-54 |
| Osmotic | 264 52.9% | 6.24E-50 | 296 59.2% | 2.70E-71 | 322 64.5% | 6.15E-92 | 243 48.6% | 1.84E-37 |
| Salt | 264 52.8% | 1.06E-49 | 258 51.8% | 1.68E-46 | 309 61.9% | 2.00E-81 | 256 51.2% | 8.25E-45 |
| UV-B | 334 67.1% | 1.36E-102 | 361 72.3% | 1.8E-127 | 335 67.3% | 1.81E-103 | 243 48.6% | 1.92E-37 |
In this table, the response to stimulus on core genes are shown, whose background frequency in TAIR is 6619/30324 (21.8%), where 6619/30324 represents having 6619 genes response to stimulus in whole 30324 genes. SF and PV represent the sample frequency and P-value, respectively. The sample frequency, e.g. 283, represents the method identifies 500 genes, in which there are 283 genes responding to stimulus.
Table 3. Response to stimulus (GO:0050896) in root samples.
| Stress Type | SPCA | PMD | CIPMD | SVM-RFE | ||||
| SF | PV | SF | PV | SF | PV | SF | PV | |
| Cold | 282 56.6% | 6.57E-62 | 291 58.2% | 1.07E-67 | 337 67.5% | 6.92E-105 | 267 53.7% | 3.49E-52 |
| Drought | 289 57.8% | 2.91E-66 | 287 57.4% | 7.60E-65 | 333 66.6% | 5.54E-101 | 273 54.8% | 8.59E-56 |
| Heat | 199 39.9% | 3.46E-17 | 205 41.1% | 1.34E-19 | 337 67.5% | 7.27E-105 | 283 56.6% | 5.63E-62 |
| Osmotic | 238 47.6% | 7.62E-35 | 223 44.6% | 2.03E-27 | 302 60.6% | 2.54E-76 | 276 55.2% | 2.86E-57 |
| Salt | 238 47.6% | 7.31E-35 | 313 62.6% | 2.75E-84 | 295 59.0% | 1.31E-70 | 264 52.9% | 7.69E-50 |
| UV-B | 211 42.2% | 5.55E-22 | 243 48.6% | 1.53E-37 | 326 65.2% | 6.85E-95 | 268 53.7% | 2.37E-52 |
As Table 2 listed, in shoot samples, only in UV-B light stress data set, CIPMD method is dominated by PMD. For other stresses data sets, CIPMD outperforms the SPCA, PMD and SVM-RFE. As Table 3 listed, in root samples, CIPMD performs better than the other three methods in all the stresses data sets except the salt stress. In salt stress data set, PMD method is superior to our method.
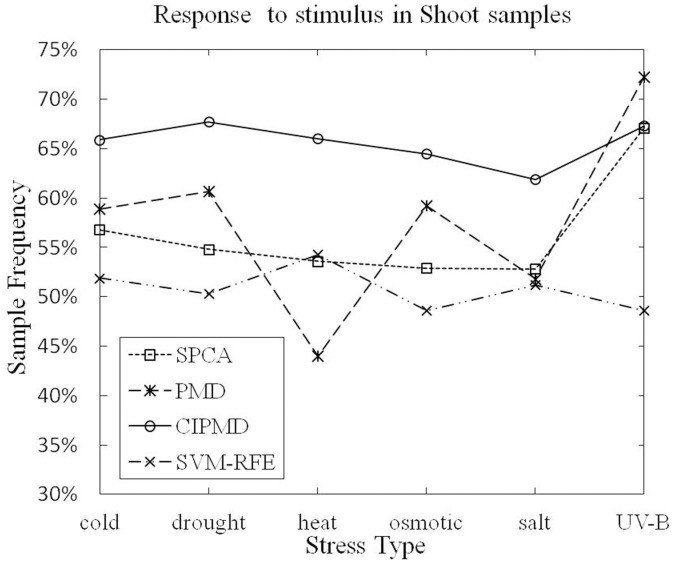
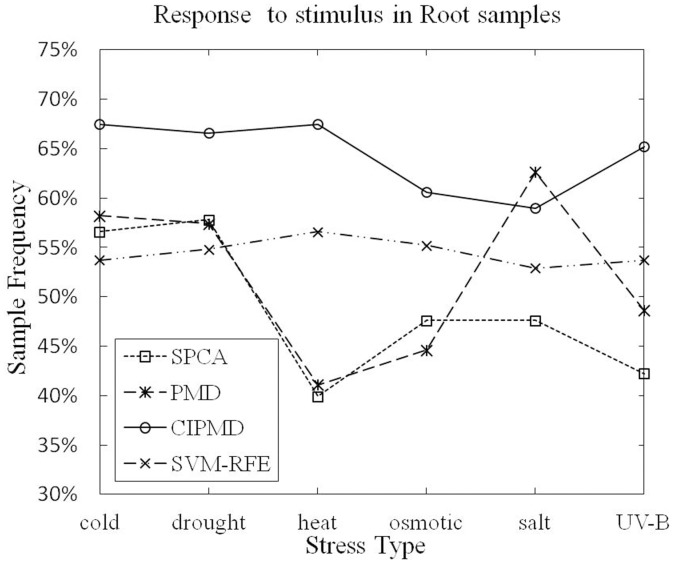
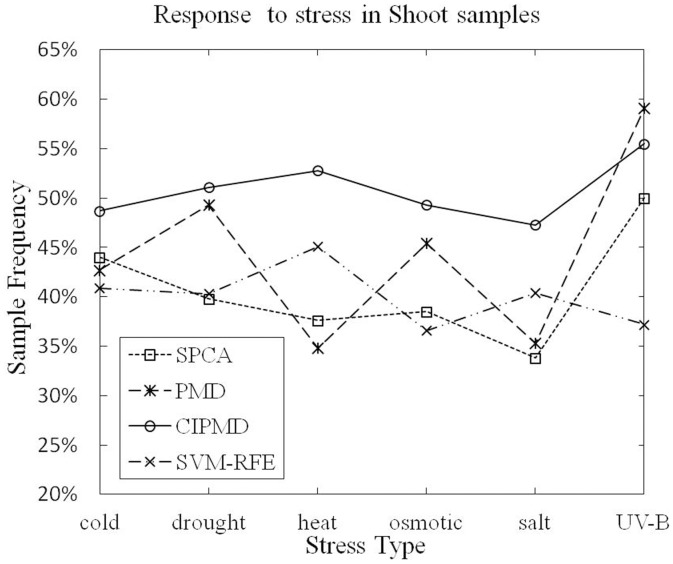
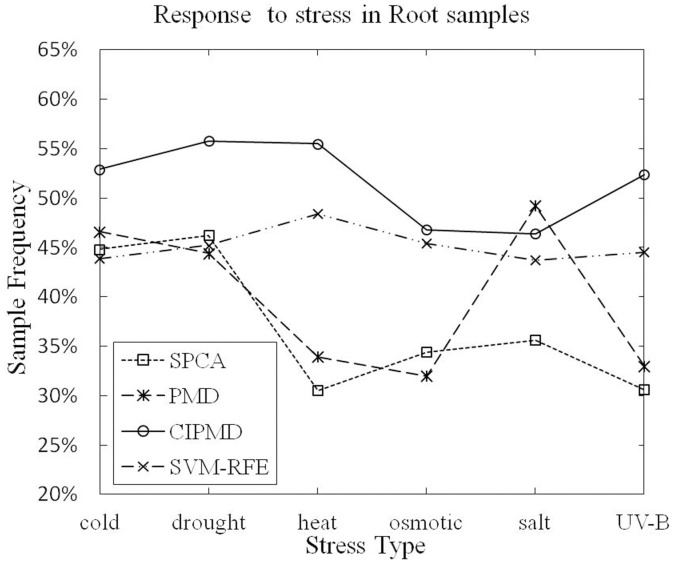
The sample frequencies of the six different stresses response to stimulus in shoot and root samples are shown in Figure 4 and Figure 5, respectively.
Figure 5. Response to stimulus (GO:0050896) in shoot samples.
From Figure 5, it can be seen that PMD has a higher data point on UV-B light stress data set than SPCA, SVM-RFE and CIPMD. However, CIPMD method is superior to PMD, SPCA and SVM-RFE in the remaining five stresses data sets of shoot samples. Figure 6 shows that only in salt stress data set, CIPMD has a lower data point than PMD. CIPMD method outperforms the other three methods in a large degree (especially in heat stress data set) in other five stresses data sets of root samples. From the two figures we can also find that SVM-RFE and CIPMD give more stable results in six different stresses data sets than PMD and SPCA methods whose results fluctuate up and down in greatly amplitudes.
Figure 6. Response to stimulus (GO:0050896) in root samples.
PMD outperforms the proposed method in some case of the experiment, e.g. the UV-B light stress data set in shoot samples and the salt stress data set in root samples, the most likely reason is that the different distributions of data lead to the different performances between methods. This problem also exists in elsewhere, for example Zheng et al. proposed a gene selection method based on Robust Principal Component Analysis (RPCA) to select plants characteristic genes, in their experiments, the number of genes responding to abiotic stimulus (GO:0009628) is selected by three methods in root samples, the performance of RPCA is equal to PMD only in UV-B stress data set, in other data sets, RPCA method is superior to the others [39].
Terms responding to stress: Table 4 and Table 5 list the gene numbers and P-value of response to stress (GO:0006950) in shoot and root samples, respectively. The superior results are marked in bold type.
Table 4. Response to stress (GO:0006950) in shoot samples.
| Stress Type | SPCA | PMD | CIPMD | SVM-RFE | ||||
| SF | PV | SF | PV | SF | PV | SF | PV | |
| Cold | 219 44.0% | 1.47E-61 | 213 42.7% | 4.44E-57 | 243 48.7% | 6.84E-80 | 204 40.9% | 1.07E-50 |
| Drought | 198 39.8% | 5.05E-47 | 246 49.3% | 2.47E-82 | 255 51.1% | 5.89E-90 | 201 40.3% | 1.02E-48 |
| Heat | 187 37.6% | 4.49E-40 | 174 34.8% | 3.51E-32 | 264 52.8% | 1.51E-97 | 225 45.1% | 1.21E-65 |
| Osmotic | 192 38.5% | 4.96E-43 | 227 45.4% | 4.12E-67 | 246 49.3% | 2.30E-82 | 183 36.6% | 2.88E-37 |
| Salt | 169 33.8% | 1.85E-29 | 176 35.3% | 1.34E-33 | 236 47.3% | 2.90E-74 | 202 40.4% | 3.32E-49 |
| UV-B | 249 50.0% | 4.18E-85 | 295 59.1% | 3.3E-127 | 277 55.5% | 1.06E-109 | 186 37.2% | 4.81E-39 |
In this table, the response to stress on core genes are shown, whose background frequency in TAIR is 4028/30324 (13.3%), where 4028/30324 represents having 4028 genes to response to stress in whole 30324.
Table 5. Response to stress (GO:0006950) in root samples.
| Stress Type | SPCA | PMD | CIPMD | SVM-RFE | ||||
| SF | PV | SF | PV | SF | PV | SF | PV | |
| Cold | 223 44.8% | 1.66E-64 | 233 46.6% | 9.92E-72 | 264 52.9% | 7.64E-98 | 218 43.9% | 7.14E-61 |
| Drought | 231 46.2% | 3.60E-70 | 222 44.4% | 2.27E-63 | 279 55.8% | 2.50E-111 | 225 45.2% | 7.69E-66 |
| Heat | 152 30.5% | 5.73E-21 | 169 33.9% | 1.39E-29 | 277 55.5% | 1.03E-109 | 242 48.4% | 1.11E-78 |
| Osmotic | 172 34.4% | 4.39E-31 | 160 32.0% | 8.07E-25 | 234 46.8% | 1.78E-72 | 227 45.4% | 6.15E-67 |
| Salt | 178 35.6% | 1.79E-34 | 246 49.2% | 3.88E-82 | 232 46.4% | 5.58E-71 | 218 43.7% | 1.76E-60 |
| UV-B | 153 30.6% | 2.26E-21 | 165 33.0% | 2.34E-27 | 262 52.4% | 9.89E-96 | 222 44.5% | 2.04E-63 |
As Table 4 listed, in shoot samples, CIPMD is superior to the other three methods in all the data sets except UV-B light stress. PMD suppresses our method only in the UV-B light stress data set. As Table 5 listed, in root samples, CIPMD is dominated by PMD only in salt-stress data set. CIPMD outperforms our competitive methods in other five stresses data sets.
The sample frequencies of response to stress in shoot and root samples are shown in Figure 7 and Figure 8, respectively.
Figure 7. Response to stress (GO:0006950) in shoot samples.
Figure 8. Response to stress (GO:0006950) in root samples.
Figure 7 shows that CIPMD method owns a lower data point in UV-B light stress data set than PMD. But in the rest five stresses data sets of shoot samples, our CIPMD is superior to the other methods. From Figure 8, it can be proved that PMD has a data point performing better than CIPMD only in salt stress data set. CIPMD method surpasses PMD and SPCA in a large extent (especially in heat stress data set) in other data sets of root samples. CIPMD outperforms SVM-RFE in all the data sets with six different stresses. Besides, both in shoot and root samples, CIPMD and SVM-RFE present more stable results than PMD and SPCA in six different stresses data sets.
Core genes responding to the stresses: The data of the drought stress in root samples and heat stress in shoot samples are analyzed to evaluate the core genes identified by our method closely related to the stresses.
For drought stress in root samples, Table 6 gives the sample frequency and P-value of response to water deprivation (GO: 0009415). The background sample frequency of response to water deprivation (GO: 0009415) in root samples is 1.4% (421/30324). As Table 6 listed, the superior results of the three methods are shown in bold type. Obviously, CIPMD can identify more genes than the other three methods.
Table 6. The numbers of response to water deprivation (GO:0009415) in root samples.
| Stress Type | SPCA | PMD | CIPMD | SVM-RFE | ||||
| SF | PV | SF | PV | SF | PV | SF | PV | |
| Drought | 44 8.8% | 1.73E-19 | 51 10.2% | 6.21E-26 | 69 13.8% | 7.8E-45 | 45 9.0% | 2.53E-20 |
Moreover, we compare the genes identified by CIPMD with the ones identified by PMD, SPCA and SVM-RFE to verify the core genes extracted by our method closely related to abiotic stresses. Table 7 lists different genes identified by CIPMD and ignored by other three methods in the first column. The column of Response to represents what stresses the genes response to, and the column of Reference denotes the searching results that the authors have already confirmed in their literatures. As Table 7 listed, all the 27 genes selected by CIPMD and neglected by PMD, SPCA and SVM-RFE can be searched in literatures. And all these core genes are indeed closely related to drought stress. Furthermore, some of the genes are also related to cold, osmotic and salt stresses.
Table 7. References about core genes responding to water deprivation in root samples.
| Gene name | Response to | References |
| At2g33380 | Drought, cold | Heyndrickx et al. (2012) [40] |
| At4g34390 | Drought | Heyndrickx et al. (2012) [40] |
| At5g62470 | Drought | Seo et al. (2009) [41] |
| At3g14050 | Drought | Heyndrickx et al. (2012) [40] |
| At3g11820 | Drought, cold | Heyndrickx et al. (2012) [40] |
| At3g19970 | Drought | Heyndrickx et al. (2012) [40] |
| At5g54490 | Drought | Heyndrickx et al. (2012) [40] |
| At5g27420 | Drought | Heyndrickx et al. (2012) [40] |
| At4g24960 | Drought, cold | Chen et al. (2002) [42] |
| At2g30550 | Drought | Heyndrickx et al. (2012) [40] |
| At3g30775 | Drought | Sharma et al. (2011) [43] |
| At3g63060 | Drought, salt, osmotic | Koops et al. (2011) [44] |
| At3g09940 | Drought | Vadassery et al. (2009) [45] |
| At4g21440 | Drought | Heyndrickx et al. (2012) [40] |
| At1g73480 | Drought, cold | Heyndrickx et al. (2012) [40] |
| At5g67340 | Drought, cold | Heyndrickx et al. (2012) [40] |
| At4g17500 | Drought | Heyndrickx et al. (2012) [40] |
| At2g17840 | Drought, cold | Kiyosue et al. (1994) [46] |
| At3g52400 | Drought, cold | Fujita et al. (2004) [47] |
| At4g05100 | Drought | Heyndrickx et al. (2012) [40] |
| At5g24590 | Drought | Heyndrickx et al. (2012) [40] |
| At5g67300 | Drought | Huang et al. (2008) [48] |
| At5g40390 | Drought | Maruyama et al. (2009) [49] |
| At3g19580 | Drought | Sakamoto et al. (2000) [50] |
| At5g45340 | Drought | Umezawa et al. (2006) [51] |
| At1g22190 | Drought, cold, osmotic | Rea et al. (2011) [52] |
| At3g57530 | Drought, cold | Heyndrickx et al. (2012) [40] |
For heat stress in shoot samples, Table 8 lists the sample frequency and P-value of response to heat (GO: 0009480). The background sample frequency of response to heat (GO: 0009480) in shoot samples is 1.0% (298/30324). In Table 8, the superior results of the four methods are marked in bold type. Wherein SVM-RFE cannot identify effective genes response to heat. It can be seen clearly that CIPMD method can identify more genes than the other methods.
Table 8. The numbers of response to heat (GO:0009408) in shoot samples.
| Stress Type | SPCA | PMD | CIPMD | SVM-RFE | ||||
| SF | PV | SF | PV | SF | PV | SF | PV | |
| Heat | 41 8.2% | 1.13E-22 | 77 15.4% | 2.37E-66 | 97 19.4% | 9.47E-96 | None | None |
In detail, we compare the genes identified by CIPMD with the ones identified by using PMD, SPCA and SVM-RFE. There are 20 different core genes identified by our method and neglected by PMD, SPCA and SVM-RFE. Among these 20 genes, 14 genes responding to heat have been confirmed in literatures. We show the verified results of the 14 genes in Table 9. The remaining genes of the 20 genes are involved in heat acclimation (GO: 0010286) which is the children of response to heat (GO: 0009408). The affirmed results in literatures of the 6 genes are listed in Table 10. From the verifications, it is obvious that all the 20 genes identified by CIPMD and ignored by PMD, SPCA and SVM-RFE are closely related with heat stress.
Table 9. References about core genes responding to heat in shoot samples.
| Gene name | Response to | References |
| At2g43630 | Heat | Heyndrickx et al. (2012) [40] |
| At1g14360 | Heat | Heyndrickx et al. (2012) [40] |
| At5g28540 | Heat | Koizumi et al. (1996) [53] |
| At2g20940 | Heat | Heyndrickx et al. (2012) [40] |
| At4g29520 | Heat | Heyndrickx et al. (2012) [40] |
| At4g29330 | Heat | Heyndrickx et al. (2012) [40] |
| At5g22060 | Heat | Heyndrickx et al. (2012) [40] |
| At1g04980 | Heat | Heyndrickx et al. (2012) [40] |
| At4g00940 | Heat | Heyndrickx et al. (2012) [40] |
| At3g10800 | Heat | Gao et al. (2008) [54] |
| At4g16660 | Heat | Heyndrickx et al. (2012) [40] |
| At1g07410 | Heat | Heyndrickx et al. (2012) [40] |
| At5g56030 | Heat | Takahashi et al (1992) [55] |
| At2g02810 | Heat | Heyndrickx et al. (2012) [40] |
Table 10. Reference about core genes involved in heat acclimation in shoot samples.
Conclusion
In this study, we proposed a novel Class-Information-based Penalized Matrix Decomposition method for identifying core genes. Our method can achieve a better identification capacity by bringing in the class information of samples based on the total scatter matrix. By integrating matrix decomposition and the PMD method, our method is appropriate to analyze the gene expression data. A large number of experiments on simulation and real gene expression data demonstrate that our CIPMD method outperforms both PMD, SPCA and SVM-RFE. Thus, our approach is effective to identify plants core genes responding to abiotic stresses.
In the future, we will focus on the biological interpretation of the core genes.
Supporting Information
The identification accuracies of the four methods with different parameters.
(XLSX)
Data Availability
The authors confirm that all data underlying the findings are fully available without restriction. Data are available from the Affymetix, CEL files are downloaded from NASCArrays [http://affy.arabidopsis.info/].
Funding Statement
This work was supported in part by the NSFC under grant No. 61202276; the Shandong Provincial Natural Science Foundation, under Grant No. ZR2013FL016; and the Foundation of Qufu Normal University, No. XJ200947. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Gill SS, Tuteja N (2010) Reactive oxygen species and antioxidant machinery in abiotic stress tolerance in crop plants. Plant Physiology and Biochemistry 48: 909–930. [DOI] [PubMed] [Google Scholar]
- 2. Allen GJ, Chu SP, Schumacher K, Shimazaki CT, Vafeados D, et al. (2000) Alteration of stimulus-specific guard cell calcium oscillations and stomatal closing in Arabidopsis det3 mutant. Science 289: 2338–2342. [DOI] [PubMed] [Google Scholar]
- 3. Ma H-S, Liang D, Shuai P, Xia X-L, Yin W-L (2010) The salt-and drought-inducible poplar GRAS protein SCL7 confers salt and drought tolerance in Arabidopsis thaliana. Journal of experimental botany 61: 4011–4019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Heller MJ (2002) DNA microarray technology: devices, systems, and applications. Annual review of biomedical engineering 4: 129–153. [DOI] [PubMed] [Google Scholar]
- 5. Sarmah CK, Samarasinghe S (2011) Microarray gene expression: A study of between-platform association of Affymetrix and cDNA arrays. Computers in biology and medicine 41: 980–986. [DOI] [PubMed] [Google Scholar]
- 6. Burleigh JG, Bansal MS, Eulenstein O, Hartmann S, Wehe A, et al. (2011) Genome-scale phylogenetics: inferring the plant tree of life from 18,896 gene trees. Systematic Biology 60: 117–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Bailey-Serres J (2013) Microgenomics: genome-scale, cell-specific monitoring of multiple gene regulation tiers. Annual review of plant biology 64: 293–325. [DOI] [PubMed] [Google Scholar]
- 8.Dudoit S, Shaffer JP, Boldrick JC (2003) Multiple hypothesis testing in microarray experiments. Statistical Science: 71–103.
- 9. Meher J (2013) Mixed PCA and Wavelet Transform based Effective Feature Extraction for Efficient Tumor Classification using DNA Microarray Gene Expression Data. Cancer 2: 110–116. [Google Scholar]
- 10. Aswani Kumar C, Srinivas S (2010) Mining associations in health care data using formal concept analysis and singular value decomposition. Journal of biological systems 18: 787–807. [Google Scholar]
- 11.Aradhya VM, Masulli F, Rovetta S (2010) A novel approach for biclustering gene expression data using modular singular value decomposition. Computational Intelligence Methods for Bioinformatics and Biostatistics: Springer. pp.254–265.
- 12. Yeung KY, Ruzzo WL (2001) Principal component analysis for clustering gene expression data. Bioinformatics 17: 763–774. [DOI] [PubMed] [Google Scholar]
- 13. Wang A, Gehan EA (2005) Gene selection for microarray data analysis using principal component analysis. Statistics in medicine 24: 2069–2087. [DOI] [PubMed] [Google Scholar]
- 14. Ma S, Kosorok MR (2009) Identification of differential gene pathways with principal component analysis. Bioinformatics 25: 882–889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Liu J-X, Wang Y-T, Zheng C-H, Sha W, Mi J-X, et al. (2013) Robust PCA based method for discovering differentially expressed genes. BMC bioinformatics 14: S3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Wang JJ-Y, Wang X, Gao X (2013) Non-negative matrix factorization by maximizing correntropy for cancer clustering. BMC bioinformatics 14: 107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wang L, Cheng H (2012) Robust sparse PCA via weighted elastic net. Pattern Recognition: Springer. pp.88–95.
- 18.Papailiopoulos DS, Dimakis AG, Korokythakis S (2013) Sparse PCA through Low-rank Approximations. arXiv preprint arXiv:13030551.
- 19. Witten DM, Tibshirani R, Hastie T (2009) A penalized matrix decomposition, with applications to sparse principal components and canonical correlation analysis. Biostatistics 10: 515–534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Liu J-X, Zheng C-H, Xu Y (2012) Extracting plants core genes responding to abiotic stresses by penalized matrix decomposition. Computers in Biology and Medicine 42: 582–589. [DOI] [PubMed] [Google Scholar]
- 21. Liu J-X, Gao Y-L, Xu Y, Zheng C-H, You J (2014) Differential Expression Analysis on RNA-Seq Count Data Based on Penalized Matrix Decomposition. IEEE Transactions on NanoBioscience 13: 12–18. [DOI] [PubMed] [Google Scholar]
- 22. Liu J-X, Xu Y, Zheng C-H, Wang Y, Yang J-Y (2012) Characteristic Gene Selection via Weighting Principal Components by Singular Values. Plos One 7: e38873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yin Y (2013) Identification of Differential Gene Pathways with Sparse Principal Component Analysis. Mathematics Theses. 126.
- 24. Zheng C-H, Zhang D, Ng VT-Y, Shiu CK, Huang D-S (2011) Molecular pattern discovery based on penalized matrix decomposition. Computational Biology and Bioinformatics, IEEE/ACM Transactions on 8: 1592–1603. [DOI] [PubMed] [Google Scholar]
- 25. Guyon I, Weston J, Barnhill S, Vapnik V (2002) Gene selection for cancer classification using support vector machines. Machine learning 46: 389–422. [Google Scholar]
- 26. Tang Y, Zhang Y-Q, Huang Z (2007) Development of two-stage SVM-RFE gene selection strategy for microarray expression data analysis. Computational Biology and Bioinformatics, IEEE/ACM Transactions on 4: 365–381. [DOI] [PubMed] [Google Scholar]
- 27. Ding Y, Wilkins D (2006) Improving the performance of SVM-RFE to select genes in microarray data. BMC bioinformatics 7: S12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Zhou X, Tuck DP (2007) MSVM-RFE: extensions of SVM-RFE for multiclass gene selection on DNA microarray data. Bioinformatics 23: 1106–1114. [DOI] [PubMed] [Google Scholar]
- 29. Duan K-B, Rajapakse JC, Wang H, Azuaje F (2005) Multiple SVM-RFE for gene selection in cancer classification with expression data. NanoBioscience, IEEE Transactions on 4: 228–234. [DOI] [PubMed] [Google Scholar]
- 30.Wang H, Yan S, Xu D, Tang X, Huang T (2007) Trace ratio vs. ratio trace for dimensionality reduction; 2007 17–22, June 2007; Minneapolis, MN. pp.1–8.
- 31. Liang F (2007) Use of SVD-based probit transformation in clustering gene expression profiles. Computational Statistics & Data Analysis 51: 6355–6366. [Google Scholar]
- 32. Journée M, Nesterov Y, Richtárik P, Sepulchre R (2010) Generalized power method for sparse principal component analysis. The Journal of Machine Learning Research 11: 517–553. [Google Scholar]
- 33. Chang C-C, Lin C-J (2011) LIBSVM: a library for support vector machines. ACM Transactions on Intelligent Systems and Technology (TIST) 2: 27. [Google Scholar]
- 34. Shen H, Huang JZ (2008) Sparse principal component analysis via regularized low rank matrix approximation. Journal of multivariate analysis 99: 1015–1034. [Google Scholar]
- 35. Craigon DJ, James N, Okyere J, Higgins J, Jotham J, et al. (2004) NASCArrays: a repository for microarray data generated by NASC's transcriptomics service. Nucleic acids research 32: D575–D577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Wu Z, Irizarry RA, Gentleman R, Murillo FM, Spencer F (2004) A model based background adjustment for oligonucleotide expression arrays. Journal of the American Statistical Association 99: 909–917. [Google Scholar]
- 37. Ashburner M, Ball CA, Blake JA, Botstein D, Butler H, et al. (2000) Gene Ontology: tool for the unification of biology. Nature genetics 25: 25–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Boyle EI, Weng S, Gollub J, Jin H, Botstein D, et al. (2004) GO:: TermFinder—open source software for accessing Gene Ontology information and finding significantly enriched Gene Ontology terms associated with a list of genes. Bioinformatics 20: 3710–3715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Zheng C-H, Liu J-X, Mi J-X, Xu Y (2012) Identifying Characteristic Genes Based on Robust Principal Component Analysis. Emerging Intelligent Computing Technology and Applications: Springer. pp.174–179.
- 40. Heyndrickx KS, Vandepoele K (2012) Systematic identification of functional plant modules through the integration of complementary data sources. Plant physiology 159: 884–901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Seo PJ, Xiang F, Qiao M, Park J-Y, Lee YN, et al. (2009) The MYB96 transcription factor mediates abscisic acid signaling during drought stress response in Arabidopsis. Plant Physiology 151: 275–289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Chen C-N, Chu C-C, Zentella R, Pan S-M, Ho T-HD (2002) AtHVA22 gene family in Arabidopsis: phylogenetic relationship, ABA and stress regulation, and tissue-specific expression. Plant molecular biology 49: 631–642. [DOI] [PubMed] [Google Scholar]
- 43. Sharma S, Villamor JG, Verslues PE (2011) Essential role of tissue-specific proline synthesis and catabolism in growth and redox balance at low water potential. Plant physiology 157: 292–304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Koops P, Pelser S, Ignatz M, Klose C, Marrocco-Selden K, et al. (2011) EDL3 is an F-box protein involved in the regulation of abscisic acid signalling in Arabidopsis thaliana. Journal of experimental botany 62: 5547–5560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Vadassery J, Tripathi S, Prasad R, Varma A, Oelmüller R (2009) Monodehydroascorbate reductase 2 and dehydroascorbate reductase 5 are crucial for a mutualistic interaction between Piriformospora indica and Arabidopsis. Journal of plant physiology 166: 1263–1274. [DOI] [PubMed] [Google Scholar]
- 46. Kiyosue T, Yamaguchi-Shinozaki K, Shinozaki K (1994) Cloning of cDNAs for genes that are early-responsive to dehydration stress (ERDs) inArabidopsis thaliana L.: identification of three ERDs as HSP cognate genes. Plant molecular biology 25: 791–798. [DOI] [PubMed] [Google Scholar]
- 47. Fujita M, Fujita Y, Maruyama K, Seki M, Hiratsu K, et al. (2004) A dehydration-induced NAC protein, RD26, is involved in a novel ABA-dependent stress-signaling pathway. The Plant Journal 39: 863–876. [DOI] [PubMed] [Google Scholar]
- 48. Huang D, Wu W, Abrams SR, Cutler AJ (2008) The relationship of drought-related gene expression in Arabidopsis thaliana to hormonal and environmental factors. Journal of experimental Botany 59: 2991–3007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Maruyama K, Takeda M, Kidokoro S, Yamada K, Sakuma Y, et al. (2009) Metabolic pathways involved in cold acclimation identified by integrated analysis of metabolites and transcripts regulated by DREB1A and DREB2A. Plant physiology 150: 1972–1980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Sakamoto H, Araki T, Meshi T, Iwabuchi M (2000) Expression of a subset of the Arabidopsis Cys (2)/His (2)-type zinc-finger protein gene family under water stress. Gene 248: 23–32. [DOI] [PubMed] [Google Scholar]
- 51. Umezawa T, Okamoto M, Kushiro T, Nambara E, Oono Y, et al. (2006) CYP707A3, a major ABA 8′-hydroxylase involved in dehydration and rehydration response in Arabidopsis thaliana. The Plant Journal 46: 171–182. [DOI] [PubMed] [Google Scholar]
- 52. Rae L, Lao NT, Kavanagh TA (2011) Regulation of multiple aquaporin genes in Arabidopsis by a pair of recently duplicated DREB transcription factors. Planta 234: 429–444. [DOI] [PubMed] [Google Scholar]
- 53. Koizumi N (1996) Isolation and responses to stress of a gene that encodes a luminal binding protein in Arabidopsis thaliana. Plant and cell physiology 37: 862–865. [DOI] [PubMed] [Google Scholar]
- 54. Gao H, Brandizzi F, Benning C, Larkin RM (2008) A membrane-tethered transcription factor defines a branch of the heat stress response in Arabidopsis thaliana. Proceedings of the National Academy of Sciences 105: 16398–16403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Takahashi T, Naito S, Komeda Y (1992) Isolation and analysis of the expression of two genes for the 81-kilodalton heat-shock proteins from Arabidopsis. Plant physiology 99: 383–390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Lim CJ, Yang KA, Hong JK, Choi JS, Yun D-J, et al. (2006) Gene expression profiles during heat acclimation in Arabidopsis thaliana suspension-culture cells. Journal of plant research 119: 373–383. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The identification accuracies of the four methods with different parameters.
(XLSX)
Data Availability Statement
The authors confirm that all data underlying the findings are fully available without restriction. Data are available from the Affymetix, CEL files are downloaded from NASCArrays [http://affy.arabidopsis.info/].