Calculation of the convective heat transfer coefficient and thermal diffusivity of cucumbers using numerical simulation and the inverse method

Abstract

Cooling of fruits and vegetables, immediately after the harvest, has been a widely used method for maximizing post-harvest life. In this paper, an optimization algorithm and a numerical solution are used to determine simultaneously the convective heat transfer coefficient, h_H, and the thermal diffusivity, α, for an individual solid with cylindrical shape, using experimental data obtained during its cooling. To this end, the one-dimensional diffusion equation in cylindrical coordinates is discretized and numerically solved through the finite volume method, with a fully implicit formulation. This solution is coupled to an optimizer based on the inverse method, in which the chi-square referring to the fit of the numerical simulation to the experimental data is used as objective function. The optimizer coupled to the numerical solution was applied to experimental data relative to the cooling of a cucumber. The obtained results for α and h_H were coherent with the values available in the literature. With the results obtained in the optimization process, the cooling kinetics of cucumbers was described in details.

Introduction

The conservation time of fruits and vegetables in natural conditions is limited to only a few days. Cooling of these products, immediately after the harvest, has been a widely used method for maximizing post-harvest life and inhibiting the growth of decay-causing microorganisms (Miyake and Hiramitsu 2011). In this sense, cooling techniques have been widely studied for several researchers (Wijewardane and Guleria 2011; Basediya et al. 2011; Samira et al. 2011; Raval et al. 2011). According to Brosnan and Sun (2001), it is necessary not only to cool the product but also to cool the product as quickly as possible, after harvest. In order to use efficient techniques for the cooling of fruits and vegetables, the heat transfer from the product to the medium should be known in details (Dincer 1995a). Thus, in the case of the heat conduction, the solution of the diffusion equation should be used in the description of the cooling process. On the other hand, the convective heat transfer coefficient h_H and thermal diffusivity α are important parameters to characterize, to model and to optimize the heat transfer processes (Erdogdu 2005). In order to determine these parameters and to describe the cooling kinetics of a product, in a general way two tools are available: the analytical and numerical tools.

Analytical solutions of the diffusion equation are found in the literature for several simple geometries such as slabs, cylinders, and spheres, among others shapes. In these solutions, it is usually assumed that these solids have constant thermo-physical properties as, for example, in Luikov (1968) and Crank (1992). In the 1990s, these solutions were used in several research works to determine the thermal diffusivity and the convective heat transfer coefficient of several agricultural products, with the objective to describe the cooling kinetics of them (Dincer 1995a, b, c, d, 1996). In these works, analytical solutions are combined with curve fitting to determine empiric expressions for α and h_H.

Although analytical models are still used (Becker and Fricke 2004; Erdogdu 2005; Erdogdu 2008; Kumar et al. 2008; Cuesta and Lamúa 2009; Raval et al. 2011), in the recent years many works use numerical solutions to describe the cooling kinetics of agricultural products. Campanõne et al. (2002) used an implicit finite-difference scheme to describe the simulation of food refrigeration. Pirozzi and Amendola (2005) determined the convective heat transfer coefficient value of strawberries, employing numerical simulation through finite differences and experimental data. A similar procedure was used by Amendola et al. (2009) to determine the convective heat transfer coefficient value for fig fruit. The authors employed numerical simulation and experimental data, using finite differences and spherical coordinates to solve the one-dimensional diffusion equation through an explicit scheme. Using finite differences and a Differential Evolution algorithm, Mariani et al. (2009) estimated the apparent thermal conductivity of carrot purée during freezing. In the last work, for instance, only the thermal conductivity was determined through optimization, since a fluxmeter was adhered to the internal wall of the container, in the interface with the product. According to the authors, “the instrument used in the experiment had allowed the measurement of the heat transfer coefficient between 400 and 2000 W m⁻² °C⁻¹”. On the other hand, Silva et al. (2011) studied the effect of the geometric representation of cucumbers on the numerical simulation of its cooling kinetics. The following geometries were used to represent the cucumber: infinite cylinder, finite cylinder, and ellipsoid. In this article, the authors assumed that the diffusion model with boundary condition of the third kind satisfactorily describes the cooling, and that the thermo-physical parameters are constant during the process. According to Silva et al. (2011), the best model in the representation of the cucumber’s shape was the ellipsoid, but the time demanded in its optimization was about 66 times greater than the time for the infinite cylinder.

As observed by Erdogdu (2008), the simultaneous determination of the thermal diffusivity and convective heat transfer coefficient is difficult to accomplish because there may be several pairs of these parameters for which the solution of the diffusion equation is fitted to a set of experimental data. In other words, the objective function may have several local minima. Thus, the simultaneous determination of the parameters of the diffusion equation through optimization is an issue which still deserves further investigation. On the other hand, although there are some articles in the literature describing the drying of agricultural products using the finite volume method (Wu et al. 2004; Carmo and Lima 2005), few works use finite volume method to describe cooling of products, particularly of an individual solid, despite the fact that this method presents a simple physical interpretation of the conservation laws.

The main objective of this paper is to present an optimization algorithm and a numerical solution for the simultaneous determination of the convective heat transfer coefficient and thermal diffusivity of a cylindrical body cooled in any medium, supposing that the position of the thermocouple which measures the temperatures is known. As a second objective, an application of the presented tools is made in a cucumber subjected to cooling air.

Material and methods

The mathematical model used in this article for the solution of the diffusion equation for a cylinder presupposes the following assumptions:

• infinite cylinder: R≪L, where R is the radius and L is the height of the cylinder;

• the solid must be homogeneous and isotropic;

• the spatial distribution of the temperature must have radial symmetry and must be initially uniform;

• the only mechanism for transport of heat within the solid is diffusion;

• the convective heat transfer coefficient is constant during the heat diffusion;

• the boundary condition is of the third kind (Cauchy), and the cooling medium temperature must be constant;

• there must be no phase change in the product during the process;

• the mass loss and the source term due to the respiration heat are negligible during the cooling of the cucumber.

Diffusion equation

For the assumptions above, the diffusion equation in cylindrical coordinates can be written as

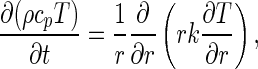1a

where ρ is the density (kg m⁻³), c_p is the specific heat (Jkg⁻¹ K⁻¹), T is the temperature (K), t is the time (s), r defines a radial position within the infinite cylinder (m), and k is the thermal conductivity (Wm⁻¹ K⁻¹). If the density and the specific heat are constant, Eq. (1a) can be written in the following way:

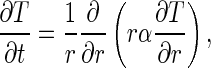1b

where α is the thermal diffusivity (m²s⁻¹).

Discretization

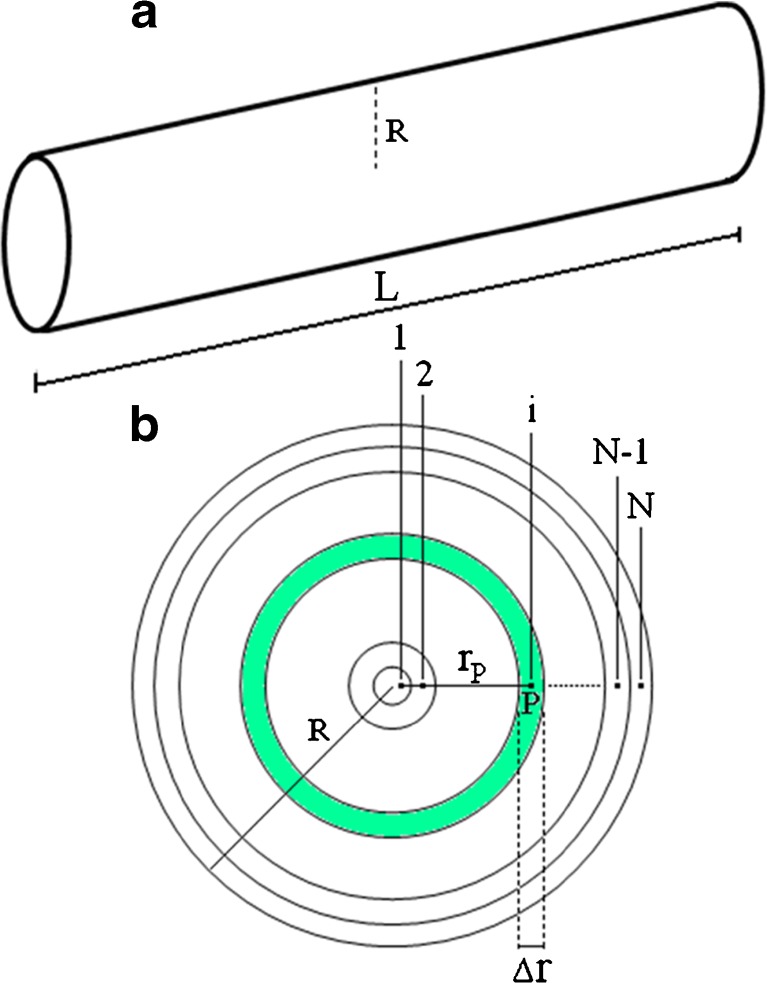
The diffusion equation will be numerically solved through the finite volume method (Patankar 1980). This choice is explained only by the experience of the authors of this article with this method. It is important to mention that the explicit formulation presents good results in problems involving discretization. However, a fully implicit formulation will be used, and this formulation was chosen because it is unconditionally stable, enabling the user of the software to be created freely can choose the number of the time step, with no restriction. To this end, a cylinder and its uniform mesh are presented Fig. 1. The thickness of the control volumes is Δr (m) and the control volume number “i” has a nodal point “P”.

Fig. 1.

a Cylinder of radius R and height L; b Uniform mesh: N control volumes with thickness Δr, and nodal points

Figure 2 shows a control volume with nodal point “P” and its neighbors to west (W) and to east (E). The lower cases “w” and “e” refer to the interfaces of the referred control volume P. Therefore, r_w and r_e are the radius of the circumferences “w” and “e”.

Fig. 2.

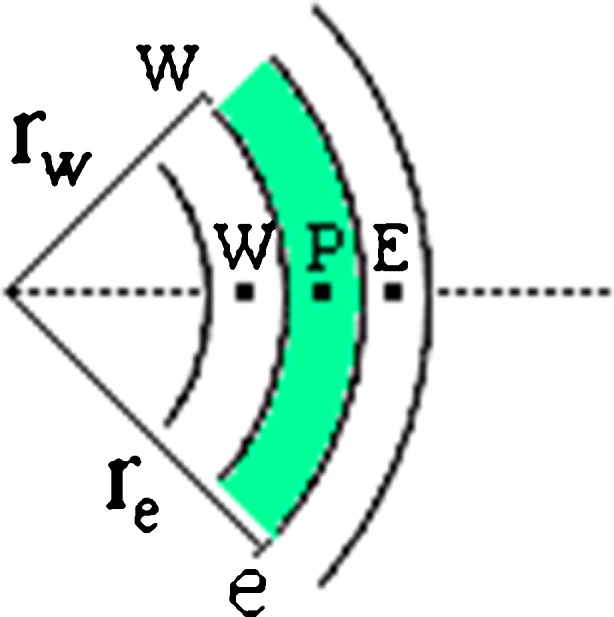
Control volume P and its neighbors to west (W) and to east (E)

Integrating Eq. (1b) with respect to space (2πr_PΔrL) and time (Δt), the following result is obtained for the control volume P:

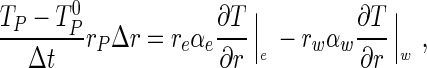2

where the superscript 0 means “former time” t and its absence means “current time” t + Δt.

Cylinder: internal volumes

The partial derivatives for an internal control volume can be approached in the following way:

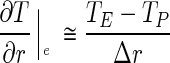3

and

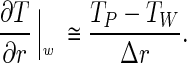4

Replacing Eqs. (3) and (4) into Eq. (2), the discretized equation for an internal volume may be written:

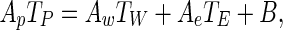5

where

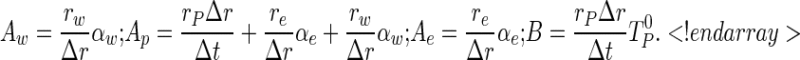6a–d

Cylinder: control volume 1

Due to the symmetry condition (flux zero in the centre), the third term of Eq. (2) is zero for the control volume 1. Thus, Eq. (2) becomes:

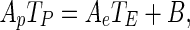7

with

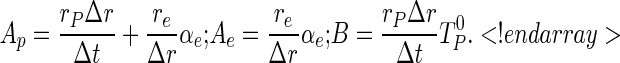(8a–c)

Cylinder: control volume N

For the control volume N, the convective boundary condition can be expressed in the following way:

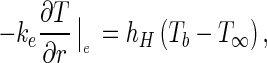9a

where h_H is the convective heat transfer coefficient (Wm⁻² K⁻¹), T_b is the temperature at the boundary (K), and T _∞ is the temperature of the cooling air (K). Dividing Eq. (9a) by the factor ρc_p, a new equation can be written for the convective boundary condition:

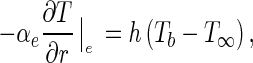9b

where h is the convective transfer coefficient (ms⁻¹). For the control volume N, Eq. (3) can be rewritten as follows:

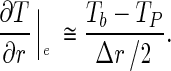10

Combining Eq. (9b) and (10), an expression for T_b is obtained:

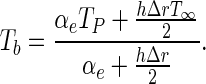11

Substituting Eq. (11) in Eq. (10), and the obtained result into Eq. (2), and taking in account Eq. (4), the following discretized equation is obtained for the control volume N:

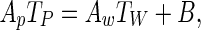12

where

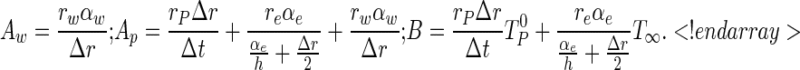13a–c

For each time step, a system of equations given by Eqs. (5), (7) and (12) can be solved by the TDMA method, i.e., tri-diagonal matrix algorithm (or Thomas algorithm) (Press et al. 1996). Once T(r,t) is numerically determined, the temperature T_b at the boundary, at a given time t, can be calculated through Eq. (11). The average value of T at a given time t may be calculated by (Silva et al. 2008):

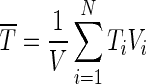14

with

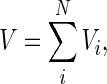15

where V_i and V respectively are the volume of the control volume “i” (m³) and the volume of the cylinder (m³).

The aforementioned system of equations can be solved for the dimensionless temperature, which is defined in the following way:

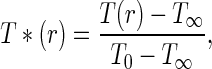16

where the initial temperature T₀ (K) is supposed uniform. In this case, for t = 0, T * (r) = 1 and, for t→∞, T * (r) = 0.

Thermal diffusivity α

For the nodal points, the process parameter α may be calculated from an appropriate relation between such parameter and the temperature T,

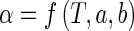17

where “a” and “b” are parameters which fit the numerical solution to the experimental data, and they are determined by optimization.

On the interfaces of the control volumes, for example “e” (Fig. 2), the following expression should be used to determine α (Patankar 1980; Silva et al. 2008):

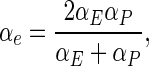18

and Eq. (18) is valid for uniform grids. Note that Eq. (18) is also valid for a constant diffusivity, with a value α. In this case, α_E = α and α_P = α; and Eq. (18) results in α_e = α.

Optimization algorithm

In order to determine the parameters α and h by optimization, the objective function was defined by the chi-square referring to the fit of the simulated curve to the experimental data of the cooling kinetics in the centre. The expression for the chi-square involving the fit of a simulated curve to the experimental data is given by (Bevington and Robinson 1992; Taylor 1997)

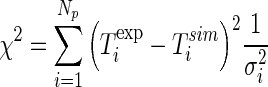19

where 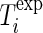is the temperature measured in the experimental point “i” (K), 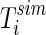is the correspondent simulated temperature (K), N_p is the number of experimental points, 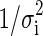is the statistical weight referring to the point “i”. In general, in the absence of information, the statistical weights are made equal to a common value, for instance 1. In Eq. (19), the chi-square depends on 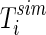, which depends on α and h. If the cooling involves an interval of temperature in which the value of h can be considered constant and the thermal diffusivity is given by Eq. (17), the parameters can be determined through the minimization of the objective function, which is accomplished in cycles involving the following steps (Silva et al. 2011):

• Step 1)

  Inform the initial values for the parameters “a”, “b” and “h”. Solve the diffusion equation and determine the chi-square;

• Step 2)

  Inform the value for the correction of “h”;

• Step 3)

  Correct the parameter “h”, maintaining the parameter “a” and “b” with constant values. Solve the diffusion equation and calculate the chi-square;

• Step 4)

  Compare the latest calculated value of the chi-square with the previous one. If the latest value is smaller, return to the step 2; otherwise, decrease the last correction of the value of “h” and proceed to step 5;

• Step 5)

  Inform the value for the correction of “a”;

• Step 6)

  Correct the parameter “a”, maintaining the parameters “b” and “h” with constant values. Solve the diffusion equation and calculate the chi-square;

• Step 7)

  Compare the latest calculated value of the chi-square with the previous one. If the latest value is smaller, return to the step 5; otherwise, decrease the last correction of the value of “a” and proceed to step 8;

• Step 8)

  Inform the value for the correction of “b”;

• Step 9)

  Correct the parameter “b”, maintaining the parameters “a” and “h” with constant values. Solve the diffusion equation and calculate the chi-square;

• Step 10)

  Compare the latest calculated value of the chi-square with the previous one. If the latest value is smaller, return to the step 8; otherwise, decrease the last correction of the value of “b” and proceed to step 11;

• Step 11)

  Begin a new cycle coming back to the step 2 until the stipulated convergence for the parameters “a”, “b” and “h” is reached.

In each cycle, the value of the correction of each parameter can be initially modest, compatible with the tolerance of convergence imposed to the problem. As an example, if the relative tolerance for h (∆h/h) is 1× 10⁻⁴ and h₀ is 1 × 10⁻⁶, then ∆h is 0.0001× 10⁻⁶ and this is the first correction for the parameter. Thus, for a given cycle, in each return to the step 2, 5 or 8, the value of the new correction can be multiplied by the factor 2. If the modest correction initially informed does not minimize the objective function, in the next cycle its value can be multiplied by the factor −1. Note that if the thermal diffusivity is supposed constant, the steps 8, 9 and 10 are not necessary. On the other hand, the initial values for the parameters can be estimated through the obtained values for similar products available in the literature, or through some empirical correlation. Another interesting aspect is that the order for the correction of the parameters was established after several tests. Although any order for the correction of the parameters results in the same final values for the parameters, the convergence is achieved more quickly using the established order.

For constant thermal diffusivity, once α and h have been determined through optimization, the Biot number (dimensionless) can be calculated by the expression (Dincer 1996):

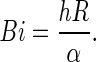20

The analysis of Eq. (1a) and (1b) makes it possible to write an expression for the thermal conductivity:

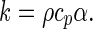21

Comparing Eq. (9a) with (9b), the following equation is obtained for the convective heat transfer coefficient:

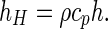22

Developed software and statistical indicators

The developed software (optimizer and solver for the diffusion equation), including the user interface, was created in a computer Intel Pentium IV with 1 GB RAM; in the studio Compaq Visual Fortran Professional Edition V. 6.6.0, using a programming language option called QuickWin Application, under the Windows XP platform. In order to analyze the quality of the fit, the statistical indicators chi-square, given by Eq. (19), and the coefficient of determination R² (Taylor 1997) are used. In addition to these, the average error, the correlation coefficient and the covariance between parameters, as well as the t-test and the variance will be used to evaluate the results. All the statistical treatment of the obtained results is performed using the LAB Fit Curve Fitting Software, available on www.labfit.net.

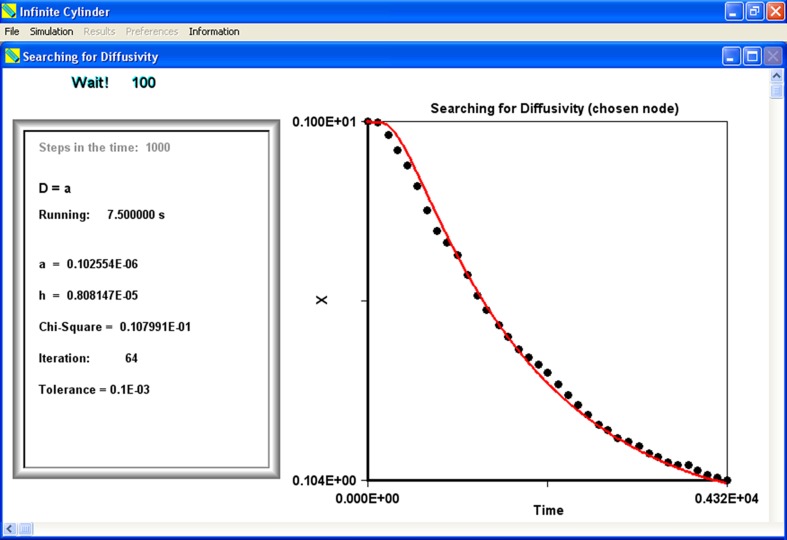
Figure 3 shows a screen of the developed software during an optimization process.

Fig. 3.

Screen of the developed software during an optimization process

Basically, the developed software can be used in two situations: 1) simulation of the cooling kinetics when the thermo-physical parameters are known; 2) determination of the parameters α and h by optimization when an experimental dataset is known.

Experimental data

Experimental data obtained by Dincer (1996) for cooling of cucumbers are explored in the present paper. The temperatures were measured with a thermocouple placed in the centre of the cucumber, and they were presented through dimensionless values determined by Eq. (16). The points of the graph that describes the cooling kinetics of the cucumber were digitized using the software xyExtract Graph Digitizer available on Internet in (http://zeus.df.ufcg.edu.br/labfit/index_xyExtract.htm). Dincer (1996) did not inform the uncertainties of the temperatures and, due to that, in the present paper, the statistical weights were made equal to 1. The dimensions of the cucumber used in the experiment were: radius R = 0.019 m and height L = 0.16 m. For these dimensions, the vegetable shape can be reasonably considered an infinite cylinder (Erdogdu and Turhan 2006). The decimal moisture content of the cucumber was X = 0.96 (wb), and the mass loss was found to be negligible. The initial temperature of the cucumber was 295 K, while the temperature of the cooling air was 277 K. Note that, although software developed in this article can include the dimensional variations of the cylinder during the cooling process, for this particular range of temperature (295–277 K) these variations were not measured by Dincer (1996) and, due to this fact, are not considered here. On the other hand, the cooling air velocity was kept at 2 ms⁻¹ and its relative humidity was 80 %.

In the present paper, the specific heat was estimated from the expression (Sweat 1986; ASHRAE 1993)

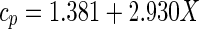23

with c_p given in kJ kg⁻¹ K⁻¹ when the moisture content X is decimal in wet basis. Using Eq. (23), the value for the specific heat of cucumbers was estimated: c_p = 4190 Jkg⁻¹ K⁻¹. Note that cucumber is 96 % water. Thus, the specific heat of the product is practically equal to the specific heat of the water. Naturally, we used an empirical expression to determine this parameter, and the value obtained herein is not exact. The density of the cucumber was determined by Fasina and Fleming (2001) for a vegetable with the same moisture content as the cucumber currently under analysis: ρ = 959 kgm⁻³.

Results and discussion

The circular section of the infinite cylinder that represents the cucumber was divided into 200 control volumes and the total time of cooling was divided into 1000 time steps. Previous study indicates that 200 control volumes and 1000 time steps could guarantee an adequate refinement for the problem under investigation. Although this number seems excessive, the position of the thermocouple within the cucumber is provided to software by the identification of the control volume where the device is placed (in this article the centre is represented by the control volume number 1). In this way, this number of control volumes allows to locate the thermocouple with good accuracy.

Constant thermal diffusivity

It must be observed that different α and h pairs can describe the cooling kinetics (Erdogdu 2008), since the objective function may have more than one minimum point. This is a problem which occurs in many optimization processes as, for example, in nonlinear regression. The Statistical Reference Datasets Project (SRDP) of the National Institute of Standards and Technology (NIST), for instance, presents 27 datasets (and initial values) with three levels of difficulty in order to certify nonlinear regression algorithms. Some of the files available are used to test whether the algorithm can detect the global minimum or if it determines parameters when another minimum is found. Initial values, physically consistent, should be chosen so that this difficulty can be worked around by the software user. Similarly, for the algorithm proposed in this paper, such difficulty must be worked around, and this can be made as will be shown below.

Boundary condition of the first kind

Initially, constant thermal diffusivity α is the only parameter to be determined by the proposed algorithm, and h will be kept at 1 × 10⁺¹⁰, which means boundary condition of the first kind. In this case, the objective function has a single minimum as noted by Silva et al. (2009). For the experimental data of cucumbers cooling, for example, using several significantly different initial values, and imposing a relative tolerance of 1 × 10⁻⁴ for the convergence, the same value for the thermal diffusivity is obtained, as can be seen in Table 1.

Table 1.

Thermal diffusivity obtained through optimization for the boundary condition of the first kind

Initial value (m2 s−1)	Result (m2 s−1)
1 × 10−10	4.490 × 10−8
5 × 10−10	4.491 × 10−8
1 × 10−9	4.491 × 10−8
5 × 10−9	4.489 × 10−8
1 × 10−8	4.491 × 10−8
5 × 10−8	4.489 × 10−8

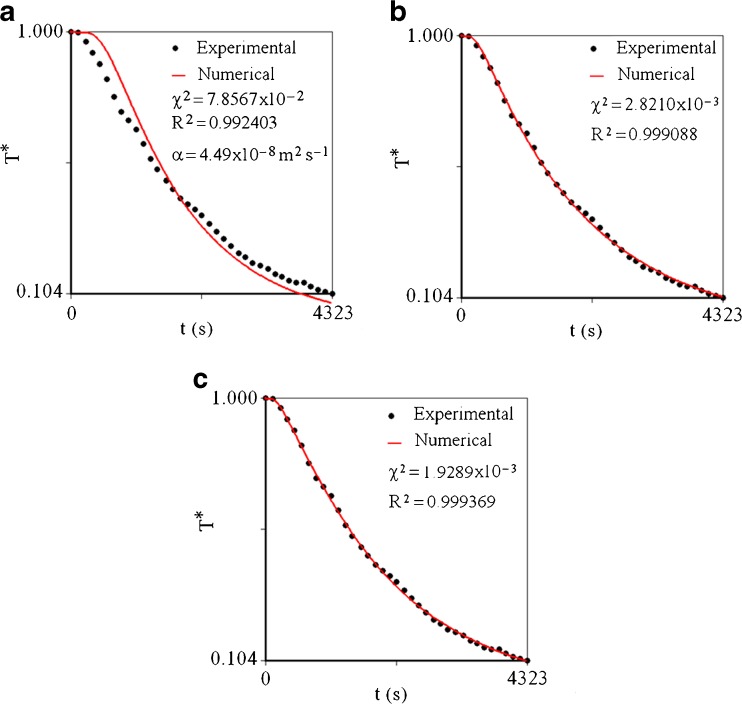
In Table 1, despite the fact that the last initial value is 500 times greater than the first, the same value was obtained for the thermal diffusivity, in all the optimizations performed. This is consistent with the results of Silva et al. (2009), who observed that there is a single value for the diffusivity that minimizes the objective function for the boundary condition of the first kind. The cooling simulation considering the boundary condition of the first type is shown in Fig. 4(a).

Fig. 4.

Cooling curve in r = 0.0 m, supposing: a Boundary condition of the first kind, b Boundary condition of the third kind with constant thermal diffusivity and c Boundary condition of the third kind with variable thermal diffusivity

An inspection of Fig. 4(a) makes it possible to state that the boundary condition of first kind is not suitable to describe cooling of cucumber. On the other hand, this condition is expressed by an infinite Biot number and, in practical terms, an “infinite Biot number” may be a value, for instance, close to 200. Another point to consider is that this inadequacy observed in Fig. 4(a) indicates that there is resistance to heat flow on the surface, so the Biot number must be much lower than 200. Furthermore, due to the resistance at the surface, a value for the thermal diffusivity greater than the one obtained in Table 1 should be expected.

Boundary condition of the third kind

For the boundary condition of third kind, using the proposed algorithm, in general an initial value two, three or four times greater than that obtained for the condition of the first kind produces satisfactory results for the simultaneous determination of α and h. On the other hand, the strong inadequacy of the solution with boundary condition of the first kind to the experimental data (Fig. 4a) makes it possible to estimate h by imposing the value of Biot number as 4, 3, 2 or 1 (values much lower than 200). If the initial value of α is estimated as 1 × 10⁻⁷ m² s⁻¹, for example, assuming Bi = 2, the initial value of h can be estimated as 1 × 10⁻⁶ m s⁻¹. Based on earlier study, the initial values for α and h were attributed respectively as 1 × 10⁻⁷ m² s⁻¹ and 1 × 10⁻⁶ m s⁻¹. Performing the optimization process as described in the “Thermal diffusivity α”, with a relative tolerance of convergence for the parameters given by 1 × 10⁻⁴, and using the solution for the diffusion equation presented in “Discretization”, it is possible to obtain the graph for the temperature in the centre (control volume 1) versus the cooling time, as shown in Fig. 4(b).

The fit of the numerical simulation to the experimental data obtained by optimization via inverse method is good, with a chi-square given by 2.8210 × 10⁻³ and a determination coefficient of 0.999088. The obtained results for the parameters can be summarized through Table 2.

Table 2.

Constant parameters determined in this article for cucumber and values from the literature for this product

	Present article	Dincer (1996)	Silva et al. (2012b)
α (m2 s−1)	1.453 × 10−7	1.45 × 10−7	1.47 × 10−7
k (W m−1 K−1)	0.5838	–	–
h (m s−1)	6.439 × 10−6	6.21 × 10−6	6.39 × 10−6
hH (W m−2 K−1)	25.87	–	–

In Table 2, the parameter h was obtained through optimization and h_H by Eq. (22). In the same way, the parameter α was obtained through optimization while the parameter k was obtained by Eq. (21). The obtained value in the present paper for α agrees with the value obtained by Dincer (1996), and the discrepancy between the two results is only 0.2 %.

With the results of Table 2, the Biot number can be calculated using Eq. (20): Bi = 0.8420. This result agrees with the one obtained by Dincer (1996), and the discrepancy between them is only 3.3 %. The advantage of the presented numerical tools with respect to the empirical expressions proposed by Dincer (1996) is that, for the numerical case, the sensor of temperature could be placed in any position within the cucumber. Besides this advantage, numerical simulations make it possible to describe the cooling kinetics in details, as it will be seen in this article. In addition, the presented numerical tool can to determine the interest parameters with variable value, as a function of the temperature, and this is not possible through the analytical tools.

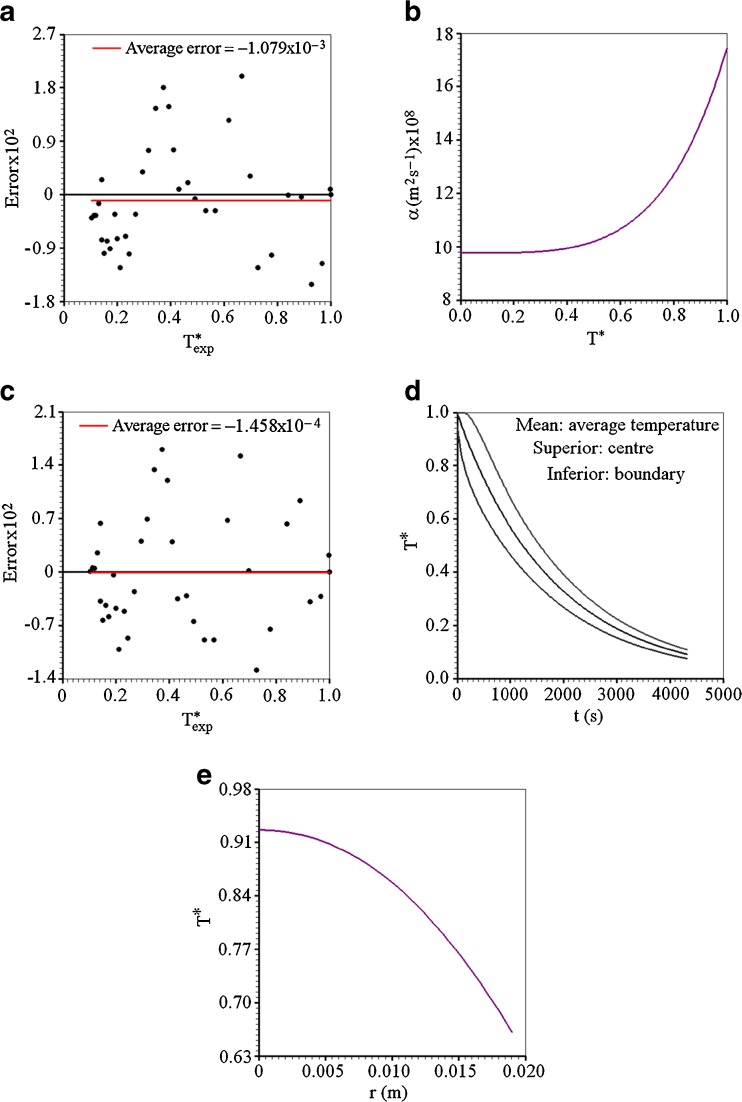
In order to investigate how much the simulated curve represents the cooling kinetics, a plot of the error as function of the dimensionless temperature is shown in Fig. 5(a).

Fig. 5.

a Dispersion and average error for constant diffusivity; b Variable thermal diffusivity versus dimensionless temperature; c Dispersion and average error for variable diffusivity; d Dimensionless temperatures: average, in the centre and on boundary; e Graph of the dimensionless temperature versus radial position after 402 s of cooling

Figure 5(a) enables to conclude that the average error is small but significant (1.079 × 10⁻³), once it is expected the value zero. Then, another model for the diffusivity should be tried, considering a value variable for this parameter.

Variable thermal diffusivity

For the interval of the temperature used in the experiment, it is well known that thermal diffusivity (and thermal conductivity) decreases when the average temperature of the product also decreases (Ansari et al. 2007; Oke et al. 2007; Kurozawa et al. 2008; Singhal et al. 2008; Ansari et al. 2009). In these papers, each value of the thermal diffusivity is determined in an experiment with the solid in a given average temperature. However, for the transient state, during the cooling, the temperature within the cucumber varies with the position (and time). Then, it is reasonable to suppose that the thermal diffusivity depends on the local temperature. Thus, in order to relate the thermal diffusivity with the local temperature, several simulations were carried out with various increasing functions. In these simulations, the convective heat transfer coefficient was considered constant. Analyzing the statistical indicators of all optimizations performed, it was observed that the dependence of the diffusivity on local temperature may be described by an expression in the following form:

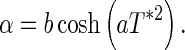24

If the thermal diffusivity is constant, the coefficients A of the discretized equations are calculated only once, and the coefficient B is calculated in each time step because its value depends on 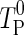, which is the value of T in the control volume P at the initial instant of each time step. However, if the parameter α is variable, the coefficients A are also calculated in each time step, due to the nonlinearities caused by the variation of this parameter. In this case, according to Silva et al. (2012a), if the time refinement is adequate, the errors due to the nonlinearities can be discarded. Thus, due to the nonlinearities on the coefficients A (Eqs. 6a–d; (8a–c); and 13a–c), introduced by the variable diffusivity, the time of cooling will be divided into 2000 steps. Attributing the initial values for the parameter “a” as a₀ = 1.0 °C^-2, b₀ = 10⁻⁷ m² s⁻¹ and h₀ = 10⁻⁶ m s⁻¹, the following results are obtained for the parameters: a = 1.202 °C⁻², b = 9.671 × 10⁻⁸ m² s⁻¹ and h = 7.763 × 10⁻⁶ m s⁻¹. The statistical indicators for the fit were χ² = 1.9289 × 10⁻³ and R² = 0.999369, and the tolerance for convergence was stipulated as 1 × 10⁻⁴. Note that the constant values for the thermal diffusivity and convective heat transfer coefficient were already determined. Thus, typical values for these quantities were assumed as initial values. An initial value was chosen for “a” assuming a moderate modification for α, when the dimensionless temperature varies from zero up to 1. On the other hand, Fig. 4(c) shows the obtained results for the cooling kinetics, supposing the thermal diffusivity is variable.

Obviously, through the statistical indicators, it can be observed that the obtained results assuming variable thermal diffusivity are better than those in which the thermal diffusivity is considered constant. Although cooling has been studied with the temperature in the dimensionless form, the obtained results are valid only for the interval from 277 up to 295 K. On the other hand, a plot of α versus T is shown in Fig. 5(b).

For the proposed model, it can be observed that, for T^* between 0 and 0.5 (corresponding to 277–286 K), the value of the thermal diffusivity is almost constant and, from 0.5 up to 1 (corresponding to 286–295 K), this parameter depends considerably of the local value of the dimensionless temperature.

For the variable diffusivity, a plot of the error as function of the dimensionless temperature is shown in Fig. 5(c).

As can be seen in Fig. 5(c), the result for the average error is practically equal to zero (−1.458 × 10⁻⁴) and the dispersion (between −1.4 × 10⁻² and 2.1 × 10⁻²) is less than the dispersion observed in Fig. 5(a) (between −1.8 × 10⁻² and 2.7 × 10⁻²). The standard deviation associated to the errors is .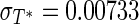

As all the thermo-physical parameters are now known, a new simulation was performed assuming 200 control volumes and a time step of 2.1615 s (cooling time divided by 2000). Equation (11) makes it possible to determine the dimensionless temperature at the boundary for each time step. In the centre, the dimensionless temperature in each time step is the value obtained for the control volume number 1. The average value of the dimensionless temperature can be calculated by Eq. (14). An idea about how much the dimensionless temperature at the boundary differs from that in the centre (and the average value) is given through Fig. 5(d).

The greater difference between dimensionless temperatures in the centre and at the boundary occurred after 402 s, and its value is 0.27151 (it is 0.92594 in the centre and 0.65443 at the boundary).

The graph of the dimensionless temperature versus the radial position r is shown at instant 402 s through Fig. 5(e).

Information about the dimensionless temperature distribution inside the cucumber, given by Fig. 5(e), is necessary in the description of its cooling because it allows for the analysis of internal stresses during the process. These thermal stresses are important because they may damage the product during the cooling process.

Equation (14) makes it possible to determine the average dimensionless temperature at any instant during the cucumber cooling. For instance, the average dimensionless temperature at the end of cooling (t = 4323 s) is 0.0904 and, with this value, the removed heat of the cucumber could be calculated.

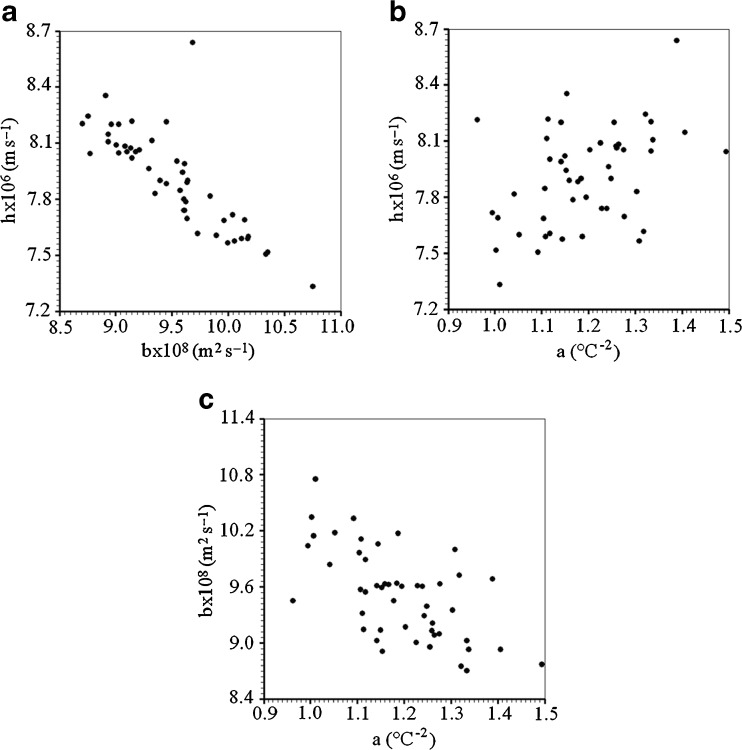
In order to estimate the uncertainties of the determined parameters and the covariance between them, 50 virtual experiments were performed as presented in Le Niliot and Lefèvre (2004). To this end, the experimental measurements were disrupted with 50 different Gaussian error distributions with zero mean value and standard deviation given by 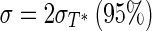. A plot showing the dispersions between “h” and “a”; “h” and “b”; and “b” and “a” is given in Fig. 6.

Fig. 6.

Dispersions between the parameters for the 50 virtual results: a h and b; b h and a; c b and a

An inspection in Fig. 6 enables to conclude that “h” decreases with an increase in “b”. On the other hand, “h” rises when “a” is increased, while “b” decreases with an increase in “a”. These results can also be seen through Table 3.

Table 3.

Elements of the correlation coefficient and covariance matrix supposing variable thermal diffusivity

	a (°C−2)	b (m2 s−1)	h (m s−1)
	Correlation	coefficient
a (°C−2)	1	−0.623412	0.412486
b (m2 s−1)	−0.623412	1	−0.813996
h (m s−1)	0.412486	−0.813996	1
	Covariance	matrix
a (°C−2)	1.34521 × 10−2	−3.42872 × 10−10	1.24181 × 10−8
b (m2 s−1)	−3.42872 × 10−10	2.24867 × 10−17	−1.00192 × 10−15
h (m s−1)	1.24181 × 10−8	−1.00192 × 10−15	6.73750 × 10−14

The average values of the parameters and also the uncertainties of them are given in Table 4.

Table 4.

Statistical treatment for the 50 virtual results supposing variable thermal diffusivity.

	Average	Standard deviation (95 %)	Standard deviation of the average (95 %)
a (°C−2)	1.1941	0.1160	0.0164
b (m2 s−1)	9.5106 × 10−8	0.4742 × 10−8	0.06771 × 10−8
h (m s−1)	7.9065 × 10−6	0.2596 × 10−6	0.0367 × 10−6

The compatibility between the values of the parameters determined through the experimental data (a = 1.202 °C⁻², b = 9.671 × 10⁻⁸ m² s⁻¹ and h = 7.763 × 10⁻⁶ m s⁻¹) and the corresponding values of the parameters obtained from the 50 virtual experiments (Table 4) is worthy of notice. For “a”, the value of the discrepancy is 0.67 %, while for “b” it is 1.7 %, and for “h” it is 1.8 %.

Student’s t-test is a statistical indicator that allows to determine the probability P(t) of a parameter given by an average value (and its uncertainty) be zero. In order to obtain information for the last results using this test, the values of “t” and P(t) are given in Table 5 for the parameters obtained through the virtual experiments.

Table 5.

t-Student test supposing variable thermal diffusivity.

	t	P(t)
a (°C−2)	72.8	0.0
b (m2 s−1)	141.5	0.0
h (m s−1)	215.4	0.0

As can be seen in Table 5, the values of “a”, “b” and “h” are significant due to the fact that, for all them, P(t) is zero.

As a final comment, although this methodology has been used by the first time for a cooling model with variable thermal diffusivity in this article, a preliminary study of the methodology was used with success to describe drying of bananas (Silva et al. 2012b), using a model with variable mass diffusivity and volume.

Conclusions

Although the present study has been applied to cooling of an individual cucumber, the proposed tools can be used to describe cooling of many products with cylindrical geometry. For the experimental dataset analyzed, the optimization process supposing constant thermal diffusivity was able to simultaneously determine the values of h and α, and the obtained results agree with the values given in the literature.

Although the consideration of constant thermal diffusivity presents satisfactory results for the cooling kinetics, the model supposing variable diffusivity is better than the constant diffusivity model. For the variable diffusivity model, it is interesting to observe that the variation of the thermal diffusivity is more significant for the dimensionless temperature (local) between 0.5 and 1.0. With respect to the calculated parameters, it is interesting to note that “h” decreases as “b” increases. On the other hand, h increases as “a” increases, while “b” decreases as “a” increases.

The proposed algorithm along with the suggested way of determining initial values is effective in the simultaneous determination of α and h. On the other hand, the determination of the uncertainties of the parameters is consistent with the standard deviation relative to the original optimization, and the t-test results in a probability zero for all parameters.

Despite the proposed tools having been applied for a cooling process, the developed study can also be applied to diffusion processes that involve the mass transfer in a product, and also the simultaneous diffusion of heat and mass.