The Parietal Reach Region Selectively Anti-Synchronizes with Dorsal Premotor Cortex during Planning

Abstract

Recent reports have indicated that oscillations shared across distant cortical regions can enhance their connectivity, but do coherent oscillations ever diminish connectivity? We investigated oscillatory activity in two distinct reach-related regions in the awake behaving monkey (Macaca mulatta): the parietal reach region (PRR) and the dorsal premotor cortex (PMd). PRR and PMd were found to oscillate at similar frequencies (beta, 15–30 Hz) during periods of fixation and movement planning. At first glance, the stronger oscillator of the two, PRR, would seem to drive the weaker, PMd. However, a more fine-grained measure, the partial spike-field coherence, revealed a different relationship. Relative to global beta-band activity in the brain, action potentials in PRR anti-synchronize with PMd oscillations. These data suggest that, rather than driving PMd during planning, PRR neurons fire in such a way that they are less likely to communicate information to PMd.

Introduction

A curious property of the cortex is that distinct regions often seem to do the same job, often facilitated by shared anatomical connections. Yet sometimes it might also be useful to downregulate these connections to preserve multiple areas' independence. On the internet, only small subsets of the nodes that could communicate actually do at any particular time, and the brain may likewise use some mechanism for isolating functional subsets of its anatomical wiring.

A great deal of recent interest has grown up around the idea that brain waves, measured as local field potentials (LFPs), thought to reflect membrane potentials (Poulet et al., 2008), could enhance communication (Fries, 2005; Buschman and Miller, 2007; Gregoriou et al., 2009; Akam and Kullman, 2010). Action potentials from one region, arriving at the peaks of an oscillation in a second, would be more likely to elicit downstream spikes (Womelsdorf et al., 2007). But the same mechanism could work in reverse: cells could time their spikes to arrive at the troughs of a distant oscillation, reducing their downstream effect. Rather than a single, synchronous oscillator, the most flexible network might be heterogeneous, linking different brain regions at different relative phases and coupling strengths.

Here, we explore whether planning a movement changes the coupling between the dorsal premotor cortex (PMd) (Cisek and Kalaska, 2005) and the parietal reach region (PRR) (Cui and Andersen, 2007). Both are strongly active before and during reaching, are monosynaptically connected (Tanné-Gariépy et al., 2002), and oscillate strongly in the beta-band during planning. Correlative studies have so far generally concluded that posterior parietal cortex drives or communicates to other regions in the beta range (Brovelli et al., 2004; Verhoef et al., 2011; Salazar et al., 2012), although there may be a confound due to power differences (see below). Yet in apparent contrast to a role in communication, beta-band activity disappears during periods of strong spiking, such as target visualization and movement (Zhang et al., 2008) and is prominent when movement is chronically suppressed, such as in Parkinson's disease (Kühn et al., 2008).

These discrepancies in the apparent role of beta oscillations could be resolved if they were found to be heterogeneous, linking different sites independently at different relative phases. Most of the data so far point to a global beta-band oscillator, broadly synchronizing parietal, frontal, and temporal cortices at various strengths, although with almost no phase lag (Salazar et al., 2012). If a subpopulation diverged from this global oscillation, and entrained or co-oscillated with another subpopulation elsewhere, this selective interaction might also affect their communication.

To reveal the particular oscillatory coupling between PRR and PMd, we use a fine-grained measure known as the partial coherence (Kocsis et al., 1999; Pesaran et al., 2008), which uses both spiking and LFP signals. The partial spike-LFP coherence regresses out the fluctuations that are common to LFPs in both regions, revealing a selective interaction between PRR spikes and PMd LFPs, which would otherwise be obscured. The exact time offset, or phase, may indicate whether the interaction serves to relatively enhance, or diminish, communication.

Materials and Methods

Two adult male rhesus monkeys (Macaca mulatta, Monkey R and Monkey L) participated in this study. All surgical and animal care procedures were conducted in accordance with National Institutes of Health guidelines and were approved by the California Institute of Technology Animal Care and Use Committee.

Recording methods.

Under sterile conditions, a stainless steel head post, a dental acrylic head cap, and a frontal and parietal recording chamber were implanted on the skull. Recordings were made from the left hemisphere of Monkey L and the right hemisphere of Monkey R. Both monkeys used their right limb for reaching. PMd and PRR were anatomically localized using structural MRI scans. PMd recordings were centered posterior and medial to the genu of the arcuate sulcus by ∼5 mm/7 mm (Monkey L/Monkey R), and PRR recordings were centered on the medial bank of the intraparietal sulcus, ∼8 mm/5 mm (L/R) anterior to the posterior extent of that sulcus. PRR recordings were located on the medial bank of the intraparietal sulcus, several millimeters anterior to previous reported PRR locations. Therefore, these recordings may actually represent tissue in-between what is often thought of as PRR, and the more anterior area 5, particularly in Monkey L. Another region was recorded 2–4 mm anterior and 3–5 mm lateral to the PRR recording sites, on the lateral bank of the sulcus. The latter recordings were conducted simultaneously with additional recordings taken in the arcuate sulcus. Of the latter two regions, the parietal site was neither reach- nor saccade-biased, and the frontal site was somewhat saccade-biased. These regions are referred to in Figure 4D (green trace). Single-unit and LFP activity was recorded from all areas using Pt/W electrodes, impedance between 0.5 and 1 MOhm, controlled by multiple-electrode microdrives (3- and 5-channel, Thomas Recordings). Spiking events and LFPs were recorded (Plexon) on separate channels, with LFPs low-pass-filtered at 200 Hz and subsampled at 1 kHz. The transfer function for the entire recording system was determined by passing a sine wave (100 μV) with a chirped profile over the relevant frequencies (1–200 Hz), with periodic simulated spikes inserted to test for any phase offset between the slow-wave and event channels. The transfer function reflected the low-pass filtering used for LFPs (3 dB at 200 Hz), as well as a low-frequency filter (3 dB at 3 Hz); there was no appreciable filtering or phase offset in our frequencies of interest (3–100 Hz). During a recording day, electrodes were simultaneously guided to both target locations. After isolating cells in both locations, the electrodes were allowed to settle into the tissue. Cells were not selected based on task-relatedness. Rather, data were collected from all cells which could be maintained in isolation.

Figure 4.

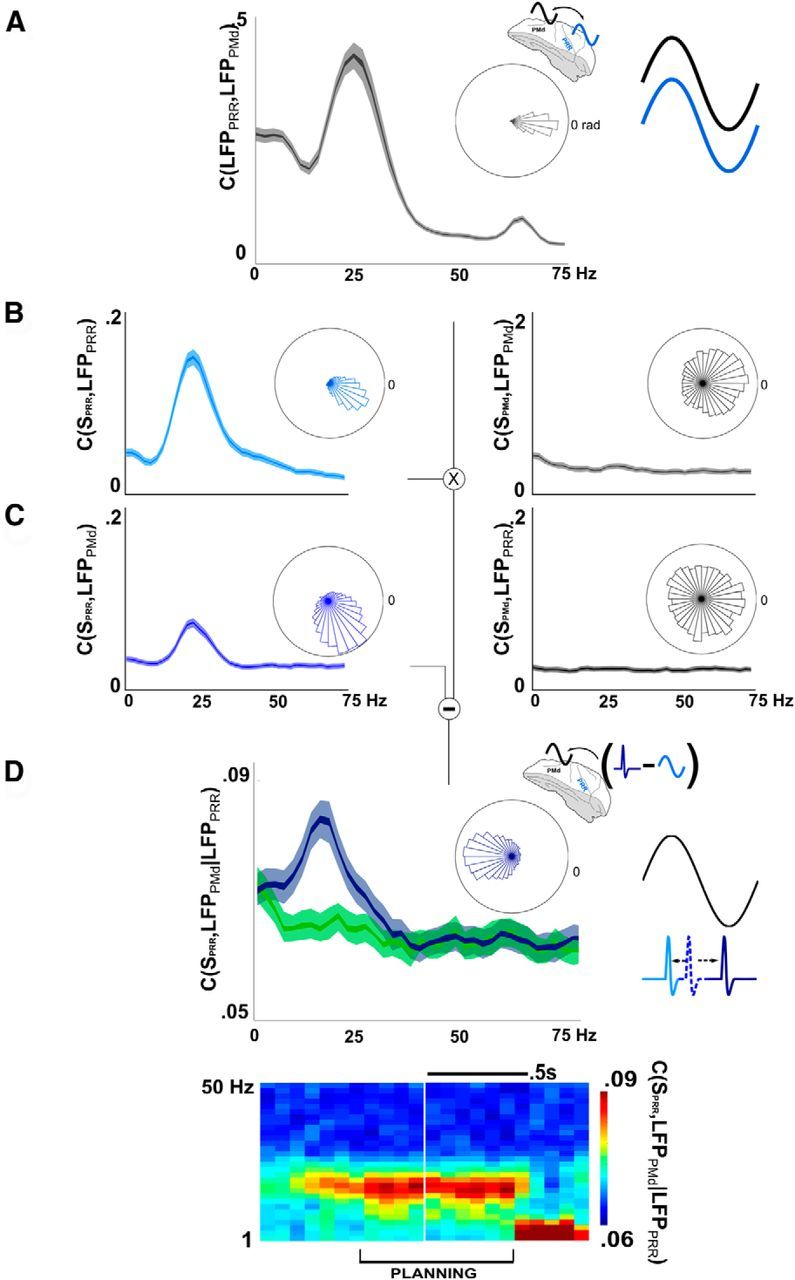
Partial coherence reveals a selective, antiphase relationship between PRR spikes and PMd LFPs. A, LFP-LFP coherence between PRR and PMd (inner and outer bands are first and 10th percentile around the median). Rose plot represents almost no phase offset between LFPs (−0.12 rad, mean PRR phase lag vs PMd). B, Spikes (S_PRR) cohere with LFPs within PRR (LFP_PRR), at a small phase lag (0.46 rad). PMd spikes also cohere to a small extent with LFPs in PMd (−0.15 rad). C, Cross-cortical spike-LFP coherence also suggests a relationship between PRR spikes and PMd LFPs (left plot; mean phase-lag of 1.05 rad). The residual difference (in the complex plane) between the cross-cortical spike-LFP coherence, C, and the cross-cortical spike-LFP coherence that would have been predicted from plots A and B, produces the partial coherence, D. The relative phase of this interaction is nearly π radians (i.e., antiphase; rose plot; mean, 3.15 rad). Like the overall beta-band effect, PRR-PMd spike-LFP coherence disappears at movement onset (coherogram, bottom, representing PRR-PMd partial spike-LFP coherence only).

Behavioral methods.

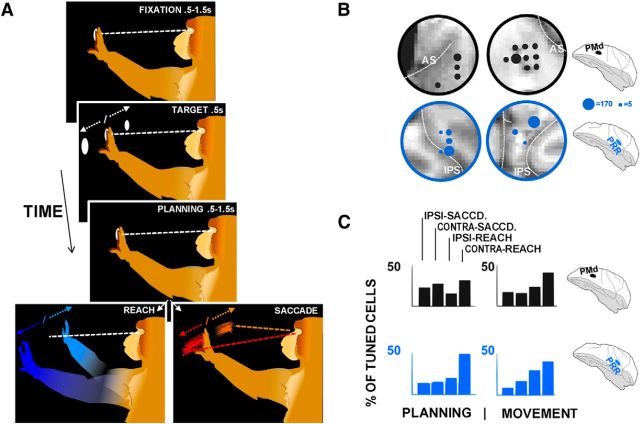
A simplified version of the tasks for both monkeys is shown in Figure 1A. Eye movements were measured using in infra-red eye tracking system (60 Hz refresh, EyeLink, SR Research), and hand movements were registered using buttons on a target board, each of which contained LEDs of multiple colors. The basic structure progressed as follows: after fixating on a central lit spot with eye and hand for 0.5–1.5 s (Table 1), the “fixation” period, the monkey saw a target simultaneously illuminated with red and green LEDs (see Fig. 1A, white LED). This two-tone target was presented in the right or left of his visual space for 0.5 s, randomly determined with 50% probability for each hemispace. Of 8 targets arranged in a square pattern, 8 inches in width, around the monkey's fixation spot, the three on the right and the three on the left were used. For the purposes of simplicity, all analyses in this manuscript average over recordings from trials with the lower, middle, and upper targets, differentiating targets by their hemispace only. After the target disappeared, the monkey was required to maintain fixation for 0.5–1.5 s, the “planning period,” after which the lit fixation spot disappeared, which was the monkey's cue to move (see Fig. 1A). Some trials required effector decisions on the part of the monkeys, and they were encouraged to randomize their choice of effectors from trial to trial (Barraclough et al., 2004). In an attempt to localize decision-related signals to the planning period, effector-decision trials were interleaved with trials in which the target changed from two-tone to a single color, either red or green, corresponding to the desired instructed effector (red for reaches, green for saccades) (Cui and Andersen, 2007). Table 1 describes the variants of this basic trial structure for the two monkeys.

Figure 1.

Task and functional similarities of PRR and PMd. A, Each monkey performed a planned-reach/saccade task, in which he held a central illuminated fixation spot with his hand and eyes as a peripheral target appeared and disappeared. After a planning period, the fixation spot disappeared, and he made either a reach or saccade to the remembered target. B, Recorded areas. Dot size corresponds to the number of cells (single and multiunit) identified in each region. C, Summary of ensemble tuning properties for each area. Top row, PMd chambers. Bottom row, PRR chambers. Left, Planning period. Right, Movement period. Each bar represents the percentage of cells tuned for ipsi-saccades, contra-saccades, ipsi-reaches, and contra-reaches, in that order, combined for both monkeys.

Table 1.

Task variants for Monkeys L and R^a

Chamber location/monkey	Arm	Fixation (s)	Bicolor target (s)	Single-color target (effector instruction, s)	Planning period (s)	Included in manuscript?	% of data per animal
R	R	0.8–1.2	0.6		0.6–1.2	Yes	50
R	R	0.8–1.2	0.6	0.6–1.2 (saccade)		No	25
R	R	0.8–1.2	0.6	0.6–1.2 (reach)		No	25
L	R	1–1.5		1 (saccade)	1–1.5	Yes	32
L	R	1–1.5		1 (reach)	1–1.5	Yes	32
L	R	0.8–1.2	0.5		0.5–1	Yes	18
L	R	0.8–1.2	0.5	0.1 (saccade)	0.5–1	Yes	9
L	R	0.8–1.2	0.5	0.1 (reach)	0.5–1	Yes	9

^aEach monkey took part in a reach-saccade task with a planning period. Monkey L used the contralateral (right) arm to the recording chamber. Monkey R used the ipsilateral (also right) arm. For Monkey R, some trials without a planning period (rows 2 and 3) were interleaved with conventional planning trials, but these trials were excluded from analysis. Any trials without an instructed effector (5th column) were decision-making trials, in which the animal was free to decide on which effector to use.

Data analysis methods.

Because of the relatively low SNR expected for cross-cortical spike-LFP coherence, calculating a coherence value required on the order of hundreds of trials. Even the most well-isolated cells exhibited some change in waveform shape over several hours. We therefore designed custom spike-sorting software, based on cluster-analysis in PCA space, which permitted the isolation of cells over the time period in which their waveforms maintained clear, slowly varying shapes. Single units were classified as those cells that had qualitatively well-separated clusters and waveforms, and 99% of interspike intervals >1 ms. LFPs experienced large and infrequent noise artifacts, caused most often by the monkey's movements. These events, identified via a threshold of 2 mV and buffered by a window of a minimum of 1 s, were likewise excluded from all analyses. Mean visually evoked times (as discussed in The role of transient responses in understanding cross-brain interaction) were the average time that the third derivative of the mean spike rate exceeded 2 SDs of the prestimulus rate distribution. Effector- and direction-selective cells were identified by calculating an ANOVA over firing rates in 20 ms bins, during the memory period, corrected for multiple comparisons. Any cell determined to be significantly tuned was classified (e.g., “contralateral reach,” “ipsilateral saccade”) according to its maximal firing rate during the time bin of the most significant difference in firing rate.

The coherence between parietal spikes S_P, and frontal LFPs F, is defined as follows:

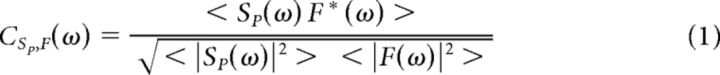where S_P(ω) and F(ω) are the frequency spectra of S_P(t) and F(t), and * denotes the complex conjugate. If S_P is a discrete signal, such as a spiking process, calculation of the coherence may be more efficient than with a continuous variable (Jarvis and Mitra, 2001). A similar calculation can be made for PMd spike, PRR LFP coherence. For the purpose of consistency in the estimate of spectral density, while also maintaining good frequency resolution, a single Slepian taper was used in calculating the spectrum. A single taper protects against high-frequency effects from the edge of the window (Bendat and Piersol, 1986) while maintaining frequency resolution. The coherence permits the calculation of an additional quantity, the partial coherence, which can filter out the effect of an explanatory signal, such as parietal LFPs, P as follows:

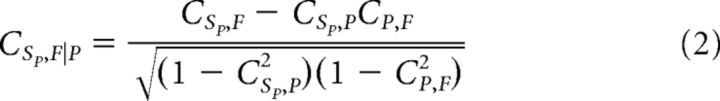Partial coherence estimates the relationship between S_P and F that is independent of P. It is derived by subtracting a linear projection of S_P onto P from S_P, and the same for F, and then calculating the coherence between the residuals. Likewise, a similar computation will estimate the partial coherence of PMd spikes and PRR LFPs. We can also calculate the extent of phase locking alone, by normalizing before averaging (similar to Vinck et al., 2012), and partializing in a similar way to Equation 2. Although beyond the scope of this manuscript, it may be of interest that these phase-locking measures produce highly similar results to Figure 4B–D (data not shown). Because there is little or no theoretical precedent in the literature for a partialized phase-locking result, we concentrate this manuscript on the use of the coherence and partial coherence.

Data for the coherence measures were collated in the following way: for a given cell and LFP pair in a given brain state, coherence was estimated in 200 ms windows, 200 windows at a time. For example, consecutive windows would be taken from one planning period, and then the next, and added to the stack of windows until 200 windows were reached. If a cell was not isolated for long enough to allow for a 200 ms stack, it was excluded. If a cell was isolated for long enough to allow for more than a single 200-window stack, all such stacks were included and considered as separate estimates. This method of using identical values for such stacks ensured consistency of the coherence measure across cells and LFPs, and for comparison to chance measures. In case of spectrograms and cohereograms (see Figs. 1B and 2D, inset), 200 ms sliding windows were taken within a trial, and windows at the same time point were then compiled across trials to calculate coherence (again, using stacks of 200). Within-area coherence was always established with LFPs taken from a different electrode than the spike in question, so as not to pollute the coherence measure with the residual of the spike measured on the same electrode. Multiunit activity was found to have a similar distribution of cross-cortical coherence to single-cell activity and was included in the figures for improved resolution.

Figure 2.

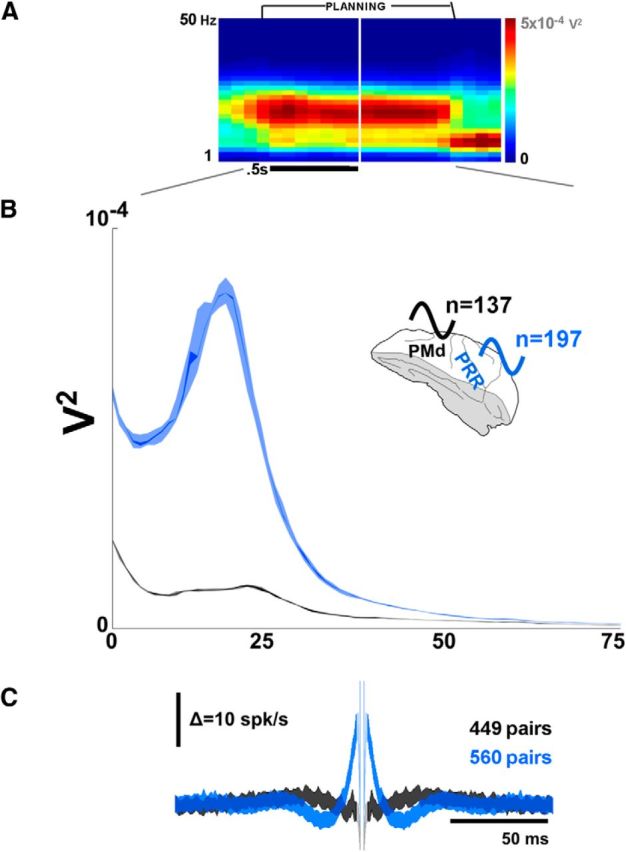
PRR and PMd have different oscillatory properties. A, Beta-band LFP activity in both brain areas emerges during the planning period. The spectrogram is averaged over both monkeys, and over PRR and PMd. B, However, differentiating by region (and averaging over the planning period) shows significantly stronger beta-band activity in PRR than PMd (p < 10⁻¹⁴, central lines are 1 percentile around the median, outer bands are 10th percentile). C, Spike-spike cross-correlation across all pairs of spikes revealed more periodicity in PRR spikes (blue) than PMd spikes (black) during the planning period.

Partial coherence could be subject to pollution by noise in the partialized signal. That is, even if a spike is perfectly time-locked to its LFP on the same electrode, it could appear to be independent if that LFP were heavily polluted by mechanical noise. To verify that the partial coherence results were not simply the result of regressing out noisy LFPs, we fit the power spectrum of all LFPs to a 1/f2 frequency profile in the log domain, between 50 and 200 Hz. We then calculated the correlation between the fit error and the partial coherence given that LFP. Although a positive correlation might have indicated an anomalous partial coherence due to noise pollution, this analysis produced slightly negative, nonsignificant correlations (Monkey L at 23 Hz, r = −0.045, p < 0.08; Monkey R at 17 Hz, r = −0.093, p < 0.06).

Frequency domain Granger causality was calculated using the method of Geweke (1982) (also used by Brovelli et al., 2004; Gregoriou et al., 2009; Verhoef et al., 2011; Salazar et al., 2012) with a history of 50 ms.

Statistical tests.

Where data are expected to be normally distributed (e.g., firing rates, mean LFP power), we use the t test/ANOVA. However, many of the data in this manuscript have non-Gaussian distributions, so we prefer in general to use a nonparametric test, the Kolmogrov–Smirnov test (K-S test). Where tests are conducted between multiple distributions (e.g., see Figs. 5 and 6), all test results are corrected for multiple comparisons.

Figure 5.

Partial spike-LFP coherence by brain state. Insets at right, Summaries of eye and hand positions during each state: yellow represents idleness; orange represents target presentation; green represents movement; black represents fixation; red represents planning. All differences are significant (p < 10⁻⁵, K-S test), except between idleness and target presentation. The idleness state is behaviorally similar to the planning and fixation states, in that the monkey's body and eyes are unmoving, and he sees no stimuli. Yet, unlike fixation and planning states, the idleness state does not elicit strong anti-synchronous beta-band activity.

Figure 6.

Partial spike-LFP coherence by planned action. Reaches and saccades (these data are Monkey L only, who used the contralateral arm to the implant site) elicited significantly different parietofrontal partial spike-LFP coherence (K-S test, p < 10⁻⁵, corrected for multiple comparisons; inner and outer lines are first and 10th percentile around the median), although differences between ipsilateral and contralateral directions are not significant (p > 0.1, K-S test).

Simulation methods.

Figure 3 shows two simulated brain regions, PRR and PMd, in two scenarios. In both scenarios, both brain regions are driven by a common driver, C, although PRR is driven with greater power than PMd. Additionally, in one scenario, spikes in PRR are connected directly to cells in region F. Details: Two sets of 128 integrate-and-fire neurons (one in PRR, one in PMd), with ∼10 Hz firing rates in each region (threshold: 0; reversal potential: −1; DC drive: 0.07, Gaussian noise stdd: 0.05), were driven by a 20 Hz beta-band source (amplitude 1; weight onto P: 0.02; weight onto F: 0.002). LFPs in both regions are calculated as the simple average of the membrane potentials of all cells. In the second version of the simulation (see Fig. 3, right column), 16 cells in P were also driven by an independent beta-band source, and these cells were connected directly to F (weight: −0.01). The same effect could be achieved by antimodulating the subset of 16 cells with an independent source that also modulated all PMd cells. Granger causality and simple and partial spike-LFP coherence were calculated as above.

Figure 3.

Amid power asymmetry, partial spike-LFP coherence reveals selective cross-cortical interactions. A, A neural simulation (I-F neurons) of a brain-wide common driver, driving PRR LFPs at greater amplitude than PMd LFPs, generates significant Granger causality, even if all signals are completely synchronous and at the same phase (Δ = difference between GC in either direction, GC(LFP_PRR,LFP_PMd) − GC(LFP_PMd,LFP_PRR)). Therefore, Granger causality does not distinguish an asymmetric common drive from a case in which PRR's spikes have a selective interaction directly with PMd (right column); displayed here as an interaction shared between a subset of PRR cells and PMd, with an antisynchronous phase; * indicates significant Granger causality, p value arbitrarily small as number of simulations increase. B, The same is true for simple spike-LFP coherence (* indicates significant simple spike-LFP coherence). However, partial spike-LFP coherence (C) between PRR spikes and PMd, with respect to PRR LFPs, can indicate whether PRR spikes interact with PMd selectively and independently of the common drive (* indicates significant partial spike-LFP coherence).

Results

Figure 1A shows the task, in which animals maintained fixation, were shown a peripheral target, and then continued to maintain fixation during a planning period of ∼0.5–1.5 s, until cued to move. Monkeys then either reached or saccaded to the peripheral target (see Materials and Methods for task details, including method of effector cueing). Figure 1B shows cortical locations in which recordings were conducted.

Figure 1C summarizes the results of the spiking responses. For each action-selective cell (ANOVA of spike rates by planned action, p < 0.05 corrected; see Materials and Methods), an identity was assigned based on the highest spike rate (ipsi-saccade, contra-saccade, ipsi-reach, contra-reach; see Materials and Methods). Both brain regions in each monkey showed a bias toward reaching movements during the movement period 150–250 ms after the cue to move (by monkey/area, % ipsi-saccade, contra-saccade, ipsi-reach, contra-reach related [total % of recorded cells that were tuned]: Monkey L/area PRR: 10, 10, 39, 41 [of 84%]; L/PMd: 14, 12, 25, 48 [75.3]; R/PRR, 9, 27, 28, 36 [35]; R/PMd, 21, 25, 23, 30 [30]). During the planning period, firing in these four regions also differentiated the animals' upcoming movements (L/RR: 8,13, 21, 58 [52]; L/PMd 20, 24, 14, 40 [58]; R/PRR, 24, 20, 20, 36 [18]; R/PMd: 28, 35, 17, 20 [31]; Monkey R also used the ipsilateral arm and had task parameters that produce somewhat weaker tuning; see Materials and Methods). The average tuning profile was less similar across areas during planning, compared with movement, with less of a reach bias in PMd.

Overall, the above analyses confirm that all four brain regions are visually responsive, contain cells that reveal the monkey's upcoming planned action, and are generally reach biased during planning and execution (Snyder et al., 1997; Cisek and Kalaska, 2005; Scherberger et al., 2005; Cui et al., 2007; Pesaran et al., 2008). These properties suggest a specialized link between PRR and PMd. However, the two regions' spiking properties were somewhat less similar during planning than during movement, which may be relevant as we uncover the way these areas interact. As a first step in understanding their interaction, we begin by assessing their individual oscillatory properties.

PRR and PMd oscillate in the beta-band, though PRR more so

PRR and PMd oscillated in the same frequency range, the beta-band, during planning. The spectrogram in Figure 2A shows the beta-band activity averaged over both monkeys and both areas (137 PMd recording sites, 197 PRR). Individually, the peak frequencies are slightly different between the two animals (peak frequencies: 17 Hz, Monkey R, PRR; 19 Hz, R, PMd; 21 Hz, Monkey L, PRR; 23 Hz, L, PMD; 20 Hz power significant, >10 Hz power, p < 10⁻³, in both animals, both regions). The adoption of beta-band oscillations by both regions confirms that they are part of the wide set of motor-related brain regions that oscillate in this frequency range, such as basal ganglia (Courtemanche et al., 2003; Kühn et al., 2008) and primary sensory and motor cortices (Murthy and Fetz, 1996).

Figure 2B illustrates that PRR oscillated much more strongly in the beta-band than did PMd (p < 10⁻²⁰ for both monkeys). The same dominance of oscillation in PRR is also visible in spiking activity. Figure 2C shows the spike-spike cross-correlation from PRR and PMd during the planning period for pairs of neurons that were simultaneously recorded (449 PMd spike-spike pairs, 560 PRR). PRR autocorrelation shows more periodicity than PMd (compare the waviness of the PRR and PMd traces). Although beta-band activity is often associated with motor cortices (Murthy and Fetz, 1996), some evidence already exists that parietal cortex has a stronger role in beta-band LFP activity (Witham et al., 2007). The data shown in Figure 2B may be the most dramatic evidence so far of the relative strength of beta-band activity in the posterior parietal cortex. Witham et al. (2007) reported an approximately threefold difference between area 5 and M1 beta-band LFP power; the PRR-PMd difference in Figure 2B is 5.9-fold (p < 10⁻¹⁰, K-S test). This power difference may indicate a heretofore unknown role for the posterior parietal lobe in a cross-brain beta-band network., more often associated with sensorimotor cortex and basal ganglia.

The difference in oscillatory power does not indicate what role beta-band oscillations play in communication. It would be tempting to assume that PRR drives PMd because it oscillates with greater power. But it could just as easily be the greatest beneficiary of a brain-wide beta-band oscillation, conducted around the brain by neural projections, or simply volume conduction. Of the available measures used for assessing how brain regions might communicate, two of the most popular, the Granger causality (Geweke, 1982; Brovelli et al., 2004; Gregoriou et al., 2009; Verhoef et al., 2011; Salazar et al., 2012) and the basic spike-LFP coherence (Womelsdorf et al., 2007; Pesaran et al., 2008; Gregoriou et al., 2009; Verhoef et al., 2011), are strongly biased by an asymmetry in power. Figure 3A shows the results of the Granger causality, applied to two simulated scenarios. The first simulation features a common driver, which drives areas PRR (here, “PRR” represents LFPs, an average over all membrane potentials) and PMd in perfect synchrony, but with different amounts of power. Despite the lack of a direct connection from PRR to PMd, the asymmetric driver generates significant PRR-to-PMd Granger causality (Δ = GC(PRR,PMd) − GC(PMd,PRR)). The PRR-to-PMd Granger causality grows stronger when a selective connection between PRR spikes and PMd LFPs is added (Fig. 3A, right column; the magnitudes could be equalized by strengthening the common driver in the left plot, making the scenarios indistinguishable to an experimenter using Granger causality).

Like the Granger causality, the simple spike-LFP coherence (Fig. 3B) has been considered a means of assessing directional interaction (Womelsdorf et al., 2007; Pesaran et al., 2008; Gregoriou et al., 2009; Verhoef et al., 2011) because spikes (S_PRR) represent the output of a region, whereas LFPs may be more representative of the inputs (Mitzdorf, 1985). However, simple spike-LFP coherence is also biased by asymmetric power (Δ = C(S_PRR,LFP_PMd) − C(S_PMd,LFP_PRR)). Essentially, any single beta-band source that drives one target more strongly than another is also likely to be represented with greater signal-to-noise, biasing both measures. The effect of asymmetric signal-to-noise on Granger causality, in particular, has been documented outside of the neuroscience literature (Nolte et al., 2008). Although this is not to say that every report of Granger causality or spike-LFP coherence is the result of asymmetric signal-to-noise, in the presence of a clear difference in power (Fig. 2), a more fine-grained measure is warranted.

The partial coherence is essentially a method of regressing out the signals common to LFPs in both regions, and it therefore removes any possible asymmetric common drive. The residual, or partial coherence, distinguishes between the scenarios with and without a selective interaction (Fig. 3C). In contrast to the Granger causality and simple spike-LFP coherence, the partial spike-LFP coherence is not necessarily meant to indicate causality or directionality. Several mechanisms could generate partial coherence, including direct drive from parietal cells to frontal, or a second common driver that weakly drives many cells in PMd and strongly drives a subset of cells in PRR. Whatever the mechanism, partial coherence is unlikely to result from a global common driver. Its existence, and its phase, may help clarify whether these two areas interact selectively and whether that interaction tends to upregulate or downregulate their communication.

Partial spike-LFP coherence reveals anti-synchrony between PRR cells and PMd LFPs

Figure 4A shows that LFPs in PRR and PMd spikes synchronize with their local electrical fields, at a phase-lag of nearly 0 (rose plot; mean lag of 0.11 rad for Monkey R, 0.21 rad for Monkey L). Although Granger causality calculated between these LFPs is highly significant (PRR-PMd>PMd-PRR, p < 10⁻²⁰, K-S test; data not shown), the LFPs are nearly perfectly in phase, which is arguably more suggestive of common modulatory activity, which could be part of a brain-wide beta-band phenomenon. Although this strong, synchronous global process is of great interest, as is its greater strength in PRR, it does not imply a direct connection.

Instead, to reveal a selective interaction between PRR and PMd, we incorporated data from single spikes. Spikes in PRR synchronize strongly with nearby LFPs (Fig. 4B, left plot), at a small phase lag. PRR spikes also synchronize with PMd LFPs (Fig. 4C, left plot), but at a larger overall phase lag, indicating a different interaction with PMd LFPs than predicted by PRR LFPs alone. Because the PRR and PMd LFPs also cohere with each other, the simple PRR-PMd spike-LFP coherence represents a mix of within-PRR and cross-PRR-PMd effects.

By removing the combined effect of within-PRR spike-LFP coherence and PRR-PMd LFP-LFP coherence using partial coherence analysis (Fig. 4D), we isolated the particular interaction of PRR spikes with PMd LFPs, independent of any global effects that might be present in PRR LFPs. The partial coherence analysis (Fig. 4D) shows that PRR spikes contain information about PMd LFPs in the beta-band, which cannot be explained by PRR LFPs themselves. Partial PRR-PMd spike-LFP coherence is significantly different from chance (at 20 Hz, p < 10⁻⁹ Monkey R; p < 10⁻²⁰ Monkey L, K-S test). These data suggest an inhomogeneity in the cortical beta-band oscillation, of the kind that might be caused by a selective interaction between PRR spikes and PMd LFPs. Of those spikes that interact selectively with PMd, most have an offset in their spike times so as to arrive at nearly a half-cycle out of phase with PMd oscillations (Fig. 4D, rose plot). At nearly π radians out of phase (3.07 rad Monkey L; 3.5 rad, Monkey R), the subset of PRR spikes that cohere selectively with PMd LFPs will arrive nearly at the trough of the subthreshold membrane potential, which will tend to reduce their effect on PMd.

The diagram in Figure 4D illustrates the partial coherence result in the time domain. The distribution of PRR spike times (average indicated by the dotted blue line) could be split into two groups: those that are predicted by the within-PRR spike-LFP coherence (light blue) and those that are not but still cohere with PMd (dark blue). The partial coherence phase indicates that the latter group actually anti-synchronize with PMd (black line, represented as inverted, as though from within the cellular membrane).

The reverse direction (PMd-PRR partial spike-LFP coherence; data not shown) is insignificant. Because the simple cross-cortical PMd-PRR spike-LFP coherence is insignificant (Fig. 4C, right), it is unlikely that any residual signal could remain after partializing. As described in Figure 3 and Materials and Methods, spikes in a more strongly driven area are more likely to cohere with LFPs in a more weakly driven area than vice-versa, which may help explain the weak PMd-PRR spike-LFP coherence.

To illustrate that the partial coherence results are not an epiphenomenon of the power asymmetry, we also present results from a second experiment, conducted in cortical regions several millimeters anterior and lateral to the PRR and PMd sites (see Materials and Methods), which were not reach-selective (i.e., cells were tuned but showed no effector bias, such as that shown in Fig. 1C). These areas had similar power differences (parietal was >6 times as powerful as frontal, p < 10⁻¹⁰, K-S test) but showed much weaker partial spike-LFP coherence (Fig. 4D, green trace; p < 10⁻⁴ Monkey R; p < 10⁻²⁰ Monkey L, K-S test; by itself, partial coherence in these nonreach regions was not significantly different from chance in Monkey R, p > 0.1, but was slightly significant in Monkey L, p < 0.01 at 20 Hz). These data suggest that the selective interaction between PRR and PMd is unlikely to be a product of unexpected, higher-order oscillatory features, or other signal-to-noise differences, but rather a true selective interaction shared between these cortical areas (see additional control analyses in Materials and Methods). All plotted results come from single-unit and multiunit spikes combined; spike-LFP coherence from single cells only is not significantly different in strength from multiunit partial coherence (KS test between memory-period single-unit and multiunit partial spike-LFP coherence at 20 Hz, p = 0.64) (Zeitler et al., 2006). Spike rate differences could in principle contribute to coherence asymmetry (Lepage et al., 2011; see in particular their Fig. 1, which details the dependence of coherence on spike rate as a function of rate), although spike rate differences are unlikely to explain this coherence asymmetry because the rates are nearly the same between parietal and frontal locations (during the planning period, the mean spike rate of well-isolated PRR units across both animals was 8.2 spike/s, vs 8.4 spike/s in PMd, two-sample t test between the log spike rates, p = 0.92).

The partial coherence indicates a point-to-point, selective interaction between PRR cells and PMd LFPs, which is independent of the synchronous oscillation, which accounts for much of the PRR LFP power (Fig. 2B) and LFP-LFP coherence (Fig. 4A). Although the phase of the interaction makes it appear to reduce communication between regions, the interaction is nevertheless shared in a highly specific way between them. These results constitute the first evidence of a direct cross-cortical spike-LFP interaction of this kind, independent of larger-scale oscillations, which are captured by PRR LFPs. Compared with what their interaction would have been if the two regions had been comodulated by a single brain-wide oscillation, the selective antiphase relationship indicates that this specific interaction is likely to reduce the effect of PRR spikes on PMd.

Planning and preparation elicit more selective anti-synchrony than passive nonmovement

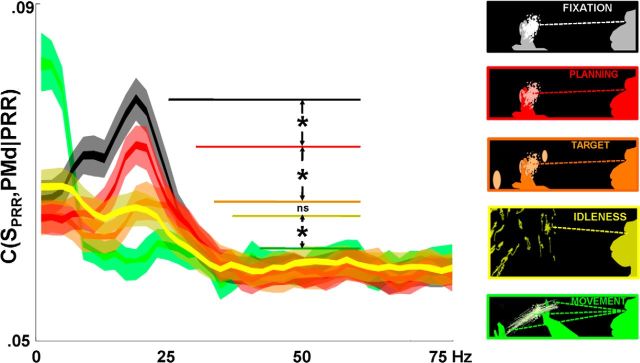
The partial coherence suggests the existence of an independent PRR-PMd interaction from the global beta-band activity in the brain. Like the global beta-band oscillation, the selective interaction is generally higher during behavioral states when the animal and environment are static and unmoving (fixation and planning), and lower during target onset and movement (Witham et al., 2007). But does this selectively down-modulating interaction appear for any static, unchanging behavioral state, as has sometimes been suggested as the role of beta-band activity (Engel and Fries, 2010), or is it more likely to occur during brain states that actively suppress movement, such as planning and preparation?

Figure 5 compares the fixation interval, target appearance interval, planning period, movement interval, and another brain state, labeled “idleness.” Idleness corresponds to periods in between behavior, where the animal is not working or moving his body, and is looking in a single direction within a darkened room (windows of time around which the animal actually generates a saccade are removed). The idleness brain state can be compared against planning periods, in which the animal is also unmoving and looking in a fixed direction, but with a particular upcoming action in mind.

PRR-PMd partial spike-LFP coherence is greater during fixation and planning periods than during target appearance, movement, and idleness periods. All comparisons between nearby states are significant to a p value of <10⁻⁵, corrected for multiple comparisons, except for the insignificant difference in partial coherence between idleness and target onset (for both monkeys). Although the animals are also unmoving during idleness, it is only during periods when they are actively planning but suppressing an upcoming movement (fixation and planning periods) that beta-band activity, and partial coherence, is high.

We can also address whether different mean spike rates contributed to the partial coherence differences across brain states (Lepage et al., 2011). Spike rates, averaged across cells in PRR, were 7.2 spike/s during the intertrial interval, 8.3 spike/s during fixation, 8.8 during target presentation, 8.2 spike/s during memory, and 9.7 spike/s during the movement period, such that the correlation between mean PRR spike rate and PRR-PMd partial coherence strength (partial coherence at 20 Hz had an amplitude of 0.076, 0.094, 0.076, 0.087, and 0.066 during corresponding periods) was r = −0.47 (p = 0.42), which does not indicate a positive relationship between spike-rate and coherence. In PMd, mean spike rates were 7.6 spike/s during the intertribal interval, 8.0 spike/s during fixation, 8.4 spike/s during target presentation, 8.4 spike/s during planning, and 8.7 spike/s during movement.

Strong low-frequency movement-period coherence (green) is typical of the movement period, but its meaning is more difficult to interpret because of large movement-related transient signals that have very low frequencies, although Pesaran et al. (2008) successfully showed that onset variations in these similar transients did not contribute to 10–15 Hz coherence.

Monkey R and Monkey L's results, individually, were slightly different from each other. Monkey L's partial coherence acted across states much as did the ensemble average shown in Figure 5 (all comparisons, p < 10⁻⁵, except idleness vs target; Monkey L's data are slightly more numerous within the ensemble). For Monkey R, planning and fixation periods were both stronger than idleness (p < 10⁻⁶), but fixation was weaker than planning (p < 0.01). Because both animals used the right arm, but only Monkey L's implant was on the left (i.e., contralateral), we reasoned that there might be an interaction between the strength of the selective interaction, and a movement plan with the contralateral arm.

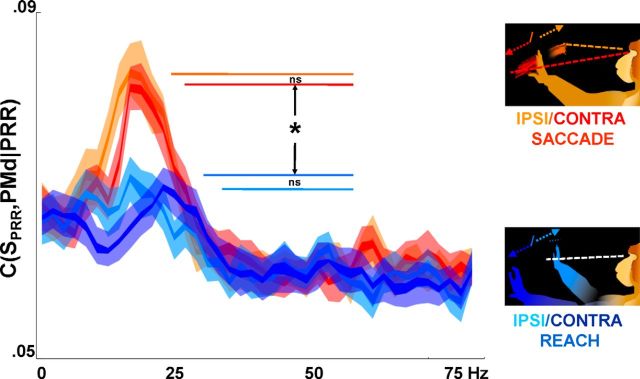
Selective anti-synchrony down-modulated by reaches with contralateral arm

The anti-synchronous PRR-PMd partial spike-LFP coherence may be related to a suppressive effect of beta-band activity on outputs. However, in advance of an action using the regions preferred effector (a reach with the contralateral arm), the anti-synchrony might need to be lifted somewhat compared with anti-synchrony during planning for other effectors. Anti-synchronous spike-LFP coherence would then be expected to be relatively less when planning reaches with the contralateral limb compared with planning eye movements.

Figure 6 shows the magnitude of the anti-synchronous, parietofrontal partial spike-LFP coherence, by direction and effector, for Monkey L. Partial coherence is indeed less during planning of reaches with the contralateral arm, whether in to the contralateral or ipsilateral spatial direction (p < 10⁻⁵, K-S test). For saccades in either direction, partial coherence is high during planning.

Consistent with Monkey R's use of the ipsilateral (right) arm, antiphase partial spike-LFP coherence remained high and did not differentiate between upcoming reaches and saccades in either direction (p > 0.1; data not shown). The plan was also more weakly discernible in Monkey R's spiking activity (Fig. 1C), which might have been partly attributable to the task variant.

Although the anti-synchronous partial coherence is weaker in advance of reaches with the preferred arm, it does not seem to be strongly affected by the visual hemifield. Figure 6 shows a difference in partial coherence between reaches and saccades, but no significant difference between ipsilateral and contralateral movement directions, suggesting that spatial attention plays little role in beta-band partial coherence of PRR spikes and PMd LFPs.

The LFP spectra and LFP-LFP coherence, which might be considered proxies for the global beta-band process, behave similarly, though not identically, to the selective process (the PRR-PMd partial spike-LFP coherence). Generally, the differences are that ipsilateral and contralateral reach plans become differentiable from each other and the reach-related signals are more powerful at higher frequencies than the saccade-related signals (consistent with Scherberger et al., 2005). In detail, ipsilateral reach plans generate more 20 Hz power than contralateral reach plans (p < 0.002, K-S test; data not shown), although both generate less than ipsilateral saccade or contralateral saccade (p < 10⁻⁴, K-S test; ipsilateral saccade not significantly different from contralateral saccade). Whereas contralateral reach generates lower PRR-PMd LFP-LFP peak coherence than ipsilateral saccade or contralateral saccade, ipsilateral reach generates slightly larger LFP-LFP coherence than either contralateral reach or either kind of saccade (contralateral reach < ipsilateral saccade/contralateral saccade, p < 10⁻¹⁰; ipsilateral reach > ipsilateral saccade/contralateral saccade, p < 10⁻¹⁰, K-S test; ipsilateral saccade not significantly different from contralateral saccade). At higher frequencies, both measures are higher for either kind of reach than for either kind of saccade (LFP power, ipsilateral saccade/contralateral saccade < ipsilateral reach/contralateral reach, 25–60 Hz, p < 10⁻³ for all combinations; LFP-LFP coherence, ipsilateral saccade/contralateral saccade < ipsilateral reach/contralateral reach, 25–60 Hz, p < 10⁻¹⁰ for all combinations). However, as Figure 6 shows, there is no frequency at which reach-related partial coherence is stronger.

These data indicate that, in advance of a reach with the contralateral arm, the anti-synchronous spike-LFP coherence may be reduced, possibly so as to facilitate communication between regions that are both tuned for the upcoming movement with the contralateral arm.

The role of transient responses in understanding cross-brain interaction

To the greatest extent possible, we assess oscillatory coupling during linear, time-independent brain states, without visual or motor transients. However, a different way to assess the interaction between areas is to monitor the time course of their responses to transient inputs. In these data, spiking in PMd responds earlier to a visual stimulus compared with PRR (Monkey L: 184.9 ms mean response time in PMd, 217 ms mean response time in PRR; Monkey R: 152 ms in PMd, 187 ms in PRR; see Materials and Methods), consistent with earlier results from our laboratory (Pesaran et al., 2008). This is further evidence that the so-called dorsal stream (Kravitz et al., 2011) may not uniformly feedforward into motor regions.

Indeed, as Figure 5 shows, and as in other recent reports (Zhang et al., 2008; Verhoef et al., 2011), beta-band oscillations are interrupted by visual stimuli. Gamma-band synchrony seems to be strongly modulated by spatial attention (Gregoriou et al., 2009). However, the insensitivity of PRR-PMd partial spike-LFP coherence to target direction (Fig. 6) makes it unlikely that spatial attention has a large effect on the selective beta-band interaction.

Discussion

These data show that, although PRR and PMd are qualitatively similar in their planning properties, PRR oscillates much more strongly in the beta-band than does PMd (Fig. 2B). These phenomena may be part of a larger gradient throughout the brain of synchronous cortical and subcortical oscillations in the beta-band (Murthy and Fetz, 1996; Courtemanche et al., 2003; Brovelli et al., 2004; Witham et al., 2007; Verhoef et al., 2011; Salazar et al., 2012), a sort of global beta-band carrier signal that drives different regions with different amounts of power. Amid this large-scale synchronous activity, we find a particular inhomogeneity between PRR spikes and PMd LFPs. PRR spikes selectively synchronize with PMd at a phase offset of π radians. This anti-synchrony may represent a reduction of the effect of PRR spikes on PMd activity, possibly explaining why PMd activity is somewhat less reach-selective during planning (Fig. 1B). This selective down-modulation of communication could selectively prevent transmission of movement-related information downstream while sparing communication within PRR and with other brain areas (Verhoef et al., 2011) that may be integral to the planning process.

A note on time-lags between regions: assuming a typical corticocortical myelenated axon conduction of speed of >5 m/s (Innocenti et al., 2013), we would expect action potentials to travel the 2+ cm between PRR and PMd in <4 ms, an order of magnitude less than the ∼50 ms period of the beta-band. Therefore, we expect that conduction velocity does not have a large effect on these results.

It is important to note that the antiphase interaction mentioned here is only relative to the overall beta-band oscillation. Both areas' LFPs still oscillate in-phase (Fig. 4A), and spikes in PRR are still timed at only a small average phase-lag to PMd LFPs (Fig. 4C), before partializing. The extent to which the large-scale beta-band synchrony in the brain contributes to information sharing awaits further study. But whatever the role of beta activity in general, Figure 4D shows that the particular relationship between PRR spikes and PMd is down-modulating in nature. This could be explained by several physiological mechanisms. The only requirement for generating this partial coherence is that two independent beta-band signals exists and that one of them engages much of the PMd LFPs, and some PRR spikes, more strongly than it does PRR LFPs. PRR and PMd could be comodulated by a large-scale common driver with asymmetric power and modulated in antiphase by a second source driving a different subset of cells. Or some PRR cells that process semi-independently of the global beta-band could also project directly to inhibitory neurons in PMd.

Although the latter possibility of a direct inhibitory projection is somewhat simpler to envision, we do not find a significant differential in overall spike rates between PRR and PMd during periods of high beta-band activity, so we do not find direct evidence that PRR spikes are actively inhibiting PMd LFPs. However, there is a reduced relationship between the two regions' encoding of the upcoming movement plan during the period of anti-synchrony (Fig. 1C), suggesting that the reach bias of PRR during planning is not communicated to PMd. Together, all of the results in this manuscript suggest the following model: most or all cells in PMd and PRR are modulated by a common beta-band source. PRR is generally more strongly modulated than PMd. Most or all cells in PMd are also modulated by an independent beta-band source. A smaller subset of PRR cells are also modulated by this second source, but in antiphase.

Put more simply, PMd diverges from the powerful beta-band oscillations present in PRR. To the extent that PRR neurons know how PMd is diverging, they fire so as to anti-synchronize with PMd. The partially coherent PRR cells do not appear to have different spiking properties or tuning than other cells in the population, so it would seem that their role in anti-cohering would simply be to obfuscate information transmission from one region to another. Moreover, although this manuscript details a particular interaction between PRR and PMd, it is still critical to understand the role beta-band may have on activity in the cortex as a whole, as well as subcortically (Murthy and Fetz, 1996; Kühn et al., 2008), and in what cases beta-band may reduce communication. The longer the oscillation period, the more a modulating signal will tend to extend beyond the timescale of the neural refractory period. So beta-band oscillations may actually reduce overall neural bandwidth simply by inhibiting them during times when they might otherwise fire (more so than with higher-frequency oscillations, such as in the gamma-band) (Gregoriou et al., 2009), contributing another factor to the overall inhibitory effect.

Beta-band activity in subcortical structures has already been identified as having an inhibitory role. The same frequency of beta-band oscillation described in this manuscript appears in the subthalamic nucleus during periods of preparation (Courtemanche et al., 2003). Also, beta-band activity is unusually strong in the subthalamic nucleus of patients and monkeys with Parkinson's disease. It may be that an overactive beta rhythm in Parkinson's disease would continually suppress movement (Kühn et al., 2008), contributing to the hypokinesia characteristic of that disease process. The present results indicate that the beta-band may also have a role in reducing corticocortical interactions, contemporaneously with the brain's suppression of movements.

There remains a question about the source of the beta-band oscillations (Hutchison et al., 2004; Wang, 2010; McCarthy et al., 2011). These data show both a special role for parietal as a powerful beta-band oscillator, and also an inhomogeneity, which implies multiple sources for the beta-band phenomenon. Further research should explore the relationship of posterior parietal with subcortical structures, to understand the way neurons change their interaction between planning and movement states in the diseased and healthy brain.