Skip to main content
PMC home page
The Journal of Neuroscience logoLink to The Journal of Neuroscience
. 2014 Sep 3;34(36):12145–12154. doi: 10.1523/JNEUROSCI.1025-14.2014

Optimal Combination of Neural Temporal Envelope and Fine Structure Cues to Explain Speech Identification in Background Noise

Il Joon Moon 1, Jong Ho Won 2, Min-Hyun Park 3,✉, D Timothy Ives 4, Kaibao Nie 5, Michael G Heinz 6,7, Christian Lorenzi 4, Jay T Rubinstein 5
PMCID: PMC4152611  PMID: 25186758

Abstract

The dichotomy between acoustic temporal envelope (ENV) and fine structure (TFS) cues has stimulated numerous studies over the past decade to understand the relative role of acoustic ENV and TFS in human speech perception. Such acoustic temporal speech cues produce distinct neural discharge patterns at the level of the auditory nerve, yet little is known about the central neural mechanisms underlying the dichotomy in speech perception between neural ENV and TFS cues. We explored the question of how the peripheral auditory system encodes neural ENV and TFS cues in steady or fluctuating background noise, and how the central auditory system combines these forms of neural information for speech identification. We sought to address this question by (1) measuring sentence identification in background noise for human subjects as a function of the degree of available acoustic TFS information and (2) examining the optimal combination of neural ENV and TFS cues to explain human speech perception performance using computational models of the peripheral auditory system and central neural observers. Speech-identification performance by human subjects decreased as the acoustic TFS information was degraded in the speech signals. The model predictions best matched human performance when a greater emphasis was placed on neural ENV coding rather than neural TFS. However, neural TFS cues were necessary to account for the full effect of background-noise modulations on human speech-identification performance.

Keywords: computational model, neural mechanism, speech perception, temporal cues

Introduction

Rate-place and temporal codes are the two primary neural codes for sound perception (Plack and Oxenham, 2005). In terms of frequency coding, the rate-place code utilizes the basilar-membrane place corresponding to the maximum discharge rate of auditory-nerve (AN) responses over the stimulus duration. However, most natural sounds fluctuate over time, therefore it is necessary to consider temporal codes that rely on shorter timescales. Any acoustic signal can be decomposed into the mathematical product of a slowly varying temporal envelope (ENVacoust) and a rapidly varying temporal fine structure (TFSacoust) (Hilbert, 1912). At the level of AN, ENVacoust is represented as variations in the discharge rate over several milliseconds (ENVneural), whereas TFSacoust is represented as phase-locking information to individual cycles of the stimulus waveform (TFSneural) (Johnson, 1980; Joris and Yin, 1992). It should be noted that complex mappings exist between the acoustic signal and its neural representation in the peripheral auditory system. For example, when acoustic signals are passed through cochlear filters, there is no one-to-one mapping between acoustic and neural ENV or TFS information (Heinz and Swaminathan, 2009; Shamma and Lorenzi, 2013).

There has been a long-standing debate about the contribution of these two acoustic features to speech intelligibility. ENVacoust information over a few spectral channels is often thought to provide sufficient information for speech intelligibility in quiet (Shannon et al., 1995), whereas TFSacoust information may play an important role when speech is presented against a complex background noise (Gnansia et al., 2009; Hopkins and Moore, 2009). However, caution should be taken to interpret these previous conclusions because TFSacoust and ENVacoust do not factor in the neural representations of these acoustic features. Furthermore it is still unclear how the central auditory system utilizes the neural information that is processed and conveyed from the peripheral auditory system.

The current study approaches the question of the neural coding of speech using psychoacoustic experiments and computational models. A recent study by Swaminathan and Heinz (2012) evaluated the contribution of peripheral ENVneural and TFSneural to speech perception in noise using a simple regression model, and showed that ENVneural was the primary contributor to speech perception. In their study, TFSneural contributed mainly in the presence of ENVneural, but rarely as the primary cue itself. However, the question of how the central auditory system utilizes such ENVneural and TFSneural information is largely unknown. To address this question, we gradually jittered the acoustic phase cues to degrade TFSacoust over 32 frequency channels with an expectation that the jittered acoustic phase cues may affect neural synchrony in AN fibers. We simulated the AN response using a computational model of peripheral auditory processing (Zilany and Bruce, 2006, 2007) to evaluate how degraded TFSacoust cues affect the encoding of TFSneural and ENVneural information. Finally, we processed the peripheral neural information using a computational neural-observer model and compared human speech identification to model predictions. In doing so, we determined the optimal combination of ENVneural and TFSneural information needed to account for speech intelligibility in steady and fluctuating noise.

Materials and Methods

Subjects.

Six native speakers of American English participated (four females and two males; five subjects between the ages of 28 and 30 and one 23 year old; mean age 27.8 years). All subjects had audiometric thresholds of 20 dB HL or less at octave frequencies between 250 and 8000 Hz in both ears. The current study was approved by the University of Washington Institutional Review Board.

Phase vocoder processing.

Figure 1 shows a schematic diagram of the Hilbert phase randomization procedure. Input waveforms, X(t), were filtered into 32 channels using an array of finite impulse-response analysis filters. They were evenly spaced on an ERBN scale between 100 and 10,000 Hz, where ERBN refers to the average value of the equivalent rectangular bandwidth (ERB) of the auditory filter for young, normal-hearing listeners at moderate sound levels (Glasberg and Moore, 1990). The bandwidth for each channel was set to 1-ERBN wide with the assumption that if vocoding is performed with analysis channels that have a similar bandwidth to auditory filters (i.e., 1-ERBN wide), the effect of the phase randomization will be primarily restricted to the temporal information encoded via neural phase locking, while the spectral information available to the central auditory system (encoded spatially on the basilar membrane in the cochlea) will be only minimally affected, if at all. In other words, the present approach explored only the role of within-channel (neural) temporal cues for speech identification. The Hilbert transform (Hilbert, 1912) was used to decompose each sub-band signal into its ENVacoust and TFSacoust. The absolute value of each sub-band analytic signal, xi(t), was taken as the sub-band ENVacoust. No additional processing was applied to the sub-band ENVacoust. The TFSacoust for each sub-band was computed as the cosine value of the angle of the analytic signal. The same analysis filters were used to filter a wideband noise, N(t), to generate a band-limited noise carrier for each sub-band, ni(t). The root mean square (RMS) value of ni(t) was set to the same RMS value as xi(t). The following equation was used to vary the extent of phase randomization:

graphic file with name zns03614-6146-m01.jpg

in which, yi(t) is the output stimulus, xi(t) is the analytic signal of the ith analysis channel, ni(t) is the filtered noise of the ith analysis channel in an analytic form, and NF is a “noise factor” from 0 to 1. As shown in Equation 1, the weighted random noise component, analytic signal [NF × ni(t)], was added to the weighted original sub-band analytic signal [(1 − NF) × xi(t)]. Then, the randomized TFSacoust was obtained by taking the cosine value of the angle of these mixed signals. The randomized TFSacoust was then modulated with the ENVacoust of the sub-band signal. Each modulated sub-band signal was subsequently filtered with the initial analysis filters. The real values of the filtered signals were then summed over all channels. For a pilot study, different types of equations were tested for the phase randomization process such as cos(angle(xi(t)) + angle(NF × ni(t))), or cos(angle(xi(t)) × [ni(t) × e−jw0(t)]NF)), where w0 is the center frequency of each analysis channel. Equation 1 was chosen because when correlations between the Hilbert TFSacoust of a vocoded signal and the corresponding original signal were computed, Equation 1 shows that, as a function of NF, the correlation coefficients decrease in a more linear fashion (Fig. 4A) than other functions tested.

Figure 1.

Figure 1.

Open in a new tab

Schematic diagram of signal processing to randomize Hilbert phase is shown. See text for details. BP, bandpass.

Figure 4.

Figure 4.

Open in a new tab

A, Mean correlation between the Hilbert TFSacoust of a vocoded signal and the corresponding original signal. Error bars show 1 SD of the mean across 10 sentences. B, C, TFSneural and ENVneural values, where the neural cross-correlation coefficients were computed between model spike-train responses to the vocoded speech and a sentence in quiet processed with NF = 0 (as a reference stimulus). Mean ρTFS and ρENV values across four AN fibers are plotted with SE bars. The IEEE sentence, the birch canoe slid on the smooth planks, was used.

Human speech-identification test procedure.

The target sentences were taken from Institute of Electrical and Electronics Engineers (IEEE) sentences (Rothauser et al., 1969), sampled at 20,000 Hz, spoken by a female speaker. The IEEE sentences were presented in either steady or amplitude-modulated, speech-shaped noise. The steady noise maskers were spectrally shaped to have the same long-term power spectrum as the IEEE sentences. The modulated noise maskers were generated by amplitude modulating the steady noise with an 8 Hz sinusoid on a logarithmic scale with a peak-to-valley ratio of 30 dB. In all trials, maskers were gated on and off with 50 ms linear ramps 500 ms before and 50 ms after the target sentences. The mixture of the target sentence and masker stimuli were then vocoded and presented monaurally to the right ear via an ER3-A insert phone at an overall target speech level of 65 dB SPL. Before actual testing, subjects listened to vocoded sentences that were processed with NF of 1 in the absence of background noise while they were presented with the sentences on the computer screen.

Speech reception thresholds (SRTs) corresponding to the 50% intelligibility level were measured using a one-up, one-down adaptive procedure. For each testing condition, subjects identified the IEEE sentences in the presence of either steady or modulated noise. Each test run started with a signal-to-noise ratio (SNR) of 6 dB, for which subjects were easily able to identify the words in the target sentence correctly. If subjects correctly identified three or more of the five keywords, the response was counted as correct and the SNR for the next sentence was decreased. If two or fewer keywords were correctly identified, the response was counted as incorrect and the SNR for the next sentence was increased. The level of the target sentence was always fixed, but the level of background noise was varied in an adaptive manner. An initial step size of 4 dB was used for the first two reversals in the adaptive track, after which the step size was fixed at 2 dB for the next six reversals. The SRT for a given track was based on the average of the SNRs corresponding to each of the last six reversals in the adaptive track. No target sentence was repeated to any subject. NF values of 0, 0.1, 0.2, 0.3, 0.5, 0.7, and 1.0 were tested in random order. For each NF value, two adaptive tracks were completed and a further adaptive track was obtained if the difference of the first two tracks exceeded 3 dB. Only about 7% of conditions across six subjects required the third adaptive track. The final threshold for each NF value was the mean of these two (or three) adaptive tracks.

Computational model of peripheral auditory processing.

A phenomenological model of the AN (Zilany and Bruce, 2006, 2007) was used to simulate spike-train responses in AN fibers to the same stimuli used in the human sentence-identification test. This model is an extension of a previously established model that has been tested extensively against neurophysiological data obtained from animals in response to both simple and complex stimuli, such as tones, broadband noise, and speech-like signals (Carney, 1993; Heinz et al., 2001; Zhang et al., 2001; Bruce et al., 2003; Tan and Carney, 2003; Zilany and Bruce, 2006, 2007). The model incorporates diverse nonlinear physiological properties of the cochlea, including compression, suppression, broadened tuning, and best-frequency shifts with increases in sound level. Inputs to the AN model were the IEEE sentence waveforms, and the output of the model was a set of spike times for four high spontaneous rate AN fibers with characteristic frequencies (CFs) of 200, 464, 1077, and 2500 Hz (CF is the frequency at which the fiber responds at the lowest sound level). These four CFs were chosen because phase locking considerably decreases above ∼2.5 kHz (Johnson, 1980).

To quantify the similarity between neural ENV or TFS responses to two different stimuli, the two sets of predicted AN spike trains were compared by computing neural cross-correlation coefficients (ρENV and ρTFS) using established techniques (Heinz and Swaminathan, 2009). Briefly, for two different stimuli passed through the AN model, one serves as a reference stimulus (A) and the other serves as a test stimulus (B). To create test stimuli, two different types of speech degradation were used: phase vocoding and adding background noise. These stimuli were passed through the AN model (Zilany and Bruce, 2006, 2007) to simulate AN spike-train responses. Shuffled autocorrelogram and shuffled cross-correlogram (SAC and SCC) analyses (Joris, 2003; Louage et al., 2004; Heinz and Swaminathan, 2009) of these spike-train responses were performed to compute neural cross-correlation coefficients (ρENV and ρTFS). These correlation coefficients describe the similarity in neural representations of ENV or TFS between the reference and test stimuli. Simulated AN spike-train responses were obtained to each of the reference (A) and test (B) stimuli, and their polarity-inverted waveforms (e.g., A+ with A−, and B+ with B−). For a given stimulus, AN responses were generated for 20 repetitions at each CF. Here, polarity inversion results in inverting the TFS but keeping ENV the same.

To quantify the strength of TFS or ENV coding to a given stimulus (A), simulated spike trains from A+ and A− were compared by creating histograms of the intervals between spikes across all pairs of repetitions (i.e., via shuffling). The shuffled autocorrelogram [SAC(A+)] was computed from spike intervals in the spike-train responses to stimulus A+, whereas the shuffled cross-polarity correlogram [SCC(A+, A−)] was computed from spike intervals between the A+ and A− spike trains. Following normalization of the histograms, TFS and ENV coding was characterized by computing “difcor” and “sumcor ” functions, respectively, as follows:

graphic file with name zns03614-6146-m02.jpg
graphic file with name zns03614-6146-m03.jpg

The peak height of the difcor or sumcor at a delay (spike interval) of zero represents the strength of TFS and ENV, respectively. To quantify the overall strength of common TFS or ENV coding between responses to stimuli A and B, a difcor or sumcor function was computed based on shuffled cross-stimulus correlograms as follows:

graphic file with name zns03614-6146-m04.jpg
graphic file with name zns03614-6146-m05.jpg

Using these difcor and sumcor functions, neural cross-correlation coefficients ranging between 0 and 1 were computed by comparing the degree of common TFS or ENV coding between A and B relative to the degree of TFS or ENV coding to A and B individually (Heinz and Swaminathan, 2009) as follows:

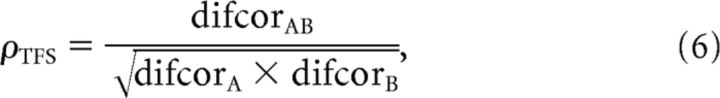graphic file with name zns03614-6146-m06.jpg
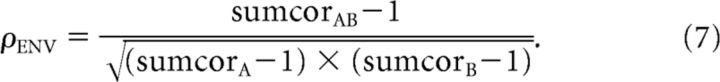graphic file with name zns03614-6146-m07.jpg

Values of ρENV and ρTFS range from near 0 for completely uncorrelated reference/test stimuli (noise floor for ρENV and ρTFS ≅ 0.1 and 0.01, respectively) to near 1 if the reference and test stimuli were perfectly correlated. For a complete illustration of the computation of ρENV and ρTFS metrics, see Heinz and Swaminathan (2009).

Computational model of the central neural observer.

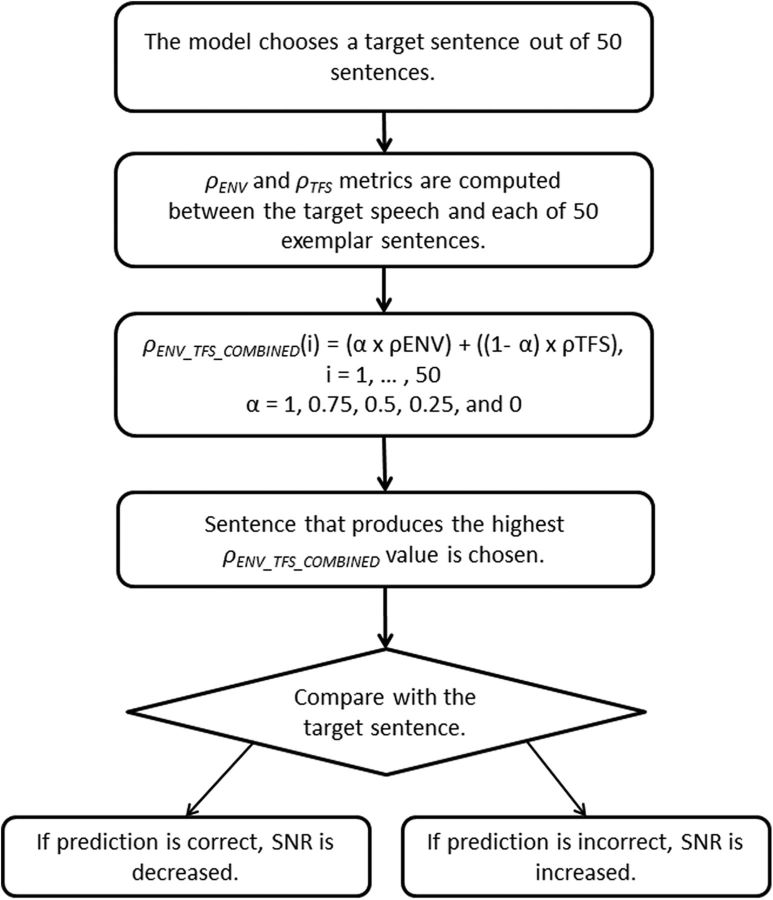
To gain further insight on how the central auditory system utilizes neural TFS and ENV information for speech perception, the sentence-identification test for human subjects was implemented using neural observers. The neural-observer sentence-identification test was conducted using the same testing paradigm as with human subjects. Human subjects were tested on an “open-set” IEEE sentence test; however, to make the computational speech-identification test more tractable, the central neural observer was provided with a set of “exemplar” sentences. Figure 2 shows the block diagram of the neural-observer computation. In each trial, the testing program randomly selected a “target” sentence out of the 50 exemplar sentences, and the peripheral model outputs were then compared between the target sentence and each of the 50 exemplar sentences. Both the target and 50 exemplars were degraded by both noise and phase vocoding at the corresponding SNR and NF. For example, for the 0 dB SNR and NF = 1 condition, when the testing program selected a target sentence randomly from the pool of 50 exemplar sentences, the background noise was added to that sentence at 0 dB SNR and the mixture of the target sentence and noise was passed through the phase vocoder with NF = 1. Here, fresh noise was generated and used for each sentence. The resulting vocoded signal was then provided to the peripheral model as a target stimulus. The 50 sentences were also degraded at the corresponding SNR and NF values; for this example, 0 dB and NF = 1. The degraded 50 exemplar sentences were provided to the peripheral model one by one. Therefore, to make a single decision, 50 different mean (across 4 CFs) ρENV and ρTFS values were computed.

Figure 2.

Figure 2.

Open in a new tab

Block diagram for the neural-observer computation. See text for details.

The neural-observer model used in this study was based upon assumptions that the central auditory system may optimally use the sensory information provided by the peripheral auditory system for the best possible speech-identification performance, depending on the acoustic environment. To simulate such a decision process, different weightings were applied to the mean ρENV and ρTFS values to compute a final decision metric for the neural observer. The following equation shows this computation:

graphic file with name zns03614-6146-m08.jpg

in which α is a weighting coefficient for ρENV, and subsequently, 1 − α is a weighting for ρTFS. Five different sets of weighting coefficients were tested (α = 1, 0.75, 0.5, 0.25, and 0).

The above procedure was performed independently for all the weightings to compare the predicted speech-identification performance by the neural-observer model. The central model had a two-step decision process. First, 50 ρENV_TFS_COMBINED values (for 50 exemplar sentences) were scanned to determine the sentence that produced the highest ρENV_TFS_COMBINED value. This sentence was saved as the predicted sentence by the central model. Second, the testing program compared the predicted sentence with the originally selected target sentence, and recorded the central neural-observer's response as either correct or incorrect. As with the speech test for human subjects, the neural-observer testing program started with an SNR of 6 dB. If the neural-observer model was not able to predict sentence identification, such a condition is marked as “n/a” in the data plot. For each testing condition, the mean threshold from six model runs was obtained.

Results

Sentence identification by human listeners

Figure 3A shows SRTs as a function of NF values. Here, a lower SRT value implies better speech-identification performance in background maskers. In general, performance was better in modulated noise (filled triangles) than in steady noise (open squares). A two-way repeated-measures ANOVA was performed to assess the effects of NF and masker type (steady or modulated noise). The main effects of NF (F(6,30) = 31.3, p < 0.001) and masker type (F(1,5) = 142.0, p < 0.001) were all highly significant. That is, as NF increased (i.e., more phase randomization), SRTs increased in both maskers, but the rate of increase for SRT values differed between the two masker types. The interaction between NF and masker type also reached significance (F(6,30) = 3.18, p = 0.015), indicating that the contribution of TFSacoust is greater for SRTs in modulated noise.

Figure 3.

Figure 3.

Open in a new tab

A, SSRTs measured from six human listeners with normal hearing in steady and modulated noise maskers as a function of NF. Error bars show 1 SEM of the mean across six subjects. B, Speech-masking release plotted as a function of NF. Error bars show 1 SEM across six subjects. Note that some error bars are invisible because the sizes of symbols are larger than the sizes of those error bars.

Speech-masking release was calculated as the SRT for steady noise minus the SRT for modulated noise. Figure 3B shows the speech-masking release as a function of NF. The amount of masking release decreased from 9.4 to 6.8 dB as NF increased from 0 to 1, creating a difference of 2.6 dB. This size of speech-masking release effect is consistent with Hopkins and Moore (2009), where they tested normal-hearing listeners using tone vocoders that preserved either 0% or 100% TFS across 32 frequency bands. There was no difference in SRTs between the first and second adaptive tracks (paired t tests, p > 0.05 for both maskers) in the sentence-identification test (i.e., there was no training effect observed).

Quantifying the effect of phase randomization on the TFSacoust, TFSneural, and ENVneural information

To estimate how the phase randomization varied the availability of TFSacoust information in the vocoded signal, correlations between the Hilbert TFSacoust (i.e., the cosine component of the analytic signal) of a vocoded signal and the corresponding original signal were computed. Ten sentences were used for this analysis. Figure 4A shows the mean correlation coefficients between the Hilbert TFSacoust of the original and vocoded signals. As NF increased from a value of 0 to 1, there was a gradual decrease in the correlation coefficients. When NF = 1 was used, the original TFSacoust information was completely degraded.

To estimate how the phase randomization varies the availability of TFSneural information in the AN, an IEEE sentence was processed with 11 NF values from 0 to 1 with a step size of 0.1. A sentence in quiet processed with NF = 0 served as a reference stimulus. Figure 4B shows mean values of ρTFS averaged across four CFs between reference and vocoded stimuli as a function of NF. As expected, ρTFS values decreased all the way to zero as NF increased from 0 to 1, which was consistent with the pattern of acoustic correlation coefficients presented in Figure 4A. This suggests that the phase randomization in the acoustic domain successfully varies the availability of TFSneural information in the AN.

It should be noted that the phase randomization in the acoustic domain may also degrade the encoding of ENVneural cues, because of the conversion of the frequency excursions of TFSacoust into dynamic variations of the output levels of the cochlear filters (i.e., ENVneural; Ghitza, 2001). The same approach was thus used to estimate the extent to which the phase randomization also alters the availability of ENVneural information in the AN. Figure 4C shows mean values of ρENV averaged across four CFs for reference and vocoded speech as a function of NF. A sentence in quiet processed with NF = 0 served as a reference stimulus. As expected, ρENV values slightly decreased as NF increased from 0 to 1. Figure 4, B and C, also shows that the phase randomization in the acoustic domain had a differential effect on TFSneural and ENVneural.

Quantifying the effect of phase randomization on TFSneural and ENVneural information in the presence of background noise

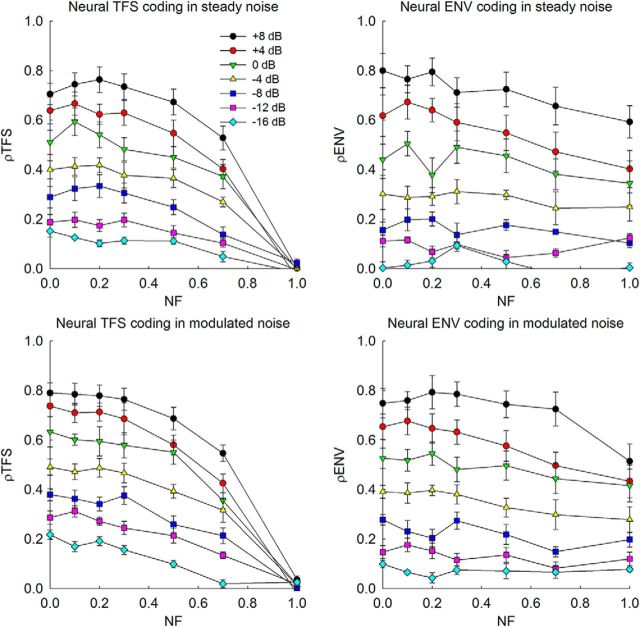
The effects of noise on the neural coding of TFS and ENV for phase-vocoded speech are shown in Figure 5. Overall, a dynamic pattern of ρTFS and ρENV values was observed. On the left side of Figure 5, mean ρTFS values averaged across four CFs in steady and modulated noise are shown on the top and bottom, respectively. Symbols represent different SNR conditions. Error bars show 1 SEM across four CFs. At each NF value, ρTFS values decreased as SNR decreased. At NF = 1, ρTFS became zero, indicating that the vocoded sentence produced completely different neural TFS coding from the original sentence. At positive SNRs, ρTFS values were relatively high and changed little until NF reached 0.5, but beyond NF = 0.5, there was a rapid decrease in ρTFS values. At negative SNRs, ρTFS values were already low, even at NF = 0. This observation illustrates the deleterious effect of adding background noise on the speech-related TFS coding in the AN. The right side of Figure 5 shows mean values of ρENV averaged across four CFs in steady and modulated noise. ρENV values measured for speech masked by noise tended to decrease as NF increased from 0 to 1, but the slopes of the functions were shallower than those for ρTFS. These data are consistent with the simulation data obtained in quiet (Fig. 4).

Figure 5.

Figure 5.

Open in a new tab

Neural coding of TFS and ENV in background noise, where the neural cross-correlation coefficients were computed between model spike-train responses to the noisy vocoded speech and a sentence in quiet processed with NF = 0 (as a reference stimulus). Symbols show different SNR conditions. Mean values and SEs across four CFs are shown. The IEEE sentence, the birch canoe slid on the smooth planks, was used.

Sentence identification predicted by the central neural observer

Figure 6 shows SRTs predicted by the central neural-observer model and obtained from six human subjects (black circles). For clarity, error bars are not plotted in Figure 5, but SEs across six model runs were generally below 1 dB. SEs across human subjects are shown in Figure 3A and they are <0.5 dB. For steady noise, the central model generally outperformed human subjects, but for modulated noise, the range of model predictions overlapped with the human data. Some patterns of the human data were well depicted by the central model. For example, the predicted SRTs of the central model consistently increased as a function of NF. When comparing steady and modulated noise, the model predicted substantially lower SNRs for modulated noise than for steady noise, consistent with human data.

Figure 6.

Figure 6.

Open in a new tab

Predicted SRTs by the central neural observer in steady and modulated noise as a function of NF. Black circles represent mean SRTs averaged across six human listeners. Symbols (red circles, green reversed triangles, yellow triangles, blue squares, and purple squares) show different ρENV weighting coefficients for the neural-observer predictions. Error bars are not plotted for clarity, but SEs across six model runs were generally below 1 dB. SEs across six human subjects can be found in Figure 3A. Note that because the neural-observer model was unable to perform the speech-identification task for NF = 1 and the ρENV weighting of 0, the data point for that condition is shown as n/a.

The central neural-observer data were generated using five different sets of weightings for ρENV and ρTFS to examine the respective effects of ENVneural and TFSneural on the intelligibility of speech (see Materials and Methods for details). When the ENVneural weighting coefficient α was set to 1, the central model used 100% of ρENV and 0% of ρTFS to conduct the sentence-identification task. Likewise, if the ENVneural weighting coefficient α was set to 0, the central model used ρTFS only without using ρENV. To quantify the difference between the human and central model predicted SRTs, the mean squared error (MSE) was computed for each model condition as follows:

graphic file with name zns03614-6146-m09.jpg

in which N indicates the number of NF values considered for computation. Except for the ρENV weighting coefficient of 0, MSE values were computed over seven NF values. For the ρENV coefficient of 0, MSE values were computed over six NF values including 0, 0.1, 0.2, 0.3, 0.5, and 0.7. Here, smaller MSE values indicate a better fit between the observed and predicted SRTs. As shown in Table 1, the central neural-observer data for the ρENV coefficient of 1 predicted the human data most accurately in steady noise. As more weighting was applied to ρTFS, the central model prediction showed a substantial decrease in SRTs in steady noise (Fig. 6), resulting in greater differences between the data from the model and human subjects (Table 1). Somewhat different patterns were observed for modulated noise. When the ρENV weighting coefficient of 0.75 was used, the smallest MSE value was observed between the human and central neural-observer model data.

Table 1.

MSE between the SRTs observed from human subjects and predicted by the central neural-observer model

ρENV:ρTFS 1:0 0.75:0.25 0.5:0.5 0.25:0.75 0:1
Steady noise 4.40 12.05 19.68 24.41 31.45
Modulated noise 1.86 0.59 1.57 14.62 3.64
Open in a new tab

Speech-masking release predicted by neural observers

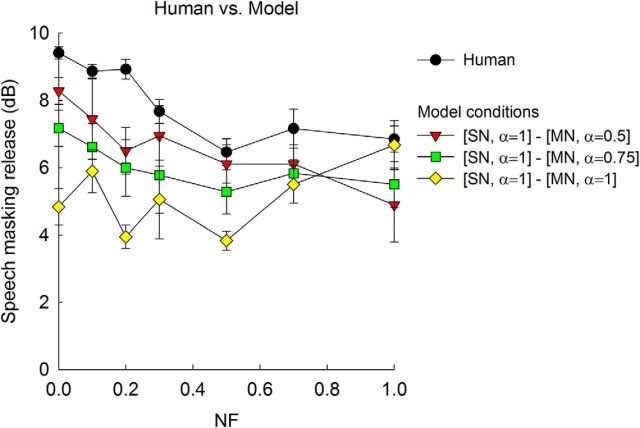
Figure 7 shows speech- masking release predicted by the central model, plotted with the data observed from human subjects. To compute the central neural-observer model prediction of speech-masking release, the ρENV weighting coefficients that showed the minimum MSE values were considered, i.e., the “best-fit” to observed SRTs was used. For steady noise, the ρENV weighting coefficient of 1 was used, and for modulated noise, the ρENV weighting coefficient 0.75 was used as these weighting coefficients produced the minimum MSE values. In addition, ρENV weighting coefficients of 1 and 0.5 also showed fairly small MSE values for modulated noise, so these ratios were also considered. In Figure 7, the central neural-observer model prediction of speech-masking release followed the pattern of human data; that is, speech-masking release decreased as NF increased. This result suggests that both human subjects and the neural-observer model increased their masking release when accurate TFSacoust cues were present (i.e., NF = 0) compared with a listening condition where TFSacoust cues were absent (i.e., NF = 1). Comparing the three model predictions, greater speech-masking release was shown when a higher weighting was given to ρTFS. Quantitatively, MSE values for the model prediction with the ρENV weighting coefficient of 0.5 for modulated noise was 2.11, whereas MSE values for the model prediction with the ρENV weighting coefficients of 0.75 and 1 for modulated noise were 3.89 and 10.16, respectively.

Figure 7.

Figure 7.

Open in a new tab

Predicted speech-masking release by the central neural-observer model. Black circles represent mean speech-masking release found for six human listeners. Red triangles represent speech-masking release predicted using the ρENV weighting of 1 for steady noise (SN) and 0.5 for modulated noise (MN). Green squares represent speech-masking release predicted using the ρENV weightings of 1 for SN, and 0.75 for MN. Yellow rhombuses represent speech-masking release predicted using the ρENV weighting of 1 for SN as well as for MN. Error bars represent 1 SE across six subjects (for human data) and across six repetitions (for the model data).

Effects of model parameters

In the current study, all model simulations were obtained with the functionality of inner and outer hair cells set to normal hearing (i.e., CIHC and COHC = 1.0) and the AN fibers had a high spontaneous rate (50 spikes per second). Input stimuli were resampled to 100 kHz before presentation to the model and scaled to best modulation level (BML). Here, BML refers to the sound level that produces maximal neural ENV coding. BMLs are typically ∼15 dB above AN fiber threshold (Joris and Yin, 1992). In this study, BMLs were computed at four different CFs for multiple input sentences to determine the overall BML, which was finally set to 35 dB SPL for all simulations in the present study. Thus, the sound level of the individual sentences used in the modeling was 35 dB SPL, which was 30 dB below the sound level used in the human speech-identification tests. However, differences in input sound level between the auditory model and human behavioral testing are consistent with many previous AN modeling studies that attempted to simulate performance of human subjects in speech-identification tests using neural responses of high spontaneous rate AN fibers (Swaminathan and Heinz, 2012; Chintanpalli and Heinz, 2013). In the AN model used in this study (Zilany and Bruce, 2006, 2007), thresholds of high spontaneous rate fibers were fitted to the lowest thresholds observed in cats (−5 dB SPL at mid-frequencies), and these fibers have rate-level functions with the typical 30–40 dB dynamic range (Miller et al., 1997). Thus, the sound levels that produced the maximum amount of neural ENV coding (best modulation levels) are quite low in the model fibers used in this study. However, given the fact that there is typically a wide range of thresholds across AN fibers, it is reasonable to expect that some fibers would exhibit essentially the same maximal neural ENV coding properties at 65 dB SPL (Joris and Yin, 1992).

To compare the effects of input sound level on the neural TFS and ENV coding, ρTFS and ρENV values were computed across four CFs between 200 and 2500 Hz. These simulations were performed using 10 different IEEE sentences presented in modulated noise at −15 dB SNR and processed with NF = 0, since the human subjects showed an average SRT of −15 dB for this listening condition. Figure 8A shows mean ρTFS and ρENV values averaged across four CFs as a function of NF for input stimulus levels of 35 and 65 dB SPL. As discussed above, a similar pattern of change in ρTFS and ρENV values as a function of NF was observed at both 35 and 65 dB SPL, suggesting that the absolute difference in input sound level between the model and behavioral speech-identification tests is unlikely to limit the conclusions from the current study.

Figure 8.

Figure 8.

Open in a new tab

Effects of input sound level, the number of CFs, and the spontaneous rate of the AN fibers on the neural TFS and ENV are evaluated. For these simulations, 10 different IEEE sentences were used. IEEE sentences were presented in modulated noise at −15 dB SNR. ρTFS and ρENV values were computed between the phase vocoded (with NF = 0) signals of the mixture (i.e., target IEEE sentence in the presence of modulated noise) and the corresponding target IEEE sentence (processed with NF = 0). A, Mean ρTFS and ρENV values averaged across four CFs (200–2500 Hz) for input stimulus of 35 and 65 dB SPL. The AN fibers were set to have a spontaneous rate of 50 spikes per second for these simulations. B, Mean ρENV values averaged across four CFs (200–2500 Hz) and seven CFs (200–8000 Hz). For these simulations, stimuli were presented at 35 dB SPL and the model was run with the spontaneous rate of 50 spikes per second. C, Mean ρTFS and ρENV values averaged across four CFs (200–2500 Hz) for three different spontaneous rates (5, 25, and 50 spikes per second). For these simulations, stimuli were presented at 35 dB SPL. Error bars represent 1 SE across 10 IEEE sentences.

In the current study, only four CFs were included between 200 and 2500 Hz for the model simulations to reduce computation time, but it may be more realistic to include higher CFs to reflect the different patterns of the AN encoding across different CFs. To evaluate the potential effect of including higher CFs, ρENV was computed for seven CFs between 200 and 8000 Hz. Note that neural TFS processing is substantially decreased above 2500 Hz (Johnson, 1980), thus only ρENV values were compared for four CFs (200–2500 Hz) and seven CFs (200–8000 Hz). Figure 8B shows that ρENV values averaged across four CFs or seven CFs were very similar, suggesting that including more CFs would not likely change the conclusions of the present study.

In the current study, all model simulations were obtained with high spontaneous rate (50 spikes per second) fibers, because the AN model has not been validated for low spontaneous rate fibers. In Figure 8C, mean ρTFS and ρENV values averaged across four CFs for three different spontaneous rates (5, 25, and 50 spikes per second) were compared as a function of NF. For these three different spontaneous rates, similar patterns of ρTFS and ρENV values were observed.

Discussion

Neural ENV and TFS coding for speech identification

In this study, a long-standing question of the neural mechanisms of speech identification in noise was explored. Our approach was unique in two aspects. From the acoustic perspective, previous vocoder studies had generally assessed the contribution of TFSneural and ENVneural cues to speech intelligibility by removing either TFSacoust or ENVacoust within each frequency band. However, this all-or-none approach may preclude a systematic assessment of the contribution of TFSneural or ENVneural on speech intelligibility. We used a phase vocoder that allows for a more gradual degradation in TFSacoust within each frequency band. From the physiological perspective, our approach provides a link between the physical sound and its representation in the AN, and a link between the peripheral sensory information and central processing for the purpose of speech perception. There are several ways to quantify TFSneural and ENVneural information in the AN. The overall strength of TFSneural and ENVneural coding in individual fibers can be quantified with synchrony-based indices (Young and Sachs, 1979; Johnson, 1980; Joris and Yin, 1992), whereas correlational or coincidence-based approaches can be used to evaluate across-fiber temporal coding (Shamma, 1985; Deng and Geisler, 1987; Carney et al., 2002). However, neither of these approaches allows for the direct assessment of the effects of degradations of TFSacoust or ENVacoust cues, because they quantify the strength of the entire temporal responses. For example, if listeners are presented with the speech signals containing TFSacoust only (Lorenzi et al., 2006), the entire ENVneural response is a combination of the independent ENVneural from the noise carrier and the speech-related ENVneural responses recovered from the TFSacoust. Cross-correlation-based metrics allows for the direct comparison of the temporal responses to original and vocoded speech, and thus provides a direct assessment of the effects of vocoding on the fidelity of speech-related cues.

Using the SCC analyses with the simulated AN responses, we showed a systematic degradation of the TFSneural and ENVneural information as a function of NF and SNR. This result is consistent with recent modeling work suggesting that jittering phase cues of the acoustic stimuli degrade the encoding of both TFSneural and ENVneural information (Heinz and Swaminathan, 2009; Shamma and Lorenzi, 2013). This dynamic interaction between the acoustic phase and the TFSneural and ENVneural information was used by the central neural-observer model. For example, at NF = 1, the original phase information was completely destroyed by the vocoder, and hence, ρTFS was near 0 (Figs. 4, 5). Thus, this condition may force listeners to use ENVneural information only. This is consistent with the fact that the central neural-observer model was unable to predict sentence identification with the ρENV weighting coefficient of 0 (Fig. 6, n/a) at NF = 1.

The central neural-observer model predicts lower SRTs when ρTFS was weighted more, demonstrating that the model prediction of speech-identification performance in noise clearly benefits from TFSneural cues. The extent to which TFSneural cues contribute to speech identification could differ for different types of maskers. For steady noise, the best fit between the SRTs observed from humans and predicted from the model was found with the ρENV weighting coefficient of 1, while for modulated noise, the ρENV weighting coefficient of 0.75 showed the best fit (Fig. 6). Furthermore, speech-masking release observed from humans was best explained when the ρENV weighting coefficient of 0.5 was used for the prediction of SRTs in modulated noise. Together, the sole use of either ENVneural or TFSneural cues does not account for human performance in all masking conditions. It may be possible that ENVneural and TFSneural cues are used optimally by the central auditory system, depending on the acoustic environment where a listener is situated.

Limitations of the current modeling approach

The model data demonstrate that it is possible to account for the effect of phase and masker type on speech identification by listeners using relatively simple decision rules that involve the use of ENVneural and TFSneural cues. Although the central model generally outperformed humans, particularly for steady noise, the fact that the model prediction replicated the pattern of human data (effects of NF and masker type) is encouraging because these models could be used in future studies investigating the effects of hearing loss on using such ENVneural/TFSneural cues or assessing the possible benefits of novel signal processing for hearing prostheses. However, it is important to acknowledge that the central model used in the present study was built on several assumptions. For example, only within-channel temporal cues were considered in the model. Also, humans were tested in open set, meaning that they do not have any exemplar sentence options available for them, but the central model was provided exemplar sentences. One can implement a closed-set speech-identification test both for humans and model simulations to minimize any procedural bias. Human listeners are able to use the top-down process for speech identification in degraded listening conditions (Warren, 1970), but the neural-observer model does not take into account such top-down processing.

The AN model used in the present study is stochastic in nature. Thus, this model takes into account the effect of internal noise at the level of the AN (Javel and Viemeister, 2000), but the model does not take into account internal noise that is generated more centrally (Vogels et al., 1989). Psychoacoustic studies on spectral and temporal auditory perception showed that human subjects (e.g., normal-hearing vs hearing-impaired subjects, or young vs older subjects) may differ strongly in terms of the central “processing efficiency,” which is their ability to use optimally the information encoded peripherally (Hall and Grose, 1994; Vinay and Moore, 2007). The model framework presented herein can readily be expanded to include the effects of reduced processing efficiency, which could potentially exist in listeners with various forms of hearing loss. For example, Lopez-Poveda and Barrios (2013) predicted the effects of the deafferentation process on temporal coding of AN fibers and how it could subsequently affect speech identification for hearing-impaired listeners. The work of Lopez-Poveda and Barrios (2013) and the present modeling study suggest that the reduction of speech-masking release that is typically associated with sensorineural hearing loss (Lorenzi et al., 2006) might result (at least in part) from the deafferentation process and the subsequent degradation of TFS coding. Altogether, the current approach could help better link the sensory information processing (i.e., from the acoustic to the peripheral neural representation) with perceptual outcomes (i.e., following processing of peripheral information into central neural information).

In the latest versions of the AN model used in this paper, simulations of the strength of phase locking (Zilany et al., 2009) and the discharge rates at saturation for higher CFs (Zilany et al., 2014) were improved. SRTs were predicted using four CFs in the current study, but it might be more realistic if more CFs were included in the advanced AN model simulations. However, even with the most recent model with more CFs, properties of ρENV and ρTFS remained quite similar as a function of NF, masker type, and SNR (data not shown). Therefore, it is unlikely that using the most recent AN model with more CFs would change the conclusions from the present study.

Implications for hearing devices and audio coding

One of the critical barriers to improving the performance of hearing prostheses is the large variability in patient outcomes, which makes it challenging or even impossible to predict hearing-aid or cochlear-implant outcomes. Patient outcome variability occurs because speech perception involves dynamic interactions between the acoustic signals (provided by hearing aids) or electric signals (provided by cochlear implants) and different biological conditions in the ears that received hearing prostheses. Hearing device signal processing has to be customized to an individual patient for the best outcomes; however, individual variability in outcomes poses a challenge. The approach presented in this paper suggests an objective and innovative way for such an optimization process. For example, the peripheral model used here was set up with the functionality of inner and outer hair cells set to normal hearing (i.e., CIHC and COHC = 1.0). These model parameters could be modified to simulate a specific hearing-loss configuration of an individual patient with hearing loss. With simulated neural responses from the customized AN model along with the prediction of speech identification by the central model, extensive evaluation of signal processing would be readily possible.

This paper also suggests that understanding the encoding and decoding of neural responses for acoustic speech signals may be crucial for the development of advanced automatic speech-recognition algorithms. Today, automatic speech recognition is widely used in desktop or tablet computers, mobile phones, home appliances, and cars. However, performance by automatic speech-recognition systems is far worse than humans, particularly in background noise (Benzeghiba et al., 2007). The performance of automatic speech-recognition systems could improve if a computational AN model were implemented as front-end processing. Such efforts have already been undertaken (Jürgens et al., 2013) and show a promising path for audio coding.

Footnotes

Research subject compensation was supported by an educational fellowship from Advanced Bionics. I.J.M. was supported by the Samsung Medical Center. J.H.W. was supported by National Institutes of Health (NIH) F31-DC009755, the University of Tennessee Health Science Center, the NeuroNet seed grant, the Hearing Health Foundation Grant, and the Todd M. Bader Grant of the Barbara Epstein Foundation, Inc. M.-H.P. was supported by the Boramae Medical Center, Seoul National University. C.L. was supported by a grant from Agence Nationale pour la Recherche (ANR) (HEARFIN project) and ANR-11-0001-02 PSL and ANR-10-LABX-0087. M.G.H. was supported by NIH R01-DC009838.

The authors declare no competing financial interests.

References

  1. Benzeghiba M, De Mori R, Deroo O, Dupont S, Erbes T, Jouvet D, Fissore L, Laface P, Mertins A, Ris C, Rose R, Tyagi V, Wellekens C. Automatic speech recognition and speech variability: a review. Speech Commun. 2007;49:763–786. doi: 10.1016/j.specom.2007.02.006. [DOI] [Google Scholar]
  2. Bruce IC, Sachs MB, Young ED. An auditory-periphery model of the effects of acoustic trauma on auditory nerve responses. J Acoust Soc Am. 2003;113:369–388. doi: 10.1121/1.1519544. [DOI] [PubMed] [Google Scholar]
  3. Carney LH. A model for the responses of low-frequency auditory-nerve fibers in cat. J Acoust Soc Am. 1993;93:401–417. doi: 10.1121/1.405620. [DOI] [PubMed] [Google Scholar]
  4. Carney LH, Heinz MG, Evilsizer ME, Gilkey RH, Colburn HS. Auditory phase opponency: a temporal model for masked detection at low frequencies. Acta Acust Acust. 2002;88:334–346. [Google Scholar]
  5. Chintanpalli A, Heinz MG. The use of confusion patterns to evaluate the neural basis for concurrent vowel identification. J Acoust Soc Am. 2013;134:2988–3000. doi: 10.1121/1.4820888. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Deng L, Geisler CD. Responses of auditory-nerve fibers to nasal consonant-vowel syllables. J Acoust Soc Am. 1987;82:1977–1988. doi: 10.1121/1.395642. [DOI] [PubMed] [Google Scholar]
  7. Ghitza O. On the upper cutoff frequency of the auditory critical-band envelope detectors in the context of speech perception. J Acoust Soc Am. 2001;110:1628–1640. doi: 10.1121/1.1396325. [DOI] [PubMed] [Google Scholar]
  8. Glasberg BR, Moore BC. Derivation of auditory filter shapes from notched-noise data. Hear Res. 1990;47:103–138. doi: 10.1016/0378-5955(90)90170-T. [DOI] [PubMed] [Google Scholar]
  9. Gnansia D, Péan V, Meyer B, Lorenzi C. Effects of spectral smearing and temporal fine structure degradation on speech masking release. J Acoust Soc Am. 2009;125:4023–4033. doi: 10.1121/1.3126344. [DOI] [PubMed] [Google Scholar]
  10. Hall JW, 3rd, Grose JH. Development of temporal resolution in children as measured by the temporal modulation transfer function. J Acoust Soc Am. 1994;96:150–154. doi: 10.1121/1.410474. [DOI] [PubMed] [Google Scholar]
  11. Heinz MG, Swaminathan J. Quantifying envelope and fine-structure coding in auditory nerve responses to chimaeric speech. J Assoc Res Otolaryngol. 2009;10:407–423. doi: 10.1007/s10162-009-0169-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Heinz MG, Colburn HS, Carney LH. Evaluating auditory performance limits: I. One-parameter discrimination using a computational model for the auditory nerve. Neural Comput. 2001;13:2273–2316. doi: 10.1162/089976601750541804. [DOI] [PubMed] [Google Scholar]
  13. Hilbert D. Grundzüge einer Allgemeinen Theorie der Linearen Integralgleichungen. Leipzig: B.G. Teubner; 1912. [Google Scholar]
  14. Hopkins K, Moore BC. The contribution of temporal fine structure to the intelligibility of speech in steady and modulated noise. J Acoust Soc Am. 2009;125:442–446. doi: 10.1121/1.3037233. [DOI] [PubMed] [Google Scholar]
  15. Javel E, Viemeister NF. Stochastic properties of cat auditory nerve responses to electric and acoustic stimuli and application to intensity discrimination. J Acoust Soc Am. 2000;107:908–921. doi: 10.1121/1.428269. [DOI] [PubMed] [Google Scholar]
  16. Johnson DH. The relationship between spike rate and synchrony in responses of auditory-nerve fibers to single tones. J Acoust Soc Am. 1980;68:1115–1122. doi: 10.1121/1.384982. [DOI] [PubMed] [Google Scholar]
  17. Joris PX. Interaural time sensitivity dominated by cochlea-induced envelope patterns. J Neurosci. 2003;23:6345–6350. doi: 10.1523/JNEUROSCI.23-15-06345.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Joris PX, Yin TC. Responses to amplitude-modulated tones in the auditory nerve of the cat. J Acoust Soc Am. 1992;91:215–232. doi: 10.1121/1.402757. [DOI] [PubMed] [Google Scholar]
  19. Jürgens T, Brand T, Clark NR, Meddis R, Brown GJ. The robustness of speech representations obtained from simulated auditory nerve fibers under different noise conditions. J Acoust Soc Am. 2013;134:EL282–EL288. doi: 10.1121/1.4817912. [DOI] [PubMed] [Google Scholar]
  20. Lopez-Poveda EA, Barrios P. Perception of stochastically undersampled sound waveforms: a model of auditory deafferentation. Front Neurosci. 2013;7:124. doi: 10.3389/fnins.2013.00124. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Lorenzi C, Gilbert G, Carn H, Garnier S, Moore BC. Speech perception problems of the hearing impaired reflect inability to use temporal fine structure. Proc Natl Acad Sci U S A. 2006;103:18866–18869. doi: 10.1073/pnas.0607364103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Louage DH, van der Heijden M, Joris PX. Temporal properties of responses to broadband noise in the auditory nerve. J Neurophysiol. 2004;91:2051–2065. doi: 10.1152/jn.00816.2003. [DOI] [PubMed] [Google Scholar]
  23. Miller RL, Schilling JR, Franck KR, Young ED. Effects of acoustic trauma on the representation of the vowel /ε/ in cat auditory nerve fibers. J Acoust Soc Am. 1997;101:3602–3616. doi: 10.1121/1.418321. [DOI] [PubMed] [Google Scholar]
  24. Plack CJ, Oxenham AJ. The psychophysics of pitch. In: Plack CJ, Oxenham AJ, Fay RR, Popper AN, editors. Pitch: neural coding and perception. New York: Springer; 2005. pp. 7–55. [Google Scholar]
  25. Rothauser EH, Chapman WD, Guttman N, Nordby KS, Silbiger HR, Urbanek GE, Weinstock M. I.E.E.E. recommended practice for speech quality measurements. IEEE Trans Audio Electroacoust. 1969;17:227–246. [Google Scholar]
  26. Shamma SA. Speech processing in the auditory system. I: the representation of speech sounds in the responses of the auditory nerve. J Acoust Soc Am. 1985;78:1612–1621. doi: 10.1121/1.392799. [DOI] [PubMed] [Google Scholar]
  27. Shamma S, Lorenzi C. On the balance of envelope and temporal fine structure in the encoding of speech in the early auditory system. J Acoust Soc Am. 2013;133:2818–2833. doi: 10.1121/1.4795783. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Shannon RV, Zeng FG, Kamath V, Wygonski J, Ekelid M. Speech recognition with primarily temporal cues. Science. 1995;270:303–304. doi: 10.1126/science.270.5234.303. [DOI] [PubMed] [Google Scholar]
  29. Swaminathan J, Heinz MG. Psychophysiological analyses demonstrate the importance of neural envelope coding for speech perception in noise. J Neurosci. 2012;32:1747–1756. doi: 10.1523/JNEUROSCI.4493-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Tan Q, Carney LH. A phenomenological model for the responses of auditory-nerve fibers. II. Nonlinear tuning with a frequency glide. J Acoust Soc Am. 2003;114:2007–2020. doi: 10.1121/1.1608963. [DOI] [PubMed] [Google Scholar]
  31. Vinay S, Moore BC. Ten(HL)-test results and psychophysical tuning curves for subjects with auditory neuropathy. Int J Audiol. 2007;46:39–46. doi: 10.1080/14992020601077992. [DOI] [PubMed] [Google Scholar]
  32. Vogels R, Spileers W, Orban GA. The response variability of striate cortical neurons in the behaving monkey. Exp Brain Res. 1989;77:432–436. doi: 10.1007/BF00275002. [DOI] [PubMed] [Google Scholar]
  33. Warren RM. Perceptual restoration of missing speech sounds. Science. 1970;167:392–393. doi: 10.1126/science.167.3917.392. [DOI] [PubMed] [Google Scholar]
  34. Young ED, Sachs MB. Representation of steady-state vowels in the temporal aspects of the discharge patterns of populations of auditory-nerve fibers. J Acoust Soc Am. 1979;66:1381–1403. doi: 10.1121/1.383532. [DOI] [PubMed] [Google Scholar]
  35. Zhang X, Heinz MG, Bruce IC, Carney LH. A phenomenological model for the responses of auditory-nerve fibers: I. Nonlinear tuning with compression and suppression. J Acoust Soc Am. 2001;109:648–670. doi: 10.1121/1.1336503. [DOI] [PubMed] [Google Scholar]
  36. Zilany MS, Bruce IC. Modeling auditory-nerve responses for high sound pressure levels in the normal and impaired auditory periphery. J Acoust Soc Am. 2006;120:1446–1466. doi: 10.1121/1.2225512. [DOI] [PubMed] [Google Scholar]
  37. Zilany MS, Bruce IC. Representation of the vowel /ε/ in normal and impaired auditory nerve fibers: model predictions of responses in cats. J Acoust Soc Am. 2007;122:402–417. doi: 10.1121/1.2735117. [DOI] [PubMed] [Google Scholar]
  38. Zilany MS, Bruce IC, Nelson PC, Carney LH. A phenomenological model of the synapse between the inner hair cell and auditory nerve: long-term adaptation with power-law dynamics. J Acoust Soc Am. 2009;126:2390–2412. doi: 10.1121/1.3238250. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Zilany MS, Bruce IC, Carney LH. Updated parameters and expanded simulation options for a model of the auditory periphery. J Acoust Soc Am. 2014;135:283–286. doi: 10.1121/1.4837815. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from The Journal of Neuroscience are provided here courtesy of Society for Neuroscience

RESOURCES