Measuring risk perceptions: What does the excessive use of 50% mean?

Abstract

Objectives

Risk perceptions are central to good health decisions. People can judge valid probabilities, but use 50% disproportionately. We hypothesized that 50% is more likely than other responses to reflect not knowing the probability, especially among individuals with low education and numeracy, and evaluated the usefulness of eliciting “don’t know” explanations.

Methods

Respondents (n=1020) judged probabilities for “living” or “dying” in the next 10 years, indicating whether they gave a good estimate or did not know the chances. They completed demographics, medical history, and numeracy questions.

Results

Overall, 50% was more likely than other probabilities to be explained as “don’t know” (vs. “a good estimate.”) Correlations of using 50% with low education and numeracy were mediated by expressing “don’t know.” Judged probabilities for survival and mortality explained as “don’t know” had lower correlations with age, diseases, and specialist visits.

Conclusions

When judging risks, 50% may reflect not knowing the probability, especially among individuals with low numeracy and education. Probabilities expressed as “don’t know” are less valid. Eliciting uncertainty could benefit theoretical models and educational efforts.

Introduction

Making good decisions involves judging the likelihood of future events. For example, perceptions of morbidity and mortality risks should be considered when making decisions about investing in health-related strategies. Subjective judgments of morbidity and mortality risks are therefore central to models of health behavior, and to intervention programs aiming to increase healthy behavior.^1-5 To inform research and educational efforts, surveys are used to measure people’s perceptions of risks. Overall, these risk perception studies suggest that, despite showing systematic biases, people can often judge valid probabilities for concrete future events.^6-11 For example, older adults’ probability judgments for living until age 75, as reported on the Health and Retirement Study (HRS), vary sensibly with their self-reported age and health behaviors, reflect actuarial life tables, and predict whether they are actually alive at age 75. ^6-8 Even adolescent respondents to the National Longitudinal Study of Youth can assess valid probabilities, for events such as getting a high-school diploma and becoming a parent by age 20, but not for dying in the next year or by age 20. ^10-11

Even though probability responses may have predictive validity, their distributions typically show excessive use of 50%, likely reflecting more than just rounding. ^{6, 12-14} Because answering 50% is especially common among less educated and low-numeracy individuals, it has been suggested that 50% may reflect not knowing what number to use. ¹³ Here, we directly asked a large national sample of Dutch participants to explain their probabilities, examining whether 50% has a different intended meaning than other probabilities, especially among individuals with low education and numeracy. We also examined whether the validity of probability responses varies by the type of explanation used.

Methods

Participants

We recruited participants from the Longitudinal Internet Studies for the Social Sciences (LISS) (http://www.lissdata.nl), drawn at random from the Netherlands’ population register. If needed, LISS offers interested individuals a computer and internet access. Participants receive €15/hour for completing monthly surveys.

Our survey was completed by 71.4% of 8143 invitees. A random subset (n=1020) received the questions analyzed here, with ages ranging from 18-95 (M=47.4; SD=15.6), 45.5% being male, and 28.7% being college-educated. The excluded respondents had similar demographics (all p>.10).

Procedure

Participants were randomly assigned to assess their probability of “living” or “dying” in the next 10 years, using a fill-in-the-blank response mode. A follow-up question asked them to explain whether they meant “a good estimate” (by selecting “I think that ‘x%’ is a relatively good estimate but I’m not quite sure it’s right” or “I think that ‘x%’ is a relatively good estimate but I don’t like to think about it too much”) or “don’t know” (by selecting “I actually have no idea about the chances” or “No one can know the chances”). These were the four main explanations expressed in cognitive interviews with Dutch individuals who thought out loud while answering our risk perception questions. We confirmed that other respondents interpreted these options as intended. A pilot-test with HRS respondents who used 50% suggested that two-thirds were willing to admit to not knowing the chances. ⁶

Here, all participants in a large national sample gave explanations, allowing us to examine whether 50% is more likely than other probabilities to be used as an expression of not knowing what number to use. Either before or after answering the probability questions, participants completed the numeracy measure developed by Lipkus and colleagues. ^{15, 16} Placement did not affect the results reported here. Participants self-reported having been diagnosed with a serious health problem like heart disease, diabetes or high cholesterol, and number of visits to medical specialists in the past year. The survey was administered in Dutch.

Results

Use of 50%

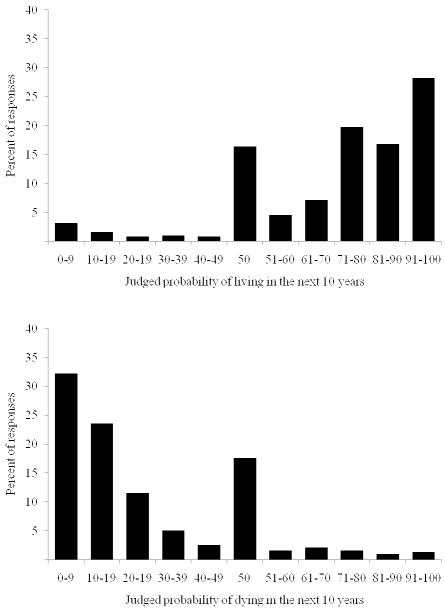
The percent of respondents answering 50% was similarly excessive in judgments of survival and mortality probabilities (17.5% vs. 16.4%, χ(1)=.25, p=.62), despite oppositely skewed distributions (Figure 1). Judged mortality probabilities were reverse-coded, so that all responses reflected survival probabilities. Consequently, the mean probability response was similar for survival and mortality, (M=77.1 vs. M=75.0, t=−1.37, p=.17). Unless noted otherwise, the reported analyses collapse survival and reverse-coded mortality probabilities.

Figure 1.

Response distributions for judged probabilities of (A) living in the next 10 years and (B) dying in the next 10 years.

Replicating previous findings, respondents who used 50% (vs. another probability) had lower levels of education, with 10.3% (vs. 19.8%) having a college degree, χ(1)=13.21, p<.001. On average, they also answered a lower proportion of the numeracy questions correctly (M=.63, SD=.23 vs. M=.67, SD=.25), t(1018)=2.15, p=.03.

Explanations for using 50%

As hypothesized, 50% was more likely than other probabilities to be explained as “don’t know” (Table 1), which held after controlling for education, numeracy, other respondent characteristics, and whether questions asked about living or dying (Table 2).

Table 1.

Percent of respondents using different explanations for their probability judgments, in overall sample, and by probability judgment, education and numeracy.

		Percent using “good estimate” explanation		Percent using “don’t know” explanation		Chi-square test comparing use of explanations
	N	Not quite sure	Don’t like to think about it	No idea	No one can know	All four	“Good estimate” vs. “Don’t know”
Overall sample	1020	16.5%	20.2%	11.6%	51.8%	-	-
Probability judgment
50%	173	6.4%	12.7%	13.9%	67.1%	χ(3)=29.07	χ(1)=27.76
Other	847	18.5%	21.7%	11.1%	48.6%	p<.001	p<.001
Education †
No college degree	676	11.8%	19.5%	10.1%	58.6%	χ(3)=54.80	χ(1)=30.40
College degree	292	27.7%	22.3%	14.0%	36.0%	p<.001	p<.001
Numeracy ‡
Low numeracy	585	11.3%	19.0%	12.1%	57.6%	χ(3)=32.86	χ(1)=24.27
High numeracy	435	23.4%	21.8%	10.8%	43.9%	p<.001	p<.001

^†A total of 968 respondents reported whether or not they had a college education.

^‡Numeracy groups were split by their median (=.73). Mean numeracy differed significantly across the four respective explanations (M=.75, SD=.22 vs. M=.69, SD=.24 vs. M=.66, SD=.23, vs. M=.63, SD=.25), F(3, 1016)=9.95, p<.001, as well as their “good estimate” (M=.71, SD=.23) vs. “don’t know” (M=.64, SD=.25), t(1018)=4.73, p<.001.

Table 2.

Logistic regression predicting use of 50% (=1) vs. other probabilities (=0).

Predictor variable	Odds ratio (OR)	95% C.I. of OR	p
Explanation for probability judgment
Good estimate, but not quite sure	-	-	-
Good estimate, but don’t like to think about it	1.60	(.74, 3.46)	.23
No idea about the chances	3.18**	(1.44, 7.01)	<.01
No one can know the chances	3.67***	(1.89, 7.15)	<.001
Control variables
College degree (vs. not)	.54**	(.35, .85)	<.01
Numeracy	1.09	(.52, 2.27)	.82
Age	1.03***	(1.02, 1.04)	<.001
Female (vs. male)	.92	(.65, 1.31)	.65
Question about living (vs. dying)	1.05	(.74, 1.49)	.78

^*p<.05;

^***p<.001.

Note: All predictors and controls were dummy variables, except for numeracy and age, which were continuous variables. A significant odds ratio below 1.00 means that 50% is less likely to be used by that group, and a significant odds ration above 1.00 means that it is more likely to be used by that group. Age was not correlated to the use of any of the four explanations (each p>.10), or their overall (“good estimate” vs. “don’t know”) categories (each p>.10).

Respondents with lower education and numeracy were relatively more likely to use “don’t know” explanations for their probability judgments (Table 1). Despite their moderate size, Pearson correlations of education (r=−.12, p<.001) and numeracy (r=−.07, p=.03) with using 50% were reduced after controlling for using “don’t know” (vs. “good estimate”) explanations (r=−.09, p<.01 for education; r=−.04, p=.16 for numeracy). Significant Sobel mediation tests (z=−3.38, p<.001 for education; z=−3.08, p<.001 for numeracy) suggested that respondents with lower levels of education and numeracy were more likely to use 50% because of not knowing what number to use.

Usefulness of explanations

To examine the validity of probability responses, we computed their correlations with age, with self-reports of having been diagnosed with a serious health problem like heart disease, diabetes, or high cholesterol (yes= 21.7%), and with number of visits to medical specialists in the past year (M=1.26; SD=2.99). As noted above, we reverse-coded judged mortality probabilities. Table 3 shows that, across all respondents, the resulting survival probabilities were valid, as seen in significant negative correlations with age, log-transformed number of specialist visits, and reporting a serious health problem, none of which differed for survival vs. mortality probabilities (p>.10).

Table 3.

Pearson correlations (r) with judged survival probabilities, as well as corresponding significance levels (p) and sample size (n).

	Age	Log of past-year specialist visits	Having been diagnosed with a serious health problem
Good estimate
…but not quite sure	r=−.54***	r=−.40***	r=−.31***
	p<.001	p<.001	p<.001
	n=168	n=168	n=168
…but don’t like to think about it	r=−.54***	r=−.25***	r=−.37***
	p<.001	p<.001	p<.001
	n=206	n=205	n=205
Don’t know
No idea about the chances	r=−.21*†‡	r=−.25**	r=−.14‡
	p=.02	p<.01	p=.13
	n=118	n=118	n=118
No one can know the chances	r=−.38***†‡	r=−.19***†	r=−.19***‡
	p<.001	p<.001	p<.001
	n=528	n=520	n=520
Overall sample	r=−.43***	r=−.25***	r=−.24***
	p<.001	p<.001	p<.001
	n=1020	n=1011	n=1011

^***p<.001.

Health problems included heart disease, diabetes and high cholesterol. We computed z-tests to examine the difference between Fisher z-transformed correlations for each “don’t know” and “good estimate” explanations. ¹⁷

^†The correlation is significantly lower than the corresponding one for “good estimate but not quite sure”

^‡This correlation is significantly lower than the corresponding one for “good estimate but don’t like to think about it”

However, these correlations were generally lower for probabilities explained as “don’t know” (vs. “good estimate”), indicating lower validity (Table 3). Z-tests comparing Fisher z-transformed correlations were not significant for each comparison, likely because some explanations were used by relatively few respondents. ¹⁷ To increase statistical power, we combined z-test results across the three outcome measures for each comparison. ¹⁷ Probabilities explained as “no idea” had significantly lower correlations than those explained as “a good estimate but I’m not quite sure” (z=−3.51, p<.001) or “a good estimate but I don’t like to think about it” (z=−3.16, p<.01). Similarly, probabilities explained as “no one can know the chances” had significantly lower correlations than those explained as “a good estimate but I’m not quite sure” (z=−3.65, p<.001) or “a good estimate but I don’t like to think about it” (z=−3.23, p<.01). A similar pattern emerged when comparing correlations for the collapsed “good estimate” and “don’t know” categories (z=−4.67, p<.001), and in partial correlations controlling for education, numeracy, and whether questions asked about living vs. dying (all z>1.88, p<.06 for comparisons between each “don’t know” vs. “good estimate” category; z=−3.55, p<.001 for comparison between collapsed categories).

Discussion

As in previous risk perception studies, a seemingly disproportionate number of respondents used 50%, when judging their probability of “living” or “dying” in the next 10 years. Researchers have proposed that 50% may represent a “don’t know” response. ^{6, 12-14} Here, we provide direct evidence that 50% is more likely than other probabilities to be explained as not knowing what number to use, especially among individuals with low education and numeracy.

Expressions of not knowing what number to use were reported with a simple follow-up question, and contained valid information about respondents’ risk perceptions. Compared to probabilities explained as “a good estimate”, those explained as “don’t know” had significantly lower correlations with age, specialist visits, and health problems. Thus, a simple follow-up question can identify respondents who do not know the risk.

One limitation is that we examined only explanations for judged probabilities of living or dying. Explanations of “don’t know” may be less common with probability questions about events that evoke less uncertainty. Asking the follow-up also increases respondent burden.

Furthermore, our follow-up did not elicit how much uncertainty about the risk respondents experienced. Recent studies in economics have found that respondents are able to express uncertainty by providing subjective probabilities for ranges of future outcomes. ^18-20 For example, judged probabilities for different inflation outcomes occurring over the next 12 months (e.g., over 12%, between 8% and 12%, between 4% and 8%, etc.) had few missing responses, with expressed uncertainty (reflected in the distribution of probabilities across outcome categories) being larger among respondents with lower numeracy and financial literacy. ¹⁸ However, such complex questions may present more respondent burden than our simple follow-up.

Our results suggest that asking respondents whether their probability judgments represent “don’t know” or a good estimate provides useful information about how well they know the risk. Not knowing one’s health risks may lead to the postponement or even avoidance of decisions to change behavior or seek medical care. Hence, eliciting uncertainty about perceived morbidity and mortality risks may help to provide insight into people’s decision-making processes and identify individuals in a need of specialized health risk communication.