Abstract
Motion estimation methods in single photon emission computed tomography (SPECT) can be classified into methods which depend on just the emission data (data-driven), or those that use some other source of information such as an external surrogate. The surrogate-based methods estimate the motion exhibited externally which may not correlate exactly with the movement of organs inside the body. The accuracy of data-driven strategies on the other hand is affected by the type and timing of motion occurrence during acquisition, the source distribution, and various degrading factors such as attenuation, scatter, and system spatial resolution. The goal of this paper is to investigate the performance of two data-driven motion estimation schemes based on the rigid-body registration of projections of motion-transformed source distributions to the acquired projection data for cardiac SPECT studies. Comparison is also made of six intensity based registration metrics to an external surrogate-based method. In the data-driven schemes, a partially reconstructed heart is used as the initial source distribution. The partially-reconstructed heart has inaccuracies due to limited angle artifacts resulting from using only a part of the SPECT projections acquired while the patient maintained the same pose. The performance of different cost functions in quantifying consistency with the SPECT projection data in the data-driven schemes was compared for clinically realistic patient motion occurring as discrete pose changes, one or two times during acquisition. The six intensity-based metrics studied were mean-squared difference (MSD), mutual information (MI), normalized mutual information (NMI), pattern intensity (PI), normalized cross-correlation (NCC) and entropy of the difference (EDI). Quantitative and qualitative analysis of the performance is reported using Monte-Carlo simulations of a realistic heart phantom including degradation factors such as attenuation, scatter and system spatial resolution. Further the visual appearance of motion-corrected images using data-driven motion estimates was compared to that obtained using the external motion-tracking system in patient studies. Pattern intensity and normalized mutual information cost functions were observed to have the best performance in terms of lowest average position error and stability with degradation of image quality of the partial reconstruction in simulations. In all patients, the visual quality of PI-based estimation was either significantly better or comparable to NMI-based estimation. Best visual quality was obtained with PI-based estimation in 1 of the 5 patient studies, and with external-surrogate based correction in 3 out of 5 patients. In the remaining patient study there was little motion and all methods yielded similar visual image quality.
Keywords: Motion estimation, Data-driven, SPECT, Motion correction
1. Introduction
Motion estimation methods in single photon emission computed tomography (SPECT) can be divided into methods which depend on just the emission data, or at least in part make use of some other source of information such as that provided by an external motion-tracking system as investigated herein. Data-driven motion estimation has the advantage of not needing the extra setup-time and cost associated with the equipment of an external tracking system. Although external motion-tracking can produce accurate real-time estimates (McNamara et al 2009), another disadvantage is the reliance on a direct correlation between internal organ motion and the externally exhibited motion. As observed from preliminary investigations using MRI of volunteers in (King et al 2009), the correlation between the motion of external markers and the motion of the heart can deteriorate in the case of arm motion involving significant movement of the shoulders and non-rigid body motions. Data-driven methods therefore offer an attractive alternative.
Most data-driven approaches use a measure of consistency between measured and estimated projections to arrive at the motion estimate. While some approaches correct for only axial and lateral translational motion in the sinogram domain (Huang et al 1992, Arata et al 1996, Lee et al 1998, Bai et al 2009), other methods aim to estimate the six-degree-of-freedom (6-DOF) transformation of the activity distribution in three-dimensions (3D) (Hutton et al 2002, Kyme et al 2003, Feng et al 2006a, Schumacher et al 2009). Unlike PET where all angles are available for every motion group, the most commonly employed current SPECT cameras involve rotation of the detector head during acquisition. The consequence of this is that for SPECT an incomplete set of angles is acquired for a given pose of the patient, making data-driven 6-DOF motion estimation in SPECT a challenging problem. Additionally, the acquisition protocol for imaging i.e., three detector heads for 360 degree acquisition in brain imaging, and two heads at 90 degrees which acquire only 180 degrees of data in a typical cardiac acquisition, has an effect on the performance of the data-driven methods due to stereoscopic effects. Kyme et al (2003) proposed a method to estimate and correct the rigid-body motion of brain SPECT studies. The method was shown to improve the image quality of motion-corrupted digital and physical Hoffman phantoms for 6-DOF motion. It was proposed that the method may be adapted to correct for gradual motion as well.
In this work two different registration-based data-driven strategies based on that of Kyme et al (2003) were considered for application in cardiac perfusion SPECT imaging. Some important differences exist between brain and cardiac imaging other than different acquisition protocols as noted before. The brain consists of oriented structures contained in a rigid skull, with fairly similar attenuation all around. The motion of the brain is well approximated as rigid. In cardiac imaging, the attenuation profile of the torso varies greatly with projection angle. Also, the assumption that motion of the heart is rigid with the rest of the chest depends upon the type of movement (King et al 2009). These differences may have an influence on the performance of a scheme similar to Kyme et al (2003) when applied to cardiac imaging, the topic of the current investigation. Further, herein different cost functions were compared in addition to the mean-squared difference (MSD) used in Kyme et al (2003) to determine if an even better correction can be obtained. Besides, in our data-driven strategy the time of motion-occurrence was obtained from the external-surrogate. Botvinik et al (1993) showed that small vertical motion of 1–2 pixels (4–8 mm) occurring for eight frames (5–6 min.) around the middle of the acquisition may cause significant artifacts in cardiac SPECT. More recently, Wheat et al (2004), analyzed 800 myocardial SPECT studies and determined 36% contained visually detectable motion. In clinical cardiac studies, we have observed using a motion–tracking system, translations on the order of 1–2 pixels (~ 5–9 mm) and rotations up to about 8 degrees (Mukherjee et al 2010a).
Herein we have investigated the sensitivity of data-driven 6-DOF motion estimation to clinically realistic motion. Two data-driven schemes with five different cost functions were compared using NCAT phantom data with motion (Segars et al 1999), with SPECT imaging simulated by the SIMIND Monte-Carlo software (Ljungberg et al 1989). The preferred scheme with the best cost function was then compared to external tracking-based motion estimation for patient studies. The use of this scheme in combination with externally measured motion was also studied to determine if further improvement over using it alone was possible. Based on this work, a realistic assessment of the accuracy of the data-driven estimation scheme was derived and areas of further improvement were identified.
2. Materials and Methods
2.1. Data-driven Motion Estimation
2.1.1. Dividing Projections into Motion Groups
The projection data were first divided into motion groups, where a group consisted of the projection angles where the patient maintained essentially the same pose. The motion transformation was then estimated between these groups. We used data-driven estimation with the best case scenario of assuming known motion groups. For patient studies, the division into motion groups was facilitated by the external-motion tracking measurements (McNamara et al 2009). In this aspect our method deviates from that of Kyme et al (2003) where a data-driven approach was used to obtain motion groups.
2.1.2 Data-driven Motion Estimation Schemes
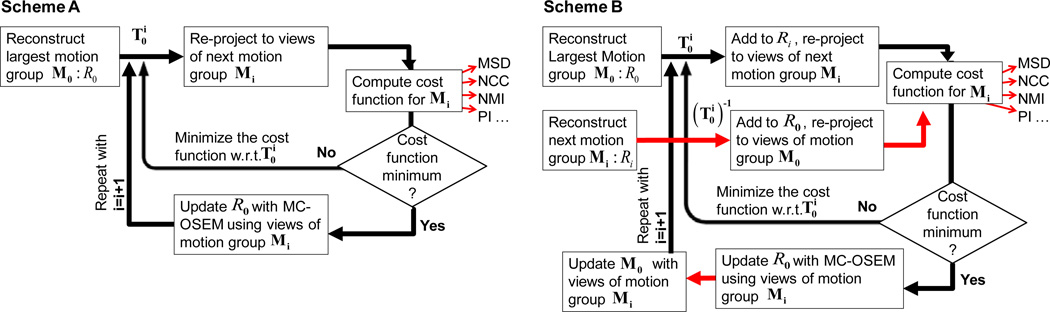
Fig. 1 shows a flowchart of the two data-driven estimation schemes used in this work. In Scheme A (Fig. 1 (a)), the largest motion group was selected as the 0th (reference) motion group (M0) and was first partially reconstructed using the Ordered Subsets Expectation Maximization (OSEM) algorithm (Hudson et al 1994) to obtain an initial motion-free model. This was then re-projected to the angles of the other motion groups, and compared for consistency with the measured projections using various cost functions described in the following section. The 6-DOF transformation of the heart from group 0 to group i where i = 1, 2, … M−1, represented by was estimated by minimizing the cost function for motion group i. Scheme A is very similar to the estimation scheme in Kyme et al (2003), with the only difference being that the transformations were always obtained relative to group 0, and the object was reconstructed at the 0th (reference) state.
Figure 1.
Figure shows two data-driven estimation schemes adapted from Kyme et al (2003) in this work. The cost functions investigated to optimize the transformations were 1) mean-squared difference (MSD), 2) total mutual information (MI), 3) total normalized mutual information (NMI), 4) average pattern intensity (PI) 5) normalized cross-correlation (NCC) and 6) entropy of the difference (EDI). (a) Scheme A: the cost function only includes the projections in motion group Mi for estimating . (b) Scheme B: the cost function includes projections at motion group Mi as well as M0 for estimating . This extra step is shown by red arrows.
Scheme B (Fig. 1 (b)) added some steps to Scheme A, wherein the next motion group Mi was also partially reconstructed (Ri) and added to R0 after inverse transforming with . The sum was then re-projected to the projection angles of M0 and the cost function for group i was computed using all angles in M0 and Mi. Thus each iteration of Scheme B involved a two-way transformation (R0 ↔Ri). For the estimation of Mi (i > 1), M0 was updated to include all projection angles up to the motion group Mi−1 for which the transformations had already been estimated. As in Scheme A, the transformation of each group with respect to the reference was estimated sequentially. In both the schemes, motion-compensated OSEM (MC-OSEM) (Feng et al 2006b) was used to update the partial reconstruction as the transformations became available.
In Kyme et al (2003), the groups were ordered such that the successive motion groups were well spaced angularly to add maximum information in each update of the reconstructed object. In our studies involving a maximum of three motion groups, the estimation proceeded with groups successively reducing in size. Once all the motion groups were estimated, a single iteration of the data-driven estimation was considered complete, and the whole process was repeated again with the full reconstruction as R0 and newly initialized transformation parameters.
2.1.3 Projector for data-driven estimation
The projection process started with a 3D Gaussian rotation combining the rotational component of the patient motion and gantry rotation, and 3D translation to align the current estimated source distribution with the patient location and gantry viewing angle. The details of this process are described in Feng et al, 2006. The employed projector models distance-dependent system spatial resolution in 3D with an incremental Gaussian blurring kernel (McCarthy et al, 1991). Attenuation was modeled during simulation of the projections; however, attenuation correction was not employed in the projector during motion estimation. This is because the attenuation map is typically aligned to the first or last motion group (in time). In general the transformation between the 0th (largest) motion group and the attenuation map was not known a priori, and therefore the cost functions were evaluated without employing attenuation and scatter correction. Additionally, in previous work (Mukherjee et al, 2011) we have observed that using attenuation correction during data-driven estimation did not lower the estimation error in cases where the attenuation map was aligned with the 0th (largest) motion group. The effect of filtering the projection and re-projection before evaluating the cost function was also investigated. A 2D-Butterworth filter of order 5 and filter cutoff 0.2 (fraction of Nyquist frequency) was employed for this purpose. The filter parameters were not optimized but chosen to closely match the values typically used for low-dose stress cardiac SPECT studies at our site.
2.1.4 Cost Functions (Consistency Metrics)
The cost functions investigated were 1) mean-squared difference (MSD) (Kyme et al 2003), 2) mutual information (MI) (Studholme et al 1999), 3) normalized mutual information (NMI) (Studholme et al 1999), 4) average pattern intensity (PI) (Wu et al 2009), 5) normalized cross-correlation (NCC) (Penney et al 1998), and 6) entropy of the difference (EDI) (Penney et al 1998). These cost functions have been used in 2D–3D registration problems in medical imaging as in Penney et al (1998) for registration of fluoroscopy to CT. The cost function for a motion group was obtained by summing a metric over the projections belonging to that group. The cost functions are defined in the following equations with P(i,p) representing the pth projection in the ith motion group, and RP(i,p) representing the corresponding re-projection, where p = {1,2,….ni}, and ni is the number of projections in the motion group. Thus, the ith motion group is represented by Mi = {Pi,1, Pi,2,…, Pi,ni}. A rectangular region of interest (ROI) was defined by visual inspection such that it enclosed the heart at all projections but excluded most of the liver and other organs. DROI is the number of pixels in this region per projection. All cost functions were computed using pixels within the ROI.
| (1) |
| (2) |
where , is the (Shannon) entropy of P(i,p), xb represents the bth bin of the histogram of P(i,p), h(x) the probability mass function obtained using pixels within ROI, and , is the joint entropy of P(i,p) and RP(i,p), where (xbx yby) represents the 2D histogram bin of P(i,p) and RP(i,p) indexed by (bx,by), and h(xbx yby) is the joint probability mass function obtained using pixels within the ROI.
| (3) |
| (4) |
where r2 is the local neighborhood size, s is a scale factor, d2 = (j − u)2 + (k − v)2, is the distance of the neighborhood pixel at (u,v) from the central pixel at (j,k), and represents the noise variance in the difference image.
| (5) |
where represents the mean intensity over the pixels within ROI in image P(i,p).
| (6) |
where H(P(i,p)) is the entropy as defined in (2), and s is a scale factor as defined in (4).
The MI, NMI, NCC and PI values are maximum for correct registration, thus the negative of their values were used for the minimization routine. The neighborhood radius r and noise variance parameter σ for PI were chosen empirically using sensitivity (defined in section 2.6) studies with the NCAT phantom. We found that σ equal to two times the average counts in the ROI of the projection data was satisfactory for our application. The scale s in PI and EDI was chosen such that the average count level in the ROI of the re-projection and actual projection were the same. For MI-based measures, use of the sum of individual projection MIs was suggested in (Clarkson et al 2000), and was shown to be better than combining all projections into a single histogram. In this work, both the methodologies (summing individual projection MIs, and pooling all projections to obtain a single MI) were tested. The cost function sensitivity to changes in pose and the accuracy of the estimates (defined in section 2.6) were compared for various motion simulations using the NCAT phantom.
2.1.5 Optimization Method
For minimization we employed the downhill simplex algorithm (Nelder and Mead 1965, Press et al 1992) which is a non-gradient based optimization methodology. In the first iteration of motion estimation, only five degrees of freedom were estimated excluding the rotation about Z-axis (gantry rotation axis) to lower the estimation error due to partial angle effects as reported in Mukherjee et al, 2011. The rotation about Z-axis was either arbitrarily fixed to be zero, or given a value obtained from the external motion tracking. In the second iteration, the optimization was initialized with seven non-degenerate points (in 6-dimensional space of transformation parameters) for estimating 6-DOF motion. To address the possibility of being trapped in a local minimum, we modified the optimization scheme so that the simplex was initialized multiple times from randomly chosen sets of points within each iteration of motion estimation. Also, the last sub-iteration was initialized with the minima obtained from previous sub-iterations. For patient studies, a hybrid scheme was employed where external-tracking estimates were used as one of the initial points of the optimization. This was done to constrain the Z-axis rotation to realistic values as otherwise the estimated rotation about Z-axis tends to be large due to limited angle artifacts (Mukherjee et al 2011).
2.2. Visual Tracking System (VTS) Based Motion Estimation During Patient Acquisition
The VTS (McNamara et al 2009) tracked the motion of retro-reflective markers attached to the chest and abdomen of patients undergoing SPECT imaging. The signal from each marker consisted of 3 one-dimensional traces corresponding to the absolute X, Y and Z location of the marker in 3D space of the SPECT coordinate system over time. Each of these traces had at least a periodic component (PM) due to respiration and a non-periodic component (NPM) that corresponds to abrupt pose changes, or slow drifts due to either patient motion or changes in respiration over time. We have developed previously a method of separating the components of PM and NPM from the marker signals using total-variation (TV) based iterative-smoothing (Mukherjee et al 2009). The 6-DOF motion of the heart within the chest was derived from the NPM traces of the chest markers using singular-value decomposition (SVD) (Strang 1998). The estimates were then used in a motion-compensated OSEM reconstruction algorithm as described in section 2.3.
2.3. Motion Correction
Motion correction within reconstruction was implemented using a motion-compensated OSEM algorithm (Feng et al 2006) to which the motion estimates - obtained from either the VTS and or the data-driven method - were given as input. Once all the transformations were estimated, the simulated data were reconstructed with all corrections (i.e., attenuation, scatter and resolution modeling). Scatter correction was done by the TEW method (Ogawa et al, 1991). Patient studies were reconstructed without scatter correction because the scatter window projections had not been acquired. The motion transformation was incorporated in the reconstruction as in (7)
| (7) |
where f(i) is an estimate of the object at the ith iteration. The iteration index i and subset index s are related by s ≡ i(modM) + 1, with the total number of subsets being M. The projections in each ordered subset are indexed by p, is the value in detector bin m of pth projection in subset s (p = 1,2…ns), and ns is the number of projections in subset s. Hmn is an element of the system matrix which has N × D elements at every projection (N the number of voxels in the 3D source distribution), Tφp is an operator that interpolates the activity distribution f to the transformed activity with the transformation given by φp. Thus, (Tφpf)(n) = f(φp (n)), where n = 1,2…N, and similarly represents the inverse transformation from the pose at pth projection in subset s to the reference.
The subsets may consist of projections from different motion groups. The transformation at each projection Tφp was therefore used to model the motion in the OSEM update. Using the method of Feng et al (2006), the activity and attenuation map were transformed to the pose at each projection within a subset using 3D Gaussian interpolation where both the gantry rotation and motion transformation were applied in a single step. The projector and the back-projector both used the transformed attenuation map for attenuation correction. The transformed activity was projected and compared with the measured data. The error (ratio of measured to estimated projection) was then back-projected and inverse-transformed to the reference motion group. The activity was reconstructed at the pose of the reference motion group.
2.4 Investigation with NCAT Phantom Studies
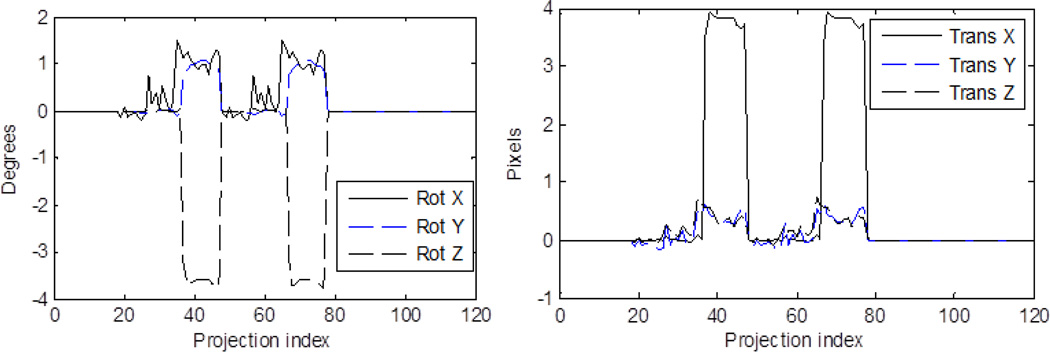
The cardiac NCAT phantom was used for simulating SPECT data using SIMIND Monte Carlo simulation software. The camera parameters were chosen to match the Philips IRIX SPECT system with a low-energy high resolution (LEHR) parallel-hole collimator using Technetium-99m sestamibi as the radiopharmaceutical. The relative concentration of activity in the liver was half that in the heart walls and in the other organs at the background level which was 1/10th of that in the heart walls. Pixel size chosen for the simulation was 4.67 mm. The simulation included attenuation, scatter and system spatial resolution. The radius of rotation was 27 cm, which was typical of clinical acquisitions. A 180° acquisition using two of the IRIX’s heads at 90° with respect to each other for a total of 60 projection angles was simulated with a) two and b) three equal-sized motion groups, with one-half and one-third the total number of angles, respectively. The total counts in the projections were scaled to 7 million (average clinical level at our site) and then Poisson noise realizations were created. Projection data were simulated with the various motions listed in Table 1. In the SPECT 3D coordinates, the Z-axis is oriented along the length of the patient, the Y-axis is oriented from back to front (PA), and X-axis is from side-to-side. Therefore, in the projection data the vertical dimension coincides with the Z-axis. The complex motion case was simulated using the motion parameters from external-tracking signals acquired during a patient study with motion. As the patient acquisitions were over 204 degrees with a total of 68 projections, the external motion signal corresponding to the last 4 angles (on each head) was discarded. The transformation parameters for the complex motion case are shown in Fig. 2. In the figure, the motion is repeated as two heads were simulated. Though the data was generated by moving the phantom at each projection angle according to the external signal, the motion estimated for the complex case using the data-driven strategy was a single transformation between two motion groups. These groups were based on the time-points of significant changes in the signal: (Group 1) projections 18–36 & 48–66 with 38 angles, and (Group 2) projections 37–47 & 67–77 with 22 angles. The “truth” for validating the data-driven estimates was also a single transformation between the average positions at these two motion groups estimated by SVD. For the complex motion case we simulated count levels of 4, 5, 6 and 7 million counts (5 datasets at each count level) for observing the variation in estimation error with noise.
Table 1.
6-DOF parameters for simulated motion cases
| Simulation Study | Translation X (mm) |
Translation Y (mm) |
Translation Z (mm) |
Rotation X (deg) |
Rotation Y (deg) |
Rotation Z (deg) |
|---|---|---|---|---|---|---|
| XTwo Translation | 10 | 0 | 0 | 0 | 0 | 0 |
| XTwo Rotation | 0 | 0 | 0 | 5 | 0 | 0 |
| YTwo Translation | 0 | 10 | 0 | 0 | 0 | 0 |
| YTwo Rotation | 0 | 0 | 0 | 0 | 5 | 0 |
| ZTwo Translation | 0 | 0 | 10 | 0 | 0 | 0 |
| ZTwo Rotation | 0 | 0 | 0 | 0 | 0 | 5 |
| XThree Translation | Group 1=10, Group 2=5 | 0 | 0 | 0 | 0 | 0 |
| XThree Rotation | 0 | 0 | 0 | Group 1=5, Group 2=2.5 | 0 | 0 |
| YThree Translation | 0 | Group 1=10, Group 2=5 | 0 | 0 | 0 | 0 |
| YThree Rotation | 0 | 0 | 0 | 0 | Group 1=5, Group 2=2.5 | 0 |
| ZThree Translation | 0 | 0 | Group 1=10, Group 2=5 | 0 | 0 | 0 |
| ZThree Rotation | 0 | 0 | 0 | 0 | 0 | Group 1=5, Group 2=2.5 |
| Complex | Object at each projection moved according to values obtained from external marker signal (fig. 2) | |||||
Figure 2.
The transformation parameters vs. the projection indices for the complex motion simulation which was based on the measured motions during a clinical cardiac SPECT study as determined by the external-tracking system. Rotation angles are shown on the left and translations about X, Y, and Z axes are shown at the right. Two camera heads acquiring over 180 degrees were simulated.
2.5 Investigation with Patient Studies
Five patient studies were acquired with external marker motion-tracking (McNamara et al 2009). Each study consisted of two rest acquisitions, where the patient was instructed to be motionless during the first study and to move during the second. Patients were requested to perform small clinically realistic movements. Movements suggested were small axial slides, side-to-side twisting, shifting or bending. In the five studies the maximum motion was about 3 cm. A transmission scan was acquired between the two rest scans. The studies were acquired on a Philips IRIX SPECT system with Tl-201 as the radiopharmaceutical, in a two-head 204 degree acquisition with 68 projections. The two reconstructed studies were compared visually after motion correction using motion estimates from both the VTS and data-driven approach. The extent of motion during transmission scan or between scans was small (< 2 mm) in these studies and was not corrected for in the reconstruction. Motion during the first rest study was also small (< 3 mm) in all patients and was not corrected in the reconstruction. The patients were requested to move solely at one time point during acquisition. Therefore, for data-driven estimation the projection data were divided into two groups based on the external marker tracking signal, with the second group corresponding to the projections where the patient moved to a new position. Also note that the patient data acquired had a single abrupt change which facilitated delineation into motion groups.
2.6 Performance Metrics
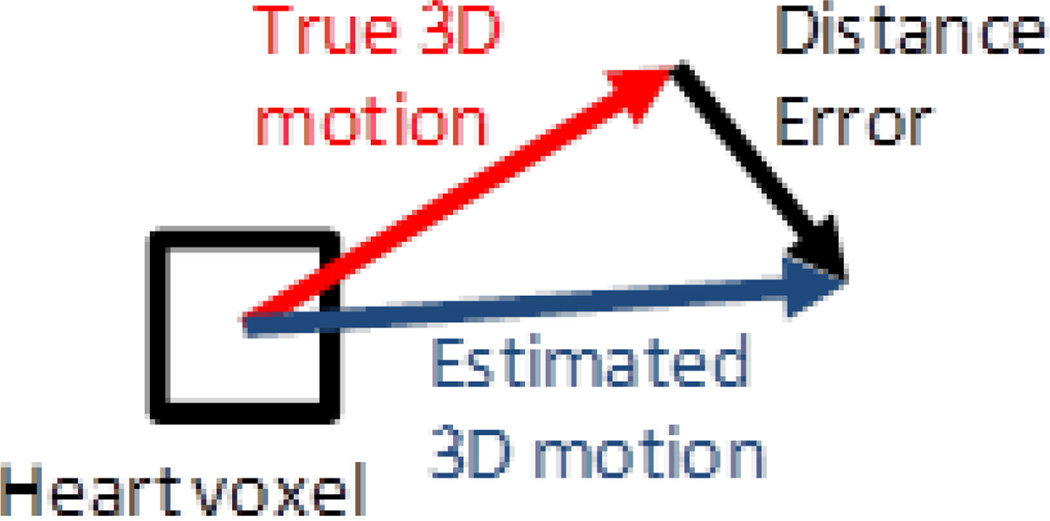
The accuracy of the estimation of the 6-DOF transformation parameters for the NCAT simulations studies was determined using the average distance error metric which is the vector difference between true and estimated motion vectors averaged over the voxels in the heart region as illustrated for a single voxel in Figure 3. This was computed as:
| (8) |
where TE represents the estimated transformation, and TA the true transformation which was known in simulation studies, and xl represents the 3D location of a voxel within the heart region. The number of voxels within the heart region is L. The heart region was obtained by segmenting the reconstructed anthropomorphic phantom when no motion was present. In NCAT studies, the heart region was known a priori while generating the phantom.
Figure 3.
The average distance error (AvDistErr) is calculated as the average of the magnitudes of distance errors for all voxels within the heart volume.
In order to test the sensitivity of the cost functions to changes in pose within the current data-driven estimation schemes (schemes A and B in Fig. 1), the cost functions were computed on a set of randomly distributed points (6-DOF transformations) around the actual transformation (truth) and including it, for all simulated motion cases. The cost functions were then compared with the AvDistErr metric computed at the same points, using the Spearman’s rank correlation (Hollander Wolfe 1973). The Spearman’s rank correlation gave a quantitative measure of how well the cost functions followed the trend in AvDistErr. The accuracy of estimation obtained using each cost function was given by the AvDistErr between the points representing the true minimum and the cost function minimum. Due to various degradations present in the SPECT projections, such as spatial resolution, noise, attenuation and scatter, the region close to the true minimum contains many local minima. Therefore, two sets of randomly distributed points (6-DOF transformations) were examined both inclusive of the true minimum: 1) Narrow: 50 points in a region ±1 pixel and ± 2 degrees on all axes about the truth, to examine the performance of cost functions close to the solution 2) Broad: 200 points in a region ± 5 pixels and ±5 degrees on all axes about the truth, to examine the performance for points far from the solution, which may occur at the beginning of the optimization process. It must be noted that the objective of this experiment is to get a preliminary assessment of the sensitivity of cost functions and decide on which scheme is preferable independent of the optimization process. The motion estimation performance will ultimately depend on the sampling of the parameter space by the optimizer used.
For patient studies, direct computation of accuracy is not possible as the truth is unknown. Therefore, the data-driven estimates were compared to the SVD-based estimates from external tracking signals using AvDistErr. The external-tracking based transformation was obtained using the average position of the chest markers at the motion groups computed by averaging over the positions at projections within the group. The transformation obtained this way was also used for motion correction using external-tracking. This was done to facilitate comparison with the data-driven method (which also estimates motion between groups) both visually and quantitatively.
For evaluating the visual image quality of the motion-corrected images via different cost functions, the images were read independently by three human-observers and then in consensus to break ties. The identities of the motion correction strategies were masked and all slices in short-axis, horizontal and vertical long-axis configurations were displayed in an interface that allowed comparison of two strategies at a time against the first rest study. The uncorrected reconstruction with motion artifacts was also included as one of the strategies. Observers chose the strategies to be displayed and ranked the strategies based on visual quality.
3. Results
3.1 Simulated Data (NCAT)
3.1.1. Preliminary assessment using randomly distributed points
Table 2 shows the results of the sensitivity and accuracy study of the cost functions using randomly generated transformations about the truth for all simulated motion cases. The spearman’s rank correlation and AvDistErr (mean and standard deviation over all motion cases) are shown for each cost function used in Scheme A and Scheme B in the narrow and broad regions defined in Section 2.6. For each cost function, a high value of the rank correlation and low AvDistErr indicates good performance. Comparing the columns, EDI was rejected from further investigation due to low rank correlation and large distance errors from the truth. Rank correlation with AvDistErr was observed to be better for all cost functions in the broad region (~ 0.7) than in the narrow region (~ 0.4) with both the schemes. This is explained by the reduced sensitivity of the cost functions to small changes in pose due to various degradations in the SPECT projections. AvDistErr values for the narrow region were approximately 4–5 mm (1 pixel) for most cost functions, though up to 7 mm for three or more motion groups. To avoid these local minima, we modified the optimization process so that it was re-initialized six times randomly with different transformation parameters.
Table 2.
Preliminary assessment of cost function accuracy (AvDistErr) and sensitivity (Spearman’s Rank Correlation) to changes in pose using randomly distributed transformations about the truth for all simulated motion cases. Note that large correlation and small AvDistErr are desired.
| MSD | NCC | PI | NMI | MI | EDI | ||
|---|---|---|---|---|---|---|---|
| Scheme A: Narrow | Spearman’s Rank Correlation | 0.45±0.16 | 0.54±0.14 | 0.36±0.19 | 0.40±0.17 | 0.37±0.14 | −0.14±0.17 |
| AvDistErr (mm) | 5.09±2.29 | 3.83±2.01 | 4.25±2.80 | 5.93±1.63 | 5.7±1.21 | 8.87±1.96 | |
| Scheme B: Narrow | Spearman’s Rank Correlation | 0.44±0.16 | 0.47±0.14 | 0.42±0.12 | 0.42±0.16 | 0.37±0.21 | −0.16±0.16 |
| AvDistErr (mm) | 5.04±1.12 | 5.28±2.71 | 4.72±2.66 | 4.76±1.68 | 5.28±1.73 | 7.94±1.63 | |
| Scheme A: Broad | Spearman’s Rank Correlation | 0.68±0.05 | 0.68±0.04 | 0.65±0.04 | 0.72±0.04 | 0.71±0.05 | −0.13±0.12 |
| AvDistErr (mm) | 8.50±9.67 | 8.55±9.67 | 7.01±9.15 | 6.86±9.15 | 1.45±3.41 | 34.56±6.72 | |
| Scheme B: Broad | Spearman’s Rank Correlation | 0.66±0.04 | 0.70±0.05 | 0.66±0.05 | 0.73±0.05 | 0.71±0.06 | −0.15±0.16 |
| AvDistErr (mm) | 4.11±7.80 | 4.81±7.80 | 7.19±9.11 | 5.74±8.83 | 0.75±2.62 | 24.28±18.73 |
Compared to Scheme A, Scheme B had better accuracy (lower AvDistErr) in the broad region for MSD, NCC, and MI, and similar accuracy for PI and NMI. In the narrow region, the accuracy of most cost functions for Schemes A and B was comparable. Thus, Scheme B was selected over Scheme A for optimization in subsequent investigations. The large variance of the accuracy values about the mean was due to a large variation in the performance of the cost functions between motion cases with two and three motion groups, with significantly worse performance in the latter. With Scheme B, the cost function MI had better accuracy than other cost functions over all motion cases. Additionally, the sensitivity of MI and NMI was significantly higher (p < 0.01) than other cost functions as determined by the Wilcoxon signed rank test (Hollander Wolfe 1973) applied to Spearman’s rank correlations obtained for the 13 simulated motion cases.
3.1.2. Comparison of the motion estimation performance of the cost functions
Pooling projections
In the computation of the NMI or MI, pooling the projection data did not yield a better estimate of the motion. The linear scaling operation used in the computation of the joint histogram with uniform bin size suppresses the effect of projections with greater attenuation by compressing the intensity range into a few bins. Therefore, the NMI/MI was computed without pooling the projections in all comparison studies.
Filtering projections
The performance was worse with 2D Butterworth filtering of the projections for MSD, NCC and PI, but was better with filtering for MI and NMI. This is expected as the contrast in the projection and re-projection images is reduced by filtering, but the joint histogram is more linear when the noise in projections is suppressed by filtering. Fig. 4 illustrates this effect for an example motion simulation with the NCAT phantom, where Fig. 4(a) is the joint histogram of the registered (aligned) re-projection of the reconstructed NCAT and the actual projection without any filtering, whereas Fig. 4(b) is the same with filtering. Thus, for comparison the projections were filtered when using MI/NMI, but not when MSD, NCC or PI was used as the cost function.
Figure 4.
Joint histogram of an aligned re-projection of a noisy reconstructed NCAT phantom (along vertical axis) with the actual projection (along horizontal axis) (a) without filtering and (b) with filtering. The bin (0, 0) is at the top left corner.
Motion Estimation Performance
A comparison of the performance of cost functions with data-driven estimation Scheme B is shown in Table 3. PI, NMI and MI were observed to perform better on average than other cost functions for NCAT data. The errors were on the order of 5 mm for the case of two motion groups, and increased up to 7 mm for one of the motion groups when three motion groups were involved for these three cost functions. This matches what is expected from the preliminary assessment. Pure translations were estimated with better accuracy than pure rotations where the errors were up to 10 mm in some cases. Larger errors of up to 1.2 cm were observed for rotational motion about Z-axis. In the case of three motion groups, the group estimated later (Group2) in the sequential estimation scheme was estimated with larger errors than the first group.
Table 3.
The average distance errors (in mm) for the different cases of known simulated motion in the NCAT phantom for the metrics investigated. XTwo, YTwo, ZTwo indicates two motion groups were simulated with motion in X, Y and Z direction respectively. XThree, YThree and ZThree are simulated similarly with three motion groups. In both cases the full 6-DOF motion model was optimized. The columns Group 1 and Group 2 refer to AvDistErr in the transformations estimated between the second and third motion groups with respect to the reference Group 0.
| MSD | NCC | PI | NMI | MI | |
|---|---|---|---|---|---|
| XTwo Translation | 3.69 | 3.78 | 2.05 | 2.94 | 5.51 |
| XTwo Rotation | 9.29 | 10.23 | 7.61 | 4.25 | 8.22 |
| YTwo Translation | 4.62 | 3.64 | 1.63 | 2.43 | 5.60 |
| YTwo Rotation | 7.52 | 5.42 | 8.83 | 6.21 | 5.14 |
| ZTwo Translation | 2.99 | 3.46 | 2.90 | 2.85 | 3.18 |
| ZTwo Rotation | 8.27 | 8.22 | 5.51 | 6.54 | 6.54 |
| Complex | 4.44 | 6.96 | 6.16 | 6.91 | 3.78 |
| Average | 5.83 | 5.96 | 4.96 | 4.59 | 5.42 |
| MSD | NCC | PI | NMI | MI | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Group 1 |
Group 2 |
Group 1 |
Group 2 |
Group 1 |
Group 2 |
Group 1 |
Group 2 |
Group 1 |
Group 2 |
|
| XThree Translation | 3.78 | 4.25 | 4.48 | 3.88 | 1.82 | 4.58 | 1.87 | 4.90 | 4.11 | 6.68 |
| XThree Rotation | 10.46 | 12.61 | 11.96 | 15.60 | 3.22 | 3.88 | 8.13 | 9.34 | 9.15 | 11.96 |
| YThree Translation | 3.88 | 8.50 | 3.74 | 6.72 | 1.26 | 3.64 | 2.62 | 3.83 | 5.51 | 5.70 |
| YThree Rotation | 7.01 | 9.11 | 4.67 | 9.81 | 1.68 | 4.44 | 2.10 | 6.21 | 4.20 | 4.76 |
| ZThree Translation | 4.20 | 8.55 | 3.78 | 8.22 | 4.30 | 7.47 | 3.97 | 4.53 | 2.52 | 4.76 |
| ZThree Rotation | 11.68 | 17.00 | 10.74 | 15.41 | 6.63 | 10.37 | 7.01 | 11.68 | 5.60 | 11.21 |
| Average | 6.83 | 10.00 | 6.56 | 9.94 | 3.15 | 5.73 | 4.28 | 6.75 | 5.18 | 7.51 |
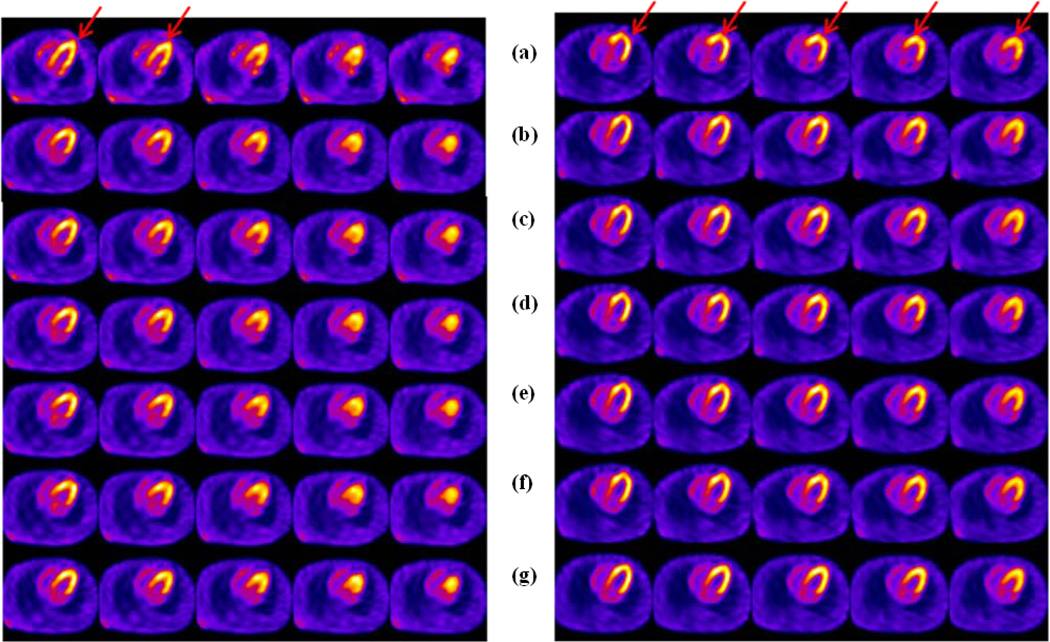
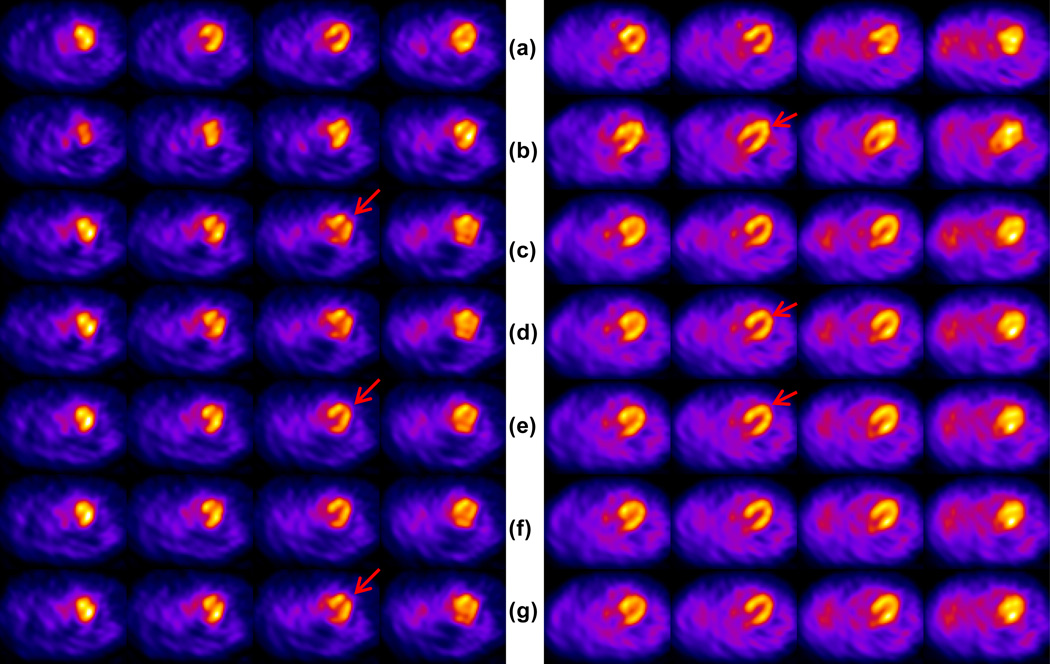
Fig. 5 (Left) shows the NCAT phantom reconstructed with the data-driven estimates for the Complex case and Fig. 5 (Right) shows the same for Zthree Rotation as defined in Table 1. For the complex motion case, lowest AvDistErr was obtained with MI. Also note that none of the cost functions were able to accurately estimate the rotation about Z-axis, but the major displacement along X-axis was estimated by most. Motion estimation performance is worst with Zthree Rotation in Table 3 and Fig. 5 (Right), where none of the cost functions produced good correction. In Table 4, noise realizations of the complex motion case with counts varying between 4 and 7 million were used to generate error-bars for each cost function. The transformation parameters estimated with each cost function for the complex motion case were compared to the “truth”. The MI-based estimates had the lowest mean AvDistErr. The error-bars imply that the AvDistErr varied 1–2 mm with noise level for all cost functions.
Figure 5.
NCAT phantom study with (Left) Complex motion and, (Right) Zthree Rotation from Table 1 for (a) uncorrected motion (b) corrected using MSD (c) corrected using NCC (d) corrected using PI (e) corrected using MI (f) corrected using NMI (g) corrected using the true motion. All cost functions are used with the data-driven Scheme B, without any prior initialization with the truth. All cost functions estimate the complex motion with errors of 4–7 mm, whereas failed to estimate the rotation about Z-axis accurately with errors up to 1 cm or more. The red arrows indicate the location of the artifacts due to motion. At the left the artifact appears as a distortion in the shape of the heart walls, whereas at the right the artifact is seen as a flattened apical region.
Table 4.
The estimated 6-DOF translations and rotations for the simulated complex motion case in Table 2. Five noise realizations of the complex motion case at four count levels- 4, 5, 6 and 7 million were used to generate error-bars for each cost function.
| Cost Function | Tx (mm) | Ty (mm) | Tz (mm) | Rotx (deg) | Roty (deg) | Rotz (deg) | AvDistErr |
|---|---|---|---|---|---|---|---|
| MSD | 13.32±3.50 | −1.67±1.45 | 0.68±1.08 | −0.66±0.31 | −0.60±0.93 | 1.03±1.30 | 6.40±1.46 |
| NCC | 12.56±2.17 | −2.51±1.70 | 0.12±1.05 | −0.49±0.93 | −1.04±0.46 | 1.82±1.88 | 6.61±0.50 |
| PI | 13.50±2.13 | −2.01±1.24 | 1.05±0.75 | −0.89±0.40 | −1.57±0.78 | 1.60±1.01 | 5.30±0.68 |
| NMI | 16.91±1.56 | −4.21±1.68 | −0.11±1.02 | −0.25±0.51 | −0.69±0.95 | 2.20±1.63 | 5.46±1.55 |
| MI | 17.24±1.90 | −4.90±0.67 | −0.34±0.45 | 0.24±0.33 | −0.79±0.19 | 2.62±1.95 | 4.32±1.10 |
| Truth | 17.62 | 1.70 | 1.15 | 0.84 | 0.94 | −3.61 | 0.00 |
3.2 Patient Studies
The cost functions PI, NMI and MI were chosen for further evaluation in patient studies based on the lower AvDistErr in NCAT studies. Table 5 shows the AvDistErr between data-driven and external tracking based estimates for five patient studies. The AvDistErr of PI and NMI-based estimates from external tracking estimates were of the order of 5–6 mm on average and less than that of MI-based estimates. NMI is expected to perform better than MI as it can account for the change in overlap region (Studholme et al 1999), and change in marginal entropies due to organs moving in or out of FOV.
Table 5.
The average distance error in mm of the data-driven estimates using PI, NMI and MI cost functions relative to the external-tracking estimates in patient studies
| Patient Study | PI | NMI | MI |
|---|---|---|---|
| 1 | 8.31 | 8.32 | 5.56 |
| 2 | 6.68 | 5.18 | 3.55 |
| 3 | 3.74 | 4.76 | 4.48 |
| 4 | 4.67 | 2.76 | 5.42 |
| 5 | 4.29 | 9.06 | 12.19 |
| Average | 5.54±1.91 | 6.02±2.62 | 6.24±3.42 |
For human-observer assessment of visual quality, the following motion-correction strategies were compared to the first rest study: 1) using external tracking, 2) data-driven using PI without the aid of external motion tracking estimates, which were used only to delineate the motion groups, 3) data-driven using PI with the aid of external motion tracking estimates for initialization, 4) data-driven using NMI without the aid of external motion tracking estimates, which were used only to delineate the motion groups, 5) data-driven using NMI with the aid of external motion tracking estimates for initialization, 6) No motion correction.
Relative performance of data-driven and external tracking based estimates
Human-observer assessment of the visual image quality is shown in Table 7. In all patients, the visual quality of PI-based estimation was either significantly better or comparable to NMI-based estimation. Compared to external-surrogate based correction, PI-based estimation produced significantly better image quality in patient 1, but worse or comparable in other patients. Best visual quality was obtained with external-surrogate based correction in 3 out of 5 patients. In all patients except patient 4, motion-correction by all strategies provided an improvement in visual image quality compared to that without motion-correction. Patient 4 exhibited very little motion externally. Thus the motion corrected reconstructions were all very similar to the one without any correction. In patient 1, better visual quality with PI-based estimate is supported by large AvDistErr from external tracking (Table 6). Fig. 6 (Left) shows patient 1, where PI-based estimate (rows e and f) produced better correction of the artifactual slit in the apex than all others as indicated by the red arrows. Fig. 6 (Right) shows patient 2 where external tracking based estimate (row g) was slightly better than the PI-based estimates (rows e and f), and significantly better than NMI based estimates (rows c and d). None of the strategies restored the shape of the heart (indicated by red arrows) to exactly what it was in the first rest study. This could be due to the following factors in the order of significance: 1) motion between emission and transmission imaging which was not corrected for thus resulting in errors in AC; 2) residual motion as the strategies corrected for motion between groups of projections; and 3) an actual change in the cardiac and respiratory motion between the first and the second rest (time gap of ~20 min) due to the prolonged time the patient spent in the imaging position. In patient 5 none of the data-driven estimates were able to correct as well as the external tracking. PI-based estimates produced the next best in visual image quality, but all data-driven strategies had a residual Z-rotation of the heart. We observed that the transition between the two motion states in patient 5 was gradual spanning over 10 projections. The poor performance of the data-driven estimates may be associated with the inability to correct for such motion as the projection data was divided into two groups for the two major motion states, causing larger extent of motion within the groups than in other studies.
Table 7.
The ranking of visual image quality achieved by the motion correction strategies based on the consensus reading by human observers. Strategies ranked were (1) External tracking only (EXT) (2) data-driven using PI (PI) (3) data-driven using PI and external tracking prior information (PIwEXT) (4) data-driven using NMI (NMI) (5) datadriven using NMI and external tracking prior information (NMIwEXT) (6) No motion correction (UNC).
| Patient Study | RankingϮ |
| 1 | PI ≡ PIwEXT>EXT>NMI ≡ NMIwEXT>UNC |
| 2 | EXT ≅ PI ≡ PIwEXT ≡ NMIwEXT>NMI>UNC |
| 3 | EXT>PI ≡ PIwEXT ≡ NMI>NMIwEXT>UNC |
| 4 | PI ≡ NMI ≡ NMIwEXT ≡ PIwEXT ≡ EXT ≡ UNC |
| 5 | EXT>PI ≡ PIwEXT>NMI ≡ NMIwEXT>UNC |
No perceivable difference : ≡, slightly better : ≅, significantly better : >
Table 6.
The estimated 6-DOF translations and rotations and the AvDistErr relative to the external tracking estimates for 5 patient studies. EXT only in the second column indicates the external surrogate-based motion tracking. PIwoEXT implies the data-driven algorithm was run freely without the aid of external motion tracking estimates, which were used only to delineate the motion groups. PIwEXT implies the data-driven algorithm was initialized using the transformation determined from the external motion tracking system as one of the seven initialization points of the simplex optimizer.
| Cases | Tx (mm) |
Ty (mm) |
Tz (mm) |
Rotx (deg) |
Roty (deg) |
Rotz (deg) |
AvDistErr (mm) |
|
|---|---|---|---|---|---|---|---|---|
| Patient 1 | PIwoEXT | −1.73 | −1.99 | 23.24 | −0.35 | −0.39 | 0.77 | 8.31 |
| PIwEXT | −1.56 | −2.04 | 22.83 | −0.85 | −0.16 | 0.65 | 9.53 | |
| EXT only | 0.82 | −0.84 | 20.08 | 3.01 | −0.27 | −0.02 | 0.00 | |
| Patient 2 | PIwoEXT | 11.65 | 3.43 | −0.63 | −0.65 | 0.11 | 1.66 | 6.68 |
| PIwEXT | 12.86 | 3.71 | 0.25 | −0.72 | −0.72 | 2.73 | 4.61 | |
| EXT only | 17.98 | 3.04 | 3.32 | −1.84 | −0.89 | 3.96 | 0.00 | |
| Patient 3 | PIwoEXT | −18.23 | 3.23 | 0.95 | −0.08 | −0.54 | −0.58 | 3.74 |
| PIwEXT | −18.39 | 3.40 | 2.84 | −0.41 | −0.71 | −0.39 | 4.54 | |
| EXT only | −28.02 | 4.67 | −1.59 | −1.27 | −4.10 | 1.77 | 0.00 | |
| Patient 4 | PIwoEXT | −0.89 | 2.63 | 2.79 | 0.19 | 0.22 | −0.78 | 4.67 |
| PIwEXT | −0.22 | −1.30 | 3.01 | 0.14 | −0.04 | −0.38 | 1.78 | |
| EXT only | 1.12 | 0.51 | 9.11 | −1.61 | 0.65 | 0.15 | 0.00 | |
| Patient 5 | PIwoEXT | −8.85 | 3.16 | −1.20 | −0.88 | 1.52 | 1.03 | 4.29 |
| PIwEXT | −7.03 | 5.53 | −1.34 | −1.26 | 1.00 | 3.43 | 4.51 | |
| EXT only | −14.43 | 2.65 | −3.55 | −0.38 | −1.06 | 3.09 | 0.00 | |
Figure 6.
Patient 1 (Left) and Patient 2 (Right) in Table 5. Rows (a) First rest study (b) Second rest study without correction (c) Second rest study corrected with the data-driven method using NMI as the cost function following Scheme B, without the aid of external motion tracking prior. (d) Second rest study corrected with the data-driven method using NMI as the cost function and external motion tracking prior following Scheme B. (e) Second rest study corrected with the data-driven method using PI as the cost function following Scheme B, without the aid of external motion tracking prior. (f) Second rest study corrected with the data-driven method using PI as the cost function and external motion tracking prior following Scheme B. (g) Same study corrected with external motion tracking estimates only. (Left) The red arrows indicate the artifactual slit at the apex due to motion, and better correction in rows (e) and (f) compared to other rows. (Right) The red arrows indicate the location of the artifact in row (b) showing elongated ventricular walls and recovery in other rows.
Relative performance of data-driven with and without external tracking based prior
Based on the human-observer assessment no significant differences were observed in the data-driven estimates with or without external-tracking based prior in patient studies 1, 4 and 5 (Table 7). In patients 2 and 3, the NMI-based data-driven method with and without external tracking prior showed significant differences but the ranking was inconsistent across patients. Table 6 shows that the AvDistErr of PI-based data-driven estimates with or without prior were within 6 mm on average of the external-tracking based estimates. The difference in AvDistErr with and without prior was less than 3 mm in all patient studies. We therefore conclude that initialization with external tracking did not affect the final solution significantly. However, constraining the rotation about Z-axis to the external-tracking based estimate during the first iteration may be favored over setting it to an arbitrarily small value, since partial angle reconstructions used in the data-driven estimation tend to estimate Z-rotation with a large error.
4. Discussion
PI and NMI-based cost functions produce more accurate estimates than other cost functions in phantom studies. In patient studies, the PI-based estimate was either comparable or better than the NMI-based estimate in terms of visual image quality. We note that NMI showed better correlation with the AvDistErr metric in the preliminary assessment reported herein, but it did not guarantee better visual quality in the consensus reading by human observers. Mutual information measures use the joint probability distribution which does not account for the spatial relationship of pixel intensities. Pattern intensity on the other hand is sensitive to differences in spatial structure in the images to be registered that are larger than the noise-related variations. Image quality indices based on structural similarity are known to correlate better with the response of human visual system (Wang et al, 2004). This may explain why PI is able to produce better visual quality than NMI in some patient studies. The lack of improvement with PI in other patient studies may be due to the difficulty of appropriately tuning the noise variance parameter, since the noise in Poisson data is signal-dependent. In our studies, we set this parameter empirically using NCAT simulations (Section 2.1.4). Therefore, the NMI-based cost function may sometimes be preferred as it involves no tuning of parameters. Filtering the projections with a 2D Butterworth filter did not improve the performance of PI due to reduced contrast. Note that all the cost functions implicitly assume a stationary noise model. Though PI may be adapted for non-stationary noise by estimating the noise-variance parameter locally, this approach was not taken as it would add to the complexity and require more free parameters to be tuned. However, variance stabilization with the Anscombe transform (Anscombe, 1948) may be used to make the noise stationary and is expected to improve the performance of the cost functions. Non-linear filtering of the projection data (Zhang, 2008) with variance stabilization may also improve data-driven estimation in general through optimal noise suppression. This will be explored in future work. We also found that in determining motion between groups of projections, computing the mutual information measure for each individual projection and adding them gives a more robust estimation than pooling all projections in one.
Preliminary assessment of the cost functions has revealed that there exist many local minima for all of the cost functions investigated with the current data-driven schemes. The problem is worse when fewer angles are acquired at any given pose as in Table 3 with three motion groups. The accuracy of the data-driven estimation schemes is also greatly affected by the type of motion to be estimated. For example, estimating the rotation about Z-axis presents a significant challenge. In our estimation scheme, the optimization was constrained to 5-DOF in the first iteration with the rotation about Z-axis set to a predefined value. Using the 5-DOF constraint in the first iteration generally leads to a better solution in the second iteration of motion estimation. However, when there is rotation about Z-axis, this may cause poor estimation. To test this possibility, we tried another set of experiments with this constraint removed, i.e. all 6-DOF were estimated in the first iteration. However, the estimation of rotation about Z-axis was not improved by this change due to the limited angle artifacts in the partial reconstructions which give an appearance of rotation about Z-axis even when no such rotation is present. Increase in the frequency of motion from a single pose change to two increased the estimation error from 4–5 mm to 7–8 mm on average in the NCAT phantom study. These problems arise due to the use of a sequential estimation technique where the partial reconstruction is gradually updated and each group’s motion is estimated sequentially. Thus errors made in estimating previous motion groups degrade the quality of the partial reconstruction when updated, and make subsequent motion estimations worse.
The sequential estimation scheme also introduces additional free parameters such as the ordering of groups. Besides, the attenuation map obtained from the transmission study acquired before the second rest is not used as it is not necessarily aligned to the largest motion group. This introduces errors in the matching of re-projected and measured data, which are solely the effect of attenuation. We hypothesize that these limitations may be averted by using a simultaneous estimation scheme where all the motion groups are estimated simultaneously in a single optimization framework, and all projections can be used to simultaneously reconstruct the object. With such a scheme, we expect the rotation about Z-axis to be estimated with greater accuracy as there will be no limited angle artifacts to confound the estimation. However, there is a fundamental limitation of data-driven estimation based on the information content of the projection data. We hypothesize that the Fisher information matrix may be used for determining the estimability of motion parameters and to examine the fundamental limit of motion severity at which the parameters are no longer estimable. This is currently being investigated in our other work.
With respect to estimating gradual ramp-like motion or increased step-like motion occurrences, we note that there is a trade-off involved between the number of motion groups and the estimation accuracy. Fewer motion groups are estimated with greater accuracy, but the transformation itself is a coarse estimation, whereas more motion groups are estimated with lower accuracy. In the current methodology more motion groups imply that the motion is estimated from less data, making the estimation more difficult. In a simultaneous estimation scheme, the number of motion parameters to be estimated increase n-fold for n motion groups. In practice, data-driven methods may need multiple iterations with successive refinements to the partitioning of projection data into motion groups for estimating such motion.
The division into motion groups in our studies has been facilitated by the availability of a secondary source of information (truth in simulations, VTS in patient studies). We did not investigate having to estimate the groups as well as the motion. We do suspect that estimating both will result in a degradation of estimation, but the extent of change in performance will be investigated in future. We do not necessarily want to exclude the external tracking information; rather we envision the best strategy to be a combination of data-driven and external tracking with a simplified external tracking device to reduce cost. Such an external device will only provide the timing information corresponding to the changes in pose of the subjects.
The AvDistErr in patient studies is not a measure of accuracy, rather a metric to compare the external and data-driven estimates. Disparity between data-driven and external-tracking based estimates may arise from multiple sources such as, inaccuracies in the data-driven estimation due to lack of enough information in the projections about the motion involved or some limitations of the estimation scheme; inaccuracies in external-tracking estimates due to poor line-of-sight during acquisition or displacement of the marker belt relative to patient body during movement; or a true breakdown in correlation between internal and external motion as observed with some types of movement (King et al 2009). We therefore use the consensus reading by human-observers to assess which estimation gives an improvement in visual image quality, which we observed did not match the relative magnitude of the AvDistErr except in patient 1. In that patient, large AvDistErr of 8 mm was associated with better visual image quality of PI-based data-driven estimation compared to the external-tracking. The visual quality is therefore affected in a complex way by the relative magnitude of the error along each axis. Additionally, the system resolution (8mm at 10 cm from the camera face) reduces the amount of intensity change in the projection data due to motion and thus AvDistErrs of 1–2 pixels may or may not be perceptible visually depending on when the motion occurred and the orientation of the patient at the time.
In patient studies, the possibility that internal organ motion and externally measured motion may not be correlated for some types of motion introduces further uncertainty in the validation of the data-driven approach. Thus, an unambiguous measure of truth is not available for a rigorous comparison of the two techniques. In future work, this issue will be resolved with the availability of a volunteer-derived XCAT with realistic internal and external motion profiles (Connolly et al 2011) both known a priori by virtue of the MRI data and the VTS tracking. Lastly, patient studies involve respiratory motion which was not corrected herein. It was also observed that the second rest studies had greater amplitude of respiratory motion for some patients, which may be associated with the anticipation of impending motion. Respiratory motion induced blurring may influence the accuracy of data-driven estimation. The extent of respiratory motion induced error will be investigated in future studies.
5. Conclusion
Our results demonstrate the feasibility of using the data-driven algorithm for 3D motion correction of cardiac SPECT imaging for infrequent motion occurrence. In summary, PI and NMI-based cost functions produce more accurate estimates than other cost functions in phantom studies. From the consensus reading by human-observers in patient studies, 3 studies had the best visual image quality with external-tracking estimate. In one study visual image quality was best with PI-based estimate. In the remaining study where little motion occurred, PI/NMI-based data-driven estimates were comparable to external tracking with no significant difference between any of the strategies. The visual quality of data-driven estimation with and without the aid of external motion tracking prior was observed to be similar in patient studies.
Acknowledgement
This work was supported by the National Institute of Biomedical Imaging and Bioengineering (NIBIB), grant R01 EB001457 and a research grant from Philips Medical systems. The contents are solely the responsibility of the authors and do not represent the official views of the NIBIB or Philips Medical Systems. The authors would like to thank Andre Z. Kyme for discussions providing valuable insight into the data-driven algorithm. UCL/UCLH receives a proportion of its research support from the UK Department of Health’s NIHR Biomedical Research Centre’s funding scheme. We would also like to acknowledge that this work is a continuation of previous investigations (Mukherjee et al, 2010b, 2011). In this paper we have evaluated the data-driven method more rigorously with rotational motion in 3D and realistic movement data extracted from patient studies. We have also studied the sensitivity of the technique with various cost functions and robustness with motion frequency and increase in noise level. Lastly, we have assessed visual quality using the consensus from multiple human-observers.
References
- Anscombe FJ. The transformation of Poisson, binomial and negative-binomial data. Biometrika. 1948;35(3/4):246–254. [Google Scholar]
- Arata LK, Pretorius PH, King MA. Correction of organ motion in SPECT using reprojection data. Proceedings of Nuclear Science Symposium. 1996;3:1456–1460. [Google Scholar]
- Bai C, Maddahi J, Kindem J, Conwell R, Gurley M, Old R. Development and evaluation of a new fully automatic motion detection and correction technique in cardiac SPECT imaging. Journal Nuclear Cardiol. 2009;16(4):580–589. doi: 10.1007/s12350-009-9096-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Botvinick EH, Zhu YY, O’Connell WJ, Dae MW. A quantitative assessment of patient motion and its effect on myocardial perfusion SPECT images. J. Nucl. Med. 1993;34:303–310. [PubMed] [Google Scholar]
- Clarkson M, Rueckert D, Hill D, Hawkes D. Multiple 2D video/3D medical image registration algorithm. Proceedings of SPIE Medical Imaging. 2000 [Google Scholar]
- Connolly CM, Konik A, Dasari PKR, Zheng S, Johnson KL, Dey J, King MA. Creation of 3D digital anthropomorphic phantoms which model actual patient non-rigid body motion as determined from MRI and position tracking studies of volunteers. Proc. SPIE. 2011:7964. [Google Scholar]
- Feng B, King MA. Estimation of 6-Degree-of-Freedom (6-DOF) Rigid-Body Patient Motion from Projection Data by the Principal-Axes Method in Iterative Reconstruction. Proceedings of Nuclear Science Symposium. 2006a;5:2695–2698. doi: 10.1109/NSSMIC.2006.356436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng B, Gifford HC, Beach RD, Boening G, Gennert MA, King MA. Use of three-dimensional gaussian interpolation in the projector/backprojector pair of iterative reconstruction for compensation of known rigid-body motion of SPECT. IEEE Trans. Med. Imag. 2006b;25:838–844. doi: 10.1109/tmi.2006.871397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hollander M, Wolfe D. Nonparametric statistical methods. Wiley-Interscience; 1999. [Google Scholar]
- Huang SC, Yu DC. Capability evaluation of a sinogram error detection and correction method in computed tomography. IEEE Trans Nucl Sci. 1992;39:1106–1101. [Google Scholar]
- Hudson H, Larkin R. Accelerated image reconstruction using ordered subsets of projection data. IEEE Trans Med Imaging. 1994;13:601–609. doi: 10.1109/42.363108. [DOI] [PubMed] [Google Scholar]
- Hutton BF, Kyme A, Lau YH, D Skerrett DW, Fulton RR. A hybrid 3d reconstruction / registration algorithm for correction of head motion in emission tomography. IEEE Trans Nucl Sci. 2002;49:188–194. [Google Scholar]
- King MA, Dey J, McNamara J, Johnson KL, Mitra J, Pretorius PH, Sun Y. MRI investigation of the relationship between the motion of external markers on the body surface and motion of the heart within the chest. Journal of Nuclear Medicine. 2009;50:587. (MeetingAbstracts) [Google Scholar]
- Konik A, Connolly CM, Johnson KL, Dasari PKR, Segars P, Pretorius PH, King MA. Digital Anthropomorphic Phantoms of Non-Rigid Human Respiratory and Voluntary Body Motions: A Tool-Set for Investigating Motion Correction in 3D Reconstruction; Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC) 2011; 2011. pp. 3572–3578. [Google Scholar]
- Konik A, Mukherjee JM, Johnson KL, Helfenbein E, Shao L, King MA. Comparison of ECG derived respiratory motion signals and pneumatic bellows for respiratory motion tracking; Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC) 2011; 2011. pp. 3925–3930. [Google Scholar]
- Kyme A, Hutton B, Hatton B, Skerrett D, Barnden L. Practical aspects of a data-driven motion correction approach for brain SPECT. Medical Imaging, IEEE Transactions on. 2003;22(6):722–729. doi: 10.1109/TMI.2003.814790. [DOI] [PubMed] [Google Scholar]
- Lee KJ, Barber DC. Use of forward projection to correct patient motion during SPECT imaging. Phys Med Biol. 1998;43:171–187. doi: 10.1088/0031-9155/43/1/011. [DOI] [PubMed] [Google Scholar]
- Ljungberg M, Strand SE. A Monte Carlo program for the simulation of scintillation camera characteristics. Comp Meth Progr Biomed. 1989;29:257–272. doi: 10.1016/0169-2607(89)90111-9. [DOI] [PubMed] [Google Scholar]
- McCarthy AW, Miller MI. Maximum likelihood SPECT in clinical computation times using mesh-connected parallel computers. IEEE Trans. Med Imag. 1991;10:426–436. doi: 10.1109/42.97593. [DOI] [PubMed] [Google Scholar]
- McNamara JE, Pretorius PH, Johnson KL, Mukherjee JM, Dey J, Gennert MA, King MA. A flexible multicamera visual-tracking system for detecting and correcting motion-induced artifacts in cardiac SPECT slices. Med Phys. 2009;36(5):1913–1923. doi: 10.1118/1.3117592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukherjee JM, McNamara JE, Johnson KL, Dey J, King MA. Estimation of Rigid-Body and Respiratory Motion of the Heart From Marker-Tracking Data for SPECT Motion Correction. Nuclear Science, IEEE Transactions on. 2009;56(1):147–155. doi: 10.1109/TNS.2008.2010319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukherjee JM, Johnson KL, McNamara JE, King MA. Quantitative study of rigid-body and respiratory motion of patients undergoing stress and rest cardiac SPECT imaging. IEEE Trans Nucl Sci. 2010a;57(3):1105–1115. doi: 10.1109/TNS.2010.2043852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukherjee JM, Pretorius PH, Johnson KL, Hutton B, King MA. Comparison of data-driven and external-surrogate based motion estimation strategies in cardiac SPECT imaging; Nuclear Science Symposium Conference Record (NSS/MIC), 2010 IEEE; 2010b. pp. 2987–2991. [Google Scholar]
- Mukherjee JM, Pretorius PH, Johnson KL, Hutton B, King MA. A comparison of cost functions for data-driven motion estimation in myocardial perfusion SPECT imaging. Proceedings of SPIE. 2011;7962 796209-796209-9. [Google Scholar]
- Nelder J, Mead R. A simplex method for function minimization. The Computer Journal. 1965;7(4):308. [Google Scholar]
- Ogawa K, Harata Y, Ichihara T, Kubo A, Hashimoto S. A practical method for position-dependent Compton-scatter correction in single photon emission CT. IEEE TransMed Imag. 1991;10:408–412. doi: 10.1109/42.97591. [DOI] [PubMed] [Google Scholar]
- Penney GP, Weese J, Little JA, Desmedt P, Hill DLG, Hawkes DJ. A Comparison of Similarity Measures for Use in 2D-3D Medical Image Registration. IEEE Trans. Med. Imag. 1998;17(4):586–595. doi: 10.1109/42.730403. [DOI] [PubMed] [Google Scholar]
- Press W, Teukolsky S, Vetterling W, Flannery B. Numerical recipes in C. Cambridge: Cambridge Univ. Press; 1992. [Google Scholar]
- Pretorius PH, King MA, Johnson KL, Mukherjee JM, Dey J, Konik A. Combined Respiratory and Rigid Body Motion Compensation in Cardiac Perfusion SPECT using a Visual Tracking System; Proceedings of IEEE Medical Imaging Conference, MIC10-3; 2011. [Google Scholar]
- Pretorius PH, Mukherjee JM, McNamara JE, Johnson KL, King MA. Evaluation of a multi-camera visual-tracking system for detecting and correcting body motion in cardiac SPECT. Journal of Nuclear Medicine. 2009;50(2):413. [Google Scholar]
- Schumacher H, Modersitzki J, Fischer B. Combined reconstruction and motion correction in SPECT imaging. IEEE Trans. Nucl. Sci. 2009;56(1):73–80. [Google Scholar]
- Segars WP, Lalush D, Tsui BMW. A realistic spline-based dynamic heart phantom. IEEE Trans. Nucl. Sci. 1999;46(3):503–506. [Google Scholar]
- Strang G. Introduction to linear algebra. Wellesley Cambridge Press; 2003. [Google Scholar]
- Studholme C, Hill D, Hawkes D. An overlap invariant entropy measure of 3D medical image alignment. Pattern recognition. 1999;32(1):71–86. [Google Scholar]
- Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: From error visibility to structural similarity. Image Processing, IEEE Transactions on. 2004;13(4):600–612. doi: 10.1109/tip.2003.819861. [DOI] [PubMed] [Google Scholar]
- Wu J, Kim M, Peters J, Chung H, Samant S. Evaluation of similarity measures for use in the intensity-based rigid 2D–3D registration for patient positioning in radiotherapy. Medical Physics. 2009;36:5391. doi: 10.1118/1.3250843. [DOI] [PubMed] [Google Scholar]
- Wheat JM, Currie GM. Incidence and characterization of patient motion in myocardial perfusion SPECT: Part 1. J. Nucl. Med. Technol. 2004;32:60–65. [PubMed] [Google Scholar]
- Zhang B, Fadili JM, Starck JL. Wavelets, ridgelets, and curvelets for Poisson noise removal. Image Processing, IEEE Transactions on. 2008;17(7):1093–1108. doi: 10.1109/TIP.2008.924386. [DOI] [PubMed] [Google Scholar]