Predicting Treatment Effects Using Biomarker Data in a Meta-Analysis of Clinical Trials

SUMMARY

A biomarker (S) measured after randomization in a clinical trial can often provide information about the true endpoint (T) and hence the effect of treatment (Z). It can usually be measured earlier and more easily than T and as such may be useful to shorten the trial length. A potential use of S is to completely replace T as a surrogate endpoint to evaluate whether the treatment is effective. Another potential use of S is to serve as an auxiliary variable to help provide information and improve the inference on the treatment effect prediction when T is not completely observed. The objective of this report is to focus on its role as an auxiliary variable and to identify situations when S can be useful to increase efficiency in predicting the treatment effect in a new trial in a multiple-trial setting. Both S and T are continuous. We find that higher efficiency gain is associated with higher trial-level correlation but not individual-level correlation when only S, but not T is measured in a new trial; but, the amount of information recovery from S is usually negligible. However, when T is partially observed in the new trial and the individual-level correlation is relatively high, there is substantial efficiency gain by using S. For design purposes, our results suggest that it is often important to collect markers that have high adjusted individual-level correlation with T and at least a small amount of data on T. The results are illustrated using simulations and an example from a glaucoma clinical trial.

1. INTRODUCTION

A biomarker (S) in a clinical trial is a type of variables intended to provide information about the true endpoint (T) and the effect of treatment (Z). It is often an intermediate physical or laboratory indicator in a disease progression process, and can be measured earlier and is often easier to collect than T. Examples of biomarkers include CD4 counts in AIDS, blood pressure and serum cholesterol level in cardiovascular disease, and prostate-specific antigen in prostate cancer studies. Early measurements are also used as biomarkers for the later measurements, such as the earlier vision test result as a biomarker for the later result in a study on patients with age-related muscular degeneration [1]. Different investigators use different terminology for the roles of the biomarkers [2]. In this paper, we call S a surrogate endpoint when the potential use of S is to completely replace T to evaluate whether the treatment is effective [3]. Alternatively, when S is used to help provide information or enhance the efficiency of the estimator of the treatment effect on T when T is not completely observed, we call S as auxiliary variables [4]. When the true endpoints are rare, later-occurring or costly to obtain, the proper use of good biomarkers can substantially reduce the trial size and duration, hence lower the expense and lead to earlier decision making.

Previous research on the biomarker has often focused on the potential role of S as a surrogate endpoint for T. In a landmark article, Prentice [3] proposed a formal definition for perfect surrogacy and provided validation criteria for a single-trial setting. The criteria require that changes in S fully capture the effect of treatment on T. This paper inspired much research in the field, but the criteria are considered too restrictive for practical use. To relax the criteria, a surrogacy measure based on the proportion of the treatment effect explained (PTE) by S was proposed [5] and further studied and extended by several other authors (e.g., [7, 8, 9]). Freedman [5] also suggested that the PTE confidence interval’s lower bound be > 0.75 for a marker to be acceptable as a surrogate endpoint. However, this requires the treatment effect on T to be very strong, which is rarely observed in practice [8, 10]. The PTE estimator is also highly variable and can be out of the [0,1] range [7, 11]; hence, its practical use is limited.

From a biological aspect, there are often multiple causal pathways leading to disease and complex mechanisms by which the treatment functions; hence, a biomarker may or may not mediate the effect of the treatment on T and the surrogacy measures are often not directly transferable from one study to another. Another problem is that S may not capture the harmful side effect of the treatment. These associated uncertainties in the use of S in replacing T to test a new treatment can lead to incorrect, even harmful conclusions [11, 12]. As a result, very few biomarkers have been accepted as valid surrogate endpoints for T and their potential use as substitutes has been less than promising.

With new biomarkers being discovered and developed at a phenomenal rate, the clinical research community continue to be extremely interested in biomarkers in clinical trials. In this paper, we focus on the use of S as an auxiliary variable in helping predict the treatment effect on T. As we shall see, this role of a biomarker proves to be more promising. One of the most common scenarios for S to be useful as an auxiliary outcome is when one has more information on S than that on T for a study population. This occurs often in practice, since patients are usually recruited into a trial sequentially in calendar time and S is observed more often and earlier than T, particularly on those enrolled early. Previous surrogacy measures are often proposed based on summary statistics in order to identify a replacement for T, and they are not usually suggested explicitly for the purpose of prediction. In the presence of individual-level data, a biomarker may actually be effective as an auxiliary outcome in enhancing inference, but not be identified as such using existing surrogacy measures. A strong association between S and T does not suffice for S to be a substitute for T; as Baker et al [13] stated, “a correlate does not make a surrogate”. However, when individual data on T exist, a strong association can inform and increase the efficiency of treatment effect prediction, as we shall demonstrate.

A number of authors have explored the role of biomarkers as auxiliary variables. However, the opinions on their values have been mixed, as noted by [14]. In much of the previous work, the information recovered from S appears to be very small [18, 4, 19] unless in rare situations when S and T are very highly correlated; however, when there is more structural relationship between S and T, it is more likely to achieve significant efficiency gain by using S [14]. Most of the work mentioned above has focused on the situation when T is the time to an event. When S and T are continuous data, Venkatraman and Begg [21] proposed fully nonparametric tests that incorporate the information from S and found that the amount of efficiency gain through S for these tests is small except in rare occasions when the correlation between S and T is extremely high. A homogeneous sample such as the single trial setting has often been considered in the previous work. When we can identify a group of trials which have similar treatment groups and patient populations, it is natural to use a meta-analytic approach to predict the treatment effect in a new trial. This approach could allow one to account for the heterogeneity among different trials and borrow information from previous trials to improve the efficiency.

In this paper, we will focus on examining the extent of information gain from S in a multiple trial setting. We will examine the situation when T is either completely missing or partially missing in a new trial when we have information on S, T and Z in the previous trials. The objective is to predict the treatment effect on T in the new trial when S and T are continuous and Z is binary. We examine the factors, particularly, the correlation between S and T and the fraction of missing T, that impact the extent of increase in the precision of the treatment effect estimate resulting from utilizing S to identify the situations when S can be beneficial. The results are intended to be of practical value and directly applicable to clinical trials.

In Section 2, we introduce a commonly used bivariate mixed model. In Section 3, we summarize several related methods used to predict the effect of Z on T in a new trial when T is either completely missing or partially missing in the new trial. The methods include those proposed by Buyse et al [10], Gail et al [22] and Henderson [23]. In Section 4, we examine the extent of information recovery from S and its relation to the correlation between S and T. In Section 5, we evaluate the methods and efficiency gain through simulations. In Section 6, we give a data example. In Section 7, we present conclusions.

2. The Model

Suppose we have n randomized trials, i = 1, …, n, where the nth trial is labeled as new and there are m_i patients in the ith trial. Let Z = 0, 1 denote the placebo and treatment groups, respectively and (S_ij, T_ij, Z_ij) represent S, T, and Z for individual j in trial i. We are interested in predicting the actual treatment effect on T in the new trial (δ_Tn) based on previous (n − 1) existing trials and whatever data is available in the nth trial. A commonly used bivariate mixed model used to describe the joint distribution of S_ij and T_ij [10] is:

$$\begin{array}{cc}\hfill & S_{\mathit{ij}}={\alpha }_0+{\alpha }_1{Z}_{\mathit{ij}}+a_{0i}+a_{1i}{Z}_{\mathit{ij}}+{∊}_{S\mathit{ij}}\hfill \\ \hfill & T_{\mathit{ij}}={\gamma }_0+{\gamma }_1{Z}_{\mathit{ij}}+r_{0i}+r_{1i}{Z}_{\mathit{ij}}+{∊}_{T\mathit{ij}}\hfill \end{array}$$ (1)

where

$$\left(\begin{array}{c}\hfill {∊}_{S\mathit{ij}}\hfill \\ \hfill {∊}_{T\mathit{ij}}\hfill \end{array}\right)~\mathrm{MVN}\left(\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}\right),\sigma =\left(\begin{array}{cc}\hfill {\sigma }_{\mathit{ss}}\hfill & \hfill {\sigma }_{\mathit{st}}\hfill \\ \hfill \hfill & \hfill {\sigma }_{\mathit{tt}}\hfill \end{array}\right)\right),$$ (2)

and

$$\left(\begin{array}{c}\hfill a_{0i}\hfill \\ \hfill r_{0i}\hfill \\ \hfill a_{1i}\hfill \\ \hfill r_{1i}\hfill \end{array}\right)~\mathrm{MVN}\left(\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right),D=\left(\begin{array}{cccc}\hfill d_{ss}\hfill & \hfill d_{st}\hfill & \hfill d_{sa}\hfill & \hfill d_{sr}\hfill \\ \hfill \hfill & \hfill d_{tt}\hfill & \hfill d_{ta}\hfill & \hfill d_{tr}\hfill \\ \hfill \hfill & \hfill \hfill & \hfill d_{aa}\hfill & \hfill d_{ar}\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill d_{rr}\hfill \end{array}\right)\right).$$ (3)

The treatment effect in the nth trial is δ_Tn = γ₁ + γ_1n. Let $Y_i^T=(S_{ij},T_{ij}),{∊}_i^T=({∊}_{Sij},{∊}_{Tij})$, β^T = (α₀, γ₀, α₁, γ₁) and ${\eta }_i^T=(a_{0i},r_{0i},a_{1i},r_{1i})$. The model (1) can be written in a general mixed model notation as Y_i = X_iβ + U_iη_i + ε_i, where β denotes the fixed effects, η_i denotes the random effects, X_i and U_i are the corresponding design matrices. The vector Y_i follows a bivariate normal distribution with mean X_iβ and variance $V_i=U_{i}D{U}_i^t+{\Sigma }_i$ where Σ_i is a 2m_i × 2m_i matrix with m_i blocks of σ on the main diagonal and zeros elsewhere.

3. Methods for Predicting the Treatment Effect δ_Tn in the New Trial

In this section, we introduce several related methods used to predict the effect of Z on T in a new trial when T is either completely missing or partially missing in the new trial.

3.1. Buyse et al Method

Buyse et al (BMBRG) [10] assumed the same model and suggested a method to estimate δ_Tn when T is completely unobserved in the nth trial. First, they fit a bivariate mixed model to the data from trial 1 through (n−1) to obtain the estimates of D, α₀, γ₀, α₁ and γ₁, denoted by $\widehat{D}$, ${\widehat{\alpha }}_0$, ${\widehat{\gamma }}_0$, ${\widehat{\alpha }}_1$ and ${\widehat{\gamma }}_1$, respectively. Second, they fit a linear regression S_nj = μ_0Sn + δ_SnZ_nj + ε_Snj in the nth trial. One then obtains that ${\widehat{a}}_{0n}={\widehat{\mu }}_{0Sn}-{\widehat{\alpha }}_0$ and ${\widehat{a}}_{1n}={\widehat{\delta }}_{Sn}-{\widehat{\alpha }}_1$ where ${\widehat{\mu }}_{0Sn}$ and ${\widehat{\delta }}_{Sn}$ are estimates of μ_0Sn and δ_Sn based on data from the nth trial. Given that β, D, σ, a_0n and a_1n are known, BMBRG showed that δ_n follows a normal distribution with conditional mean

$$E\left({\delta }_{Tn}\right)={\gamma }_1+\left(d_{\mathit{sr}}{d}_{\mathit{ar}}\right){\left(\begin{array}{cc}\hfill d_{\mathit{ss}}\hfill & \hfill d_{\mathit{sa}}\hfill \\ \hfill d_{\mathit{sa}}\hfill & \hfill d_{\mathit{aa}}\hfill \end{array}\right)}^{-1}\left(\begin{array}{c}\hfill a_{0n}\hfill \\ \hfill a_{1n}\hfill \end{array}\right),$$ (4)

and conditional variance

$$\mathit{var}\left({\delta }_{Tn}\right)=d_{\mathit{rr}}-\left(d_{\mathit{sr}}{d}_{\mathit{ar}}\right){\left(\begin{array}{cc}\hfill d_{\mathit{ss}}\hfill & \hfill d_{\mathit{sa}}\hfill \\ \hfill d_{\mathit{sa}}\hfill & \hfill d_{\mathit{aa}}\hfill \end{array}\right)}^{-1}\left(\begin{array}{c}\hfill d_{\mathit{sr}}\hfill \\ \hfill d_{\mathit{ar}}\hfill \end{array}\right).$$ (5)

While various methods can be used to obtain the estimate for δ_Tn, denoted by ${\widehat{\delta }}_{Tn}$, in our simulations, we replace β, D, σ, a_0n and a_1n with their estimates in equations (4) and (5) as often done in practice. Specifically, we obtain β, D and σ using a restricted maximum likelihood method from PROC MIXED in SAS. We estimate μ_0Sn and δ_Sn using PROC GLM in SAS and then obtain the estimates for a_0n and a_1n. However, this often leads to underestimation of $var\left({\widehat{\delta }}_{Tn}\right)$.

3.2. Gail et al Method

Gail et al (GPHC) [22] proposed to estimate δ_Tn without involving models for the joint distribution of (S_ij, T_ij) at the individual level. The method applies to the situation when T is completely unobserved in the nth trial. Let ${\mu }_{Ti}^T=({\mu }_{0Ti},{\mu }_{1Ti})$ represent the marginal means of T in the Z = 0 and 1 groups in the ith trial and similarly for ${\mu }_{Si}^T=({\mu }_{0Si},{\mu }_{1Si})$. GPHC assume that ${({\mu }_{0Ti},{\mu }_{0Si},{\mu }_{1Ti},{\mu }_{1Si})}^T$ follows a multivariate normal distribution with covariance φ where φ is a 4 × 4 matrix representing the between-trial variance; hence, its estimate ${({\widehat{\mu }}_{0Ti},{\widehat{\mu }}_{0Si},{\widehat{\mu }}_{1Ti},{\widehat{\mu }}_{1Si})}^T$ follows a multivariate normal distribution with the covariance φ +ω_i where ω_i is a 4 × 4 matrix with two block diagonal matrices denoting the within-trial variance for each treatment group. The elements of μ_Ti, μ_Si, and φ are connected with the parameters in the model (1) in the following way: μ_0Ti = γ₀ + r_0i, μ_1Ti = γ₀ + r_0i + γ₁ + r_1i, μ_0Si = α₀ + a_0i, μ_1Si + α₀ + a_0i + α₁ + a_1i, φ₁₁ = d_tt + d_bb + 2d_tb, φ₁₂ = d_ts + d_ab + d_ta + d_sb, φ₁₃ = d_tt + d_tb, φ₁₄ = d_ts + d_sb, φ₂₂ = d_ss + d_aa + 2d_sa, φ₂₃ = d_st + d_ta, φ₂₄ = d_ss + d_sa, φ₃₃ = d_tt, φ₃₄ = d_st and , φ₄₄ = d_ss.

GPHC show that μ_Tn given ${\widehat{\mu }}_{Sn}$ (and β, φ and ω) follows a normal distribution with mean

$$E\left({\mu }_{Tn}\right)=\left(\begin{array}{c}\hfill {\gamma }_0\hfill \\ \hfill {\gamma }_0+{\gamma }_1\hfill \end{array}\right)+\left(\begin{array}{cc}\hfill {\phi }_{12}\hfill & \hfill {\phi }_{14}\hfill \\ \hfill {\phi }_{23}\hfill & \hfill {\phi }_{34}\hfill \end{array}\right){\left(\begin{array}{cc}\hfill {\phi }_{22}+{\omega }_{22n}\hfill & \hfill {\phi }_{24}\hfill \\ \hfill {\phi }_{24}\hfill & \hfill {\phi }_{44}+{\omega }_{44n}\hfill \end{array}\right)}^{-1}\left(\begin{array}{c}\hfill a_{0n}\hfill \\ \hfill a_{0n}+a_{1n}\hfill \end{array}\right),$$

and variance

$$\mathit{var}\left({\mu }_{Tn}\right)=\left(\begin{array}{cc}\hfill {\phi }_{11}\hfill & \hfill {\phi }_{13}\hfill \\ \hfill {\phi }_{13}\hfill & \hfill {\phi }_{33}\hfill \end{array}\right)-\left(\begin{array}{cc}\hfill {\phi }_{12}\hfill & \hfill {\phi }_{14}\hfill \\ \hfill {\phi }_{23}\hfill & \hfill {\phi }_{34}\hfill \end{array}\right){\left(\begin{array}{cc}\hfill {\phi }_{22}+{\omega }_{22n}\hfill & \hfill {\phi }_{24}\hfill \\ \hfill {\phi }_{24}\hfill & \hfill {\phi }_{44}+{\omega }_{44n}\hfill \end{array}\right)}^{-1}{\left(\begin{array}{cc}\hfill {\phi }_{12}\hfill & \hfill {\phi }_{14}\hfill \\ \hfill {\phi }_{23}\hfill & \hfill {\phi }_{34}\hfill \end{array}\right)}^T,$$

where ω_22n denotes the variance of ${\widehat{\mu }}_{0Sn}$ and ω_44n for ${\widehat{\mu }}_{1Sn}$.

The treatment effect on T in the new trial, δ_Tn, has mean

$$E\left({\delta }_{Tn}\right)=(-11)E\left({\mu }_{Tn}\right),$$ (6)

and variance

$$\mathit{var}\left({\delta }_{Tn}\right)=(-11)\mathit{var}\left({\mu }_{Tn}\right)\left(\begin{array}{c}\hfill -1\hfill \\ \hfill 1\hfill \end{array}\right).$$ (7)

If we drop the terms w_22n and w_44n from the above expressions, we obtain the identical expressions as those of the BMBRG mean and variance. The GPHC formula takes into account the uncertainty associated with estimating a_0n and a_1n while BMBRG does not. Similar to BMBRG, GPHC also assume that β, D and σ are known in deriving equations (6) and (7). Since the uncertainties of β, D and σ are not accounted for here, $var\left({\widehat{\delta }}_{Tn}\right)$ is often underestimated. Gail et al (2000) noted that this method is analogous to the generalized estimating equations (GEE) [6]. We note that the GEE approach can handle the situation when T is partially observed in the new trial, thus the GPHC method could be generalized and would be worthy of further investigation.

To estimate δ_Tn and $var\left({\widehat{\delta }}_{Tn}\right)$, in our simulations, we first obtain $\widehat{\phi }+{\widehat{\omega }}_i$ by calculating the covariances of the treatment- and trial-specific means where $\widehat{\phi }$ and ${\widehat{\omega }}_i$ denote the estimates of φ and ω_i, respectively. We then calculate the treatment-specific covariances of S and T within each trial and then average them over different trials to obtain ${\widehat{\omega }}_i$. From these, we calculate $\widehat{\phi }$. We calculate the overall treatment-specific means as ${\widehat{\gamma }}_0$ and ${\widehat{\gamma }}_1$ (i.e., the estimates of γ₀ and γ₁) and the variances for each treatment group in the new trial for ${\widehat{\omega }}_{22n}$ and ${\widehat{\omega }}_{44n}$ (i.e., the estimates of ω_22n and ω_44n). We estimate μ_0Sn and μ_1Sn and then calculate a_0n and a_1n. Then we plug in these estimates into (6) and (7) to obtain the mean and variance for ${\widehat{\delta }}_{Tn}$.

3.3. Henderson Method (HD)

While both BMBRG and GPHC methods only apply to the situation when T is completely missing in the new trial, the HD method applies to the situations when T is either completely missing, partially missing or completely observed in the new trial. Using the general mixed model notation, we can obtain the estimates of β and η_n (denoted by $\widehat{\beta }$ and ${\widehat{\eta }}_n$) by solving the mixed model equation which is described by Henderson [23] (details in Appendix A) and their sum follows a normal distribution with mean

$$E(\widehat{\beta }+{\widehat{\eta }}_n)=\beta +{\mathit{DU}}_n^T{V}_n^{-1}(Y_n-X_n\beta ).$$ (8)

and variance

$$\begin{array}{cc}\hfill & \mathit{var}\left(\widehat{\beta }+{\widehat{\eta }}_n-\beta -{\eta }_n\right)={\left(\sum _{i=1}^n{X}_i^T{V}_i^{-1}{X}_i\right)}^{-1}+D-{\mathit{DU}}_n^T{V}_n^{-1}{U}_{n}D+{\mathit{DU}}_n^T{V}_n^{-1}{X}_n\hfill \\ \hfill & {\left(\sum _{i=1}^n{X}_i^T{V}_i^{-1}{X}_i\right)}^{-1}{X}_n^T{V}_n^{-1}{U}_{n}D-2{\mathit{DU}}_n^T{V}_n^{-1}{X}_n{\left(\sum _{i=1}^n{X}_i^T{V}_i^{-1}{X}_i\right)}^{-1}.\hfill \end{array}$$

The treatment effect for the nth trial has mean

$$E\left({\widehat{\delta }}_{Tn}\right)=\left(0001\right)(\beta +{\eta }_n)$$ (9)

and variance

$$\mathit{var}\left({\widehat{\delta }}_{Tn}\right)=\left(0001\right)\mathit{var}(\widehat{\beta }+{\widehat{\eta }}_n-\beta -{\eta }_n){\left(0001\right)}^T.$$ (10)

Note that ${\widehat{\eta }}_n$ is the best linear unbiased predictor (BLUP) and can be derived as an empirical Bayes estimator [25, 26]. When T is completely missing in the nth trial, the expression of $E\left({\widehat{\delta }}_{Tn}\right)$ in (9) is exactly the same as the GPHC estimate in (6). Different from GPHC and BMBRG, the variance formula in (10) accounts for the uncertainty associated with estimating β, but it treats D and σ as known quantities. In the implementations, we obtain these estimates using PROC MIXED in SAS.

3.4. Empirical Bayes Estimate and Conditional Posterior Variance (EB-CPV)

Let r be the number of patients in the new trial on whom we have information on both S and T. The empirical Bayesian estimate of δ_Tn can be obtained as the posterior mode estimate when we assume flat priors for the fixed effects and multivariate normal priors for the random effects [26]. Its expression is identical to the HD estimate in equation (9) [26]. When β, D and σ are known, the conditional posterior variance (CPV) of δ_Tn can approximate the variance of ${\widehat{\delta }}_{Tn}$ [28]. We obtain the CPV of δ_Tn as (details in Appendix C):

$$\mathit{var}\left({\delta }_{Tn}\right)=\left(01\right){({\Psi }_d^{-1}+{\Phi }_e^{-1})}^{-1}{\left(01\right)}^T,$$ (11)

where, Ψ_d is a function only of the between-trial covariances given by ${\Psi }_{11}-{\Psi }_{12}{\Psi }_{22}^{-1}{\Psi }_{21}$ and Φ_e is a function only of the within-trial covariances given by ${\Phi }_e=\left(\begin{array}{cc}\hfill {\varphi }_{11}\hfill & \hfill {\varphi }_{12}\hfill \\ \hfill {\varphi }_{12}\hfill & \hfill {\varphi }_{22}\hfill \end{array}\right)$. The elements of Ψ_d and Φ_e are listed below:

$$\begin{array}{cc}\hfill & {\Psi }_{11}=\left(\begin{array}{cc}\hfill d_{\mathit{tt}}\hfill & \hfill d_{\mathit{tr}}\hfill \\ \hfill d_{\mathit{tr}}\hfill & \hfill d_{\mathit{rr}}\hfill \end{array}\right),{\Psi }_{12}=\left(\begin{array}{cc}\hfill d_{\mathit{st}}\hfill & \hfill d_{\mathit{ta}}\hfill \\ \hfill d_{\mathit{sr}}\hfill & \hfill d_{\mathit{ar}}\hfill \end{array}\right),{\Psi }_{21}=\left(\begin{array}{cc}\hfill d_{\mathit{st}}\hfill & \hfill d_{\mathit{sr}}\hfill \\ \hfill d_{\mathit{sr}}\hfill & \hfill d_{\mathit{ar}}\hfill \end{array}\right),\hfill \\ \hfill & {\Psi }_{22}=\left(\begin{array}{cc}\hfill d_{\mathit{ss}}\hfill & \hfill d_{\mathit{sa}}\hfill \\ \hfill d_{\mathit{sa}}\hfill & \hfill d_{\mathit{aa}}\hfill \end{array}\right),{\varphi }_{11}=\frac{({\sigma }_{\mathit{tt}}-{\sigma }_{\mathit{st}}^2{\sigma }_{\mathit{ss}}^{-1}){\sum }_{j=1}^r{Z}_{\mathit{nj}}^2}{r{\sum }_{j=1}^r{Z}_{\mathit{nj}}^2-{\left({\sum }_{j=1}^r{Z}_{\mathit{nj}}\right)}^2},\hfill \\ \hfill & {\varphi }_{12}=\frac{({\sigma }_{\mathit{tt}}-{\sigma }_{\mathit{st}}^2{\sigma }_{\mathit{ss}}^{-1}){\sum }_{j=1}^r{Z}_{\mathit{nj}}}{r{\sum }_{j=1}^r{Z}_{\mathit{nj}}^2-{\left({\sum }_{j=1}^r{Z}_{\mathit{nj}}\right)}^2},{\varphi }_{22}=\frac{r({\sigma }_{tt}-{\sigma }_{\mathit{st}}^2{\sigma }_{\mathit{ss}}^{-1})}{r{\sum }_{j=1}^r{Z}_{\mathit{nj}}^2-{\left({\sum }_{j=1}^r{Z}_{\mathit{nj}}\right)}^2}.\hfill \end{array}$$

When T is completely missing in the nth trial, i.e., r = 0, the CPV simplifies to:

$$\mathit{var}\left({\delta }_{Tn}\right)=\left(01\right){\Psi }_d{\left(01\right)}^T,$$ (12)

an expression equivalent to the BMBRG variance formula in (5). The CPV formula can be viewed as the generalization of the BMBRG variance formula. Note that the CPV underestimates the prediction variance because they treat β, D, σ, a_0n and a_1n as known quantities. Morris [29] and Ghosh and Rao [28] showed that a better estimator of the prediction variance can be obtained by adding to the CPV a second term that takes into account the uncertainty about all parameters.

3.5. Bayesian Estimation (denoted by Bayes)

An alternative method to obtain the distributions of the parameters of interest is a fully Bayesian estimation method which is also applicable when T is either partially missing or completely missing. We assume flat priors for the fixed effects, i.e., p(α₀) ∝ 1, p(γ₀) ∝ 1, p(α₁) ∝ 1, and p(γ₁) ∝ 1, and vague priors for the rest of parameters, specifically, σ⁻¹ ~ W (a, E) and D^-−1 ~ W (c, F), where W refers to the Wishart distribution. We use a = 3, c = 5, E = (a + 1)⁻¹I₂ and F = (c + 1)⁻¹I₄. A data augmentation method is used to implement the procedure (details in Appendix B). The Bayesian estimation method naturally takes into consideration the uncertainty associated with estimating every parameter [27], but it can be sensitive to the prior specifications. While it is computationally intensive to conduct extensive simulations to evaluate the properties of this method, it is very feasible to analyze data using this method.

4. Efficiency Gain and Correlation

In this section, we study the precision of the predicted treatment effects (${\widehat{\delta }}_{Tn}$) and the factors that impact the precision, particularly, the correlation between S and T and the fraction of missingness.

4.1. Correlation

In a multiple-trial setting, with a bivariate mixed model assumption, the treatment adjusted individual-level or within-trial correlation between S and T is $R_{indiv}^2={\sigma }_{st}^2∕{\sigma }_{ss}{\sigma }_{tt}$. The trial-level correlation between S and T is defined by Buyse et al [10] as

$$R_{\text{trial}}^2=\frac{\left(d_{\mathit{sr}}{d}_{\mathit{ar}}\right){\left(\begin{array}{cc}\hfill d_{\mathit{ss}}\hfill & \hfill d_{\mathit{sa}}\hfill \\ \hfill d_{\mathit{sa}}\hfill & \hfill d_{\mathit{aa}}\hfill \end{array}\right)}^{-1}\left(\begin{array}{c}\hfill d_{\mathit{sr}}\hfill \\ \hfill d_{\mathit{ar}}\hfill \end{array}\right)}{d_{\mathit{rr}}}.$$

The between-trial correlation $R_{trial}^2$ assesses how well the treatment effect on T in the new trial can be predicted by that on S. While $R_{trial}^2$ is identified as the key factor that impacts the degree of efficiency gain from S in the research by Buyse et al [10] and Gail et al [22], as we shall see in the following, $R_{indiv}^2$ plays an even more important role than $R_{trial}^2$ in obtaining substantial efficiency gain from S with respect to the estimated treatment effect on T when T is partially observed.

4.2. Prediction Precision and Correlation

We examine the impacts of $R_{indiv}^2$ and $R_{trial}^2$ on the prediction precision using the CPV formula in equation (11). We note that when there is an equal number of patients per treatment group in the new trial, the elements of Φ_e in CPV simplify to

$${\varphi }_{11}=\frac{2{\sigma }_{\mathit{tt}}(1-R_{\text{indiv}}^2)}{r},{\varphi }_{12}=\frac{2{\sigma }_{\mathit{tt}}(1-R_{\text{indiv}}^2)}{r},{\varphi }_{22}=\frac{4{\sigma }_{\mathit{tt}}(1-R_{\text{indiv}}^2)}{r}.$$

When T is completely missing in the new trial, the CPV simplifies to $var\left({\delta }_{Tn}\right)=d_{rr}(1-R_{trial}^2)$; hence, the factors that determine the precision of the predictor of the treatment effect on T are $R_{trial}^2$ and d_rr which are between-trial level. When T is partially observed, the additional important factors are within-trial level including $R_{indiv}^2$, σ_tt and r. Since the within-trial covariances in Φ_e are usually significantly smaller than the between-trial covariances in Ψ_d, we find that Φ_e usually dominates and Ψ_d has a negligible impact on the CPV. Although the CPV usually underestimates the prediction variance, our simulation studies show that it usually accounts for the majority of the total variance, and a comparison between (11) and (12) should suffice to provide algebraic intuition about the prediction variance.

5. Simulations

5.1. The Setup

We conduct simulation studies to evaluate the bias, efficiency and coverage rates of the confidence intervals for the predicted treatment effect in a new trial using the above methods. For comparison purposes, we also estimate δ_Tn based on observed T using the simple estimate without any distributional assumption (denoted by SIMPLE). That is, ${\widehat{\delta }}_{Tn}={\Sigma }_k{T}_{nk1}∕m_{n1}-{\Sigma }_l{T}_{nl0}∕m_{n0}$, where T_nk1 represents T on patient k in the Z = 1 group in the nth trial and similarly for T_nl0, m_n1 represents the number of patients in the Z = 1 group in the nth trial and similarly for m_n0.

We generate 500 data sets based on the bivariate mixed model in (1). We assume equal number of patients per trial and let m_i = m. The parameter specifications are: β^T = (1, 2, 1, 1), d_ss = 0.5, d_tt = 0.2, d_aa = 3.5, d_rr = 1.6, σ_ss = 1 and σ_tt = 0.3. To examine the impact of the trial-level correlation, we vary the correlation matrices for the random effects: $\left(\begin{array}{cccc}\hfill 1\hfill & \hfill 0.57\hfill & \hfill 0.37\hfill & \hfill 0.22\hfill \\ \hfill 0.57\hfill & \hfill 1\hfill & \hfill 0.24\hfill & \hfill 0.21\hfill \\ \hfill 0.37\hfill & \hfill 0.24\hfill & \hfill 1\hfill & \hfill 0.3\hfill \\ \hfill 0.22\hfill & \hfill 0.21\hfill & \hfill 0.3\hfill & \hfill 1\hfill \end{array}\right)$, $\left(\begin{array}{cccc}\hfill 1\hfill & \hfill 0.57\hfill & \hfill 0.37\hfill & \hfill 0.22\hfill \\ \hfill 0.57\hfill & \hfill 1\hfill & \hfill 0.24\hfill & \hfill 0.21\hfill \\ \hfill 0.37\hfill & \hfill 0.24\hfill & \hfill 1\hfill & \hfill 0.7\hfill \\ \hfill 0.22\hfill & \hfill 0.21\hfill & \hfill 0.7\hfill & \hfill 1\hfill \end{array}\right)$ and $\left(\begin{array}{cccc}\hfill 1\hfill & \hfill 0.57\hfill & \hfill 0.37\hfill & \hfill 0.22\hfill \\ \hfill 0.57\hfill & \hfill 1\hfill & \hfill 0.24\hfill & \hfill 0.21\hfill \\ \hfill 0.37\hfill & \hfill 0.24\hfill & \hfill 1\hfill & \hfill 0.9\hfill \\ \hfill 0.22\hfill & \hfill 0.21\hfill & \hfill 0.9\hfill & \hfill 1\hfill \end{array}\right)$, which correspond to $R_{trial}^2=0.1$, 0.5 and 0.8, respectively. To examine the impact of the individual-level correlation, we vary $R_{indiv}^2$ from 0.1, 0.5, to 0.9. We vary n, m, and the percentage of missingness in the new trial (denoted by p). For each different data set, we have a different underlying true treatment effect δ_Tn because δ_Tn is not fixed and follows a known distribution. Its average across 500 data sets is denoted by ${\stackrel{‒}{\delta }}_{Tn}$. For each data set and each method used, we obtain ${\widehat{\delta }}_{Tn}$, its standard error, its CI as ${\widehat{\delta }}_{Tn}\pm 1.96\times \left(\text{standard error}\right)$ and an indicator variable for whether the 95% CI contains δ_Tn or not. Let ${\overline{\widehat{\delta }}}_{Tn}$ denote the average of ${\widehat{\delta }}_{Tn}$ across 500 data sets. We examine the method’s performance by its average bias $(\mathrm{Bias}={\overline{\widehat{\delta }}}_{Tn}-{\stackrel{‒}{\delta }}_{Tn})$, the average standard error (SE), the root mean squared error $(\mathrm{RMSE}=\sqrt{\Sigma {({\widehat{\delta }}_{Tn}-{\delta }_{Tn})}^2∕500})$, and the coverage rate (CR) over all simulated data sets. As we will see all estimates are unbiased, the relative efficiency (RE) of two estimators can be approximated by the inverse of the ratio of the two corresponding RMSE²s.

5.2. Method Evaluation

In Table I, we present Bias, RMSE, SE and CR of ${\widehat{\delta }}_{Tn}$ using the respective methods including SIMPLE, HD, BMBRG, GPHC, Bayes and EB-CPV from simulations with various combinations of n, m, and the percentage of missingness. We let $R_{indiv}^2=0.5$ and $R_{trial}^2=0.5$. When T is completely or 50% observed in the new trial, SIMPLE and HD generate estimates which are unbiased, have similar RMSE and confidence intervals with nominal-level or close- to-nominal-level coverage rates; on the other hand, CPV consistently gives underestimated prediction variances (i.e., SE < RMSE).

Table I.

Simulation results based on 500 data sets. β^T= (1, 2,1,1), d_ss = 0.5, d_tt = 0.2, d_aa = 3.5, d_rr = 1.6, σ_ss = 1, σ_tt = 0.3, $R_{indiv}^2=0.5$ and $R_{trial}^2=0.5$

n	m	%Missing	Methods	Bias	RMSE	SE	CR
10	100	0%	SIMPLE	−0.005	0.111	0.109	95.0
			HD	−0.005	0.112	0.106	94.8
			Bayes	−0.006	0.112	0.109	94.8
			EB-CPV	−0.005*	0.112*	0.093†	90.8
		50%	SIMPLE	−0.002	0.149	0.139	95.4
			HD	0.000	0.143	0.139	94.0
			Bayes	−0.004	0.145	0.145	94.8
			EB-CPV	0.000*	0.143*	0.132†	91.2
		100%	BMBRG	−0.013	1.193	0.736	76.6
			GPHC	−0.010	1.125	0.755	80.2
			HD	−0.011	1.125	0.795	82.0
			Bayes	−0.037	1.139	1.105	94.8
40	100	0%	SIMPLE	−0.005	0.111	0.109	95.0
			HD	−0.005	0.110	0.108	95.0
			EB-CPV	−0.005*	0.110*	0.093†	91.4
		50%	SIMPLE	−0.002	0.149	0.155	95.4
			HD	0.003	0.140	0.142	95.8
			EB-CPV	0.003*	0.140*	0.130†	93.2
		100%	BMBRG	−0.008	0.965	0.887	92.8
			GPHC	−0.008	0.965	0.877	92.6
			HD	−0.008	0.965	0.869	92.4
40	300	0%	SIMPLE	0.002	0.063	0.063	94.2
			HD	0.002	0.063	0.063	94.4
			EB-CPV	0.002*	0.063*	0.066†	90.9
		50%	SIMPLE	−0.002	0.089	0.090	94.4
			HD	0.000	0.085	0.083	93.6
			EB-CPV	0.000*	0.085*	0.077†	91.4
		100%	BMBRG	−0.002	0.920	0.868	93.8
			GPHC	−0.002	0.919	0.871	93.8
			HD	−0.002	0.919	0.882	94.0
55	100	0%	SIMPLE	−0.005	0.111	0.109	95.0
			HD	−0.005	0.110	0.108	95.0
			EB-CPV	−0.005*	0.110*	0.094†	90.8
		50%	SIMPLE	−0.002	0.149	0.155	95.4
			HD	0.002	0.140	0.142	95.8
			EB-CPV	0.002*	0.140*	0.131†	93.4
		100%	BMBRG	−0.033	0.950	0.883	93.8
			GPHC	−0.033	0.948	0.898	94.0
			HD	−0.033	0.948	0.898	94.2

SIMPLE: simple estimate. HD: Henderson method. Bayes: Bayesian estimation. CPV: conditional posterior variance. BMBRG: method by Buyse et al [10]. GPHC: method by Gail et al [22]. EB-CPV: EB estimate with CPV variance.

^*obtained using HD.

^†obtained using CPV.

When T is completely missing in the new trial, BMBRG, GPHC and HD all underestimate the variances of ${\widehat{\delta }}_{Tn}$. When the number of the trials is relatively large (n = 40, 55), the extent of underestimation is minor; however, with a small number of trials (n = 10), the extent can be more severe and the coverage rates can be less than 85%. Although HD is expected to have better CR than GPHC and GPHC is expected to be better than BMBRG because they account for more uncertainty of the parameters, the advantages of HD and GPHC over BMBRG are small and all methods give similar CRs. The Bayes method we used gives more precise estimates of the variances and the coverage rates are around the 95% nominal level.

The SIMPLE and HD methods give estimates with similar precision which shows that the efficiency gain from the bivariate normal assumption is small. When T is partially or completely observed, the increase in m can improve the precision of the estimates while a larger n does not necessarily improve much precision. When T is completely missing, there is a minor gain in the precision when n and m increase.

5.3. R $R_{indiv}^2$, $R_{trial}^2$, Percentage of Missingness and Information Recovery from S

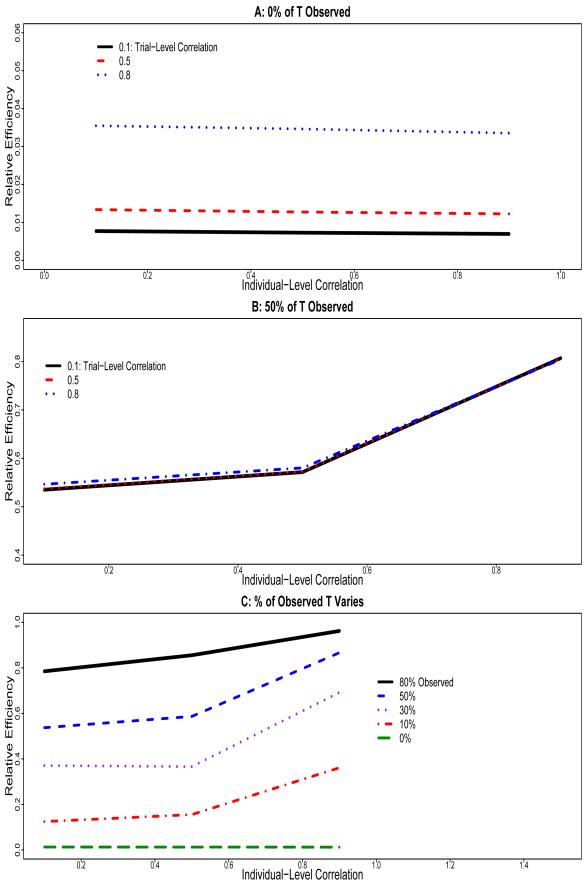
Figure 1A shows the relatively efficiency of ${\widehat{\delta }}_{Tn}$ when T is completely missing in the new trial compared to the estimate before any deletion in T occurs using the HD method. Relative efficiency is defined as the inverse of the ratio of the two variances. We vary $R_{indiv}^2$ and $R_{trial}^2$ and let n = 40 and m = 100. We find that while the increases in $R_{indiv}^2$ have negligible impact on the precision, the increase in $R_{trial}^2$ can improve the precision more than any other factor. These findings agree with the algebraic intuition from the CPV variance formula in (12). Relative to the estimate based on completely observed data, the relative efficiency varies from 0.7%, 1.2% to 3.4% as we increase $R_{trial}^2$ from 0.1, 0.5 to 0.8. As a result, when we completely rely on S and summary statistics from previous trials to predict ${\widehat{\delta }}_{Tn}$, the extent of information recovery is often limited and the precision of ${\widehat{\delta }}_{Tn}$ is usually insufficient to be clinically useful.

Figure 1.

Simulation results based on 500 data sets. Relative efficiency of the new treatment effect estimate using S when T is not completely observed to that when T is completely observed. A: 0% of T Observed in the new trial; B: 50% of T observed in the new trial; C: Percentage of Observed T Varies in the new trial.

Figure 1B presents the relative efficiency of ${\widehat{\delta }}_{Tn}$ when T is 50% missing compared with the estimate before any deletion of T using the HD method. We find that high $R_{indiv}^2$ can lead to a large gain of efficiency from the use of S. When $R_{indiv}^2$ is large (e.g., 0.7 or 0.9), most of the information on δ_Tn is recovered from S and the precision of the estimate is close to that when T is completely observed. On the other hand, the magnitude of $R_{trial}^2$ does not have much impact on the amount of efficiency gain from S. The observations here are in agreement with the CPV variance formula in (11).

Figure 1C shows the relative efficiency of ${\widehat{\delta }}_{Tn}$ when T is partially or completely missing compared with the estimate before any deletion of T. Naturally, the higher the proportion of available T, the smaller the RMSE, and thus the greater the precision for the treatment effect prediction. Interestingly, we find that there is a substantial efficiency gain from the information on S with even a small fraction of observed T, particularly when $R_{indiv}^2$ is high. For example, when 30% T are observed, the lost information due to missingness is almost completely recovered from S when $R_{indiv}^2=0.9$.

6. Data Analysis: a Glaucoma Study

The evaluation of the extent of information recovery from S in predicting the treatment effect on T in a new trial is illustrated using the Collaborative Initial Glaucoma Treatment Study (CIGTS) [30]. Glaucoma is a group of diseases that cause vision loss and is a leading cause of blindness. High pressure in the eyes, i.e. intraocular pressure (IOP), is a major risk factor of glaucoma. The CIGTS is a randomized multi-center clinical trial to compare the effects of two types of treatments, surgery and medicine, on reducing IOP among glaucoma patients. Patients are enrolled between 1993 and 1997. A total of 607 patients are included in the study and among them, 307 are randomly assigned into the medicine group. IOP (recorded in mmHg) has been measured at different time points following the treatment. For the purpose of this paper, we take the IOP measurement at month 96 as T and that at month 12 as S. We assume that the IOP measurements are normally distributed. To evaluate the situation of a meta-analysis where data are from different trials; we treat the different centers in the CIGTS study as independent trials testing a similar group of treatments. A preliminary analysis of these data shows that the estimate of the between-trial variances, $\widehat{D}$, is non-positive definite. Mimicing the approach of Gail et. al. [22], we rescale up the data size by simulating S_ij and T_ij from bivariate normal distributions for each trial and treatment group with the trial-specific and treatment-specific means and variance-covariances from the real data. Nonetheless, our results are generalizable. The CIGTS study includes 14 centers from which we delete five centers (i.e., 5, 7, 12, 13, 14) either because they had too few observations or because of non-positive definite covariance matrices within center. We also deleted two outliers that are greater than 35mmHg. For the centers included (n = 9), we increase the sample sizes to 335, 176, 385, 264, 539, 368, 286, 528, and 319. The trial-specific and treatment-specific means and correlations for S and T are listed in Table II.

Table II.

Description of Pseudodata in Glaucoma study: Treatment-Specific Means and Individual-Level Correlations for Each Center

Center	Sample Size	Medicine	Surgery	Individual-level Correlation
		(Means of S, T)	(Means of S, T)	Medicine	Surgery
1	670	(17.63, 16.52)	(13.76, 14.59)	0.367	0.608
2	352	(17.22, 16.42)	(14.63, 12.98)	−0.455	0.467
3	770	(19.27, 17.58)	(15.81, 16.17)	0.589	0.548
4	528	(17.17, 15.51)	(10.93, 12.88)	0.176	0.540
5	1078	(18.52, 18.67)	(14.99, 15.32)	0.435	0.407
6	736	(18.62, 18.89)	(15.13, 17.11)	−0.16	−0.0056
7	572	(18.35, 15.34)	(14.59, 14.53)	0.177	0.396
8	1056	(18.59, 16.16)	(13.60, 13.72)	0.31	0.95
9	638	(17.56, 16.82)	(14.19, 14.61)	0.042	0.756

The HD method is used to fit the rescaled data for which $\widehat{D}$ is positive definite and the estimates of $R_{trial}^2$ and $R_{indiv}^2$, denoted by ${\widehat{R}}_{trial}^2$ and ${\widehat{R}}_{indiv}^2$, are obtained as 0.25 and 0.15, respectively. We randomly select Center 8 as the new trial and delete some proportion of T in Center 8 to examine the extent of efficiency gain through the use of S. The missing mechanism is missing completely at random [24]. The results are listed in Table III. Without missing T, ${\widehat{\delta }}_{Tn}$ is −2.45 with the standard error of 0.29. When T is completely missing, ${\widehat{\delta }}_{Tn}$ is 1.58 with the standard error of 0.79. When 20% or 50% of T are missing, the precision of ${\widehat{\delta }}_{Tn}$ using S is comparable to that based on completely observed T. Even with 80% missing, the SE is substantially smaller than that when 100% of T is missing. For further illustration, we treat Center 9 as a new trial and obtain similar results. With this rescaled data, we have artificially increased the sample size by approximately five fold for each trial, hence, the power to detect the treatment effect is much larger than the original data. When δ_Tn is predicted solely based on S, the relatively efficiency is only about 10% compared to that when T is not missing, and ${\widehat{\delta }}_{Tn}$ reaches the significance level of 0.05 for Center 9 and is not quite significant for center 8. In this particular study we completely observe S by the end of year 1998 but only start to observe T in year 2001, thus by solely relying on S to predict δ_Tn, we can significantly shorten the trial length, but the result is only of borderline significance. In practice many trials do not have such strong effect so when δ_Tn is predicted solely based on S, the substantial loss in precision often results in failure to detect any real treatment effect difference. In the CIGTS, by October 2002, about 20% of T would have been observed and the treatment effect is clearly significant, illustrating the benefit of significant increase in the precision of ${\widehat{\delta }}_{Tn}$ by utilizing a small fraction of T. There is a also a considerable time saving compared to collecting T on all subjects, which would have required follow-up to 2005.

Table III.

Estimate treatment effect on IOP at the 96th month utilizing information from early IOP measures at the 12^th month in the glaucoma study.

p	Estimate	Standard Error	p-value
center = 8
SIMPLE†	−2.45	0.29	< .0001
No missing‡	−2.33	0.22	< .0001
100% missing‡	−1.58	0.79	0.063
90% missing‡	−1.50	0.47	0.0059
80% missing‡	−2.37	0.39	< .0001
50% missing‡	−2.61	0.29	< .0001
20% missing‡	−2.19	0.23	< .0001
center = 9
SIMPLE†	−2.21	0.30	< .0001
No missing‡	−2.32	0.27	< .0001
100% missing‡	−2.68	0.82	0.0053
90% missing‡	−2.19	0.61	0.0023
80% missing‡	−2.30	0.49	< .0002
50% missing‡	−2.04	0.36	< .0001
20% missing‡	−2.15	0.30	< .0001

^†Based on complete data before any deletion.

^‡HD method was used.

7. DISCUSSION

In this report, we examine the role of biomarkers as auxiliary variables in predicting the treatment effect and identify situations when biomarkers can be beneficial in a multiple-trial setting. While previous literature on the use of biomarkers as substitutes for the true endpoints has been mostly negative and the proposed surrogate measures are often not useful in practice, we show that it is possible for S to be useful as auxiliary variables in helping provide information and enhancing the inference on T. Although a high correlation between S and T does not qualify S as a good surrogate [13], we show that the correlation is a critical measure in determining the extent of information recovery from S.

In a multiple-trial setting, when T is completely unobserved, $R_{indiv}^2$ has little impact on the amount of information recovered from S; on the other hand, the higher the $R_{trial}^2$, the higher the efficiency gain from S. However, even with a relatively high $R_{trial}^2$, the predicted treatment effect based on data from other trials and biomarkers in the new trial solely is usually too imprecise to be clinically useful. On the other hand, when the predicted treatment effect on T solely based on S would be sufficient to detect the difference in the treatment effect, the benefit of reducing the trial length can be enormous. Examples include the situation when the statistical power to detect treatment effect is very large or when $R_{trial}^2$ is close to 1 such as the ovarian cancer example in [10]. However, these cases are usually rare in practice. On the contrary, when T is partially observed in the new trial, we find that a high $R_{indiv}^2$ is a very important determinant in increasing the precision of the predicted treatment effect from S but the impact of $R_{trial}^2$ is negligible. With even a small fraction of T and a high $R_{indiv}^2$, the information on the treatment effect is mostly recovered and the prediction precision is close to that when T is completely observed. It appears that some data on T are essential to provide the basis for individual-level predictions of T from S and take advantage of the distributional assumption between S and T, and hence to give a much more efficient treatment estimate.

We compare the BMBRG, GPHC and HD methods when T is completely missing. Each method gave unbiased estimates; but the variances were underestimated, particularly when the number of the trials was small. Either a bootstrap [22] or fully Bayesian or measurement-error approach [15] could remedy this problem. When T is partially observed, we use two methods: HD and EB-CPV. We find that the underestimation of the variance from the HD method becomes negligible but CPV consistently underestimates the variance. We note that we only consider the case of missing T being missing completely at random and that all methods are applicable when the missing mechanism is missing at random [24].

In conclusion, biomarkers would seem to have a useful role as auxiliary variables. Future research should focus on their roles as auxiliary variables and identify scenarios when biomarkers can increase the precision of the treatment effect. For design purposes, our results suggest that it is often important to collect at least some data on the true endpoint and more information on biomarkers which have high adjusted individual-level correlations with the true endpoint. With appropriate utilization of high quality biomarkers in estimating the treatment effect when the true endpoint is not completely observed, one can reach a desired level of precision earlier, hence shortening the study period and reducing the cost. In our study, we consider continuous S and T. For future research, it would also be interesting to investigate the factors that impact the efficiency gain and the extent of it when S and T are other types of data such as binary, categorical and time to an event.

8. APPENDIX A: Henderson Method [23]

Let Y = Xβ+Uη+ε, where the vectors Y, η and ε and the matrix X are obtained from stacking the vectors Y_i, η_i and ε_i and the matrices X_i, respectively, underneath each other, and where U is the block-diagonal matrix with blocks U_i on the main diagonal and zeros elsewhere. Let $\mathcal{D}$ and Σ be block-diagonal with blocks D and Σ_i on the main diagonal and zeros elsewhere. We have the following relationships: $E\left(\eta \right)=0,E\left(∊\right)=0,\mathrm{var}\left(\eta \right)=\mathcal{D}$, var(ε) = Σ, cov(η, ε) = 0 and we let $\mathcal{V}=U\mathcal{D}{U}^T+\Sigma$. The estimates of $\mathcal{D}$, Σ and $\mathcal{V}$ are denoted by $\widehat{\mathcal{D}}$, $\widehat{\Sigma }$ and $\widehat{\mathcal{V}}$. Henderson [23] proposed a method to obtain estimates of β and η by solving the mixed model equation as follows:

$$\left[\begin{array}{cc}\hfill X^T{\widehat{\Sigma }}^{-1}X\hfill & \hfill X^T{\widehat{\Sigma }}^{-1}U\hfill \\ \hfill U^T{\widehat{\Sigma }}^{-1}X\hfill & \hfill U^T{\widehat{\Sigma }}^{-1}U+{\widehat{\mathcal{D}}}^{-1}\hfill \end{array}\right]\left[\begin{array}{c}\hfill \widehat{\beta }\hfill \\ \hfill \widehat{\eta }\hfill \end{array}\right]=\left[\begin{array}{c}\hfill X^T{\widehat{\Sigma }}^{-1}Y\hfill \\ \hfill U^T{\widehat{\Sigma }}^{-1}Y\hfill \end{array}\right]$$

The solution can be written as:

$$\begin{array}{cc}\hfill & \widehat{\beta }={\left(X^T{\widehat{\mathcal{V}}}^{-1}X\right)}^{-1}{X}^T{\widehat{\mathcal{V}}}^{-1}Y\hfill \\ \hfill & \widehat{\eta }=\widehat{\mathcal{D}}{U}^T{\widehat{\mathcal{V}}}^{-1}(Y-X\widehat{\beta }).\hfill \end{array}$$

The covariance matrix of $(\widehat{\beta }-\beta ,\widehat{\eta }-\eta )$ is

$$C={\left[\begin{array}{cc}\hfill X^T{\Sigma }^{-1}X\hfill & \hfill X^T{\Sigma }^{-1}U\hfill \\ \hfill U^T{\Sigma }^{-1}X\hfill & \hfill U^T{\Sigma }^{-1}U+{\mathcal{D}}^{-1}\hfill \end{array}\right]}^{-1}.$$

McLean and Sanders (1988) [33] and McLean, Sanders and Stroup (1991) [34] show that C can also be written as

$$C={\left[\begin{array}{cc}\hfill C_{11}\hfill & \hfill C_{21}\hfill \\ \hfill C_{21}\hfill & \hfill C_{22}\hfill \end{array}\right]}^{-1}$$

where

$$\begin{array}{cc}\hfill C_{11}=& {\left(X^T{\mathcal{V}}^{-1}X\right)}^{-1},\hfill \\ \hfill C_{21}=& -\mathcal{D}{U}^T{\mathcal{V}}^{-1}X{C}_{11},\hfill \\ \hfill C_{22}=& {(U^T{\Sigma }^{-1}U+{\mathcal{D}}^{-1})}^{-1}-C_{21}{X}^T{\mathcal{V}}^{-1}U\mathcal{D}\hfill \\ \hfill =& \mathcal{D}-\mathcal{D}{U}^T{\mathcal{V}}^{-1}U\mathcal{D}-C_{21}{X}^T{\mathcal{V}}^{-1}U\mathcal{D}.\hfill \end{array}$$

In practice, the estimate, $\widehat{C}$, is often obtained by substituting $\mathcal{D}$ and Σ in C with their estimates, as we have done in this paper. From the above, we canDobtain the expression for the mean and variance for $\widehat{\beta }+{\widehat{\eta }}_n$ as follows:

$$\begin{array}{cc}\hfill & E(\widehat{\beta }+{\widehat{\eta }}_n)=\beta +{\mathit{DU}}_n^T{V}_n^{-1}(Y_n-X_n\beta ),\hfill \\ \hfill & \mathit{var}(\widehat{\beta }-\beta +{\widehat{\eta }}_n-{\eta }_n)={\left(X^T{\mathcal{V}}^{-1}X\right)}^{-1}+D-{\mathit{DU}}_n^T{V}_n^{-1}{U}_{n}D+{\mathit{DU}}_n^T{V}_n^{-1}{X}_n\hfill \\ \hfill & {\left(X^T{\mathcal{V}}^{-1}X\right)}^{-1}{X}_n^T{V}_n^{-1}{U}_{n}D-2{\mathit{DU}}_n^T{V}_n^{-1}{X}_n{\left(X^T{\mathcal{V}}^{-1}X\right)}^{-1}\hfill \\ \hfill =& {\left(\sum _{i=1}^n{X}_i^T{V}_i^{-1}{X}_i\right)}^{-1}+D-{\mathit{DU}}_n^T{V}_n^{-1}{U}_{n}D+{\mathit{DU}}_n^T{V}_n^{-1}{X}_n\hfill \\ \hfill & {\left(\sum _{i=1}^n{X}_i^T{V}_i^{-1}{X}_i\right)}^{-1}{X}_n^T{V}_n^{-1}{U}_{n}D-2D{U}_n^T{V}_n^{-1}{X}_n{\left(\sum _{i=1}^n{X}_i^T{V}_i^{-1}{X}_i\right)}^{-1}.\hfill \end{array}$$

9. APPENDIX B: BAYESIAN ESTIMATION

Iterate the following two steps until the parameters reach convergence:

Step 1: Impute missing T_nj’s from a normal distribution with mean and variance:

$$\begin{array}{cc}\hfill E(T_{\mathit{nj}}\mid S_{\mathit{nj}},Z_{\mathit{nj}})=& {\gamma }_0+r_{0n}-{\sigma }_{\mathit{st}}{\sigma }_{\mathit{ss}}^{-1}({\alpha }_0+a_{0n})\hfill \\ \hfill +& ({\gamma }_1+r_{1n}-{\sigma }_{\mathit{st}}{\sigma }_{\mathit{ss}}^{-1}({\alpha }_1+a_{1n}\left)\right)Z_{\mathit{nj}}+{\sigma }_{\mathit{st}}{\sigma }_{\mathit{ss}}^{-1}{S}_{\mathit{nj}},\hfill \\ \hfill \mathit{var}(T_{\mathit{nj}}\mid S_{\mathit{nj}},Z_{\mathit{nj}})=& {\sigma }_{\mathit{tt}}-{\sigma }_{\mathit{st}}^2{\sigma }_{\mathit{ss}}^{-1}\hfill \end{array}$$

Step 2: Apply Gibbs sampling to the complete data to estimate the parameters:

$$\begin{array}{cc}\hfill & D^{-1}\mid \eta ~W(n+c,{(\sum _{i=1}^n{\eta }_i{\eta }_i^T+F^{-1})}^{-1})\hfill \\ \hfill & {\sigma }^{-1}\mid X,Y,Z,\beta ,\eta ~W{(\sum _{i=1}^n{m}_i+a,(\mathit{VS}+E^{-1})}^{-1})\hfill \\ \hfill & {\eta }_i\mid X,Y,Z,\sigma ,D~\mathit{MVN}(\mathit{VE}\times (\sum _{j=1}^{m_i}{Z}_{\mathit{ij}}^T{\sigma }^{-1}(Y_{\mathit{ij}}-X_{\mathit{ij}}\beta )),\mathit{VE})\hfill \\ \hfill & \beta \mid X,Y,Z,{\eta }_i,\sigma ~\mathit{MVN}(\mathit{VB}\times (\sum _{i=1}^n\sum _{j=1}^{m_i}{X}_{\mathit{ij}}{\sigma }^{-1}(Y_{\mathit{ij}}-U_{\mathit{ij}}{\eta }_i)),\mathit{VB})\hfill \end{array}$$

where,

$$\begin{array}{cc}\hfill & \mathit{VS}=\sum _{i=1}^n\sum _{j=1}^{m_i}(Y_{\mathit{ij}}-X_{\mathit{ij}}\beta -U_{\mathit{ij}}{\eta }_i){(Y_{\mathit{ij}}-X_{\mathit{ij}}\beta -U_{\mathit{ij}}{\eta }_i)}^T,\hfill \\ \hfill & \mathit{VB}={\left(\sum _{i=1}^n\sum _{j=1}^{m_i}{X}_{\mathit{ij}}^T{\sigma }^{-1}{X}_{\mathit{ij}}\right)}^{-1},\hfill \\ \hfill & \mathit{VE}={(\sum _{j=1}^{m_i}{U}_{\mathit{ij}}^T{\sigma }^{-1}{U}_{\mathit{ij}}+D^{-1})}^{-1}.\hfill \end{array}$$

From the distributions of β and η_i, we can obtain the distribution of δ_Tn.

10. APPENDIX C: CONDITIONAL POSTERIOR VARIANCE OF δ_Tn

Let α₀ + a_0i = μ_0Si, γ₀ + r_0i = μ_0Ti, α₁ + a_1i = δ_Si and γ₁ + r_1i = δ_Ti. We can rewrite the model (1) as

$$\begin{array}{cc}\hfill & S_{\mathit{ij}}={\mu }_{0Si}+{\delta }_{\mathit{Si}}{Z}_{\mathit{ij}}+{∊}_{\mathit{Sij}}\hfill \\ \hfill & T_{\mathit{ij}}={\mu }_{0Ti}+{\delta }_{\mathit{Ti}}{Z}_{\mathit{ij}}+{∊}_{\mathit{Tij}}.\hfill \end{array}$$

Assume there are r observations with both S and T observed and m_n – r observations with just S observed in the nth trial. The likelihood can be written as:

$$\begin{array}{cc}\hfill & L(\varphi \mid S,t,Z)\hfill \\ \hfill =& \left\{\prod _{i=1}^{n-1}\left[\prod _{j=1}^{m_i}N(Y_{\mathit{ij}}\mid \beta ,{\eta }_i,\sigma ,D,Z_{\mathit{ij}})\right]\right\}\hfill \\ \hfill & \left\{\prod _{j=1}^{r}N(Y_{\mathit{nj}}\mid {\eta }_n,\beta ,Z_{\mathit{nj}},\sigma ,D)\prod _{j=1}^{m_n-r}N(S_{\mathit{nj}}\mid {\mu }_{0_{\mathit{sn}},}{\delta }_{\mathit{sn}},Z_{\mathit{nj}},{\sigma }_{\mathit{ss}})\right\}\hfill \\ \hfill =& \prod _{i=1}^{n-1}\left[\prod _{j=1}^{m_i}\frac{1}{\sqrt{2\pi }{\mid \sigma \mid }^{1∕2}}\exp \left\{-\frac{1}{2}{\left(\begin{array}{c}\hfill S_{\mathit{ij}}-{\mu }_{0\mathit{Si}}-{\delta }_{\mathit{Si}}{Z}_{\mathit{ij}}\hfill \\ \hfill T_{\mathit{ij}}-{\mu }_{0\mathit{Ti}}-{\delta }_{\mathit{Ti}}{Z}_{\mathit{ij}}\hfill \end{array}\right)}^T{\sigma }^{-1}\left(\begin{array}{c}\hfill S_{\mathit{ij}}-{\mu }_{0\mathit{Si}}-{\delta }_{\mathit{Si}}{Z}_{\mathit{ij}}\hfill \\ \hfill T_{\mathit{ij}}-{\mu }_{0\mathit{Ti}}-{\delta }_{\mathit{Ti}}{Z}_{\mathit{ij}}\hfill \end{array}\right)\right\}\right]\hfill \\ \hfill & \prod _{j=1}^r\frac{1}{\sqrt{2\pi }{\mid \sigma \mid }^{1∕2}}\exp \left\{-\frac{1}{2}{\left(\begin{array}{c}\hfill S_{\mathit{nj}}-{\mu }_{0\mathit{Sn}}-{\delta }_{\mathit{Sn}}{Z}_{\mathit{nj}}\hfill \\ \hfill T_{\mathit{nj}}-{\mu }_{0\mathit{Tn}}-{\delta }_{\mathit{Tn}}{Z}_{\mathit{nj}}\hfill \end{array}\right)}^T{\sigma }^{-1}\left(\begin{array}{c}\hfill S_{\mathit{nj}}-{\mu }_{0\mathit{Sn}}-{\delta }_{\mathit{Sn}}{Z}_{\mathit{nj}}\hfill \\ \hfill T_{\mathit{nj}}-{\mu }_{0\mathit{Tn}}-{\delta }_{\mathit{Tn}}{Z}_{\mathit{nj}}\hfill \end{array}\right)\right\}\hfill \\ \hfill & \prod _{j=r}^{m_n-r}\frac{1}{\sqrt{2\pi }{\mid \sigma \mid }^{1∕2}}\exp \left\{-\frac{1}{2}{(S_{\mathit{nj}}-{\mu }_{0\mathit{Sn}}-{\delta }_{\mathit{Sn}}{Z}_{\mathit{nj}})}^2\right\}\hfill \\ \hfill & \prod _{i=1}^n\frac{1}{\sqrt{2\pi }{\mid D\mid }^{1∕2}}\exp \left\{-\frac{1}{2}{\left(\begin{array}{c}\hfill {\mu }_{0\mathit{Si}}-{\alpha }_0\hfill \\ \hfill {\mu }_{0\mathit{Ti}}-{\gamma }_0\hfill \\ \hfill {\delta }_{\mathit{Si}}-{\alpha }_1\hfill \\ \hfill {\delta }_{\mathit{Ti}}-{\gamma }_1\hfill \end{array}\right)}^T{D}^{-1}\left(\begin{array}{c}\hfill {\mu }_{0\mathit{Si}}-{\alpha }_0\hfill \\ \hfill {\mu }_{0\mathit{Ti}}-{\gamma }_0\hfill \\ \hfill {\delta }_{\mathit{Si}}-{\alpha }_1\hfill \\ \hfill {\delta }_{\mathit{Ti}}-{\gamma }_1\hfill \end{array}\right)\right\},\hfill \end{array}$$

which is proportional to the posterior density when we assume flat priors for the fixed effects and multivariate normal distributions for the random effects. The conditional posterior distributions of μ_0Tn and δ_Tn given the data and all other parameters are proportional to:

$$\begin{array}{cc}\hfill \begin{array}{c}\hfill {\mu }_0{T}_n\hfill \\ \hfill {\delta }_{T_n}\hfill \end{array}\mid \cdot \propto & \prod _{j=1}^r\frac{1}{\sqrt{2\pi }{\mid \sigma \mid }^{1∕2}}\exp \left\{-\frac{1}{2}{\mathit{ME}}^T\times {\sigma }^{-1}\times \mathit{ME}\right\}\hfill \\ \hfill & \frac{1}{\sqrt{2\pi }{\mid D\mid }^{1∕2}}\exp \left\{-\frac{1}{2}{\left(\begin{array}{c}\hfill {\mu }_{0\mathit{Sn}}-{\alpha }_0\hfill \\ \hfill {\mu }_{0\mathit{Tn}}-{\gamma }_0\hfill \\ \hfill {\delta }_{\mathit{Sn}}-{\alpha }_1\hfill \\ \hfill {\delta }_{\mathit{Tn}}-{\gamma }_1\hfill \end{array}\right)}^T{D}^{-1}\left(\begin{array}{c}\hfill {\mu }_{0\mathit{Sn}}-{\alpha }_0\hfill \\ \hfill {\mu }_{0\mathit{Tn}}-{\gamma }_0\hfill \\ \hfill {\delta }_{\mathit{Sn}}-{\alpha }_1\hfill \\ \hfill {\delta }_{\mathit{Tn}}-{\gamma }_1\hfill \end{array}\right)\right\}\hfill \\ \hfill \propto & \exp \left\{-\frac{1}{2}\sum _{j=1}^r{[T_{\mathit{nj}}-{\mu }_{0\mathit{Tn}}-{\delta }_{\mathit{Tn}}{Z}_{\mathit{nj}}-{\sigma }_{\mathit{st}}{\sigma }_{\mathit{ss}}^{-1}(S_{\mathit{nj}}-{\mu }_{0\mathit{Sn}}-{\alpha }_n{Z}_{\mathit{nj}}\left)\right]}^2\times q^{-1}\right\}\hfill \\ \hfill & \times \exp \left\{\frac{1}{2}{\mathit{MD}}^T\times {({\Psi }_{11}-{\Psi }_{12}{\Psi }_{22}^{-1}{\Psi }_{21})}^{-1}\times \mathit{MD}\right\}\hfill \\ \hfill =& A\times B.\hfill \end{array}$$ (13)

where

$$\begin{array}{cc}\hfill & {\Psi }_{11}=\left(\begin{array}{cc}\hfill d_{\mathit{tt}}\hfill & \hfill d_{\mathit{tr}}\hfill \\ \hfill d_{\mathit{tr}}\hfill & \hfill d_{\mathit{rr}}\hfill \end{array}\right),{\Psi }_{12}=\left(\begin{array}{cc}\hfill d_{\mathit{st}}\hfill & \hfill d_{\mathit{ta}}\hfill \\ \hfill d_{\mathit{sr}}\hfill & \hfill d_{\mathit{ar}}\hfill \end{array}\right),{\Psi }_{21}=\left(\begin{array}{cc}\hfill d_{\mathit{st}}\hfill & \hfill d_{\mathit{sr}}\hfill \\ \hfill d_{\mathit{ta}}\hfill & \hfill d_{\mathit{ar}}\hfill \end{array}\right),{\Psi }_{22}=\left(\begin{array}{cc}\hfill d_{\mathit{ss}}\hfill & \hfill d_{\mathit{sa}}\hfill \\ \hfill d_{\mathit{sa}}\hfill & \hfill d_{\mathit{aa}}\hfill \end{array}\right),\hfill \\ \hfill & \mathit{ME}=\left(\begin{array}{c}\hfill S_{\mathit{nj}}-{\mu }_{0\mathit{Sn}}-{\delta }_{\mathit{Sn}}{Z}_{\mathit{nj}}\hfill \\ \hfill T_{\mathit{nj}}-{\mu }_{0\mathit{Tn}}-{\delta }_{\mathit{Tn}}{Z}_{\mathit{nj}}\hfill \end{array}\right),\mathit{MD}=\left(\begin{array}{c}\hfill {\mu }_{0\mathit{Tn}}-{\gamma }_0\hfill \\ \hfill {\delta }_{\mathit{Tn}}-{\gamma }_1\hfill \end{array}\right)-{\Psi }_{12}{\Psi }_{22}^{-1}\left(\begin{array}{c}\hfill {\mu }_{0\mathit{Sn}}-{\alpha }_0\hfill \\ \hfill {\delta }_{\mathit{Sn}}-{\alpha }_1\hfill \end{array}\right).\hfill \\ \hfill & \text{and}q={\sigma }_{\mathit{tt}}-{\sigma }_{\mathit{st}}^2{\sigma }_{\mathit{ss}}^{-1}.\hfill \end{array}$$

The covariance contribution for μ_0Tn and δ_Tn from term B is ${\Psi }_d={\Psi }_{11}-{\Psi }_{12}{\Psi }_{22}^{-1}{\Psi }_{21}$.

We define $Q_{nj}=T_{nj}-{\sigma }_{st}{\sigma }_{ss}^{-1}(S_{nj}-{\mu }_{0Sn}-{\alpha }_n{Z}_{nj})$. From (13),

$$\begin{array}{cc}\hfill & A=\exp \left\{-\frac{1}{2}\sum {(Q_{\mathit{nj}}-{\mu }_{0\mathit{Tn}}-{\delta }_{\mathit{Tn}}{Z}_{\mathit{nj}})}^2{q}^{-1}\right\}\hfill \\ \hfill & =\exp \{-\frac{1}{2}[\frac{\sum Z_{\mathit{nj}}^2}{q}{\delta }_{\mathit{Tn}}^2+\frac{r}{q}{\mu }_{0\mathit{Tn}}^2+\frac{\sum Q_{\mathit{nj}}^2}{q}-2\frac{{\mu }_{0\mathit{Tn}}\sum Q_{\mathit{nj}}}{q}\phantom{]}\phantom{\}}\hfill \\ \hfill & \phantom{\{}\phantom{[}-2\frac{{\delta }_{\mathit{Tn}}\sum Z_{\mathit{nj}}{Q}_{\mathit{nj}}}{q}+2\frac{{\mu }_{0\mathit{Tn}}{\delta }_{\mathit{Tn}}\sum Z_{\mathit{nj}}}{q}]\}.\hfill \end{array}$$

A is proportional to a bivariate normal density. The covariance contribution from term A is defined as ${\Phi }_e=\left(\begin{array}{cc}\hfill {\varphi }_{11}\hfill & \hfill {\varphi }_{12}\hfill \\ \hfill {\varphi }_{12}\hfill & \hfill {\varphi }_{22}\hfill \end{array}\right)$, where

$$\begin{array}{cc}\hfill & {\varphi }_{11}=\frac{({\sigma }_{\mathit{tt}}-{\sigma }_{\mathit{st}}^2{\sigma }_{\mathit{ss}}^{-1}){\sum }_{j=1}^r{Z}_{\mathit{nj}}^2}{r{\sum }_{j=1}^r{Z}_{\mathit{nj}}^2-{\left({\sum }_{j=1}^r{Z}_{\mathit{nj}}\right)}^2},\hfill \\ \hfill & {\varphi }_{12}=\frac{({\sigma }_{\mathit{tt}}-{\sigma }_{\mathit{st}}^2{\sigma }_{\mathit{ss}}^{-1}){\sum }_{j=1}^r{Z}_{\mathit{nj}}}{r{\sum }_{j=1}^r{Z}_{\mathit{nj}}^2-{\left({\sum }_{j=1}^r{Z}_{\mathit{nj}}\right)}^2},\hfill \\ \hfill & {\varphi }_{22}=\frac{r({\sigma }_{\mathit{tt}}-{\sigma }_{\mathit{st}}^2{\sigma }_{\mathit{ss}}^{-1})}{r{\sum }_{j=1}^r{Z}_{\mathit{nj}}^2-{\left({\sum }_{j=1}^r{Z}_{\mathit{nj}}\right)}^2}.\hfill \end{array}$$

Combining the variance contributions from terms A and B, we can obtain the conditional posterior covariance for μ_0Tn and δ_Tn as: ${({\Phi }_e^{-1}+{\Psi }_d^{-1})}^{-1}$. The corresponding conditional posterior variance for ( 0 1 ) ${({\Phi }_e^{-1}+{\Psi }_d^{-1})}^{-1}$ ( 0 1 )^T.