Recent Developments in Molecular Simulation Approaches to Study Spherical Virus Capsids

Abstract

Viruses are a particularly challenging systems to study via molecular simulation methods. Virus capsids typically consist of over 100 subunit proteins and reach dimensions of over 100 nm; solvated viruses capsid systems can be over 1 million atoms in size. In this review, I will present recent developments which have attempted to overcome the significant computational expense to perform simulations which can inform experimental studies, make useful predictions about biological phenomena and calculate material properties relevant to nanotechnology design efforts.

1 Introduction

Viruses are parasitic entities, which can infect all domains of life. Virus structures span a variety of shapes and sizes, have numerous distinct structural features and utilize a diversity of mechanisms to complete their infection and replication processes. Viruses can contain either an RNA or DNA genome, and for both RNA and DNA, the genome may be single-stranded (ss) or double-stranded (ds). Viruses are classified by their genome type and the mechanism the virus uses to produce mRNA from its genome[1]. The protein shell (capsid) which surrounds the genomic material can display a variety of surface features, including pores, canyons, spikes and pillars. The capsid may be surrounded by a lipid membrane (enveloped) or naked (non-enveloped) or may even have an internal membrane[2]. The recent discovery of giant viruses has called into question whether viruses should be classified as living or non-living entities. These giant viruses are larger and have more complex genomes than singled-cell organisms[3, 4].

Even though there is great divergence in the structure and mechanisms employed by various viruses, a common physical constraint exists for all of these system. This is the fact that the viral genome must encode for a capsid to enclose the genome, to protect it during the transport from one cell to another during the proliferation of the viral infection. The difficultly of doing this is most easily understood for the viruses on the opposite end of the virosphere from the giant viruses, the small spherical viruses. For example the hepatitis B virus (HBV) genome is only 3.2 kb long, encoding four genes, only one of which is used to make the capsid. The genome is far too large for a single copy of the capsid protein to somehow encapsidate and protect the genome. The solution to this predicament was first touched on by Crick and Watson[5], where they realized that since the size of capsids are much larger than any single protein, a capsid must contain multiple copies of the capsid protein. They proposed the capsids were assembling into a high symmetry order platonic solid shape, the largest of which is the icosahedron (and dodecahedron), which would contain 60 subunits. While 60 subunits appeared sufficient to form a shell in the smallest spherical viruses, it was clear, given protein sizes are fairly consistent, that 60 subunits would not be enough to form the larger shells that were being observed (ca. 1950s and early 1960s). The solution to this was put forth by Caspar and Klug[6], who showed that icosahedral symmetry could still be used in capsid structures containing greater that 60 subunits. This is accomplished by allowing the subunits to exists in slightly different symmetry environments, both pentamers and hexamers, which is known as the principle of quasi-equivalence. This concept provided a scalable design for capsids in which 12 pentamers exist at the vertices of the icosahedron, but a variable number of hexamers can be packed in-between the pentamers to form shells of different diameters. Icosahedral capsids are classified by their triangulation number, T ; the set of allowable T-numbers is given by T = h² + k² + hk, where h and k take on only zero, or positive integer values. h and k represents the number of “steps” in different directions required to traverse from one pentamer to another, where steps are taken from the center of one capsomer (hexamer or pentamer) to another. Since all icosahedral capsids have 12 pentamers, larger T numbers represent larger capsids; the number of protein subunits in a given capsid is 60T, and the number of different symmetry environments a subunit may exist in is T.

It is quite remarkable that the evolutionary pressures that viruses face have pushed them to the mathematical limit. The icosahedral rotation group (I), which describes the symmetry of spherical virus capsids is an order 60 symmetry and is the largest rotation group of any discrete point group symmetry. So how are viruses capable of assemblying such a highly organized structure? Does the virus use complex machinery in the cell to facilitate the formation of the capsid? It turns out that the organization of the capsid is encoded into the protein subunit itself, as evidenced by the ability to self-assemble icosahedral capsids from purified capsid proteins in the absence of nucleic acids[7]. The specificity of the protein-protein interactions in a capsid is, in many cases, sufficient to dictate the organization of the icosahedral capsid. It is conceivable that an optimal subunit shape exists that can exhibit these symmetry characteristics. Indeed capsids proteins do display folds which are distinct from other non-capsid proteins[8], and by far the most prevalent being the jelly-roll fold[9]. The topology of the jelly-roll fold as well as the subunit organization in a T = 1 and T = 3 capsid are presented in Fig. 1.

Figure 1.

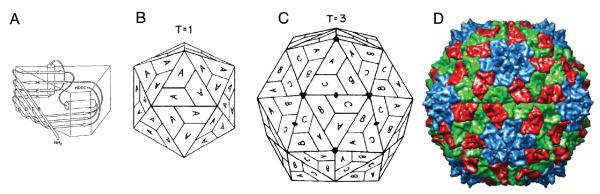
Icosahedral capsid structural organization. A) The topology of the jelly-roll fold presents a trapezoidal shape which can be optimally tiled on an icosahedral lattice. B) T = 1 shell in which all subunits are in identical environments (only pentamers). C) T = 3 shell in which three (slightly) different symmetry environments exist (denoted by subunit A, B and C). All shells larger than T = 1 consists of pentamers and hexamers. D) Structure of the SBMV T = 3 capsid (pdbid:4sbv), in which the trapezoidal shape and subunit organization can be clearly seen. Colors correspond to the subunits in (C) as follows: blue = A, red = B, green = C. Subfigures A,B and C are reproduced with permission from [10].

The subject of this review is to highlight the role of molecular simulation in understanding the dynamics and mechanics of spherical virus capsids. I will discuss models ranging from all-atom classical models to various flavors of coarse grained models. It should be noted that there has been significant theoretical work as well as non-particle based numerical simulations to understand these properties as well. I will not go into depth on these topics, but some of the highlights include mathematical theories on the assembly and organization of virus structures; notable contributions include those by Mannige and Brooks[11–13] and Twarock and coworkers[14–17]. Thermodynamic and kinetic treatments of capsid organization, assembly and mechanics have included important contributions from Bruinsma, Gelbart, Zandi, Reguera and Rudnick[18–23], Zlotnick[24–26] and Hagan[27]. The mechanical properties of capsids have been heavily studied, using continuum elasticity by Nelson and Widom[28, 29], Bruisnma and Gelbart[30–32] and Podgornick[33–36], who has focused on electrostatic contributions. Finite element simulations have complemented these theoretical and also experimental studies on capsid mechanics, in particular the work by Klug[37–42]. Molecular simulation and these other approaches are in most instances complementary and can provide different perspectives on the same phenomena. One advantage molecular simulations has is the ability to provide mechanistic insights. Depending on the granularity of the model, these insights may be translated into biochemically testable hypotheses and have the potential to form a basis to inhibit virus assembly or other stages of the viral infection cycle.

2 All-atom Modeling

2.1 Full Capsid Simulations

The use of modern all-atom molecular mechanics force fields, such as CHARMM22/CMAP[43] or AMBER-99SB[44], have had great success in describing the dynamics and thermodynamics of proteins and other biological macromolecules. It is desirable to extend this level of accuracy to virus capsid simulations, but the computational cost of such calculations is immense. Given the high cost, it is unlikely these simulations can be extended to time-scales which are relevant to biological processes, or even to observe motions along the lowest frequency modes. However, a few groups have made the Herculean effort to compute all-atom dynamics of complete virus capsids. In 2006, Schulten and coworkers performed simulations on the T = 1 satellite tobacco mosaic virus (STMV), both for empty capsids and with a model for the RNA genome core[45]. These simulations were performed in explicit TIP3P water, resulting in systems sizes of over 1 million atoms. The simulations were run for ~ 10 ns, and the major conclusion was that the RNA acts to stabilize and preserve the symmetry of the capsids. In the absence of RNA the capsid was unstable, broke symmetry and began to collapse. Given the short timescale of the simulation it is somewhat surprising that such large deformations were observed, but STMV has not been shown to form stable shells without RNA present. Zink and Grubmüller preformed simulations on the T = 3 southern bean mosaic virus (SBMV) capsid, shown in Fig. 1D, solvated explicitly with TIP4P water; the simulation system was 4.5 million atoms[46]. The system was equilibrated for 13 ns and then force-probe simulations were performed to compare with AFM nanoindendation studies. While SBMV has not been studied experimentally via AFM, the elastic constants computed in this work were an order of magnitude larger than has been observed experimentally for other capsids[47]. This likely overestimation, was probably due to the force loading rate being ~ 8 orders of magnitude faster than experimental rates[48], and the model probe tip was much smaller than AFM tips. May and Brooks performed a simulation of a mutant T = 1 capsid of Sesbania mosaic virus (SeMV), shown in Fig. 2, in explicit TIP3P water for ~ 30 ns; the system size exceeded 800,000 atoms[49]. The SeMV capsid was stable in that simulation and the purpose was to compare the equilibrium fluctuations in the all-atom full capsid simulation with dynamics generated by a multiscale model (more on this below). Recently, van der Spoel computed trajectories for the T = 1 satellite tobacco necrosis virus (STNV) capsid, solvated with TIP3P water; the system size was 1.2 million atoms[50]. These simulations on the STNV capsid were performed on the 1 μs timescale, far exceeding any of the previous studies. In that study, they examined the role of structural Ca⁺² ions in stabilizing the capsid. When the Ca⁺² ions were removed, the capsid swelled by an amount consistent with experimental measurements. One other notable work, also performed by Schulten, was in the construction of an atomistic model of the mature HIV-1 capsid[51]. HIV does not have a spherical/icosahedral capsid, it has a cone structure, but is made from hexamers and 12 pentamers of capsid proteins. Using a multistage approach, involving flexible-fitting to cryo-EM densities, a complete modelfor the full capsid was built and solvated, resulting in a 64 million atom system. This massive system was simulated for 100 ns on the Blue Waters supercomputer and remained stable during the simulation. It is the hope that this all-atom model will enable development of new HIV-1 therapeutics.

Figure 2.

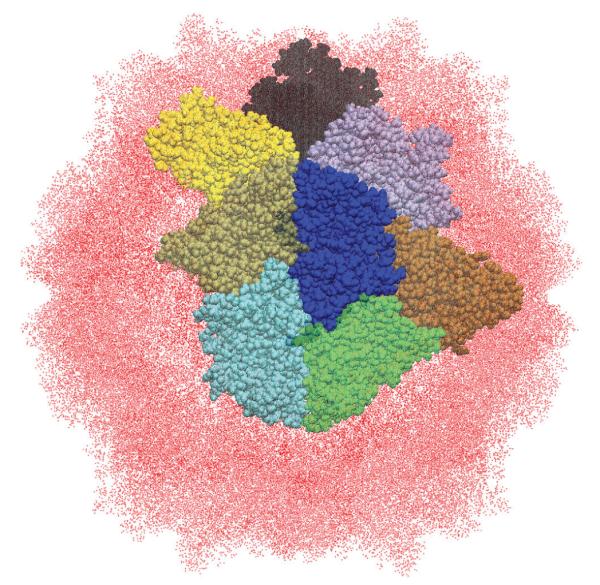
In the RSBC method only a single asymmetric unit is explicitly simulation. For the SeMV T = 1 (pdbid :1×36)particle shown here, the central blue subunit would be explicitly simulated. The surrounding colored subunits are “images” of the central subunit, related by one of the icosahedral rotations.

2.2 Symmetry Constrained Simulations

The advancements in high performance computing and improved MD algorithms have enabled the full capsids simulations, consisting of millions of atoms, as discussed above. However, the high degree of symmetry in spherical capsids, allows for a way to reduce the system size, without disrupting the integrity of the capsid, or introducing edge effects. This can be accomplished by employing rotational symmetry boundary conditions(RSBC)[52], which can be implemented with the CHARMM IMAGES facility[53]. The concept is the same as in regular periodic boundary conditions, but where the regular method is used to construct a semi-infinite system, the RSBC method uses a closed point group symmetry to model a finite system (see Fig. 2). The major benefit in capsid simulations is that the asymmetric unit may be simulated under icosahedral symmetry conditions, effectively reducing the system size 60-fold compared to the full capsid system. The method was introduced by Pettitt over 20 years ago, but has seen limited usage. The major proponents of the method have been May and Brooks[49, 54–57] and Post[58–61].

May and Brooks have primarily used the method to generate equilibrium dynamics of capsids and extract a scaling factor which feeds into their multiscale approach for calculating elastic properties. Most recently they used the RSBC method to study conformational changes related to the maturation of the T = 7 bacteriophage HK97[54], see Fig. 5A-B. In that work, they constructed a pathway between known structures of that capsid; immature (Prohead II) and mature (Head I). The pathway was refined using the harmonic Fourier beads method[62, 63] and umbrella sampling simulations were performed to compute a potential of mean force (PMF) along the transition. The overall ΔG between the end points was in reasonable agreement with differential scanning calorimetry (DSC) measurements[64] on the same states. They also performed constant pH MD[65] during the umbrella sampling simulations and estimated pK_as for the histidines and acidic amino acids. From the pK_as, ΔΔGs were estimated based on the Wyman-Tanford linkage equation[66, 67] to understand how pH is influencing the free-energy landscape. They observed that different segments of the pathway respond differently to acidification, in a manner consistent with in vitro studies.

Figure 5.

Maturation transition of T = 7 HK97. A) The immature Prohead II (pdbid:3e8k) B) The mature Head II (pdbid:10hg). C) The first non degenerate normal mode for Prohead II, is a breathing/expansion model. D) The second non-degenerate normal mode is concentrated at the pentamers and contributes to the faceted morphology of Head II. Pentamers are blue in C and D)

The work by Post has focused on human rhinovirus (HRV) 14 and its interaction with the antiviral WIN 52084 molecule, which inhibits viral replication by preventing uncoating of the capsid. HRV-14 is a pseudo T = 3 capsid, indicating the capsid has a T = 1 architecture (only pentamers), but the “subunit” in this case would be a 3 protein unit. Using icosahedral RSBC they observed that WIN 52084 increased configurational entropy at the binding site while simultaneously increasing flexibility in loops away from the binding pocket[61]. Expanding upon that observation, they conducted simulations of a pentamer under dodecahedral RSBC to study long range correlated motions[60]. In the absence of WIN 52084 they observed breathing motions of the capsid and long range correlations between the motions of regions of the capsid that get externalized during uncoating. WIN 52084 acts to disrupt the breathing and correlated motions, suggesting this is the mechanism of antiviral activity.

The RSBC method provides a considerable computational advantage compared to explicitly modeling a full virus capsid. While structural studies indicate icosahedrally symmetric capsids are thermodynamically favorable[68], clearly a system undergoing thermal fluctuations will not maintain perfect symmetry. This raises the issue of whether the RSBC is introducing artifacts to the dynamics. There are two possible sources of errors the RSBC method may introduce; one local and one global. The local effect could arise due to interactions around the symmetry axes, at which an explicitly modeled atom is interacting with multiple images of itself. Post investigated this effect by comparing the dynamics around symmetry constrained and unconstrained axes and found the radial distribution functions were negligibly different. The global effect of icosahedrally constrained simulations was observed by May and Brooks, when they compared fluctuation spectra between full capsid and icosahedral RSBC simulations[49]. In that work, the virus surface was discretized and the fluctuations were projected onto a spherical harmonic basis. The spectra differed significantly, marked by the icosahedrally constrained capsid having the largest projections onto the icosahedrally symmetric spherical harmonics, which is a sensible observation. It has been shown that the lowest frequency normal modes of capsids are not icosahedrally symmetric[69] so it is not surprising that the absence of those non-icosahedral modes would result in different long-wavelength dynamics. May and Brooks were interested in continuum properties and therefore the incorporation of the lowest frequency modes was important, but in other studies where the properties of interest are molecular in nature and more localized, the global modes may not be as relevant.

3 Multiscale and Coarse Grained Modeling

3.1 Mechanical Properties of Capsids

Intense interest in the mechanical properties of virus capsids arose after measurements revealed the forces exerted by packaged DNA on bacteriophage capsids was in the range of 50 pN[70] and the pressure inside the capsids could be as high as 50 atm[71]. These are remarkably high forces and it was quite surprising that a capsid, thought to be held together by relatively weak protein-protein interactions[72], could be so mechanically robust. This led to a series of experimental studies using the method of AFM nanoindentation in which a force versus displacement (FZ) curve is determined from which a spring constant, k, for the capsid can be measured. For empty capsids, thin shell elastic theory can be reasonably applied, and from k an estimate of the capsid 3-dimensional Young’s modulus, E, can be obtained. Numerous viruses have been analyzed using this method, the results of which have been recently reviewed[47]. While AFM provides a method to directly probe the properties of the capsid, and being a single-particle method the heterogeneity of the sample can be analyzed, it is a somewhat blunt tool, given the tip radius is typically ~ 20 nm. Simulations methods have been successful in predicting the mechanical properties of capsids, and can give insight into the molecular basis for these properties. The interest in the mechanical properties of capsids is two-fold, one is biological the other technological. Understanding how the mechanical properties of the capsid are derived and how those properties change as a function of environment, ligand/receptor binding or different stages of the viral life cycle can give insight into the mechanisms of viral processes. On the technology front, the utilization of viruses for applications such as gene delivery and biomedical imaging[73] has become fashionable, and the design of nanodevices may depend critically on the mechanical properties of the shell.

Two approaches have been taken to calculate mechanical properties from molecular simulations. One method is to perform an in silico nanoindentation experiment, the other is to relate equilibrium fluctuations to an elastic Hamiltonian. May and Brooks developed a theoretical framework and multiscale approach to calculate the 2D Young’s modulus, Y, and bending modulus, κ, of capsids from equilibrium simulations[49]. In that study they examined the SeMV T = 1 mutant (Fig. 2) using nonlinear 2D shell elasticity theory and by describing the deformations of the shell in a spherical harmonic basis, they derived an expression for the total elastic energy of the capsid,

$$E=\frac{1}{2}\sum _l\left(8b+k\frac{l(l-1)(l+1)(l+2)}{R^2}\right){\mid {\widehat{\alpha }}_l\mid }^2,$$ (1)

where R is the radius of the shell, ${\mid {\widehat{a}}_l\mid }^2\equiv {\sum }_{m=-l}^{+l}{a}_{\mathit{lm}}{a}_{\mathit{lm}}^{\ast }$, a_lm is the amplitude of harmonic Y_lm and b is the sum of the Lamé parameters, which can be related to Y. From equipartition of energy among the modes the following relation was developed

$$\langle {\mid {\widehat{\alpha }}_l\mid }^2\rangle =\frac{K_{B}T}{8b+k\frac{l(l-1)(l+1)(l+2)}{R^2}},$$ (2)

which was used to fit the equilibrium spectra and estimate Y and κ. In the initial study the equilibrium dynamics were generated using an all-atom full capsid approach and a multiscale approach. In the multiscale method an elastic network model (ENM) was constructed to describe the interactions within the capsid. The potential energy of the ENM is given by

$$U_{\mathit{ENM}}=\frac{k}{2}\sum _{r_{\mathit{ij}}^0<R_c}{(r_{\mathit{ij}}-r_{\mathit{ij}}^0)}^2,$$ (3)

where r_ij is the separation distance between “nodes” of the network, chosen to be Cα atoms in this work, $r_{\mathit{ij}}^0$ is the separation distance in the initial structure, typically an experimentally determined structure, and k is the uniform spring constant between interacting nodes. Only those atoms separated by less than the cutoff, R_c, are considered to be interacting; May and Brooks used a cutoff of 12 Å. Normal mode analysis (NMA) can be performed on the ENM, by constructing a Hessian matrix of the second derivatives of U_ENM, and diagonalizing the Hessian to obtain the normal modes. The modes can then be used to generate a trajectory according to

$$\Delta {\mathbf{r}}_i\left(t\right)=\sum _{j=7}^N\frac{C}{{\omega }_j}{\mathbf{a}}_{\mathit{ij}}\mathit{cos}({\omega }_{j}t+{\varphi }_j)$$ (4)

where the displacement of atom i is given by a sum over normal modes j = 7,.., N. a_ij is the ith component of mode j, ω_j and ϕ_j are the frequency and phase shift (chosen randomly) of mode j. C is an amplitude factor, which for May and Brooks was an arbitrary factor. The sum over modes, may be restricted to the lower frequency range of the mode spectrum, if the global, collective dynamics are of interest. This was the case for May and Brooks and they only considered the slowest 1000 modes; the first 6 modes are rigid body motions and are not considered. Since the spring constant in the network is arbitrary, May and Brooks performed a renormalization procedure in which the spectral intensity computed from the ENM dynamics was rescaled according to the a scaling factor derived from an all-atom simulation of just the asymmetric unit of the T = 1 SeMV under icosahedral RSBC. This was justified by the observation that the sum of the spectral intensities was conserved between an all-atom full capsid simulation and the RSBC system, which was rationalized as a manifestation of energy conservation. With the rescaled network, May and Brooks were able to estimate Y and κ for SeMV in a range consistent with theoretical estimates[28, 31].

To connect their calculations to AFM experiments May and Brooks decomposed a finite element indentation simulation on T = 3 cowpea chlorotic mottle virus (CCMV) onto a spherical harmonic basis, and observed this mode of deformation is predominantly characterized by the l = 1 harmonic[56]. Using the multiscale approach, they were able to estimate E based upon the l = 1 mode and observed agreement between their calculations and experimental AFM measurements. They went on to perform these calculations on the immature and mature states of HK97 and observed good agreement with experimental measurements[57]. In a separate study[55], they showed that the spherical (immature) to faceted (mature) transition that HK97 undergoes during maturation could be rationalized in terms of the Foppl-von Kármán number,

$$\gamma =\frac{{\mathit{YR}}^2}{k}$$ (5)

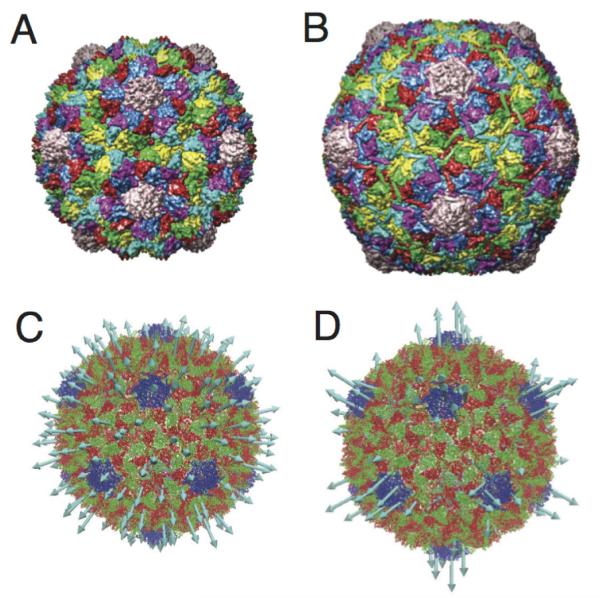
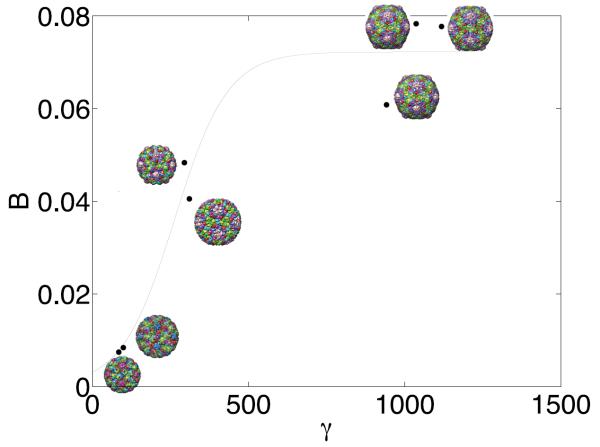
according to the theory of Nelson[28]. May and Brooks went on to calculate γ for a series of capsid structures and found that the larger T = 7 capsids displayed a strong dependence between the capsid shape and γ, whereas smaller T = 3 capsid did not. That correlation for the large T = 7 capsids is shown in Fig. 3, where B represents a degree of buckling (analogous to asphericity); the inflection point in the curve-fit to the data, representing a crossover from a spherical to faceted regime, was in excellent agreement with the theoretical estimate of γ = 260[31].

Figure 3.

Predicted γ-values versus the buckling shape factor B, shows large γ correlates with faceted configurations. Reproduced with permission from [55].

The alternative approach that has been taken to use molecular models to determine elastic properties of capsids is to deform the capsids in a manner analogous to the AFM nanoindenation procedure. As discussed above, using an all-atom description to model capsid nanoindentation, will likely result in the system being pushed far from equilibrium, because the computational expense necessitates fast loading rates. Therefore, coarse-grained models are attractive because they potentially can capture the essential physics and allow for loading rates closer to experimental timescales. Schulten and coworkers employed a shape-based CG (SBCG) model in which the mapping was approximately 150 atoms per CG bead to study nanoindentation of empty T = 4 HBV capsids[74]. This model effectively fixes the subunit shape and the CG beads interact through bond and angle terms, as well as Lennard-Jones (LJ) and Coulomb potentials. When the SBCG model was introduced, the strength of the LJ interaction was uniform (∊ = 4 kcal/mol), but in the study of HBV the model was adjusted to account for specific interactions, which were required to maintain the capsid size and shape. With this model, they were able to perform indentation at a rate of 2.3 * 10⁶ nm/s, which is still 3-4 orders of magnitude faster than typical experimental rates. The model was able to produce reversible deformation at smaller deformations and irreversible deformation for large deformations, which is observed in experimental systems. The model was able to attribute this characteristic to local shifting of the monomer-monomer interactions and bending of the monomer subunits. The SBCG model and expiremental and simulated FZ curves are shown in Fig. 4.

Figure 4.

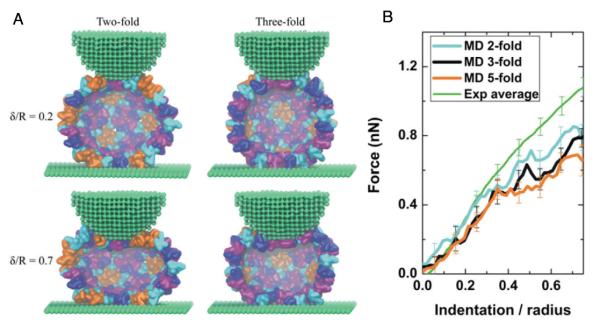
Simulated AFM nanoidentation of HBV capsid. A) Simulation snapshots for deformations along different symmetry axes using the SBCG model. B) Comparison between experimental and SBCG FZ curves shows good agreement, particularly for small deformations. Reproduced with permission from [42].

In a recent study by Barsegov, the mechanics and underlying energy landscape of CCMV were investigated[75]. This studied utilized a structure-based model, commonly called a Gō-model, which they term a self-organized polymer (SOP) model. The SOP model represents each residue by a single particle at the Cα position. The force field of the SOP consists of a finite extensible nonlinear elastic term to model the bonded backbone interactions, and non bonded terms for the native $\left(U_{\mathit{NB}}^{\mathit{ATT}}\right)$ and non-native $\left(U_{\mathit{NB}}^{\mathit{REP}}\right)$ contacts. Native contacts are those residues which fall with a cutoff distance (8 Å) in the pdb structure, these interactions have the form

$$U_{\mathit{NB}}^{\mathit{ATT}}=\sum _{i,j=i+3}{∊}_n\left[{\left(\frac{r_{\mathit{ij}}^0}{r_{\mathit{ij}}}\right)}^{12}-2{\left(\frac{r_{\mathit{ij}}^0}{r_{\mathit{ij}}}\right)}^6\right]{\Delta }_{\mathit{ij}}$$ (6)

$$U_{\mathit{NB}}^{\mathit{REP}}=\sum _{i,j=i+2}{∊}_r{\left(\frac{{\sigma }_r}{r_{\mathit{ij}}}\right)}^6+\sum _{i,j=i+3}{∊}_r{\left(\frac{{\sigma }_r}{r_{\mathit{ij}}}\right)}^6(1-{\Delta }_{\mathit{ij}})$$ (7)

where, $r_{\mathit{ij}}^0$ is the distance between residues in the native state and Δ_ij = 1 for native interactions and is zero otherwise. This model was implemented to run on GPU architectures, which allowed for nanoindentation simulations to be performed at rates comparable to experimental loading rates. The simulations were able to reproduce the experimentally determined spring constant and display reversible/irreversible deformations in a manner consistent with experimental observations. They did detailed analysis on their Force-indentation (FZ) curves to calculate the reversible work and performed umbrella sampling simulations to determine ΔG, ΔH and TΔS during indentation. One of the major conclusions was that capsid collapse was an enthalpically driven process. Other work using CG based models includes a comprehensive study by Cieplak and Robbins, in which they performed nanoidentation on 35 different capsid using a structure based model[76].

In a study on human adenovirus (HAdV), which is a pseudo T = 25 capsid, with a diameter over 90 nm, the influence of cellular host factors on the mechanical properties of the capsid were examined by AFM. It was observed that binding of integrin at the 5-fold axis had an effect to weaken the stiffness at the 5-fold, but to also increase the stiffness at the 2-fold axis[77]. Because of the large size of the (HAdV), a very coarse-model was used by May to investigate this effect, an elastic model of a Mackay icosahedron. It was observed that in this simple geometric model, if the springs at the 5-fold axis were softened the normal modes describing a deformation along the 2-fold axis were characterized by high frequency (stiffer) modes than when the 5-fold vertex was not softened. This result implies the coupling between the mechanical response at different vertices in a capsid may be a generic geometric effect.

3.2 Capsid Conformational Changes

Several viruses have been identified, which undergo large structural transitions, and structural data, either x-ray or cryo-EM, is available on multiple states of the system. Particularly if these states are stages in the viral life cycle and are related to infectivity of the virus particle, understanding the mechanism and thermodynamics of the conformational change pathway would provide valuable insights. Understanding the thermodynamics, through PMF calculations, are challenging because the potential energy function should not be biased toward a particular state (as it is in ENM and Gō-models). The work by May, Arora and Brooks[54], discussed above, presents PMF calculations using an all-atom potential, but otherwise little progress has been made in this area. However the use of CG models has been effective in identifying potential pathways of conformational change. Tama and Brooks performed NMA using a Cα-based ENM on the full capsid of several viruses which undergo a swelling transition [69, 78]. In that study the protein subunits were treated as rigid blocks and it was shown that just one or two of the lowest frequency icosahedral (non-degenerate) normal modes could account for 90% of the displacement between the swollen and unswollen states. The systems that were examined were T = 3 CCMV, T = 4 nudaurelia capensis virus (NωV), and T = 7 HK97. For CCMV and NωV only the lowest mode was needed to describe the deformations, whereas HK97 required the two lowest modes. This observation was rationalized because CCMV and NωV are spherical in both states and only require a single mode to account for the expansion, whereas HK97 both expands and changes morphology from spherical to icosahedral. These studies supported the concept that functional dynamics of capsids are dictated by their structure and only the lowest frequency icosahedral mode(s), are needed to describe these motions. Other normal mode based analyses of HK97 maturation has been performed in a symmetry constrained manner[79], and using a Gaussian network model (GNM) in which the coupling between nonicosahedral and icosahedral motions were examined[80]. Fig. 5 presents the structures of the immature and mature form of HK97, as well as the first and second non-degenerate normal modes.

The question of symmetric versus non symmetric motions in the HK97 maturation pathway was evaluated through MD simulations using a coarse-grained (Cα-based) structure-based model by May, Feng and Brooks[81]. In this model the non-bonded native contacts have a different functional form from the SOP model. The native contacts potential in the May model is

$$U_{\mathit{ij}}={∊}_{\mathit{ij}}\left[5{\left(\frac{{\sigma }_{\mathit{ij}}}{r_{\mathit{ij}}}\right)}^{12}-6{\left(\frac{{\sigma }_{\mathit{ij}}}{r_{\mathit{ij}}}\right)}^{10}\right]$$ (8)

where ∊_ij is determined by the residue pair type and the hydrogen bonding in the native structure. The attractive term scaling as $r_{\mathit{ij}}^{-10}$, creates a narrower energy well than the standard 12-6 LJ potential. The larger σ_ij values in a Cα-based model, result in a flatter energy minimum compared to all-atom LJ potentials. The use of a power 10 attractive term counteracts the well-flattening feature inherent to the coarse-grain model. In this work the native state was chosen as the mature form (Head II) of HK97 and simulations were performed using the immature (Prohead II) structure. The nature of the a coarse-grained structure-based model is a relatively smooth downhill potential, and therefore trajectories could be observed which transitioned from the immature to mature state. These computations were e cient enough, that they were able to generate an ensemble of trajectories and evaluate the heterogeneity of the pathways. Pathways which closely maintained icosahedral symmetry and others which significantly broke symmetry were observed. Examining the ensemble of 66 pathways showed the icosahedral modes accounted for the majority of the motion along the maturation pathways, and the low frequency non-icosahedral modes made little contribution. Interestingly, all of the pathways followed a common mechanism initiated by reorganization of the pentamers followed by the hexamers, which is consistent with conclusions from the GNM study[80].

4 Outlook

There are other areas of molecular modeling of viruses which I have not touched upon in this review. The study of viral capsid assembly, which has been a very fertile area of investigation, was recently reviewed by Hagan[82]. Major contributors to that field include Hagan[83–86], Rapaport[87–89] and Nguyen and Brooks[90–92]. Recently these studies have moved beyond empty capsid assembly and have begun to examining the influence of packaging RNA during assembly[84, 93]. Also not discussed here are the many nonicosahedral viruses that have been studied by the techniques of molecular modeling. Many of these non-icosahedral viruses are significant human health threats, including HIV[51, 94–96], Lassa Virus [97] and Influenza[98–100], and are an important and active area of investigation.

For the foreseeable future coarse-grain models will continue to play a significant role in understanding these complex viral nanomachines. While coarse-grain models may lack the quantitative details of all-atom models, the insights from these models into the mechanism, kinetics and energetics of viral processes and properties can shape they way think about these systems and guide the design of experiments to probe their behavior. These insights from CG models can form the basis for more refined simulations. Certainly one of the hopes is that computational methods will aid in the design of antiviral therapeutics. Since drugs must be highly specific, all-atom or even quantum mechanical models will be required to assess potential drug molecules. Both the CG and higher level modeling efforts will benefit from continued improvements in hardware and algorithms for MD. Enhanced sampling methods, such as meta-dynamics[101] and replica-exchange[102], will be valuable tools in understanding conformational changes and exploring the free energy landscapes underlying these dynamics.

Currently a major push in the field has been to better understand the capsid-genome interactions. The use of asymmetric cryo-EM reconstructions to obtain structural information on the packaging motors of tailed dsDNA phages[103] and the use of single-molecule methods to measure the forces during genome packaging and ejection[104], make this an area where molecular modeling may play a significant role in the future. Molecular modeling of virus capsids is a nascent field, only about ten years old. Many great insights have come forth in the first ten years of investigations, one can barely imagine the advances we will see in the next decade.