Abstract
The development of residual dipolar coupling (RDC) in protein NMR spectroscopy, over a decade ago, has become a useful and almost routine tool for accurate protein solution structure determination. RDCs provide orientation information of magnetic dipole–dipole interaction vectors within a common reference frame. Its measurement requires a nonisotropic orientation, through a direct or indirect magnetic field alignment, of the protein in solution. There has been recent progress in the developments of alignment methods to allow the measurement of RDC and of methods to analyze the resulting data. In this chapter we briefly go through the mathematical expressions for the RDC and common descriptions of the alignment tensor, which may be represented using either Saupe order or the principal order matrix. Then we review the latest developments in alignment media. In particular we looked at the lipid-compatible media that allow the measurement of RDCs for membrane proteins. Other methods including conservative surface residue mutation have been invented to obtain up to five orthogonal alignment tensors that provide a potential for de novo structure and dynamics study using RDCs exclusively. We then discuss approximations assumed in RDC interpretations and different views on dynamics uncovered from the RDC method. In addition to routine usage of RDCs in refining a single structure, novel applications such as ensemble refinement against RDCs have been implemented to represent protein structure and dynamics in solution. The RDC application also extends to the study of protein–substrate interaction as well as to solving quaternary structure of oligomer in equilibrium with a monomer, opening an avenue for RDCs in high-order protein structure determination.
Keywords: RDC, Alignment medium, Ensemble, Dynamics, Oligomer
1 Introduction
Solution NMR spectroscopy is a powerful technique to study protein structure and dynamics at the atomic level. The method relies on a variety of experimental restraints to determine protein structure. These include the nuclear Overhauser effects (NOEs) that provide interproton distances, the J-coupling constants that depend on dihedral angles [1–3], the paramagnetic relaxation enhancement (PRE) that is distance dependent with respect to the paramagnetic center [4], and the residual dipolar couplings (RDC) that report on internuclei vector orientations. NOE typically measures interproton distances of less than 5 Å and J-coupling probes spin nuclear interactions within a few bonds away and they are therefore local in nature. In contrast, PRE can measure distances up to 20–30 Å from the paramagnetic center. In this respect RDC is unique. It can provide relative orientations among internuclei vectors irrespective of their distance separations. This unique property of RDC has opened up new possibilities in using NMR to study phenomena that were previously unattainable.
In the presence of a magnetic field, RDCs arise when the proteins in solution weakly align relative to the field, thus creating an anisotropic condition. The direction of the alignment of the protein molecules in the magnetic field is commonly referred to as the alignment tensor frame. Under such anisotropic condition, with the presence of an external field, a magnetic dipole–dipole interaction does not average to zero and yields a measurable dipolar coupling. The magnitude of the dipolar coupling depends on the angle between the internuclei vector and the external magnetic field as well as the internuclei distance. If the dipolar interaction is between two covalently bonded nuclei, then the internuclear distance is fixed and only the orientation dependence remains. A typical measurement may report hundreds of RDCs within a protein that correspond to bond directions within the alignment tensor frame, providing orientation restraints for protein structure determination.
There are at least two approaches to create weak alignment conditions for measuring RDCs. One is to take advantage of the large magnetic susceptibility of a protein where its interaction with the magnetic field could produce a weak alignment [5, 6]. The other is to mix the protein sample with a medium that can be mechanically manipulated to create an anisotropic matrix or one containing supramolecules with substantially large susceptibility anisotropy that can be aligned under an external magnetic field. The interaction between the proteins and the media in turn could induce weak alignment of the proteins [7]. The latter approach creates a degree of alignment that is roughly one order of magnitude stronger than the former one, significantly larger than the experimental error, and thus is more practical for general applications.
A common usage of RDCs is to include them with other NMR restraints in refining a protein structure. For studies of large or membrane associated proteins, where high level of deuteration is required to achieve narrower line-widths, the number of observed NOEs will be reduced greatly. Therefore RDC restraints are necessary [8]. In this chapter we will focus on a short description on how RDC was developed, its practical mathematical expressions, and novel methods used in creating different alignment conditions that would allow more proteins to be studied using RDCs. We will describe RDC data interpretations and some common approximations. Finally we will discuss the most recent RDC applications in ensemble structure refinement, protein–ligand, and protein high-order structure determinations.
2 Theoretical Expressions
Dipolar coupling measures the interaction between two magnetic nuclei in an external field B0. If the vector connecting nuclei A and B is parallel to the field B0, the coupling is at its strongest with a magnitude Dmax, which is given by Eq. (1), where μ0 is the vacuum permeability, h is Planck’s constant, γA and γB are the gyromagnetic ratios of nuclei A and B, respectively, and rAB is the distance between nuclei A and B. In some expressions vacuum permeability μ0 was assumed and therefore omitted in the Dmax expression, and there will be a factor of 4π difference in the denominator of Eq. (1). Dmax is bond type dependent and usually on the order of 103 Hz, e.g., Dmax for protein backbone amide 1H–15N spin nuclei pair is 21.66 kHz with an assumed bond length of 1.04 Å. Because of diffusive motion the direction of the internuclei vector fluctuates relative to the B0 direction and therefore the dipolar coupling has to be evaluated with respect to every possible orientation. This orientation dependency follows the second order Legendre polynomials. Shown in Eq. (2) is the expression for the dipolar coupling D of an internuclei vector with a fixed distance (which is the case for bonded nuclei), where Θ is the instantaneous angle between the dipole–dipole or bond vector and B0 (Fig. 1), and the angular bracket indicates time or population average. The average for D will be zero if Eq. (2) is integrated over the variable Θ that covers the surface of a sphere, corresponding to all possible orientation for an isotropic diffusing molecule. However, due to a weak alignment causing a nonisotropic sampling of orientations, the average of D is not zero. In practice, adjusting the concentration of the alignment media can allow between an equivalent of 0.1–1% fractions of protein molecules being aligned and it results in a value for D to be within ±20 Hz for 1H–15N vectors, referred to as RDC.
Fig. 1.
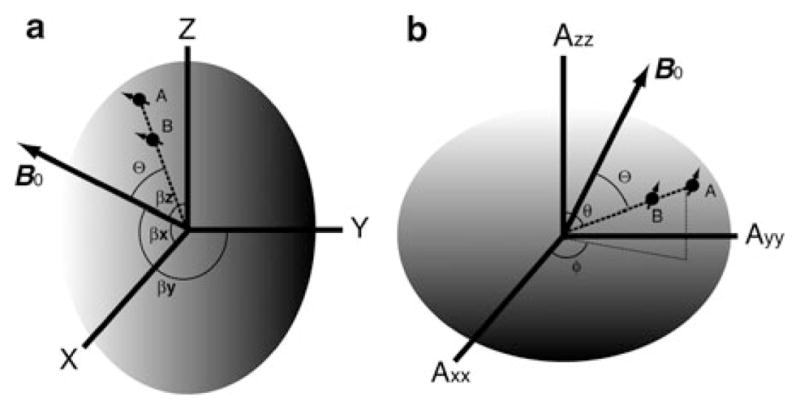
Illustrations of relationships between RDC internuclei vector AB and an arbitrary molecular frame (a) and the alignment tensor frame (b). A protein molecule, carrying spin nuclei A and B, is represented using an ellipsoid. B0 is the external field. Θ is the instantaneous angle between the internuclei vector AB and B0. βx,y,z specify the projection angles of B0 onto each axis of a molecular frame. Polar angle θ; and azimuth angle ϕ are spherical coordinates of the vector AB in the alignment tensor frame
| (1) |
| (2) |
| (3) |
| (4) |
The equation for RDC, Eq. (2), could be rewritten in the form of the expectation value for a vector in a Saupe order matrix, i.e., Eqs. (3, 4) [9]. The x, y, z in Eq. (3) are directional cosines of a bond vector in an arbitrary molecular frame (Fig. 1a), the most convenient would be an existing PDB coordinate frame; Saupe element Sij is the averaged projection of axes of the molecular frame onto the direction of B0 with βx,y,z (Fig. 1a) specifying the projection angle for each axis; δij is Kronecker delta. The Saupe matrix is symmetric and traceless and contains five unknown variables, i.e., Sxx, Syy, Sxy, Sxz, and Syz. The product on the right side of Eq. (3) is a scalar, the value of which equals the average of the second order Legendre polynomials in Eq. (2). The aforementioned 10−3 to 10−4 (0.1–1%) scaling in the dipolar coupling is contained within all Saupe order elements. Since the five unknowns in the Saupe matrix are common to all bond vectors or RDC measurements in one aligned protein sample, in theory with more than five RDC bond vectors pointing in different directions one could solve the Saupe matrix. Prestegard and coworkers have written a protocol for solving the five Saupe unknowns using the singular-value-decomposition (SVD) method to obtain alignment parameters [10].
| (5) |
| (6) |
| (7) |
One can diagonalize the Saupe matrix to obtain the alignment parameters. Diagonalization of the Saupe matrix results in the principal order matrix and Euler rotation matrices T(α,β,γ) and T*(α,β,γ), where α, β, and γ are Euler angles and * indicates conjugate transpose (Eq. (5)). The Euler rotation of Cartesian coordinates in the molecular frame xyz of Eq. (3) results in a set of new coordinates x′y′z′ Eq. (6) for the bond vector within the principle order frame (Fig. 1b). The principal order matrix equals the alignment tensor matrix with its Eigenvalues, Axx, Ayy, Azz in Eq. (5), representing the alignment order in the corresponding tensor direction. There are different conventions in describing the alignment order parameters. For instance, one can keep the S representation for Eigenvalues in the alignment tensor matrix, i.e., Szz, etc. Alternatively, the Azz, notation which is equivalent to 2Szz/3 in the diagonalized Saupe matrix can be used [11].
Following the convention in Eq. (5), and in analogy to Sxx and Syy of the diagonalized Saupe matrix, there are the following relationships: Axx = Azz(−1/2 + 3R/4) and Ayy = Azz(−1/2−3R/4), where R is the rhombicity which can be in the range of 0–2/3, with the convention that |Azz| ≥ |Ayy| ≥ |Axx|. Because Azz, on the order of 10−3 to 10−4, is not a convenient number, Azz can be replaced with a more convenient Da (= 3DmaxAzz/4) representation, which allows for an easier comparison among different alignment conditions. Here is an alternative to using the five Saupe unknowns. We use Da to specify the alignment order of a sample, rhombicity R to describe asymmetry of the alignment tensor, and three Euler angles to define the tensor directions instead. With Euler angles one could conveniently visualize the tensor within a molecular frame. Further simplifications can be made by using spherical coordinates, i.e., polar angle θ and azimuth angle ϕ, to replace x′y′z′ (Fig. 1b). After substituting Da, rhombicity R, and the spherical coordinates in the alignment frame into Eqs. (5, 6), one will end up with a more familiar expression for RDC Eq. (7). It is essential to keep in mind that Eq. (2) and Eq. (7) are the similar formula, and the only difference is that the latter carries no ensemble averages.
3 Alignment Methods
Dipolar coupling manifests itself as an additional coupling to the scalar or J-coupling. RDC measurements normally require two NMR samples prepared in parallel, one with and the other without the presence of an aligning medium, corresponding to an isotropic and an anisotropic samples, respectively. An identical NMR pulse sequence is applied to both samples to measure the J and J + D values. The difference yields the dipolar coupling D. Therefore any pulse sequences developed to measure J-coupling are applicable for measuring dipolar coupling. There are two general methods to determine J + D value under anisotropic conditions, measuring direct splitting on NMR spectra and fitting a J-modulated intensity [12]. Methods for measuring DH–N, DHα–Cα, DCα–C′, DN–C′, DH–C′, and DH–H were extensively reviewed [11, 13, 14]. Here we focus on ways of adjusting alignment conditions and improvement in measurement accuracy.
A number of liquid-crystalline media have been employed to generate weak alignment for solution protein samples. The utilization and mechanisms of the commonly used alignment media have been reviewed previously [11, 15] and they include bicelles made of dimyristoylphosphatidylcholine (DMPC) and dihex-anoylphosphatidylcholine (DHPC) [16, 17], filamentous phages Pf1 [18] or fd [19], stretched [20, 21] or compressed [22] polyacrylamide gel, and poly(ethylene glycol)/hexanol mixture [23]. In addition, one can also add charged molecules into the alignment media to generate different alignment tensors for protein molecules [24, 25]. Though the pool of alignment media seems large, the demand for new media still exists for several reasons. One reason is that when there are more choices of alignment media the chance of finding a compatible one for challenging proteins or membrane proteins increases. The second reason is that any additional orthogonal alignment tensors from new alignment media add new information and can potentially better define bond vector orientation and dynamics. This has a promising potential for de novo protein structure determination. Recent additions in alignment media include charged gel [26], novel DNA based media [27, 28], and collagen gel [29]. The physical interactions between proteins and the medium are almost exclusively to be either steric and/or electrostatic, which could potentially limit the ability to obtain a complete set of five orthogonal alignment tensors. However, recent developments such as conservative mutation on protein surface [30] and use of composite media [31] may overcome these limitations. To improve measurement accuracy by providing more consistent reference (isotropic) data, approaches such as extracting RDCs from two samples at different concentrations of alignment media [32] and application of a new two-stage NMR tube [33] have been proposed.
3.1 Charged Polyacrylamide Gel
Mechanically stretched [21] or compressed [22] polyacrylamide gel medium is a promising medium for measuring RDCs on membrane proteins that are reconstituted in micelles or bicelles. This is due to its inertness and inability to react with detergents. However, to establish weak alignment that is practical, it is necessary to polymerize at least 7% (w/v) acrylamide in a sample [34]. At such concentration the narrow pore size of the gel matrix limits protein diffusion, resulting in peak line-width broadening. Meier et al. [35] initially showed a sufficient alignment order was achieved by copolymerizing only 2% (w/v) acryl-amide and acrylic acid, leading to an anionic polymer. Cierpicki and Bushweller [26] used acrylamide (<5% w/v) with different charged polymer units to generate alignment order. In addition to anions, positive charges were introduced by addition of (3-acrylamidopropyl)-trimethylammonium chloride or N-(2-acryloamidoethyl)-triethylammonium iodide. With such a charged gel, satisfactory sample stability and NMR spectra quality were obtained using integral membrane protein OmpA dissolved in dodecylphosphocholine (DPC) micelles. The RDCs obtained from the charged gel were directly used for membrane protein structure determination.
3.2 DNA Based Media
Nucleic acids carry a relatively stronger magnetic susceptibility than proteins and seldom react with detergent. In the continuous effort to develop detergent compatible alignment media, Douglas et al. [27] initially exploited DNA nanotubes as alignment media. Two bundles of six DNA strands in 7,000-base length were linked through base-pairing sticky ends to form a micron-long DNA filament. The trans-membrane helices of a T-cell receptor reconstituted in DPC/SDS bicelles were aligned in a cosolvent of DNA nanotubes at a concentration of 28 mg/mL. The measured DH–N and DHα–Cα were shown to be consistent with the protein structure determined without RDC.
To ease the DNA nanotube medium preparation and reduce the cost, Lorieau et al. [28] used potassium salt of dinucleotide (d(GpG)) that would tetramerize through guanosine hydrogen bonds at a concentration of 10 mg/mL. The G-tetrad DNA, similar to bacteriophage Pf1, is strongly negatively charged. However, different from phage Pf1, its liquid crystalline phase is chiral nematic and the director can run perpendicular to the external field. Analysis of RDCs collected on a mutant of protein GB3 aligned in G-tetrad DNA showed the obtained alignment tensor carried the same directions as those in phage Pf1, but the sign of Da switched [28]. In this case, it is the electrostatic interaction between alignment medium and protein that determine the uniqueness of the alignment tensor. Nevertheless, G-tetrad DNA allowed RDC measurements on the fusion peptide of the influenza viral hemagglutinin solubilized in DPC micelles [36].
3.3 Collagen Gel
Collagen proteins, abundant in mammals, are made of trimer of polypeptide chains. Each chain is rich in proline or hydroxyl-proline, glycine, and others, which together form an extended left-handed polyproline-II structure [37]. Three copies of such chains form a right-handed helix, carrying a weak magnetic moment. For in vitro use the rat tail tendon type I collagen monomers were prepared [38] and stored in acidic buffer at 4 °C. At pH 6–8 and temperatures over 30 °C the collagen helices will polymerize and cross-link through amino acid side chains, e.g., lysine. When such reactions occur in the presence of magnetic field, weak alignment can be achieved [29]. At a concentration of 13 mg/mL, a sample with collagens polymerized in the presence of magnetic field yielded deuteron splitting of 20 Hz, usually sufficient for dipolar coupling [29].
3.4 Composite Media
As mentioned before, the nature of alignment forces, either steric or electrostatic, could limit the number of orthogonal alignment tensors we can observe experimentally. However, Ruan and Tolman [31] showed the interference of the two alignment forces could produce one additional orthogonal tensor. They polymerized 5% (w/v) polyacrylamide gel together with 3–4 mg/mL of bacteriophage Pf1 in the presence of the magnetic field. A special tube with a cross section size of 7 × 5 mm was filled with both media and positioned at a maximal angle of 55° to field B0 (Fig. 2). The gel was dried, later soaked with protein sample, and stretched into a 5-mm NMR tube. Phages were assumed to be field aligned and trapped at the direction because their motions were inhibited by polymerized acrylamide. Essentially, the direction of phages formed a tilting angle with the direction of gel stretch. Proteins were subject to interfered alignment forces, resulting in both strong steric and electrostatic interactions. Surprisingly, the measured alignment tensors at different tilting angles are not a simple linear combination of those obtained from individual alignment using phage or acrylamide gel alone. As reported [31], at least three orthogonal tensors were solved for a ubiquitin sample subjected to composite alignment media. The same group also reported that the unambiguous bond direction might be determined with only three orthogonal alignment tensors [39].
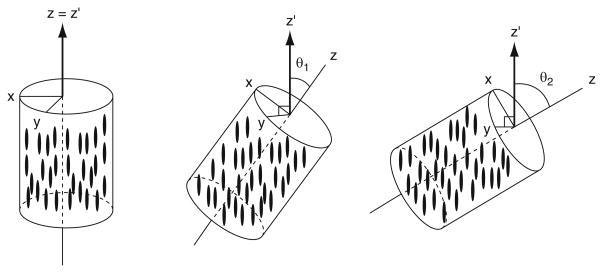
Fig. 2.
Variation of alignment using stretched polyacrylamide gels (SAG) and bacteriophage Pf1, which has been embedded and aligned (along z′) at different angles relative to the long axis (z) of the sample. The gels were cast in an approximately ellipsoidal (squashed cylinder) geometry, with dimensions of 5, 7, and 10 mm along the x, y, and z axes, respectively. The gels were then dried, rehydrated, and stretched to fit within a 4.2 mm i.d. NMR tube. (Reprinted with permission from [31])
3.5 Conservative Mutation
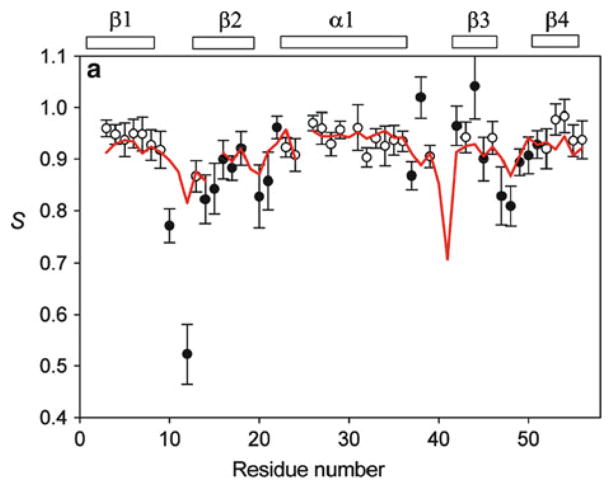
The surface charge of Pf1 phage is heavily negative and proteins will be aligned according to its surface electrostatic potentials [40]. Yao and Bax [30] carefully modified the surface charge distribution of the 6-kDa protein GB3 by either conservatively mutating one or two residues at each time, e.g., K to E, or keeping the histidine-tag at terminus of the native GB3. The backbone structure was later found to be unperturbed in those modified proteins. A total of six mutant proteins were found to align quite differently with respect to the B0 field and five singular values were obtained (Fig. 3). With this well-defined system, the amplitude and direction of RDC bond dynamics up to the millisecond (ms) were unambiguously obtained and compared to nanosecond to picosecond (ns–ps) dynamics from spin relaxation measurements (Fig. 4) [41]. Interestingly, Yao et al. found both RDC and relaxation measurements showed the same amount of flexibility for residues in regular secondary structures. Bond vectors within loop regions, however, were shown by RDC to have larger amplitude of motions compared to what were suggested from the relaxation data [41].
Fig. 3.
Alignment tensor orientations relative to the ribbon backbone structure of GB3 for six mutants, all in liquid-crystalline Pf1 medium. The six tensors are for A – K19AD47K; B –K19ED40N; C – K19EK4A-C-His-tag; D – K19EK4A-N-His-tag; E – K19AT11K; F – K19EK4A. Diagonalized tensor elements, Dxx (red), Dyy (green), and Dzz (blue) have magnitudes proportional to the length of the corresponding lines. (Reprinted with permission from [30])
Fig. 4.
Experimental order parameters, S, of NH bond vectors in GB3 derived from iterative Direct Interpretation of Dipolar Couplings (DIDC) using all six sets of RDCs. The red line marks the order parameters derived from 15N relaxation. Filled symbols represent residues for which the fully anisotropic model was required to get a satisfactory fit to the data, while, for open symbols, the isotropic internal motion model was able to fit the RDCs to within the experimental noise. (Reprinted with permission from [41])
3.6 RDC/RCSA Accuracy Improvement
In addition to RDC, protein alignment creates slight chemical shift changes for the aligned sample relative to the isotropic sample. The chemical shift difference, named residual chemical shift anisotropy (RCSA), comes from the projection of the chemical shift tensor, which is not averaged to zero, onto the alignment tensor. RCSA is also a long range structural restraint, providing orientation dependences generally complementary to RDCs [42–44]. The solvent used in the isotropic protein sample usually differs from that in the anisotropic sample. This can introduce errors in measuring both dipolar couplings and chemical shift differences. Such error may be below the measurement accuracy for RDCs, on the order of 0.1–1 Hz. However, RCSA, which is on the order of parts per billion (ppb), may be greatly affected. The solvent effect can be removed by measuring several aligned samples at increasing alignment orders and extrapolating the RCSA values to zero concentration [32]. The methods were applied to backbone 15N [32] and 13C′ [45] RCSA measurements.
Another way to overcome this is to measure isotropic sample under the same unaligned medium. Liu and Prestegard [33] developed a two-stage NMR tube with two different internal diameters (I.D.) at upper and lower parts of an open-ended NMR tube. For isotropic condition the protein sample was soaked into polyacryl-amide gel in 5 mm I.D. part, then the same piece of gel was pulled and stretched into the 3 mm I.D. part by vacuum created using a syringe at the other end of the two-stage tube, resulting anisotropic condition. The method allows for higher accuracy measurements for both RDC and RCSA.
Aside from using both aligned and unaligned samples for RDC and RCSA, one may also keep a single sample that contains alignment media for both isotropic and anisotropic measurements. Upon the application of magic angle spinning, similar to what is used in solid state NMR, the alignment effect for bicelles [46] or phage [47] was removed. In this way the measurement will not contain any solvent effects.
4 Interpretation and Implementation
Measured RDC values are representative averages of the whole ensemble of dipolar interactions within protein molecules in solution. Such an ensemble should include all protein conformers interconverting at time scales faster than the inverse of RDC values (1/D). For instance, the observed dipolar coupling is affected by the internuclei or bond vectors that stretch and vibrate on a femtosecond to nanosecond (fs–ns) time scale, the protein domain reorientation on a nanosecond to microsecond (ns–μs) time scale, and conformational change that ranges from nanoseconds, e.g., unstructured terminus, to milliseconds. It is nearly impossible to describe protein structure and dynamics using RDC values without any assumptions. Some approximations have to be made in interpreting RDC measurements.
4.1 Approximations
Most RDCs except for DH–H [48] are measured on fixed internuclei distances such as bond vectors or geometries within the peptide plane so that in Eqs (1) and (2) a constant internuclei distance rAB in Dmax is assumed. This in itself is an approximation because the effective bond lengths vary due to dynamic processes. For instance, Yao et al. [49] determined the average protein backbone H–N bond length to be 1.01–1.02 Å. However, for deriving the true alignment order an effective value of 1.04 Å was proven proper and used extensively to account for H–N bond libration dynamics [50]. A slight increase in effective bond length for RDC analysis also applies to Hα–Cα bonds. On the other hand, bond lengths for heavy nuclei, e.g., Cα–C′, are consistent with values reported from crystallography studies [50].
By expressing RDC using Eq. (3), where the Saupe matrix is multiplied by bond directional cosines within a local molecular frame, we assume protein conformational change does not affect the alignment tensor. Thus Eq. (3) is an approximation to Eq. (2), in which the average bracket over the second order Legendre polynomial is applied. This approximation is valid when RDCs from the structured part of the proteins are analyzed. For small proteins GB3 [41, 51] and ubiquitin [52] the model free (MF) order parameter from 15N spin relaxation analysis and the order parameter derived from RDC analysis were strongly correlated. These indicate that the effect of slow motion dynamics on microsecond to millisecond time scales on RDC may be negligible and a single structure representation is sufficient for the structured part of proteins within the current experimental uncertainty [53].
When the dynamics involve large scale amplitudes of motion, e.g., the MF order parameter S2 <0.6, multiple structures may exist and each one of them is subjected to its own alignment tensor that may vary significantly due to different steric, and electrostatic interactions of each conformer to the alignment media. Specifically for unfolded proteins it becomes challenging to separate intrinsic bond dynamics from Saupe order parameters in the laboratory frame because local motion and the overall perturbed diffusive motions are coupled [54]. Monte-Carlo simulation of an ensemble of conformers and the following comparison to measurements remain the only option to interpret RDCs in a flexible system [55, 56]. The application of RDCs to study protein in an unfolded state is an active research field [57–59]. For instance, efforts have been made to represent the conformational space of urea denatured ubiquitin with as few as 200 conformers, which seem to reproduce measured RDCs [59]. However, additional specific bond type RDC scaling factors had to be applied for H–N, Hα–Cα, etc., which indicate different amounts of motion along bond vectors within a peptide plane [57, 59].
4.2 Common Applications of RDC
The most common use of RDCs is for structure validation and refinement. Given structure coordinates determined either from X-ray crystallography or solution NMR, one can readily fit RDC data to the corresponding bond vector directions within the molecular frame. Any programs that utilize Eqs (3) or (5) in a chi-square minimization routine or formal software packages such as PALES [60, 61] and REDCAT [62] which implement the SVD algorithm can be employed to carry out the numerical fitting. The fitting will result in the optimized alignment tensor and values that best matched the measured RDCs. To quantify the agreement between a structure and measured dipolar couplings, Cornilescu et al. [63] proposed quality factor Q. This factor can better determine the quality of the fit than Pearson’s correlation R. Shown in (8) is the expression for the Q factor where rms refers to root mean square. It provides an estimate of average disagreement in percentage between measured and calculated dipolar couplings. A Q factor of 40%, roughly corresponding to Pearson’s R of 0.9, are commonly found on structures with 2–3 Å resolution; and a Q value of 20% or less indicates the structure is at high resolution (1.5 Å) and accuracy. Clore and Garrett [64] suggested an alternative form to replace the denominator of (8) in the case of a limited RDC sampling over all of the possible orientations. A thorough discussion on Q factor can be found elsewhere [65].
| (8) |
| (9) |
For solution structure determination, RDC is normally not included as a potential term (9) during the initial structure calculation in a simulated annealing protocol in a program such as Xplor-NIH [66, 67]. Due to directional degeneracy associated with RDC restraints, as described in the theoretical expression section, multiple local potential minima will hinder the successful search for the right conformation. Typically a rough tertiary fold of protein is obtained first with the use of NOE restraints and such a fold can be used as a starting structure for the next simulated annealing procedure with the combined NOE and RDC restraints. The procedure to include RDC restraints in a program such as Xplor-NIH uses four pseudo-atoms (OXYZ) [68] to represent the alignment tensor directions [69]. The RDC force constant, k in (9), can be increased gradually as the temperature is being lowered in the simulated annealing. In the end it is ideal to adjust the force constant k so that the deviation from the measured RDCs matches the experimental error.
4.3 Ensemble Minimization
As discussed before, RDC reflects the ensemble averaged dipolar coupling and incorporates a wide range of time scales up to milliseconds. During RDC restrained structure calculations we made approximations by assuming a single conformer. The question remains whether it is reasonable to keep this assumption in all cases. Clore and Schwieters [52] initially employed a two-member ensemble minimization to test whether a better agreement between measured and calculated RDC data could be achieved, and whether it was statistically significant. The ensemble algorithm proposed by Clore and Schwieters [52] kept a user-defined number of conformers during the course of a simulated annealing, and any evaluated physical quantity, e.g., Dcalc, is linearly averaged among individual conformers. After refining the ubiquitin structure with DH–N data sets collected in 11 different alignment media, and a couple of other heteronuclear RDCs, they found a single conformer in most cases is sufficient to yield a good quality factor Q less than 20%. The structure was validated against the DHα–Cα data set that was not being applied as a restraint. A 15% reduction in Q value was obtained with an ensemble size of two, which was statistically significant. In addition, several residues were found to be undergoing anisotropic motion and can be better represented by the two-member ensemble (Fig. 5a) [52]. Later a simulated annealing with an ensemble size of four to eight on protein GB3 had been found to be optimal [71]. The consensus is that other than residues having large amplitude or anisotropic motions, most structured residues can be represented with a single structure for monomeric small proteins because the accuracy of NMR structural coordinates is well within the measurement uncertainty of the RDCs.
Fig. 5.
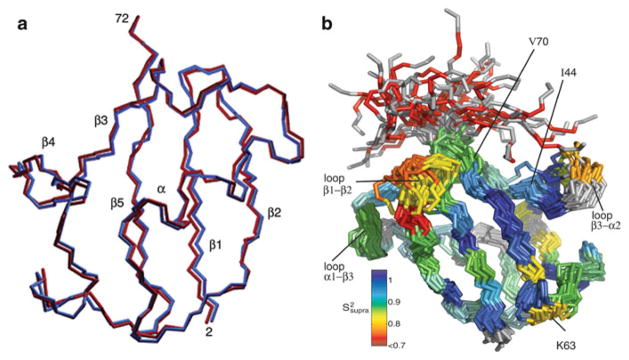
Structure ensemble of Ubiquitin. (a) Two members (shown in red and blue) of a typical ensemble from the two-member size calculation. (Reprinted with permission from [52].) (b) Backbone trace of 40 randomly chosen structures from the ensemble. Residues are colored by the amount of additional (slower than-τc) mobility as compared with the Lipari-Szabo order parameters. (Reprinted with permission from [70])
Other studies on ensemble minimization reveal a relatively larger conformational sampling for ubiquitin [72]. In another study, an ensemble of around 100 ubiquitin structures was generated using NMR restrained simulated annealing and molecular dynamics. Interestingly, such an ensemble covers structural heterogeneity observed in 40 or so ubiquitin–ligand complex crystal structures (Fig. 5b) [70]. RDC restraints used in such ensemble minimizations were measured in over 30 different alignment media [73]. The biological implication is that ligand induced ubiquitin conformers preexist in its structural ensemble. Further, the ubiquitin N–H order parameters derived from RDC analysis [73–76] were overall lower by 0.1–0.2 than that of MF order parameter derived from relaxation data [77], indicating an appreciable amount of microsecond to millisecond motion that was not observed in spin relaxation measurement. It is nevertheless an interesting and different conclusion from other findings on ubiquitin [52] and GB3 [41].
Besides backbone dynamics for monomeric proteins, ensemble minimization may be better suited for studying relatively slower and larger scale protein domain dynamics and structure. Liu et al. [78] implemented ensemble minimization to characterize the dynamic structure of a membrane-anchored ADP ribosylation factor (Arf). The yeast Arf is composed of flexibly joined C-terminal domain and the short N-terminal helix that interacts with the membrane. The Arf protein anchored on DMPC/DHPC bicelles were aligned in a negatively charged polyacrylamide gel, and the resulting alignment order parameters Da and R for C- and N-terminal domains are 8.6 Hz and 0.29, and 4.7 Hz and 0.61, respectively. The differences in alignment order indicate significant interdomain motions. A three-member ensemble minimization significantly increased the linear correlation coefficient between measured and back-calculated RDC (Fig. 6) and PRE data on the N-terminal helix. Such dynamics could be crucial for Arf to function as a regulator of effectors GTP/GDP.
Fig. 6.
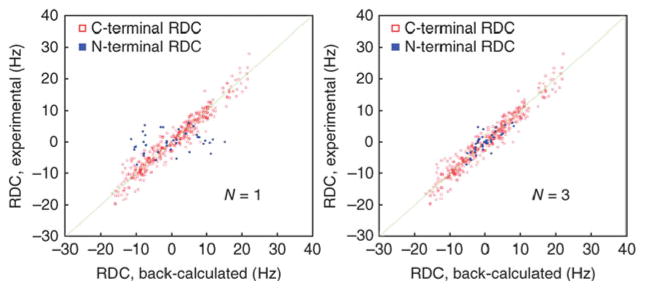
Ensemble structural fitting to RDCs. Agreement between experimental and back-calculated RDCs for a one-state ensemble (left) and a three-state ensemble (right). Data include NH, NC′, and phenyl CH (the latter two are normalized to NH). RDCs are collected in positive and negative gels. (Reprinted with permission from [78])
4.4 Structure of a Ligand in a Bound State
The conformational ensemble described previously represents a continuous distribution of conformers and no significant protein fold or high-order structural change within the ensemble members was taken into account. Other systems may also be composed of discrete conformers in equilibrium; for instance, large structural differences could exist between free and bound states of ligand molecules in the presence of their receptors. Generally the NMR signals from the ligands in this type of equilibrium are dominated by the ligands in the free states. RDCs can play a role in solving ligand structure in the bound form not generally accessible by other techniques.
Photo-activated retina rhodopsin, a G-protein coupled receptor (GPCR), is a major component in purple membranes (PM). Due to the high structural content of helices in GPCR, GPCR rich PM disks align in the presence of a magnetic field with the membrane normal being parallel to the field [79, 80]. The binding of the GDP-bound form of the heterotrimeric G protein transducin (Gt) to the light activated MII intermediate of the rhodopsin activates the visual signal transduction pathway. A peptide consisting of the C terminal ten residues of the α-subunit of transducin (Gtα) is capable of competing with Gt for binding and was studied using NMR spectroscopy [81]. In the presence of light, Gtα transiently binds activated GPCR that is embedded in membrane disks of bovine retina. Since these disks were aligned in the magnetic field, RDCs for Gtα could be observed. The measured RDCs followed a time-decay course after light activation, while GPCR returned to its inactive state. The decay time constant is on the order of 1 h that allowed rapid acquisition of 2D 1H–15N and 1H–13C spectra on the Gtα peptide sample. The RDC values at zero time were obtained from extrapolation of multiple RDCs collected along a time decay curve. The structure and orientation of the peptide in the bound state to GPCR were derived from RDCs and transferred NOEs [81]. The validity of such use of RDCs relies on two conditions. The first condition is the fast exchange between the free and bound states of Gtα that allows the observation of only one set of resonances of the free state. The other condition is that the free Gtα peptides are not aligned in GPCR enriched PM media so that alignment contribution all comes from the bound state. Indeed the alignment order of the system was weak with a Da value of only 1.6 Hz.
In the above case, the ligand receptor GPCR is naturally buried in bicelles, which by itself is the alignment medium. This ensures strong alignment order for bound ligand molecules. However, for a general study protein receptors are not necessarily buried in any disks that could be aligned; thus the alignment order for ligand molecules in equilibrium with its free form would be too weak to be observed. Seidel et al. [82] demonstrated a method of anchoring polyhistidine-tagged protein receptors onto the bicelles that were doped with histidine-tag binding lipid molecules. This increased the alignment order of the protein–ligand complex and prevented measurements of the protein RDCs. The RDCs of the bound ligand in fast exchange with free ligand molecules, however, were observed and they could be used to map the ligand configuration on the protein receptors.
4.5 Structure of Oligomeric State
RDCs are very useful in improving the structure determination of a monomeric protein. In addition, they can be utilized to establish quaternary structure of symmetric oligomers. Prestegard and coworkers have developed methods to determine dimer structure using RDC data [83, 84]. The underlying principle is that the rotational symmetric C2 axis of any protein dimer should be parallel to one axis of the alignment tensor of the dimer. By solving alignment tensor axes from different alignment media, one could identify the common tensor axis that should be parallel to the symmetric axis [85, 86]. Bacillus subtilis proteins YkuJ dimerize with strong affinity and its Kd is on the order of 10−9 M [83]. When working at the typical NMR protein concentration (~0.1–1.0 mM) the measured RDC would primarily reflect the dimer structure. The crystal structure of YkuJ is a tetramer and there are two possible configurations for a dimer structure. Wang et al. [83] aligned the protein using two alignment media, 5% poly(ethylene glycol)/hexanol and 10 mg/mL phage Pf1. Both yielded different alignment tensor directions. However, the x axes from the two tensors were close to each other and were believed to be the symmetric axis of the dimer. The further rotation and docking procedure with energy minimization yielded dimer structure very close to one possible dimer structure observed in the crystal structure of the tetramer. Prestegard and colleagues further extended this approach to study structures of weakly associated dimer. The Staphylococcus epidermidis proteins SeR13 weakly dimerize at a Kd on the order of 10−3 M [84]. The measured RDCs were the weighted average of monomer and dimer states and the resulting alignment tensor from direct fitting would be the average of both monomer and dimer alignment tensors. Lee et al. [84] circumvented this by deriving the exact Kd value from concentration dependent chemical shift values, then extrapolating the RDCs as a function of protein concentration together with the Kd to yield pure RDC data set for the dimer. The rest of the work to determine the dimer structure was similar to the previous approach [83], but with the additional restraints from chemical shift perturbation and paramagnetic surface perturbation data that helped identifying newly buried surface residues upon dimerization.
5 Conclusion
Some additional reviews [11, 65, 87] can be found on RDC topics with different emphasis such as methods [69, 88, 89], theories [13, 14, 90], and dynamics [15]. In this chapter we have briefly summarized the theoretical expressions for the widely used RDCs and common descriptions for magnetic alignment under either Saupe order matrix or alignment tensor representations. RDCs have become notably more relevant in solution structure and dynamics studies for larger system due to the fact that the number of NOEs diminishes. In some cases RDCs may be the sole major experimental NMR restraints for determining domain positions in large systems of over 100 kDa [8]. With its essentiality in mind, more alignment media are being explored. The more choices available, the higher the chance biologically important proteins and membrane proteins reconstituted in micelles or bicelles can be aligned without any interference with the media. More RDC measurements on large and multidomain proteins can reveal their quaternary structure and dynamics manifested through differences in alignment order. However, caution should be exercised in RDC data interpretations because a single RDC data set may not be able to separate differences in domain positions and dynamics simultaneously. Cross-validating the results with different RDCs under another orthogonal alignment tensor, rotational diffusion tensors from spin relaxation, and small angle X-ray scattering that are sensitive to the protein overall shape should help overcome this problem.
Acknowledgments
We thank Nils-Alexander Lakomek for helpful discussion. This work was supported by the Intramural Research Program of the NIH, National Heart, Lung, and Blood Institute.
References
- 1.Wuthrich K. Determination of 3-dimensional protein structures in solution by nuclear-magnetic-resonance – an overview. Methods Enzymol. 1989;177:125–131. doi: 10.1016/0076-6879(89)77008-7. [DOI] [PubMed] [Google Scholar]
- 2.Bax A. Two-dimensional NMR and protein-structure. Annu Rev Biochem. 1989;58:223–256. doi: 10.1146/annurev.bi.58.070189.001255. [DOI] [PubMed] [Google Scholar]
- 3.Clore GM, Gronenborn AM. Multidimensional heteronuclear nuclear-magnetic-resonance of proteins. Nucl Magn Reson Pt C. 1994;239:349–363. doi: 10.1016/s0076-6879(94)39013-4. [DOI] [PubMed] [Google Scholar]
- 4.Clore GM, Tang C, Iwahara J. Elucidating transient macromolecular interactions using paramagnetic relaxation enhancement. Curr Opin Struct Biol. 2007;17(5):603–616. doi: 10.1016/j.sbi.2007.08.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Tolman JR, et al. Nuclear magnetic dipole interactions in field-oriented proteins –information for structure determination in solution. Proc Natl Acad Sci USA. 1995;92(20):9279–9283. doi: 10.1073/pnas.92.20.9279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tjandra N, Grzesiek S, Bax A. Magnetic field dependence of nitrogen-proton J splittings in 15N-enriched human ubiquitin resulting from relaxation interference and residual dipolar coupling. J Am Chem Soc. 1996;118(26):6264–6272. [Google Scholar]
- 7.Tjandra N, Bax A. Direct measurement of distances and angles in biomolecules by NMR in a dilute liquid crystalline medium. Science. 1997;278(5340):1111–1114. doi: 10.1126/science.278.5340.1111. [DOI] [PubMed] [Google Scholar]
- 8.Schwieters CD, et al. Solution structure of the 128 kDa enzyme I dimer from Escherichia coli and its 146 kDa complex with HPr using residual dipolar couplings and small- and wide-angle X-ray scattering. J Am Chem Soc. 2010;132(37):13026–13045. doi: 10.1021/ja105485b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Saupe A. Recent results in field of liquid crystals. Angew Chem Int Ed. 1968;7(2):97. [Google Scholar]
- 10.Losonczi JA, et al. Order matrix analysis of residual dipolar couplings using singular value decomposition. J Magn Reson. 1999;138(2):334–342. doi: 10.1006/jmre.1999.1754. [DOI] [PubMed] [Google Scholar]
- 11.Bax A, Kontaxis G, Tjandra N. Dipolar couplings in macromolecular structure determination. Nucl Magn Reson Biol Macromol B. 2001;339:127–174. doi: 10.1016/s0076-6879(01)39313-8. [DOI] [PubMed] [Google Scholar]
- 12.Bax A, et al. Measurement of homonuclear and heteronuclear J-couplings from quantitative J-correlation. Nucl Magn Reson C. 1994;239:79–105. doi: 10.1016/s0076-6879(94)39004-5. [DOI] [PubMed] [Google Scholar]
- 13.Prestegard JH, Al-Hashimi HM, Tolman JR. NMR structures of biomolecules using field oriented media and residual dipolar couplings. Quart Rev Biophys. 2000;33(4):371–424. doi: 10.1017/s0033583500003656. [DOI] [PubMed] [Google Scholar]
- 14.Prestegard JH, et al. Determination of protein backbone structures from residual dipolar couplings. Nucl Magn Reson Biol Macromol C. 2005;394:175. doi: 10.1016/S0076-6879(05)94007-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tolman JR, Ruan K. NMR residual dipolar couplings as probes of biomolecular dynamics. Chem Rev. 2006;106(5):1720–1736. doi: 10.1021/cr040429z. [DOI] [PubMed] [Google Scholar]
- 16.Bax A, Tjandra N. High-resolution heteronuclear NMR of human ubiquitin in an aqueous liquid crystalline medium. J Biomol NMR. 1997;10(3):289–292. doi: 10.1023/a:1018308717741. [DOI] [PubMed] [Google Scholar]
- 17.Ottiger M, Bax A. Characterization of magnetically oriented phospholipid micelles for measurement of dipolar couplings in macromolecules. J Biomol NMR. 1998;12(3):361–372. doi: 10.1023/a:1008366116644. [DOI] [PubMed] [Google Scholar]
- 18.Hansen MR, Mueller L, Pardi A. Tunable alignment of macromolecules by filamentous phage yields dipolar coupling interactions. Nat Struct Biol. 1998;5(12):1065–1074. doi: 10.1038/4176. [DOI] [PubMed] [Google Scholar]
- 19.Clore GM, Starich MR, Gronenborn AM. Measurement of residual dipolar couplings of macromolecules aligned in the nematic phase of a colloidal suspension of rod-shaped viruses. J Am Chem Soc. 1998;120(40):10571–10572. [Google Scholar]
- 20.Sass HJ, et al. Solution NMR of proteins within polyacrylamide gels: diffusional properties and residual alignment by mechanical stress or embedding of oriented purple membranes. J Biomol NMR. 2000;18(4):303–309. doi: 10.1023/a:1026703605147. [DOI] [PubMed] [Google Scholar]
- 21.Chou JJ, et al. A simple apparatus for generating stretched polyacrylamide gels, yielding uniform alignment of proteins and detergent micelles. J Biomol NMR. 2001;21(4):377–382. doi: 10.1023/a:1013336502594. [DOI] [PubMed] [Google Scholar]
- 22.Tycko R, Blanco FJ, Ishii Y. Alignment of biopolymers in strained gels: a new way to create detectable dipole-dipole couplings in high-resolution biomolecular NMR. J Am Chem Soc. 2000;122(38):9340–9341. [Google Scholar]
- 23.Ruckert M, Otting G. Alignment of biological macromolecules in novel nonionic liquid crystalline media for NMR experiments. J Am Chem Soc. 2000;122(32):7793–7797. [Google Scholar]
- 24.Losonczi JA, Prestegard JH. Improved dilute bicelle solutions for high-resolution NMR of biological macromolecules. J Biomol NMR. 1998;12(3):447–451. doi: 10.1023/a:1008302110884. [DOI] [PubMed] [Google Scholar]
- 25.Wang H, et al. A liquid crystalline medium for measuring residual dipolar couplings over a wide range of temperatures. J Biomol NMR. 1998;12(3):443–446. [Google Scholar]
- 26.Cierpicki T, Bushweller JH. Charged gels as orienting media for measurement of residual dipolar couplings in soluble and integral membrane proteins. J Am Chem Soc. 2004;126(49):16259–16266. doi: 10.1021/ja046054g. [DOI] [PubMed] [Google Scholar]
- 27.Douglas SM, Chou JJ, Shih WM. DNA-nanotube-induced alignment of membrane proteins for NMR structure determination. Proc Natl Acad Sci USA. 2007;104(16):6644–6648. doi: 10.1073/pnas.0700930104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lorieau J, Yao LS, Bax A. Liquid crystalline phase of G-tetrad DNA for NMR study of detergent-solubilized proteins. J Am Chem Soc. 2008;130(24):7536. doi: 10.1021/ja801729f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ma JH, Goldberg GI, Tjandra N. Weak alignment of biomacromolecules in collagen gels: an alternative way to yield residual dipolar couplings for NMR measurements. J Am Chem Soc. 2008;130(48):16148. doi: 10.1021/ja807064k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Yao LS, Bax A. Modulating protein alignment in a liquid-crystalline medium through conservative mutagenesis. J Am Chem Soc. 2007;129(37):11326. doi: 10.1021/ja073937+. [DOI] [PubMed] [Google Scholar]
- 31.Ruan K, Tolman JR. Composite alignment media for the measurement of independent sets of NMR residual dipolar couplings. J Am Chem Soc. 2005;127(43):15032–15033. doi: 10.1021/ja055520e. [DOI] [PubMed] [Google Scholar]
- 32.Burton RA, Tjandra N. Determination of the residue-specific 15N CSA tensor principal components using multiple alignment media. J Biomol NMR. 2006;35(4):249–259. doi: 10.1007/s10858-006-9037-6. [DOI] [PubMed] [Google Scholar]
- 33.Liu YZ, Prestegard JH. A device for the measurement of residual chemical shift anisotropy and residual dipolar coupling in soluble and membrane-associated proteins. J Biomol NMR. 2010;47(4):249–258. doi: 10.1007/s10858-010-9427-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ishii Y, Markus MA, Tycko R. Controlling residual dipolar couplings in high-resolution NMR of proteins by strain induced alignment in a gel. J Biomol NMR. 2001;21(2):141–151. doi: 10.1023/a:1012417721455. [DOI] [PubMed] [Google Scholar]
- 35.Meier S, Haussinger D, Grzesiek S. Charged acrylamide copolymer gels as media for weak alignment. J Biomol NMR. 2002;24(4):351–356. doi: 10.1023/a:1021609207024. [DOI] [PubMed] [Google Scholar]
- 36.Lorieau JL, Louis JM, Bax A. The complete influenza hemagglutinin fusion domain adopts a tight helical hairpin arrangement at the lipid:water interface. Proc Natl Acad Sci USA. 2010;107(25):11341–11346. doi: 10.1073/pnas.1006142107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Bella J, et al. Crystal-structure and molecular-structure of a collagen-like peptide at 1.9-Angstrom resolution. Science. 1994;266(5182):75–81. doi: 10.1126/science.7695699. [DOI] [PubMed] [Google Scholar]
- 38.Saffarian S, et al. Interstitial collagenase is a Brownian ratchet driven by proteolysis of collagen. Science. 2004;306(5693):108–111. doi: 10.1126/science.1099179. [DOI] [PubMed] [Google Scholar]
- 39.Ruan K, Briggman KB, Tolman JR. De novo determination of internuclear vector orientations from residual dipolar couplings measured in three independent alignment media. J Biomol NMR. 2008;41(2):61–76. doi: 10.1007/s10858-008-9240-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zweckstetter M, Hummer G, Bax A. Prediction of charge-induced molecular alignment of biomolecules dissolved in dilute liquid-crystalline phases. Biophys J. 2004;86(6):3444–3460. doi: 10.1529/biophysj.103.035790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Yao L, et al. Simultaneous NMR study of protein structure and dynamics using conservative mutagenesis. J Phys Chem B. 2008;112(19):6045–6056. doi: 10.1021/jp0772124. [DOI] [PubMed] [Google Scholar]
- 42.Sanders CR, et al. Magnetically-oriented phospholipid micelles as a tool for the study of membrane-associated molecules. Prog Nucl Magn Reson Spectrosc. 1994;26:421–444. [Google Scholar]
- 43.Lipsitz RS, Tjandra N. 15N chemical shift anisotropy in protein structure refinement and comparison with NH residual dipolar couplings. J Magn Reson. 2003;164(1):171–176. doi: 10.1016/s1090-7807(03)00176-9. [DOI] [PubMed] [Google Scholar]
- 44.Tjandra N, Suzuki M, Chang SL. Refinement of protein structure against non-redundant carbonyl 13C NMR relaxation. J Biomol NMR. 2007;38(3):243–253. doi: 10.1007/s10858-007-9165-7. [DOI] [PubMed] [Google Scholar]
- 45.Burton RA, Tjandra N. Residue-specific 13C′ CSA tensor principal components for ubiquitin: correlation between tensor components and hydrogen bonding. J Am Chem Soc. 2007;129(5):1321–1326. doi: 10.1021/ja066835c. [DOI] [PubMed] [Google Scholar]
- 46.Kurita J, et al. Measurement of 15N chemical shift anisotropy in a protein dissolved in a dilute liquid crystalline medium with the application of magic angle sample spinning. J Magn Reson. 2003;163(1):163–173. doi: 10.1016/s1090-7807(03)00080-6. [DOI] [PubMed] [Google Scholar]
- 47.Yao LS, et al. Site-specific backbone amide 15N chemical shift anisotropy tensors in a small protein from liquid crystal and cross-correlated relaxation measurements. J Am Chem Soc. 2010;132(12):4295–4309. doi: 10.1021/ja910186u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Boisbouvier J, Delaglio F, Bax A. Direct observation of dipolar couplings between distant protons in weekly aligned nucleic acids. Proc Natl Acad Sci USA. 2003;100(20):11333–11338. doi: 10.1073/pnas.1534664100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Yao LS, et al. NMR determination of amide N-H equilibrium bond length from concerted dipolar coupling measurements. J Am Chem Soc. 2008;130(49):16518. doi: 10.1021/ja805654f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ottiger M, Bax A. Determination of relative N-HN N-C′, Cα-C′, and Cα-Hα effective bond lengths in a protein by NMR in a dilute liquid crystalline phase. J Am Chem Soc. 1998;120 (47):12334–12341. [Google Scholar]
- 51.Clore GM, Schwieters CD. Amplitudes of protein backbone dynamics and correlated motions in a small alpha/beta protein: correspondence of dipolar coupling and heteronuclear relaxation measurements. Biochemistry. 2004;43(33):10678–10691. doi: 10.1021/bi049357w. [DOI] [PubMed] [Google Scholar]
- 52.Clore GM, Schwieters CD. How much backbone motion in ubiquitin is required to account for dipolar coupling data measured in multiple alignment media as assessed by independent cross-validation? J Am Chem Soc. 2004;126(9):2923–2938. doi: 10.1021/ja0386804. [DOI] [PubMed] [Google Scholar]
- 53.Bax A, Tjandra N. Are proteins even floppier than we thought? Nat Struct Biol. 1997;4(4):254–256. doi: 10.1038/nsb0497-254. [DOI] [PubMed] [Google Scholar]
- 54.Fredriksson K, et al. On the interpretation of residual dipolar couplings as reporters of molecular dynamics. J Am Chem Soc. 2004;126(39):12646–12650. doi: 10.1021/ja048287d. [DOI] [PubMed] [Google Scholar]
- 55.Louhivuori M, et al. On the origin of residual dipolar couplings from denatured proteins. J Am Chem Soc. 2003;125(50):15647–15650. doi: 10.1021/ja035427v. [DOI] [PubMed] [Google Scholar]
- 56.Jha AK, et al. Statistical coil model of the unfolded state: resolving the reconciliation problem. Proc Natl Acad Sci USA. 2005;102(37):13099–13104. doi: 10.1073/pnas.0506078102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Meier S, Grzesiek S, Blackledge M. Mapping the conformational landscape of urea-denatured ubiquitin using residual dipolar couplings. J Am Chem Soc. 2007;129(31):9799–9807. doi: 10.1021/ja0724339. [DOI] [PubMed] [Google Scholar]
- 58.Esteban-Martin S, Fenwick RB, Salvatella X. Refinement of ensembles describing unstructured proteins using NMR residual dipolar couplings. J Am Chem Soc. 2010;132(13):4626–4632. doi: 10.1021/ja906995x. [DOI] [PubMed] [Google Scholar]
- 59.Nodet G, et al. Quantitative description of backbone conformational sampling of unfolded proteins at amino acid resolution from NMR residual dipolar couplings. J Am Chem Soc. 2009;131(49):17908–17918. doi: 10.1021/ja9069024. [DOI] [PubMed] [Google Scholar]
- 60.Zweckstetter M, Bax A. Prediction of sterically induced alignment in a dilute liquid crystalline phase: aid to protein structure determination by NMR. J Am Chem Soc. 2000;122(15):3791–3792. [Google Scholar]
- 61.Zweckstetter M. NMR: prediction of molecular alignment from structure using the PALES software. Nat Protoc. 2008;3(4):679–690. doi: 10.1038/nprot.2008.36. [DOI] [PubMed] [Google Scholar]
- 62.Valafar H, Prestegard JH. REDCAT: a residual dipolar coupling analysis tool. J Magn Reson. 2004;167(2):228–241. doi: 10.1016/j.jmr.2003.12.012. [DOI] [PubMed] [Google Scholar]
- 63.Cornilescu G, et al. Validation of protein structure from anisotropic carbonyl chemical shifts in a dilute liquid crystalline phase. J Am Chem Soc. 1998;120(27):6836–6837. [Google Scholar]
- 64.Clore GM, Garrett DS. R-factor, free R, and complete cross-validation for dipolar coupling refinement of NMR structures. J Am Chem Soc. 1999;121(39):9008–9012. [Google Scholar]
- 65.Bax A. Weak alignment offers new NMR opportunities to study protein structure and dynamics. Protein Sci. 2003;12(1):1–16. doi: 10.1110/ps.0233303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Schwieters CD, Kuszewski JJ, Clore GM. Using Xplor-NIH for NMR molecular structure determination. Prog Nucl Magn Reson Spectrosc. 2006;48(1):47–62. [Google Scholar]
- 67.Schwieters CD, et al. The Xplor-NIH NMR molecular structure determination package. J Magn Reson. 2003;160(1):65–73. doi: 10.1016/s1090-7807(02)00014-9. [DOI] [PubMed] [Google Scholar]
- 68.Tjandra N, et al. Defining long range order in NMR structure determination from the dependence of heteronuclear relaxation times on rotational diffusion anisotropy. Nat Struct Biol. 1997;4(6):443–449. doi: 10.1038/nsb0697-443. [DOI] [PubMed] [Google Scholar]
- 69.de Alba E, Tjandra N. Residual dipolar couplings in protein structure determination. Methods Mol Biol. 2004;278:89–106. doi: 10.1385/1-59259-809-9:089. [DOI] [PubMed] [Google Scholar]
- 70.Lange OF, et al. Recognition dynamics up to microseconds revealed from an RDC-derived ubiquitin ensemble in solution. Science. 2008;320(5882):1471–1475. doi: 10.1126/science.1157092. [DOI] [PubMed] [Google Scholar]
- 71.Clore GM, Schwieters CD. Concordance of residual dipolar couplings, backbone order parameters and crystallographic B-factors for a small alpha/beta protein: a unified picture of high probability, fast atomic motions in proteins. J Mol Biol. 2006;355(5):879–886. doi: 10.1016/j.jmb.2005.11.042. [DOI] [PubMed] [Google Scholar]
- 72.Lindorff-Larsen K, et al. Simultaneous determination of protein structure and dynamics. Nature. 2005;433(7022):128–132. doi: 10.1038/nature03199. [DOI] [PubMed] [Google Scholar]
- 73.Lakomek NA, et al. Self-consistent residual dipolar coupling based model-free analysis for the robust determination of nanosecond to microsecond protein dynamics. J Biomol NMR. 2008;41(3):139–155. doi: 10.1007/s10858-008-9244-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Lakomek NA, et al. A thorough dynamic interpretation of residual dipolar couplings in ubiquitin. J Biomol NMR. 2006;34(2):101–115. doi: 10.1007/s10858-005-5686-0. [DOI] [PubMed] [Google Scholar]
- 75.Peti W, et al. Model-free analysis of protein backbone motion from residual dipolar couplings. J Am Chem Soc. 2002;124(20):5822–5833. doi: 10.1021/ja011883c. [DOI] [PubMed] [Google Scholar]
- 76.Meiler J, et al. Model-free approach to the dynamic interpretation of residual dipolar couplings in globular proteins. J Am Chem Soc. 2001;123(25):6098–6107. doi: 10.1021/ja010002z. [DOI] [PubMed] [Google Scholar]
- 77.Chang SL, Tjandra N. Temperature dependence of protein backbone motion from carbonyl 13C and amide 15N NMR relaxation. J Magn Reson. 2005;174(1):43–53. doi: 10.1016/j.jmr.2005.01.008. [DOI] [PubMed] [Google Scholar]
- 78.Liu YZ, Kahn RA, Prestegard JH. Dynamic structure of membrane-anchored Arf·GTP. Nat Struct Mol Biol. 2010;17(7):876. doi: 10.1038/nsmb.1853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Lewis BA, et al. Magnetic birefringence studies of dilute purple membrane suspensions. Biophys J. 1985;47(2):143–150. doi: 10.1016/s0006-3495(85)83888-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Koenig BW, et al. NMR measurement of dipolar couplings in proteins aligned by transient binding to purple membrane fragments. J Am Chem Soc. 1999;121(6):1385–1386. [Google Scholar]
- 81.Koenig BW, et al. Structure and orientation of a G protein fragment in the receptor bound state from residual dipolar couplings. J Mol Biol. 2002;322(2):441–461. doi: 10.1016/s0022-2836(02)00745-3. [DOI] [PubMed] [Google Scholar]
- 82.Seidel RD, Zhuang TD, Prestegard JH. Bound-state residual dipolar couplings for rapidly exchanging ligands of His-tagged proteins. J Am Chem Soc. 2007;129(15):4834–4839. doi: 10.1021/ja069145h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Wang X, et al. RDC-assisted modeling of symmetric protein homo-oligomers. Protein Sci. 2008;17(5):899–907. doi: 10.1110/ps.073395108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Lee HW, et al. Three-dimensional structure of the weakly associated protein homodimer SeR13 using RDCs and paramagnetic surface mapping. Protein Sci. 2010;19(9):1673–1685. doi: 10.1002/pro.447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Al-Hashimi HM, Bolon PJ, Prestegard JH. Molecular symmetry as an aid to geometry determination in ligand protein complexes. J Magn Reson. 2000;142(1):153–158. doi: 10.1006/jmre.1999.1937. [DOI] [PubMed] [Google Scholar]
- 86.Bewley CA, Clore GM. Determination of the relative orientation of the two halves of the domain-swapped dimer of cyanovirin-N in solution using dipolar couplings and rigid body minimization. J Am Chem Socety. 2000;122(25):6009–6016. [Google Scholar]
- 87.Bax A, Grishaev A. Weak alignment NMR: a hawk-eyed view of biomolecular structure. Curr Opin Struct Biol. 2005;15(5):563–570. doi: 10.1016/j.sbi.2005.08.006. [DOI] [PubMed] [Google Scholar]
- 88.Tjandra N. Establishing a degree of order: obtaining high-resolution NMR structures from molecular alignment. Struct Fold Des. 1999;7(9):R205–R211. doi: 10.1016/s0969-2126(99)80167-1. [DOI] [PubMed] [Google Scholar]
- 89.Lipsitz RS, Tjandra N. Residual dipolar couplings in NMR structure analysis. Annu Rev Biophys Biomol Struct. 2004;33:387–413. doi: 10.1146/annurev.biophys.33.110502.140306. [DOI] [PubMed] [Google Scholar]
- 90.Prestegard JH, Bougault CM, Kishore AI. Residual dipolar couplings in structure determination of biomolecules. Chem Rev. 2004;104(8):3519–3540. doi: 10.1021/cr030419i. [DOI] [PubMed] [Google Scholar]