Abstract
Affect is increasingly recognized as central to decision making. However, it is not clear whether affect can be used to predict choice. To address this issue, we conducted 4 studies designed to create and test a model that could predict choice from affect. In Study 1, we used an image rating task to develop a model that predicted approach–avoidance motivations. This model quantified the role of two basic dimensions of affect—valence and arousal—in determining choice. We then tested the predictive power of this model for two types of decisions involving images: preference based selections (Study 2) and risk–reward trade-offs (Study 3). In both cases, the model derived in Study 1 predicted choice and outperformed competing models drawn from well-established theoretical views. Finally, we showed that this model has ecological validity: It predicted choices between news articles on the basis of headlines (Study 4). These findings have implications for diverse fields, including neuroeconomics and judgment and decision making.
Keywords: choice, affect, valence, arousal, decision making
Traditional theories of human decision making have ignored the role of affect. They have posited that choices were made by perfectly rational decision makers who cognitively assessed available options and chose the option that maximized utility (Friedman & Savage, 1952).
The first critiques of traditional decision-making theories came from behavioral decision researchers who identified cognitive biases and simplifying heuristics that often ran counter to purely rational decision making (e.g., Tversky & Kahneman, 1974). These critiques led to more realistic models that were better aligned with how people actually decided in real life. Nevertheless, these theories adhered to earlier cognitive perspectives and generally continued to ignore the role of affect in decision making (Loewenstein & Lerner, 2003).
More recently, decision researchers have acknowledged that affect is crucially involved in decision making. This realization has arisen in part from demonstrations that patients with deficits in affective— but not cognitive—processing have impaired decision making (e.g., Bechara, 2004). Spurred by this and related evidence, affect decision theorists have proposed that affect is not only involved in decision making but is, in fact, the common currency used to assign value to all decision options (Peters, Västfjäll, Gärling, & Slovic, 2006). Decision makers are said to compare the affective state that is likely to occur if they pick a particular option with the affective states that would result from other available options (Loewenstein & Lerner, 2003).
According to this framework, a person deciding whether to go to a party at a friend’s house or to a concert would compare the affect associated with going to the party with the affect associated with going to the concert. He or she would choose on the basis of the more favorable affective state. Such a process could occur even if the decision options involve considerations that are not purely affective. In such cases, decision makers are said to decompose complex thoughts into affective states (Mellers, 2000; Pfister & Böhm, 2008) that are then compared with each other. Hence many, if not all, decisions may be made via affective comparisons.
Thus, in a few short decades, affect has come from having no role in theories of decision making to potentially becoming an explaining mechanism underlying all decisions. However, a key gap remains in that no quantitative model explains how people compare two affective states and choose the one they prefer.
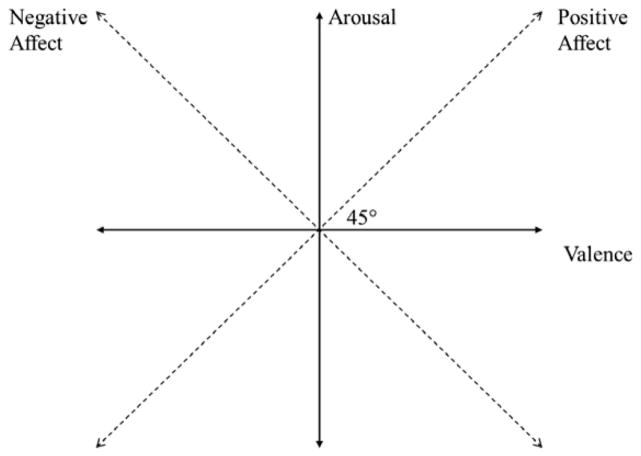
Our goal in this article is to create such a quantitative model. To create this model, we begin with two fundamental dimensions of affect: valence and arousal. The first, valence, represents the pleasantness or unpleasantness of the affect. The second, arousal, represents the degree of activation associated with the affect. These two dimensions capture most of the variance in self-reported mood ratings (Barrett & Russell, 1999; Osgood, Suci, & Tannenbaum, 1957; Russell, 1980). In addition, cross-cultural (Larsen & Diener, 1992), neurobiological (Posner et al., 2009), and developmental data (Russell & Bullock, 1985) demonstrate that—as Wundt (1912) postulated—valence and arousal are core components of affective states. Valence and arousal are often drawn as perpendicular dimensions to create an affective 2-space (see Figure 1).
Figure 1.
A plot of affective space along commonly used affective dimensions. Valence and arousal are plotted along the x- and y-axes, respectively. Positive affect/activation (PA) and its orthogonal dimension, negative affect/activation (NA), are alternative dimensions at a 45° rotation.
There are two opposing views as to how valence and arousal might predict choice. The first view is that only valence matters. On this view, choice consists of picking the option that is associated with a more pleasant affect (i.e., the higher the valence, the more preferred the associated affect). This valence-only view is supported by several influential theoretical approaches (Bower, 1981, 1991; Elster, 1998; Isen, Shalker, Clark, & Karp, 1978). It is also supported by the mainstream approach–avoidance literature, which posits the “primacy of the valence dimension” (Lang, 1995, p. 374). Approach motivations are theorized to increase with increasing valence and avoidance motivations are theorized to increase with decreasing valence (see Elliot & Covington, 2001, for a review). These motivations are thought to be the drivers of choice: Researchers (Tooby & Cosmides, 1990; Zajonc, 1998) have argued that approach–avoid motivations determine all subsequent responses.
The second view begins by rotating the valence and arousal dimensions by 45° (see Figure 1). The rotated dimensions, orthogonal to each other, are usually called positive affect or positive activation (PA) and negative affect or negative activation (NA; Watson & Tellegen, 1985). Some theorists suggest that increasing scores along the PA dimension represent an increasing approach motivation and increasing scores along the NA dimension represent an increasing avoid motivation (Watson, Wiese, Vaidya, & Tellegen, 1999). Because PA and NA bisect the valence-arousal axes, they receive equal contributions from valence and arousal; thus, according to this view (subsequently referred to as the equal-weights view), approach and avoidance motivations are a function of equal parts of valence and arousal.
Both the valence-only view and the equal-weights view provide the basis to construct models that predict choice on the basis of affect. For example, assume that one is trying to decide between Option 1 (vanilla ice cream) with valence v1 and arousal a1 and Option 2 (chocolate ice cream) with valence v2 and arousal a2. The valence-only model would predict that Option 1 would be picked if v1 > v2 and Option 2 would be picked if v2 >v1. The equal weights model would predict that Option 1 would be picked if a1 + v1 > a2 + v2 and Option 2 would be picked if a2 + v2 > a1 + v1.
Thus, both the valence-only model and the equal-weights model seek to predict choice on the basis of linear combinations of valence and arousal. The valence-only model assigns 1 as a coefficient to valence and 0 as coefficient to arousal; the equal-weights model assigns equal coefficients to valence and arousal. Because neither of these models has been empirically tested, it is unknown whether it is possible to successfully model choice—predict choice with accuracy significantly better than chance— using either of these models. Further, it is unknown whether there is a linear combination of valence and arousal that models choice across affective space better than any other linear combination, including those represented in the valence-only model and the equal-choice model.
In the four-study sequence presented below, we—for the first time— empirically demonstrate that it is possible to systematically model choice using two dimensions of affect, valence and arousal. Further, we found that arousal does indeed play a role in predicting choice (i.e., the valence-only model is not optimal) and, when sampling across all of affective space, its relative contribution in predicting choice is less than that of valence (i.e., the equal-weights model is not optimal).
In Study 1, we asked participants to rate a set of affective images on valence and arousal. We regressed these ratings with self-reported wanting and identified a linear combination of valence and arousal that best fit predictions of wanting ratings. In two subsequent studies, we tested whether this best-fit model would outpredict the valence-only model and the equal-weights model in the domain of behavioral decisions involving affective images. Specifically, in Study 2, we examined choices that involve preference behavioral decisions between two images, and, in Study 3, we examined choices involving risk–reward behavioral decisions in which the reward of seeing a positive image had to be compared with the risk of having to view a negative image. In Study 4, we tested whether the best-fit model derived in Study 1 and used in Studies 2 and 3 (using images) could predict decisions in a more realistic and ecologically valid domain: picking which articles to read on the basis of newspaper style headlines.
Study 1: Deriving a Model to Predict Wanting From Affect
Our goal in Study 1 was to determine what combination of arousal and valence ratings best predicted self-reported wanting (approach) ratings for a set of images that spanned affective 2-space.
Method
Forty-six students (21 women) viewed 50 pictures drawn principally from the International Affective Picture System (IAPS), a picture set developed to provide a set of normative emotional stimuli across a wide range of affective categories (Lang, Bradley, & Cuthbert, 2008). The valence/arousal mean and variance of the 50 chosen pictures was nearly identical to that for the entire IAPS set.1
Participants were first shown each of the 50 pictures for 500 ms. The brief glimpse was intended to ensure that participants did not fully process the picture and could therefore feel that it would be rewarding (or punishing) to see the picture for a longer time. They were asked to rate (on a scale of 1 to 7) how much they wanted to see the picture again for a longer duration (wanting ratings). A rating of 1 indicated strong not wanting and 7 indicated strong wanting. After completing the wanting ratings, participants were asked to rate the same 50 pictures on valence and arousal (on a scale of 1 to 7). They were specifically instructed to rate the valence and arousal they themselves felt rather than the valence and arousal felt by people depicted in the images.
Results and Discussion
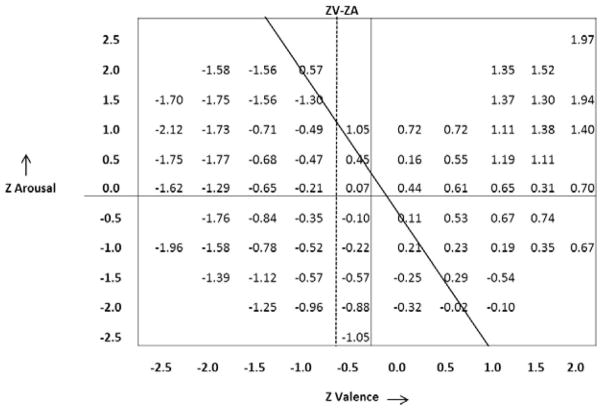
The valence, arousal, and wanting ratings were converted to z scores using per-subject mean and standard deviation scores. Figure 2 shows wanting z scores (ZW) for each 0.5 ≥ 0.5 cell (z units) in affective 2-space where the x-axis is the valence z score (ZV) and the y-axis is the arousal z score (ZA).
Figure 2.
A plot of affective space with wanting z scores (ZW) plotted for each 0.5 × 0.5 cell of Valence × Arousal z scores (ZV and ZA, respectively). Wanting tends to increase from left to right with increasing valence z scores. To the right of the dashed line (ZV = −0.5), wanting tends to increase from bottom to top with increasing arousal. The trend is generally reversed on the left of the dashed line. The area to the right and top of the solid diagonal line is generally the approach region (positive ZW) and to the left bottom is generally the avoid region (negative ZW).
It is possible to approximate the approach (ZW ≥ 0) and avoid (ZW < 0) regions with the diagonal line shown in Figure 2. The fact that this line is angled (and not vertical) suggests that arousal does play a role in predicting wanting. Notably, there are stimuli eliciting (modest) negative valence and very high arousal—such as a jet fighter firing a missile—that are in the approach region. Some erotic images also fall in this category. Correspondingly, there are images eliciting (modest) positive valence and very low arousal—such as a dull abstract shape—that are in the avoid region.
Two further trends are apparent in the wanting z scores. First, they generally appear to increase with valence. Wanting z scores for images with high negative valence scores are generally negative, and wanting z scores for images with highly positive z scores are generally positive. Valence therefore appears to be a predictor of wanting. Second, in the region defined by ZV ≥ −0.5, wanting scores generally increase with increasing arousal. In the ZV < −0.5 region, wanting scores generally decrease with increasing arousal. Arousal therefore also appears to be a predictor of wanting, but its effect appears to flip across the vertical line defined by ZV = −0.5. We therefore separately fitted valence and arousal to wanting for ZV < −0.5 and ZV ≥ −0.5.
We used multiple regression analysis to determine the respective contributions of valence (ZV) and arousal (ZA) in predicting wanting (ZW).2 In the region ZV ≥ −0.5, the two predictors explained 44% of the variance (R2 = .44), F(2, 1598) = 449.2, p < .001. Both valence and arousal predicted wanting; the regression coefficient of valence was 0.53 (95% CI [0.51, 0.56], p < .001) and the regression coefficient of arousal was 0.25 (95% CI [0.21, 0.27], p < .001). In the region ZV < −0.5, the two predictors explained 52% of the variance (R2 = .52), F(2, 698) = 291.7, p < .001. Both valence and arousal predicted wanting; the regression coefficient of valence was 0.67 (95% CI [0.62, 0.73], p < .001) and the regression coefficient of arousal was 0.14 (95% CI [0.08, 0.20], p < .001). The contribution of valence was greater than the contribution of arousal in predicting wanting in both regions (p < .001).
We designate this model consisting of the derived linear coefficients of valence and arousal as the best-fit model. The coefficient for arousal in the best-fit model is significantly different from zero (p < .001), which is evidence against the valence-only model; the coefficient of arousal is also significantly less that the coefficient for valence (p < .001), which is evidence against the equal-weights model.
In sum, the above results demonstrate the following: (a) Both valence and arousal predict wanting and (b) valence influences wanting more than arousal influences wanting.
Study 2: Using the Best-Fit Model to Predict Preference Decisions
In Study 2, we analyzed how participants decided between a pair of images. The goal of Study 2 was to (a) test whether the best-fit model identified in Study 1 could predict such choices above chance and (b) whether the best-fit model could outpredict the valence-only and equal-weights models.
Method
Twenty-two students (12 women) viewed a set of 160 images (145 IAPS images and 15 others) for 500 ms each and rated the affect created by each image on the dimensions of valence and arousal in a procedure identical to that described in Study 1. In a second task, the 160 pictures were then re-presented as 80 pairs. The same set of pairs was used for all participants. The pairs were chosen in a manner as to ensure a diverse sampling across affective space.
Within a pair, one picture was designated Picture 1 and the other was designated Picture 2. Picture 1 and Picture 2 were counterbalanced for valence and arousal (IAPS population ratings). Participants were shown Picture 1 for 500 ms, which was followed by Picture 2 for 500 ms. They were asked to choose which of the two pictures they wanted to see for a longer duration. The chosen picture was displayed for 4 s, a duration long enough to ensure that the preferred picture was viewed and processed; this attached real affective consequences to each choice.
Results and Discussion
We determined the preference predictions of each model as follows. The valence-only model would pick the higher valenced picture; the equal-weights model would pick the picture with higher PA, measured by valence + arousal, or—if both pictures were negatively valenced—with lower NA, measured by (−valence) + (−arousal) scores; the best-fit model would pick the picture with higher scores for the best-fit linear combination derived in Study 1: (0.53 × valence + 0.24 × arousal) in the ZV ≥ −0.5 region and the best-fit linear combination (0.67 × valence × 0.14 × arousal) in the ZV < −0.5 region.
The best-fit model predicted choice for 74.2% of trials (95% CI [72.16%, 76.24%]). The valence-only model predicted actual choice for 66.81% of trials (95% CI [64.61%, 69.01%]). The equal-weights model predicted choice for 70.17% of trials (95% CI [68.03%, 72.30%]). The differences between the best-fit and both competing models were highly significant (for McNemar’s test, best-fit vs. valence-only χ2 = 41.06, p < .0001, odds ratio = 1.96; best-fit vs. equal-weights χ2 = 12.96, p < .0001, odds ratio = 1.82).
Study 2 yielded unambiguous results showing that (a) it is possible to predict behavioral choice concerning affect at levels above chance using all three models and (b) the best-fit model has the highest predictive accuracy for decisions involving preferences. In Study 3, we wanted to extend our findings to test decisions that required the participant to weigh expected rewards and risks.
Study 3: Using the Best-Fit Model to Predict Risk–Reward Decisions
In Study 3, participants had the choice to risk seeing a negative picture for the reward of seeing a positive one or to play it safe and ensure that they saw neither picture. The goal of Study 3 was to test whether the best-fit model identified in Study 1 and tested in Study 2 could (a) model actual risk–reward choices and (b) out-predict the valence-only and equal-weights models for actual risk–reward choices.
Method
Twenty students (10 women) viewed 100 images (85 IAPS images and 15 others) for 500 ms each and rated them on the dimensions of valence and arousal in a procedure identical to that used in Studies 1 and 2.
The 100 pictures were re-presented as 50 pairs. The reward picture was positively valenced (IAPS population ratings) and the risk picture was negatively valenced. The reward and risk pictures were counterbalanced and shown for 500 ms each. Subjects were asked to make a choice to proceed or skip. If they elected to proceed, they were shown either picture—with 50% probability—for 4 s. If they elected to skip, they were shown a blank screen for 4 s (this ensured that subjects would not skip only to shorten the experiment).
Results and Discussion
The approach–avoidance literature defines the region for which valence > 0 as the approach region. We use this definition for the valence-only model. For the equal-fit model, we defined the approach region as the region for which PA > 0. For the best-fit model, we defined the approach region as the region for which ZW > 0 in Study 1 (approximately represented as the area to the right of the angled line in Figure 2).
We predicted that if the average z score valence and arousal of the risk and reward pictures lay in the approach region, the proceed option would be chosen. Otherwise, we predicted that the skip option would be chosen. Because the approach region of the best-fit model differs from those of the valence-only and the equal-weights models, the models differ in their proceed and skip predictions. These differential predictions were tested against actual subject choices.
The best-fit model predicted actual choice for 76.2% of the trials (95% CI [73.5%, 78.8%]); the valence-only model was predictive for 69.1% of trials (95% CI [66.2%, 71.9%]); the equal-weights model was predictive for 71.8% of trials (95% CI [69%, 74.6%]). The differences between the best-fit and both competing models were highly significant (for McNemar’s test, best fit vs. valence only χ2 = 21.39, p < .0001, odds ratio = 1.89; best fit vs. equal weights χ2 = 19.26, p < .0001, odds ratio = 2.69).
We observed no sex-based differences in participant choices. Further studies are required to examine if there are additional (individual difference) drivers that apply to the risk–reward decision context but not to the simpler preference-based decision contexts examined in Study 2.
Study 3 showed that the best-fit model could predict risk–reward decisions. However, it remained unknown whether the best-fit model could be extended to decision domains other than those involving images.
Study 4: Testing the Ecological Validity of the Best-Fit Model
In Study 4, we analyzed how participants decided between a pair of news article headlines. This is a choice context that could be used to test ecological validity of the best-fit model because users choose to click or avoid Internet articles millions of times every day on the basis of their headlines.
The goal of Study 4 was to (a) test whether the best-fit model identified in Study 1 could predict choices outside the image domain above chance and (b) whether the best-fit model could outpredict the valence-only and equal-weights models.
Method
Thirty-six participants (16 women) viewed a set of 50 headlines that were written in the style of newspaper (or news website) headlines. The headlines were written to differ in the valence and arousal they elicited. Pilot ratings indicated that as anticipated, valence and arousal ratings elicited by these headlines spanned the full affective 2-space. Valence ranking ranged from 1 to 7 with a mean of 4.24 and arousal rankings ranged from 1 to 7 with a mean 4.16.
In the first task, participants were asked rate each headline on the dimensions of valence and arousal in a procedure identical to that described in Study 1. In a second task, the 50 headlines were then re-presented as 25 pairs. The same set of pairs was used for all participants. The pairs were chosen to ensure a diverse sampling across affective space. An example pair included (a) “The Quiet Pleasures of Redwood Groves” and (b) “Group Promotes Having Sex on High Mountain Peaks.”
Participants were shown each headline pair in turn. They were asked to pick the headline of the article they were more interested in reading. They were told that later, they would be asked to read articles corresponding to some (but not all) of the choices they made. However, participants did not know which of their choices would later prove to be consequential. This ensured that each choice had to be treated as being important.
The participants made 25 choices. At the end of the 25 choices, they were asked to read articles corresponding to two of their choices.
Results and Discussion
We determined the preference predictions of each model using a procedure identical to the one used in Study 2. The best-fit model (the one identified in Study 1 and confirmed in Studies 2 and 3 using IAPS) predicted choice for 73% of headline pairs (95% CI [70.0%, 75.8%]). The valence-only model predicted actual choice for 52% of trials (95% CI [48.7%, 55.2%]), which is indistinguishable from chance. The equal-weights model predicted choice for 64% of trials (95% CI [60.8%, 67.1%]). The differences between the best-fit and both competing models were highly significant (for McNemar’s test, best-fit vs. valence-only χ2 = 109.42, p < .0001, odds ratio = 3.82; best-fit vs. equal-weights χ2 = 25.29, p < .0001, odds ratio = 1.94).
Study 4 yielded unambiguous results showing that (a) it is possible to predict choice in a domain other than images at levels above chance using the best-fit and equal-weights models and (b) the best-fit model derived in Study 1 using images has the highest predictive accuracy for decisions involving picking articles on the basis of headlines preferences, an everyday choice context for many individuals.
General Discussion
In this article, we identified a linear combination of valence and arousal ratings that best matched self-reported wanting ratings for stimuli that spanned affective 2-space. This best-fit model better predicted relative preference and risk–reward choices compared with predictions based on the canonical valence-only and equal-weights models.
The two main contributions of the current article are that (a) we have demonstrated a way to model approach–avoidance behavior—and hence choice—from affect, and (b) we have shown that although both valence and arousal predict choice across affective 2-space, valence has a relatively greater impact than arousal. This contradicts the two prior canonical views that assumed that only valence matters in predicting choice and valence and arousal matter equally.
It has long been clear that valence plays a role in choice (Schneirla, 1959). Research on the role of arousal in choice is more recent and, unsurprisingly, less settled. Arousal has been shown to play a role in social transmission (Berger, 2011), which could potentially be related to personal choice. Ariely and Loewenstein (2006) have demonstrated that arousal broadens the category of things that are attractive. Such a broadening could impact approach–avoidance behaviors. A related explanation is that arousal is associated with the salience of a stimulus. Salient events require immediate behavioral responses and therefore impact motivation (Cooper & Knutson, 2008).
The best-fit model offers new insights regarding the mechanisms underlying affective choice. We believe that these insights have broad implications across many other fields in psychology. For example, neuroeconomists have suggested that various neural systems are involved in decision making, but little is known about how options with different values are compared with each other (Rangel, Camerer, & Montague, 2008). The best-fit model provides a testable common currency.
Another broad implication of the best-fit model is for understanding individual differences in decision making and personality. Individuals may be more or less arousal focused or valence focused (cf. Feldman, 1995). These differences may be associated with differences in labeling of affective experience, specific personality traits, and particular decision-making tendencies.
The best-fit model might be further developed in three ways. First, in future studies, researchers could analyze rotation angles associated with discrete emotions. It is conceivable that discrete emotions have unique rotation angles and hence a predictable approach–avoidance signature. Further, discrete emotions may incrementally predict approach–avoid tendencies after valence and arousal have been partialed out. Such evidence could bolster the claim for the utility of a discrete emotions perspective. Second, the above studies featured North American participants. It remains unknown whether differing ideal affects (Tsai, 2007) for participants from different cultures impact the best-fit model. Third, the best-fit model as derived in Study 1 relies on reportable affect. It is likely that using alternative physiological and neural measures could improve the best-fit model or identify alternative ways to predict choice from affect.
Footnotes
Exact IAPS picture numbers are available on request.
We tested all regression models for fixed as well as random effects. There were no slope-related random effects. Intercept-related random effects were factored in to the fixed model by using subject-level z scores as dependent variables. We thus reported results from fixed regression models.
Contributor Information
Gaurav Suri, Stanford University.
Gal Sheppes, Tel Aviv University.
James J. Gross, Stanford University
References
- Ariely D, Loewenstein G. The heat of the moment: The effect of sexual arousal on sexual decision making. Journal of Behavioral Decision Making. 2006;19:87–98. doi: 10.1002/bdm.501. [DOI] [Google Scholar]
- Barrett LF, Russell JA. The structure of current affect: Controversies and emerging consensus. Current Directions in Psychological Science. 1999;8:10–14. doi: 10.1111/1467-8721.00003. [DOI] [Google Scholar]
- Bechara A. The role of emotion in decision-making: Evidence from neurological patients with orbitofrontal damage. Brain and Cognition. 2004;55:30– 40. doi: 10.1016/j.bandc.2003.04.001. [DOI] [PubMed] [Google Scholar]
- Berger J. Arousal increases social transmission of information. Psychological Science. 2011;22:891– 893. doi: 10.1177/0956797611413294. [DOI] [PubMed] [Google Scholar]
- Bower GH. Mood and memory. American Psychologist. 1981;36:129–148. doi: 10.1037/0003-066X.36.2.129. [DOI] [PubMed] [Google Scholar]
- Bower GH. Mood congruity of social judgments. In: Forgas J, editor. Emotion and social judgments. Oxford, United Kingdom: Pergamon; 1991. pp. 31–54. [Google Scholar]
- Cooper JC, Knutson B. Valence and salience contribute to nucleus accumbens activation. Neuro Image. 2008;39:538–547. doi: 10.1016/j.neuroimage.2007.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elliot A, Covington M. Approach and avoidance motivation. Educational Psychology Review. 2001;13:73–92. doi: 10.1023/A:1009009018235. [DOI] [Google Scholar]
- Elster J. Emotions and economic theory. Journal of Economic Literature. 1998;36:47–74. [Google Scholar]
- Feldman LA. Valence focus and arousal focus: Individual differences in the structure of affective experience. Journal of Personality and Social Psychology. 1995;69:153–166. doi: 10.1037/0022-3514.69.1.153. [DOI] [Google Scholar]
- Friedman M, Savage LJ. The expected utility hypothesis and the measurability of utility. Journal of Political Economy. 1952;60:463– 474. doi: 10.1086/257308. [DOI] [Google Scholar]
- Isen AM, Shalker TE, Clark M, Karp L. Affect, accessibility of material in memory, and behavior: A cognitive loop? Journal of Personality and Social Psychology. 1978;36:1–12. doi: 10.1037/0022-3514.36.1.1. [DOI] [PubMed] [Google Scholar]
- Lang PJ. The emotion probe: Studies of motivation and attention. American Psychologist. 1995;50:372–385. doi: 10.1037/0003-066X.50.5.372. [DOI] [PubMed] [Google Scholar]
- Lang PJ, Bradley BN, Cuthbert BN. Technical Report A-8. Gainesville: University of Florida; 2008. International affective picture system (IAPS): Affective ratings of pictures and instruction manual. [Google Scholar]
- Larsen RJ, Diener E. Promises and problems with the circumplex model of emotion. In: Clark MS, editor. Review of personality and social psychology: Emotion. Vol. 13. Newbury Park, CA: Sage; 1992. pp. 25–59. [Google Scholar]
- Loewenstein GF, Lerner JS. The role of affect in decision making. In: Davidson RJ, Scherer KR, Goldsmith HH, editors. Handbook of affective sciences. Oxford, United Kingdom: Oxford University Press; 2003. pp. 619–642. [Google Scholar]
- Mellers BA. Choice and the relative pleasure of consequences. Psychological Bulletin. 2000;126:910–924. doi: 10.1037/0033-2909.126.6.910. [DOI] [PubMed] [Google Scholar]
- Osgood CE, Suci GJ, Tannenbaum PH. The measurement of meaning. Urbana: University of Illinois; 1957. [Google Scholar]
- Peters E, Västfjäll D, Gärling T, Slovic P. Affect and decision making: A “hot” topic. Journal of Behavioral Decision Making. 2006;19:79– 85. doi: 10.1002/bdm.528. [DOI] [Google Scholar]
- Pfister HR, Böhm G. The multiplicity of emotions: A framework of emotional functions in decision making. Judgment and Decision Making. 2008;3:5–17. [Google Scholar]
- Posner J, Russell JA, Gerber A, Gorman D, Colibazzi T, Yu S, Peterson BS. The neurophysiological bases of emotion: An fMRI study of the affective circumplex using emotion-denoting words. Human Brain Mapping. 2009;30:883– 895. doi: 10.1002/hbm.20553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rangel A, Camerer C, Montague PR. A framework for studying the neurobiology of value-based decision making. Nature Reviews Neuroscience. 2008;9:545–556. doi: 10.1038/nrn2357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russell J. A circumplex model of affect. Journal of Personality and Social Psychology. 1980;39:1161–1178. doi: 10.1037/h0077714. [DOI] [PubMed] [Google Scholar]
- Russell JA, Bullock M. Multidimensional scaling of emotional facial expressions: Similarity from preschoolers to adults. Journal of Personality and Social Psychology. 1985;48:1290–1298. doi: 10.1037/0022-3514.48.5.1290. [DOI] [Google Scholar]
- Schneirla TC. An evolutionary and developmental theory of biphasic processes underlying approach and withdrawal. In: Jones M, editor. Nebraska Symposium on Motivation. Lincoln: University of Nebraska Press; 1959. pp. 1–42. [Google Scholar]
- Tooby J, Cosmides L. The past explains the present: Emotional adaptions and the structure of ancestral environments. Ethology and Sociobiology. 1990;11:375– 424. doi: 10.1016/0162-3095(90)90017-Z. [DOI] [Google Scholar]
- Tsai JL. Ideal affect: Cultural causes and behavioral consequences. Perspectives on Psychological Science. 2007;2:242–259. doi: 10.1111/j.1745-6916.2007.00043.x. [DOI] [PubMed] [Google Scholar]
- Tversky A, Kahneman D. Judgment under uncertainty: Heuristics and biases. Science. 1974 Sep 27;185:1124–1131. doi: 10.1126/science.185.4157.1124. [DOI] [PubMed] [Google Scholar]
- Watson D, Tellegen A. Toward a consensual structure of mood. Psychological Bulletin. 1985;98:219–235. doi: 10.1037/0033-2909.98.2.219. [DOI] [PubMed] [Google Scholar]
- Watson D, Wiese D, Vaidya J, Tellegen A. The two general activation systems of affect: Structural findings, evolutionary considerations, and psychobiological evidence. Journal of Personality and Social Psychology. 1999;76:820– 838. doi: 10.1037/0022-3514.76.5.820. [DOI] [Google Scholar]
- Wundt W. An introduction to psychology. New York, NY: Macmillan; 1912. [DOI] [Google Scholar]
- Zajonc R. Emotion. In: Gilbert D, Fiske S, Lindzey G, editors. The handbook of social psychology. 4. New York, NY: McGraw-Hill; 1998. pp. 591–632. [Google Scholar]