Accelerated Intensity Frailty Model for Recurrent Events Data

Summary

In this article we propose an accelerated intensity frailty (AIF) model for recurrent events data and derive a test for the variance of frailty. In addition, we develop a kernel-smoothing-based EM algorithm for estimating regression coefficients and the baseline intensity function. The variance of the resulting estimator for regression parameters is obtained by a numerical differentiation method. Simulation studies are conducted to evaluate the finite sample performance of the proposed estimator under practical settings and demonstrate the efficiency gain over the Gehan rank estimator based on the AFT model for counting process (Lin et al., 1998, Biometrika 85, 605–618). Our method is further illustrated with an application to a bladder tumor recurrence data.

1. Introduction

Recurrent events data are frequently encountered in areas of industry, economics, public health and medical research, where subjects may experience repeated occurrences of the same type of events. Examples include recurrent tumors, infections, asthma attacks and car warranty claims, and many others (Cook and Lawless, 2007). A number of methods have been developed for analysis of recurrent events data. One popular approach is to model the intensity function of the counting process for recurrent events, such as the well known Andersen-Gill model (Andersen and Gill, 1982), which assumes a Cox-type multiplicative intensity function. Under the Andersen-Gill model, the underlying counting process becomes a nonhomogeneous Poisson process adjusting for covariates. However, the multiplicative intensity function is likely to be too stringent in practice due to the within-subject dependency and it generally requires the adjustment of complicated time-dependent covariates. Alternatively, marginal approaches have been widely studied, for example, Cox regression model for the marginal hazard functions of time to recurrent events (Wei et al., 1989) and the marginal models for the mean/rate functions of the counting process for recurrent events (Pepe and Cai, 1993; Lawless and Nadeau, 1995; Lawless et al., 1997; Lin et al., 2000). In many applications, the within-subject dependence of recurrent events is also of primary interest. To study the within-subject dependence, the random effect/frailty models have been proposed, for example the multiplicative intensity frailty model (Andersen et al., 1993). Its associated nonparametric maximum likelihood estimation and asymptotic theory have been investigated by many authors (e.g. Murphy, 1994, 1995; Parner, 1998).

In addition to the Cox-type regression models for recurrent events data, many other semiparametric models have also been studied in the literature, such as the accelerated failure time (AFT) model for counting process (Lin et al., 1998; Jin et al., 2006), the linear transformation models for gap times or counting process (Lu, 2005; Zeng and Lin, 2007) and the additive intensity/rate models (Schaubel et al., 2006; Liu and Wu, 2011). They provide useful alternatives for the Cox-type regression models.

In this paper, we propose an accelerated intensity frailty (AIF) model for recurrent events data. A similar model was also studied by Strawderman (2006) for gap times using an EM-like algorithm. However, Strawderman’s estimator does not maximize the likelihood function and its variance needs to be obtained using the bootstrap method. Here, we develop the nonparametric maximum likelihood estimation (NPMLE) method for the proposed model based on a kernel-smoothing aided EM algorithm. The remainder of the paper is organized as follows. Section 2 introduces the AIF model for recurrent events data. A test for the variance of the frailty is derived in Section 3. Section 4 presents our NPMLE estimators and the corresponding variance estimation procedure via numerical differentiation. The large sample properties of the NPMLE estimators are also briefly discussed. Simulation studies and an application to a bladder tumor recurrence data are provided in Section 5. Some conclusions and discussions are given in Section 6.

2. AIF Model

Let $N_i^{*}(t)$, i = 1,⋯, n, be the number of events observed on subject i by time t in the absence of censoring, and X_i be a p-dimensional vector of baseline covariates. With censoring, we only observe $N_i(t)=N_i^{*}(t\mathrm{\Lambda }{C}_i)$, where C_i is the censoring time and a Λ b denotes the minimum of a and b. Then N_i(t) is a counting process with the jumps only at the observed recurrence times 0 < T_i1 < ⋯ < T_i,ni ≤ C_i, where T_ij is the time to the jth recurrence and n_i is the total number of observed recurrences on subject i. Given covariates X_i and a random effect α_i, the conditional intensity function of $N_i^{*}(t)$ is specified by

$$\lambda (t|{\mathbf{X}}_i,{\alpha }_i)={\alpha }_i{e}^{{\beta }_0^{\prime }{\mathbf{X}}_i}{\lambda }_0(t{e}^{{\beta }_0^{\prime }{\mathbf{X}}_i}),$$ (1)

where λ₀(·) is an unspecified baseline intensity function, and α_i is a positive random variable with mean 1 to ensure the identifiability of the baseline intensity function and is assumed to be independent of X_i. When there is only one recurrent event per subject, model (1) becomes the accelerated failure time frailty model for survival times, which has been studied by various authors (e.g. Lambert et al., 2004; Klein et al., 1999; Pan, 2001; Zhang and Peng, 2007). Under model (1), conditional on α_i and X_i, $N_i^{*}(t)$ is a nonhomogeneous Poisson process with mean ${\alpha }_i{\mathrm{\Lambda }}_0(t{e}^{{\beta }_0^{\prime }{\mathbf{X}}_i})$, where ${\mathrm{\Lambda }}_0(t)={\int }_0^t\lambda 0(s)ds$. Therefore, we have $E\{N_i^{*}(t)|{\mathbf{X}}_i\}={\mathrm{\Lambda }}_0(t{e}^{{\beta }_0^{\prime }{\mathbf{X}}_i})$, which coincides with the marginal AFT model for counting process studied by Lin et al. (1998) and Jin et al. (2006). Here the frailty α_i is to describe the association among gap times of consecutive events for the same subject, the larger the variance of α_i the stronger the association. Throughout the paper, it is assumed that C_i is independent of $N_i^{*}(·)$ given {X_i, α_i} and C_i is independent of α_i.

3. Frailty Variance Test based on Gehan Rank Estimator

It is of interest to test whether the variance of the frailty is zero in the AIF model, i.e. H₀ : Var(α_i) = 0, since it implies that gap times between consecutive recurrences are conditionally independent given covariates. Note that the AIF model implies the marginal AFT model for counting process (Lin et al., 1998). Therefore, the Gehan rank estimator proposed byLin et al. (1998) is a consistent estimator regardless of the distribution of the frailty including the case with α_i ≡ 1. Let β̂_G denote the Gehan rank estimator of β₀ and ${\widehat{\mathrm{\Lambda }}}_G(t;{\widehat{\beta }}_G)={\sum }_{i=1}^n{\int }_0^{t}d{N}_i(s{e}^{-{\widehat{\beta }}_G^{\prime }{\mathbf{X}}_i})/{\sum }_{j=1}^n{Y}_j(s;{\widehat{\beta }}_G)$ denote the estimator of Λ₀ proposed by Lin et al. (1998), where Y_j(s; β) = I{C̃_j(β) ≥ s} and C̃_j(β) = C_je^{β′ X_j}. Under H₀, the total number of events n_i on subject i is a Poisson random variable with mean ${\mathrm{\Lambda }}_0(C_i{e}^{{\beta }_0^{\prime }{\mathbf{X}}_i})$ and variance ${\mathrm{\Lambda }}_0(C_i{e}^{{\beta }_0^{\prime }{\mathbf{X}}_i})$, while under the alternative Var(α_i) > 0, the variance of n_i is larger than the mean. This motivates us to consider the following test statistic

$$T_n=\sum _{i=1}^n[{\{n_i-{\widehat{\mathrm{\Lambda }}}_G(C_i{e}^{{\widehat{\beta }}_G^{\prime }{\mathbf{X}}_i};{\widehat{\beta }}_G)\}}^2-{\widehat{\mathrm{\Lambda }}}_G(C_i{e}^{{\widehat{\beta }}_G^{\prime }{\mathbf{X}}_i};{\widehat{\beta }}_G)],$$

and reject H₀ when T_n > c. A similar test statistic is also studied in Dean and Lawless (1989) for detecting overdispersion in Poisson regression. Under H₀, it can be shown that n^−1/2T_n is asymptotically normally distributed with mean zero based on the asymptotic results established in Lin et al. (1998). To compute the variance of the test statistic T_n, we adopt the resampling technique developed by Lin et al. (1998). Specifically, we consider the perturbed test statistic:

$$T_n^{*}=\sum _{i=1}^n[{\widehat{\mathrm{\Lambda }}}_G^2(C_i{e}^{{\widehat{\beta }}_G^{\prime }{\mathbf{X}}_i};{\widehat{\beta }}_G)-{\widehat{\mathrm{\Lambda }}}_G^2(C_i{e}^{{\widehat{\beta }}_G^{*\prime }{\mathbf{X}}_i};{\widehat{\beta }}_G)-(2n_i+1)\{{\widehat{\mathrm{\Lambda }}}_G(C_i{e}^{{\widehat{\beta }}_G^{\prime }{\mathbf{X}}_i};{\widehat{\beta }}_G)-{\widehat{\mathrm{\Lambda }}}_G(C_i{e}^{{\widehat{\beta }}_G^{*\prime }{\mathbf{X}}_i};{\widehat{\beta }}_G)\left\}\right]+\sum _{i=1}^n(V_i-1)\{n_i^2+{\widehat{\mathrm{\Lambda }}}_G^2(C_i{e}^{{\widehat{\beta }}_G^{\prime }{\mathbf{X}}_i};{\widehat{\beta }}_G)-(2n_i+1){\widehat{\mathrm{\Lambda }}}_G(C_i{e}^{{\widehat{\beta }}_G^{\prime }{\mathbf{X}}_i};{\widehat{\beta }}_G)\}+\sum _{i=1}^n{\widehat{W}}_i\{2{\widehat{\mathrm{\Lambda }}}_G(C_i{e}^{{\widehat{\beta }}_G^{\prime }{\mathbf{X}}_i};{\widehat{\beta }}_G)-(2n_i+1)\},$$

where V₁,⋯, V_n are i.i.d. positive random variables with mean 1 and variance 1,

$${\widehat{W}}_i={\widehat{\mathrm{\Lambda }}}_G(C_i{e}^{{\widehat{\beta }}_G^{\prime }{\mathbf{X}}_i};{\widehat{\beta }}_G)-{\widehat{\mathrm{\Lambda }}}_G(C_i{e}^{{\widehat{\beta }}_G^{\prime }{\mathbf{X}}_i};{\widehat{\beta }}_G^{*})+\sum _{j=1}^n(V_j-1){\int }_0^{C_i{e}^{{\widehat{\beta }}_G^{\prime }{\mathbf{X}}_i}}\frac{d{M}_j(s;{\widehat{\beta }}_G)}{{\sum }_{k=1}^n{Y}_k(s;{\widehat{\beta }}_G)},$$

dM_j(t; β) = dN_j(te^−β′X_j) − Y_j(t; β)dΛ̂_G(t; β), ${\widehat{\beta }}_G^{*}$ is the perturbed estimator for β obtained based on the same set of random variables V_i’s as proposed inLin et al. (1998). Following the same arguments as in Lin et al. (1998), it can be shown that conditional on observed data, $n^{-1/2}{T}_n^{*}$ has the same limiting distribution as n^−1/2T_n under H₀. Therefore, we can use the empirical distribution of $n^{-1/2}{T}_n^{*}$ to calculate the critical value c.

4. Proposed Estimation Method

Assume that Var(α_i) > 0. We develop an EM algorithm to obtain the nonparametric maximum likelihood estimators for the AIF model. Specifically, let f_α(·; θ) denote the density function of α_i, where θ is a scalar parameter related to the variance of frailty. In practice, a variety of distributions can be used for the frailty, such as gamma distribution (Clayton, 1978) and log-normal distribution (McGilchrist and Aisbett, 1991). Then the complete log-likelihood, up to a constant independent of parameters, can be written as

$$l_n^c(\beta ,\mathrm{\Lambda },\theta )=l_{n,1}^c(\theta )+l_{n,2}^c(\beta ,\mathrm{\Lambda }),$$

where

$$l_{n,1}^c(\theta )=n^{-1}\sum _{i=1}^n\{n_i\text{log}{\alpha }_i+\text{log}{f}_{\alpha }({\alpha }_i;\theta )\},$$ (2)

$$l_{n,2}^c(\beta ,\mathrm{\Lambda })=n^{-1}\sum _{i=1}^n(\sum _{j=1}^{n_i}[\beta \prime {\mathbf{X}}_i+\text{log}\lambda \{{\tilde{T}}_{ij}(\beta )\}]-{\alpha }_i\mathrm{\Lambda }\{{\tilde{C}}_i(\beta )\left\}\right),$$ (3)

with $\mathrm{\Lambda }(t)={\int }_0^t\lambda (s)ds\text{and}{\tilde{T}}_{ij}(\beta )=T_{ij}{e}^{\beta \prime {\mathbf{X}}_i}$.

In the E-step, we compute the conditional expectations E(α_i|𝒪,Ω̂^[k]), E(log α_i|𝒪,Ω^[k]) and E{log f_α(α_i; θ)|𝒪,Ω̂^[k]}, where Ω̂^[k] = (β̂^[k],Λ̂^[k],θ̂ ^[k]) denote the current estimates at step k and 𝒪 = {(T_ij, C_i, X_i), i = 1,⋯, n; j = 1,⋯, n_i} denote the observed data. The above expectations can be calculated as the integrals of the corresponding terms with respect to the following conditional density:

$$f({\alpha }_i|𝒪,{\widehat{\mathrm{\Omega }}}^{[k]})=\frac{f_{\alpha }({\alpha }_i;{\widehat{\theta }}^{[k]}){\alpha }_i^{ni}{e}^{-{\alpha }_i{\widehat{\mathrm{\Lambda }}}^{[k]}\{{\tilde{C}}_i({\widehat{\beta }}^{[k]})\}}}{{\int }_0^{\infty }{f}_{\alpha }({\alpha }_i;{\widehat{\theta }}^{[k]}{\alpha }_i^{n_i}{e}^{-{\alpha }_i{\widehat{\mathrm{\Lambda }}}^{[k]}\{{\tilde{C}}_i({\widehat{\beta }}^{[k]})\}}d{\alpha }_i)}.$$

For instance, when the frailty follows a gamma distribution with the density f_α(x; θ) = x^β−1e^−βxββ/Γ(β) with $\mathrm{\Gamma }(\theta )={\int }_0^{\infty }{t}^{\theta -1}{e}^{-t}dt$, we have

$${\widehat{\alpha }}_i^{[k]}\equiv E({\alpha }_i|𝒪,{\widehat{\mathrm{\Omega }}}^{[k]})=(n_i+{\widehat{\theta }}^{[k]})/[{\widehat{\theta }}^{[k]}+{\widehat{\mathrm{\Lambda }}}^{[k]}\{{\tilde{C}}_i({\widehat{\beta }}^{[k]})\}],E_{2,i}^{[k]}\equiv E(\text{log}{\alpha }_i|𝒪,{\widehat{\mathrm{\Omega }}}^{[k]})=\mathrm{\Psi }(n_i+{\widehat{\theta }}^{[k]})-\text{log}[{\widehat{\theta }}^{[k]}+{\tilde{\mathrm{\Lambda }}}^{[k]}\{{\tilde{C}}_i({\widehat{\beta }}^{[k]})\}],$$

and

$$E_{3,i}^{[k]}\equiv E\{\text{log}{f}_{\alpha }({\alpha }_i;\theta )|𝒪{\widehat{\mathrm{\Omega }}}^{[k]}\}=(\theta -1)E_{2,i}^{[k]}-\theta {\widehat{\alpha }}_i^{[k]}+\theta \text{log}\theta -\text{log}\mathrm{\Gamma }(\theta ),$$

where Ψ(x) = Γ′(x)/Γ(x) is the digamma function. For other frailty distributions where there are no closed forms for these conditional expectations, such as the log-normal distribution, we use gaussian quadrature method to calculate the integrals. Therefore, the conditional expectations of (2) and (3) given 𝒪 and Ω̂^[k] are respectively,

$$E\{l_{n,2}^c(\theta )|𝒪,{\widehat{\mathrm{\Omega }}}^{[k]}\}=n^{-1}\sum _{i=1}^n(n_i{E}_{2,i}^{[k]}+E_{3,i}^{[k]}),$$ (4)

$$E\{l_{n,2}^c(\beta ,\mathrm{\Lambda })|𝒪,{\widehat{\mathrm{\Omega }}}^{[k]}\}=n^{-1}\sum _{i=1}^n(\sum _{j=1}^{n_i}[\beta \prime {\mathbf{X}}_i+\text{log}\lambda \{{\tilde{T}}_{ij}(\beta )\}]-{\widehat{\alpha }}_i^{[k]}\mathrm{\Lambda }\{{\tilde{C}}_i(\beta )\}).$$ (5)

In the M-step, we maximize (4) and (5), respectively. Maximization of (4) can be achieved easily using standard gradient-based algorithms. Here, we used the “optim” function in R, and denote the maximizer of (4) by θ̂^[k+1]. Based on model (1) and the conditional independent censoring assumption, the intensity function of the counting process $N_i(t{e}^{-{\beta }_0^{\prime }{\mathbf{X}}_i})$ given α_i and X_i is I{C̃_i(β) ≥ t}α_iλ₀(t). Therefore, given β₀ = β and ${\alpha }_i={\widehat{\alpha }}_i^{[k]}$, the nonparametric maximum likelihood estimator of Λ₀(t) is given by

$${\widehat{\mathrm{\Lambda }}}^{[k]}(t;\beta )=\sum _{i=1}^n{\int }_0^t\frac{d{N}_i(s{e}^{-\beta \prime {\mathbf{X}}_i})}{{\sum }_{j=1}^{n}I\{{\tilde{C}}_j(\beta )\ge s\}{\widehat{\alpha }}_j^{[k]}}.$$

Let ΔΛ̂^[k](t; β) denote the jump of Λ̂^[k](t; β) at t. Due to the fact that ${\sum }_{i=1}^n{\widehat{\alpha }}_i^{[k]}{\widehat{\mathrm{\Lambda }}}^{[k]}\{{\tilde{C}}_i(\beta );\beta \}={\sum }_{i=1}^n{n}_i$, the resulting profile likelihood function of β from (5) is

$$l_{n,2}^{[k]}(\beta )=n^{-1}\sum _{i=1}^n(\sum _{j=1}^{n_i}[\beta \prime {\mathbf{X}}_i+\text{log}\mathrm{\Delta }{\widehat{\mathrm{\Lambda }}}^{[k]}\{{\tilde{T}}_{ij}(\beta );\beta \}]-n_i),$$

which is discrete and can not achieve its maximum with finite values of β as noted by Zeng and Lin (2007) for the nonparametric maximum likelihood estimation in the standard AFT model. Smoothing is needed to approximate maximization. Note that $d{\widehat{\mathrm{\Lambda }}}^{[k]}(t;\beta )={\sum }_{i=1}^{n}d{N}_i(t{e}^{-\beta \prime {\mathbf{X}}_i})/{\sum }_{j=1}^{n}I\{\tilde{C}j(\beta )\ge t\}{\widehat{\alpha }}_j^{[k]}$ and the indicator function I{C̃_j(β) ≥ t} can be approximated by the smooth function ${\int }_{-\infty }^{\{{\tilde{C}}_j(\beta )-t\}/h_n}K(u)du$ as h_n → 0, where K(·) is a smooth symmetric kernel density with bandwidth h_n. Then, given β and ${\widehat{\alpha }}_i^{[k]}’k$, a smoothed nonparametric maximum likelihood estimator of λ₀(t) can be obtained by

$${\widehat{\lambda }}^{[k]}(t;\beta )=\frac{h_n^{-1}{\sum }_{i=1}^n{\int }_0^{\infty }K\{(s-t)/h_n\}d{N}_i(s{e}^{-\beta \prime {\mathbf{X}}_i})}{{\sum }_{j=1}^n{\widehat{\alpha }}_j^{[k]}{\int }_{-\infty }^{\{{\tilde{C}}_j(\beta )-t\}/h_n}K(u)du}-\frac{h_n^{-1}{\sum }_{i=1}^n{\sum }_{j=1}^{n_i}K[\{{\tilde{T}}_{ij}(\beta )-t\}/h_n]}{{\sum }_{j=1}^n{\widehat{\alpha }}_j^{[k]}{\int }_{-\infty }^{\{{\tilde{C}}_j(\beta )-t\}/h_n}K(u)du}.$$

.

Therefore, the smoothed profile likelihood function of β is

$${\tilde{l}}_{n,2}^{[k]}(\beta )=n^{-1}\sum _{i=1}^n(\sum _{j=1}^n[\beta \prime {\mathbf{X}}_i+\text{log}{\widehat{\lambda }}^{[k]}\{{\tilde{T}}_{ij}(\beta );\beta \}]-n_i).$$ (6)

Denote the maximizer of (6) by ${\widehat{\mathrm{\Lambda }}}^{[k+1]}(t)={\int }_0^t{\widehat{\lambda }}^{[k]}(s;{\widehat{\beta }}^{[k+1]})ds$.

From initial estimators Ω̂^[0] = (β̂^[0],θ̂^[0],Λ̂^[0]), we iterate between the E-step and M-step until a pre-determined convergence criterion is satisfied. In our implementation, we chose β̂^[0] = β̂_G, θ̂^[0] = 1. Setting k = −1 and ${\widehat{\alpha }}_i^{[-1]}\equiv 1$ in λ̂^[k](t; β̂^[0]), we obtain Λ̂^[0]. Our limited numerical experience suggests that the proposed EM algorithm is not sensitive to the choice of θ̂^[0] since β̂_G is a consistent estimator of β₀ regardless of the frailty distribution. Denote the estimators of β, θ and Λ(·) at convergence by β̂_n, θ̂_n and Λ̂_n(·), respectively. Following the techniques used by Liu et al. (2013) for studying the kernel-smoothing aided nonparametric maximum likelihood estimation in the AFT frailty model with clustered survival data, it can be shown that under certain regularity conditions, and $n{h}_n^2\to \infty \text{and}n{h}_n^4\to 0$ as n → ∞, the proposed estimators are consistent, and β̂_n and θ̂_n are asymptotically normal and semiparametrically efficient. The proofs are given in the Web Appendix.

To estimate the variance of β̂_n, we use the EM-aided numerical differentiation method proposed by Chen and Little (1999), which numerically computes the empirical Fisher Information matrix of the observed profile likelihood. Specifically, write

$$E\{l_{n,1}^c(\theta )+l_{n,2}^c(\beta ,\mathrm{\Lambda })|𝒪,\mathrm{\Omega }\}=\frac{1}{n}\sum _{i=1}^n{\tilde{l}}_i(\beta ,\mathrm{\Lambda },\theta ).$$

We perturb the jth component of β̂_n by a small value d and denote the pair of perturbed estimates by β̂_n,j− = (β̂_n,1,⋯, β̂_n,j − d,⋯, β̂_n,p) and β̂_n,j+ = (β̂_n,1,⋯, β̂_n,j + d, ⋯, β̂_n,p) for j = 1,⋯, p. Fix β at β̂_n,j− and run the EM Algorithm until convergence. Denote the estimates of Λ and θ at convergence by Λ̂_n,j− and θ̂_n,j−, respectively. Similarly, we can obtain the estimates Λ̂_n,j+ and θ̂_n,j+. For i = 1,⋯, n and j = 1,⋯, p, define

$${\tilde{S}}_{ij}=\{{\tilde{l}}_i({\tilde{\beta }}_{n,j+},{\widehat{\mathrm{\Lambda }}}_{n,j+},{\widehat{\theta }}_{n,j+})-{\tilde{l}}_i({\widehat{\beta }}_{n,j-},{\widehat{\mathrm{\Lambda }}}_{n,j-},{\widehat{\theta }}_{n,j-})\}/(2d).$$

Let S̃_i = (S̃_i1,⋯, S̃_ip)′ and ${\widehat{I}}_n={\sum }_{i=1}^n{\tilde{S}}_i{\tilde{S}}_i^{\prime }$. Then the variance-covariance matrix of β̂_n can be estimated by ${\widehat{I}}_n^{-1}$.

5. Numerical Studies

5.1 Simulations

We generate recurrent events data from the proposed AIF model with two covariates X_i = (X_i1, X_i2)′, where X_i1 follows Bernoulli(0.5) and X_i2 follows uniform [−1,1]. In addition, we consider two frailty distributions: gamma frailty with mean 1 and variance σ₂ = 1/θ and log-normal frailty with mean 1 and variance σ₂ = e_θ − 1; and two functions for Λ₀(t): Λ₀(t) = log(t + 1) and Λ₀(t) = −log[1 − Φ{log(t)}], where Φ is the standard normal cumulative distribution function. We set β₀ = (−1,1)′ and σ₂ = 2, 1 or 0.5 for gamma frailty and 2.32, 1.72 or 0.65 for log-normal frailty. The censoring time C_i’s are generated from uniform [0, τ_c], where τ_c is chosen to yield an average of 2 and 4 events per subject. Given α_i, C_i and X_i, the number of observed recurrent events n_i for subject i is generated from a poisson distribution with mean ${\alpha }_i{\mathrm{\Lambda }}_0(C_i{e}^{{\beta }_0^{\prime }{\mathbf{X}}_i})$. Following similar arguments given inLiang et al. (2009), conditional on (C_i, X_i, n_i), the recurrent event times 0 < T_i1 < ⋯ < T_ini < C_i of subject i are obtained as the order statistics of a set of i.i.d random variables with the joint density function

$$p(t_{i1},\cdots t_{i{n}_i}|C_i,{\mathbf{X}}_i,n_i)=n_i!\prod _{j=1}^{n_i}\frac{{\lambda }_0(t_{ij}{e}^{{\beta }_0^{\prime }{\mathbf{X}}_i})e^{{\beta }_0^{\prime }{\mathbf{X}}_i}}{{\mathrm{\Lambda }}_0(C_i{e}^{{\beta }_0^{\prime }{\mathbf{X}}_i})}.$$

For each scenario, we consider 500 simulation runs with the sample size of n = 100. In our method, we use Gaussian kernel for computational convenience. But other kernel functions, such as Epanechnikov kernel, can also be used. To select the bandwidth parameter h_n, we set h_n = ζn^−1/3 based on the asymptotic results, where ζ is a positive constant. In our simulation study, we find that ζ between 2 and 3 generally works well in all scenarios for the gamma and log-normal frailties. In general, a cross-validation method can be used to select the best ζ.

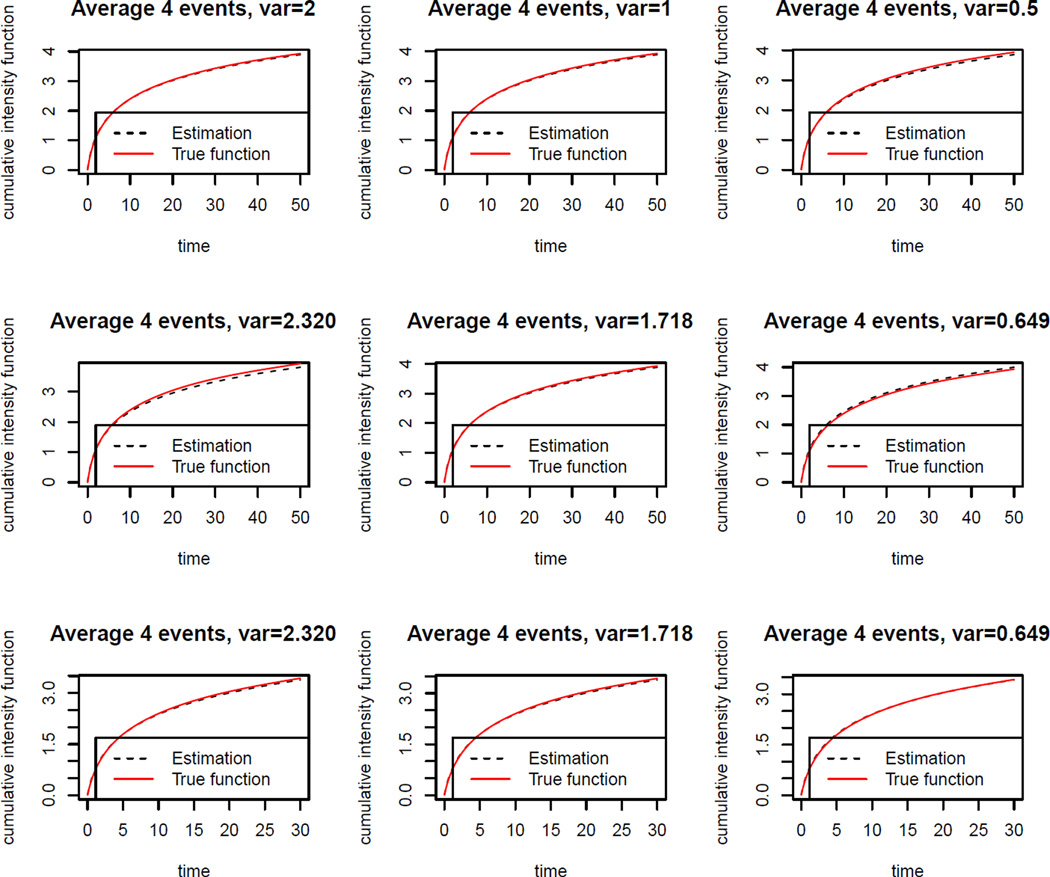
For comparison, we also considered the Gehan rank estimator (denoted by GehanR) proposed byLin et al. (1998). The simulation results are summarized in Tables 1–2. We observe that both estimators for the regression parameters are nearly unbiased under all settings and the averages of estimated standard errors obtained using the proposed EM-aided numerical differentiation method for the NPMLE are close to their standard deviations with the empirical coverage probabilities of 95% confidence intervals close to the nominal level. In addition, the NPMLE is more efficient than the GehanR in almost all cases, and the gain is more substantial when the variance of frailty is big, for example, when σ²=2 for gamma frailty and Λ₀(t) = log(t + 1), the relative efficiency (RE) for β₁ (defined as the sample variance of GehanR divided by the sample variance of NPMLE) is 1.88 and 5.59 for 2 and 4 events per subject, respectively, and it is 2.21 and 7.43 for log-normal frailty with σ₂ = 2.32. This agrees with our expectation since when there is a strong dependence among recurrent event times, by effectively accounting for the association via a frailty, the NPMLE is expected to be more efficient than the GehanR assuming the working independence. Moreover, the biases of the NPMLE for the variance of the frailty are relatively small, especially when the number of events per subject is large. We note that the biases of the frailty variance estimates under the log-normal frailty are relatively larger than those under the gamma frailty, which may be partly due to the numerical integration used in the kernel smoothing based EM algorithm. To assess the estimation of Λ₀(t) using our method, we plot the mean of estimated curves Λ̂_n(t) versus the true curve Λ₀(t), see the first and second rows of Figure 1. For illustration, here we only report the results for the cases with 4 averaged number of events per subject and Λ₀(t) = log(t + 1). It is observed that the estimated curves are close to the true curves for all the settings.

Table 1.

Simulation results for gamma frailty: AVG, average number of events per subject; SD, sample standard deviation; SE, mean of estimated standard errors; CP, empirical coverage probability of 95% Wald-type confidence interval; RE, relative efficiency of NPMLE compared with GehanR.

						NPMLE			GehanR
AVG	σ2	Bias	SD	β	Bias	SD	SE	CP(%)	Bias	SD	RE
Λ0(t)=log(t + 1)
2	2	−0.117	.454	−1	0.096	.502	.482	92.6	0.087	.689	1.884
				1	−0.063	.435	.427	95.4	−0.026	.582	1.790
4	2	−0.056	.358	−1	0.015	.437	.435	93.8	0.137	1.033	5.588
				1	0.008	.388	.388	96.2	−0.070	.907	5.465
2	1	0.006	.217	−1	0.042	.465	.463	96.0	0.001	.514	1.222
				1	−0.036	.392	.414	94.6	−0.025	.450	1.318
4	1	0.002	.191	−1	−0.004	.410	.419	94.6	0.011	.766	3.491
				1	−0.007	.351	.376	96.2	−0.031	.685	3.809
2	0.5	0.087	.150	−1	0.028	.413	.435	94.6	0.017	.454	1.208
				1	−0.025	.359	.386	96.0	−0.031	.380	1.120
4	0.5	0.022	.107	−1	0.023	.383	.401	95.6	0.040	.649	2.871
				1	−0.016	.351	.358	94.8	−0.064	.547	2.429
Λ0(t)=−log{1 − Φ(log t)}
2	2	−0.031	.495	−1	0.085	.321	.336	95.8	0.025	.390	1.476
				1	−0.090	.293	.301	95.0	−0.011	.343	1.370
4	2	−0.025	.399	−1	0.066	.365	.402	95.4	0.049	.470	1.658
				1	−0.038	.330	.349	94.8	−0.007	.405	1.506
2	1	0.051	.242	−1	0.024	.279	.305	96.0	−0.002	.308	1.219
				1	−0.031	.246	.276	96.0	−0.007	.276	1.259
4	1	0.013	.201	−1	0.057	.263	.268	95.2	0.007	.336	1.632
				1	−0.037	.237	.242	94.2	−0.009	.304	1.645
2	0.5	0.093	.158	−1	−0.006	.253	.275	96.2	−0.000	.268	1.122
				1	−0.004	.237	.248	95.6	−0.016	.227	0.917
4	0.5	0.023	.117	−1	−0.003	.248	.241	94.6	−0.012	.293	1.396
				1	−0.011	.209	.215	94.2	−0.010	.240	1.319

Table 2.

Simulation results for lognormal frailty: AVG, average number of events per subject; SD, sample standard deviation; SE, mean of estimated standard errors; CP, empirical coverage probability of 95% Wald-type confidence interval; RE, relative efficiency of NPMLE compared with GehanR.

						NPMLE			GehanR
AVG	σ2	Bias	SD	β	Bias	SD	SE	CP(%)	Bias	SD	RE
Λ0(t)=log(t + 1)
2	2.320	−0.308	.769	−1	0.052	.491	.469	93.4	−0.001	.730	2.210
				1	−0.027	.414	.417	94.6	−0.029	.587	2.010
4	2.320	−0.136	.779	−1	0.046	.398	.460	96.4	0.019	1.085	7.432
				1	−0.022	.367	.411	95.8	−0.025	.876	5.697
2	1.718	−0.121	.572	−1	0.055	.475	.464	94.0	0.003	.663	1.948
				1	0.04	.406	.415	95.2	−0.022	.556	1.875
4	1.718	−0.045	.523	−1	0.016	.406	.410	94.8	0.015	.985	5.886
				1	−0.014	.382	.363	94.0	−0.011	.773	4.095
2	0.649	0.128	.235	−1	0.009	.405	.439	95.4	−0.022	.479	1.399
				1	−0.000	.374	.390	95.8	0.009	.414	1.225
4	0.649	0.061	.189	−1	−0.006	.378	.392	95.8	0.001	.692	3.351
				1	0.028	.344	.346	94.8	0.012	.575	2.794
Λ0(t)=−log{1 − Φ(log t)}
2	2.320	−0.371	.731	−1	0.045	.329	.309	96.0	−0.015	.413	1.576
				1	−0.054	.287	.279	93.2	−0.011	.359	1.565
4	2.320	−0.305	.744	−1	0.052	.337	.337	95.0	−0.009	.506	2.254
				1	−0.018	.299	.297	94.2	−0.015	.413	1.908
2	1.718	−0.153	.572	−1	0.009	.293	.282	93.8	−0.019	.377	1.656
				1	−0.018	.262	.254	94.4	−0.009	.328	1.567
4	1.718	−0.216	.484	−1	0.052	.286	.292	95.0	−0.009	.451	2.487
				1	−0.05	.257	.257	93.6	−0.012	.370	2.073
2	0.649	0.088	.257	−1	−0.009	.281	.272	94.0	−0.02	.296	1.110
				1	0.026	.233	.245	96.4	0.005	.244	1.097
4	0.649	−0.011	.177	−1	0.006	.243	.249	95.0	−0.017	.322	1.756
				1	−0.012	.215	.222	95.6	0.008	.265	1.519

Figure 1.

Estimation of Λ₀(t): the first row is for the gamma frailty, the second row is for the log-normal frailty and the third row is for the misspecified frailty.

Next, we conduct a sensitivity analysis to study the performance of the proposed NPMLE when the frailty distribution is misspecified. Specifically, here the frailty is generated from the log-normal distribution, but the NPMLE is computed based on the gamma frailty in the EM algorithm. The simulation results are given in Table 3. It can be seen that the NPMLE for the regression parameters still shows very small biases that are comparable to those reported in Table 2 when the log-normal frailty distribution is correctly specified, and the means of estimated standard errors are close to the standard deviations with proper coverage probabilities. However, the variance of the frailty is seriously underestimated when the log-normal frailty is misspecified as the gamma frailty. In addition, based on the NPMLE estimates of Λ₀(t) given in the third row of Figure 1, the mean estimated curves are still close to the true curves under the misspecification of the frailty distribution. In summary, the NPMLE shows relatively robust performance to the misspecification of the frailty distribution for estimation of β₀ and Λ₀(·). One possible explanation is that parameters β₀ and Λ₀(·) in the AIF model have the same marginal interpretation as those in the AFT model for counting process (Lin et al., 1998).

Table 3.

Sensitivity analysis results for misspecified gamma frailty distribution: AVG, average number of events per subject; SD, sample standard deviation; SE, mean of estimated standard errors; CP, empirical coverage probability of 95% Wald-type confidence interval.

		Λ0(t)=log(t + 1)						Λ0(t) = −log{1 − Φ(log t)}
AVG	σ2	Bias(σ̂2)	SD(σ̂2)	Bias	SD	SE	CP(%)	Bias(σ̂2)	SD(σ̂2)	Bias	SD	SE	CP(%)
2	2.320	−1.021	.367	0.030	.485	.495	94.6	−0.973	.383	0.019	.313	.331	96.6
				−0.019	.422	.446	95.0			−0.044	.293	.303	94.4
4	2.320	−1.085	.278	0.021	.427	.426	94.8	−1.082	.296	0.033	.322	.348	95.4
				0.005	.392	.384	93.0			−0.017	.285	.308	95.0
2	1.718	−0.632	.294	0.042	.488	.491	93.8	−0.596	.311	0.002	.303	.303	95.2
				0.011	.414	.442	96.8			−0.013	.270	.276	96.2
4	1.718	−0.692	.225	0.014	.419	.420	94.8	−0.678	.242	0.049	.297	.284	94.2
				−0.018	.384	.374	94.2			−0.049	.259	.256	94.2
2	0.649	−0.057	.159	−0.000	.415	.425	95.0	−0.054	.183	−0.013	.286	.271	93.8
				0.012	.388	.381	94.0			0.032	.235	.246	94.6
4	0.649	−0.117	.118	−0.000	.381	.398	96.2	−0.114	.128	0.009	.247	.263	96.4
				0.028	.346	.354	94.8			−0.012	.216	.235	96.2

In addition, we compare our proposed NPMLE with a maximum kernel smoothed pseudo likelihood estimator assuming working independence, denoted by MPSLE. Specifically, to obtain MPSLE, we set α_i ≡ 1, i = 1,⋯, n, in the log likelihood function $l_{n,2}^c(\beta ,\mathrm{\Lambda })$ given in (3), and apply similar kernel smoothing techniques to obtain the smoothed pseudo profile log likelihood function for β. MPSLE of β is the maximizer of the resulting smoothed pseudo profile log likelihood function. We consider the same simulation settings with Λ₀(t) = log(t + 1). The results are given in the Supplementary Materials. Based on the results, we observe that our proposed NPMLE is more efficient than MPSLE for almost all the scenarios, and the efficiency gain is big for the cases with large frailty variance and large average number of recurrences per subject. In addition, MPSLE is generally more efficient than Gehan rank estimator. Finally, we conduct the proposed frailty variance test in Section 3 and consider the same simulation settings with the average number of recurrence per subject as 2. Overall, the proposed test gives reasonable power for both gamma and log-normal frailties, and two choices of baseline intensity functions. For example, for gamma frailty, the power ranges from 0.835 to 0.945, while for the log-normal frailty, it ranges from 0.635 to 0.77. The detailed simulation results are given in the Supplementary Materials.

5.2 Analysis of Bladder Tumor Recurrence Data

We apply our estimation method to a bladder tumor recurrence data from a study conducted by the Veterans Administration Co-operative Urological Group between 1971 and 1976. The study enrolled 118 patients with bladder tumor, who were randomly assigned to one of the three treatment groups, placebo, thiotepa and pyridoxine. As in the analysis conducted byLin et al. (1998), we only focus on two groups, placebo and thiotepa, with the total number of patients n = 86. Among them, 48 received placebo with 87 total recurrences, while 38 received thiotepa with 45 total recurrences. The maximum number of recurrences is 9, but there are 39 patients who never experienced any tumor recurrence in the study duration, showing the big heterogeneity among patients in terms of tumor recurrence, partly due to the differences in covariates and censoring times. The prognostic covariates include treatment (1 if treated with placebo and 0 otherwise), diameter of the largest initial tumor (in centimeters), and number of initial tumors.

Lin et al. (1998) conducted a goodness-of-fit test for the counting process based marginal AFT model, and found no evidence against this model for the bladder tumor recurrence data. To test the dependence of tumor recurrence times after adjusting for baseline covariates, we conduct the test proposed in Section 3 for the null hypothesis H₀ : Var(α_i) = 0. We consider a one sided test with the significance level 0.05 based on 1000 resampled test statistics. The empirical p-value is 0.022, which rejects the null hypothesis and indicates the within-subject dependency of tumor recurrence times even after adjusting for covariates.

Next, we analyze the data using our proposed method with the gamma and log-normal frailties. The corresponding estimators are denoted by NPMLE_g and NPMLE_l, respectively. The bandwidth parameters are chosen as the same as in the simulation study. For comparison, we also compute the Gehan rank estimator, denoted by GehanR. The results are given in Table 4. We observe that the NPMLE_g and NPMLE_l give very similar estimates, which suggests that the proposed NPMLE method for the regression coefficients is not sensitive to the choice of the frailty distribution. The estimated variance of frailty is 0.837 for the gamma frailty and 0.893 for the log-normal frailty. In addition, our NPMLEs give more significant p-values compared to the GehanR, indicating possible efficiency gain by taking into account the association of tumor recurrence times. Both methods find that treatment and number of initial tumors have significant effects on the mean number of bladder tumor recurrences, but initial size does not. In particular, the treatment thiotepa is effective in reducing the mean number of bladder tumor recurrences.

Table 4.

Analysis results for bladder tumor data: Est., point estimates of the regression coefficients; SE, estimated standard errors; pv, p-value of the statistic.

	NPMLEg			NPMLEl			GehanR
	Est.	SE	pv	Est.	SE	pv	Est.	SE	pv
Treatment	0.623	0.274	0.023	0.612	0.244	0.012	0.657	0.314	0.036
Initial number	0.462	0.098	0.000	0.450	0.081	0.000	0.218	0.086	0.011
Initial size	−0.030	0.090	0.739	−0.041	0.078	0.599	−0.022	0.101	0.828

6. Concluding Remarks and Discussions

In this paper, we propose an AIF model for recurrent events data and develop its associated nonparametric maximum likelihood estimation using kernel smoothing based EM algorithm. The numerical studies show that our estimators may have substantial efficiency gain compared to the Gehan rank estimator, especially when the dependence of recurrent event times is strong. Moreover, our limited sensitivity analysis shows that the proposed estimators for regression coefficients and baseline cumulative intensity function are not sensitive to the choice of the frailty distribution. Theoretical properties of the proposed estimators under the misspecification of the frailty distribution need to be further investigated along the line ofKosorok et al. (2004).

In the proposed AIF model, the baseline intensity function is multiplied by a frailty variate to facilitate the developed kernel smoothing based EM estimation. It is also of interest to consider the case that the frailty variate affects the time scale directly. The derivation of the associated nonparametric maximum likelihood estimation will become more challenging and deserve a full investigation. In addition, the frailty distribution in the AIF model needs to be specified in advance. Knowing the frailty distribution can help with the prediction, for example, predicting the next recurrent event time given all the previous recurrent event times and covariates. However, there are relatively fewer works available for determining the most appropriate frailty distribution. Among them available,Choi et al. (2001) proposed an empirical Bayes test for checking the gamma frailty assumption in the multiplicative intensity frailty model. It is an interesting question that warrants our future research.