Change Detection, Multiple Controllers, and Dynamic Environments: Insights from the brain

Abstract

Foundational studies in decision making focused on behavior as the most accessible and reliable data on which to build theories of choice. More recent work, however, has incorporated neural data to provide insights unavailable from behavior alone. Among other contributions, these studies have validated reinforcement learning models by demonstrating neural signals posited on the basis of behavioral work in classical and operant conditioning. In such models, the values of actions or options are updated incrementally based on the difference between expectations and outcomes, resulting in the gradual acquisition of stable behavior. By contrast, natural environments are often dynamic, including sudden, unsignaled shifts in reinforcement contingencies. Such rapid changes may necessitate frequent shifts in the behavioral mode, requiring dynamic sensitivity to environmental changes. Recently, we proposed a model in which cingulate cortex plays a key role in detecting behaviorally-relevant environmental changes and facilitating the update of multiple behavioral strategies. Here, we connect this framework to a model developed to handle the analogous problem in motor control. We offer a tentative dictionary of control signals in terms of brain structures and highlight key differences between motor and decision systems that may be important in evaluating the model.

Prying open the black box of the decision maker to study the brain inside offers the potential to advance our understanding of behavior in situations where the reward contingencies present in their environment change abruptly. By investigating the system responsible for translating environmental inputs into behavioral outputs, we may discover the underlying algorithms responsible for choice behavior and formulate a systematic account of decision making. Indeed, because real agents are biological organisms with behaviors adapted to a broad set of nested and competing goals— from maximization of evolutionary fitness to food intake, reproduction, and competition, to minimization of free energy or motor error or sensory uncertainty (Friston, 2010; Knill & Pouget, 2004; Todorov, 2004; Todorov & Jordan, 2002)—a formulation of decision making in these terms may resolve apparent behavioral paradoxes by subsuming principles like rationality within a more accurately formulated biological optimization framework (Giraldeau & Caraco, 2000; Smith, 1982; D. W. Stephens, Brown, & Ydenberg, 2007; D.W. Stephens & Krebs, 1986).

Among this program’s early successes, the most promising involves the discovery of a neural basis for reinforcement learning models developed in both machine learning and conditioning experiments in animals (Mackintosh, 1974; Pearce & Bouton, 2001; Pearce & Hall, 1980; Rescorla & Wagner, 1972; Sutton & Barto, 1998). In such models, the algorithm attempts to set the value of a relevant parameter in a model of action selection. This parameter may be the associative strength of a cue, for example, or the value of an action. Reinforcement learning models posit that, subsequent to environmental feedback, the relevant parameter, v, should be updated according to

$$v\leftarrow v+\alpha (ṽ-v)$$

where ṽ is the observed value of the parameter and α is a learning rate. That is, when v is predicted and ṽ observed, the algorithm shifts the estimate of v incrementally in the direction of ṽ. In the most common situation, v is the reward value of a given action, and the second term is proportional to the difference between the observed and predicted rewards, the so-called reward prediction error (RPE) (Sutton & Barto, 1998).

In typical learning problems, we are interested in updating V(s), the reward value (summed over all future actions) of the present state of the world, given a model for action selection. Most often, actions are assumed to be selected by examining the options available at s and choosing the one most likely to maximize V(s′), the value in the subsequent state. However, during learning, agents must also explore the space of possible alternative actions, which may yield higher-value outcomes. To do so, they often employ a second system for handling this explore/exploit tradeoff, the “actor” of so-called “actor-critic” theories, which is responsible for translating valuation into action (Sutton & Barto, 1998). By occasionally choosing unknown or undersampled options, the actor computational module gathers information about the rewards accruing to alternative strategies. The critic, a separate computational module, then uses the RPE for these outcomes to update the value function. Over the course of learning, as the critic converges on an optimal behavioral response, the need for exploration diminishes, and the actor simply chooses options that maximize the value function (Rescorla & Wagner, 1972; Sutton & Barto, 1998).

However, more efficient models also adjust learning rates in response to changes in environmental contingencies. Unexpected outcomes may signal a need to renew or accelerate learning, as in attentional theories of conditioning (Pearce & Bouton, 2001; Pearce & Hall, 1980). These theories posit an additional “surprise,” “salience,” or “attentional” signal proportional to the unexpectedness of an outcome, which subsequently increases learning rate. Indeed, both the RPE and the surprise signal are integrated in online Bayesian models of learning like the Kalman filter (Courville, Daw, & Touretzky, 2006; Daw & Courville, 2008; Dayan & Kakade, 2001; Dayan, Kakade, & Montague, 2000).

Mounting evidence suggests that these models, grounded in machine learning and classical and operant conditioning experiments, are instantiated in the brain. Most famously, in studies of single neurons recorded in monkeys performing a classical conditioning task, Schultz and collaborators showed that a RPE signal is encoded in the firing of dopamine-releasing neurons located in the substantia nigra pars compacta and the ventral tegmental area of the midbrain (Schultz, 2007; Schultz, Dayan, & Montague, 1997). That is, these neurons fired in response to receipt of unexpected rewards but only to cues, not receipt, of predicted rewards. More recently, Deisseroth and collaborators have demonstrated that this signal is sufficient for place preference conditioning in mice (Adamantidis et al., 2011; Tsai et al., 2009). In addition surprise-like signals conforming to the assumptions of Pearce-Hall models have been observed in midbrain, amygdala, and cortex (Bromberg-Martin, Matsumoto, & Hikosaka, 2010; Hayden, Heilbronner, Pearson, & Platt, 2011; Roesch, Calu, Esber, & Schoenbaum, 2010). In the cortical case, single neurons in the anterior cingulate cortex (ACC) of monkeys performing a choice task between risky options fired more strongly to unexpected than expected outcomes (Hayden, Heilbronner, et al., 2011). Visual cues informed monkeys of the relative probability of receiving each of two potential outcomes (a large or small reward), with probabilities varied parametrically. As in the case of amygdala, the ACC neurons’ firing was modulated by the surprisingness of the event, whatever the outcome. Received large rewards that were a priori unlikely elicited greater neural activity than those that were a priori unlikely, and the same was true for small rewards. Taken together, these results strongly suggest that neural circuits implement an RL-like algorithm for both learning and action selection.

The necessity of change detection

Despite these advances, it remains abundantly clear that the natural environments in which many decisions are made are not amenable to the most naïve forms of reinforcement learning. In dynamic environments, the underlying values of options may drift, requiring a continual updating of estimates (Behrens, Woolrich, Walton, & Rushworth, 2007; Daw, O'Doherty, Dayan, Seymour, & Dolan, 2006; Pearson, Hayden, Raghavachari, & Platt, 2009). Variability in returns requires that decision makers alter their learning rates—faster for more rapidly changing environments, slower for more static ones—in a way that makes the best use of the available data (Courville et al., 2006; Daw & Courville, 2008; Dayan et al., 2000; Gallistel, Mark, King, & Latham, 2001). When the quantities to be learned are moving targets, more and more sophisticated assumptions about the environment come into play, and the problem of estimating the values of available options becomes a sophisticated problem in optimal filtering.

Furthermore, environments do not always change smoothly and gradually. Sudden jumps in the value of options—for instance, the discovery that a piece of fruit is rotten, or that a nearby bush contains a predator—may drastically alter outcome contingencies associated with particular choices and thus require rapid behavioral adaptation. In such cases, the incremental approach of reinforcement learning may prove maladaptive (Gallistel et al., 2001; Pearson, Heilbronner, Barack, Hayden, & Platt, 2011; Wolpert & Kawato, 1998). A more effective approach may require rapidly shifting between behavioral strategies. Indeed, this is precisely what agents do when confronted with sudden changes (Gallistel et al., 2001; Nassar, Wilson, Heasly, & Gold, 2010). They make an inference (often Bayesian) about the existence of a shift in the environment and switch strategies entirely.

Consider, for example, a situation in which an animal is presented with a pair of options inside an experimental apparatus, perhaps two levers tied to differing reward schedules. Furthermore, assume that the entire apparatus can be configured in two or more states in which the optimal behavioral responses differ. For instance, in one state, both levers may be programmed to yield equal reward every five and every ten presses, respectively (i.e., fixed-ratio schedules, FR 5 and FR 10). In that case, the optimal response is for the animal to ignore the lever associated with the more stringent FR schedule. In the second, state, however, both levers are programmed with variable interval (VI) reinforcement schedules, in which case matching behavior is the reward-maximizing response. Finally, assume that the apparatus shifts between these two reward contingencies unpredictably with a given hazard function, which encodes the probability density of switching in the next moment as a function time since the last switch.

Likewise, in multi-agent competitive situations, animals may be required to change behavioral modes (e.g., producer vs scrounger, hawk vs dove) in response to an opponent’s strategy (Smith, 1982). This may be true either across opponents (when a player’s type is fixed but hidden) or across time against a single opponent, herself capable of adopting multiple behavioral modes. Here in particular, the ability to detect sudden change in the world and react appropriately should prove valuable.

How is an animal to respond? In the first scenario, the most simplistic RL framework simply updates the value of pressing each lever each time the animal receives a reward. The values of the respective levers are updated independently, and each time the state of the apparatus changes, the value of each lever gradually changes via the update equation given above. In other words, each time world changes, the animal begins the process of learning all over again.

But an optimal agent is capable of much better performance. A model-based RL algorithm might learn, for instance, that the values of the levers are strongly correlated and thus learning about one lever yields information about the other. A Bayesian agent might use knowledge of the hazard function and recent outcomes to infer the probability that the underlying state of the apparatus has changed. Indeed, experiments have shown that animals are capable of making rapid changes between behavioral patterns in response to sudden changes in reward contingency, changes much too fast to be based on naïve reinforcement learning (Daw & Courville, 2008; Gallistel et al., 2001). In this case, the animal changes behavior abruptly soon after the change in reward contingencies, close to the performance of an ideal observer.

At issue, of course, is not what performance is mathematically possible, but what performance is possible with biologically plausible online learning algorithms. To a first approximation, the ability to respond to such sudden jumps in the state of the world requires two key ingredients: 1) a set of neural algorithms capable of detecting sudden environmental change and, 2) a set of algorithms for rapidly adjusting behavior. The problem of change detection in response to noisy signals has received significant attention in the statistics literature (Adams & MacKay, 2007; Wilson, Nassar, & Gold, 2010), but the connection with underlying biology remains to be made. As for the second ingredient, there is always the possibility, once change is detected, of increasing the learning rate in an RL algorithm so that only recent outcomes contribute. In general, this will result in faster but noisier learning, with the added disadvantage of throwing away information pertinent to the previous environment. That is, if the previous state of the world ever recurs, a decision maker using this approach would need to relearn her behavioral response to each set of environmental contingencies from scratch.

Alternatively, agents could learn multiple, separately maintained strategies, with the option of switching between them as conditions warrant. Such a system would have the advantages of rapid adaptation to environmental change and access to well-learned, specialized systems on demand, albeit with the computational burden of updating, storing, and selecting among the multiple models. An algorithm for precisely such a system, called MOSAIC (Wolpert & Kawato, 1998), has been proposed for optimal motor control. Here we review data on the anatomical substrates of change detection and then propose a tentative identification of elements of the MOSAIC model with neural circuits within the brain.

Change detection in the brain

Clearly, if change detection comprises a core competency for decision makers in dynamic and uncertain environments, change detection algorithms should be instantiated within the brain. However, the problem of change detection is embedded within the larger problem of learning, for which we have a better understanding of the underlying biology. In broad strokes, learning is known to depend crucially on the basal ganglia, particularly the ventral striatum/nucleus accumbens (Balleine, Liljeholm, & Ostlund, 2009; Graybiel, Aosaki, Flaherty, & Kimura, 1994; Knutson, Adams, Fong, & Hommer, 2001). The basal ganglia are thought to filter wide-ranging inputs from cortex for conjunctions of signals relevant for triggering learned behaviors, and for implementing these behaviors by modulating cortico-basal ganglia-thalamo-cortical loops (Houk & Davis, 1994). In addition, other brainstem structures such as the VTA (Schultz, 2007), habenula (Matsumoto & Hikosaka, 2007), and the rostromedial tegmental nucleus (Hong, Jhou, Smith, Saleem, & Hikosaka, 2011) are known to be part of a circuit responsible for processing rewards, aversive outcomes, and prediction errors (Bromberg-Martin et al., 2010), while the amygdala carries salience signals useful for adjusting learning rates (Roesch et al., 2010; Schoenbaum, Chiba, & Gallagher, 1998). In the cortex, dopaminergic signals project primarily to frontal areas, in particular orbitofrontal and anterior cingulate regions, thought to be important for cue-related prediction (Schoenbaum, Roesch, Stalnaker, & Takahashi, 2009) and action valuation (Amiez, Joseph, & Procyk, 2006; Kennerley, Behrens, & Wallis, 2011; Kennerley, Walton, Behrens, Buckley, & Rushworth, 2006; Wallis, 2011), respectively. More lateral prefrontal regions are thought to implement executive control functions, including strategic decision making (Barraclough, Conroy, & Lee, 2004; Bechara, Tranel, & Damasio, 2000; Venkatraman, Payne, Bettman, Luce, & Huettel, 2009). Though the overall picture remains incomplete, these regions are all known to make important contributions to the learning of simple action patterns and outcome associations.

Yet the question of which, if any, brain structures contribute to change detection and consequent switching between behavioral modes has received comparatively little attention, probably due to the difficulty of characterizing behavior in dynamic environments (Behrens et al., 2007; Daw, O'Doherty, et al., 2006; Gittins, 1979; Whittle, 1988). A handful of experiments have implicated frontopolar regions (hypothesized to sit atop the executive hierarchy (Boorman, Behrens, Woolrich, & Rushworth, 2009; Christoff & Gabrieli, 2000; Soon, Brass, Heinze, & Haynes, 2008; Tsujimoto, Genovesio, & Wise, 2011)) and posterior midline regions (Behrens et al., 2007; Daw, O'Doherty, et al., 2006; Pearson et al., 2009) in behavioral adjustment in the face of continuously changing reward contingencies, with these regions more active in cases of exploratory behavior. More generally, one of these regions, the posterior cingulate cortex (CGp), is thought to be involved in the type of inwardly-directed cognition necessary for long-term strategic planning (Gerlach, Spreng, Gilmore, & Schacter, 2011; Leech, Braga, & Sharp, 2012; Spreng, Stevens, Chamberlain, Gilmore, & Schacter, 2010).

In a recent work (Pearson et al., 2011), we reviewed evidence for the hypothesis that CGp is part of a circuit involved in detecting environmental change and signaling the need for commensurate changes in behavioral mode. As work in non-human primates has shown, CGp firing rates encode a filtered sum of rewards received over the last several trials (Hayden, Nair, McCoy, & Platt, 2008), encode the volatility of uncertain rewards in monkeys choosing between risky and safe options (McCoy & Platt, 2005), and signal exploratory versus exploitative choices in a task with dynamically changing rewards (Pearson et al., 2009). Moreover, when CGp neurons are electrically stimulated, this causes a switch in choice preference from preferred to less preferred options (Hayden et al., 2008). In each case, across a variety of value-based decision tasks, CGp encodes a key variable necessary to reallocating behavior, and stimulation of this area plays a causal role in effecting behavioral change. All of this is commensurate with a role for CGp in accumulating evidence of environmental change and signaling a need to alter behavioral mode. In keeping with numerous theories of change detection, we hypothesized that this signal might represent the log posterior odds of a shift in the underlying environment, a Bayesian measure of confidence in the brain’s current model of the world (Pearson et al., 2011). In our model, the anterior cingulate cortex captures local, moment-to-moment information about outcomes, and this information is subsequently maintained online and filtered by CGp. Unexpected outcomes contribute evidence for a change in the outcome contingencies of the environment, with multiple such outcomes resulting in a change in behavior. Below, we examine a previously published model for how multiple such strategies may be learned and adjudicated, suggesting a potential correspondence between brain areas in our model and components of the learning algorithm.

Multiple controllers for flexible behavior: the MOSAIC model

As we have noted above, the need for rapid adaption to changing environmental contingencies argues for the inadequacy of a single incremental system implementing reinforcement learning to account for all behavioral change. This holds true not only for decision making, but for the systems responsible for motor control, where the timescale of behavioral adjustment is often much faster. Here again, the suggestion that the brain maintains multiple strategies or control systems, with the option of switching between them as evidence warrants, forms the basis for a compelling proposal, which Wolpert, Kawato, and collaborators dubbed “modular selection and identification for control” (MOSAIC) (Haruno, Wolpert, & Kawato, 2001,2003; Sugimoto, Haruno, Doya, & Kawato, 2012; Wolpert & Kawato, 1998). In MOSAIC, the brain maintains and learns multiple control modules for movement, each to be implemented under a broad set of conditions.

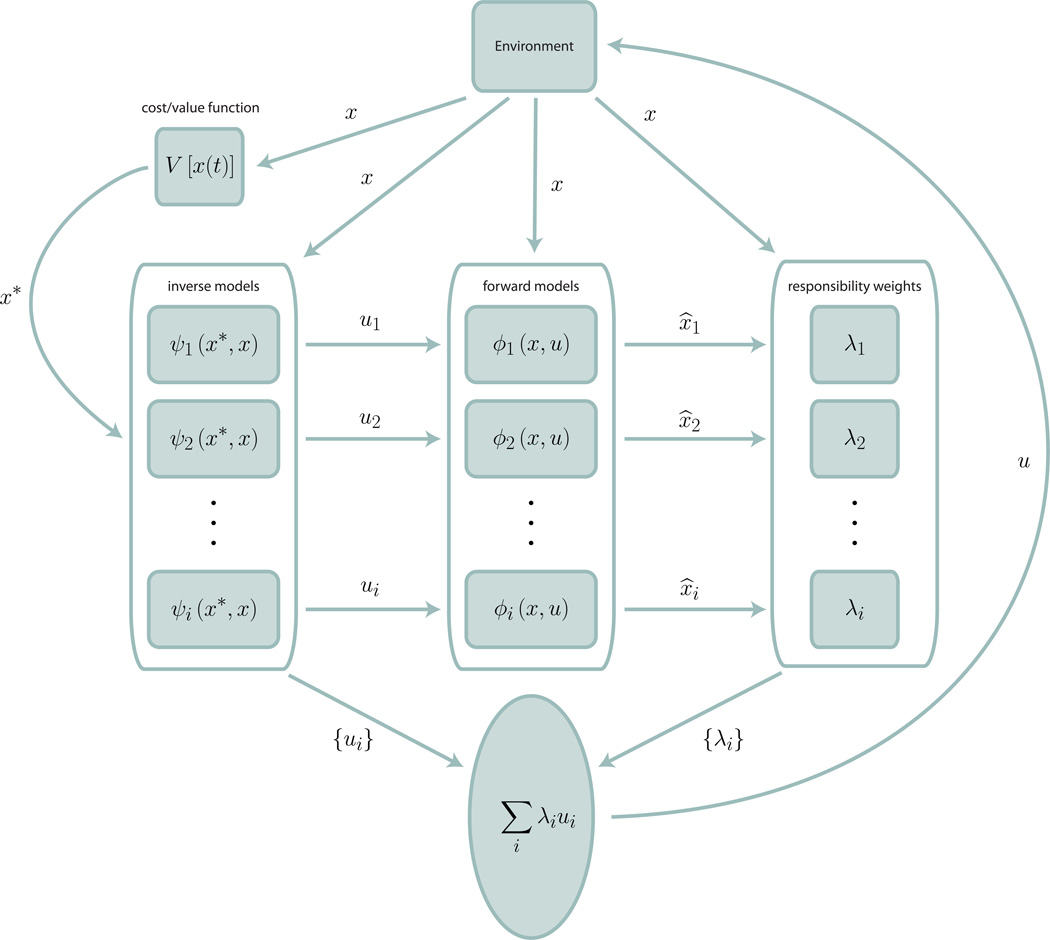
Figure 1 shows a schematic of this computational process. More specifically, for each module, given a state of the world represented by the vector × and a control signal given by u, both at time t, we have both a forward model for how the system evolves

$$x_{t+1}=\varphi (x_t,u_t)$$

and an inverse model for control given a desired state of the system, x*

$$u_t=\psi (x_{t+1}^{*},x_t)$$

such that the two are inverses of one another:

$$x_{t+1}^{*}=\varphi (x_t,\psi (x_{t+1}^{*},x_t))$$

Figure 1.

The MOSAIC control model. In MOSAIC, multiple forward and inverse models, corresponding to multiple systems of control, combine to produce a single control signal, u. Control signals u_i from the various inverse models are combined according to responsibility weights λ_i, which are calculated from the discrepancy between the observed state of the environment, x (that is, all available sensory information, plus reinforcement from the environment) and each model’s prediction, x̂_i. These weights represent a confidence in the applicability of each model to the current state of the environment, and apportion learning across the different models (not pictured). This scheme allows for simultaneous learning of and rapid switching between multiple control systems.

That is, for each control module—in our case, behavioral mode—agents both make predictions about the environment’s response to their actions and the necessary actions required for desired environmental responses. The rat presented with two levers in an apparatus in one of two possible states behaves as if making predictions for each lever for each possible state, and determines which actions are most likely to lead to maximal reward given current evidence for each state of the apparatus.

In practice, the desired state of the system is determined by minimizing some cost function (equivalent to maximizing the value function in typical RL models), and modules are learned by performing gradient descent on the parameters of the forward model:

$$\delta w\propto -(\mathrm{x̂}-x)·{\nabla }_w\varphi$$

where x̂ is the prediction of the forward model and x is the measured state of the environment. In other words, the animal adjusts its behavior incrementally in the direction of improved prediction.

The key idea behind MOSAIC is that all such models learn and operate simultaneously. This is done through the assignment of a responsibility weight λ to each model, encapsulating an internal estimate of confidence in that model’s predictions:

$$\lambda =\frac{e^{-{|x-{\mathrm{x̂}}^i|}^2/{\sigma }^2}}{{\sum }_i{e}^{-{|x-{\mathrm{x̂}}^i|}^2/{\sigma }^2}}$$

That is, λ is determined by a normalized error measurement between the observed state of the world (sensory evidence, reward rates, etc.) and each model’s prediction. In a Bayesian context, this responsibility weight may be defined as a posterior confidence in the correctness of each model, updated as new data are observed. These weights can then be used to make averaged predictions (x̂ = ∑_iλ_ix̂ⁱ) and control signals (u = ∑_iλ_iuⁱ) across models and thus differentially update models according to their applicability to the current environment:

$$\delta w_i\propto -{\lambda }_i({\mathrm{x̂}}^i-x)·{\nabla }_w\varphi$$

In this way, models that do not accurately predict the dynamics of the current environment are minimally updated, while models that apply in the current context are more strongly updated. Thus, model switching and model learning happen within the same prediction error framework, which can be given a Bayesian formulation in terms of optimal inference about the world (Friston, 2011; Todorov, 2004; Todorov & Jordan, 2002; Wolpert & Kawato, 1998).

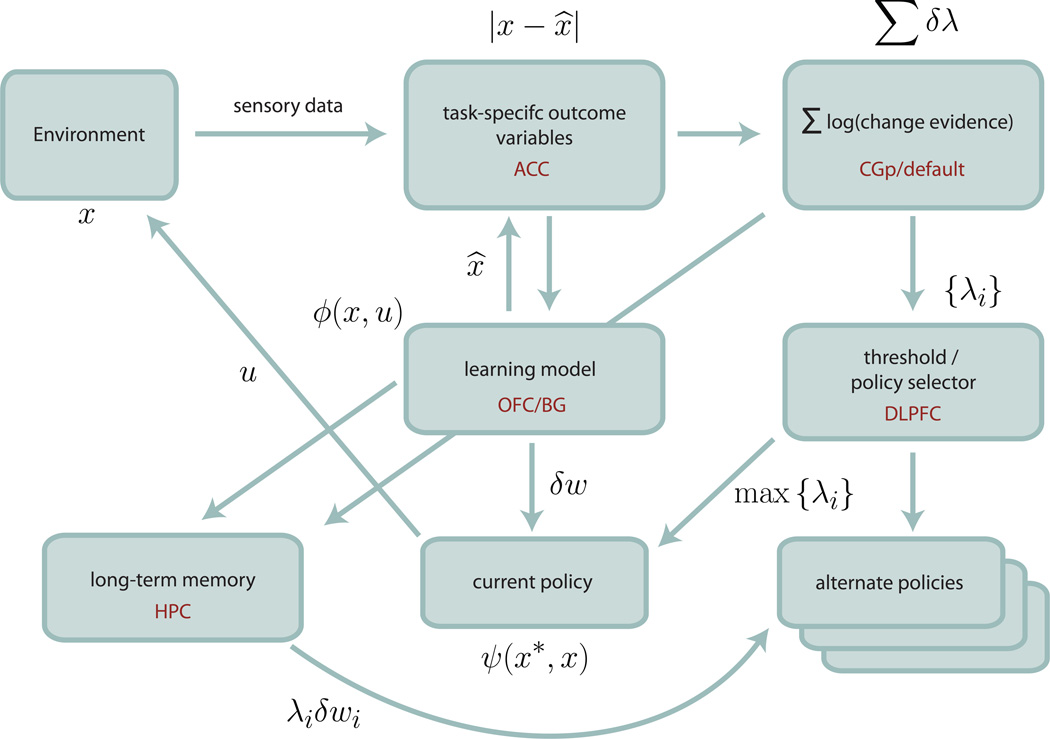
The MOSAIC formulation provides a natural formalization of our change detection model, as illustrated in Figure 2. (Pearson et al., 2011). Predictions of environmental states and rewards take the place of limb positions, with prediction errors (signed and unsigned) encoded in ACC. These errors are accumulated across trials in CGp, in a signal that can be viewed as useful for incremental updating of the responsibility weight. In other words, the accumulated errors across trials track the change in model confidence associated with a shift in the underlying environment. Moreover, these signals should gate learning by apportioning the RL update of model parameters in accordance with responsibility weight, potentially through modulatory connections with parahippocampal gyrus.

Figure 2.

A multiple controller model of decision making. Sensory feedback from the environment is divided into task-specific variables, which are compared with forward predictions to form errors, |x − x̂|. These errors are used to both update the currently active policy (δw) and the responsibility weights for both the current an alternative models δλ_i. Change detection corresponds to the accumulation of sufficient error from the current policy (∑δλ), which results in the selection of a new control module corresponding to maximum responsibility weight. Tentative identifications for the anatomical substrate of model elements are listed in red, though each component is likely to involve multiple regions, and a given region may be associated with multiple functions.

In the case of the rat confronted by a pair of levers, in an apparatus in one of two states, MOSAIC predicts that with each lever press, the rat behaves as if making a prediction for the outcome of the lever press for each of the two states, weighted by an estimate of the probability that each state obtains. At the neural level, ACC signals the difference between expectation and result for individual trials, while CGp accumulates this information, analogous to the responsibility weight. As evidence for an environmental shift builds, CGp firing should increase, with behavior shifting between modes when this firing reaches a critical threshold. Thus activity in the change detection circuit should precede a behavioral switch, as suggested by results in previous studies (Hayden et al., 2008; Pearson et al., 2009).

However, several key differences complicate the adaptation of MOSAIC from motor to decision systems. First, because the neural distinction between motor planning and output and the decision process is poorly understood at present. Neural representations for pure value and for value as tied to specific movements may overlap to varying degrees in separate neural circuits. Second, and more clearly for our purposes, the primary inference problem in motor control is that of effecting a desired movement, apart from its reward value. The key unknown is the physics of the object being manipulated, not the cost function determining efficient muscle movement, which is taken as given. In most decision-making formulations, however, we are interested in costs apart from the motor outputs that make decisions manifest, and it is the value function of different actions that changes between environments (though the forward Markov model governing state transitions may also change). Fortunately, MOSAIC can also adapt to multiple cost functions, successfully transitioning between them (Sugimoto et al., 2012). More importantly, while CGp neurons do appear to encode outcomes across multiple trials, they also appear to react more strongly to violations of expectation than would be anticipated from a gradual transition from one model to another. This suggests either a very small region of overlap in model predictions, a low tolerance for errors when making inference (small σ²), or perhaps both. Indeed, such rapid shifts in beliefs are often the result of Bayesian, rather than gradient descent, inferences (Gallistel et al., 2001).

More intriguing, however, may be the contrast between the predictions of MOSAIC for motor control and our application of its formalism to decision making. By now, it is well known that subjects performing many perceptual and simple motor tasks exhibit Bayesian-like inference (Braun, Ortega, & Wolpert, 2009; Gold & Shadlen, 2007; Raposo, Sheppard, Schrater, & Churchland, 2012; Trommershäuser, Maloney, & Landy, 2008), but in simple decision tasks involving probabilities given in mathematical or written form produce strong departures from optimality (Gigerenzer & Selten, 2002; Gilovich, Griffin, & Kahneman, 2002; Trommershäuser et al., 2008). Furthermore, while the graded nature of muscular control may allow for composition of control signals from different models (weighted by responsibility weights), the discrete nature of many choice paradigms renders this process latent, at best. Lastly, working memory, attentional, or other representational constraints may also limit the number of models that may be effectively tracked or evaluated. Together, these factors lead us to conjecture that a MOSAIC-like model for decision making might strongly limit the number of nonzero responsibility weights, in much the same way that cue competition enforces parsimony in classical conditioning (Gallistel & Gibbon, 2000). In this case, models would need to be evaluated one (or perhaps two) at a time, in a manner more akin to hypothesis testing. Such a constraint would represent a key difference between decision and motor or perceptual systems.

Discussion

We have proposed an identification of major components of the brain’s system for decision making with elements of MOSAIC, a modular model of control. The learning processes necessary to adaptive decision making face many of the same issues as those of motor control, including the need to maintain and refine multiple controllers for a variety of tasks and environments, and MOSAIC offers a convenient formalization of and solution to this dilemma. We suggest that cingulate cortex plays a key role in signaling both feedback from actions and model confidence, and in particular that the posterior cingulate cortex plays a key role in the switch between models and modulation of learning in the face of changing environmental contingencies. We also propose, in contradistinction to multi-module accounts of motor control, that decision systems suffer from a cognitive bandwidth limit on the number of models that may be countenanced or simultaneously updated. Thus, while sensation and movement may often exhibit Bayesian integration over models, many cognitively demanding decisions do not. Such a suggestion was also recently made in a model of learning in open and dynamic environments, where it was proposed that only a few models, perhaps four or fewer, could receive simultaneous consideration, with only the highest posterior probability model updated by learning (Collins & Koechlin, 2012).

Testing these theories presents a challenge for neural studies of decision making. Most decision tasks consist of repeated choices of a few types and are essentially static. More dynamic tasks (Daw, Courville, & Touretzky, 2006; Nassar et al., 2010; Pearson et al., 2009) are difficult to analyze and may not have known optimal solutions. But tasks capable of studying dynamic decision making should clearly satisfy some key conditions. First, they must exhibit reliable behavioral control, regular enough to be modeled mathematically (Gold & Shadlen, 2007; Hayden, Pearson, & Platt, 2011). Second, they must require inference about environmental change of a nontrivial type, which poses a training challenge for non-human subject. Finally, they must require the implementation of multiple decision strategies unique enough to be disambiguated behaviorally.

Nevertheless, dynamic decision making forces us to confront the brain in its most natural functional context. By focusing on the feedback and control aspects of decision algorithms, we stand to learn much more about the interacting networks that give rise to its most flexible processing, as well as its most intriguing cognitive phenomena.