Identifying ligand binding sites and poses using GPU-accelerated Hamiltonian replica exchange molecular dynamics

Abstract

We present a method to identify small molecule ligand binding sites and orientations to a given protein crystal structure using GPU-accelerated Hamiltonian replica exchange molecular dynamics simulations. The Hamiltonians used vary from the physical end state of protein interacting with the ligand to a unphysical end state where the ligand does not interact with the protein. As replicas explore the space of Hamiltonians interpolating between these states the ligand can rapidly escape local minima and explore potential binding sites. Geometric restraints keep the ligands within the protein volume, and a potential energy pathway designed to increase phase space overlap between intermediates ensures good mixing. Because of the rigorous statistical mechanical nature of the Hamiltonian exchange framework, we can also extract binding free energy estimates at all putative binding sites, which agree well with free energies computed from occupation probabilities. We present results of this methodology on the T4 lysozyme L99A model system with four ligands, including one non-binder as a control. We find that our methodology identifies the crystallographic binding sites consistently and accurately for the small number of ligands considered here and gives free energies consistent with experiment. We are also able to analyze the contribution of individual binding sites on the overall binding affinity. Our methodology points to near term potential applications in early-stage drug discovery.

II. INTRODUCTION

Determining small molecule binding sites and bound poses is an important part of the drug discovery process. When the co-crystal structure of a lead compound is unavailable, rationalizing affinity changes in a lead compound series and designing molecules with improved binding can prove challenging. Even when the binding site is known, additional sites with varying druggability may exist, and targeting these alternative sites may produce desirable biological responses and hence provide new opportunities for drug discovery.

With rapid development in processing power and molecular simulation algorithms, computational methods are now playing an important role in predicting protein-ligand binding properties, especially in early-stage drug discovery. Docking methods, the most widely used class of structure-based drug design methods, aim to rapidly generate a comprehensive set of conformations of the protein-ligand complex and rank them using scoring functions with varying complexity and accuracy. Though docking methods can quickly rank and often identify binding locations and poses, the accuracy of docking is limited by a number of factors, including the effectiveness of semi-empirical scoring functions, the difficulty of including solvation effects, and the difficulty of representing a statistical mechanical ensemble with one or a few configurations. Docking is therefore problematic in projects requiring detailed and reliable knowledge of ligand binding location and its interactions with the target in the binding pocket [1].

A number of studies have worked to fix many of these issues. Some studies have successfully improved docking methodologies by introducing receptor flexibility [2], explicit water molecules [3], or even using post-docking methods to rescore the entire complex ensemble [4, 5]. Nevertheless, as shown by studies evaluating and comparing different docking programs, their intrinsic limitations, such as a low level of physical detail and lack of statistical mechanical sampling, make them unable to consistently identify ligand binding sites and poses [6–8]. Other structure-based drug design methods that are specifically designed for identifying binding sites based on geometric properties [9–11] or that are knowledge-based [12–14] have also been used with varying success, but these methods are only useful when the sites are well-defined pockets. Moreover, extensive usage of fitted models and parameters makes them less reliable for systems for which they were not parameterized.

In contrast with the cheap but approximate docking methods to study protein-ligand binding are more rigorous, physical-based techniques such as molecular dynamics (MD) and Monte Carlo (MC) simulations, which historically have been used much less commonly in the drug design process because of their expense. With an all-atom representation of the protein and potentially explicit solvent, MD simulations can provide microscopic information about protein-ligand interactions, predict and calculate properties based on statistical averages of an ensemble of conformations, and have been shown to be capable of accurately predicting binding affinities in model systems [15–17]. In theory, MD simulations of a protein with a known ligand will eventually converge to the true distribution of bound structures if run sufficiently (though impractically) long with an accurate force field. Free energy calculation methods [18] can then in principle be used to either decide between the predicted poses or compare them with experimental data.

In reality, optimizing these simulation tools individually and assembling them together to produce useful predictions on a timeline consistent with a realistic drug design pipeline is still an unsolved problem. The rapid development of computer power and techniques such as GPU-accelerated simulations [19, 20], increasingly accurate biomolecular force fields [21–23] and implicit solvent models [24–26] and even simulation machines designed specifically for MD simulations [27, 28] may have made these problems much more amenable to computation. However, many issues must still be addressed to enable simulations of sufficient accuracy to be useful in drug design or discovery. Among these issues, poor or insufficient sampling is undoubtedly the most stubborn one [29]. A ligand in an MD simulation can easily become kinetically trapped for long periods of time, effectively preventing it from visiting the relevant parts of conformational space. This leads to incorrect sampling of the ensemble and results in the computed binding affinities or observed binding modes that are sensitive to the initial configuration. In fact, without adequate sampling, even a perfect force field would be of limited use. As argued by Mobley [29] in a recent review, we are still running unconverged simulations with unsampled configurations on a daily basis, hoping that the unsampled ones are not essential to ligand binding or other events of interest. Overcoming this sampling problem could lead to direct use of more physical methods to understand and predict small molecule binding.

Because of these computational limits, knowledge of the binding site is usually a prerequisite in standard ligand binding free energy calculation methods. A crystal structure of a related small molecule or, alternatively, a putative initial structure generated by docking tools is often used as the starting configuration to increase the likelihood that the free energy calculations can at least converge within the binding site. However, with the increased simulation power and improved simulation tools, may directly physical molecular simulation techniques be used to identify the ensemble of binding locations and poses both accurately and relatively quickly without the prior knowledge of the binding site? Using cheaper docking-based tools and other structure-based drug design methods are options to create a binding ensemble [30], but in many cases the emphasis on making the process fast discards the physics required to obtain properly weighted ensembles.

In this study, we investigate whether sufficiently optimized accelerated MD simulations in implicit solvent can discover binding sites and binding modes without prior knowledge of the binding site, even in a highly buried binding pocket. Many studies have investigated enhanced sampling methods for accelerating the rate at which MD can sample relevant conformations [31–37], and we focus specifically on Hamiltonian replica exchange molecular dynamics (HREMD) in this paper. In Hamiltonian replica exchange methods, individual replicas can visit a range of predefined Hamiltonians during the course of a simulation, with pairs of replicas accepting proposed exchanges of Hamiltonians according to a modified Metropolis criterion. The convergence properties of the system can vary drastically with different Hamiltonians, allowing kinetic barriers present in one Hamiltonian to be avoided in another Hamiltonian if a proper set is designed.

HREMD has been proven to improve sampling in free energy calculations over the use of independent simulations at fixed Hamiltonians [32]. However, because of the large gap between the time scale that current computers can achieve and the time scale of most relevant biomolecular motions, we must further optimize HREMD [38] or combine it with other enhanced sampling methods to fully explore the biophysical configurations of interest in protein-ligand binding. We accelerate sampling beyond that typically achieved by HREMD, without sacrificing thermodynamic accuracy, by restraining the uncoupled ligand to the vicinity of the protein by a flat-bottom potential in all states, using multiple coupled and uncoupled states, Monte Carlo simulation techniques, and GPU-accelerated molecular dynamics with the OpenMM toolkit [20, 39]. Because of the rigorous statistical mechanical nature of the Hamiltonian exchange framework, we can also extract binding free energy estimates at all putative binding sites using the multistate Bennett acceptance ratio (MBAR) algorithm [40].

The methodology presented here has many similarities to that used by Gallicchio et al. in the Binding Energy Distribution Analysis Method (BEDAM) [41], in that Hamiltonian replica exchange in an implicit solvent system is used to enhance sampling. However, in our case no binding site is assumed, the Hamiltonian is designed to explicitly maximize phase space overlap between replicas, and no restraints are placed on the protein. A number of other less conceptually central sampling enhancements are also added as discussed below.

To test the methodology presented in this paper, we examine a model protein-ligand binding system consisting of the engineered L99A mutant of T4 lysozyme and a series of small aromatic ligands. This model system has been widely used by a number of researchers to test the accuracy of free energy methods [15, 16, 42]. T4 lysozyme L99A has a small, buried, hydrophobic internal pocket that has proven to be a difficult target for a number of docking methods [43–46]. Importantly, the crystallographic binding structures and binding free energies are well characterized for this system, allowing us to directly validate our methodology.

III. THEORY AND COMPUTATIONAL METHODS

A. System preparation

Protein parameterization

The T4 lysozyme L99A benzene-bound structure (PDB accession code 181L) was used for this study. The protein was parameterized with the AMBER parm96 forcefield [23] using LEaP from the AmberTools11 [47] (chosen to be consistent with previous studies of this system) [15].

Ligand parameterization

Ligand structures were created from IUPAC names using the OpenEye OEChem toolkit (version 2.3.2). Mobley et al. have shown that the semi-empirical quantum mechanical AM1-BCC charge model [48, 49] for small molecules works almost as well as ab initio methods in calculating binding free energies for implicit systems [50]. This treatment was used to derive charges for the ligand, and the other parameters were assigned from AMBER GAFF force fields [23, 51] using the ANTECHAMBER package [52].

B. Docking

To compare the performance of traditional docking methods and our methodology, AutoDock (version 4.2) was used to dock the same four ligands to the protein [53, 54]. Each ligand was docked twice, once with an entirely rigid protein and once with three flexible residues, Val111, Val103 and Leu118. The three flexible residues were chosen based on their reorientation observed in X-ray structures in response to ligand binding previously reported [15]. All docking was performed to the same PDB structure 181L, the co-crystal of the mutant with benzene. The protein for rigid and flexible docking was prepared according to standard AutoDockTools procedures, adding hydrogens to the original files and assigning Gasteiger partial charges. The AutoDock default grid spacing was used, with the grid box sizes for all docking set to be the box size, which effectively covers the entire protein volume. The number of genetic algorithms runs was set at 50, resulting in 50 final poses.

This setup is only partially blind, as the bound structure used is the actual crystal structure for one of the four ligands, so there is some degree of preorganization of the docking site for a bound ligand. Additionally, in the case of the flexible docking, only the residues which are known to potentially move in alternate crystal structures were made flexible. This therefore represents in many ways a best case scenario for docking.

C. Simulation Methodology

The HREMD-based simulations utilized a modified version of the open-source Python alchemical free energy code YANK, which is built on the OpenMM GPU-accelerated molecular simulation library [20, 39]. We performed our simulations using a generalized Born (GB) implicit representation of water [25]. A Langevin dynamics integrator with a 2 fs time step and a 0.1 ps⁻¹ collision frequency was used, with a bath temperature of 298 K, and bonds to hydrogen were constrained by the CCMA method [55]. A flat-bottom restraint was implemented to keep the ligand in the vicinity of the protein while allowing it to sample in an unbiased way all spatially available and physically reasonable conformational space consistent with binding. The specific choices made for this potential are described below. Hamiltonian replica exchange [32] was used to improve sampling, along with a number of improvements described below. Simulations were run on GPU computing resources provided by XSEDE, including the NCSA Forge and Lincoln clusters.

All preliminary tests of simulation parameters and the 10-fold replicate test of simulation consistency were performed with 1-methylpyrrole, a known binder. The ability of our approach to differentiate binders from non-binders was then examined by introducing another three ligands: benzene, a small binder, p-xylene, a larger binder which requires conformational change of Val111, and phenol, a nonbinder, as a control [15]. By using p-xylene, the ability of the method to sample all relevant biomolecular motions of the protein can be examined. The system used in our simulations is shown in Fig. 1.

FIG. 1. Protein system and small molecule ligands used in this study.

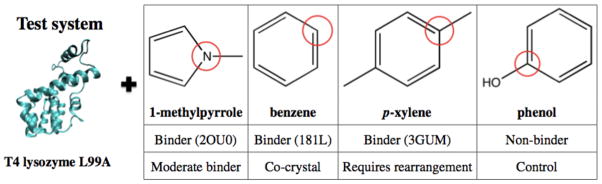
The T4 lysozyme L99A and four ligands, including one non-binder were examined. The ligand atoms closest to the centroids, used to define the location of the ligand in subsequent analysis, are circled in red.

With sufficient sampling of all relevant binding states, the simulations here can also be used to calculate the protein-ligand free energy of binding. For this purpose, we additionally performed HREMD simulations of the ligand alone, in implicit solvent, with the same parameters as described above.

Flat-bottomed restraint

It is common in free energy calculations to use restraints to keep the ligand close to the putative binding site, especially in alchemical states that have weakened interactions with the protein [56, 57]. These restraints prevent the ligand from drifting through the simulation box, a process which has very long correlation time. In our case, we use the tendency of the uncoupled ligand to wander to our advantage in order to identify new binding sites. A restraint to a single binding site would defeat this objective. However, we still wish to keep the ligand near the protein, as the time the ligand spends in the solvent is not of interest. We therefore used a flat-bottomed restraint to keep the ligand close to the protein, as the implicit solvent treatment would otherwise allow the ligand to drift off. A flat potential was used inside a cutoff radius (r₀) with harmonic restraining walls outside of this radius, using the equation:

$$U(r)=\{\begin{array}{ll}0\hfill & \text{if}r\le r_0\hfill \\ \frac{1}{2}k{(r-r_0)}^2\hfill & \text{if}r>r_0\hfill \end{array}$$ (1)

where U(r) is the restraining potential, k is the spring constant, r is the distance between the protein and ligand centers of geometry, and r₀ is the cutoff radius.

We set r₀ at half the maximum distance between protein atoms plus a 5 Å buffer so that the entire protein with a buffer zone for surface binding sites was within the cutoff. We set the spring constant k = 5.92 kcal/mol/Ų, such that at 1 Å away from the cutoff, the potential energy rises to 5k_BT. This minimizes the amount of time the ligand spends away from the protein. In this case, we obtain a cutoff of 35.34 Å from the center of the protein for this system. This restraint is present regardless of the degree the ligand is coupled to the protein. We validated our flat-bottom restraint and integration scheme for physical consistency as described in the Supporting Information. In the case of a less spherical protein, the amount of time spent sampling configurations away from the protein surface could be minimized using a more complicated shape such as an ellipsoid constrained along the protein axes.

Hamiltonian replica exchange molecular dynamics (HREMD)

In MD simulations of protein-ligand complexes, ligands are highly likely to get kinetically trapped in local minima in the free energy surface, potentially for tens of microseconds. [58, 59] These trapping events prevent the ligands from visiting other potential binding sites. Our proposed solution to this problem is to use Hamiltonian replica exchange molecular dynamics (HREMD) between coupled and uncoupled ligand states. Typically in HREMD, N copies of simulations at different intermediates along the coupling pathway are run in parallel, with Monte Carlo exchanges between neighboring replicas. This process allows sampling at one Hamiltonian state with short correlation times to be shared by exchange with other Hamiltonians with longer correlation times. In our particular implementation, starting the fully interacting state, charges are first scaled to zero, followed by removing the Lennard-Jones interactions between ligand and protein through soft-core potentials [60–62], leaving an uncharged molecule decoupled from the protein at the other end state. Replicas are periodically swapped (exchanged) using the standard Metropolis criterion. The state of physical interest is fully coupled state, in which all protein-ligand interactions are turned on. However, by including partially and fully uncoupled states in our simulation we allow the ligands to escape from kinetically trapped states, such as nonspecific binding minima, on the time scale of tens or hundreds of picoseconds rather than microseconds. Here, we use a Langevin integrator, but in principle the integrator of user’s choice can be used to perform the MD (or alternately, MC).

In order to efficiently discover putative ligand binding sites and geometries when such information is unavailable, we made a number of modifications to the standard Hamiltonian replica exchange algorithm and Langevin dynamics [32]. These included Gibbs sampling moves in state space, Monte Carlo translation and rotation moves, seeding all replicas with independent initial configurations, and using multiple coupled and uncoupled states.

Gibbs sampling for replica exchange

Recently, it was shown that replica exchange algorithms can be considered a form of Gibbs sampling, with approaches that speed mixing in the permutation of thermodynamic state indices associated with replica coordinates also speeding overall mixing of the whole simulation Markov chain [38]. We make use of this scheme here by attempting many swaps of randomly selected replica pairs (i, j), accepted with the acceptance criteria described in Eq. 24 of Ref. [38]. We attempt a total of K⁵ swaps each iteration, where K is the total number of alchemical states, to ensure the replicas are thoroughly mixed. Thus, instead of only jumping to the nearest neighbors, a given replica can jump to any Hamiltonian that is allowed with a probability that obeys detailed balance. In previous test cases, this increased the rate of sampling between 2 and 100 times, depending on the observables and systems examined, with negligible increase in computational cost [38]. The potential energy matrix of each configuration calculated at all alchemical states is calculated and stored for later MBAR analysis.

Monte Carlo ligand translational/rotational moves

To further enhance conformational sampling, we introduced Monte Carlo translational and rotational moves, carried out immediately prior to dynamics with each iteration of Hamiltonian exchange. For these moves, a random displacement of the ligand atoms is attempted, with the trial displacement in each dimension drawn from a normal distribution with 1 nm standard deviation, and acceptance or rejection determined by the Metropolis criterion. A rotational move is chosen by drawing a rotation matrix uniformly over rotation space by generating a uniform quaternion (a uniform element of SO(3)) and translating it into a rotation matrix, with rotations accepted or rejected by the Metropolis criterion.

Seeding replicas with independent starting configurations

To eliminate biasing from the starting configuration, we initialized the simulations with random starting configurations in the allowed simulation space at all replicas. We applied random rotational and translational moves to the initial bound configurations of all replicas using the scheme described in the previous section without Metropolization. Translational moves were proposed by generating three random numbers from 0 to 2 nm corresponding to (x, y, z) translation from the initial bound configurations, followed by a rotational move as described above. This starting location was rejected if any atom was less than 3 Å from any protein atom.

Using multiple fully coupled and fully uncoupled states

Standard HREMD uses only one fully coupled state and one fully uncoupled state. We can increase the amount of physically meaningful sampling by using multiple fully coupled states. By also using multiple fully uncoupled states, we increase the chance of a ligand being exchanged into a fully uncoupled state, gaining the ability to move freely around the simulation box.

In our HREMD simulations, the potential energy can be expressed in terms of two coupling parameters:

$$U(X)=U_0(x)+U_{\mathit{elec}}(X,{\lambda }_{\mathit{elec}})+U_{LJ}(X,{\lambda }_{LJ})$$ (2)

where U₀ is the potential of the system with the noninteracting ligand. U_elec and U_LJ are the Lennard-Jones and electrostatic potentials. λ_elec and λ_LJ ∈ [0,1] are the corresponding coupling parameters. Note that the flat-bottom restraint and the ligand torsion, angle, and bond potentials are fully turned on in all states and therefore part of U₀.

For simulations of the ligand in complex, we use 24 total states, as this number is easily portable between configurations of 6 or 8 GPUs per CPU on the computing clusters simulations were run on. In this study, one iteration is defined as the period in MD time steps between replica exchanges. The MD time step was 2 fs, with 500 time steps between exchanges, making each iteration 1 ps long. Smaller number of time steps per iteration allows for more exchanges in state space in a given unit time, and thus for faster transitions of ligands in and out of putative binding sites [63]. However, at some point as exchanges become more frequent there is a tradeoff between the computational overhead required to perform state exchanges and the acceleration of binding transitions due to the exchanges. We ran a series of 1 ns simulations with different numbers of time steps per iteration (250, 500, 1000, 2500). We chose 500 steps for our performance runs, because with 250 MD iterations per swap the percentage of time spent performing exchanges was about twice as much as that for 500. The total time taken was independent of whether Gibbs sampling or standard Metropolis neighbor exchange was performed. The particular tradeoffs involved in choosing this exchange frequency are highly sensitive to the particular CUDA implementation and the networking details of the computers on which simulations are run, and should not be taken as definitive for all hardware or software configurations.

We performed a series of runs using a beta version of the code to examine the sensitivity of the simulation efficiency on simulation parameters, including the number and spacing of intermediate states, the number of additional fully coupled and fully uncoupled states, and the size of the Monte Carlo displacements. The results showed that other than having sufficiently close spacing of intermediate states in space, sampling was not very sensitive to these simulation parameters, and thus no attempt at extensive optimization was made. A table of simulation parameters tested is included as Supplementary Material.

For these simulations, 1 nm was used for the maximum MC displacement distance. The ligand was discharged (charge annihilation) and then decoupled (Lennard-Jones decoupling) by scaling the potentials over a series of coupling parameters (λ_elec: 1.0,0.85, 0.65, 0.35, 0; λ_LJ: 1.0, 0.95, 0.90, 0.85, 0.80, 0.70, 0.60, 0.50, 0.40, 0.30, 0.20, 0.10, 0.0), which were chosen to make sure that replica exchange transitions probabilities between neighboring states were approximately equal across the entire transformation. Six fully coupled and three fully uncoupled states were used, for a total of 24 states. One equilibrium iteration was followed by production runs performed for 15000 iterations (15 ns/replica).

For the ligand in solvent HREMD simulations (decoupling the ligand in implicit solvent), we used only three states—the fully coupled state, the state with the ligand fully discharged and the state with the ligand fully discharged and decoupled—as this number is sufficient to guarantee full mixing between states in implicit solvent. All other simulation parameters were the same as in ligand-protein complex simulations.

D. Production runs

To test simulation consistency and repeatability, we performed ten separate independent runs of the 1-methylpyrrole/T4 lysozyme L99A system starting from random configurations for 15 ns per replica. We then compared clustering patterns between these ten independent runs. Simulations starting from different configurations, if run sufficiently long, should converge to the same clusters at the fully coupled states, within some statistical noise.

We also performed simulations with two other binders and one other non-binder was also performed to see if this methodology was able to differentiate binders from non-binders. For the p-xylene case, a conformational change from the crystal structure of Val111 is required for the lig-and to bind, which provides a good opportunity to test the ability of our method to sample relevant biomolecular motions and ligand motions.

Binding site identification

The configurations sampled at all of the fully coupled (i.e., fully interacting) states were analyzed together to give final predictions of putative binding sites. In the analysis, the location of the ligand at any given configuration was determined by the ligand atom closest to the center of geometry of the ligand, circled in red in Fig. 1.

Protein alignment

Both the protein and ligand were flexible during our simulations. To be able to cluster all ligand binding locations, all protein conformations from all complexes had to be aligned to provide information on ligand locations relative to the protein. Alignments used the Kabsch algorithm [64, 65] as implemented by Bosco K. Ho [66]. All configurations were aligned to the alpha carbons of the crystal structure.

Clustering analysis

After alignment, the samples from all fully coupled states were clustered using the Density-Based Scan Algorithm with Noise (DBSCAN) [67]. The rationale behind this choice of clustering algorithm lies in the nature of the data. We do not know ahead of time how many alternative binding sites are possible, though it is likely that the densities at these locations are moderately well-defined, because the exponential nature of the Boltzmann distribution means that low free energy configurations will have high density compared to the non-binding locations. However, there is also likely to be nonspecific binding density. We therefore expect distinct clusters, with some moderate noise, but we do not know number of clusters beforehand. These requirements make K-means and hierarchical clustering algorithms less useful. Density-based clustering methods that cluster results based on the density of data points appear more applicable.

To simplify the clustering, we began the clustering process with a grid-based density analysis. Starting from atomic coordinates of the protein, a three-dimensional cube with 36 Å edge length, just large enough to fit the observed data sampled during the flat-bottom restrained simulation, was centered on the center of geometry of the system and filled with a 2 Å-resolution grid defining 46656 cells of 8 ų volume each. A 2 Å edge length was chosen based on the standard tolerance for the approximate maximum allowable fluctuations from crystal structure. The uniform density over all nonempty cells was calculated, and all cells with fewer than 8 times the background density were discarded. The factor of 8 was chosen for this model system because, clusters that appeared visually distinct could not be separated by the clustering algorithms with a density cutoff factor less than 8. This choice of low density to exclude from the clustering introduces a small amount of bias, which we address later.

After this filtering, the DBSCAN algorithm was used to cluster the results [67]. We used 1% of total number of the remaining samples after low density filtering as the criteria for defining a cluster. Without this filtering removing the low density volumes, the DBSCAN algorithm tended to give large amorphous clusters. This initial filtering of the density gave well-defined clusters in all cases examined. The most populated cluster was then identified as the most probable binding site, with the the centroids of the clusters used to define the locations of the binding sites.

Binding pose identification

The binding configuration of the ligand is determined not only by the location of its center of geometry, but also by the orientation and conformation of the ligand within the binding site. It is therefore important to further analyze these clusters to find the most probable binding orientations and poses.

In order to identify poses, we ran LIGPLOT for each observed pose in the predicted binding sites [68]. The LIGPLOT program generates both lists of observed interactions (such as hydrogen bonding, π-π stacking, and hydrophobic contact interactions) and schematic 2-D representation of protein-ligand complexes in terms of these interactions. We first examined the hydrophobic interaction patterns of all the poses at each location by counting the interactions predicted by LIGPLOT. We then identified interactions that were frequently formed for low-RMSD structures and classified the poses based on possession of sets of these predicted interactions.

However, because of the small size of the ligands and the partial freedom they have to reorient in the binding site, it is impossible to uniquely specify low RMSD configurations based solely on lists of observed contacts. We therefore default to classifying clusters based on the average RMSD values of all the poses in the most populated cluster from the ligand in the co-crystal structure after alpha carbon alignment in order demonstrate the performance of the methodology. This procedure requires having a crystal structure with the ligand of interest, but we anticipate that pose identification based on specific protein-ligand contacts in a crystal structure-agnostic method should work much more effectively than it worked here for other more complicated binding sites with larger, more chemically diverse ligands.

E. Computing binding free energies

Because the simulation algorithm presented here generates samples from all the intermediate states connecting the coupled and uncoupled states, we can use free energy perturbation and reweighting techniques to calculate binding free energies. In this case, we use the multistate Bennett acceptance ratio (MBAR) method to calculate free energies [40], as implemented as the pymbar Python code [69]. Because exchanging between alchemical intermediates using the Metropolis criteria or Gibbs sampling already requires calculating the differences between the potential energy function applied to each sampled configuration, no additional information is required to analyze the resulting energy using MBAR.

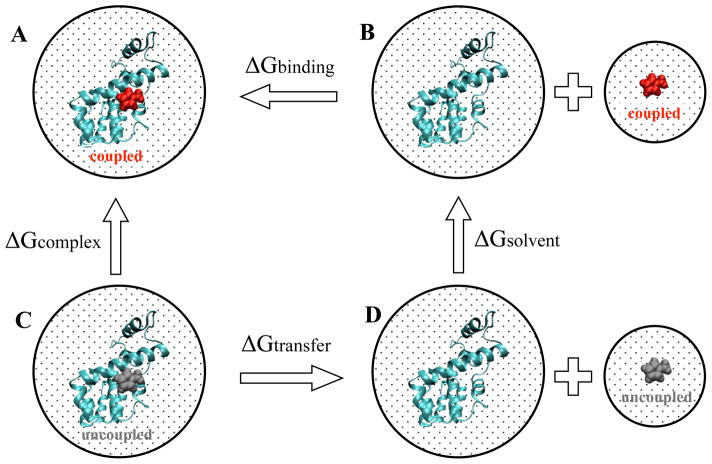
As shown in Fig. 2, to calculate the binding free energy (B to A), the ligand is first decoupled from the solvent (B to D), as described in the Methods, transferred into the protein binding site (D to C), and coupled with the protein (C to A), closing the cycle. The dotted box represents the implicit solvent environment. Grey and red ligands represent decoupled and coupled ligands, respectively. ΔG_solvent and ΔG_complex are the free energies of decoupling the ligand in solvent and complex, respectively. To calculate ΔG_solvent, a HREMD simulation of ligand in implicit solvent was also performed for each ligand.

FIG. 2. Thermodynamic cycle for calculating binding free energy.

To calculate the binding free energy (B to A), the ligand is first decoupled from the solvent (B to D), transferred into the protein binding site (D to C), and coupled with the protein (C to A), closing the cycle. The dotted box represents the implicit solvent environment. Grey and red ligands represent decoupled and coupled ligands, respectively. ΔG_solvent and ΔG_complex are the free energies of decoupling the ligand in solvent and complex, respectively.

The free energy of then transferring the ideal gas ligand out of the simulation box (ΔG_transfer) is equal to k_BT times the ratio of the volumes the ideal gas ligand is sampling. We will then have for the overall binding free energy:

$$\mathrm{\Delta }{G}_{\mathit{binding}}=\mathrm{\Delta }{G}_{\mathit{solvent}}-\mathrm{\Delta }{G}_{\mathit{complex}}+k_{B}Tln\frac{V^{\circ }}{V_{\mathit{binding}}}$$ (3)

where ΔG_solvent and ΔG_complex are the free energy of decoupling the ligand in solvent and complex and V^∘ and V_sphere are the standard-state volumes for a single molecule in a box of size 1 L/N_A and V_binding is the volume of the binding site, which may change depending on the most appropriate definition of binding site. k_B and T are the Boltzmann constant and temperature in Kelvin, respectively.

ΔG_complex can be calculated by:

$$\mathrm{\Delta }{G}_{\mathit{complex}}=-k_B\mathit{T}lnQ/V^{\circ }$$ (4)

where Q is canonical partition function, which is given by:

$$Q={\int }_V{\mathrm{e}}^{-U/k_{B}T}\mathrm{d}\overrightarrow{\mathbf{x}}$$ (5)

where U is the potential energy as a function of the coordinates x⃗ and V is the phase space volume of x⃗ over which we sample.

In our study, because we spatially locate our ligands within the protein configurational space, we can calculate not only the overall free energy of the ligand binding to the protein, but also the binding free energy with respect to all potential binding sites considered jointly and the binding free energies of ligand binding to individual binding sites. The difference between these three binding free energies is the configurational volume over which we integrate to calculate the partition function.

Overall binding free energies calculations

The overall binding free energy is the free energy of the ligand considering the entire simulation volume, with partition function given by:

$$Q_{\mathit{overall}}={\int }_{V_{\mathit{overall}}}{\mathrm{e}}^{-U/k_{B}T}\mathrm{d}\overrightarrow{\mathbf{x}}$$ (6)

where V_overall is total volume inside the flat-bottom sphere. In the limit of box that does not extend far beyond the edge of the protein, and with a sufficiently large binding affinity, this would be the free energy consistent with an experimental measurement of protein association anywhere on the protein.

Binding free energies of individual sites

We can also calculate the binding free energies of the ligand to individual binding sites. Using the grid constructed during the grid-based density analysis, we define a site as the volume made up of the smallest number of cells that include all the samples from that cluster. The partition function for the site is given by:

$$Q_{\mathit{site}}={\int }_{V_{\mathit{site}}}{\mathrm{e}}^{-U/k_{B}T}\mathrm{d}\overrightarrow{\mathbf{x}}$$ (7)

where the only difference is that V_site is volume within an individual binding site. This free energy will be equivalent to the binding free energy calculated for a method that requires binding in a specific location of a protein, such as fluorescence polarization competition assays. MBAR is applied to all samples that occur in that defined binding volume, over all intermediate and final states.

Binding free energies over all sites

We introduce a final measure, all-site binding free energies, which is the binding free energy over all the bound clusters considered together. Here, we are interested in the binding affinity over the volume defined by all known specific binding clusters previous identified. The partition function is given by:

$$Q_{\mathit{all}\mathit{sites}}={\int }_{V_{\mathit{all}\mathit{sites}}}{\mathrm{e}}^{-U/k_{B}T}\mathrm{d}\overrightarrow{\mathbf{x}}$$ (8)

where V_{all sites} represents the volume of all individual binding sites combined. This should be nearly equal to the binding affinity over the entire protein (ΔG_overall), but excludes probability associated with isolated ligands in the water box alone, and thus may be more comparable for many experimental definitions of binding affinity such as by isothermal calorimetry (ITC) or surface plasmon resonance (SPR) than the overall binding affinity. Because of the granularity of the boxes, it may also exclude some probability density at the edge of clusters that spills into neighboring boxes without reaching the density cutoff, an approximation that we analyze later. MBAR is applied to the samples that occur over the joint volume of all binding sites, over all intermediate and final states. Because the partition function in MBAR is a weighted sum over all samples, each sample can be assigned to a binding cluster, and we strictly satisfy:

$$Q_{\mathit{all}\mathit{sites}}=\sum _{i=1}^{N_{\mathit{clusters}}}{Q}_{\mathit{site},i}$$ (9)

or alternatively:

$$\mathrm{\Delta }{G}_{\mathit{all}\mathit{sites}}=-k_{B}Tln\left(\sum _{i=1}^{N_{\mathit{clusters}}}{e}^{-\mathrm{\Delta }{G}_{\mathit{site},i}/k_{B}T}\right)$$ (10)

This study, there are a few cases where more than one cluster has samples in a single box volume, which means that this relationship is only approximately correct because of double counting. In the case, the differences are less than 0.1 kcal/mol, so we do not attempt to define binding site volume at a finer grain or split the boxes between clusters.

IV. RESULTS AND DISCUSSION

A. Binding sites are consistently identified in repeated trials

To test the statistical robustness of our methodology, we performed ten independent simulation runs of the 1-methylpyrrole/T4 lysozyme L99A system. We analyzed the configuration distribution from all fully coupled states for each independent run individually and compared them.

Between six and twelve clusters were identified for each of the ten copies, with a total of seventeen independent clusters observed among all simulations. For statistical consistency, we are interested mainly in the most common clusters. After we discarded the six singletons which occurred in only one simulation, eleven sites were left that appeared in multiple simulations. The occupancy O of a specific site i, the probability of observing this location in a run, is defined as:

$$O_i=\frac{1}{N_{\mathit{trials}}}\sum _{j=1}^{N_{\mathrm{found}}}\frac{N_{i,j}}{N_{\mathit{total},j}}$$ (11)

N_found is the number of times a cluster is found in site i across all N_trials = 10 trial simulations, N_i,j is the number of samples observed in site i in trial j, and N_total,j is the total of number of samples in the observed clusters. This is a slight approximation, as if a cluster is not observed, the volume still has nonzero density. Since the cutoff for a cluster is ¡1%, approximation does not appreciably change the results.

Table I shows the analysis of the eleven sites identified from our ten runs, with their physical locations in the protein shown by the first eleven positions in Fig. 3a. In Fig. 3a, a location is represented by a sphere with diameter of 2 Å (the grid resolution). Black indicates the experimental binding location. The eleven sites were numbered based on the occupancy fractions occurrence, and by frequencies if occupancy fractions were the same. Of eleven sites, three are observed in all ten runs, two of whose occupancies are larger than 0.2 in all ten runs.

TABLE I. Computed site occupancies and free energies.

Quantitative analysis of the eleven putative binding sites identified from ten simulation runs. Frequency is the number of trial runs (out of ten) observed at this site. Occupancies from direct observation of the fully interacting states are calculated via Eq. 11, while free energies are estimated from these occupancies by Eq. 13. Free energies are computed at each binding site using MBAR and samples collected from all intermediates confined to the binding sites (Eq.7), with occupancy estimated from the calculated free energies via Eq.12. Of eleven putative binding sites discovered in total, three are observed in all ten runs. Site 1, the most populated location in all runs, is located in the binding pocket, indicating that we can identify the binding location consistently. All free energies in kcal/mol. Error bars in the first ligand are standard deviations over the ten runs.

		From Direct Observation		From Free Energy Calculation
Site	Frequency	ΔGsite	Occupancy	ΔGsite	Occupancy
1	10	−3.239±0.292	0.467 ± 0.046	−3.482 ± 0.261	0.364 ± 0.101
2	10	−2.784±0.213	0.211 ± 0.024	−3.043 ± 0.182	0.173 ± 0.044
3	10	−2.142±0.176	0.075 ± 0.010	−2.612 ± 0.206	0.084 ± 0.027
4	8	−2.103±0.154	0.060 ± 0.008	−2.587 ± 0.152	0.080 ± 0.019
5	8	−1.889±0.149	0.048 ± 0.008	−2.566 ± 0.131	0.077 ± 0.016
6	6	−1.804±0.104	0.042 ± 0.005	−2.538 ± 0.119	0.074 ± 0.014
7	5	−1.708±0.109	0.035 ± 0.005	−1.893 ± 0.123	0.025 ± 0.005
8	7	−1.596±0.138	0.029 ± 0.008	−2.599 ± 0.103	0.082 ± 0.013
9	5	−1.263±0.114	0.016 ± 0.005	−1.820 ± 0.091	0.022 ± 0.003
10	4	−1.347±0.098	0.010 ± 0.003	−1.613 ± 0.118	0.016 ± 0.003
11	3	−0.765±0.001	0.007 ± 0.000	−0.672 ± 0.019	0.003 ± 0.000

FIG. 3. Fifteen binding sites identified from all simulation runs.

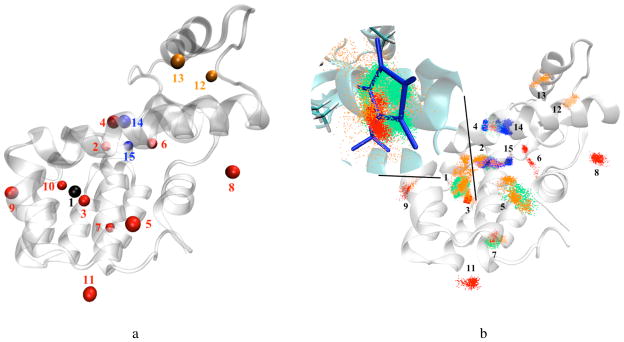
(a) The centroid of each site is represented by a sphere, with diameter of 2 Å (the grid resolution). Black indicates the crystallographic binding site. Black and red locations together are the eleven sites for 1-methylpyrrole, with benzene sites as a subset of these. Pink and blue represent additional sites exclusively for p-xylene and phenol, respectively. (b) The binding site predictions for one run of 1-methylpyrrole (red), benzene (green), p-xylene (orange) and phenol (blue). Each point represents the center of geometry at the fully coupled states after grid-based density filtering and clustering. In the inset of the nonpolar binding pocket, all the protein residues within 6 Å of the ligand are shown.

Importantly, site 1 is the most populated in all ten independent runs and is located at the crystallographic ligand binding site, indicating that we can identify this experimentally observed binding location consistently. Site 2 is also observed in all runs and has an average occupancy of more than 0.2. Though not as populated, site 3 is also observed in all runs. However, as indicated from Fig. 3a, site 3 is very close to site 1 and could be interpreted as “spillover” from site 1. All the other sites occur with much lower probability and can be best interpreted as weaker nonspecific binding locations. The clusters in Fig. 3b show the binding location predictions (with the same numbering system) for all four molecules after conducting the grid-based density analysis, each point representing a conformation at the fully coupled states, with only one of the ten runs shown (in red) for 1-methylpyrrole. As shown in Fig. 3b, the volume of site 1 for 1-methylpyrrole is relatively small despite having almost half of the total samples, indicating that density at the binding site is well-localized.

Free energy differences are simply k_BT times the log ratios of the relative probabilities of the two states. We should therefore be able to directly compare the ranking of the sites by occupancy measured by direct observation to the free energies calculated for each site. Free energies of binding to each site are computed as described Section III E using Eq. 7, and are shown in Table I, where they can be compared directly to the occupancies. The ranking of the free energies of the sites agrees with that of the occupancies in almost all cases, though there are some differences outside of statistical error. The free energy difference between the top two binding sites is only 0.44 kcal/mol, suggesting that there may exist at least one potential binding site other than the experimental binding site. The fact that low-frequency clusters are not consistently observed in all simulations indicate that the simulations are not entirely converged. This may explain the difference in binding affinity between rarer clusters, although the convergence of the dominant binding sites does appear adequate based on agreement between the two ways of calculating relative affinity between clusters.

To better understand the consistency between free energies and occupancies, we can estimate an occupancy for each site based on its free energy. We estimated the occupancies O_i from the free energies ΔG_i as:

$$O_i=\frac{{\mathrm{e}}^{-\mathrm{\Delta }{G}_i/k_{B}T}}{{\sum }_{i=1}^{N_{\mathit{trials}}}{\mathrm{e}}^{-\mathrm{\Delta }{G}_i/k_{B}T}}$$ (12)

where G_i is the ΔG_site for location i. Uncertainties for each site free energy are the standard deviation of the free energy over the ten independent runs, and are the uncertainty in a single calculation, not in the mean.

We can also estimate each cluster’s free energy based on the directly observed occupancy of the cluster in the fully interacting states. Each cluster’s relative free energy is equal to:

$$\mathrm{\Delta }{G}_i=-k_{B}Tln\frac{O_i}{O_{\mathit{far}}}$$ (13)

where G_i and O_i are ΔG_site and occupancy for site i. O_far is the occupancy of the “cluster” of samples far away from the protein as to be effectively noninteracting. This cluster serves as a reference, because the transfer of the ligand to this volume should have ΔG_site = 0. We define this cluster as those samples found between r=r_cutoff and r_cutoff − 5 Å in the fully coupled state.

As shown in Table I, the occupancies calculated both ways as well as the free energies calculated both ways are in relatively good agreement within statistical error, indicating that our definition of the occupancy and the free energy calculation methodology are consistent. The free energy calculations in principle contain more information, since they incorporate the potential energies, as well as the location information the occupancies contain, and also include samples from multiple intermediate states. Interestingly, however, the uncertainties in occupancies and free energies calculated starting from either directly observed occupancies or using MBAR are similar.

B. The dominant binding site can be identified accurately across multiple molecules

To test the accuracy of our methodology in identifying binding sites across a range of ligands, we examined the predicted sites of four ligands binding to the same protein, one of which (phenol) is known not to bind experimentally. All methods were the same, except that each of the three additional ligand binding runs was run only once, instead of ten times.

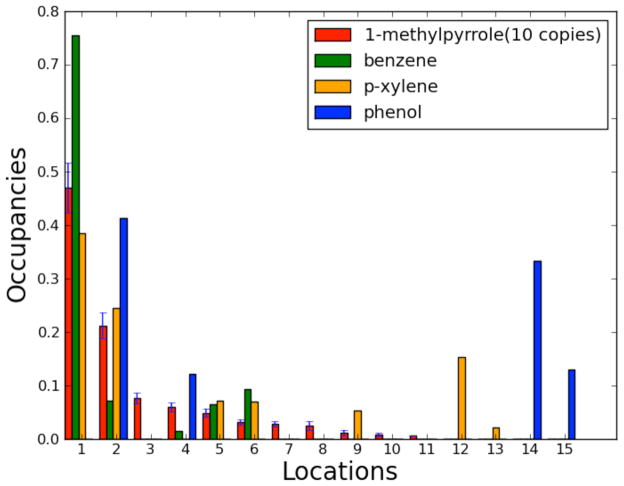
Fig. 4 shows the site occupancies for four molecules. For 1-methylpyrrole, the statistical error in a single run (not in the mean) was calculated over the 10 runs, while values for only one run were used for the other three ligands. Since many of the same binding sites were observed in simulations of the different molecules, we used the same numbering systems described in the previous section for the 1-methylpyrrole runs, adding newly identified sites to the initial eleven sites.

FIG. 4. Binding site fractional occupancies.

The three binders share similar binding patterns, and are labeled by extending the numbering scheme from the 1-methylpyrrole simulations. Site 1, located at experimental binding location, is the most populated site for all three binders. However, no samples above background are observed in the binding site for the nonbinder, phenol.

As shown in Fig. 4, since the three binders share similar binding patterns, the total number of potential binding sites identified on the protein only increases by four when additional ligands are analyzed, with two of the sites from the non-binder, phenol. These four additional sites are the last four sites numbered sites in Fig. 3a. Pink and blue represent additional sites observed for p-xylene and phenol, respectively. The green, orange and blue clusters in Fig. 3b are the binding site predictions for benzene, p-xylene and phenol. Each point represents a conformation at the fully coupled state, with the low density sites filtered out. The binding site at the crystallographically observed binding cavity (site 1) is identified as the most populated site for all three binders. Additionally, no binding cluster of any density above background is identified at this location for simulations of the non-binder. This suggests that, at least for this model system and small set of ligands, we can identify the binding location accurately and consistently and differentiate the binders from non-binders.

C. Binding poses can also be identified

1. Pose prediction at site 1 for 1-methylpyrrole

After the binding site (site 1) was successfully identified, we further examined the poses found at that site. From the 10 runs of the 1-methylpyrrole/T4 lysozyme L99A system, we took the set of ligands in the most populated cluster, which is also the experimental binding cluster, and examined the poses of the ligand configurations in this location.

We initially attempted to analyze the poses based on the hydrophobic interaction contacts made between the ligand and the protein predicted by the LIGPLOT program. Although there were a number of hydrophobic interactions correlated with low RMSD binding, there was no single hydrophobic interaction pattern that could be conclusively identified with low RMSD binding, suggesting that it is not possible to identify the most representative pose by hydrophobic interaction patterns alone for this system. This was determined by using one run of 1-methylpyrrole system as a training set to determine patterns of contacts associated with low RMSD and then testing these patterns on a second run to see if low RMSD structures were identified. However, no pattern in hydrophobic binding was identified that could consistently identify poses within 1 Å RMSD. We hypothesize that it is difficult to determine binding patterns from contacts is this case because it is an engineered ligand binding system with a large hydrophobic binding surface (up to 20 contacts), with similar contributions to binding energy. Such as consensus pose procedure based on observed contacts is more likely to work for systems with important hydrogen-bonding patterns systems and more complex ligands.

We therefore focus on identifying poses based on RMSD from crystal structure. We calculate the RMSD for all four molecules with respect to the co-crystal poses (Table II and Table III). All RMSD values are symmetry corrected. Although we ran all docking and simulations with the benzene co-crystal structure, we calculated RMSDs from the experimental crystal structures of 1-methylpyrrole and p-xylene (PDB accession code 2OU0 and 3GUM) after aligning the alpha carbons to incorporate the conformational differences between the complexes.

TABLE II.

Average ligand RMSD (in Å) from crystal structures of AutoDock and the methodology presented in this paper. For AutoDock, the average RMSD was calculated over 50 top poses, while for our methodology, this was calculated over all poses in the 8 ų predicted binding locations, with the standard deviation for 1-methylpyrrole. For the nonbinder phenol, since there is no crystal structure available, we use the co-crystal ligand benzene with phenol in order to identify whether docking incorrectly places the ligands in the binding site. All RMSDs are symmetry corrected.

Molecules	Rigid AutoDock	Flexible AutoDock Our methodology
1-methylpyrrole	1.84	1.87	1.93 ± 0.09
benzene	1.62	2.30	2.32
p-xylene	2.32	3.76	3.14
phenola	11.21	12.87	N/A

^aAs compared to the binding cavity in benzene co-crystal structure.

TABLE III.

Percentages (%) of poses with RMSD from crystal structure less than 2 Å for AutoDock and the methodology presented in this paper. The standard error for 1-methylpyrrole was calculated over the ten runs. For the nonbinder phenol, since there is no crystal structure available, we replaced the benzene co-crystal ligand with phenol and computed RMSD to the resulting structure. All RMSDs are symmetry corrected.

Molecules	Rigid AutoDock	Flexible AutoDock Our methodology
1-methylpyrrole	46.0	50.0	43.3 ± 2.8
benzene	52.0	30.0	33.4
p-xylene	36.0	20.0	19.1
phenola	2.0	4.0	0.0

^aAs compared to the binding cavity in benzene co-crystal structure.

Fig. 5 shows 100 typical poses of each binder at the binding site are shown. 1-methylpyrrole is primarily oriented the same way in all configurations, as can be seen by the essentially stationary single nitrogen. Benzene has somewhat more conformational variation, as can be expected with the highly symmetrical ligand, but still has relatively little motion. However, p-xylene has significant conformational variation in the binding site, which we discuss in the next section.

FIG. 5. Superimposed poses (100 each) at the experimental binding site for all three binders for 1-methylpyrrole, benzene and p-xylene.

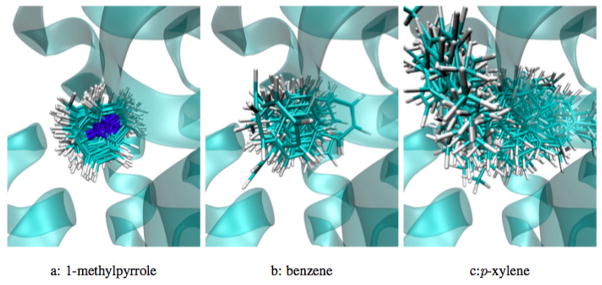
For 1-methylpyrrole and benzene, configurational noise is limited, while p-xylene transitions between two different clusters during the simulation.

2. The role of Val111 in binding

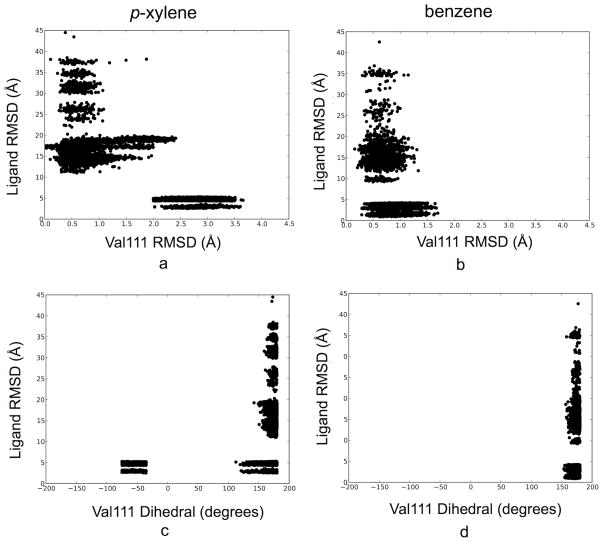
One of the challenges involved in simulations of ligand binding is capturing correlated motions involving both ligand and protein. T4 lysozyme L99A is a good model system to test the power of this methodology to overcome this sampling problem. Previous simulations have shown that p-xylene cannot bind to the same configuration of the binding cavity as smaller ligands; instead, a rotamer change of Val111 is first required. In simulations with p-xylene placed in the binding cavity, the occluded nature of the pocket makes this rotamer motion is extremely slow, often occurring on time scales beyond that of typical simulations [15]. In this study, we monitored movement of Val111 during the HREMD simulations of p-xylene and benzene. Fig. 6 shows the RMSD of the two ligands from their crystal structure with respect to the RMSD of Val111 from the crystal structure for (a) p-xylene and (b) benzene as well as the ligand RMSD of the ligands versus against the Val111 χ dihedral angle (C-C_α-C_β-C_γ) in (c) and (d). Each dot is a conformation at each iteration. Because we are comparing the ligand pose to the crystal structure pose, low ligand RMSD corresponds to the ligand being in the crystallographic binding site.

FIG. 6. Correlation between ligand binding site occupation and Val111 displacement for p-xylene and benzene.

RMSD of the ligand from the crystal structure with respect to the RMSD of Val111 from the crystal structure (upper graphs) and the Val111 χ dihedral angle (C-C_α-C_β-C_γ) (lower graphs) for p-xylene (left side, a and c) and benzene (right side b and d). All calculations are of fully interacting ligands. Val111 must move for p-xylene binding to occur, either by a torsional angle rotation or by backbone motion, but benzene binding is independent.

As shown in Fig. 6a, the ligand binding and the conformational change of Val111 for p-xylene are highly correlated. When p-xylene enters the binding site, Val111 is necessarily displaced; if it is not, no binding occurs. For benzene binding (Fig. 6b), Val111 stays in the initial location regardless of whether the ligand is bound or not. This demonstrates that our HREMD decoupling strategy can significantly accelerate such coupled configurational changes on binding that requires long simulations of at least multiple nanoseconds in standard MD simulations [15]. HREMD does this by removing the ligand from the pocket so that the transition can occur.

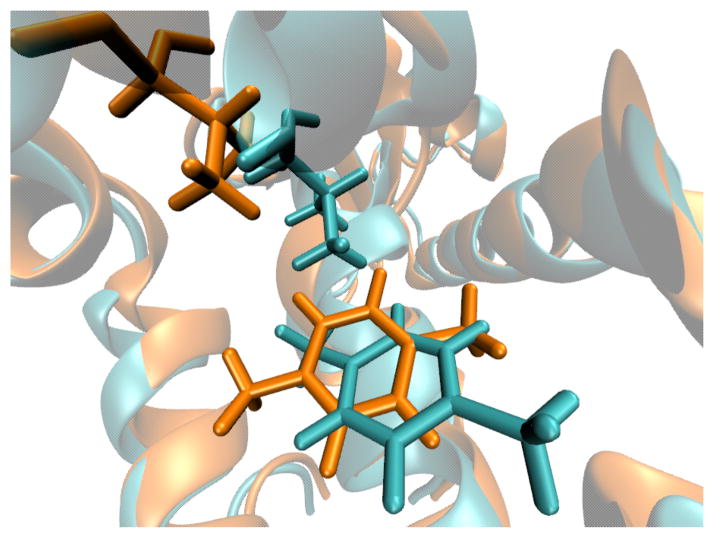
If we look directly at the Val111 dihedral angle (C-C_α-C_β-C_γ), the correlation between binding of ligand and the conformational change of Val111 is not complete. There are in fact configurations that have low p-xylene RMSD, but where the dihedral corresponds to the small binder crystal structure. This occurs because the protein backbone shifts out, allowing Val111 to move, a binding mode not observed in previous free energy calculations. Fig. 7 shows two low RMSD structures from each of the two clusters. Cyan and orange are used for the dihedral shift (RMSD=0.34Å) and alternative backbone shift (RMSD=2.87Å) structures, respectively. It is not clear if this observed difference in binding modes from previous simulations is due to force field errors, the implicit solvent errors, lack of the protein relaxation with the ligand absent in previous simulations, or some other unknown reason.

FIG. 7. Two representative structures observed in the simulation of p-xylene.

Cyan and orange are crystal-like (RMSD=0.3 Å from crystal) and alternative (RMSD=2.87 Å from crystal) structures, respectively. In the crystal-like structure, Val111 dihedral changes from the configuration found in the apo or small binder crystals. In the alternative structure, Val111 shifts away via backbone motion.

To quantify the relative frequency of the two binding modes, we clustered all the conformations in the binding site of p-xylene. Only two clusters with more than 10 percent of all the conformations are present, with respective occupancies of 0.53 and 0.32. By comparing to the p-xylene crystal structure, we found that cluster one has a 0.56 A average RMSD with respect to the crystal structure while cluster two has a 3.03 Å average RMSD. There are thus two primary binding modes in this location-defined cluster that can be distinguished by their orientation.

One unrelated but important observation from Fig. 6 is that there are no ligand observations in the range of 5 Å and 10 Å for either benzene or p-xylene in the interacting state, indicating that there is no physical entry route for the ligand. Instead, it hops back and forth between bulk and the binding site via the unphysical decoupling pathway.

D. Comparison of docking and our modified HREMD methodology

It is instructive to compare the performance of docking methods to our methodology. The T4 lysozyme L99A system has proven a challenging case for UCSF’s DOCK program as well as other docking programs [43–46]. Therefore, as an additional check we attempted molecular docking to identify binding sites and poses, in our case using AutoDock. We first compared the average ligand RMSD from the crystal structures for all binders in both cases. For AutoDock, the average RMSD was calculated over 50 top poses, while for our modified HREMD, the average RMSD was calculated over all poses at the highest probability binding location. We also compared the percentages of poses with RMSD (from the experimental co-crystal structure for each ligand after alpha carbon alignment) with values less than 2 Å. Since there is since there is no crystal structure for the nonbinder phenol, we used the benzene co-crystal and replaced the benzene with phenol and used RMSDs to that modeled crystal structure to see if either approach incorrectly placed phenol into the binding site. Results are shown in Table II and III.

Surprisingly, AutoDock and the more sophisticated methodology produced comparable results for the binding site locations. Fraction within a given RMSD does not mean exactly the same thing when comparing the two methods. In the docking runs, only 50 poses were generated out of hundreds of thousands of attempts while in our simulations, all poses in the binding configuration are counted. Instead, it should be considered only an indication of whether the crystallographic binding site can be identified. Rigid docking outperforms flexible docking substantially for two binders, which is especially interesting in the case of p-xylene. Since we know that Val11 must readjust from the small-binder crystal structure in both experiment and simulations for binding to actually occur, the better performance of rigid docking indicates that the good performance may be a statistical fluke, and that it is only recognizing a hollow hydrophobic site. Tests on wider sets of ligands may be required to further compare the methods.

E. Binding free energies can be accurately calculated

Though the initial goal of this study was not to calculate the binding free energies, the fact that our methodology was modified from a free energy calculation tool made it straightforward. We calculated the free energies of ligand binding to different sites, as shown in Table I. The ordering of the sites using free energies matches the ordering using occupancies well, though not perfectly. The free energy of ligand binding to the most populated binding site is substantially more favorable than those of other sites, confirming that a single site is dominant, though not overwhelmingly so, at only 2–3 times the occupancy of the next most frequently occupied site.

Additionally, we were able to calculate the overall free energies of different ligands associated with the protein, over the entire simulation volume, as shown in Table IV. The overall free energies generally match the experimental values to within statistical noise. In Table IV, we also compare all-site binding free energies and binding free to the dominant binding site to the the overall free energies. For the non-binder phenol ΔG_site is close to zero since the experimental site was not observed as the one of the predicted potential clusters. The errors for the 10-replica 1-methylpyrrole simulations are calculated using the standard deviation in the free energy over the ten simulations, while the errors for the rest are calculated using the statistical uncertainty estimate for MBAR.

TABLE IV.

Comparisons between calculated and experimental binding free energies of four different molecules in kcal/mol. G_site is the binding free energy to the most populated cluster, which except for phenol is the binding cavity. The binding energy of phenol to the binding cavity is −0.16± 0.53 kcal/mol. ΔG_{all sites} is the binding energy over all specifically-bound clusters, while ΔG_overall is over the entire protein. ΔG_explicit are explicit solvent simulations from Ref. [15].

Molecules	ΔGsite	ΔGall sites	ΔGoverall	ΔGexplicit	ΔGexperimental
1-methylpyrrole	−3.48 ± 0.26	−4.15 ± 0.25	−5.05 ± 0.21	−4.32 ± 0.08	−4.44
benzene	−4.26 ± 0.71	−5.15 ± 0.80	−6.01 ± 0.81	−4.56 ± 0.20	−5.19
p-xylene	−4.01 ± 0.89	−4.94 ± 0.85	−5.72 ± 0.95	−3.54± 0.17	−4.67
phenol	−1.03± 0.32	−1.78 ± 0.47	−2.32 ± 0.58	−1.26 ± 0.09	> −2.74

As a comparison, we also include in Table IV the explicit solvent calculations of the same ligands from Mobley et al. [15], which were calculated assuming binding to only a single site. We observe that these binding calculations are relatively consistent with our results. They are in particularly close agreement with the free energy of binding to the highest occupancy site, though the statistical noise is somewhat too high to reach any strong conclusions. Gallicchio et al., using a different choice of force field and implicit solvation model, but also assuming a single binding site, calculated a binding free energy of −4.01 ± 0.04 kcal/mol for benzene and −1.40 ± 0.03 for phenol [41]. This agrees with our single site calculation for benzene, but is more favorable for binding for phenol. The number for phenol in Table IV is for the most favorable binding site for phenol, not the hydrophobic pocket, which has a binding affinity −0.16 kcal/mol. The binding free energies of other molecules examined by Gallicchio et al. were also underestimated, similar to Mobley et al. ‘s explicit solvent calculations. This underestimation may be due to the contribution of alternate sites to the free energy of binding, but may also be explained by a host of other force-field factors.

In the limit of tight binding and a sufficiently small simulation box, the overall free energy should be slightly more favorable than the all-sites free energy, because the overall free energy also includes the completely nonspecific binding to the protein and the low concentration in the simulated volume near the protein. However, in this study this discrepancy approaches 1 kcal/mol. This difference appears to in part be because of the granularity of the clustering algorithm, which omits density outside the cluster if it falls below the 8 times average density background. We performed an alternate binding calculation for the 1-methylpyrrole case in which we set the energies of all samples not in the set of grid cubes assigned to binding site clusters equal to energies drawn from the samples away from the protein. In this case, the overall binding affinity changed from −5.05 to −4.19 kcal/mol, indicating that the difference between the all-site free energy and overall free energy was due to samples associated with the protein, not samples at other locations in the box. However, it is still unclear how much of the weight is due to samples from the binding sites that were not included in the clustering because of the grid granularity and how much is due to samples weakly associated to the protein but not part of any binding cluster. With these missing densities, all-site binding affinities would be shifted somewhat towards the overall binding affinity, and the individual site binding affinities would also become slightly more favorable.

F. Discussion

One of the difficulties in GPU-accelerated MD simulations is parallelization of a single simulation across multiple GPUs. The highly parallelized replica structure of HREMD made it suitable to run on multiple GPUs, since we can parallelize up to one GPU per replica. As a result, we were able to generate 15-ns simulations for all 24 alchemical states in about 6.3 days of wall time, using 6 GPUs at 4 replicas per GPU, running at approximately 10 ns/day/GPU in GPU time per single replica. This time scale makes such calculations already potentially useful for drug discovery. Optimized OpenMM GPU code without the alchemical state code achieved 40 ns/day on the same same machine and on the same systems. This indicates that with properly optimized code and given the rapid development of GPU processor technology, the wall-clock time for studies such as this will decrease significantly in the very near future.

Some parameters involved in our simulations, such as the number of fully coupled states, the number of fully uncoupled states and the Monte Carlo displacement, could potentially be further optimized, as our initial optimization tests of these parameters were fairly coarse grained. The results (in Supporting Information) suggest that in most cases, the sampling is not sensitive to these parameters, though a full optimization is beyond the scope of the current study. A rigorous exploration of these parameters over longer time scale may reveal additional ways to further improve the efficiency of the methods presented in this study. There are a large number of potential ways to improve efficiency of simulations, including optimization of the OpenMM CUDA implementation and adding Monte Carlo moves of ligand and protein torsional angles. Such improvements could further bring the convergence time down from days to hours, making such simulations a more useful tool in drug design pipelines.

We have found that optimized HREMD simulations in implicit solvent can identify binding sites and binding modes in a model system without prior knowledge of the binding site, even in a highly buried binding pocket. Since we start the simulations from random starting configurations, no binding site information is needed. As a result, our methodology can potentially be used to conduct low-throughput virtual screening, even when no binding site information is available. In low-throughput virtual screening, especially in the lead optimization stage, the accuracy presented here may be sufficient, and the relatively moderate computational cost will either now or soon be accessible.

However, it is important to recognize that this is a test of only four molecules and a single, relatively small protein. The demonstrated ability of modified HREMD methods presented here to sample multiple binding sites will be independent of the system. However, the success in finding the binding site and the agreement of binding affinities may not be nearly as transferable. This study is meant as an exploration of the utility of modified HREMD to sample between binding sites, and is only a proof-of-principle.

Despite the general success of this methodology, there are a few flaws in the clustering approach presented here. One problem is that more than one cluster can contain samples in the same grid volume, leading to the inability to uniquely decompose a binding site into separate clusters. However, this leads to a relatively low amount of error, less than 0.1 kcal/mol in this study. Another problem is that there are some samples belonging to the binding cluster that are omitted because they partially fall into another box that falls below the overall density cutoff. Overcoming these problems would require either additional data in order to use a smaller grid, or a more robust density-based clustering algorithm, technical problems that can presumably be overcome with sufficient work, but which are not required for the level of precision presented in this study.

We find that for at least the moderate affinity ligands in this study, the free energy of binding sites other than the most likely binding site contributes nonnegligibly to the total free energy, with these alternate binding sites contributing between 0.7 and 0.9 kcal/mol to the overall binding free energy. Although this contribution is likely to be less in tight binding molecules that have a very tight binding mode, this observation does mean that the exact binding affinity can depend significantly on the way the binding site is defined and the method used to calculate it. This effect may possibly be a reason that binding affinities measured in Mobley et al. ‘s and Gallicchio et al. ‘s studies of binding to the crystallographic binding cavity of this system were consistently less favorable than experiment by about this amount [15, 41], though there are certainly no lack of other possible explanations for this discrepancy. This distribution of binding sites, if it does translate into a typical experimental system, may also be important for fragment-based drug design studies, as there may be multiple binding sites that are worth targeting in a single protein.

We also compared the alternative binding sites observed directly with the experimental electron densities deposited in the Protein Data Bank to see if unassigned densities could be correlated with these putative binding sites. We examined all binding sites with threshold occupancy of 0.1 in the simulations, as density lower than this is unlikely to be observed above noise. For benzene, no alternative sites have occupancies larger than 0.1, so no search is necessary. For p-xylene, we did not observe any apparent electron densities in the volumes of the two putative sites with occupancies larger than the threshold. For 1-methylpyrrole, two ligands were proposed in the crystal structure, one of which is an alternative site with a lower density than the binding site. However, this alternative site was not predicted by our methodology. For the single computationally predicted alternative site with 1-methylpyrrole with an occupancy higher than 0.1, we observed some unassigned electron density, but it was not distinguishable from water. Interestingly, the structure Met106 ligand in contact with this binding site volume was ambiguous, with two different conformations of Met106 proposed to fill the volume in the coordinates, but this may be unconnected. The simulations do appear to be fairly well converged, at least with respect to the two most populous binding sites, which suggests that either the force field and/or implicit solvent model is creating spurious density, or there is some other physical reason for this binding site not being present in experimental crystal structures.

V. CONCLUSIONS

In this study, we used a modified version of Hamiltonian replica exchange among alchemical intermediates combined with Monte Carlo ligand displacement/rotation moves to identify putative binding location and poses in the T4 lysozyme L99A model system starting from random initial ligand positions. Our results suggest that this methodology can identify the binding sites consistently and accurately. Moreover, we can identify the correct binding orientations within these binding sites relatively accurately. Last but not least, we can not only calculate the overall free energies of binding using MBAR, but can also decompose the contributions to the overall binding free energy both in terms of individual binding sites and all binding sites combined, demonstrating the extent to which the ensemble of weak binders may contribute nonnegligibly to the overall free energy. With the wider availability of GPU simulation resources, this methodology may be a stepping-off point for further improved drug discovery methods when no co-crystal ligand information is available.