A Quadrature-Based Tunable Radio-Frequency Sensor for the Detection and Analysis of Aqueous Solutions

Abstract

A highly tunable and sensitive radio-frequency (RF) sensor is presented for the measurement of aqueous-solution dielectric properties. Two quadrature hybrids are utilized to achieve destructive interference that eliminates the probing signals at both measurement ports. As a result, weak signals of material-under-test (MUT) are elevated for high sensitivity detections at different frequencies. The sensor is demonstrated through measuring 2-propanol-water solution permittivity at 0.01 mole fraction concentration level from ~4 GHz to ~12 GHz. De-ionized water and methanol-water solution are used to calibrate the sensor for quantitative MUT analysis through our proposed model. Micro-meter coplanar waveguides (CPW) are fabricated as RF sensing electrodes. A polydimethylsiloxane (PDMS) microfluidic channel is employed to introduce 250 nL liquid, of which ~1 nL is effectively the MUT. The permittivity and the relaxation time of 2-propanol-water solution are obtained. Compared with our power divider based sensors, the differential reflection coefficients in this work provide additional information that complements the transmission coefficient methods.

I. Introduction

Label-free detection and analysis of molecular compositions in aqueous solutions are of great interest for the development of high-performance micro-total-analysis-system (μ-TAS). A potential approach is to measure the changes of dielectric permittivity and relaxation time of solutions at very low concentration levels [1], where the solute molecules may not interact with each other and the changes may be molecule specific. Thus, high sensitivity and broadband (i.e., 3-octave or wider) radio-frequency (RF) measurements are essential. The measurements are also important for the studies of molecular structures and dynamics, such as H-bond rearrangement dynamics [2], dipole moment of the specific solute and the solute—solvent interface [3]. Furthermore, the measurement methods are likely to be of great interest for single cell and single particle investigations [4], [5].

Nevertheless, achieving high-sensitivity and broadband RF measurements simultaneously has been a difficult challenge since the conditions for the two operations often contradict each other. Transmission line based techniques, such as the coplanar waveguide (CPW) based approaches [6], are usually broadband. Miniaturizing the critical dimensions can improve CPW absolute sensitivity, but not the sensitivity for low concentration level measurements. Resonator-based RF sensors achieve high sensitivities [7]–[9], but the sensitivities are reduced significantly for lossy material-under-test (MUT) due to degraded effective quality factors (Q_eff). Furthermore, these resonator-based sensors lack broadband frequency capabilities unless tuning techniques are introduced [10], [11]. Moreover, there is a lack of sensitivity tuning in these approaches.

Recently, we proposed an interference-based simple technique to simultaneously address the above mentioned challenges on sensitivity and frequency tuning capability [12]. Power dividers, millimeter sized coplanar waveguides (CPW) and large (~200 μL) polydimethylsiloxane (PDMS) wells are used therein. The technique shares the basic interference operating principle with the RF sensors [13], [14] and the microwave bridges [15], where only transmission scattering parameters are available. In this work, we show that interference-based sensors can be implemented with broadband quadrature hybrids. As a result, reflection and coupling scattering parameters also provide MUT information that complements results from transmission scattering parameters. Furthermore, micrometer CPWs and microfluidic channels are built to handle nL liquid volumes, instead of μL in [12]. In Section II, the quadrature-hybrid-based RF sensor and its operation are introduced. Section III presents the measurement results of 2-propanol-water solutions, and Section IV concludes the letter.

II. A Quadrature Based RF Sensor

A. Sensor Design Considerations

Fig. 1 shows the schematic of the RF sensor. Two broadband quadrature hybrids are used for RF probing signal division and combination. Off-chip tuning components, continuously tunable phase shifters (Φ) and attenuators (R), are introduced to tune the electrical balance of the two branches as well as the operating frequencies. One phase shifter and one attenuator can also be used, but with less operation flexibility. The probing signal is usually of very low phase noise. Hence it is highly coherent and can be effectively considered as a single frequency signal in this analysis. CPW structures, shown in Fig. 1(b), are used to probe MUT in PDMS microfluidic channels.

Fig. 1.

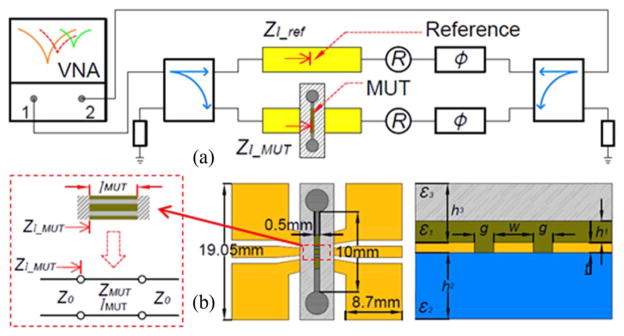
(a) A schematic of the RF sensor under test. (b) The top and cross section views of the sensing zone, where w = 6 μm, g = 7.2 μm, t = 0.5 μm (gold), h₁ = 50 μm (channel), h₂ = 1 mm, h₃ = 2 mm (PDMS), ε₁: MUT permittivity, ε₂: 3.75, ε₃: 2.3.

To obtain high measurement sensitivity, we exploit destructive interference processes to suppress probing signals at the output ports, i.e., 180° phase difference between reference and MUT branches. As a result, weak MUT signals are elevated for measurements. Adjustments with phase shifters and attenuators are necessary due to non-ideal device performance. Different from our power-divider based sensor [12], reflections at both port 1 and 2 in Fig. 1(a) are also differential signals between reference and MUT branches. Thus, the reflection scattering parameters are also sensitive to MUT property changes, which will be further discussed below.

A 500 μm wide PDMS channel is built and attached to the CPW in MUT branch in Fig. 1. Aqueous solutions are injected into and extracted from the channel through two soft plastic tubes (not shown) that are attached to the circular openings of the channel, shown in Fig. 1.

B. MUT Property Extraction

For reasons similar to those in [12], DI water and methanol-water solution (at 0.01 mole fraction) are used to calibrate the sensor and determine the unknown parameters of the tuning components before the MUT liquid (2-propanol-water solution at 0.01 mole fraction) is measured. The permittivity of calibration liquids are obtained from reported data [2]. As a result, three different measurements are conducted at each frequency point.

DI water is first used as reference MUT. The sensor is tuned to a desired sensitivity at each target frequency f₀, i.e., a desired |S₂₁|_min level (Fig. 2). The obtained scattering parameters are our reference data and can be described by

Fig. 2.

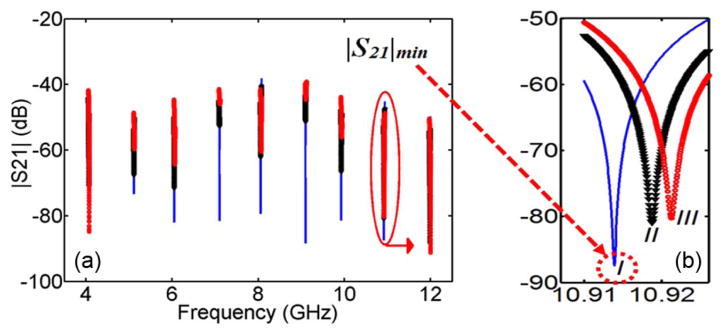
(a) S₂₁ magnitude. (b) Zoom-in view at ~11 GHz (solid line, I: DI water; triangles, II: methanol-water; circles, III: 2-propanol-water).

$$S_{21,w}=K_{1}exp(-{\gamma }_{\mathit{air}}{l}_{\mathit{ref}})+K_{2}exp(-{\gamma }_w{l}_{\mathit{MUT}})$$ (1)

$$S_{11,w}=C_1(Z_{l\_\mathit{ref},\mathit{air}}-Z_0)/(Z_{l\_\mathit{ref},\mathit{air}}+Z_0)+C_2(Z_{l\_\mathit{MUT},w}-Z_0)/(Z_{l\_\mathit{MUT},w}+Z_0).$$ (2)

Then methanol-water solution is measured, followed by 2-propanol-water solution measurements. In this process, |S₂₁|_min and corresponding frequency will shift due to the change of MUT. Equations similar to (1) & (2) can be used to describe corresponding S_21,m,p & S_11,m,p. Subscripts w,m and p are for water, methanol-water, and 2-propanol-water. In these equations, the propagation constants of the CPW section are γ_w,m,p; the physical lengths of reference and MUT sections are l_ref,MUT. The coefficients K₁, K₂, C₁ and C₂ describe the effects of all the other sensor components except the MUT sections. Impedance Z_{l_ref} and Z_{l_MUT,w,m,p} are marked in Fig. 1(a). They can be derived using the equivalent circuit in Fig. 1(b) and the characteristic impedances of reference and MUT CPW sections, Z_ref,air and Z_MUT,w,m,p, can be obtained from [16]

$$\begin{array}{l}{Z}_{\mathit{MUT},w,m,p}=\frac{1}{(C_{\mathit{cpw}}{v}_{ph})}=\frac{\sqrt{{\epsilon }_{\mathit{eff},w,m,p}}}{(C_{\mathit{cpw}}{c}_0)}\\ =\frac{1}{\left(c_0\sqrt{2\left(2a_0+a_1\left({\epsilon }_{1,\mathrm{w},\mathrm{m},\mathrm{p}}^{\prime }-{\epsilon }_3\right)+a_2({\epsilon }_2^{\prime }-1)+a_3({\epsilon }_3^{\prime }-1)\right)a_0}\right)}\end{array}$$ (3)

where a_i (i = 0,1,2,3) can be found in [16]. Then you have

$$\frac{S_{21,m}-S_{21,w}}{S_{21,p}-S_{21,w}}=\frac{exp(-{\gamma }_m{l}_{\mathit{MUT}})-exp(-{\gamma }_w{l}_{\mathit{MUT}})}{exp(-{\gamma }_p{l}_{\mathit{MUT}})-exp(-{\gamma }_w{l}_{\mathit{MUT}})}$$ (4)

$$\frac{S_{11,m}-S_{11,w}}{S_{11,p}-S_{11,w}}=\frac{\frac{Z_{l\_\mathit{MUT},m}-Z_0}{Z_{l\_\mathit{MUT},m}+Z_0}-\frac{Z_{l-\mathit{MUT},w}-Z_0}{Z_{l\_\mathit{MUT},w}+Z_0}}{\frac{Z_{l\_\mathit{MUT},p}-Z_0}{Z_{l\_\mathit{MUT},p}+Z_0}-\frac{Z_{l\_\mathit{MUT},w}-Z_0}{Z_{l\_\mathit{MUT},w}+Z_0}}.$$ (5)

The term “exp(−γ_pl_MUT)” at frequency f_p, which corresponds to |S₂₁|_min,p, can be calculated through (4) and |S₂₁|_min,w,m. So the term ‘tanh(−γ_pl_MUT)’ in Z_{l_MUT,w,m,p} can be determined. According to Z_{l_MUT,w,m,p}, (3), and (5), the real part of the 2-propanol-water solution permittivity, ${\epsilon }_{1,p}^{\prime }$, can be obtained. In this process, Z_{l_MUT,w,m} is calculated at frequency f_p.

It seems that ${\epsilon }_{1,p}^{\prime }$, can be also obtained directly from the phase constant β_p in term ‘exp(−γ_pl_MUT)’ without using S₁₁ through

$${\beta }_p=2\pi f\sqrt{{\epsilon }_0{\mu }_0}\times \sqrt{\frac{\left(2a_0+a_1\left({\epsilon }_{1,\mathrm{p}}^{\prime }-{\epsilon }_3^{\prime }\right)+a_2\left({\epsilon }_2^{\prime }-1\right)+a_3\left({\epsilon }_3^{\prime }-1\right)\right)}{(2a_0)}}.$$ (6)

Unfortunately, β_p is of the form

$${\beta }_p=\frac{1}{l_{\mathit{MUT}}}\left(2n\pi -\mathit{imag}\left(ln\frac{exp(-{\gamma }_p{l}_{\mathit{MUT}})}{\mid exp(-{\gamma }_p{l}_{\mathit{MUT}})\mid }\right)\right),n=\dots ,-2,-1,0,1,2,\dots$$ (7)

Thus, additional information is needed to determine n, which is 0 only when the reference branch and the MUT branch in Fig. 1(a) are almost identical. The use of S₁₁, i.e., quadrature-based sensor in Fig. 1(a), addressed this issue in this work.

The imaginary part ${\epsilon }_{1,p}^{″}$ can be calculated by using the attenuation constant α_p from the term “exp(−γ_pl_MUT)”. The constant can be described as

$${\alpha }_p=\frac{\pi a_1{\epsilon }_{1,p}^{″}}{\left({\lambda }_0\sqrt{2\left(2a_0+a_1\left({\epsilon }_{1,\mathrm{p}}^{\prime }-{\epsilon }_3^{\prime }\right)+a_2\left({\epsilon }_2^{\prime }-1\right)+a_3\left({\epsilon }_3^{\prime }-1\right)\right)a_0}\right)}.$$ (8)

Table I shows that for the CPW MUT sections in Fig. 1(b), results obtained from the models above agree with HFSS full-wave simulation analysis reasonably well.

TABLE I.

Comparison Between Model and HFSS Simulation (Format: mag∠rad)

f (GHz)	(S21,m-S21,w)/(S21,p-S21,w)		(S11,m-S11,w)/(S11,p-S11,w)
	Model	HFSS	Model	HFSS
4	0.34∠-0.09	0.26∠0.28	0.35∠-0.04	0.30∠0.16
8	0.32∠-0.02	0.46∠0.32	0.32∠-0.02	0.41∠0.39
11	0.31∠0.01	0.33∠-0.01	0.31∠-0.01	0.33∠0.02

III. Measurement Results

The solution of 2-propanol-water at 0.01 mole fraction is measured. Experimental S₂₁ and S₁₁ at different frequencies are shown in Fig. 2 and 3, respectively. The results show that our quadrature-based RF sensor is widely tunable and highly sensitive even though no particular efforts have been attempted to achieve the highest possible sensitivity, which is ultimately determined by the insertion loss of the circuit components and the VNA dynamic range. It also shows that with liquid, the effective quality factor, Q_eff = f₀/Δf_{3 dB}, calculated from S₂₁ magnitude, is 5.05 × 10⁴, which is very high compared with currently available RF sensors [7].

Fig. 3.

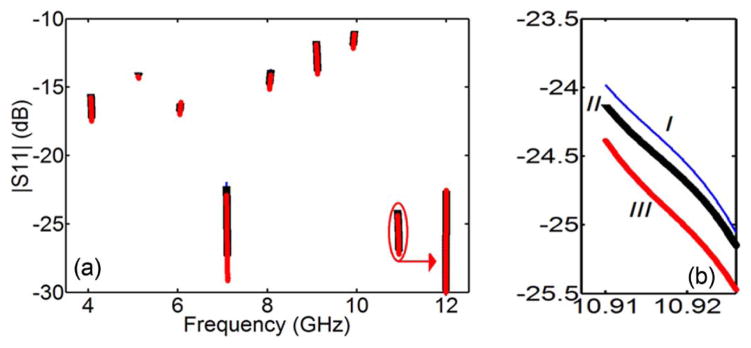
(a) S₁₁ magnitude. (b) Zoom-in view at ~11 GHz (solid line, I: DI water; triangles, II: methanol-water; circles, III: 2-propanol-water).

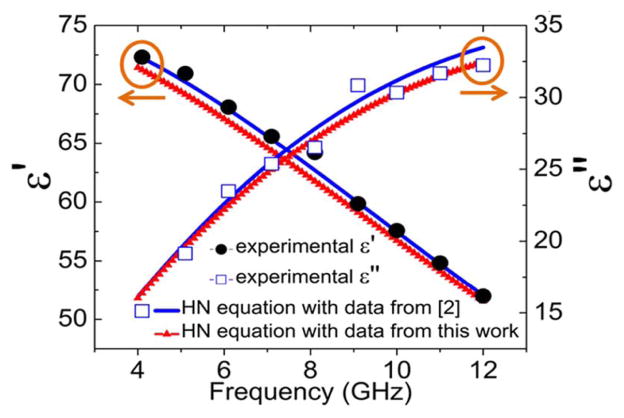
The extracted 2-propanol-water solution permittivity is shown in Fig. 4. The Havriliak–Negami(HN) equation [2]

Fig. 4.

Obtained permittivity, ε = ε′ − jε″, of 2-propanol-water solution.

$$\epsilon (f)={\epsilon }_{\infty }+\mathrm{\Delta }\epsilon /{(1+{(j2\pi f\tau )}^{\beta })}^{\alpha }$$ (9)

can be used to fit the measured data through a least-square fitting approach, shown in the same figure. In (9), ε_∞ is solution permittivity at infinite high frequency, Δε is the permittivity change between high and low frequencies, τ is the relaxation time, and α and β are fitting constants. The obtained τ is 9.45 ps, which is close to 9.59 ps reported in [3]. The rest of the parameters are ε_∞ = 5.3, Δε = 70.5, α = 1 and β = 0.98. The results obtained with quadrature-based and power divider-based [12] sensors agree reasonably well, e.g., at 5 GHz, ε is 70.89 − j17.75 in [12] and 70.92 − j19.15 in Fig. 4. The slight difference may be caused by liquid handling and possible solution concentration level difference.

IV. Conclusion

The liquid volume that is directly above the CPW signal line and signal-ground gaps in Fig. 1 is 0.51 nL. Therefore, the effective MUT volume is comparable with that of other RF sensors, e.g., [8]. The insets in Figs. 2 and 3 indicate that much smaller MUT volumes and much lower solute concentration levels can be accurately measured. Additionally, the implementation of the presented RF sensor is flexible in terms of RF sensing electrodes, the number and arrangement of attenuators and phase-shifters.

In summary, broadband quadrature hybrids are used in conjunction with tunable phase-shifters and attenuators to build a highly sensitive and tunable RF sensor. Micrometer CPWs are fabricated on 1 mm thick fused silica substrates as broadband RF sensing electrodes. Microfluidic channels are built to introduce aqueous solutions for calibrations and characterizations. A model is presented to extract dielectric permittivity values and the relaxation time of liquids from measured scattering parameters. It is expected that the sensor will find wide applications in RF μ-TAS developments. Further work is needed to investigate potential sensitivity disparity between |S₂₁|_min and |S₁₁| in Figs. 2 and 3, the scaling of CPW dimensions and operation frequencies, the automation and miniaturization of the sensors.