Stability of delayed memristive neural networks with time-varying impulses

Abstract

This paper addresses the stability problem on the memristive neural networks with time-varying impulses. Based on the memristor theory and neural network theory, the model of the memristor-based neural network is established. Different from the most publications on memristive networks with fixed-time impulse effects, we consider the case of time-varying impulses. Both the destabilizing and stabilizing impulses exist in the model simultaneously. Through controlling the time intervals of the stabilizing and destabilizing impulses, we ensure the effect of the impulses is stabilizing. Several sufficient conditions for the globally exponentially stability of memristive neural networks with time-varying impulses are proposed. The simulation results demonstrate the effectiveness of the theoretical results.

Introduction

Memristor was originally postulated by Chua in 1971 (Chua 1971; Chua and Kang 1976) and fabricated by scientists at the Hewlett-Packard (HP) research team (Strukov et al. 2008; Tour and He 2008). It has been proposed as synapse emulation because of their similar transmission characteristics and the particular device advantage such as nanoscale, low energy dissipation which are significant for the designing and optimizing of the neuromorphic circuits (Strukov et al. 2008; Tour and He 2008; Cantley et al. 2011; Kim et al. 2011). Therefore, one can apply memristor to build memristor-based neural networks to emulate the human brain. In recent years, dynamics analysis of memristor-based recurrent neural networks has been attracted increasing attention (Hu and Wang 2010; Wen et al. 2012a, b; Wu et al. 2012; Wen and Zeng 2012; Wang and Shen 2013; Zhang et al. 2012; Wu and Zeng 2012a, b; Guo et al. 2013). In Hu and Wang (2010), the dynamical analysis of memristor-based recurrent neural networks was studied and the global uniform asymptotic stability was investigated by constructing proper Lyapunov functions and using the differential inclusion theory. Following, the stability and synchronization control of memristor-based recurrent neural networks have been further investigated (Wen et al. 2012a, b; Wu et al. 2012; Wen and Zeng 2012; Wang and Shen 2013; Zhang et al. 2012; Wu and Zeng 2012a, b; Guo et al. 2013). As well known, memristor-based neural networks exhibit state-dependent nonlinear switching behaviors because of the abrupt changes at certain instants during the dynamical processes. Therefore, it is more complicated to study the stabilization of memristor-based neural networks. So, recently, many researchers begin to turn their attentions to construct the general memristor-based neural networks and analyze the dynamic behavior (Wen et al. 2012a, b; Wu et al. 2012). In this paper, we focus on the general memristor-based neural networks constructed in Wen et al. (2012a, b), Wu et al. (2012).

In the implementation of artificial memristive neural networks, time delays are unavoidable due to finite switching speeds of amplifiers and may cause undesirable dynamic behavior such as oscillation, instability and chaos (He et al. 2013a, b; Wang et al. 2012). On the other hand, the state of electronic networks is often subject to instantaneous perturbations and experiences abrupt change at certain instants that is the impulsive effects. Therefore, memristive neural networks model with delays and impulsive effects should be more accurate to describe the evolutionary process of the system. During the last few years, there has been increasing interest in the stability problem in delayed impulsive neural networks (Lu et al. 2010; Hu et al. 2012; Chen and Zheng 2009; Yang and Xu 2007; Hu et al. 2010; Liu and Liu 2007; Liu et al. 2011; Lu et al. 2011, 2012; Guan et al. 2006; Yang and Xu 2005; Zhang et al. 2006). In Liu et al. (2011), synchronization for nonlinear stochastic dynamical networks was investigated using pinning impulsive strategy. In Guan et al. (2006), a new class of hybrid impulsive models has been introduced and some good results about asymptotic stability properties have been obtained by using the “average dwell time” concept. In general, there are two kinds of impulsive effects in dynamical systems. An impulsive sequence is said to be destabilizing if the impulsive effects can suppress the stability of dynamical systems. Conversely, an impulsive is said to be stabilizing if it can enhance the stability of dynamic systems. Stability of neural networks with stabilizing impulses or destabilizing has been studied in many papers (Lu et al. 2010; Hu et al. 2012; Chen and Zheng 2009; Yang and Xu 2007; Hu et al. 2010; Liu and Liu 2007; Liu et al. 2011; Lu et al. Lu et al. 2011, 2012; Guan et al. 2006; Yang and Xu 2005; Zhang et al. 2006). When the impulsive effects are stabilizing, the frequency of the impulses should not be too low. In most of the literature (Lu et al. 2010; Hu et al. 2012; Chen and Zheng 2009; Yang and Xu 2007; Hu et al. 2010; Liu and Liu 2007; Liu et al. 2011; Lu et al. 2011, 2012; Guan et al. 2006; Yang and Xu 2005) only investigate the stability problem when the impulses are stabilizing and the upper bound of the impulse intervals is used to guarantee the frequency of the impulses. When the impulsive effects are destabilizing, the lower bound of the impulsive intervals can be used to ensure that the impulses do not occur too frequently. For instance, in the Yang and Xu (2005), Zhang et al. (2006), the authors consider such kind of impulsive effects. In all those literature, it is implicitly assumed that the destabilizing and stabilizing impulses occur separately. However, in practice, many electronic biological systems are often subject to instantaneous disturbance and then exposed to time-varying impulsive strength, and both the destabilizing and stabilizing impulses might exist in the practical systems.

Motivated by the aforementioned discussion, different from the previous works, in this paper, we shall formulate the memristive neural networks with time-varying impulses in which the destabilizing and stabilizing impulse are considered simultaneously and deal with its global exponential stability. The upper and lower bounds of stabilizing and destabilizing impulsive intervals are defined, respectively to describe the impulsive sequences such that the destabilizing impulses do not occur frequently and the frequency of the stabilizing impulses should not be too law. By using the differential inclusion theory and the Lyapunov method, the sufficient criteria will be obtained under the stability of delayed memristor-based neural networks with time-varying impulses is guaranteed.

The organization of this paper is as follows. Model description and the preliminaries are introduced in “Model description and preliminaries” section. Some algebraic conditions concerning global exponential stability are derived in “Main results” section. Numerical simulations are given in “Numerical example” section. Finally, this paper ends by the conclusions in “Conclusions” section.

Model description and preliminaries

Model description

Several memristor-based recurrent neural networks have been constructed, such as those in Hu and Wang (2010), Wen et al. (2012a, b), Wu et al. (2012), Wen and Zeng (2012), Wang and Shen (2013), Zhang et al. (2012), Wu and Zeng (2012a, b), Guo et al. (2013). Based on these works, in this paper, we consider a more general class of memristive neural networks with time-varying impulses described by the following equations:

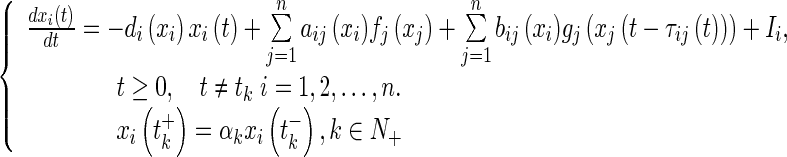1

where 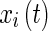is the state variable of the ith neuron, d_i is the ith self-feedback connection weight, 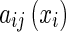and 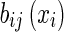are, respectively, connection weights and those associated with time delays. I_i is the ith external constant input. 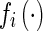and 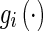are the ith activation functions and those associated with time delays satisfying the following Assumption 2. The time-delay 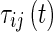is a bounded function, i.e., 0 ≤ τ_ij(t) ≤ τ where τ ≥ 0 is a constant. 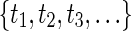is a sequence of strictly increasing impulsive moments, 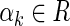represents the strength of impulses. We assume that x_i(t) is right continuous at t = t_k, i.e., 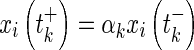. Therefore, the solution of (1) are the piecewise right-hand continuous functions with discontinuities at t = t_k for .

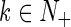Remark 1

The parameter α_k in the equality 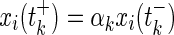describes the influence of impulses on the absolute value of the state. When , the absolute value of the state is enlarged. Thus the impulses may be viewed as destabilizing impulses. When 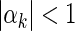, the absolute value of the state is reduced, thus the impulses may be viewed as stabilizing impulses.

Remark 2

In this paper, both stabilizing and destabilizing impulses are considered into the model simultaneously. we assume that the impulsive strengths of destabilizing impulses takes value from a finite set 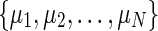and the impulsive strengths of stabilizing impulses take values from 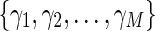, where 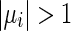,,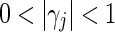 for 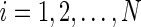,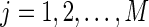. We assume that denote the activation time of the destabilizing impulses with impulsive strength μ_i and the activation time of the stabilizing impulses with impulsive strength γ_i, respectively. The following assumption is given to enforce the upper and lower bounds of stabilizing and destabilizing impulses, respectively.

Assumption 1

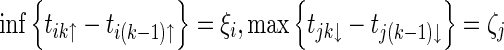where .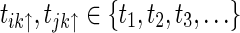

Assumption 2

For 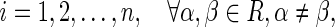then neuron activation function 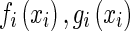in (1) are bounded and satisfy

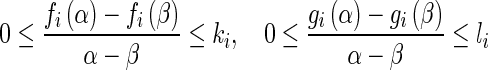2

where k_i, l_i are nonnegative constants.

Preliminaries

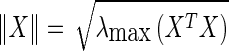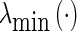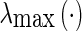For convenience, we first make the following preparations. R⁺ and Rⁿ denote, respectively, the set of nonnegative real numbers and the n-dimensional Euclidean space. For,, let denotes the Euclidean vector norm, and the induced matrix norm. and denote the minimum and maximum eigenvalues of the corresponding matrix, respectively. For continuous functions 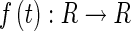, 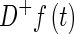is called the upper right Dini derivative defined as 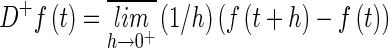. N₊ denotes the set of positive integers.

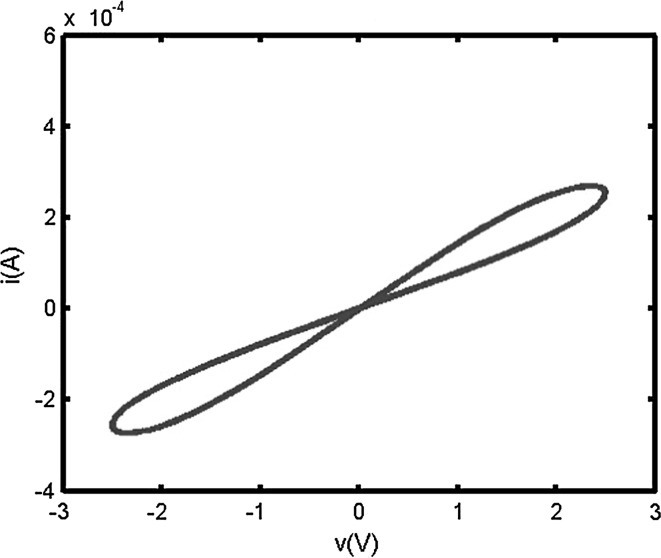
As we well known, memristor is a switchable device. It follows from its construction and fundamental circuit laws that the memristance is nonlinear and time-varying. Hence, the current–voltage characteristic of a memristor showed in Fig. 1. According to piecewise linear model (Hu and Wang 2010; Wen et al. 2012a, b) and the previous work (Wu et al. 2012; Wen and Zeng 2012; Wang and Shen 2013; Zhang et al. 2012; Wu and Zeng 2012a, b; Guo et al. 2013), we let

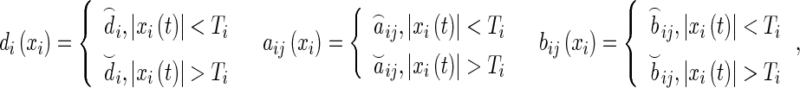Here, T_i > 0, are memristive switching rules and 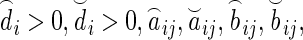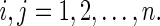are constants relating to memristance.

Fig. 1.

The typical current–voltage characteristic of memristor. It is a pinched hysteresis loop

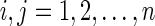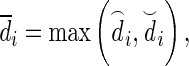
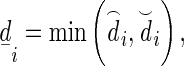
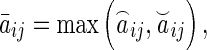
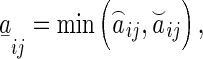
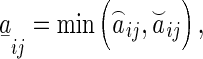
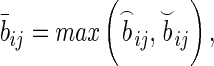
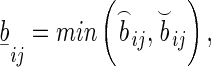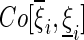Let, for , and denote the convex hull of 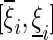. Clearly, in this paper, we have .

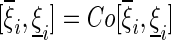Now, according to the literature (Hu and Wang 2010; Wen et al. 2012a, b), by applying the theories of set-valued maps and differential inclusion, we have from (1)

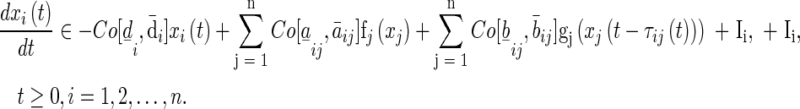3

Or, equivalently, for 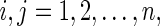there exist

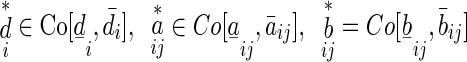such that

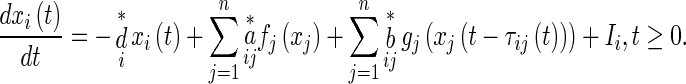4

Definition 1

Aconstant vector 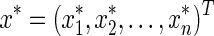is said to be an equilibrium point of network (1), if for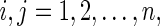

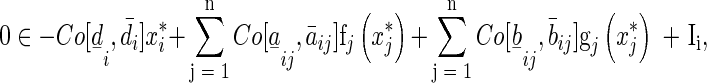5

Or, equivalently, for 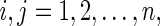there exist

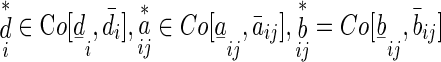such that

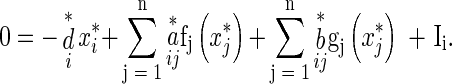6

If 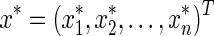is an equilibrium point of network (1), then by letting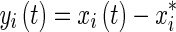, 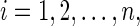we have

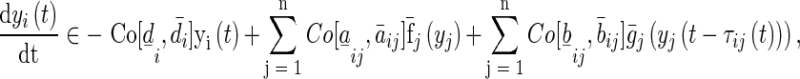7

Or, equivalently, there exist 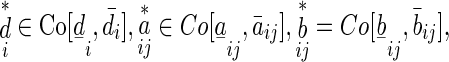such that

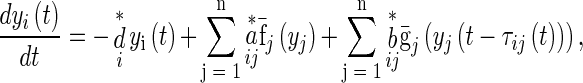8

Obviously, 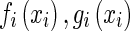satisfy Assumption 1 and we can easily see that 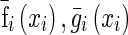also satisfy the following assumption:

Assumption 3

For 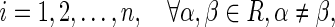then neuron activation function 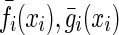in (5) and (6) are bounded and satisfy

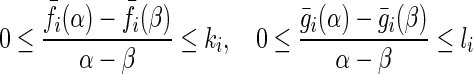9

where 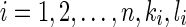are nonnegative constants.

Definition 2

If there exist constants 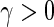, 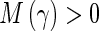and 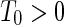such that for any initial values

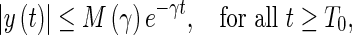then system (10) is said to be exponentially stable with exponential convergence rate γ.

For further deriving the global exponential stability conditions, the following lemmas are needed.

Lemma 1

Filippov (1960) Under Assumption2, there is at least a local solutionx(t) of system (1) with the initial conditions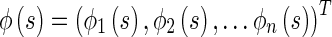, , 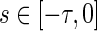which is essentially bounded. Moreover, this local solution x(t) can be extended to the interval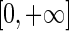in the sense of Filippov.

Under Assumption 2, and 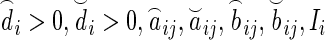, are all constant numbers, from the references (Wu et al. 2012; Hu et al. 2012), in order to study the memristive neural network (1), we can turn to the qualitative analysis of the relevant differential inclusion (3).

Lemma 2

Baæinov and Simeonov (1989) Let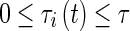. 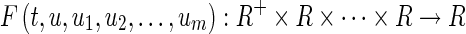be nondecreasing in u_ifor each fixe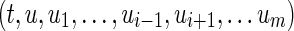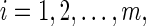d, and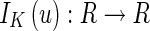be nondecreasing in u. Suppose that

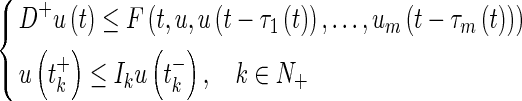and

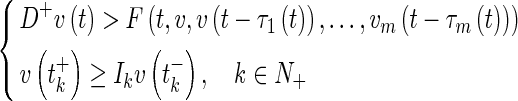Then, for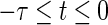implies that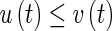, for.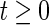

In the following section, the paper aims to analysis the globally exponential stability of the system (1).

Main results

The main results of the paper are given in the following theorem.

Theorem 1

Consider the memristive neural networks (1), suppose that Assumptions 1 and 2 hold. Then, the memristive neural network (1) with time-varying impulses will be globally exponentially stable if the following inequality holds

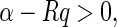where

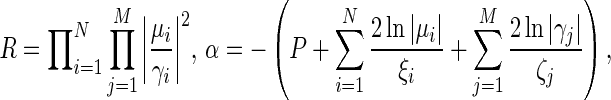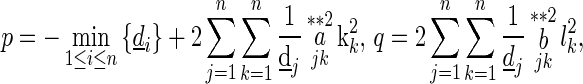here,

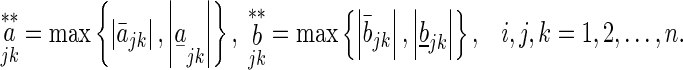Proof

We choose a Lyapunov functional for system (5) or (6) as

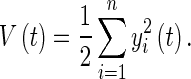10

The upper and right Dini derivative of V(t) along the trajectories of the system (5) or (6) is

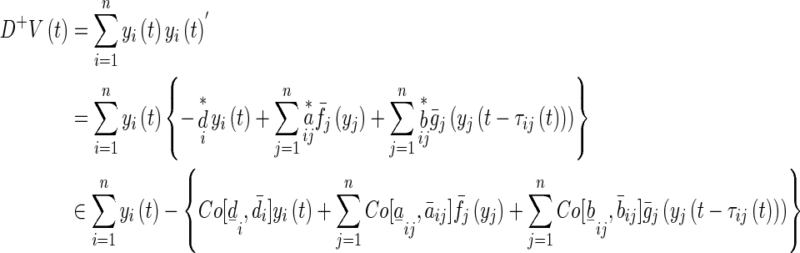11

From Assumption 3, we have

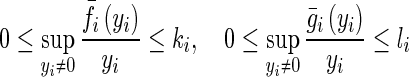12

where 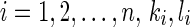are nonnegative constants.By (11) and (12), we get

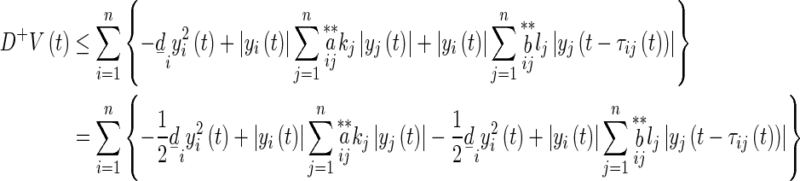13

By mean-value inequality, we have

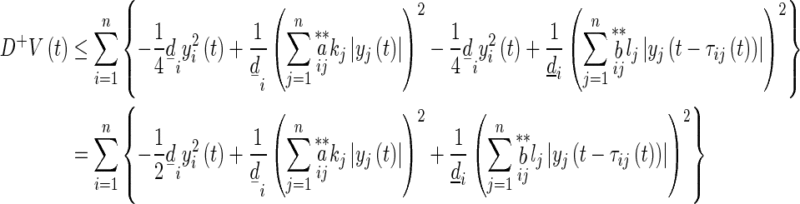14

By Cauchy–Schwarz inequality, we obtain

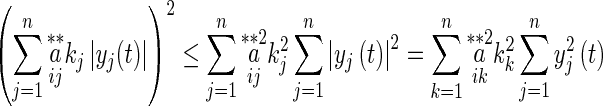15

and

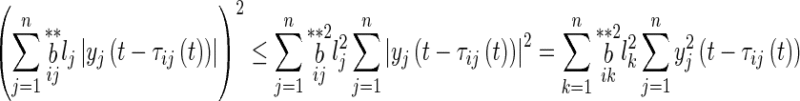16

It follows from (15) and (16) that

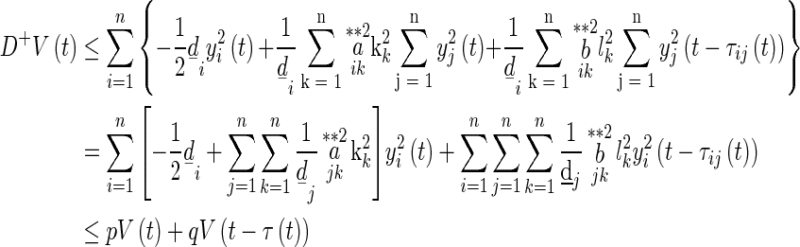17

where 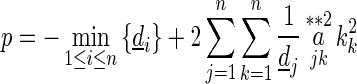, , 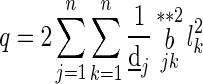. For t = t_k, from the second equation of (1), we get

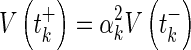18

For any σ > 0, let 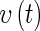be a unique solution of the following impulsive delay system

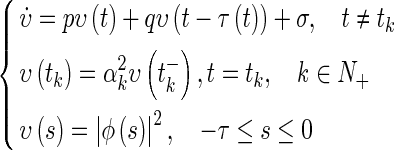19

Note that 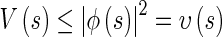, for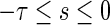. Then it follows from (17), (18) and Lemma 2 that

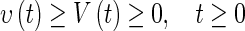20

By the formula for the variation of parameters, it follows from (19) that

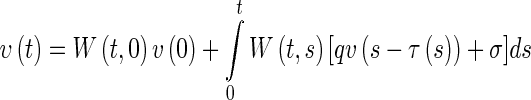where 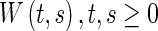is the Cauchy matrix of linear system

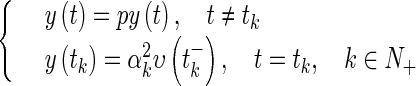21

According to the representation of the Cauchy matrix, one can obtain the following estimation

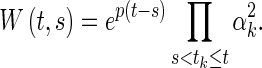22

For any t > 0, if there exist an s such that there are N_i destabilizing impulses and M_j stabilizing impulses in the interval (s, t), then from Assumption 1, we can easily get 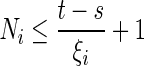, , 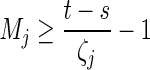then it follows from Assumption 1 and (22) that

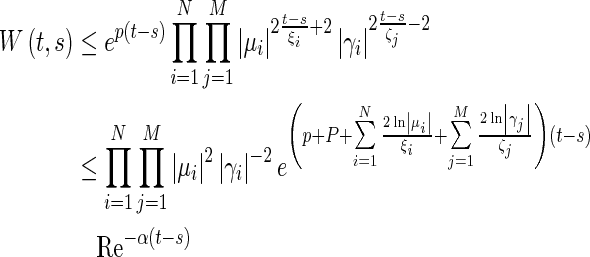23

where 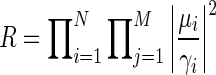, 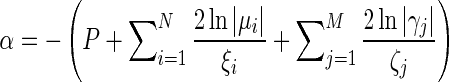. Let 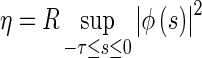then we can get that

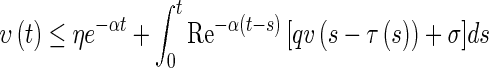24

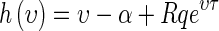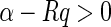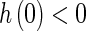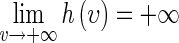Let . It follows from that , , and 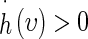. Therefore there is unique 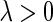such that 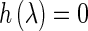.On the other hand, it is obvious that 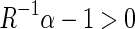. Hence,

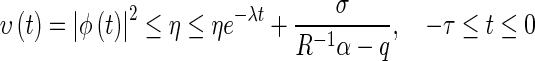25

So it suffices to prove

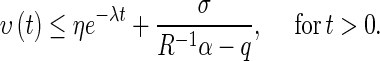By the contrary, there exist t > 0 such that

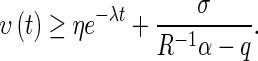We set

Then 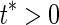and 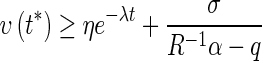. Thus, for ,

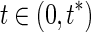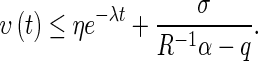From (24) and (25), one observes that

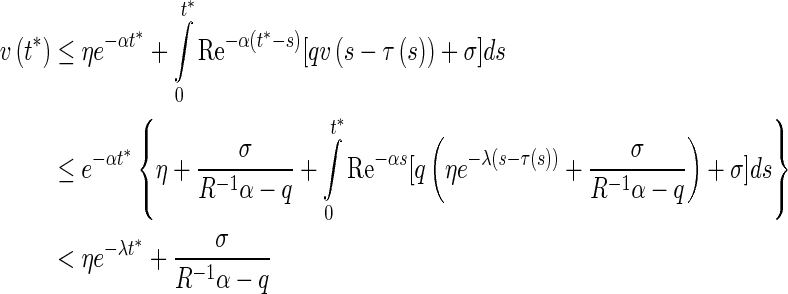26

This is a contradiction. Thus, 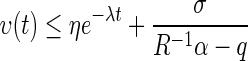, for t > 0, holds. Letting 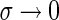, we can get from (15) that 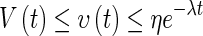. By Definition 1, the solution y(t) of the memristive neural network (1) is exponentially stable. This completes the proof.

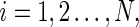
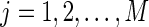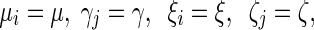
In order to show the influence of the stabilizing impulses and destabilizing impulses clearly, we assume that both the destabilizing and stabilizing impulses are time-invariant, i.e., for , 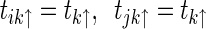. Then we get the following corollary.

Corollary 1

Consider the memristive neural networks (1). Suppose that Assumptions 1 and 2 hold. Then, the memristive neural network (1) with time-invariant impulses will be globally exponentially stable if the following inequality holds

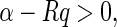where

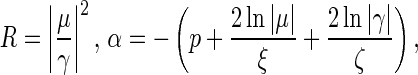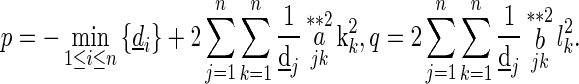Here,.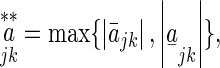

Proof

Corollary 1 can be similarly proved as Theorem 1. So the process will be omitted here.

Numerical example

In this section, we will present an example to illustrate the effectiveness of our results. Let us consider a two-dimensional memristive neural network

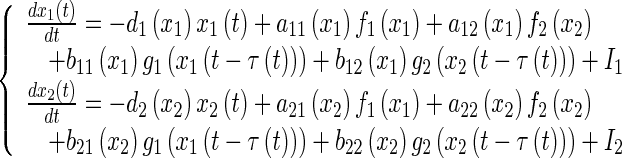27

where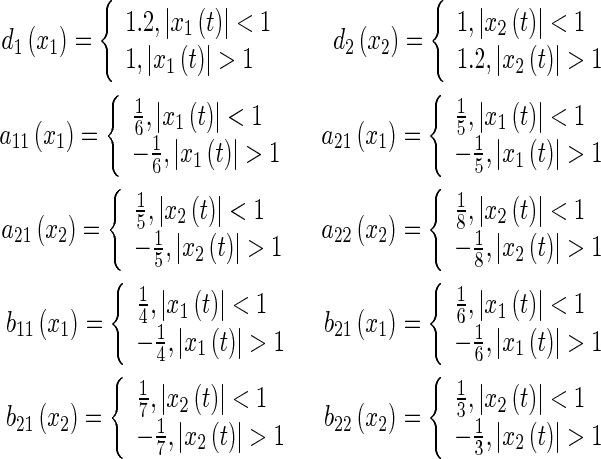Therefore,

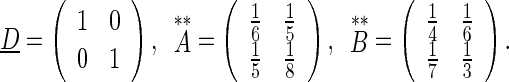Let 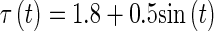, , 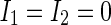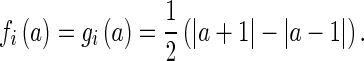By simple calculation, we get 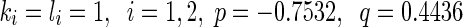. For the time-varying impulses, we Choose the impulsive strengths of destabilizing impulses 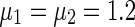, the impulsive strength of stabilizing impulses 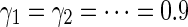, and the lower bounds of stabilizing 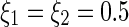. According to Corollary 1 that the neural network (27) can be stabilized if the maximum impulsive interval ζ of the stabilizing impulsive sequence is not more than 0.2755. 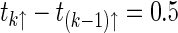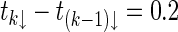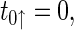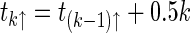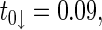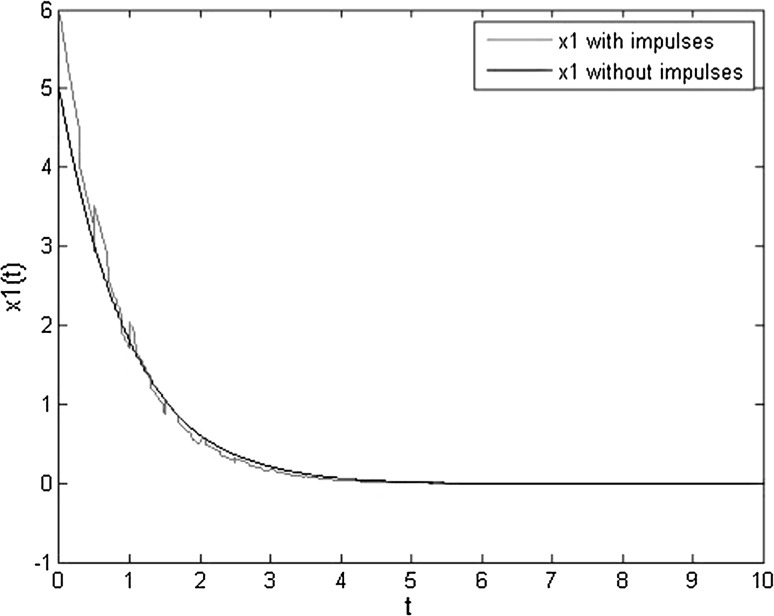If we let , the whole impulses can be described as, for destabilizing impulses and 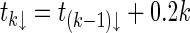for stabilizing impulses then the corresponding trajectories of the impulsive neural networks (1) are plotted as shown in Fig. 2, where one observes that, when 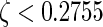, the neural networks (1) can be stabilized.

Fig. 2.

State trajectories of the memristive neural networks (10) with different conditions: a without impulses (blue); b the maximum impulsive interval of the stabilizing impulsive is 0.2 (green). (Color figure online)

Conclusions

In this paper, we investigated the exponential stability analysis problem for a class of general memristor-based neural networks with time-varying delay and time-varying impulses. To investigate the dynamic properties of the system, under the framework of Filippov’s solution, we can turn to the qualitative analysis of a relevant differential inclusion. By using the Lyapunov method, the stability conditions were obtained. A numerical example was also given to illustrate effectiveness of the theoretical results.