Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Sep 5;4:6290. doi: 10.1038/srep06290

Characteristics of the transmission of autoregressive sub-patterns in financial time series

Xiangyun Gao 1,2,3,4, Haizhong An 1,2,3,a, Wei Fang 1,2,3, Xuan Huang 1,2,3, Huajiao Li 1,2,3, Weiqiong Zhong 1,2,3
PMCID: PMC4155334  PMID: 25189200

Abstract

There are many types of autoregressive patterns in financial time series, and they form a transmission process. Here, we define autoregressive patterns quantitatively through an econometrical regression model. We present a computational algorithm that sets the autoregressive patterns as nodes and transmissions between patterns as edges, and then converts the transmission process of autoregressive patterns in a time series into a network. We utilised daily Shanghai (securities) composite index time series to study the transmission characteristics of autoregressive patterns. We found statistically significant evidence that the financial market is not random and that there are similar characteristics between parts and whole time series. A few types of autoregressive sub-patterns and transmission patterns drive the oscillations of the financial market. A clustering effect on fluctuations appears in the transmission process, and certain non-major autoregressive sub-patterns have high media capabilities in the financial time series. Different stock indexes exhibit similar characteristics in the transmission of fluctuation information. This work not only proposes a distinctive perspective for analysing financial time series but also provides important information for investors.

A financial market is a complex system whose behaviour is usually characterized as a financial time series1. Therefore, we can understand the structures and characteristics of a financial market by analysing the financial time series. Many researchers have proposed various time series models based on econometrics, e.g., the autoregressive integrated moving average model (ARIMA)2, bilinear time series model3, autoregressive conditional heteroskedasticity model (ARCH)4, generalized autoregressive conditional heteroskedasticity model (GARCH)5, threshold autoregression model6 and neural network models7,8. In non-linear analysis, researchers applied wavelet transform, analytic signal approach, multiscale entropy, multifractality and recurrence quantification analysis, etc., to quantify the complexity of time series, including issues such as characteristics, identifications and dynamics9,10,11,12,13,14,15,16.

However, there is another issue with time series: the transmission of fluctuation information. Most financial time series have the characteristic of fluctuation, and autoregressive equations can reflect the fluctuation information. Different sub-periods of the whole time series exhibit different autoregressive sub-patterns. If a long-term financial time series is divided into many fragments (sub-periods), the entire autoregressive pattern of the long-term financial time series can be described by the union of all the autoregressive sub-patterns: Sub_patterni. As the number of fragments increases, it obtains more autoregressive sub-patterns and creates a more detailed characterisation of the entire autoregressive pattern of the long-term financial time series. The evolution of the autoregressive sub-patterns forms a time-varying process of transmission, which can help us learn the fluctuant trend of financial time series. In the process of transmission, there are different types of autoregressive sub-patterns that transform into each other and form a transmission complex network (TCN).

To understand the characteristics of the autoregressive sub-patterns transmission, we should analyse the TCN. Complex network theory provides a good analysis approach. The core idea of complex network theory is to capture the essential characteristics of a real system by analysing the network structure of the system17,18,19. Dynamical information in time series can be identified using complex network theory. Zhang, Small and Xu found that the structure of the corresponding network depended on the dynamics of the series20,21. Researchers divided time series into fragments with fixed sizes and then constructed a corresponding complex network model to analyse the structure characteristics in the time series22,23,24. Lacasa et al. proposed the famous visibility graph algorithm, which can map all types of time series into networks25. Then, the Hurst exponent of fractional Brownian motion is studied using the visibility algorithm26. Thus far, the visibility algorithm has been used in many areas27,28. In our previous studies29,30,31, we have researched the transmission characteristics of correlation modes in time series based on complex network theory. We found power law distributions, ‘small-world' behaviour and transmission media in the process of the transmission.

In this paper, we investigated the transmission characteristics of autoregressive sub-patterns in financial time series. First, we proposed a new algorithm that maps the transmission of autoregressive sub-patterns into networks. Then, we studied the distributions of autoregressive sub-patterns, transmission pattern, the fluctuation clustering effect and the transmission media in the process of transmission, using the complex network analytical approach.

Data

The Shanghai (securities) composite index is used in this study. The index contains 5629 data points from December 19, 1990 to December 31, 2013 (http://app.finance.ifeng.com/hq/stock_daily.php?code=sh000001). The Shanghai (securities) composite index reflects the overall trend of the Shanghai stock exchange markets.

Definition of the autoregressive sub-patterns in financial time series

To define the autoregressive sub-patterns in financial time series, we first divided the financial time series into m dimensions. The fluctuation of each dimension can be represented by an autoregressive sub-pattern. Then, we defined the scale of the dimension as ω. The scale is the length of the dimension, i.e., each dimension contains ω time-series data.

graphic file with name srep06290-m1.jpg

where Yi is i-th dimension. This process utilises a sliding data-window to divide the time series into fragments. Yi + 1 contains 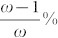Inline graphic of the information of Yi. The advantage of the sliding-window method is that it retains the feature of memory and transitivity between dimensions29,30,31. Thus, the number of dimensions m = n − ω + 1 (where n = 5629 is the number of observations).

Second, we built a regression equation for each dimension. The regression model of the j-th dimension can be described as follows:

graphic file with name srep06290-m2.jpg

where yj is the j-th Shanghai (securities) composite index, βj and αj are the parameters of the regression and εj is the residual error. The logarithmic process of y can remove the exponential trend.

We observed the autoregressive sub-patterns through the forms of autoregression of the financial time series. Then, we utilised the most basic and effective ordinary least squares (OLS) method to evaluate the values of the two parameters, β and α. Hence, we can obtain a series of values for parameters α and Inline graphic. Each combination of the two parameters involves a regression equation that describes the autoregressive sub-pattern of a dimension with scale ω.

Third, we allocated parameters β and α to the different intervals. We defined 0.05 as the interval extent of parameter α and 0.1 as the interval extent of parameter β. In addition, the significance of the regression model was tested by a Student's test, and the autocorrelation of the residual errors was tested by the Durbin-Watson (D-W) test. If the regression model of a dimension does not pass the significance test, we marked it as ‘P', and if the autocorrelation of the residues in a dimension did not pass the D-W test, we marked it as ‘D'. Thus, the combination of the parameters can be allocated into different intervals defined as autoregressive sub-patterns Sub_patterni. For example, the parameters of the i-th dimension are αi = 0.926, βi = 0.531, and the dimension passes both the significance test and the D-W test. Thus, Sub_patterni = α(0.9,0.95]β(0.5,0.6] reflects the autoregressive sub-pattern of the dimension. Several of the sub-patterns are marked as ‘P', ‘D' or ‘PD'. The results of the significance test depend on p-values. If the p-value is less than 5%, the model passes the significance test. A different scale ω (sample size) needs a different D-W test standard. Here, we referenced the ‘Durbin-Watson d statistic: significance points of dl and du at the 0.01 level of significance'32. This step can utilise the limited patterns to show the intrinsic transmission characteristics between the continuous patterns; it is necessary to construct the transmission networks.

Mapping the transmission of autoregressive sub-patterns into complex networks

Based on the above, we obtained the sequence of the autoregressive sub-patterns. This means that the autoregressive sub-patterns evolve into each other over time: 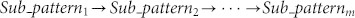Inline graphic (m = n − ω + 1). However, there are only a few types of autoregressive sub-patterns (the number of types of autoregressive sub-patterns less than m). Therefore, we defined the types of autoregressive sub-patterns as nodes and the transmissions over time as edges. The weight of an edge is the frequency of the transmission between two types of autoregressive sub-patterns. Thus, we mapped the transmission of autoregressive sub-patterns in the financial time series into a directed and weighted transmission complex network (TCN). As an example, we took the scale of the dimension ω = 50, as shown in Fig. 1.

Figure 1. Transmission complex network of autoregressive sub-patterns in Shanghai (securities) composite index time series.

Figure 1

Open in a new tab

(The scale of dimension ω = 50, with different colours representing different clusters. For details, please see analysis of clustering effect).

Results

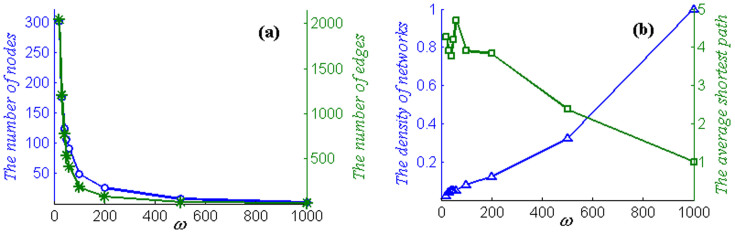
The TCN contains different types of autoregressive sub-patterns in financial time series and reflects the relationships between different sub-patterns. Each type of autoregressive sub-pattern plays a role in the topological structure of the TCN. Thus, we can observe the transmission characteristics of the fluctuation sub-patterns in financial time series through analysis of the TCN. Complex network theory provides many indices to identify the major autoregressive sub-patterns, clusters and transmission media. Moreover, we can set different scales of the dimension ω depending on the needs of the analysis. If the goal is to study the transmission characteristics of autoregressive sub-patterns based on short periods, scale ω can be set to a smaller value. If the goal is to understand the transmission characteristics based on long periods, scale ω can be set to a larger value. With an increase in scale ω, the numbers of nodes and edges in the corresponding complex networks decrease (Fig. 2 (a)). When ω = 500 the number of nodes is only eight, and the number of nodes is only three when ω = 1000. An increase in scale ω will hide the characteristics of diversity of the autoregressive sub-patterns. Thus, if the value of scale ω is too large, it is meaningless for studying the transmission of the autoregressive sub-patterns in financial time series. From Fig. 2 (b), on the one hand, when the values of scale ω are less than 100, the densities of the networks are less than 0.05. However, the density of the networks increases quickly with an increase in scale ω; when ω = 1000, the density of the networks reaches 1. On the another hand, the length of the average shortest path of networks decrease with an increase in scale ω. If a type of sub-pattern transforms into another, it will convert via only a few types of sub-patterns (fewer than 5).

Figure 2. Sensitivity analysis on ω.

Figure 2

Open in a new tab

(a) Number of nodes and edges for different values of scale ω. (b) Density of networks and average shortest path for different values of scale ω.

We took the scale of the dimension ω = 50 as an example, and the entire financial time series is divided into m = n − ω + 1 = 5580 dimensions. Then, we constructed the regression equations of the dimension and corresponding model tests 5580 times. The proportion of the dimensions that passes both the significance test and the D-W test is 94.01%, which also ensures the effectiveness of the study. After defining the autoregressive sub-patterns, we obtained 5580 autoregressive sub-patterns. However, only 106 types of sub-patterns appear in the TCN.

Major autoregressive sub-patterns in the transmission process (nodes)

We identified the major autoregressive sub-patterns through the transmission ability of the autoregressive sub-patterns, which can be measured by the weighted out-degree of the nodes. The weighted out-degree is a comprehensive indicator of the local information for a node; it considers not only the number of neighbouring nodes but also the weight between neighbours. The weighted out-degree of node 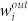Inline graphic is defined as

graphic file with name srep06290-m3.jpg

where Ni is the set of neighbours of node i, and wij is the weight from node i to node j. Nodes with greater out-degree weights are shown larger in Fig. 1 and have corresponding autoregressive sub-patterns with greater transmission abilities.

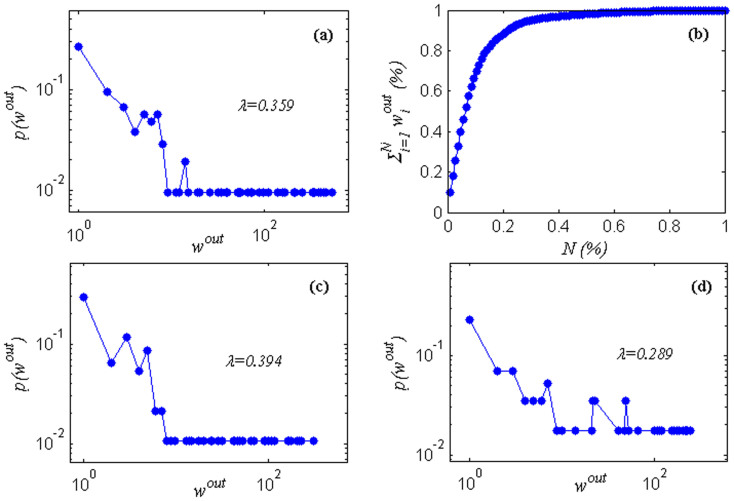
The weighted out-degree of a node in TCN follows a power-law distribution 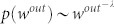Inline graphic, as shown in Fig. 3 (a). From Fig. 3 (b), we see that 14.28% of the autoregressive sub-patterns (15 types) shoulder 80.21% of the transmission ability in the TCN. This implies that a few types of autoregressive sub-patterns play a major role in the process of the transmission and that Shanghai securities market is statistically significantly not random under. A few types of autoregressive sub-patterns drive the oscillations of the financial market.

Figure 3. Distributions of the weighted out-degree of node.

Figure 3

Open in a new tab

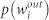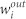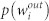(a) Double-logarithmic plot between the weighted out-degree of node Inline graphic and Inline graphic (the whole time series). (b) Cumulative distribution of the weighted out-degree of the node (sorted by the value of the weight out-degree of the nodes in descending order, N = 1,2,…,106). (c) Double-logarithmic plot between the weighted out-degree of node Inline graphic and Inline graphic (the first part of the time series). 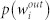(d) Double-logarithmic plot between the weighted out-degree of node Inline graphic and Inline graphic (the second part of the time series).

Moreover, to look further into the parts of the studied time series, we evenly divided the whole studied time series into two parts; the first part is from December 19, 1990 to July 2, 2002, and the second part is from July 3, 2002 to December 31, 2013. We found that both distributions of the transmission ability follow power-law distribution Inline graphic, as shown in Fig. 3 (c) and (d). The distributions of transmission ability between parts and whole have similar characteristics.

Transmission patterns (edges)

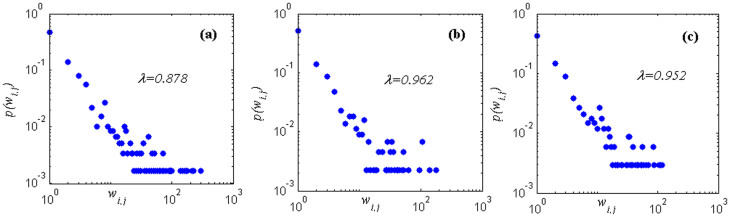
From the process above, we analysed the major autoregressive sub-patterns in the transmission process from the perspective of nodes. We also focused on transmission patterns between any two autoregressive sub-patterns (edges). The dualistic transmission pattern is defined as two nodes and the edge between them, i.e. Sub_patterni → Sub_patternj. There are 106 types of autoregressive sub-patterns in the TCN. Thus, theoretically, there are 1062 = 11,236 types of transmission patterns between two autoregressive sub-patterns but only 590 directed and weighted edges in the TCN. This means that 590 types of transmission patterns are present in the transmission process. From Fig. 4, we see that the distributions of the weights of the whole and the parts follow the power-law distribution 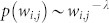Inline graphic. The result shows that there are just a few types of major transmission patterns.

Figure 4. Distributions of the weights of edges in TCN.

Figure 4

Open in a new tab

(a) Double-logarithmic plot between weights of the edges wi,j and p(wi,j) (the whole time series). (b) Double-logarithmic plot between weights of the edges wi,j and p(wi,j) (the first part of the time series). (c) Double-logarithmic plot between weights of the edges wi,j and p(wi,j) (the second part of the time series).

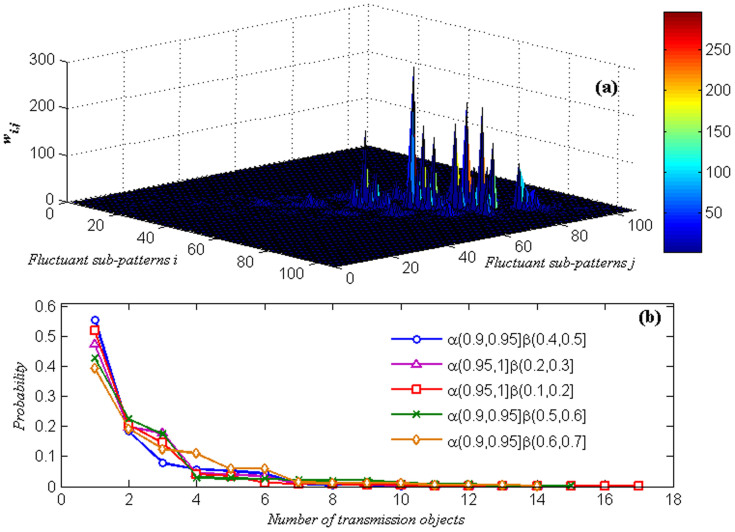
Although there are hundreds of types of autoregressive sub-patterns (106 nodes) and transmission patterns (590 edges), the major transmission patterns concentrate in a small area, as shown in Fig. 5 (a). Thus, there are significant laws and features in the transmission process of autoregressive sub-patterns in financial time series. In Shanghai stock exchange markets, the autoregressive sub-patterns do not transmit to others randomly. Rather, the transmission of fluctuation information is controlled by a few types of transmission patterns. In particular, certain autoregressive sub-patterns transmit into themselves. For example, transmission patterns α(0.9,0.95]β(0.4,0.5] → α(0.9,0.95]β(0.4,0.5], α(0.95,1]β(0.1,0.2] → α(0.95,1]β(0.1,0.2] and α(0.95,1]β(0.2,0.3] → α(0.95,1]β(0.2,0.3].

Figure 5. Transmission ability between autoregressive sub-patterns.

Figure 5

Open in a new tab

(a) Distributions of the transmission ability between two autoregressive sub-patterns. The transmission direction is from autoregressive sub-pattern i to j (i, j = 1,2,…,106). (b) The transmission probabilities of the major fluctuant sub-patterns (with a weighted out-degree of no less than 380).

Moreover, each type of autoregressive sub-pattern has many different transmission objects, but only a few types of autoregressive sub-patterns can be transferred with higher probability. The transmission probabilities of the major autoregressive sub-patterns (the top 5) are shown in Fig. 5 (b). Thus, the transmission patterns of major autoregressive sub-patterns are relatively stable in the transmission process.

Clustering effect on fluctuation in the transmission process

The analysis of clusters in the TCN can help us to understand the fluctuation clustering effect in the transmission process. The clustering effect on fluctuation is that some autoregressive sub-patterns transfer into each other more frequently rather than transferring into others in the process of the transmission; i.e., a type of autoregressive sub-pattern usually accompanies certain autoregressive sub-patterns. There are high transmission probabilities between these sub-patterns, and these sub-patterns form a sub-network. A sub-network is defined as a group of nodes that have a high density of edges within them but a lower density of edges between groups33. Blondel34 provided an algorithm to divide the TCN into clusters accurately and efficiently. The algorithm is based on modularity in the networks. (For details on the algorithm of dividing clusters, please see Ref. [25].)

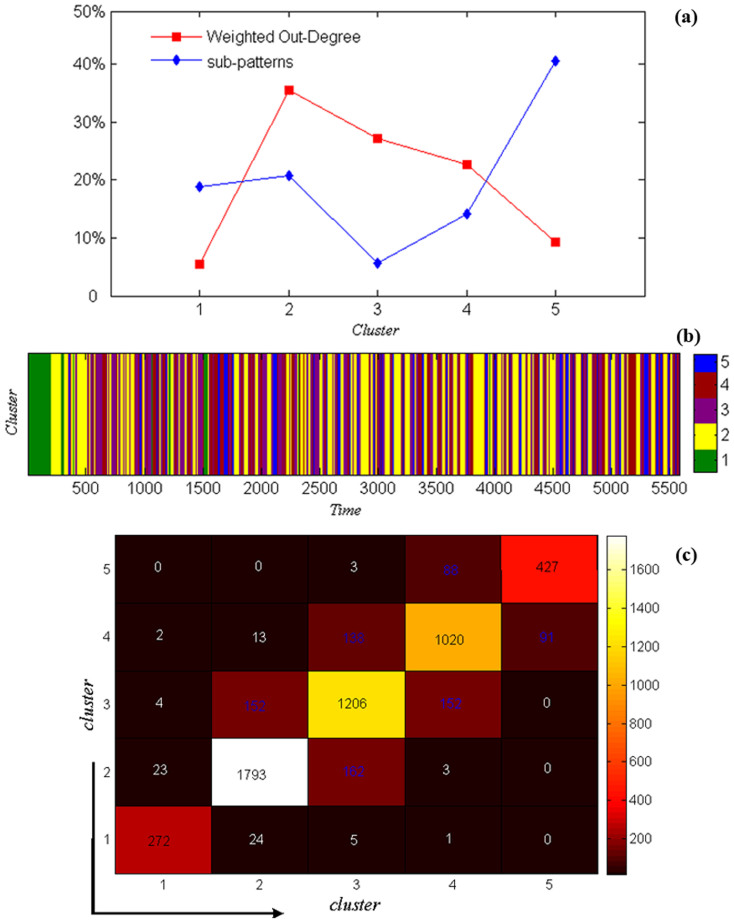
The results show that there are five clusters in the TCN (Fig. 1 shows different colours representing different clusters; 1-green, 2-yellow, 3-purple, 4-red and 5-blue). Fig. 6 (a) indicates that there is a relatively negative correlation between the number of types and the sum of the weighted out-degree of clusters. Thus, the cluster has strong transmission ability with only a few types of autoregressive sub-patterns.

Figure 6. Clustering effect in the transmission process.

Figure 6

Open in a new tab

(a) Number of sub-patterns and sum of the weight out-degree of each cluster (%). (b) Distribution of five clusters over time. (c) Distribution of transmission ability between clusters. The direction of transmission is from the vertical axis to the horizontal axis.

There are three major clusters in the TCN, clusters 2, 3 and 4, which have 85.30% transmission ability. The appearance of major clusters can imply a stable signal in the fluctuation of the financial time series and can provide investors with the important information that the financial time series fluctuates around a certain major cluster for a period. For example, although the Shanghai (securities) composite index time series experienced periods of sharp increase and sharp decline from 2006 to 2008 (time = 3691 to 4247), the autoregressive sub-patterns were relatively stable. In particular, cluster 2 shows an obvious clustering effect on fluctuation (see Fig. 6 (b)). However, clusters 1 and 5 contain 59.43% of the types of autoregressive sub-patterns, and the sum of weighted out-degree only accounts for 14.70% in the TCN. The appearance of clusters 1 or 5 can reflect an unstable signal for investors, implying that the autoregressive sub-patterns vary during corresponding periods. For example, at the beginning of the Shanghai securities market, the stock market mechanism was not perfect. Regulation with respect to daily price limits was in abeyance on May 21, 1992. Thus, the stock price was guided by the markets, and in only 5 days, the Shanghai (securities) composite index increased from 616.99 to 1421.57 (increasing as much as 130.40%). This turbulent period is marked by cluster 1 (the green areas in Fig. 6 (b)).

Moreover, different clusters have different autoregressive sub-patterns. The primary autoregressive sub-patterns of the three major clusters are α(0.95,1]β(0,0.4] (cluster 2), α(0.9,0.95]β(0.4,0.7] (cluster 3) and α(0.85,0.9]β(0.7,1] (cluster 4).Thus, investors can reference different autoregressive sub-patterns in different periods with a corresponding fluctuation clustering effect.

Transmission abilities differ between different clusters. The transmission ability TA,B between cluster A and cluster B is defined as

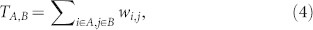graphic file with name srep06290-m4.jpg

where wi,j is the weight from node i to node j, node i belongs to cluster A and node j belongs to cluster B.

Fig. 6 (c) shows that there are three levels in the distribution of the transmission ability between clusters. The first level is that high transmission ability occurs in the interior of a cluster, which also proves that the cluster partition is effective. The second level of transmission ability occurs between clusters 2 and 3, clusters 3 and 4, and clusters 4 and 5. 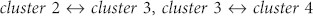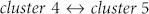This means that the changing of autoregressive sub-patterns in the transmission process mainly occurs in three cases: Inline graphic and Inline graphic. In the third level, the transmission ability is weak between these clusters. For example, cluster 1, 2 or 3 is difficult to transmit to cluster 5, and cluster 5 is difficult to transmit to cluster 1, 2 or 3. Thus, there are transmission media between the clusters that enable one autoregressive sub-pattern to transmit to another autoregressive sub-pattern.

Transmission media

If an autoregressive sub-pattern stands in the shortest path between two patterns, it plays the role of transmission media in the transmission process. The level of the transmission media effect can reflect the ability to control information in the transmission process. Only by transmitting through these media can certain autoregressive sub-patterns transmit to others. The transmission media play an important role in the topological structure of complex networks35. In the TCN, especially, the transmission media between fluctuation clusters are the necessary conditions for the significant changing of autoregressive sub-patterns, which can provide investors with important information on likely future changes. Thus, we can evaluate the normalised betweenness centralities of nodes that can denote the media ability of each autoregressive sub-pattern in the TCN36. The normalised betweenness centrality BCi of node i can be defined as

graphic file with name srep06290-m5.jpg

where gjk(i) is the number of shortest paths between nodes j and k that pass node i. gjk is the total number of shortest paths between nodes j and k. For higher normalised betweenness centralities, the media ability is stronger.

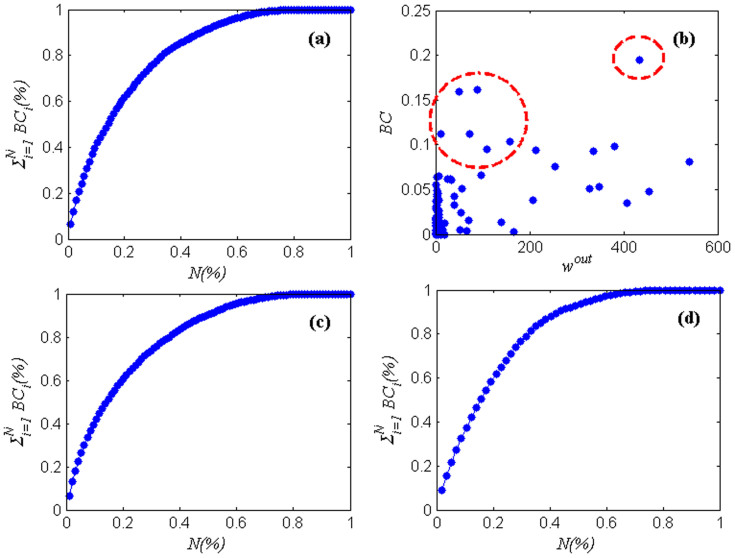
Fig. 7 (a) indicates that 25.47% of the autoregressive sub-patterns (21 types) shoulder 70.62% of the media ability, and the top 3 autoregressive sub-patterns shoulder 16.57% of the media ability in TCN. Thus, these autoregressive sub-patterns with high media abilities are significant for information changing and transmission in the Shanghai securities market. Autoregressive sub-patterns with high media ability play an important role in controlling information. In particular, the autoregressive sub-pattern α(0.95,1]β(0.1,0.2] (BC = 0.196, wout = 434) has the highest media ability and third transmission ability in the TCN, occupying an important position in the transmission process. We also found that certain lower-weighted out-degree autoregressive sub-patterns have higher media ability. Thus, although these autoregressive sub-patterns are not major factors in the financial market, they are important in mediating roles in the transmission process (see Fig. 7 (b)), e.g., α(0.8,0.85]β(1.1,1.2] (BC = 0.163, wout = 88) and α(0.75,0.8]β(1.5,1.6] (BC = 0.161, wout = 51). From the perspective of betweenness centrality of the network, these autoregressive sub-patterns imply a precursor to market changes. We should pay attention to these autoregressive sub-patterns. Moreover, the fluctuation of financial markets is not an uncorrelated random process. The law of fluctuation of financial time series is better understood by identifying the media in the transmission process of autoregressive sub-patterns.

Figure 7. Distributions of the normalised betweenness centrality in TCN.

Figure 7

Open in a new tab

(a) Cumulative distribution of the normalised betweenness centrality of node (sort by value of the normalised betweenness centrality of nodes in descending order, N = 1,2,…,106, the whole time series). (b) Distribution between weighted out-degree and normalised betweenness centrality. (c) Cumulative distribution of the normalised betweenness centrality of node (sort by value of the normalised betweenness centrality of nodes in descending order, N = 1,2,…,94, the first part of the time series). (d) Cumulative distribution of the normalised betweenness centrality of node (sort by value of the normalised betweenness centrality of nodes in descending order, N = 1,2,…,57, the second part of the time series).

Moreover, the media abilities of the whole and parts time series also have some similar features. A minority of types of sub-patterns shoulder the majority of the media ability. In the first part of the time series, 27.65% of the autoregressive sub-patterns (26 types) shoulder 71.17% of the media ability (see Fig. 7 (c)), and in the second part of the time series, 26.31% of the autoregressive sub-patterns (15 types) shoulder 71.07% of the media ability (see Fig. 7 (d)).

Discussion and Conclusions

We used 23 years of daily financial time series to study the features of transmission of the autoregressive sub-patterns. This study is different from other studies because researchers usually analyze the fluctuation of financial time series; however, our research focuses on the transmission of fluctuation, which is hidden in the fluctuation process of financial time series. Hence, we used an econometrical regression model to define the autoregressive sub-patterns quantitatively. Then, we contributed a directed and weighted transmission complex network from the financial time series.

We found that a few types of autoregressive sub-patterns drive the oscillations of the financial market. A few types of major transmission sub-patterns concentrate in a small area. The major autoregressive sub-patterns have stable transmission sub-patterns. There is a fluctuation clustering effect in the transmission process of autoregressive sub-patterns, and three levels exist in the distribution of transmission ability between clusters. The conversion of fluctuation clustering has three cases: 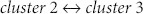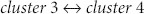Inline graphic, Inline graphic and Inline graphic. Other cases need transmission media to transmit, and the autoregressive sub-patterns that control the fluctuation transmission information in the financial time series can be identified by measuring the media abilities. Certain non-major autoregressive sub-patterns have high media abilities that play an important role in the transmission process. There are similar characteristic of the distributions of the transmission ability, the weights of edges and the normalised betweenness centrality of nodes between parts and whole.

These results show that the financial market is statistically significantly not random and provides important information for investors. First, investors should refer to different autoregressive parameters according to their terms of investment. Different observation periods lengths have different autoregressive sub-patterns. For example, for 50-day investment decisions, α(0.9,0.95]β(0.4,0.5] is the most important autoregressive sub-pattern. However, for 100-day investment decisions, investors should refer to a different autoregressive sub-pattern, because α(0.95,1]β(0.1,0.2] is the most important autoregressive sub-pattern (Table S1). Second, based on the present sub-pattern, investors could determine the probability and range of the next sub-pattern according to the results of the transmission pattern, clustering effect, and media ability. For example, if the present sub-pattern is in cluster 5, the next sub-pattern may be in cluster 5 or cluster 4 (see Fig. 6 (c)).

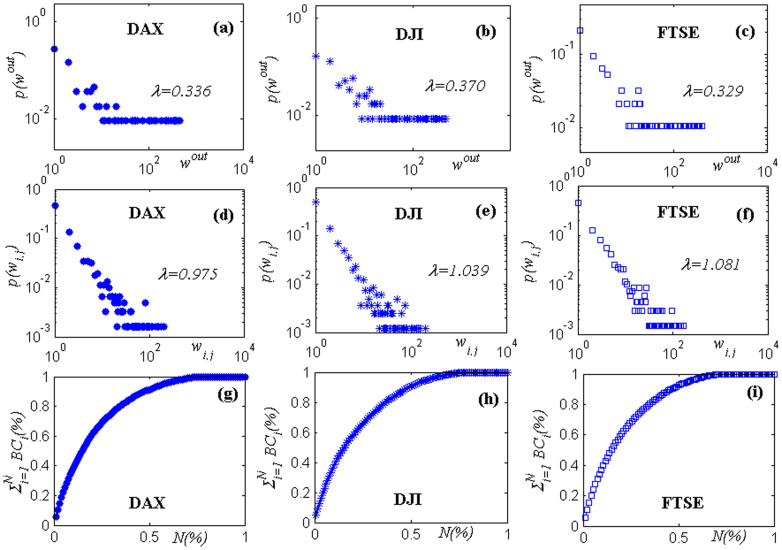
Moreover, we selected three other major stock indexes to study the transmission characteristics of the autoregressive sub-patterns (see Fig. 8). The three major stock indexes were the Deutscher Aktienindex Germany daily data (DAX), the Dow Jones Industrial Average Index (DJI) and the Financial Times Stock Exchange Index (FTSE), which contain 5696 (from July 1, 1991 to December 30, 2013), 5968 (from April 25, 1990 to December 31, 2013) and 5462 (from May 20, 1992 to December 31, 2013) data points, respectively. All of the distributions of the weighted out-degree of nodes and the weights of edges follow power law distribution. The power exponents of the distributions of the weighted out-degree are approximately 0.3, and the power exponents of the distributions of the weights of edges are approximately 1.0. Approximately 35% of the sub-patterns shoulder more than 80% of the media ability. These results indicate that these stock indexes exhibit similar transmission characteristics with the fluctuation information.

Figure 8. Distributions of weighted out-degree of nodes, weights of edges and cumulative distribution of normalised betweenness centrality of nodes of three different stock indexes: DAX, DJI and FTSE.

Figure 8

Open in a new tab

(a), (b) and (c) are the distributions of the weighted out-degree of nodes. (d), (e) and (f) are the distributions of the weights of edges. (g), (h) and (i) are the cumulative distribution of the normalised betweenness centrality of nodes.

In this study, our primary goal was to provide an approach to study transmission characteristics of autoregressive sub-patterns in time series. This can help us understand different characteristics of the transmissions based on different periods. However, financial time series are affected by various factors. Future analyses based on this study will consider these factors to study transmission characteristics of autoregressive sub-patterns under different time scales ω and different financial time series.

Author Contributions

H.A. and X.G. designed research; X.G., W.F. and X.H. performed research; W.F. and H.L. contributed new reagents/analytic tools; X.G., H.A., X.H., H.L. and W.Z. analysed data; and X.G. and X.H. wrote the paper. All authors reviewed the manuscript.

Supplementary Material

Supplementary Information

Table S1

srep06290-s1.pdf (156.9KB, pdf)

Acknowledgments

This research is supported by grants from the National Natural Science Foundation of China (Grant No. 71173199), the Fundamental Research Funds for the Central Universities (Grant No.2-9-2013-04) and the Science and Technology Innovation Fund of the China University of Geosciences (Beijing).

References

  1. Munnix M. C. et al. Identifying States of a Financial Market. Sci. Rep. 2, 644 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Box G. E. & Pierce D. A. Distribution of residual autocorrelations in autoregressive-integrated moving average time series models. J. Am. Stati. Assoc. 65, 1509–1526 (1970). [Google Scholar]
  3. Granger C. W. J. & Andersen A. P. An introduction to bilinear time series models. (Vandenhoeck und Ruprecht Göttingen, 1978). [Google Scholar]
  4. Engle R. F. Autoregressive conditional heteroscedasticity with estimates of the variance of united-kingdom inflation. Econometrica 50, 987–1007 (1982). [Google Scholar]
  5. Bollerslev T. Generalized autoregressive conditional heteroskedasticity. J. Econometrics 31, 307–327 (1986). [Google Scholar]
  6. Tong H. & Lim K. S. Threshold autoregression, limit-cycles and cyclical data. J. Roy. Stat. Soc. B 42, 245–292 (1980). [Google Scholar]
  7. Zhang G. P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 50, 159–175 (2003). [Google Scholar]
  8. Hansen J. V. & Nelson R. D. Neural networks and traditional time series methods: A synergistic combination in state economic forecasts. Ieee T. Neural Networ. 8, 863–873 (1997). [DOI] [PubMed] [Google Scholar]
  9. Ivanov P. C. et al. Scaling behaviour of heartbeat intervals obtained by wavelet-based time-series analysis. Nature 383, 323–327 (1996). [DOI] [PubMed] [Google Scholar]
  10. Schulte-Frohlinde V. et al. Noise effects on the complex patterns of abnormal heartbeats. Phys. Rev. Lett. 87 (2001). [DOI] [PubMed] [Google Scholar]
  11. Costa M., Goldberger A. L. & Peng C. K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 89 (2002). [DOI] [PubMed] [Google Scholar]
  12. Kantelhardt J. W. et al. Multifractal detrended fluctuation analysis of nonstationary time series. Physica A 316, 87–114 (2002). [Google Scholar]
  13. Amaral L. A. N. et al. Behavioral-independence features of complex heartbeat dynamics. Phys. Rev. Lett. 86, 6026–6029 (2001). [DOI] [PubMed] [Google Scholar]
  14. Zbilut J. P. & Webber C. L. Embeddings and delays as derived from quantification of recurrence plots. Phys. Lett. A 171, 199–203 (1992). [Google Scholar]
  15. Strozzi F., Zaldivar J. M. & Zbilut J. P. Recurrence quantification analysis and state space divergence reconstruction for financial time series analysis. Physica A 376 (2007). [Google Scholar]
  16. Zbilut J. P. & Webber C. L. Recurrence quantification analysis: Introduction and historical context. Int. J. Bifurcat. Chaos 17, 3477–3481 (2007). [Google Scholar]
  17. Barabási A.-L. & Albert R. Emergence of scaling in random networks. Science 286, 509–512 (1999). [DOI] [PubMed] [Google Scholar]
  18. Watts D. J. & Strogatz S. H. Collective dynamics of ‘small-world'networks. Nature 393, 440–442 (1998). [DOI] [PubMed] [Google Scholar]
  19. Newman M. E. & Watts D. J. Renormalization group analysis of the small-world network model. Phys. Lett. A 263, 341–346 (1999). [Google Scholar]
  20. Zhang J. & Small M. Complex network from pseudoperiodic time series: Topology versus dynamics. Phys. Rev. Lett. 96, 238701 (2006). [DOI] [PubMed] [Google Scholar]
  21. Xu X., Zhang J. & Small M. Superfamily phenomena and motifs of networks induced from time series. Proc. Natl. Acad. Sci. USA 105, 19601–19605 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Yang Y. & Yang H. Complex network-based time series analysis. Physica A 387, 1381–1386 (2008). [Google Scholar]
  23. Jiang Z., Yang H. & Wang J. Complexities of human promoter sequences. Physica A 388, 1299–1302 (2009). [Google Scholar]
  24. Donner R. V., Zou Y., Donges J. F., Marwan N. & Kurths J. Recurrence networks—A novel paradigm for nonlinear time series analysis. New J. Phys. 12, 033025 (2010). [Google Scholar]
  25. Lacasa L., Luque B., Ballesteros F., Luque J. & Nuño J. C. From time series to complex networks: The visibility graph. Proc. Natl. Acad. Sci. USA 105, 4972–4975 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Lacasa L., Luque B., Luque J. & Nuno J. C. The visibility graph: A new method for estimating the Hurst exponent of fractional Brownian motion. EPL (Europhysics Letters) 86, 30001 (2009). [Google Scholar]
  27. Qian M.-C., Jiang Z.-Q. & Zhou W.-X. Universal and nonuniversal allometric scaling behaviors in the visibility graphs of world stock market indices. J. Phys. A - Math. Theor. 43, 335002 (2010). [Google Scholar]
  28. Yang Y., Wang J., Yang H. & Mang J. Visibility graph approach to exchange rate series. Physica A 388, 4431–4437 (2009). [Google Scholar]
  29. Gao X. Y., An H. Z. & Fang W. Research on fluctuation of bivariate correlation of time series based on complex networks theory. Acta Phys. Sin. 61, 098902 (2012). [Google Scholar]
  30. Gao X. Y., An H. Z., Liu H. H. & Ding Y. H. Analysis on the topological properties of the linkage complex network between crude oil future price and spot price. Acta Phys. Sin. 60, 068902 (2011). [Google Scholar]
  31. An H., Gao X., Fang W., Huang X. & Ding Y. The role of fluctuating modes of autocorrelation in crude oil prices. Physica A 393, 382–390 (2014). [Google Scholar]
  32. Gujarati D. N. & Porter D. C. Basic Econometrics. 972–973 (McGraw Hill Higher Education, 2009). [Google Scholar]
  33. Mucha P. J., Richardson T., Macon K., Porter M. A. & Onnela J.-P. Community structure in time-dependent, multiscale, and multiplex networks. Science 328, 876–878 (2010). [DOI] [PubMed] [Google Scholar]
  34. Blondel V. D., Guillaume J.-L., Lambiotte R. & Lefebvre E. Fast unfolding of communities in large networks. J. Stat. Mech - Theory E. 2008, P10008 (2008). [Google Scholar]
  35. Freeman L. C. Centrality in social networks conceptual clarification. Soc. Network. 1, 215–239 (1979). [Google Scholar]
  36. Goh K.-I., Oh E., Kahng B. & Kim D. Betweenness centrality correlation in social networks. Phys. Rev. E 67, 017101 (2003). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Table S1

srep06290-s1.pdf (156.9KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES