Abstract
Wet-chemistry methods have crucial advantages for the synthesis of nanostructures, including simple, low-cost, large-area, and low-temperature deposition on almost arbitrary substrates. Nevertheless, the rational design of improved wet-chemistry procedures is extremely difficult because, in practice, only post-synthesis characterization is possible. In fact, the only methods for on-line monitoring the growth of nanostructures in liquids are complex, expensive and introduce intricate artifacts. Here we demonstrate that electro-mechanically resonating substrates and in-situ temperature sensors easily enable an accurate real-time investigation of reaction kinetics and, in combination with conventional SEM imaging, greatly facilitate the rational design of optimized synthesis procedures; in particular, such a simple approach provides useful insight for the development of processes where one or more key parameters are dynamically adjusted. As a proof-of-concept, first, we accurately characterize a process for fabricating arrays of ZnO nanorods; afterwards, we design a dynamic-temperature process that, in comparison with the corresponding constant-temperature procedure, is almost-ideally energy efficient and results in ZnO nanorods with improved characteristics in terms of length, aspect ratio, and total deposited nanorods mass. This is a major step towards the rational design of dynamic procedures for the solution growth of nanostructures.
Wet-chemistry methods1 are very widely used for growing nanostructures because of many crucial advantages, including simple, low-cost, large-area, and low-temperature deposition on almost arbitrary substrates. Nevertheless, the properties of solution-grown nanostructures are typically affected by large spread and poor reproducibility, which are likely the consequences of limited understanding of the nucleation and growth mechanisms, poor process characterizations, and insufficient insight for rational process design2. An ideal strategy for overcoming these issues would be to monitor in real-time the nanostructures synthesis in liquids which, however, is substantially more complex than for other growth methods3. A powerful tool for monitoring the surface nucleation and growth in solution is liquid-cell TEM (Transmission Electron Microscope)4,5,6,7,8 which allows to observe, with atomic-level resolution, the early formation and aggregation of nanoparticles as well as the straightening of the chain5. On the other hand, liquid-cell electron microscopy requires sophisticated test microfluidic devices because of the extremely small penetration depth of electrons into liquids5,6,7,8; clearly, such an experimental setup is completely different from conventional wet-chemistry (standard, large glass containers). Moreover, high-energy probing electron beams can affect nanostructures growth and add intricate artifacts such as heating, charging, production of free radicals, radiolysis, and bubbling. Electromagnetic waves can also be used, instead of electrons, as probes for obtaining real-time information on the growth of nanostructures, both at system level or at single nanostructure level2,9,10,11,12; however, even in these cases, the experimental set-up is complex (e.g. requiring synchrotron accelerators) and can introduce awkward side-effects due to the high photon intensity, such as the formation of highly reactive radicals. In conclusion, microscopy approaches can provide unique insight into the mechanisms of nanostructures nucleation and growth, including at single-nanostructure level, but, first, are extremely complex and expensive, and, second, are not easy to be applied to the optimization of conventional wet-chemistry syntheses (e.g. it would be impossible to use the TEM for monitoring the growth in typical glass containers and on time-scales of many hours).
Therefore, at present, there are no effective tools for on-line monitoring, even at system level, the growth of nanostructures during conventional wet-chemistry processes. As a result, the accurate characterization of reaction kinetics is extraordinarily complex. In fact, since only post-synthesis analyses are possible, studying the reaction kinetics requires, for each experimental condition (defined by all the relevant parameters, including temperature, concentrations of all the chemicals,…), several tests performed with different growth-times and followed by the systematic post-synthesis analysis of all the samples (e.g.13,14,15,16). Additionally, even the simple determination of the minimum temperature for a certain growth process would require many distinct experiments. Besides, on-line monitoring could greatly facilitate the rational design of improved synthesis procedures, with special reference to the dynamic control of process parameters. In fact, though, at present, process parameters (e.g. temperature and chemical concentrations) are generally kept constant, it has already been demonstrated that proper adjustments of process parameters during the synthesis can be very beneficial17,18. Finally, on-line monitoring can enable the implementation of feedback19 assisted solution growth, which may obviously result in an even more accurate control of the nanostructures properties.
Here, we use electro-mechanically resonating substrates and in-situ temperature sensors for on-line monitoring, at system-level and with negligible artifacts, the solution growth of ZnO nanostructures; in particular, first, we accurately study a process for fabricating arrays of high density, well separated, vertically aligned ZnO nanorods and then, based on this characterization and on conventional Scanning Electron Microscope (SEM) imaging, we design a dynamic-temperature control process that, in comparison with constant-temperature syntheses, is almost-ideally energy efficient and results in nanorods with improved characteristics in terms of length, aspect ratio, and total deposited nanorods mass.
Results
Among many techniques for monitoring chemical reactions at liquid/solid interfaces4, quartz crystal microbalances (QCMs) or, more in general, electro-mechanical resonators, are uniquely simple and low-cost. Nevertheless, as observed by Zaera4, surprisingly, these devices have been almost exclusively used for biochemical sensing, most likely because of poor communication among different disciplines. In fact, viscous coupling, surface roughness, surface stresses, and both the liquid conductance and dielectric constant may complicate the use of electro-mechanical resonators in liquids21 and can largely reduce the quality factor. However, in most practical cases the reduction of the quality factor may simply be solved by using, instead of oscillator circuits, network analyzers which, besides providing more accurate information (i.e. measurement of the impedance within a certain bandwidth rather than only of the resonating frequency), can characterize resonators even when the quality factors become very low due to liquid parasitics (liquid conductance and liquid capacitance) or to the high deposited nanowires mass. Moreover, with reference to the effects on the resonant frequency of viscous coupling, surface roughness, surface stresses, liquid conductance and liquid dielectric constant, by comparing the resonant frequencies in-liquid and after emersion, we found that the in-liquid resonant frequency measurement can still provide a reasonable estimation (around ±7.5% error) of the in-air resonant frequency, which is directly proportional to the total nanorods deposited-mass (see Supplementary Information). We also stress that these spurious effects may be similar in similar experiments and, therefore, their contributions can compensate when performing comparative studies (e.g. growth experiments with two slightly different chemical concentrations). Finally, we mention that in extreme cases of nutrient solutions with very high ion concentrations and, therefore, very high liquid conductivities, it would be possible to insert the resonator in a chamber so that only one electrode is exposed to the liquid environment (i.e. no parasitic liquid conductance between the two electrodes). Among all possible electro-mechanical resonators, we have chosen the simplest and most widely used type, i.e. standard, low cost, commercially available AT-cut quartz crystals; however, since the addition of a seed-layer may enable nanostructures growth on practically all substrates1, any type of electro-mechanical resonators suitable for in-liquid operations, eventually coated by a passivation layer and by a seed-layer, could be used.
For small mass loading Δm, the variation Δfm of the quartz resonant frequency in air can be described by the Sauerbrey equation
 |
where fR,IN is the initial resonant frequency, S is the piezoelectric active area, µQ and ρQ are the shear stiffness and the mass density of the quartz, respectively. In practice, a 20 MHz QCM, even in liquids (i.e. with a resolution for the resonant frequency measurement around 10 Hz), can easily detect mass changes per unit area as low as 10 ng/cm2, i.e. 100 ag/μm2, which is enough to detect particles in the small nanometer range. As an example ZnO nanoparticles with a number density of 10/μm2 and an hemispheric morphology with 10 nm radius would have a weight per unit area around 120 ag/μm2. Therefore, ultra-low cost electromechanical resonators, like commercial quartz crystal microbalances (prices less than 1$) are already suitable for detecting minuscule nanoparticles and, analogously, extremely small variations of the lengths (fractions of nanometers) of nanostructures growing on the substrate. We also mention that it would be possible to reach even higher sensitivities by using high-performance electromechanical resonators22. Obviously, electromechanical resonators only detect nanoparticles attached to their surfaces and, therefore, are only sensitive to the growth of nanostructures on the substrate and not to other colloidal nanoparticles which remain in solution.
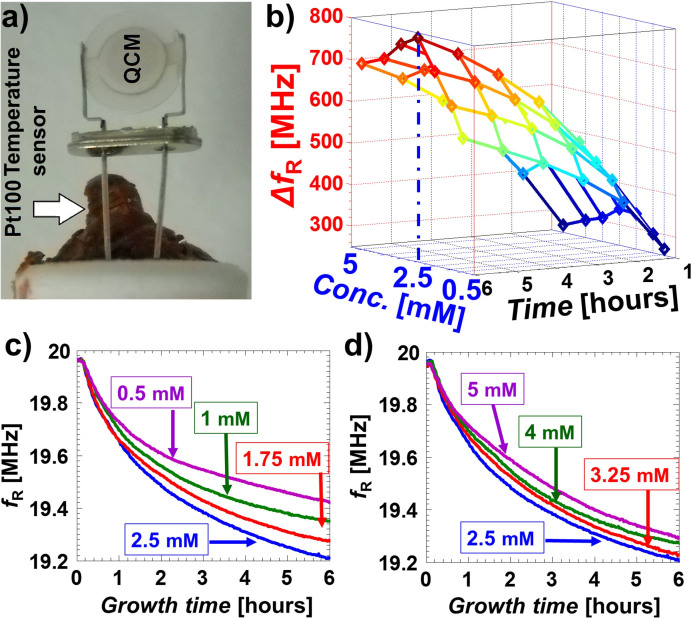
With reference to nanostructures, we focused on the synthesis of arrays of ZnO nanorods because of their wide applications including nanogenerators23,24,25,26, laser27,28, piezotronics29,30, piezo-photo-tronics30,31,32 and sensors with superior performances20,33,34. As an illustrative example, we have considered an extremely simple, single-step, double-sided method for growing high-density, well-separated, vertically aligned ZnO nanorods on quartz resonators by means of the most typical nutrient solution20, i.e. DI water containing an equimolar concentrations of zinc nitrate and HMTA35. As shown in figure 1(a), in order to on-line monitor the ZnO nanostructures reaction kinetics, as a uniquely simple arrangement, we have immersed inside a sealed Pyrex bottle containing the standard nutrient solution a Teflon bar supporting both the quartz resonator and the adjacent Pt100 resistive temperature sensor, preliminarily covered by an inert, high-temperature silicone paste in order to avoid parasitic electrical paths between its terminals. The very small distance (around 5 mm) between the temperature sensor and the substrate and the relatively high thermal conductivity of the nutrient solution allow to accurately measure the substrate temperature. First, we kept a constant 90°C solution temperature and varied the equimolar zinc nitrate and HMTA concentrations from 0.5 mM to 5 mM; figure 1(b) shows the variation with time of the resonant frequency (with respect to the initial resonant frequency) for different concentrations of zinc nitrate and HMTA and at different time intervals (time step equal to one hour); figure 1(c) (0.5 mM to 2.5 mM) and 1(d) (2.5 mM to 5 mM) show the time evolution of the resonant frequencies due to the growth of ZnO nanostructures. Though Eq. (1) relates the resonant frequency variation to the mass variation, we prefer to explicitly report in the graphs only the resonant frequencies because these frequencies are directly measured; by contrast, an accurate on-line estimation of the mass deposited on the quartz would require to estimate the variation of the resonant frequency associated to liquid loading, which also depends on the surface roughness. However, by comparing the resonant frequencies in-liquid and after emersion, we found that the in-liquid resonant frequency measurement can still provide a reasonable estimation (around ±7.5% error) of the in-air resonant frequency, which is directly proportional to the total nanorods deposited-mass (see Supplementary Information); moreover, when performing comparative analyses of the reaction kinetics the effects of similar liquid loadings would obviously be similar. Remarkably, the excellent mass-resolution of microbalances allows to distinguish minimal differences among the kinetics relative to slightly different experimental conditions (e.g. with reference to figure 1(c) and 1(d), it would be very difficult to obtain such accurate information on reaction kinetics from the analyses of SEM images). We also performed test experiments with quartzes having different resonant frequencies, with or without on-line monitoring, and verified that on-line monitoring results in negligible artifacts (see Fig. S1 in the Supplementary Information).
Figure 1. On line monitoring of ZnO nanostructures reaction kinetics with different equimolar concentrations of the reagents (zinc nitrate and HMTA).
(a) Photograph of the quartz crystal microbalance and the adjacent Pt100 resistive temperature sensor, both supported by a Teflon bar; the temperature sensor is covered by an inert high-temperature silicone paste. (b) Reaction kinetics, at 90°C, quantified by the variation, for different growth times (time-step equal to one-hour), of the resonant frequency at different concentrations. (c) and (d) Resonant frequencies of the quartz-substrates versus time during the nanorods growth, at 90°C, for different equimolar concentrations of HMTA and zinc nitrate, ranging from 0.5 mM to 2.5 mM (c) and from 2.5 mM to 5 mM (d).
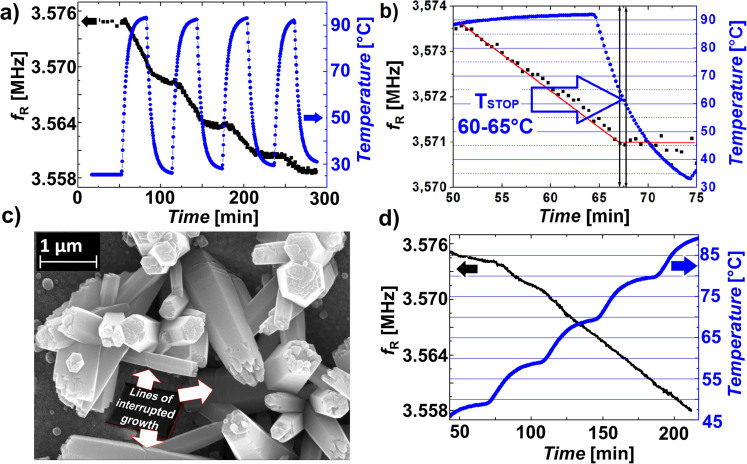
The ability to on-line monitor the in-liquid synthesis of nanostructures offers the opportunity to study, with unprecedented ease and accuracy, the effects of temperature. For instance, figure 2(a) shows that cyclically moving the growth container from a hot bath (92°C) to a cold bath (25°C for 30 minutes) and vice versa, the nanostructure growth is enabled or disabled at high and low temperatures, respectively. Figure 2(b) shows a similar experiment with a very clear interruption of the growth when the temperature goes below the threshold temperature (between 60°C and 65°C). The evaluation of the threshold temperature, which would be much more complex and time consuming with conventional approaches, can be crucial for the rational design of improved processes (see later). Our results also show that cycled stop-and-go growth processes obtained by alternating low (25°C) and high (92°C) temperatures do not significantly modify the growth rate (see Fig. S2 in the Supplementary Information), even when the stop-and-go phases degrade the single-crystal nature of the nanorods, as in case of figure 2(c) which shows lines of interrupted growth and the conversion of a single nanorod into many entangled ZnO nanostructures. Figure 2(d) shows the microbalance resonant frequency and the temperature in an experiment performed with an increasing stepped temperature (room temperature, 50°C, 60°C, 70°C, 80°C, 90°C), thus confirming that the regular growth starts only above 60°C; once the temperature goes above the threshold, further increases do not appreciably modify the rate of nanorods-mass deposition.
Figure 2. Experiments with time-varying temperature for quartzes with nominal initial resonant frequency 3.579 MHz and equimolar 5 mM concentration of zinc nitrate and HMTA.
(a) fR and temperature when the Pyrex container is cyclically moved from hot bath (92°C) to cold bath (25°C for 30 minutes) and vice versa. (b) Identification of the threshold temperature (between 60°C and 65°C); the growth rate is not significantly changed until the temperature stays above the threshold. (c) SEM images of nanostructures grown with alternating stop-and-go phases that degrade their single-crystal nature, as evident from the lines of interrupted growth and from the conversion of single nanorods into many entangled ZnO nanostructures. (d) fR and temperature during growth with time-dependent temperature (10°C steps from 50°C to 90°C); the growth rate is not significantly modified by increases of temperature above the threshold.
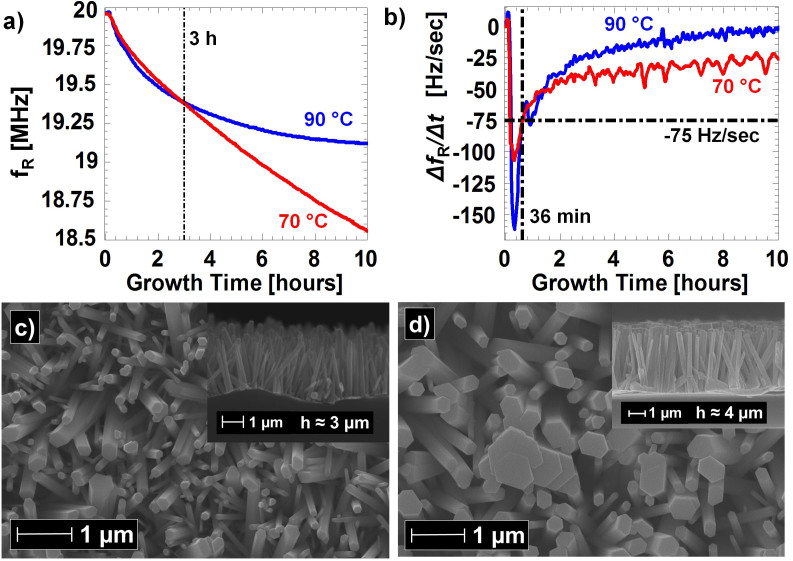
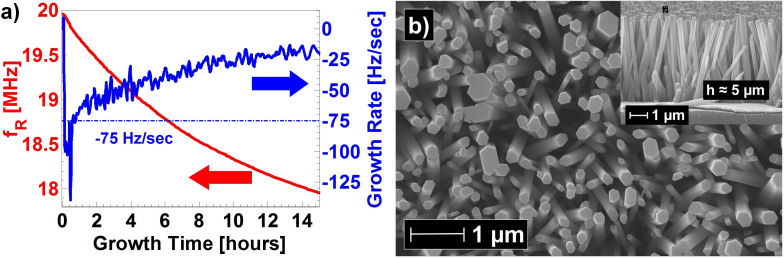
In principle, wet-chemistry synthesis procedures can take advantage of the dynamic control of the key process parameters, such as chemical concentrations or temperature. For instance, it has already been shown that, in presence of a seed layer and of polyethylenimine (PEI), temperature variations during the synthesis can prove useful and, as an example, reducing, after 10 minutes, the temperature by a few degrees (88°C to 85°C) allowed to avoid the fusion at the roots of ZnO nanowires17; similarly, a stepped increase of the temperature can improve the crystallinity of ZnO nanowires18. However, obviously, the development of dynamic-parameters processes is complicated by the absence of effective tools for on-line monitoring. Here we demonstrate that the proposed method for in-situ tracking the reaction kinetics and the solution temperature, in combination with conventional SEM imaging, can greatly facilitate the rational design of dynamic-parameters procedures for the solution-growth of ZnO nanorods. Specifically, first, we have optimized the reagents concentration (figure 1). Second, we found the threshold temperature for the solution growth (between 60°C and 65°C, see figure 2(b)). Third, we verified that even in presence of large temperature variations, if the temperature remains above the threshold, the growth continues (figure 2) and the crystallinity of the nanorods is preserved, as evident from the nearly perfect hexagonal cross-section of the nanorods. Fourth, as shown in figures 3(a) (resonant frequencies) and 3(b) (derivatives of the resonant frequencies), we have characterized the conventional constant-temperature process at 90°C and at 70°C (70°C is slightly, but reliably, above the threshold temperature and thus is the best choice for minimizing the energy-consumption associated to the synthesis); as evident in figures 3(a) and 3(b), at higher temperatures, the nanorods growth, though initially favored, since the reactions in solution are also enhanced by higher temperatures, at longer times, slows down and finally saturates because of shortage of reactants (also in agreement with previous investigations on the decay of the concentration of zinc ions in solution36). Fifth, SEM imaging confirms that nanorods grown at 90°C are shorter than nanorods grown at 70°C (see inset of figures 3(c) and 3(d)); we mention that, in order to allow fair comparisons, we considered the SEM images of the best nanorods we could obtain at 90°C, i.e. samples taken out in proximity of the saturation, as, consistently with13, we also observed that keeping the nanorods in solution for excessive times may result in a slow and gradual dissolution of parts of the nanorods due to the low concentration of zinc ions in solution. Sixth, SEM imaging also shows that nanorods grown at 90°C have smaller diameters than nanorods grown at 70°C (see figures 3(c) and 3(d)), consistently with the early saturation of the 90°C synthesis. Based on these considerations, we have designed a dynamic-temperature control process that, in comparison with conventional constant-temperature methods, is almost-ideally energy efficient and results in nanorods with improved characteristics in terms of length, aspect ratio, and total deposited mass on the substrate. In practice, as shown in figure 4(a), we started the synthesis at 90°C, thus achieving faster initial growth and smaller diameters, and then, in order to avoid excessive consumption of reactants and growth-saturation, we reduced the temperature to 70°C when the derivative of the resonant frequency reached about –75 Hz/s (i.e. the value where the derivatives of the resonant frequencies obtained in the constant-temperatures experiments intersect, see figure 3(b)). In these 90°C–70°C experiments, in comparison with the best 70°C (lengths and aspect ratios around 3.9 µm and 13.5, respectively) and 90°C experiments (lengths around 2.7 µm and aspect ratio of about 13.5), we obtained nanorods with higher length (up to 5 µm) and aspect ratios (up to 20); as expected, the diameter, average 280 nm, was smaller than the diameter of nanorods grown at 70°C, average 310 nm, but obviously larger than nanorods grown at a 90°C, average 200 nm (at 90°C the shortage of reactants also suppresses the lateral growth). For instance, figure 4(b) shows nanorods grown with the proposed 90°C–70°C process for 15 hours.
Figure 3. Constant-temperature procedures for the solution-growth of ZnO nanorods (90°C and 70°C).
(a) Resonant frequencies of quartz substrates during syntheses performed at 90°C and at 70°C. (b) Derivatives, with respect to time, of the resonant frequencies of quartz substrates during syntheses performed at 90°C and at 70°C (the synthesis at 70°C is initially slower but becomes faster after about 36 minutes). (c) Top view SEM images of the ZnO nanorods grown at 90°C (cross-section in the top-right inset). (d) Top view SEM image of the ZnO nanorods grown at 70°C (cross-section in the top-right inset).
Figure 4. Dynamic-temperature procedure for the solution-growth of ZnO nanorods (90°C – 70°C).
(a) Resonant frequency and its derivative for a synthesis started at 90°C and continued at 70°C after the derivative of the resonant frequency reached about - 75 Hz/s. (b) Top view SEM image of the nanorods grown with the proposed two-temperatures dynamic process (cross-section in the top-right inset; the nanorods have enhanced length and aspect ratio, see text).
The large reduction of temperature to a value only slightly larger than the threshold temperature for most of the synthesis duration allows to obtain an almost-ideal energy efficiency (obviously, the short period at higher temperature gives a comparably minor contribution to the total energy consumption), while keeping the advantages of initiating the growth at higher temperature; in particular, reducing the temperature from 90°C to 70°C results in about 40% energy saving for an environment temperature of 21°C. We stress that the energy efficiency can obviously be crucial for environmentally-friendly syntheses, especially in view of the so many possible high-volume applications of ZnO nanowires and, more in general, of quasi-1D nanostructures grown in solution.
Remarkably, though using the microbalance and the in-situ temperature sensor has been instrumental to the rational design of the proposed process, for maximum simplicity, the solution temperature can be reduced after an initial high-temperature phase without any monitoring system and, therefore, without a resonating substrate. In order to explore this possibility, we compared the three types of synthesis (90°C, 70°C, and 90°C–70°C) on silicon covered by a gold thin film without the assistance of real-time monitoring. In the 90°C–70°C experiment, we reduced the temperature after 36 min (i.e. similar to the on-line monitoring experiment). The results are in good agreement with the experiments on electromechanical resonators (see Fig. S3 in the Supplementary Information).
Discussion
Despite many previous studies on the wet-chemistry of ZnO nanostructures, with the exception of extremely complex and expensive approaches (e.g. in-liquid TEM or x-rays) there are no methods for real-time monitoring the growth of ZnO nanostructures in liquids, so that the only option is to perform, for each experimental condition (i.e. all the relevant parameters, such as temperature and concentrations of chemicals, kept constant), a multitude of growth-experiments, each one with a distinct growth-time, followed by the brute-force systematic investigation (e.g. by SEM) of all the samples. Such an approach, of course, would be extremely expensive and time-consuming; for these reasons, there are only very few accurate investigations on the kinetics of wet-chemistry synthesis of ZnO nanostructures, and, in most studies, only basic information are given (e.g. it may be mentioned that the growth saturates and that nanowires can have a certain maximum length, but the exact kinetics and how the growth saturates are almost never discussed).
Our approach allows to characterize the kinetics of the growth with unprecedentedly high accuracy; for instance, we found that, with our growth method, 2.5 mM (equimolar concentration of HMTA and zinc nitrate) is the best concentration for fastest nanowires growth at 90°C (Figures 1b, 1c, 1d); moreover, we have also determined the threshold temperature for growth with a single experiment (Figure 2b).
The complexity of measuring the kinetics of wet-chemistry processes has long been an obstacle towards the rational design of improved processes; for this reason, only very simple processes are generally adopted and, in particular, though, obviously, constant growth-conditions are sub-optimal, very few “dynamic” wet-chemistry processes have been reported so far, with special reference to dynamic changes of the temperature. In fact, though, of course, dynamic adjustments of the temperature may have advantages, the growth-temperature is almost always kept constant because it would not be easy to decide when and how the temperature should be changed. By contrast, as a demonstration of the practical relevance of our more accurate kinetics-characterization, we have rationally designed a dynamic-temperature growth process which allows to simultaneously minimize power consumption and grow ZnO nanorods with improved characteristics in terms of length, aspect ratio, and total deposited nanorods mass. Remarkably, we have also verified that, once the process has been rationally improved by taking advantage of electro-mechanical resonators and in-situ temperature sensors, the same improvements are found on non-resonating substrates (Figure S3 and related discussion). Though we have considered as an especially relevant example the optimization of the recipe based only on zinc nitrate and hexamine (almost neutral pH, compatible with biological elements, no aggressive and dangerous chemicals), our approach is general and represents a major step towards the effective rational design of dynamic procedures for the solution growth of nanostructures.
In conclusion, the real-time monitoring of nanostructures growth in liquids, at both system and single-nanostructure levels, is very complex as both liquid-cell TEM and in-situ X-ray microscopes are expensive, cause intricate artifacts, and are restricted to impractically small solution volumes and short growth times. As a result, in wet-chemistry syntheses the accurate characterization of the reaction kinetics is very difficult and, consequently, the rational design and the optimization of wet-chemistry procedures is very challenging. Here, we demonstrated that electro-mechanically resonating substrates and in-situ temperature sensors can provide, without artifacts, real-time system-level information on the reaction kinetics of wet-chemistry procedures. As a proof of concept, we have chosen the simplest and most widely used types of electromechanical resonators, AT quartz crystals, as substrates and monitored the high-density growth of ZnO nanorods by measuring both the resonant-frequency and the substrate temperature. The proposed approach is extremely simple and low cost, can be applied to any type of electro-mechanical resonators, introduces negligible artifacts, and offers important insights into growth reactions and their kinetics; as an especially significant example, we have studied the kinetics of ZnO nanorods syntheses at different temperatures and with different chemicals concentrations, the optimum concentration of reagents, and the reaction threshold temperature. Afterwards, we have shown that combining our results with standard post-synthesis SEM analysis can greatly facilitate the rational design of optimized wet-chemistry fabrication procedures and, as an example, we have proposed an almost-ideally efficient, dynamic-temperature synthesis process which, in comparison with conventional constant temperature methods, yields nanorods with improved length, aspect ratio, and total deposited mass. Our on-line monitoring approach is extremely simple and low cost and does not introduce detectable artifacts. The proposed strategy, besides enabling an accurate characterization of reactions kinetics and an effective process optimization, opens the way to the rational design of fabrication procedures with dynamic control of process parameters, including feedback-assisted solution growth.
Methods
We used commercial quartzes with silver electrodes as electro-mechanical resonators; for generality, we considered several types of low-cost AT-cut quartzes with different initial resonant frequencies equal to:
20 MHz (Fox Electronics FOXLF200-20),
15 MHz (Euroquartz 14.7456MHz HC49/30/50/-40+85/18pF/ATF),
10 MHz (Euroquartz 10.000MHz HC49/30/50/-40+85/18pF/ATF)
3.5789 MHz (Euroquartz 3.579545MHz HC49/30/50/-40+85/18pF/ATF).
The cap of the quartzes has been opened by cutting the metallic cover near the base (see20 for details). The nutrient solution was prepared by mixing in DI water (ρ > 18 MΩ·cm) equimolar concentrations of zinc nitrate and hexamethylenetetramine (HMTA) bought from Sigma Aldrich. Each quartz was kept vertical in the middle of a sealed Pyrex container by means of a Teflon bar which also supported a Pt100 resistive temperature sensor covered by an inert high-temperature silicone paste for avoiding parasitic parallel resistances between the terminals of the Pt100 sensor (see figure 1(a)). The Pyrex container was heated by immersion inside a pre-heated thermal bath. The admittances of the quartz substrates were continuously recorded by an Agilent E5070 network analyzer. SEM images were taken with a FE-SEM (LEO SUPRA 1250, Oberkochen, Germany) after covering the samples with thin gold layers.
Author Contributions
A.O. and C.F. conceived and designed the experiments. A.O. performed all the experiments and the measurements. A.O. and C.F. analyzed the data, discussed the results, and wrote the manuscript.
Supplementary Material
Supplementary Information
Acknowledgments
The authors thank Massimo Palmacci and Ivan Pini for help with preparing the experimental equipment. The authors thank Dr. Giuseppe Arrabito for stimulating discussions. This research has been supported by the Italian Institute of Technology (Project Seed - API NANE) and by MIUR (FIRB – Futuro in Ricerca 2010 Project “Nanogeneratori di ossido di zinco ad altissima efficienza per l'alimentazione di microsistemi impiantabili e di reti wireless di sensori”).
References
- Xu S. & Wang Z. L. One-dimensional ZnO nanostructures: Solution growth and functional properties. Nano Res. 4, 1013–1098 (2011). [Google Scholar]
- Sun Y. Watching nanoparticle kinetics in liquid. Mater. Today 15, 140–147 (2012). [Google Scholar]
- Ross F. M. Controlling nanowire structures through real time growth studies. Reports Prog. Phys. 73, 114501 (2010). [Google Scholar]
- Zaera F. Probing liquid/solid interfaces at the molecular level. Chem. Rev. 112, 2920–86 (2012). [DOI] [PubMed] [Google Scholar]
- Liao H.-G., Cui L., Whitelam S. & Zheng H. Real-time imaging of Pt3Fe nanorod growth in solution. Science 336, 1011–1014 (2012). [DOI] [PubMed] [Google Scholar]
- Yuk J. M. et al. High-Resolution EM of Colloidal Nanocrystal Growth Using Graphene Liquid Cells. Science 336, 61–64 (2012). [DOI] [PubMed] [Google Scholar]
- Liu Y., Tai K. & Dillon S. J. Growth-kinetics and morphological evolution of ZnO precipitated from solution. Chem. Mater. 25, 2927–2933 (2013). [Google Scholar]
- Williamson M. J., Tromp R. M., Vereecken P. M., Hull R. & Ross F. M. Dynamic microscopy of nanoscale cluster growth at the solid-liquid interface. Nat. Mater. 2, 532–6 (2003). [DOI] [PubMed] [Google Scholar]
- Sun Y. et al. Nanophase Evolution at Semiconductor/Electrolyte Interface in Situ Probed by Time-Resolved High-Energy Synchrotron X-ray Diffraction. Nano Lett. 10, 3747–3753 (2010). [DOI] [PubMed] [Google Scholar]
- Sun Y. & Wang Y. Monitoring of Galvanic Replacement Reaction between Silver Nanowires and HAuCl4 by In Situ Transmission X-ray Microscopy. Nano Lett. 11, 4386–4392 (2011). [DOI] [PubMed] [Google Scholar]
- Abécassis B., Testard F., Spalla O. & Barboux P. Probing in situ the nucleation and growth of gold nanoparticles by small-angle X-ray scattering. Nano Lett. 7, 1723–7 (2007). [DOI] [PubMed] [Google Scholar]
- Abécassis B., Testard F., Kong Q., Francois B. & Spalla O. Influence of Monomer Feeding on a Fast Gold Nanoparticles Synthesis: Time-Resolved XANES and SAXS Experiments. Langmuir 26, 13847–13854 (2010). [DOI] [PubMed] [Google Scholar]
- Tian J.-H. et al. Improved seedless hydrothermal synthesis of dense and ultralong ZnO nanowires. Nanotechnology 22, 245601 (2011). [DOI] [PubMed] [Google Scholar]
- Xu S., Lao C., Weintraub B. & Wang Z. L. Density-controlled growth of aligned ZnO nanowire arrays by seedless chemical approach on smooth surfaces. J. Mater. Res. 23, 2072–2077 (2011). [Google Scholar]
- Xu S. et al. Optimizing and Improving the Growth Quality of ZnO Nanowire Arrays Guided by Statistical Design of Experiments. ACS Nano 3, 1803–12 (2009). [DOI] [PubMed] [Google Scholar]
- Layek A. et al. A Generalized Three-Stage Mechanism of ZnO Nanoparticle Formation in Homogeneous Liquid Medium. J. Phys. Chem. C 116, 24757–24769 (2012). [Google Scholar]
- Xu C. & Gao D. Two-Stage Hydrothermal Growth of Long ZnO Nanowires for Efficient TiO2 Nanotube-Based Dye-Sensitized Solar Cells. J. Phys. Chem. C 116, 7236–7241 (2012). [Google Scholar]
- Liu K., Wu W., Chen B., Chen X. & Zhang N. Continuous growth and improved PL property of ZnO nanoarrays with assistance of polyethylenimine. Nanoscale 5, 5986–5993 (2013). [DOI] [PubMed] [Google Scholar]
- Falconi C. et al. Electronic interfaces. Sensors Actuators B Chem. 121, 295–329 (2007). [Google Scholar]
- Orsini A., Medaglia P. G., Scarpellini D., Pizzoferrato R. & Falconi C. Towards high-performance, low-cost quartz sensors with high-density, well-separated, vertically aligned ZnO nanowires by low-temperature, seed-less, single-step, double-sided growth. Nanotechnology 24, 355503 (2013). [DOI] [PubMed] [Google Scholar]
- Auge J., Hauptmann P., Eichelbaum F. & Rösler S. Quartz crystal microbalance sensor in liquids. Sensors Actuators B Chem. 19, 518–522 (1994). [Google Scholar]
- Rinaldi M., Zuniga C. & Piazza G. 5-10 GHz AlN Contour-Mode Nanoelectromechanical Resonators. in 2009 IEEE 22nd Int. Conf. Micro Electro Mech. Syst. 916–919 (IEEE, 2009). doi:10.1109/MEMSYS.2009.4805533. [Google Scholar]
- Wang X., Song J., Liu J. & Wang Z. L. Direct-current nanogenerator driven by ultrasonic waves. Science 316, 102–5 (2007). [DOI] [PubMed] [Google Scholar]
- Romano G. et al. Piezoelectric potential in vertically aligned nanowires for high output nanogenerators. Nanotechnology 22, 465401 (2011). [DOI] [PubMed] [Google Scholar]
- Xu S. et al. Self-powered nanowire devices. Nat. Nanotechnol. 5, 366–73 (2010). [DOI] [PubMed] [Google Scholar]
- Falconi C., Mantini G., D'Amico A. & Wang Z. L. Studying piezoelectric nanowires and nanowalls for energy harvesting. Sensors Actuators B Chem. 139, 511–519 (2009). [Google Scholar]
- Gargas D. J., Gao H., Wang H. & Yang P. High quantum efficiency of band-edge emission from ZnO nanowires. Nano Lett. 11, 3792–6 (2011). [DOI] [PubMed] [Google Scholar]
- Chu S. et al. Electrically pumped waveguide lasing from ZnO nanowires. Nat. Nanotechnol. 6, 506–510 (2011). [DOI] [PubMed] [Google Scholar]
- Wu W., Wei Y. & Wang Z. L. Strain-gated piezotronic logic nanodevices. Adv. Mater. 22, 4711–5 (2010). [DOI] [PubMed] [Google Scholar]
- Wang Z. L. Progress in Piezotronics and Piezo-Phototronics. Adv. Mater. 24, 4632–4646 (2012). [DOI] [PubMed] [Google Scholar]
- Zhou J. et al. Flexible piezotronic strain sensor. Nano Lett. 8, 3035–40 (2008). [DOI] [PubMed] [Google Scholar]
- Araneo R., Lovat G., Burghignoli P. & Falconi C. Piezo-Semiconductive Quasi-1D Nanodevices with or without Anti-Symmetry. Adv. Mater. 24, 4719–24 (2012). [DOI] [PubMed] [Google Scholar]
- Lee D. et al. Enhanced mass sensitivity of ZnO nanorod-grown quartz crystal microbalances. Sensors Actuators B Chem. 135, 444–448 (2009). [Google Scholar]
- Ko W., Jung N., Lee M., Yun M. & Jeon S. Electronic Nose Based on Multipatterns of ZnO Nanorods on a Quartz Resonator with Remote Electrodes. ACS Nano 7, 6685–6690 (2013). [DOI] [PubMed] [Google Scholar]
- Vayssieres L. Growth of Arrayed Nanorods and Nanowires of ZnO from Aqueous Solutions. Adv. Mater. 15, 464–466 (2003). [Google Scholar]
- Ashfold M. N. R., Doherty R. P., Ndifor-Angwafor N. G., Riley D. J. & Sun Y. The kinetics of the hydrothermal growth of ZnO nanostructures. Thin Solid Films 515, 8679–8683 (2007). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Information