Structural and energetic determinants of tyrosylprotein sulfotransferase sulfation specificity

Abstract

Motivation: Tyrosine sulfation is a type of post-translational modification (PTM) catalyzed by tyrosylprotein sulfotransferases (TPST). The modification plays a crucial role in mediating protein–protein interactions in many biologically important processes. There is no well-defined sequence motif for TPST sulfation, and the underlying determinants of TPST sulfation specificity remains elusive. Here, we perform molecular modeling to uncover the structural and energetic determinants of TPST sulfation specificity.

Results: We estimate the binding affinities between TPST and peptides around tyrosines of both sulfated and non-sulfated proteins to differentiate them. We find that better differentiation is achieved after including energy costs associated with local unfolding of the tyrosine-containing peptide in a host protein, which depends on both the peptide’s secondary structures and solvent accessibility. Local unfolding renders buried peptide—with ordered structures—thermodynamically available for TPST binding. Our results suggest that both thermodynamic availability of the peptide and its binding affinity to the enzyme are important for TPST sulfation specificity, and their interplay results into great variations in sequences and structures of sulfated peptides. We expect our method to be useful in predicting potential sulfation sites and transferable to other TPST variants. Our study may also shed light on other PTM systems without well-defined sequence and structural specificities.

Availability and implementation: All the data and scripts used in the work are available at http://dlab.clemson.edu/research/Sulfation.

Contact: fding@clemson.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

After their synthesis in the ribosome, many proteins undergo post-translational modifications (PTM) such as glycosylation, phosphorylation and peptide hydrolysis before reaching their fully functional forms. Tyrosine sulfation is a common PTM occurring on many proteins that transit through the Golgi apparatus, such as extracellular matrix proteins, serine protease inhibitors and G-protein coupled receptors (Stone et al., 2009). So far hundreds of tyrosine-sulfated proteins have been identified, and more are likely to be discovered. A list of sulfated proteins can be obtained from the UniProt database (Bairoch et al., 2005). A major functional role of tyrosine sulfation is to mediate protein–protein interactions (Kehoe and Bertozzi, 2000). Sulfation is vital for many biological functions as indicated in studies showing that postnatal viability, vision, fertility and growth are affected in mice in the absence of sulfation (Ouyang et al., 2002; Borghei et al., 2006). The functioning of many proteins, including P-selectin glycoprotein ligand-1 (Pouyani and Seed, 1995; Wilkins et al., 1995), chemokine receptors (Simpson et al., 2009), platelet glycoprotein Ib (Uff et al., 2002; Zarpellon et al., 2011), depends on tyrosine sulfation. For example, the sulfation of tyrosine in the chemokine receptor CCR5 is necessary for HIV-1 gp120 mediated entry of HIV into CD4+ T-lymphocytes (Choe et al., 2003). A detailed understanding of the molecular mechanism of tyrosine sulfation is therefore important for manipulating such modifications, regulating cell signaling and drug development.

Sulfation is catalyzed by the tyrosylprotein sulfotransferase (TPST) enzymes, which reside inside the Golgi apparatus. The process involves the transfer of a sulfo-group from a bound 3′-phosphoadenosine-5′-phosphosulfate (PAPS) to the phenol group of tyrosine. In humans, two isoforms, TPST-1 and TPST-2, are found with 64% sequence identity between them (Teramoto et al., 2013). The functional differences between the isoforms or the necessity of two such isoforms are not well-established. Sulfation occurs only on specific tyrosines in proteins. Even though up to 1% of tyrosines in a cell’s proteome can be sulfated (Önnerfjord et al., 2004), the location of sulfated tyrosines are not known for many proteins. Hence, neither the exact role of sulfated tyrosines in these proteins nor the mechanism by which the tyrosines are selected for sulfation is fully understood. Analysis of the amino acid sequences flanking sulfated tyrosines suggested some general features such as the presence of acidic and small residues, absence of disulfide bonds or glycosylated residues and a reduced number of hydrophobic residues in the vicinity of sulfated tyrosines (Rosenquist and Nicholas, 1993). However, there are also many exceptions to these general characteristics of sequence specificity. For example, mutational studies reported an enhanced sulfation efficiency when tyrosines were flanked by basic residues (Bundgaard et al., 1997). Therefore, in contrast to other PTMs such as N-glycosylation, which recognizes structurally available NX(T/S) triplets (Marshall, 1974), a well-defined sequence specificity for tyrosine sulfation cannot be established.

Owing to the lack of obvious sequence patterns, sophisticated statistical tools have been developed to predict potential locations of sulfation sites in a given protein. Sulfinator (Monigatti et al., 2002) constructed four different hidden Markov models to recognize sulfated tyrosine residues depending on their locations in the sequence: near N-terminal, near C-terminal, in the center of a window of at least 25 amino acids and in windows containing multiple tyrosines. In PredSulSite (Huang et al., 2012), physicochemical properties of amino acids along with predicted secondary structures and amino acid sequence order are considered in a supported vector machine (SVM). The SVM algorithm has also been applied in another predictor based on predicted secondary structures and solvent accessible surface area (Chang et al., 2009). These statistics-based tools work satisfactorily in their test cases and have been useful in experimental studies of protein sulfation (Goff et al., 2003; Keykhosravani et al., 2005). However, these training-based statistical methods depend heavily on the quality of the training set, such as the coverage and completeness, which is not the case for the increasing list of sulfated proteins identified experimentally. As a result, many exceptions were observed in cases beyond the training sets (Monigatti et al., 2006; Önnerfjord et al., 2004), and these methods are also not transferable to other TPST variants, such as recently discovered bacterial TPSTs (Han et al., 2012). Most importantly, many of these methods are sequence-based and the constructed predictors lack structural or physicochemical insights to the molecular mechanism of tyrosine selection by TPST enzyme.

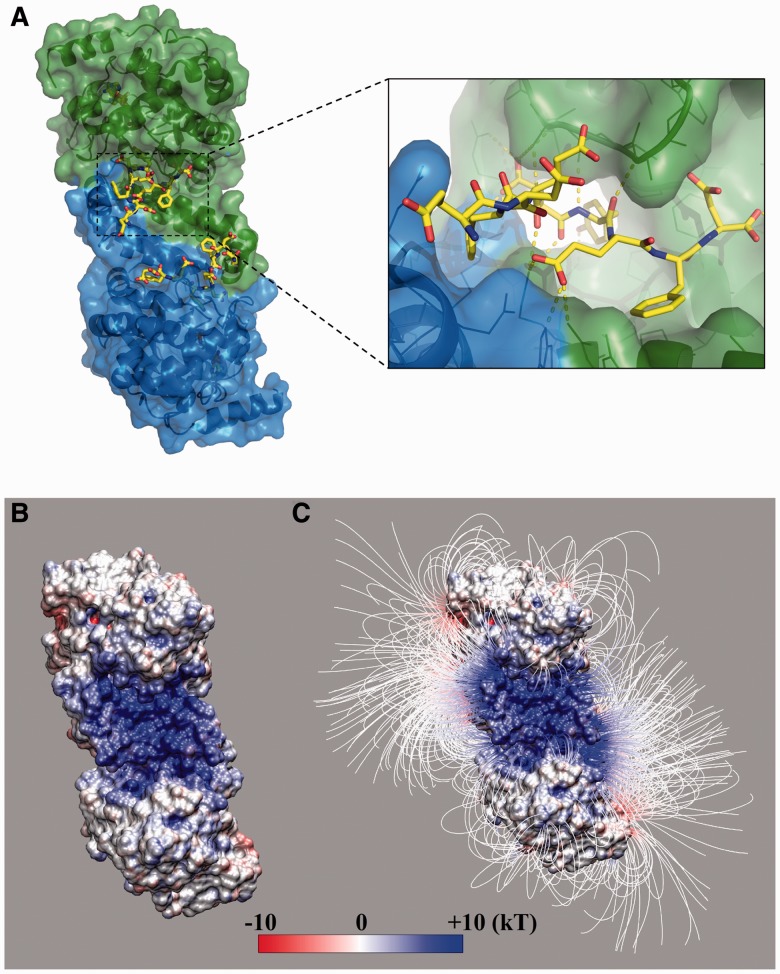
Recently, a high-resolution structure of human TPST-2 (Fig. 1A) has been solved at 1.9 Å resolution in complex with a high-affinity peptide using X-ray crystallography (Teramoto et al., 2013), making it possible to study the structural and energetic determinants of TPST sulfation specificity. In this work, we adapt Eris (Yin et al., 2007a), a method developed to compute protein stability changes on mutations, to estimate the binding affinities between TPST-2 and various peptide substrates to differentiate sulfated and non-sulfated sequences that have been experimentally verified. We find that the peptide–TPST binding affinities cannot separate the sulfated and non-sulfated sequences satisfactorily. Better differentiation is achieved after including energy costs associated with local unfolding of the tyrosine-containing peptides in the host protein, which depends on both the peptide’s secondary structures and solvent accessibility. The thermodynamic population of the locally unfolded peptides determines the availability of the peptide for TPST binding and subsequent catalysis. Therefore, our study suggests that both the thermodynamics accessibility of a peptide and its binding affinity to TPST are important for sulfation. The interplay of these two factors allows a great variety in sequences and structures of sulfated peptides, where a buried peptide with well-defined secondary structure might be sulfated if the peptide undergoes local unfolding, making itself available for enzyme binding.

Fig. 1.

The structure of TPST-2 dimer. (A) The TPST-2 dimer (Teramoto et al., 2013) with bound substrate peptide (yellow) and PAPS analog. (B) Electrostatic potential and (C) field lines of the enzyme after removing the substrate peptide. The binding pocket has a high positive electrostatic potential, and hence, the peptides with net negative charge can be driven into the pocket by electrostatic interactions

2 MATERIALS AND METHODS

2.1 Electrostatic analysis

To determine how the electrostatic interactions guide the peptides to the protein, the electrostatic potential and force surrounding the protein were calculated using Delphi (Li et al., 2012) after removing the peptide from the binding site. The following parameters were used for the calculation: scale = 2.0 grids/Å; grid size 280 × 280 × 280; and dielectric constants of 2.0 and 80.0 for protein and water environment, respectively. The force field used for the calculations was AMBER (Lindorff-Larsen et al., 2010). VMD graphics tool (Humphrey et al., 1996) was used to visualize the electrostatic surface and field lines.

2.2 Protein–peptide binding affinity

The relative binding affinity of a given peptide with respect to the reference peptide can be quantified as

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{bind}={\left(G^{complex}-G^{prot}-G^{pep}\right)}_{mut}-{\left(G^{complex}-G^{prot}-G^{pep}\right)}_{ref}$$

where the superscript complex denotes the enzyme–peptide complex; prot and pep refer to the protein and peptide in their unbound states, respectively; the subscript mut denotes mutations of a given peptide with respect to the reference peptide indicated by the subscript ref. Because the absolute free energy is difficult to measure, the free energy difference between the folded and unfolded states, i.e. the stability ΔG, is most commonly used. The unfolded state of the complex corresponds to the unfolded protein and peptide, and thus ΔΔG_bind = (ΔG^complex − ΔG^prot − ΔG^pep)_mut − (ΔG^complex − ΔG^prot − ΔG^pep)_ref. Because the protein sequence is not changing,

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{bind}=\mathrm{\Delta }\mathrm{\Delta }{G}^{complex}-\mathrm{\Delta }\mathrm{\Delta }{G}^{pep}$$ (1)

where ΔΔG^complex and ΔΔG^pep refer to the mutation-induced stability changes for the complex and peptide, respectively.

2.3 Estimation of stability change on mutations

We used Eris to estimate the stability changes on mutations (Yin et al., 2007a). Eris uses the backbone-dependent rotamer library to model protein side-chain conformations (Dunbrack and Cohen, 1997). Given the vast side-chain rotameric space, the optimal packing was searched via a Monte Carlo-based simulated annealing algorithm, where the rotameric space of side chains was sampled according to the Metropolis criteria and the simulation temperature is gradually reduced till the acceptance rate is below a pre-defined threshold. The stability of a given sequence and corresponding structural conformation was evaluated with the Medusa force field (Ding and Dokholyan, 2006), which includes van der Waals, solvation, hydrogen bonds, electrostatics, statistical potential for backbone-dependent amino acid identity and rotamer and reference energy for the unfolded states. The atom types and corresponding van der Waals interaction parameters were taken from CHARMM (Brooks et al., 1983). The solvation energy was approximated by the Lazaridis–Karplus implicit solvent model (Lazaridis and Karplus, 1999). The distance- and angle-dependent hydrogen bond interaction parameters were adapted from Kortemme and Baker (2002). We used the Debye–Hückel approximation to model the screened charge–charge interactions at the physiological condition, namely pH ∼ 7 and salt concentration ∼0.1 M, and the corresponding Debye length was ∼10 Å. The weights for different energy terms and the reference energy of unfolded state were determined by recapitulating the native amino acid sequence of a set of high-resolution protein structures (Yin et al., 2008).

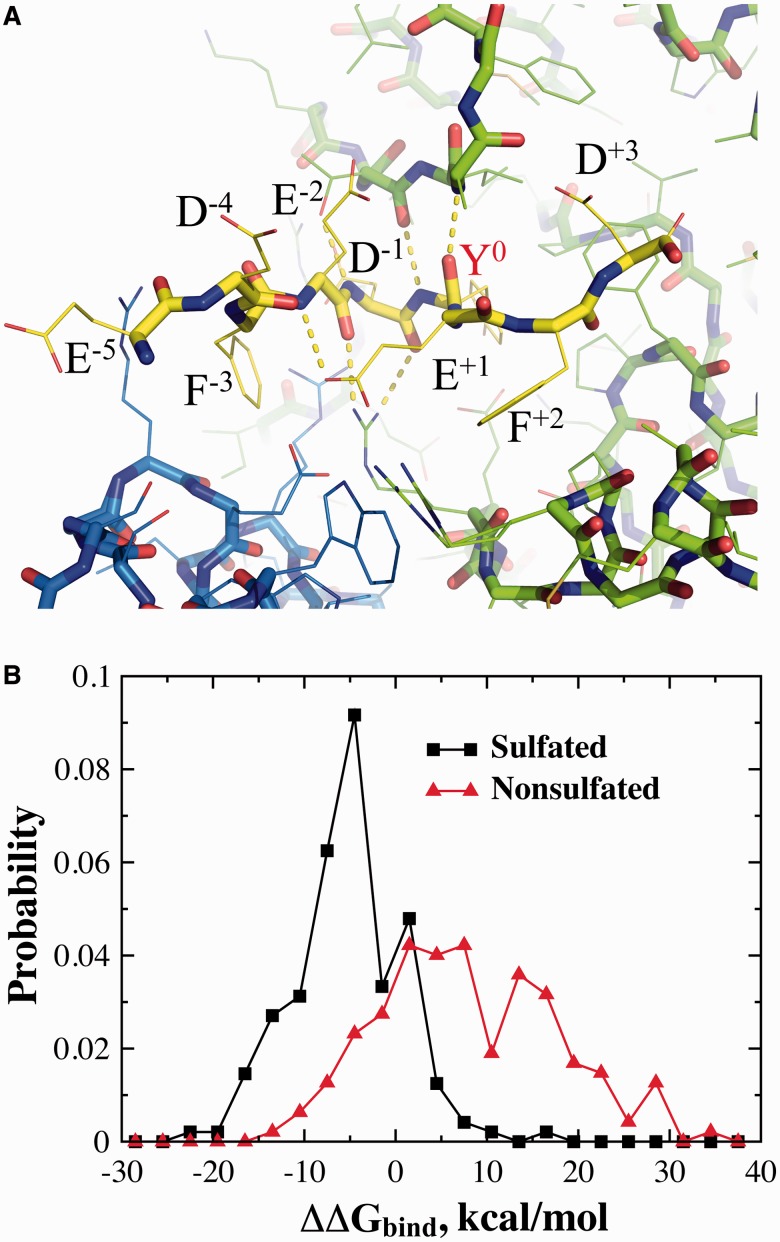
Owing to the stochastic nature of the simulated annealing algorithm, multiple simulations were often performed to compute the average stability of a given sequence. We used the PDB structure of 3AP1 (Teramoto et al., 2013) to model the bound complexes (Fig. 2A). We chose a nine-residue window with the sulfated tyrosine as the sixth residue similar to the reference peptide in the crystallography structure. It has been experimentally shown that these flanking residues are important for both TPST binding and catalysis (Lin et al., 1992). For a given mutation, 100 independent simulations were performed for both the native and mutant protein (or protein–peptide complex). The stability was estimated as the average value over all simulations, and the mutation-induced stability change was then obtained as the difference between mutant and wild type.

Fig. 2.

The estimation of protein–peptide binding affinity. (A) The structure of the reference nine-residue peptide in the TPST-2 binding pocket as obtained from X-ray crystallography structure, with the sulfated tyrosine positioned as the sixth residue (Y⁰). The neighboring residues and their positions (superscript) relative to the tyrosine are also marked. (B) The probability density of peptide–enzyme binding scores (ΔΔG_bind) for the peptides both sulfated and non-sulfated peptides

2.4 Positive and negative datasets

To test whether a parameter can be used to differentiate the sulfated and non-sulfated proteins, we compiled a list of experimentally verified sulfated peptide/proteins (positive dataset) and a list of non-sulfated peptide/proteins (negative dataset). For the positive dataset, we collected a list of 160 non-redundant tyrosine-sulfated peptide/proteins by combining both Sulfinator (Monigatti et al., 2002) and dbPTM (Lu et al., 2012) datasets, which were extracted from the UniProt database (Bairoch et al., 2005). Many proteins had more than one sulfated tyrosine. Similarly, based on Sulfinator, a list of 159 peptide–proteins was constructed for the secreted proteins that do not undergo sulfation.

2.5 Secondary structures and relative solvent accessibility predictions

We used the NetSurfP (Petersen et al., 2009), a protein surface accessibility and secondary structure prediction web-server, to estimate a peptide’s structural propensity in terms of relative solvent accessibility, P_rsa, and various secondary strucutres, P_α, P_β and P_coil. A benchmark study by the developers (Petersen et al., 2009) indicated that the prediction accuracy of NetSurfP is comparable with other best publicly available methods. With the input of the sequence of a host protein, the profiles of relative solvent accessibility and secondary structures—α-helix, β-sheet and random coil—were obtained for all residues. We computed the average propensities, P_α, P_β, P_coil and P_rsa, over the nine-residue window around a given tyrosine of interest.

2.6 Z-score and Z-score minimization

For a given parameter χ, derived for both the sulfated and non-sulfated sequences, we defined the Z-score:

$$Z=\frac{{\langle \chi \rangle }_{sulfated}-{\langle \chi \rangle }_{nonsulfated}}{\delta {\left(\chi \right)}_{sulfated}+\delta {\left(\chi \right)}_{nonsulfated}}$$ (2)

where δχ is the standard deviation. The averaging was done separately for all peptides belonging to sulfated and non-sulfated datasets. The Z-score quantifies the separation between the χ-value distributions of the two datasets.

To determine the coefficients E_α, E_β and E_rsa in the effective energy E^eff, we minimized the Z-score of E^eff using a Monte Carlo-based simulated annealing. We gradually decreased the Monte Carlo temperature, and at each temperature multiple rounds of perturbations of the coefficients were applied. The acceptance or rejection of perturbations was determined according to the Metropolis criteria. As the Monte Carlo temperature approaches zero, the Z-score was minimized stochastically. Multiple independent simulations with different random seeds were performed to ensure the convergence.

3 RESULTS

The TPSP-2 enzyme has an N-terminal cytoplasmic domain, a transmembrane domain anchoring the protein in the Golgi membrane, a putative stem region and a luminal domain that catalyzes the tyrosine sulfation (Teramoto et al., 2013). The protein exists as a homodimer and the structure of the catalytic domain has been solved recently in its dimeric form (Teramoto et al., 2013) (PDB ID: 3AP1, Fig. 1A). The peptide binds to a well-defined deep pocket, a part of which is at the inter-monomer interface (Fig. 1A).

3.1 The role of electrostatics in peptide binding

The peptide-binding pocket of the enzyme is rich in positively charged residues. Electrostatics analysis using Delphi (Li et al., 2012) (see Section 2) indicates that the electrostatic potential near the binding pocket is highly positive (Fig. 1B). Even more, the electrostatic field lines form an electrostatic funnel, which can drive a negatively charged substrate toward the pocket (Fig. 1C). Many sulfated peptides have a net negative charge, typically originating from acidic groups positioned near the tyrosine. For example, in many cases the sulfated tyrosines are flanked by two acidic residues, providing local net charge of −2e. This feature was believed to be a necessary requirement for all sulfated tyrosines (Hortin et al., 1986). The more recent discovery of sulfated tyrosines not flanked by acidic residues has called into question this requirement (Bundgaard et al., 1997). However, the net negative charge may still be present because of more distant acidic residues. The observation that TPSP dimer forms such a prominent positive electrostatic patch at the dimer interface suggests that electrostatic interactions between the TPSP and the peptide are an important feature for the binding and perhaps for the specificity of the recognition. To reveal the interplay between binding affinity and specificity, we use the protein–peptide complex structure to estimate the binding affinities of both sulfated and non-sulfated peptides to investigate the specificity of TPST recognition.

3.2 Protein–peptide binding energy

In the complex structure, the peptide conformation is stabilized by several hydrogen bonds with the enzyme, including both backbones and side chains (Fig. 1A) (Teramoto et al., 2013). To be catalyzed by the enzyme, a substrate peptide has to assume an appropriate conformation in the pocket such that specific TPST–peptide interactions can be established. Therefore, it is expected that the corresponding binding affinity would vary significantly with the amino acid sequences, which in turn would be crucial for the selectivity of peptide sequences for TPST sulfation. Because it is difficult to estimate the absolute value of binding affinity ΔG, we computed the change in binding affinity, ΔΔG_bind, due to mutations with respect to the reference peptide in the X-ray crystallography structure of the TPST–peptide complex (see Section 2). We use Eris (Yin et al., 2007a) to estimate the stability changes on mutations, where the inter-atomic interactions is modeled with the Medusa force field (Ding and Dokholyan, 2006). The Medusa force field includes major physical interactions that govern the binding between peptide and receptor, including van der Waals, solvation, hydrogen bonds and electrostatics (see Section 2). The Eris/Medusa method has been shown efficient in recapitulating protein stability changes on mutations with a high correlation between predictions and experimental measurements (Yin et al., 2007a, b). For the peptides, a window of nine residues is used with the tyrosine of our interest at the sixth position as for the reference peptide in the complex structure (Fig. 2A).

We first test whether the peptide-binding affinity is the driving force for tyrosine sulfation by TPST. We constructed a list of sulfated and non-sulfated proteins that are experimentally validated (see Section 2). If the peptide-binding energy is the determinant for the TPST sulfation specificity, the sulfated sequences should have stronger affinities or lower binding energies than the non-sulfated sequences. We compute the probability densities of the Eris-derived relative binding affinity ΔΔG_bind for sulfated and non-sulfated sequences (Fig. 2B). As expected, the sulfated sequences, in general, have lower ΔΔG_bind values compared with the non-sulfated sequences. Thus, the peptide-binding affinity plays a crucial role in the sulfation selection process. However, it is also clear from Figure 2B that a significant separation of the two sets of sequences is not achieved on the basis of ΔΔG_bind values alone. To quantify the separation of two datasets, the standard score (i.e. Z-score, see Section 2) is calculated to determine if the separation of two Gaussian-like distributions is statistically significant. Z-score quantifies the separation with respect to the standard deviations. A larger absolute Z-score value indicates a more significant separation of the two distributions. The Z-score for the two distributions is −0.83, indicating that the separation is within one standard deviation and thus two datasets are not well-separated according the peptide-binding affinity alone. Thus, even though the binding affinity plays an important role in the selection process, there are additional factors that contribute to the selection of tyrosines by TPST.

3.3 Local unfolding of the tyrosine-containing peptide

It has been reported that many of the tyrosines that undergo sulfation are positioned in unstructured regions of the host protein, although some sulfated peptides contain ordered secondary structures (Chang et al., 2009; Huang et al., 2012). In their native structures, peptides that fold into α-helix or β-sheet structures in the host protein would not be able to fit into the TPST binding pocket (Figs 1 and 2A). In other words, these peptides with well-defined secondary structures would need to locally unfold to bind to the enzyme. The unfolding of secondary structures requires energy, making the binding less favorable. Additionally, to bind to the enzyme, the peptide segment also needs to break tertiary contacts, if any, with respect to the rest of the host protein. The energy cost associated with losing these tertiary contacts also makes the recognition by the enzyme unfavorable. The number of tertiary contacts is inversely proportionally to the solvent-accessible surface area (Ding et al., 2012). Next, we examine the secondary structures and solvent accessibility of the sulfated and non-sulfated peptides in the corresponding host proteins.

The majority of proteins in the UniProt datasets do not have experimentally determined 3D structures available. As a result, the secondary structures and solvent accessibilities of the peptides in our sulfated and non-sulfated datasets cannot be derived directly from the structure of their host proteins. On the other hand, bioinformatics tools have been developed to predict protein secondary structures and solvent accessibility from sequences with significant accuracy. We use the web-server NetSurfP (Petersen et al., 2009) to estimate the propensity of a peptide in terms of relative solvent accessibility, P_rsa, and secondary structure elements, P_α, P_β and P_coil (See Section 2). We find that compared with the non-sulfated sequences the sulfated ones tend to have weaker propensities for ordered secondary structures (Fig. 3A and B), and consequently higher propensity for random coils (Fig. 3C), although the differences are relatively small with major overlaps of the distributions. Similarly, as expected, the sulfated sequences also have slightly higher probability to be solvent-exposed than those non-sulfated sequences (Fig. 3D). Therefore, local unfolding of the peptide in the host protein—including both unfolding of the ordered secondary structures and losing tertiary contacts with respect to the rest of the protein, the energy cost of which is inversely proportional to the solvent accessibility—is also important for the recognition of the tyrosine-containing peptide by TPST. The thermodynamic population of the locally unfolded peptides, determined by the energy cost, is available to bind the enzyme. Similar partial unfolding of protein substrates has also been observed for proteolytic cleavage of proteins (Hubbard et al., 1994) as well as for both N- (Marshall, 1974) and O-glycosylation (Hansen et al., 1998) sites.

Fig. 3.

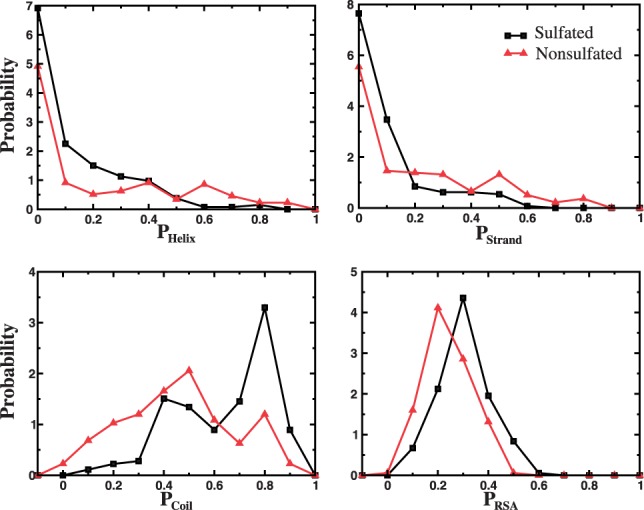
Secondary structures and solvent accessibility of peptides in host proteins. The normalized probability density of peptides in the dataset used, with respect to their propensities to form α-helix, β-strand and random coil secondary structures, and their relative solvent accessibility

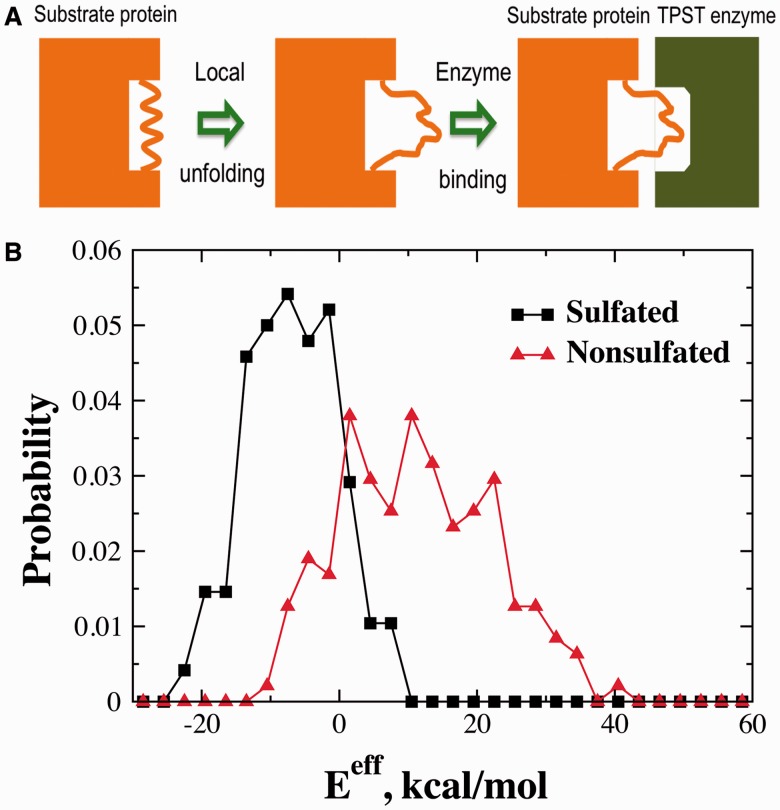
3.4 An effective energy for sulfation

Our analysis above suggests that the thermodynamic availability of the peptide—i.e. the probability of the peptide to be locally unfolded and thus accessible for enzyme binding—is also important for TPST sulfation (Fig. 4A). We propose a simple energy cost function for local unfolding of the peptide, E_αP_α + E_βP_β − E_rsaP_rsa, where the coefficients E_α and E_β are the energy costs for the unfolding of α-helix and β-sheet, respectively. The coefficient E_rsa corresponds to the energy cost for losing tertiary contacts. Thus, the total effective energy for TPST sulfation can be approximated as E^eff = E_αP_α + E_βP_β − E_rsaP_rsa + ΔΔG_bind + C, where C is an arbitrary reference coefficient.

Fig. 4.

Effective sulfation energy. (A) A schematic of tyrosine sulfation where the tyrosine-containing peptide is structured and/or buried. For the sulfation to occur, substrate protein undergoes a local unfolding around the sulfated tyrosine. (B) The probability density of the effective binding energy E^eff for sulfated and non-sulfated sequences. E^eff separates the two sets of sequences more effectively, compared with ΔΔG_bind (Fig. 3B). The reference coefficient C of E^eff is chosen as −14.6 kcal/mol so that the two distributions intersect around zero. The Z-score between the two distributions is −1.03

We parameterize the coefficients E_α, E_β and E_rsa by minimizing the Z-score of E^eff values between the sulfated and non-sulfated datasets (see Section 2), E_α = 19.1 kcal/mol, E_β = 24.7 kcal/mol and E_rsa = 7.5 kcal/mol. We notice that these energy coefficients are physically sound. For instance, if all the nine residues of the peptide are forming a helix, the average energy cost for breaking a backbone hydrogen bond on unfolding would be ∼2 kcal/mol, which is close to the estimated energy of a single hydrogen bond (Deechongkit et al., 2004). The distributions of E^eff for sulfated and non-sulfated datasets are shown in Figure 4B. Compared with ΔΔG_bind, the separation between the two datasets with the effective sulfation energy is significantly improved with the Z-score decreased from −0.83 to −1.03. Therefore, with the effective sulfation energy E^eff the distributions of the sulfated and non-sulfated sequences are now separated by approximately one standard deviation.

Our results suggest that the substrate peptide’s structural properties in the host protein and its binding affinity to the enzyme are both important for the recognition by TPST. One interesting question is which term in the effective energy contributes the most in differentiating the two datasets. To answer this, we compute the Z-score for each term separately. The values for the peptide-binding energy ΔΔG_bind, propensities of α-helix P_α, β-sheet P_β and relative solvent accessibility P_rsa in the host proteins, are −0.83, −0.23, −0.29 and 0.42, respectively. Therefore, the peptide-binding affinity plays a major role for TPST specificity while the thermodynamic availability of the peptide in its host protein also plays a significant role. These two factors together determine the TPST sulfation specificity, resulting into great variations in both sequences and structures of the sulfated proteins.

A better separation between sulfated and non-sulfated sequences with E^eff than other parameters allows us to use E^eff as the predictor to estimate whether a peptide is potentially sulfated. The E^eff distributions of sulfated and non-sulfated proteins are both Gaussian-like (Fig. 4B). We choose a cutoff value E_c corresponding to the intersection of these two distributions such that a protein has a high probability of being sulfated than non-sulfated if E^eff < E_c. We set the reference coefficient C of E^eff as −14.6 kcal/mol so that E_c = 0. As a result, the error rates for both sulfated (i.e. sulfated proteins with E^eff > 0) and nonsulfated (i.e. non-sulfated proteins with E^eff < 0) equal to ∼15%. Using the same datasets, we compare the performance of our method with respect to two existing sulfation prediction servers, Sulfinator (Monigatti et al., 2002) and PredSulSite (Huang et al., 2012). Sulfinator successfully predicts 126 of 160 sulfated and 155 of 159 non-sulfated sites, resulting in error rates of ∼21 and ∼2.5%, respectively. PredSulSite succeeds in predicting 94 of 160 sulfated and 158 of 159 non-sulfated sites, and thus, the corresponding error rates are ∼41 and ∼0.6%. Interestingly, both Sulfinator and PredSulSite have a high success rate for non-sulfated sequences but with a sacrifice of the success rate for sulfated sequences. On average, our structure-based method has similar prediction accuracy as these statistics-based tools with a better prediction of the sulfated sequences. Next, we examine the applications of effective sulfation energy E^eff in two case studies that are not included in the datasets.

3.5 Sulfated tyrosines in HIV-1 antibodies

Two human monoclonal HIV antibodies, 412d and 47e, have been identified and purified from patients. The antibodies contain sulfated tyrosines in their variable loops (i.e. CDR3) that compete with the sulfated CCR5 receptor for the glycoprotein gp120 of HIV-1. It has been shown that tyrosine sulfation is critical for both antibody binding and the efficiency of the viral infection (Choe et al., 2003; Farzan et al., 1999). Antibody 412d has four tyrosines (Y96, Y100, Y100c and Y100l, Table 1) in the CDR3 loop, and antibody 47e has three tyrosines (Y100a, Y100g and Y100h) in the loop. The question is which tyrosine or tyrosines are sulfated by TPST.

Table 1.

The relative binding energy ΔΔG_bind and the effective sulfation energy E^eff are computed for different tyrosines of interest for HIV antibodies, 412d and 47e

Antibody	Index	ΔΔGbind	EαPα	EβPβ	−ErsaPrsa	Eeff
47e	Y100a	−1.51	0	0	−2.94	−19.05
	Y100g	24.54	0	0	−2.61	7.33
	Y100h	22.21	0	0	−2.39	5.22
412d	Y96	31.60	0	10.99	−1.76	26.23
	Y100	25.59	0	0	−2.83	8.16
	Y100c	7.03	0	0	−3.01	−10.58
	Y100l	28.62	0	2.75	−1.65	15.12

Note: The unit is kcal/mol. The contributions of secondary structure unfolding and solvent exposure are also shown. The sequence of the variable loop, CDR3, in the antibody 47e is GGEDGDYLSDPFYYNHGMDVW, where the examined tyrosines are 100a, 100 g and 100 h, shown in boldface and underlined. The CDR3 sequence of the antibody 412d is YCASPYPNDYNDYAPEEGMSWYFDL, where the examined tyrosines are 96, 100, 100C and 100L. The experimentally validated tyrosines that undergo sulfation are highlighted using boldface font.

We compute for each tyrosine the corresponding nine-residue peptide’s relative binding affinities, ΔΔG_bind, and also the effective sulfation energy E^eff (Table 1). Because all tyrosines are positioned in the variable loop, the correction of E^eff compared with ΔΔG_bind is relatively small. For antibody 47e, Y100a has the lowest ΔΔG_bind among the three tyrosines and corresponds to the only one with E^eff <0, suggesting Y100a has been sulfated by TPST. The corresponding values are also consistent with other sulfated sequences, suggesting that Y100a is sulfated (Figs 2B and 4B). The result is consistent with mutagenesis experiments (Choe et al., 2003). For antibody 412d, we find that Y100c has significantly lower values of ΔΔG_bind and E^eff than other three tyrosines, and the corresponding negative E^eff value suggests that it is sulfated. However, mutagenesis experiment found that Y100 is also sulfated in addition to Y100c. The unfavorable ΔΔG_bind and E^eff values of Y100 in our calculations are caused by its upstream proline residue P97, which has strong preference for the backbone dihedral angles. The particular proline residue is not compatible with the backbone conformation of the TPST–ligand complex, resulting in an unfavorable conformation. The artifact can be resolved by modeling the backbone conformational flexibility, whose accurate and rapid characterization is still computationally challenging and is the subject for the future studies. Taking together, our method can be used to predict the potential sulfation sites although there is room for improvement.

3.6 Sulfation efficiency

Incomplete sulfation is often observed for many sulfated proteins. For example, gastrin, a regulator of gastric acid secretion for digestion, is partially sulfated (Bundgaard et al., 1997). Systematic mutagenesis studies have been applied to understand the sequence dependence of the sulfation efficiency, where the extent of sulfation was measured for many mutants with mutations around the sulfated tyrosine (Bundgaard et al., 1997). The extent of sulfation measurement is more quantitative than the all-or-none descriptions of the sulfated and non-sulfated datasets. In addition to the descriptive insight of the sequence dependence of sulfation efficiency derived from the previous mutational studies, a more quantitative analysis is necessary. We hypothesize that the extent of sulfation should depend on both the thermodynamic availability of the peptide and the peptide-binding affinity, which are described by the effective sulfation energy, E^eff. We postulate that the sulfation efficiency should monotonically decrease with respect to the sulfation energy. For wild type and mutant gastrin (see Supplementary Table S1 for the list of mutations), we compute the ΔΔG_bind and E^eff and presented the scatterplot with respect to the sulfation efficiency in Figure 5. Although many mutations are single-amino acid substitutions, some mutations induce changes in secondary structure propensities, and thus significantly affect the energy cost for local unfolding with respect to the host protein. As a result, we observe a significant difference between ΔΔG_bind and E^eff in terms of correlation with respect to sulfation efficiency. As expected, we find a better correlation between the sulfation efficiency and E^eff than that of ΔΔG_bind. Using a linear regression, we find that absolute value of the correlation coefficient is improved from 0.31 for ΔΔG_bind to 0.53 for E^eff. Owing to inaccuracies in both experimental measurements and computational estimation of the effective energy, we do not expect a perfect correlation. Moreover, we also do not expect a linear correlation between the extent of sulfation and the sulfation energy for a wide range of energies, although the linear approximation can exist within a certain energy window. Therefore, the independent test suggests that the simple effective energy of sulfation can be used to predict the sulfation efficiency in incomplete sulfation.

Fig. 5.

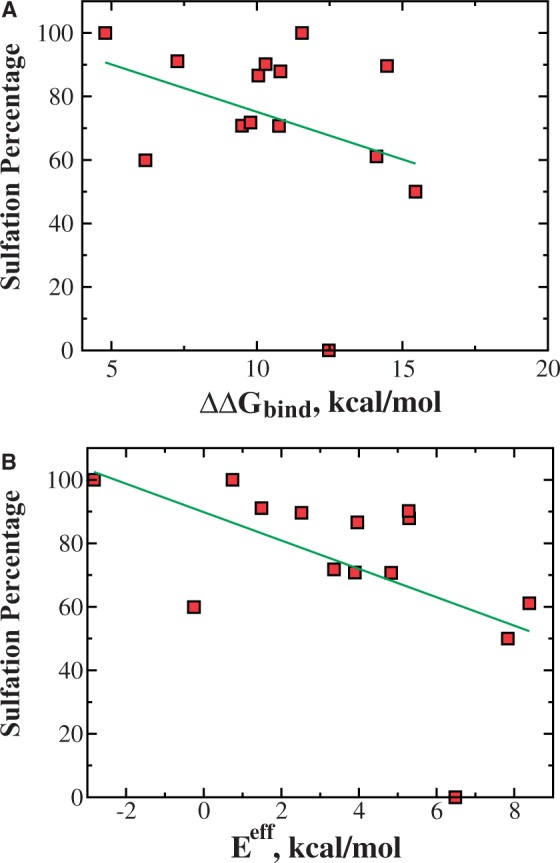
Correlation between sulfation efficiency and sulfation energy. (A) The scatterplot of the experimentally determined sulfation efficiency and computed relative peptide-binding affinity ΔΔG_bind for gastrin and its 13 mutants. Two quantities show weak correlation, with a Pearson correlation coefficient of −0.31. (B) Better correlation is achieved by using effective sulfation energy E^eff in which energy costs for unfolding and desolvation are incorporated. The correlation coefficient is improved to −0.53

3.7 TPST-1 isoform

Our estimation of relative peptide-binding affinity is based on the structure of TPST-2. The question is whether TPST-1 and TPST-2 have different binding affinities with respect to a given peptide. Because the sequence identity between two isoforms is 64% (sequence similarity is ∼78%), we expect their structures are highly similar to each other. We align the two sequences and build the homology model for TPST-1 using TPST-2 as the template (Fig. S1). We find that the peptide-binding pocket is almost identical for both isoforms with only two mutations near the N-terminal of the peptide (Supplementary Fig. S1B). One of the mutations is arginine to lysine, which maintains the charge. Therefore, we postulate that a peptide would have similar binding affinities with respect to TPST-1 and TPST-2. To test this hypothesis, we calculated the relative binding affinities ΔΔG_bind of HIV-1 antibodies and gastrin mutants to TPST-1 using the homology model. The ΔΔG_bind values of TPST-1 and TPST-2 highly correlate with each other with the Pearson correlation coefficient r = 0.98 (see the scatterplot in Supplementary Fig. S2). The slope of a linear fit is 1.07 with an offset of 0.28, suggesting that peptides have similar binding affinities to the two isoforms. Because other terms in the effective sulfation energy depend only on the structure of a substrate protein instead of the receptor, we expect that the effective sulfation energies E^eff with respect to the two isoforms are also similar, and thus no significant differences in terms of binding specificity and the sulfation specificity are observed.

In summary, using structure-based molecular modeling approaches, we have identified both structural and energetic determinants for TPST sulfation specificity. Our results suggest that both the thermodynamic availability of the peptide in a host protein and its binding affinity to the enzyme are important for TPST sulfation specificity. The thermodynamic availability of a peptide is determined by the energy cost of peptide local unfolding, where the peptide loses both tertiary and secondary interactions that stabilize its native structure in the host protein. The binding of the peptide by TPST is determined by its interactions with the residues in the binding pockets. The interplay of both peptide thermodynamic availability and enzyme-binding affinity in determining the TPST sulfation specificity leads to great variety in sulfated sequences and structures. We have developed an effective sulfation energy function that combines both the energy cost for peptide local unfolding and the binding affinity. Case studies suggest that the simple sulfation energy function can be used to predict the potential sulfation sites and the sulfation efficiency for incomplete sulfation. The benchmark study indicates that the predictive power of our structure-based sulfation predictor is comparable with other statistics-based tools with a better positive sulfation-predication rate. Besides the dependence of structural availability, the major differences between structure-based and statistics-based methods include computational efficiency and transferability. Owing to a large number of calculations of inter-atomic interactions in our structure-based method, the statistics-based methods are often computationally more efficient. However, as our method is based on physical interaction, we expect it to be transferable to other applications, such as estimating the effect of mutations in the TPST enzyme on sulfation specificity and sulfation prediction for other TPST variants, including the recently discovered bacterial TPSTs. (Han et al., 2012). We also expect that the proposed sulfation mechanism is also applicable to other post-translational modification systems where the sequence or structural specificities are not well-defined.

Funding: National Institutes of Health (R01GM093937 to L.L. and E.A.) (in part) and the startup funds from Clemson University (to F.D. and to M.B.).

Conflict of Interest: none declared.