Cognitive and behavioral attention in children with math difficulties

Abstract

Cognitive assessments and behavioral ratings of attention were used to examine the relation of inattention to math performance in children. Third grade students with math difficulties (MD; n = 17) and math and reading difficulties (MDRD; n = 35) were administered the Attentional Network Test (ANT), as well as achievement and intelligence measures. Strengths and Weaknesses of ADHD-Symptoms and Normal-Behavior-IV (SWAN-IV) Inattention ratings were collected from teachers. Two comparison groups were also recruited: a typically achieving group (n = 23) and a group that responded to a math-tutoring intervention (responders; n = 54). On the ANT, children with MD and MDRD did not perform significantly different than typically achieving children or responders on measures of alerting and orienting attention and executive control. All subgroups did demonstrate performance patterns that were expected on the ANT. However, performance across blocks of the task was inconsistent, suggesting poor reliability. There were no relations between ANT performance and SWAN-IV behavioral inattention scores, though behavioral ratings of inattention correlated significantly with math performance. Children with MD and MDRD may have more difficulty with distraction and attention to detail in contextual situations, as opposed to impulsive responding in these settings. The lack of relation between cognitive attention and math performance may suggest that either the ANT does not assess the relevant attention constructs associated with math difficulties or may parallel studies of attention deficit/hyperactivity disorder (ADHD) in which cognitive and behavioral assessments are weakly related.

Several recent studies have reported that behavioral ratings of attention are sensitive to math difficulties in children, with teacher ratings of inattention accounting for unique variances in math performance (Cirino, Fletcher, Ewing-Cobbs, Barnes, & Fuchs, 2007; Fuchs et al., 2005; Fuchs et al., 2006). Other studies have shown a relation between cognitive measures of attention and mathematical performance (Huckeba, Chapieski, Hiscock, & Glaze, 2008; Lindsay, Tomazic, Levine, & Accardo, 2001; van der Sluis, de Jong, & van der Leij, 2004). Although behavioral and cognitive assessments measure attention using different methods, both demonstrate a relation to math achievement and math difficulties. What remains unclear is how they relate in the context of one another, which is important to demonstrate for purposes of articulating a model that can accommodate both types of attention with regard to math difficulties. Behavioral attention is consistent with diagnostic criteria for attention deficit/hyperactivity disorder (ADHD) and is evaluated through perceptions of an individual’s behavior; however, there is currently no framework to examine what properties of attention these behavioral ratings represent. Cognitive attention, in contrast, can be represented in a theoretical framework consisting of different processes of attention. One such framework is Posner’s model of attention (Posner & Peterson, 1990; Posner & Rothbart, 2007).

The purpose of the present study was to evaluate cognitive assessments of attention in children with math difficulties (MD) and how these assessments relate to behaviorally assessed attention. We review studies related to both types of attention. We then present an analysis of an attention network task and behavioral ratings to address whether these constructs have unique or overlapping variance in relation to math performance.

Behavioral Attention

Several studies have documented significant relations between ratings of attention and a variety of mathematical skills. Fuchs et al. (2006) examined the contribution of attention to different aspects of mathematical performance, including arithmetic, algorithmic computation, and arithmetic word problems. Unique and direct relations were found between attentive behavior, as measured by the Strengths and Weaknesses of ADHD-Symptoms and Normal-Behavior (SWAN) scale (Swanson et al., 2008), and a composite measure of arithmetic skills. Fuchs et al. (2006) found that teacher ratings of attentive behavior, evaluated using the SWAN, were the most robust predictor for mathematical performance, even in relation to cognitive assessment of arithmetic skill. Cirino et al. (2007) examined individuals with MD who varied in reading difficulties (RD). They also found a relation between the SWAN and measures of arithmetic performance but not measures of counting knowledge and estimation response times. The removal of behavioral inattention as a covariate from group comparisons did not alter the overall pattern of results. In a treatment study in which individuals were identified as at risk for MD and randomly assigned to a tutoring or control group, Fuchs et al. (2005) found that teacher ratings of attention/distractibility on the short form of the Social Skills Rating System (SSRS; Gresham & Elliot, 1990) were the most robust predictor of treatment outcome. For basic fact fluency and math computations, teacher ratings of inattention, but not impulsivity, were unique predictors of performance.

These studies show that behavioral ratings of inattention are a significant correlate of math or MD status. While such behavioral ratings may indeed reflect inattention as a cognitive process, other explanations are possible. First, inattentive behaviors may interfere with a child persevering on math tasks. Second, teachers may not be instructing in a way that is useful to children with MD who show inattentive behavior. Third, the inattention ratings may reflect concerns about academic performance and are not specific to inattention (Fuchs et al., 2005, 2006). Regardless of the explanation, behavioral ratings of inattention account for significant and unique variance in math performance and are associated with MD.

Cognitive Attention

Cognitive assessments of attention attempt to assess specific components of attention and may be tied to different theoretical models. However, there are various theoretical frameworks of cognitive attention, and models focus on different components. The components most often examined with regard to math achievement include sustained attention, inhibition, shifting, and working memory. However, we know of no study that evaluates the relation of math achievement systematically within a model-based framework of cognitive attention. Table 1 summarizes studies that address both mathematics and cognitive attention.

Table 1.

Studies on the Relation between Cognitive Measures of Attention and Mathematical Skills.

Study	Attention Processes	Findings
Censabella and Noël (2008)	Inhibitory control
van der Sluis et al. (2004)	Inhibition Shifting	*(when task involves both inhibition and shifting)
Lindsay et al. (2001)	Sustained attention Inhibition of prepotent responses	*
Huckeba et al. (2008)	Sustained attention Inhibition of prepotent responses	* * (to a lesser degree than sustained attention)

Note.

^*Indicates significant findings.

Lindsay et al. (2001) examined cognitive attention in children with MD by using the Conners’ Continuous Performance Test (CPT; Conners, 1994), a measure of sustained attention that requires inhibition of prepotent responses. Children with MD were less consistent in response latency compared with controls, even as they made more omission errors (failed to press a key when required). There was no significant difference between the two groups on the percentage of commission errors. According to Lindsay et al., the high number of omission errors made by the MD group may reflect a loss of “attentiveness.” However, a high percentage of commission errors, rather than omission errors, indicates an impulsive response pattern and is usually associated with low arithmetic scores. The high number of omission errors may be due more to distractibility than impulsivity. The participant may show a loss of attention during the task and fail to respond to relevant stimuli, whereas their attention is reinstated when they see the target, hence the lack of commission errors.

In a sample of children with Tourette syndrome (TS) and an age-matched comparison group, Huckeba et al. (2008) found that attentional deficits were significantly related to poor arithmetic skill. Children were given various math measures as well as the Test of Variables of Attention (TOVA; Greenberg, 1990, 1993). Children with TS were grouped based on their mean z scores from three scales of the TOVA: commission errors, omission errors, and response time. Three groups were formed: the high-, mid-, and low-attention subgroups. Only the low-attention subgroup differed significantly from the comparison group on all three TOVA variables. Response time was most closely associated with arithmetic performance in the Tourette syndrome group and may reflect deficient arousal to stimuli (Huckeba et al., 2008).

Several studies have examined inhibitory control in relation to working memory in children with MD (Bull & Scerif, 2001; Passolunghi & Siegel, 2001). Inhibition may be related to math skills due to the need to correctly access representations of math facts and other aspects of math in working memory. Inhibitory control is often interpreted as part of the attention domain because of the requirements for response selection and inhibition (Nigg, 2000). Using various tasks measuring working memory and inhibitory control, these studies indicate that children with MD have difficulty inhibiting prepotent information as well as trouble maintaining information in working memory (Bull & Scerif, 2001). Censabella and Noël (2008) evaluated inhibitory functions and found no significant differences in inhibition processes between children with MD and controls. These authors concluded that the inhibition deficiency in MD may be due to a more passive inhibition, and that MD results from specific deficits in numerical processing (Butterworth, 2005) as opposed to overall deficits in general attentional abilities (such as inhibition).

Van der Sluis et al. (2004) focused on both the inhibition and shifting capabilities of children with MD. On separate inhibition and shifting tasks, van der Sluis et al. found that the two groups of learners did not differ. By contrast, on a measure that combined inhibition and shifting, children with MD showed significantly poorer performance. This raises the possibility that difficulty in activating and coordinating different executive functions at the same time may result in poorer arithmetic performance in children with MD.

This review of literature examining mathematics and cognitive attention suggests that different components of cognitive attention are associated with mathematical skill depending on the model emphasized in the study and used to select measures. Sustained attention, inhibition of prepotent responses, and coordination of different executive functions involved in attention have each been implicated as being related to mathematical skills.

Rationale for the Present Study

The role of attention in children with MD is currently not well delineated because of the different ways in which the construct is operationalized. Behavioral assessments are based on parent and teacher perceptions of behavior and also may differ according to context (school vs. home). Although behavioral assessments of attention are more consistent with criteria for ADHD and may be more practical, they measure more overt behaviors and do not clearly map onto a theoretical framework of attention. Difficulty arises because behavioral ratings of attention do not have a clear theoretical framework, and it is therefore difficult to map these directly onto cognitive aspects of attention. For example, ratings may tap and not differentiate several processes of attention combining some items that represent impulsivity or disinhibition and items that represent focusing and directing attention. Comparisons of behavioral ratings with assessments based on a cognitive model may help address what specific attentional processes most closely map onto behavioral ratings. It is important to attempt to relate the two types of attention assessment because the cognitive models derive from a theoretical framework, but the behavioral ratings have shown strong predictive relationships with mathematics.

One model that may help relate behavioral ratings and cognitive assessments of attention is Posner’s model of attention (Posner & Petersen, 1990). According to Posner and Petersen attention is carried out by a network of anatomical areas that carry out specific cognitive attentional processes. Alerting involves arousal of attention and maintaining an alert state and is associated with right frontal and parietal areas; orienting is the selection of information from sensory input and is associated with the superior parietal lobes, temporal-parietal junction, and superior colliculus; executive attention is resolving conflict among responses and is associated with the anterior cingulate cortex and prefrontal cortex (Fan, McCandliss, Sommer, Raz, & Posner, 2002; Posner & Rothbart, 2007). Posner’s Flanker Task (Posner & Petersen, 1990) was developed as a task of spatial attention in which participants are presented target stimuli to the left or right of a fixation point, as well as valid, invalid, and neutral cues; accuracy and reaction time in this measure are based on whether the cue is valid or not.

The Attentional Network Task (ANT; Fan et al., 2002) was developed to help operationalize components of the Posner model, and examining performance on such a measure may help to conceptualize the attentional capacities of children with MD. By mapping behavioral ratings on this cognitive attention network, we may be better able to understand the relationship between them and, therefore, to help elucidate the apparent lack of theoretical framework behind behavioral ratings. To date, the relation between MD and specific aspects of attention has not been sufficiently examined. In the present study, we sought to elucidate these relations, wherein two scenarios seem possible.

First, children with MD may have difficulty with aspects of attention that more predominantly involve focusing and directing attention. In this scenario, alerting and orienting network performance on the ANT may overlap with behavioral ratings of inattention in children with MD. If this scenario is correct, groups with MD would differ from typically achieving children on assessments of alerting and orienting networks. Executive control performance would not differ between groups, since this is likely associated more with impulsivity and disinhibition.

Alternatively, there may be no association between behavioral ratings of inattention and focusing and directing attention on a cognitive task, in which case children with MD may have more difficulty with executive attention. Under this scenario, there would be weak relations of cognitive performance and behavior ratings, which is consistent with research on ADHD showing weak relations of cognitive assessments and behavioral rating of inattention (DuPaul, Anastopoulos, Shelton, Guevremont, & Metevia, 1992; Lui & Tannock, 2007) that may be context dependent. Children with MD would have more difficulty than controls on an assessment of executive control, and there would be indications of problems with attention persistence (e.g., an interaction of trial block and group showing progressively poorer performance by children with MD over time).

Most previous studies of students who struggle with math do not specifically consider the persistence of the math problem (Mazzocco, 2007) or the adequacy of instruction in math (Fletcher, Lyon, Fuchs, & Barnes, 2007). Because this response-to-intervention (RTI) framework (VanDerHeyden & Burns, 2010) is underutilized for describing the cognitive characteristics of MD students, we capitalized on a unique opportunity to evaluate cognitive and behavioral measures of attention in the context of responsiveness to tutorial intervention. We hypothesized that the attentional performance of students with MD who responded to math intervention would be similar to typically achieving children and would differentiate these groups from students who failed to respond.

METHOD

Participants

The participants for this study come in part from Fuchs et al. (2009), which is a third grade intervention study with students with MD (n = 70) and math and reading difficulties (MDRD; n = 63). MD in that study was defined as performance less than the 26th percentile on a calculation screening measure and greater than the 39th percentile on a reading measure, and MDRD was defined by performances below the 26th percentile on both a calculation screening measure and a reading measure. All students were required to have a T-score of 30 on both the Vocabulary and Matrix Reasoning subtests of the Wechsler Abbreviated Scale of Intelligence (WASI) (Wechsler, 1999) for inclusion. These students were randomly assigned to a 14-week tutoring intervention. Further details on participant ascertainment and study findings can be found in the original study (Fuchs et al., 2009).

For purposes of the present study, we reclassified students who completed the Fuchs et al. (2009) intervention as responders or nonresponders. In order to follow an RTI framework, the posttest Wide Range Achievement Test-3 (WRAT-3) scores were used to form groups based on mathematical ability and intervention response. Students whose posttest WRAT-3 Arithmetic scores were greater than the 30th percentile at the end of the tutoring were classified as responders to the intervention (n = 54). The remaining students were grouped as either having only MD (n = 17) or MDRD (n = 35). We chose the 30th percentile to ensure that only children with no math difficulties were included in the responder group. A variety of approaches involving final status postintervention as well as growth during the intervention had been used to assess intervention response. In general, most of the evidence in reading studies shows that final status models are sufficient, with little value added from assessments of growth in the intervention (Kim, Petscher, Schatschneider, & Foorman, 2010). There is little research on assessing inadequate responders to math instruction, where a variety of approaches to determining group classification are apparent (Bryant, Bryant, Gersten, Scammacca, & Chavez, 2008; Jordan, Hanich, & Kaplan, 2003). The approach used in this article simply establishes that children who have not had an opportunity to learn are distinguished from children whose math problems are more intractable.

In addition, because the Fuchs et al. (2009) study focused only on students with MD/MDRD, we then recruited an additional subgroup of typically achieving children. A typically achieving group was recruited specifically for the current study from third grade classrooms from one of the schools in the same school district in Houston used for intervention; the teachers nominated 32 students based on mathematical performance in the classroom indicating “average” achievers. To ensure typical development of math skills, the students were evaluated with the WRAT-3 Arithmetic measure. Following criteria used for determining final status at the end of the intervention study, eligible students (n = 23) scored above the 30th percentile on the WRAT-3 Reading and Arithmetic sub-tests. If eligible, students also were administered the ANT and a descriptive measure of nonverbal reasoning ability (WASI Matrices).

Sociodemographic and IQ information is presented by study group in Table 2. All four groups, MD (n = 17), MDRD (n = 35), responders (n = 54), and typical children (n = 23), were comparable on gender, χ²(3, N = 127) = 2.80, p = .42, and ethnicity, χ²(4, N = 127) = 4.88, p = .40 (where MD and MDRD groups were combined for ethnicity to account for the low number of Hispanic children in the MD group). Significantly more children in the MDRD group received reduced/free lunch at school, χ²(3, N = 127) = 7.86, p < .05. In addition and more interestingly, children in the adequate-responder group were significantly younger than children in the other three groups, F(3, 128) = 10.69, p < .01. These findings are consistent with other studies of inadequate responders to reading intervention (Nelson, Benner, & Gonzales, 2003).

Table 2.

Sociodemographic Information and Group Selection Data.

	Group		Responders	Typical
	MD	MDRD
n	17	35	54	23
Age (years: M ± SD)*	9.37 ± 0.45a	9.47 ± 0.45a	8.99 ± 0.39b	9.28 ± 0.37a
Gender – n (%)
Female	4(24%)	16(47%)	23(43%)	10(43%)
Male	13(76%)	18(53%)	30(57%)	13(57%)
Ethnicity – n (%)*
African American	13(76%)	23(68%)	31(58%)	12(52%)
Hispanic	0(0%)	10(29%)	13(25%)	9(39%)
Other	4(24%)	1(3%)	9(17%)	3(9%)
Reduced/Free Lunch Status- n (%)*
Yes	12(71%)	31(91%)	37(70%)	14(61%)
No	5(29%)	3(9%)	16(30%)	9(39%)
WASI Matrices T-Score (M ± SD)*	42.18 ± 9.87a,c	38.71 ± 8.06a	46.15 ± 10.19c	54.78 ± 9.14b
WRAT Reading Standard Score (M ± SD)*	103.29 ± 6.38a,c	76.14 ± 11.96b	99.83 ± 12.05a	106.83 ± 6.96c
WRAT Math Standard Score (M ± SD)*	85.59 ± 4.32a	82.46 ± 7.047a	104.46 ± 9.39b	106.13 ± 6.60b

Note. Demographic data was missing for one participant in the MDRD and Responder groups.

^*Significant difference between groups at p < .05.

There were expected differences among the groups on IQ and achievement, illustrating that the selection criteria appropriately differentiated the groups. Typical children demonstrated significantly higher WASI Matrix Reasoning scores than children in the other four groups, F(3, 128) = 14.21, p < .01. Children with MDRD performed significantly lower on the WRAT reading subtest than the other three groups, F(3, 128) = 52.79, p < .01. Interestingly, children with MDRD demonstrated significantly lower WASI Matrix Reasoning subtests scores than responders, F(1, 128) = 13.21 p < .01. Responders performed significantly worse than typical children on the WRAT reading subtest, F(1, 128) = 6.90, p < .01.

Group-Selection Measures

IQ and achievement measures were administered to establish exclusion criteria for intellectual deficiency, reading status, and responsiveness to the tutoring intervention.

Achievement

The WRAT-3 comprises arithmetic calculations and word reading subtests (Wilkinson, 1993). Arithmetic requires counting, identification of numbers, number comparisons, and computations that increase in difficulty. Reading involves identification of letters and words. These WRAT-3 subtests have adequate internal consistency (r > .90) and strong criterion validity (Wilkinson, 1993). Standard scores were analyzed in this study.

Intelligence

Two subtests of the Wechsler Abbreviated Scale of Intelligence (WASI; Wechsler, 1999), a measure of general intellectual ability, were included: Vocabulary and Matrix Reasoning. The internal consistency for both subtests is .92 or higher (Sattler, 2001). The Vocabulary subtest measures verbal knowledge, expressive vocabulary, and foundation of information. The Matrix Reasoning subtest measures nonverbal reasoning through four types of tasks: serial reasoning, pattern completion, classification, and analogy. The Matrix Reasoning subtest of the WASI was the only subtest collected for the typically achieving group because time limits precluded administration of the Vocabulary subtest for the this group. Although both WASI subtests were used in identifying the MD, MDRD, and responder groups for intervention, we used only Matrix Reasoning in this study.

Other Math Measures

Other assessments of math were Basic Facts Addition and Subtraction and the Double-Digit Addition and Subtraction test (Fuchs, Hamlett, & Powell, 2003). The Double-Digit Addition and Subtraction test (Fuchs et al., 2003) comprises two subtests. The first provides students with 5 minutes to complete 20 two-digit by two-digit addition problems with and without regrouping. The second subtest provides students with 5 minutes to complete 20 two-digit by two-digit subtraction problems with and without regrouping. Coefficient alpha in the present study was .93 (Fuchs, 2008). Following Fuchs et al. (2008), these measures were used to create a composite of math performance for correlational analyses.

Cognitive Attention Measures

The ANT (Fan et al., 2002) combines cued reaction time (Posner, 1980) and flanker tasks (Eriksen & Eriksen, 1974). Stimuli were presented through E-Prime, an experiment application, on a Mac laptop. Stimuli consisted of a row of five horizontal black lines, with arrowheads pointing right or left. The target was the arrowhead pointing to the left or right in the center of the line. The target was flanked on either side by two arrows in the same direction (congruent condition), in the opposite direction (incongruent condition), or by lines (neutral condition) (Fan et al., 2002). Students determined whether a central arrow points left or right by pressing the corresponding button. In the child version of the ANT, the arrows were placed inside colorful cartoon fish in a row, and the child was instructed to help feed the center fish by pressing a button corresponding with the direction the center fish is swimming (the direction of the arrow inside the fish). To add an orienting component, the arrows appeared above or below fixation points and may or may not be accompanied by spatial cues (Fan et al., 2002). There are four types of cues: a central cue, a double cue, a spatial cue, or no cue. One of these types of cues preceded each target. In the central cue condition, an asterisk is presented at the location of the fixation cross. In the double-cue condition, an asterisk appears above and below the fixation cross. The spatial cue involves a single asterisk presented in the same position of the upcoming target (Rueda et al., 2004). Except when spatial cues were present, the location of the target was always uncertain. Responses were recorded using two input keys on a joystick. The task is made up of three blocks.

The Alerting score was calculated as the median response time to the double cues minus the median response time to the no cues (computed within each flanker condition). The median of these three subtraction scores was computed. The Orienting score was calculated as the median response time to the central cues minus the median response time to the spatial cues (computed within each flanker condition). The median of these three subtraction scores was computed. The Conflict score was calculated as the median response time to congruent flankers minus the response time to the incongruent flankers (computed within each flanker condition). The median of these three subtraction scores was computed (Fan et al., 2002).

The efficiency of the three attentional networks (Alerting, Orienting, and Conflict) is assessed by a set of cognitive subtractions. According to Fan et al. (2002), these subtractions are less reliable than the mean of raw reaction time (RT) scores. The conflict network is the most reliable, with a test-retest reliability of r = .77; however, the alerting (r = .52) and orienting (r = .61) networks show less than adequate reliability (Fan et al., 2002).

Attentive Behavior Measure

The SWAN-IV is an 18-item teacher rating scale of behavioral inattention. Behaviors, corresponding to the criteria for ADHD from the Diagnostic and Statistical Manual of Mental Disorders, text revision (American Psychiatric Association, 2000) are rated on a 7-point Likert scale; the ratings range from −3 to +3, with more negative scores corresponding with problematic behavior. In the present study, we reported results from the Inattentive Behavior subscale as the average of Items 1–9. The SWAN-IV has been shown to significantly correlate with other dimensional assessments of behavioral inattention (Swanson et al., 2008). Coefficient alpha for inattention and hyperactivity/impulsivity in this sample was .97 (Fuchs et al., 2006).

Procedure

Students with MD and MDRD were assessed in the spring of third grade (2007) as part of a tutoring study (see Fuchs et al. [2008] for details of the intervention). Participants were tested in a quiet setting, and computer testing of the ANT was approximately 15 minutes. Students were individually administered the WASI subtests, the Arithmetic and Reading WRAT-3 subtests, and a math assessment battery. In May, the ANT was then administered individually on Mac laptops by trained examiners. Teachers were asked to complete the SWAN-IV rating scale for all participants in the fall of third grade.

The typically achieving group was tested separately in May of 2009 because Fuchs et al. (2008) did not evaluate typically developing children. Third grade students were administered the ANT individually on Mac laptops by trained examiners and were then individually administered the WASI Matrix Reasoning, the Arithmetic and Reading WRAT-3 subtests, Basic Facts Addition and Subtraction, and the Double-Digit Addition and Subtraction test. Teachers were not available to provide SWAN-IV behavioral ratings for the typically achieving group, but no child was identified or treated for attention disorder.

Data Analysis

A trial-by-trial dataset was explored to inspect variability and outliers. Trials in which reaction times were less than 100 ms or greater than 1700 ms were removed from analyses (Fan et al., 2002). Distributions of the reaction times were examined after these exclusions and determined to be normally distributed. Research questions were tested with correlations as well as with analyses of variance (ANOVAs). Details on how each hypothesis was addressed are embedded in the results below. In all analyses, sociodemographic information, including age and free lunch status, was treated as a covariate. Because many children also had reading difficulties, an additional analysis treated reading as a covariate. There were no substantive differences in the pattern of results with or without covariates; therefore, they are not reported below.

RESULTS

Data Screening

Examination of invalid trials resulted in the removal of 5% of trials. This high number of invalid trials is most likely due to participants taking too long to respond. Follow up to this analysis revealed that children in the typical group had significantly more invalid trials (M = 10.22; SD = 7.62) than those in the MD group (M = 6.53; SD = 4.91) and responder group (M = 5.46; SD = 5.15), F(1, 128) = 4.12, p < .04 and F(1,128) = 11.31, p < .001, respectively. Children with MDRD (M = 8.26; SD = 5.32) also had significantly more invalid trials than the responder group, F(1, 128) = 5.14, p < .03, but did not differ from the other groups. These mean differences are small and consistent with previous findings on the rate of invalid trials (Fan et al., 2002).

Alerting Network Score

Table 3 presents means and standard deviations for each ANT component. A one-way ANOVA for the ANT Alerting effect revealed no significant group differences, F(3, 125) = 1.42, p < .24. This suggests that children in each group performed similarly when alerting their attention in this task. Analysis of reaction times for the Alerting subtraction components (e.g., median reaction times across flankers of the no and double cues) also revealed no significant group differences on these scores, F(3, 128) = 0.45, p < .72 and F(3, 128) = 0.47, p < .71. Most effect sizes were in the small-to-moderate range (.20–.50), except for the comparison of MDRD versus Typical groups (d = .08), which was negligible.

Table 3.

Means and Standard Deviations for ANT Network Scores.

Group	Alerting		Orienting		Conflict
	Mean	SD	Mean	SD	Mean	SD
MD	28.25	77.15	26.31	79.22	112.27	91.14
MDRD	63.21	77.60	51.25	60.54	100.70	95.94
Responder	49.51	52.64	33.50	77.33	85.65	73.15
Typical	69.03	83.51	37.86	52.14	70.15	55.45

Orienting Network Score

A one-way ANOVA on the ANT Orienting effect revealed no significant group differences, F(3, 125) = 0.66, p < .58. Children in each group performed similarly when orienting their attention to the spatial cues. Analysis of reaction times for the Orienting subtraction components (e.g., median reaction times across flankers of the central and spatial cues) also did not yield significant group differences, F(3, 128) = 0.59, p < .62 and F(3, 128) = 0.62, p < .60. For pairwise comparisons, effect sizes ranged from .06–.36 (smaller effects).

Conflict Network Score

A one-way ANOVA on the ANT Conflict effect also revealed no significant group differences, F(3, 125) = 1.18, p < .32, suggesting that children in the four groups performed similarly when utilizing their attention to resolve conflict. Analysis of reaction times for the Conflict subtraction components (e.g., median reaction times across cues of the congruent and incongruent cues) also did not yield group differences, F(3, 128) = 0.36, p < .78 and F(3, 128) = 0.78, p < .51. For pairwise comparisons, effect sizes ranged from .14–.38 (smaller effects).

Reliability

The reliability of the ANT task was analyzed because null results were found when analyzing network scores and studies have found varying estimates of reliability for the ANT. Reliability was analyzed by computing Pearson correlations across blocks of the test. Table 4 shows the Pearson correlations among measures of the three attentional networks for each of the three blocks. Correlations for the Alerting and Orienting scores across blocks were negligible (r = −.13–.08), and those for the Conflict scores were also low(r = .12–.30). Overall, there appears to be little stability across blocks in terms of these difference scores comprising the ANT domains of interest.

Table 4.

Pearson Correlations for ANT Network and Component Scores.

	Block 1			Block 2
	Alerting	Orienting	Conflict	Alerting	Orienting	Conflict
Block 1
Alerting
Orienting
Conflict
Block 2
Alerting	−.04
Orienting		.02
Conflict			.30*
Block 3
Alerting	−.13			.0009
Orienting		.08			.00
Conflict			.12			.23*

Note.

^*Correlation is significant at the .05 level.

Determining reliability is often an issue when using difference scores; reliable difference scores can be found only when using tests that are reliable at each time they are given and that have low correlations with each other (Crocker & Algina, 2008). Therefore, Pearson correlations of the scores that make up each ANT subtraction were also analyzed across blocks. Correlations for each cue and flanker component across blocks were statistically significant and higher than the difference scores, though not strong in terms of stability (range: r = .18–.55, median: r = .39).

Factorial Design

Given the weak reliability of the network scores across blocks, we utilized the constituent components of each in a factorial design to further evaluate the impact of group on ANT performance and to evaluate whether the ANT was performing as expected. The network effects consist primarily of combinations of cues and flankers, and therefore a repeated measures multivariate analysis of variance (MANOVA) was performed to examine the relation between block (3), flanker (congruent, incongruent, neutral), cue (none, double, central, spatial), and group (MD, MDRD, Typical, Responder). In these analyses, group was treated as the between-subjects factor and block, flanker, and cue were each treated as within-subjects factors. There was not a significant Block × Flanker × Cue × Group interaction, F(36, 305) = 1.31, p < .12. Therefore, scores were collapsed across blocks.

A significant Flanker × Cue × Group interaction was found, F(18, 340) = 1.91; p < .01. To further explore this interaction, we examined the interaction between cue and group within each level of flanker. We looked at two types of cues at a time: no cue versus double cue to examine the effect of having a cue present and central cue versus spatial cue to examine the orienting component of a spatial cue. A significant Cue × Group interaction was found within congruent flanker trials, F(3, 125) = 3.07, p < .03. A significant Cue × Group interaction was also found within incongruent flanker trials, F(3, 125) = 3.71, p < .01. However, there were no significant findings when examining cue within congruent and incongruent flanker trials for each of the four groups. These findings are most likely due to the low power that occurs when using small sample sizes. No other significant Cue × Group interactions were found within the congruent, incongruent, and neutral flankers.

Children, regardless of group, responded significantly faster to double cues than no cues, significantly faster to spatial cues than central cues, and significantly faster to congruent than incongruent flankers. A cue-validity effect refers to the response pattern of reaction times expected; children are expected to respond more quickly to a cue that identifies the correct location of the upcoming target than if there is no cue or a central cue (Dennis et al., 2005) and are expected to respond faster to congruent than incongruent flankers. The expected pattern of responses was found and all groups displayed a cue-validity effect. Figure 1 shows that children responded faster to double cues than no cue, faster to spatial cues than central cues, and faster to congruent than incongruent flankers. The clear effects of cue validity in the ANT show that children performed on the task as expected; however, these results are clearer and more reliable when analyzed with a factorial design as opposed to the created difference scores.

Figure 1.

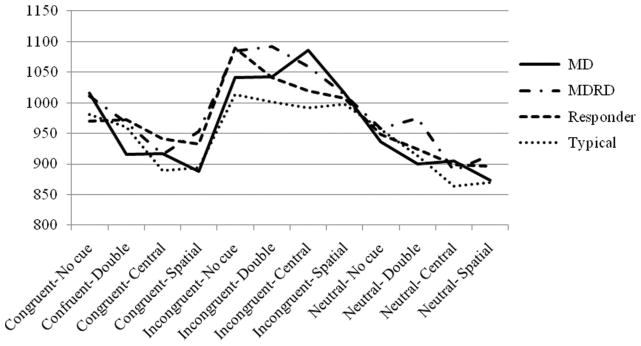
Median reaction time (in milliseconds) on the ANT by cue and flanker.

Behavior Ratings and Math Difficulties

Table 5 shows means and standard deviations for SWAN-IV inattention scores. Children in the responder group were rated as less inattentive than children in the MD and MDRD groups, F(1, 103) = 15.06, p < .01 and F(1, 103) = 16.87, p < .01, respectively. There was no significant difference in behavioral ratings of attention between children with MD and MDRD, F(1,103) = 0.36; p < .55. A multivariate analysis of covariance (MANCOVA) examining the three ANT network scores was performed with SWAN-IV inattention scores treated as a covariate. No significant difference was found when performing this analysis with SWAN-IV ratings as a covariate, F(6, 192) = 0.71, p < .65.

Table 5.

Means and Standard Deviations for SWAN Inattention Scores.

Group	SWAN Inattention Score
	Mean	SD
MD	−11.35	11.35
MDRD	−9.47	8.37
Responder	0.02	11.43
Typical	NA	NA

Pearson correlations between inattention, the math performance composite, and Alerting/Orienting scores in children with MD/MDRD revealed a significant correlation between teacher ratings of inattention and math performance, r = .45. Correlations were not significant between inattention and Alerting network scores, r = −.03, and Orienting network scores, r =−.16. There were also no significant correlations between math performance and Alerting network scores, r = −.04, and Orienting network scores, r = −.09. Given the absence of associations of ANT performance and math group and the less than adequate reliability of the ANT measures, this result is not surprising.

DISCUSSION

In one scenario, we hypothesized that if children with MD/MDRD have more difficulty with focusing and directing attention, they would perform more poorly when alerting their attention to cues than responders and typically achieving children. Under this scenario, we predicted that children with MD/MDRD would have more difficulty alerting and orienting their attention in a cognitive assessment of attention. We found that children with MD/MDRD did not significantly differ from typically achieving children and responders when alerting or orienting their attention to the task.

Under the second scenario, children with MD/MDRD were expected to perform differently on manipulating their attention as measured by the conflict network, which involves executive attention (Fan et al., 2002). However, children with MD/MDRD did not perform significantly different than typical children or responders on a measure of executive control.

What about behavioral attention? We hypothesized a strong relation of alerting and orienting network scores with SWAN-IV behavioral inattention scores, which did not occur. Consistent with previous findings in ADHD (DuPaul et al., 1992; Lui & Tannock, 2007), correlations between cognitive measures of attention and behavioral rating of attention were small and not statistically significant. However, behavioral ratings of inattention correlated significantly with math performance. The absence of relations of ANT performance and math group and the significant relations between SWAN-IV behavioral ratings and math group may indicate that behavioral ratings assess unique aspects of attentional difficulties in children with MD/MDRD. Although behavioral ratings are strongly predictive of attentional difficulties, these ratings (SWAN) did not map well onto the cognitive framework of the ANT task. It is unclear whether this inability to map behavioral ratings (SWAN) onto the cognitive framework of the ANT is due to their lack of construct overlap or due at least in part to the weak demonstrated reliability of the cognitive task as it was used in this study.

Although Fan et al. (2002) found moderate reliability of the three network scores, other studies have found lower reliabilities for this version of the ANT. For example, in a study of typically developing children, Rueda et al. (2004) also calculated the reliability of ANT network scores with an odd-even split-half correlation. Reliability scores were weak for the alerting, r = .37, and orienting, r = .02, networks, and modest for the conflict, r = .59, network. Lawrence, Eskes, and Klein (2009) obtained even lower values: alerting, r = .07, orienting, r = −.01, and conflict, r = .24, networks. Our findings are in accordance with Lawrence et al. (2009), documenting that the alerting, orienting, and conflict networks all had poor test-retest reliability, which is at least in part due to the use of difference scores (Bereiter, 1967; Crocker & Algina, 2008). Pearson correlations were low even when analyzing reaction times to different cues that comprise the three networks, suggesting that these are difficult to assess with the task as used here.

Because of less than adequate reliability for these difference scores, we used a factorial design approach to examine the relation between group, the four different cues, and the three flankers. A significant interaction was found between cue and group within both congruent and incongruent flanker trials. However, there were no significant findings when examining cue within congruent and incongruent flanker trials for each of the four groups, which is likely due to the low power that occurs when using small sample sizes.

In terms of a cue-validity effect, children were expected to perform faster when a double cue alerted them to an impending target as opposed to no cue and to perform faster to a spatial cue that oriented their attention to where an upcoming target would be compared with a central cue. In the present study, all groups displayed a cue-validity effect. This shows that the ANT task is working correctly but may not be the correct task to use in order to differentiate between children with MD and typically achieving children. These results are more clear and reliable when analyzed with a factorial design as opposed to the created difference scores.

In this study, we had the unique opportunity to examine responders to tutorial interventions on cognitive and behavioral measures of attention. As hypothesized, responders did not perform differently than typically achieving children on the ANT. Children who responded to the math intervention were not expected to have trouble with alerting and orienting attentional processes, since they were able to grasp math facts and concepts after a tutorial program. However, it should be taken into account that many of the responders still have reading difficulties. Since reading scores were treated as a covariate, they did not affect results; these reading difficulties did not seem to affect the responders’ performance.

One explanation of the lack of relation between cognitive attention and math performance is that the ANT does not assess the constructs that are associated with math difficulties. Perhaps Posner’s model of three attentional networks is not the best theoretical framework to conceptualize attentional difficulties in children with MD. Previous studies have found that children with math difficulties have poor sustained attention and exhibit disinhibition (Table 1). In terms of sustained attention, other studies have shown that a significant group-by-block interaction on a version of Posner’s Flanker Task from which the ANT was derived can be interpreted as an index of sustained attention that shows the expected poorer performance over time in children with ADHD (Brewer et al., 2001); however, children with MD/MDRD did not show a significant group-by-block interaction on the ANT. These findings indicate that children with MD/MDRD may not have difficulty with sustained attention, although a more direct test would involve a CPT measure like that used by Lindsay et al. (2001) to examine sustained attention in children with MD/MDRD. The ANT does not directly assess the construct of disinhibition, an aspect of cognitive attention that has been related to children with MD (Table 1). Perhaps cognitive assessment of attention would be more sensitive to math difficulties if a task measuring inhibition was used, such as a Stop Signal or other Go/No-Go task.

These findings must be understood in light of several key limitations of the present study in which children’s performance on the ANT was not strongly related to math performance. In addition to the reliability issues, the sample size may not have been adequate to detect what were mostly small effect sizes, for which a very large number of participants would be required to detect statistically significant interaction effects. Also, the sample included a high percentage of children in lower socioeconomic status households. This may affect results because children may perform poorly on math tasks because of lack of instruction as opposed to overall mathematical capability. Another possible limitation is the large number of responders compared to children with MD/MDRD, meaning many children in the sample no longer had math difficulties when introduced to adequate tutoring interventions.

With these limitations in mind, we tentatively draw the following set of conclusions. First, behavioral ratings suggest that children with MD have more difficulty with distraction and attention to detail in contextual situations, as opposed to impulsive responding. Like Fuchs et al. (2006), teacher ratings of inattention highly correlate with mathematical performance. However, behavioral ratings are not necessarily a measure of cognitive inattention; behavioral ratings of attention may reflect other factors such as the teacher’s perception of the child’s academic achievement. These aspects of performance were not captured by the ANT. Although this study showed the patterns expected on the ANT, the reliability was poor, which limits correlational analyses. The ANT is used as a measure of cognitive attention because the task itself does make sense theoretically based on Posner’s model of attention; however, this task may be an example of a measure that has validity without reliability. In demonstrating the poor reliability of the ANT, we suggest that the ANT is not found to be reliable in various clinical populations and therefore should not be used as a reliable measure of cognitive attention. Future studies may use a more reliable test to measure attentional networks and other cognitive components of attention in children with MD. Performance on other cognitive measures involving disinhibition might also be included to examine the relation between math performance and inhibitory aspects of cognitive attention. By examining other aspects of cognitive attention, the relation of attention and math performance can be better understood. However, given the weak relations of cognitive and behavioral assessments of inattention generally reported in the literature (DuPaul et al., 1992), these two approaches to assessment may not be strongly related.