Geodesic Distances to Landmarks for Dense Correspondence on Ensembles of Complex Shapes

Abstract

Establishing correspondence points across a set of biomedical shapes is an important technology for a variety of applications that rely on statistical analysis of individual subjects and populations. The inherent complexity (e.g. cortical surface shapes) and variability (e.g. cardiac chambers) evident in many biomedical shapes introduce signifi-cant challenges in finding a useful set of dense correspondences. Application specific strategies, such as registration of simplified (e.g. inflated or smoothed) surfaces or relying on manually placed landmarks, provide some improvement but suffer from limitations including increased computational complexity and ambiguity in landmark placement. This paper proposes a method for dense point correspondence on shape ensembles using geodesic distances to a priori landmarks as features. A novel set of numerical techniques for fast computation of geodesic distances to point sets is used to extract these features. The proposed method minimizes the ensemble entropy based on these features, resulting in isometry invariant correspondences in a very general, flexible framework.

1 Introduction

Establishing point correspondence between two or more shapes is a key algorithmic component in many medical image analysis applications. Various technical strategies—including registration, alignment to a template or matching features/measurements—have been used to study not only geometric changes in shape, but also image and model measurements relevant to specific applications. While many systems rely on alignment to a common template, the literature shows some advantages in building correspondences in an unbiased way by using an entire ensemble of subjects [1]. Automatic correspondence optimization has benefited from recent approaches like the spherical harmonics (SPHARM) description [2], which implicitly computes dense correspondences across shapes using a continuous one-to-one mapping of each shape to the unit sphere. The Minimum Description Length (MDL) method [3] also relies on spherical parameterization to compute correspondences but is computationally expensive and thus rendered impractical. The point distribution model given by Cates et al [4] provides a flexible framework to establish dense point correspondences across shapes in a nonparametric fashion, without the constraint of a particular parameterization or topology.

The inherent complexity of certain classes of biomedical shapes presents significant challenges in the establishment of point correspondences. For instance, studies of degenerative conditions such as autism and Alzheimer's disease benefit from the analysis of local cortical thickness measurements of the brain and rely on shape matching for valid comparison between subjects. Some of these techniques are initialized using manually delineated surface features (major sulci) to drive the matching procedure [5,6]. The many folds of the cortex can easily cause sulci to cross over each other and become aligned with the wrong features in the target or template. Widely used software packages such as FreeSurfer and BrainVoyager use cortex inflation—a process of removing cortical folds and then, typically, mapping to a sphere—to overcome the complexity in matching cortical surfaces. One of the goals of this work is to avoid this intermediate, inflated representation.

Correspondence based on point positions is sensitive not only to shape complexity, but also to anatomical variability in shapes. This can lead to inconsistent correspondences on surfaces where it is diffcult to automatically match landmarks across a wide range of shapes. An example is the structural analysis of the left atrium (LA), which is of particular interest in atrial fibrillation (AF) studies. Recent advances in MRI have enhanced structural imaging of the LA but a high degree of variability in the LA anatomy presents a significant challenge in automatic identification of anatomically significant landmarks for quantitative analysis. The incorporation of a sparse set anatomically based landmark features, identified by either an expert or some automated process, can dramatically improve dense automatic correspondence in these scenarios.

The strategy in this paper is motivated by two observations. First is the relative success of alignment techniques, such as [5], that rely on nearly isometric, smooth mappings to simplified parameterizations in order to find appropriate deformations to templates. This suggests that positions on the surface rather than the ambient space are an important in anatomical alignment. The second observation is the success of landmark-distance-based features in recognizing shapes in computer vision applications [7,8,9]. Although these methods rely on combinatorial matching algorithms, which are not particularly well suited to the applications we address here, these works do demonstrate that collections of geodesic distances are rich, nearly complete, descriptions of shapes.

2 Technical Background

The proposed method (geodesic distance method) builds on the correspondence optimization method proposed in [4] as well as efficient parallel solvers for the eikonal equation on triangular meshes proposed by Fu et al [10]. Here we give a brief review of the results from these works that are relevant to our method.

Correspondence Optimization

We define a surface $\mathcal{S}\subset {\mathbb{R}}^d$ (e.g., d = 3 for volumes), as a smooth, closed manifold of codimension one. We sample $\mathcal{S}$ using a discrete set of N points that are considered as random variables Z = (X₁, X₂, . . . , X_N)^T, $\mathbf{X}\in {\mathbb{R}}^d$ drawn from a probability density function (PDF), p(X). An ensemble comprised of M surfaces, ε = z¹, . . . , z^M can be described by a Nd×M matrix of particle positions $P=\left({\mathbf{x}}_j^k\right)$, where k = 1, . . . , M and j = 1, . . . , N. Let ${\mathbf{z}}^k\in {\mathbb{R}}^{Nd}$ be an instance of a random variable Z, then, modelling p(Z) parametrically as a Gaussian with covariance Σ gives the entropy $H\left(\mathbf{Z}\right)\approx \frac{1}{2}\log \mid \Sigma \mid =\frac{1}{2}{\sum }_{j=1}^{Nd}\log {\lambda }_j$, where λ_j are the eigenvalues of Σ. We estimate the covariance from the data, letting Y denote the matrix of (centered) points for the ensemble, which gives Σ = (1/(M − 1))Y Y ^T . Because N > M, we perform the computations on the dual space (dimension M). Thus, we have the cost function G associated with the ensemble entropy:

$$\log \mid \Sigma \mid \approx G\left(P\right)=\log \mid \frac{1}{M-1}{Y}^{T}Y,\mid \text{and}-\frac{\partial G}{\partial P}=Y{(Y^{T}Y+\alpha I)}^{-1}.$$ (1)

where |·| is the matrix determinant. The combined ensemble and shape cost function is defined by Q = H(Z) − Σ_k H(P ^k). The optimization process of this cost function is defined via gradient descent, by moving individual points on the surface, as described in [4].

Fast Geodesic Distance Computation

The proposed method requires the computation of geodesic distances to landmarks (points/curves) at all correspondence positions. Performing these calculations over large ensembles of shapes is prohibitive without the use of fast, parallel algorithms for solving the hyperbolic partial differential equations (PDE) as well as extremely fast graphics processing units (GPUs). One such method, the fast iterative method (FIM) [11] formulates the distance between each point a on the surface and every other point, as the solution to the eikonal equation |∇u| = 1, using the boundary condition u(a) = 0. An extension of FIM for triangular meshes [10] that performs fast computation of geodesic distances between vertices on a triangle mesh is used to compute geodesic distance features.

3 Methodology

Rather than use absolute particle positions, as in [4], we propose to leverage manually placed landmarks (points/curves) to guide correspondence optimization via geodesic distances to these landmarks. Consider a manifold $\mathcal{M}\subset {\mathbb{R}}^d$ with a point x and a landmark l. We can define a mapping $D:\mathcal{M}\to \mathbb{R}$, where D(x, l) is the geodesic distance of point x to the landmark l. Given a triangulated surface to describe $\mathcal{M}$ and a point set to describe landmark l, we can use the FIM method [10] to compute D(x, l) for all points $x\subset \mathcal{M}$ by setting appropriate boundary conditions on the eikonal equation. In practice, we compute these distances to all points on the mesh and interpolate these discrete samples onto the triangle faces, as in [12]. Given an ensemble of shapes, as described in Sec. 2 and a set of T landmarks (points/curves) for each shape, we can represent particle j on shape k as a vector of geodesic distances: ${\tilde{p}}_j^k=(D(x_j^k,l_1^k),\dots ,D(x_j^k,l_T^k))$ from T landmarks. Using the entropy minimization framework from Sec. 2, the ensemble entropy term in (1) can be modified to compute covariance of the geodesic distance features instead of particle positions, giving

$$G\left(\tilde{P}\right)=\log \mid \frac{1}{M-1}{\tilde{Y}}^T\tilde{Y}\mid$$ (2)

where, Ỹ is the matrix of geodesic distances to all landmarks at a correspondence point minus the mean geodesic distance to all landmarks for the same point across the ensemble. The derivative ∂G/∂P is computed by the chain rule as

$$-\frac{\partial G}{\partial P}=J^T{({\tilde{Y}}^T\tilde{Y}+\alpha I)}^{-1}$$ (3)

where J is the Jacobian matrix given by ∂D/∂P and computed as a block diagonal matrix with diagonal blocks of T × d submatrices of partial derivatives, computed numerically by projecting the correspondence points on to the surface. This gradient is used to update point correspondences in accordance with the optimization described in [4].

Proof-of-Concept Experiment

Computational solid geometry methods were used to compute the intersection of a pair of ellipsoids with axes a, b and c, with a larger ellipsoid with axes A, B and C, to create a coffee bean shape with two slots—thus simulating an element of the cortical surface folds. The slots were then moved and scaled stochastically, to create a population of 10 coffee bean shapes. The position of the slots was chosen from a uniform distribution in the range [−B/3, B/3], and the width was sampled from a Gaussian distribution of μ = 8 and σ = 2. The number of correspondences was set to 1024.

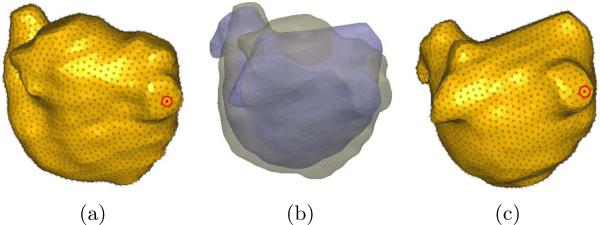
First, correspondences were distributed across the ensemble using the original formulation from [4]. The sole use of point positions, coupled with the complexity of the shape led to inconsistent correspondences, and the method failed to compute a valid mean shape (Fig. 1(a)). Next, fixed landmarks were introduced (3 each in the two slots and 1 on the ridge between them) into the original formulation and the experiment was repeated. Fixed landmarks improved the consistency of correspondences, but position information alone is not isometry invariant, and thus resulted in a suboptimal mean shape (Fig. 1(b)). Finally, geodesic distances to these fixed landmarks were computed as described above and used to optimize correspondences in the proposed method. This resulted in isometry invariant, consistent correspondences, as evidenced by the mean shape (Fig. 1(c)).

Fig. 1.

Mean shapes from: (a) particle based automatic correspondence [4] , (b) including fixed landmarks, and (c) and proposed method using geodesic distance features

4 Results and Discussion

Validation on Cortical Surfaces

T1- and T2-weighted MRI scans were acquired for paediatric 2-year-old subjects as part of the Infant Brain Imaging Study (IBIS) network (http://www.ibis-network.org). Ten of these subjects were randomly selected for this study. A single subject was selected as template and an expert manually labelled 13 major curves on the template surface: superior temporal (STS), inferior temporal (ITS), medial-temporo-occipital (MTOS), central (CS), precentral (PreCS), postcentral (PostCS), inferior frontal (IFS) and superior frontal (SFS), intraparietal (IPS), cingulate (CingS), calcarine (CalcS), occipito-parietal (OPS), and sylvian (SylS) sulcus. Only left hemispheres were used. The input data was a set of segmented left hemispheres, with 13 sulcal curves each. 6 of these curves were selected as landmark curves (as shown in Table 1) and geodesic distances to these curves were used as features to optimize 6144 correspondences on each cortical surface. Sulcal depth was also used as an additional feature to guide the correspondence optimization. Two views of the mean shape computed from this model are shown in Fig. 2. Note that it is possible to identify all of the major sulci, including the ones not used in the optimization. Given the lack of ground truth for cortical surface data, we validate these results via analyses of surface measures (depth, thickness) and cross-validation based on the geodesic distance features. A cross-subject variance estimate of sulcal depth was computed over all correspondences across all shapes in the ensemble. The mean and std. deviation values of 1.39918 and 0.769351 were found to be consistent with the literature. Additionally, a cross-subject variance estimate of the cortical thickness was also performed, since the use of sulcal depth as a feature biases the previous test. The mean and std. deviation values of 0.494561 and 0.392878 were also found to be consistent with the literature [13].

Table 1.

Comparison of average dissimilarity per curve between proposed (top) and CIVET (bottom) methods, for curves used in correspondence optimization (left) and unseen curves (right)

	Curves used in optimization						Unseen curves
	CingS	CS	IPS	STS	SFS	SylS	CalcS	IFS	ITS	MTOS	OPS	PostCS	PreCS
Proposed	3.42	2.18	7.19	6.79	4.67	3.75	2.31	4.63	8.43	5.00	3.69	6.61	5.24
CIVET	3.49	2.90	10.68	9.95	4.55	3.54	2.08	4.95	11.32	5.41	3.97	8.61	7.15

Fig. 2.

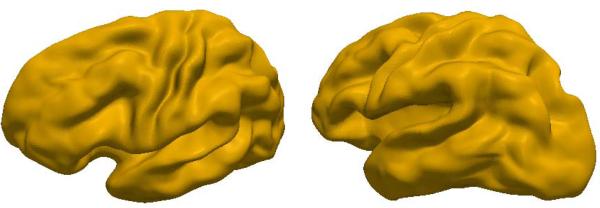
Two views of the mean shape of the ensemble of left hemisphere cortical surfaces

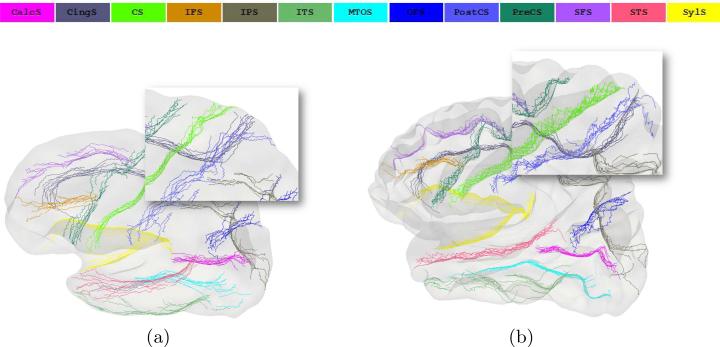
Next, each set of curves was warped onto the mean space via thin plate spline warping and curve alignment was compared to the output of the CIVET pipeline, where major sulcal curves were initially mapped onto the common unit sphere by the surface registration method [14], and then further projected onto the template surface by a one-to-one mapping between the sphere and the template. Figure 3 shows a visual comparison of curve alignment from the geodesic distance method (a) with curve alignment from the CIVET pipeline (b). In general, alignment for curves used as features in the geodesic distance method was better than the CIVET result, while maintaining the smoothness of the curves. For unseen curves, CIVET alignment appears to be better, however this may be achieved at the cost of smoothness, as shown in the inset images for the CS curve. We also quantify sulcal curve alignment in Table 1, by looking at the average dissimilarity per curve, computed in a pair-wise manner using all points on the curve, over all pairs of shapes. Table 1 indicates that the geodesic distance method aligns 4 of the 6 curves used as features better than the CIVET pipeline. Moreover, the same is true for 6 of the remaining 7 unseen curves. These values indicate that the correspondences are consistent and isometry invariant, even for sulci that are not part of the landmark set. Thus the geodesic distance method provides a framework for further statistical analysis of the cortical surface without the need for inflation.

Fig. 3.

Alignment of cortical curves in the mean space using the geodesic distance method (a) and the CIVET pipeline (b). Note that the two surface templates are different: mean template from geodesic distance method (a), MNI template (b).

Application to AF

Thirteen shapes were retrospectively chosen from a database of patients who presented to the University of Utah for AF and underwent late-gadolinium enhancement (LGE) MRI to imaging. There were 6 patients with a pair of scans (pre- and post-ablation), and 1 singular post-ablation scan. The input data for the proposed model consisted of segmentations of the LA and attached LA appendage, created by experts using Corview (www.corview.org). Landmark positions were manually identified using Corview for each of the pulmonary veins (left- and right-inferior and left- and right-superior) and the center of the mitral valve. As the most recognizable landmarks of LA, these structures are also the most appropriate features to drive correspondence across subjects. Using a feature vector of distances to each of these landmarks, 2560 correspondences were distributed on the LA shapes. Given the variability of the LA, clustering the results into multiple means might be more interesting for specific applications. While such clustering is beyond the scope of this work, we can analyze the median shapes for each group, reconstructed using the correspondences. Figure 4 shows median shapes for the pre-ablation (a) and post-ablation (c) groups. A particular point is highlighted to display the proximity of the correspondences. An overlay of the group median shapes is shown in Fig. 4(b) to describe the variability present in the pre- and post-ablation groups. In future work, we hope to better model variability of important structures in the LA by adopting an anatomically-based coordinate system that explicitly incorporates their positional information.

Fig. 4.

Reconstructed median shapes for the pre-ablation (a) and post-ablation (c) groups, highlighting a particular correspondence. Overlay of the two median shapes, showing the high degree of variability (b).