Acidification Asymmetrically Affects Voltage-dependent Anion Channel Implicating the Involvement of Salt Bridges

Background: VDAC voltage gating depends on pH.

Results: Acidification asymmetrically and reversibly enhances VDAC closure.

Conclusion: pH-sensitive formation of stable salt bridges in the cytosolic side of VDAC explains its asymmetrical response to acidification.

Significance: The pronounced sensitivity of the cytosolic side of VDAC to acidification provides new insights into the protective effect of cytosolic acidification during ischemia.

Abstract

The voltage-dependent anion channel (VDAC) is the major pathway for ATP, ADP, and other respiratory substrates through the mitochondrial outer membrane, constituting a crucial point of mitochondrial metabolism regulation. VDAC is characterized by its ability to “gate” between an open and several “closed” states under applied voltage. In the early stages of tumorigenesis or during ischemia, partial or total absence of oxygen supply to cells results in cytosolic acidification. Motivated by these facts, we investigated the effects of pH variations on VDAC gating properties. We reconstituted VDAC into planar lipid membranes and found that acidification reversibly increases its voltage-dependent gating. Furthermore, both VDAC anion selectivity and single channel conductance increased with acidification, in agreement with the titration of the negatively charged VDAC residues at low pH values. Analysis of the pH dependences of the gating and open channel parameters yielded similar pK_a values close to 4.0. We also found that the response of VDAC gating to acidification was highly asymmetric. The presumably cytosolic (cis) side of the channel was the most sensitive to acidification, whereas the mitochondrial intermembrane space (trans) side barely responded to pH changes. Molecular dynamic simulations suggested that stable salt bridges at the cis side, which are susceptible to disruption upon acidification, contribute to this asymmetry. The pronounced sensitivity of the cis side to pH variations found here in vitro might provide helpful insights into the regulatory role of VDAC in the protective effect of cytosolic acidification during ischemia in vivo.

Introduction

The voltage-dependent anion channel (VDAC)⁴ controls the fluxes of ATP, ADP, and other respiratory substrates across the mitochondrial outer membrane by using its characteristic ability to switch or “gate” between the open, high conducting, and so-called “closed,” low conducting states. Experiments with VDAC reconstituted into planar lipid membranes demonstrate that at low voltages (<30 mV) VDAC forms a channel of 4.1 ± 0.1 nS in 1 m KCl, pH 7.4, whereas different lower conductive states, around 2 nS, are predominant at high positive or negative applied voltages (>30 mV) (1). Transitions between open and closed states involve large structural rearrangements of the protein (2) that alter its ion selectivity (3). Although most of the negatively charged mitochondrial metabolites go through the anion-selective open state (1, 4–9), the closed states are cation-selective and thus virtually impermeable to the negatively charged ATP (6, 7) and most likely to other metabolites. Improved knowledge of the molecular mechanisms by which VDAC controls the transport of metabolites across mitochondrial outer membranes would provide insights into the regulation of mitochondrial respiration and metabolism in healthy and pathological conditions.

It has been generally accepted that the sensitivity of VDAC to the applied voltage depends on the charge state of the residues that constitute its “voltage sensor.” In previous studies, the role of charged residues in VDAC gating was investigated by either increasing (1, 10) or decreasing (11) the pH of the membrane-surrounding solution. Specifically, an increased pH reduced the voltage sensitivity of VDAC; higher voltages were required to close the channels in electrophysiological experiments at higher pH values. In addition, introduction of multiple negative charges by modifying amino groups with succinic anhydride also resulted in a decrease of voltage sensitivity (1, 12, 13). In both cases, a decrease in the net positive charge of the channel resulted in a decrease in voltage sensitivity. These data implied that VDAC gating should also respond to acidification, in which case the net channel charge should become more positive. The corresponding experiments demonstrated that acidification does indeed increase VDAC voltage sensitivity (11, 14).

Previous biophysical studies also probed for potential structural rearrangements brought on by extremely acidic pH conditions. Circular dichroism (CD) and electron microscopy (EM) measurements reported that fungal VDAC underwent reversible conformational changes at pH values below 5 (15, 16), suggesting channel closure at low pH even without applied voltage (15). However, the response of VDAC to asymmetric acidification was not addressed.

We reconstituted VDAC into planar lipid membranes to investigate the effect of acidic pH conditions on channel gating and studied the channel behavior over a range of pH values from 7.4 to 3.5. Our observations confirmed that VDAC voltage-induced closure is enhanced as the pH decreases from 7.4 to 3.5. Furthermore, the preference for the closed states of VDAC upon acidification is fully reversible when pH is restored to a neutral value. The selectivity of VDAC for anions increases up to 3-fold at pH values below 4, in agreement with the titration of negative charges. The conductance of the open state also increases with acidification.

Previous studies reported an asymmetric gating of the channel with respect to the polarity of the applied voltage (1, 17). Here, we demonstrate that the response of VDAC to acidification is also highly asymmetric with respect to the side of the membrane where pH has been changed. The cis side of the channel, presumably the cytosolic side (18, 19), is most sensitive to acidification, whereas the trans side, presumably the mitochondrial side of the channel, is barely responsive to pH changes. Using molecular dynamics simulations, we found that the number of salt bridges that can potentially be disrupted at low pH is significantly higher in the cytosolic side compared with the mitochondrial side. This finding could help to explain the asymmetric response of channel gating to acidification.

This asymmetric response to pH might have potential physiological importance for pathologies that are associated with a total or partial lack of oxygen supply (anoxia or hypoxia, respectively), such as ischemia/reperfusion injury. Ischemia involves a temporal cytosolic acidification, which protects cells from death during early ischemic stress (20–22), which is followed by a reperfusion stage in which pH is restored to neutral, leading to cell death. The asymmetric sensitivity of VDAC to acidification in favor of the cytosolic side of the channel and the full reversibility of this pH response may provide new insights into this “pH paradox” of ischemia/reperfusion injury.

EXPERIMENTAL PROCEDURES

VDAC Isolation and Purification from Rat Liver Mitochondria

Frozen mitochondrial membrane fractions from rat liver were kindly provided by Marco Colombini (University of Maryland, College Park). VDAC was isolated from the membrane fraction by the standard method (23) and then purified on a hydroxyapatite/celite (2:1) column following the method described previously (24).

VDAC Reconstitution Experiments

Planar lipid membranes were formed on a 70–90-μm diameter orifice in the 15-μm thick Teflon partition that separated two compartments filled with aqueous solutions of 1 m KCl buffered with 5 mm HEPES at pH 7.4 as described previously (17). Lipid monolayers for membrane formation were made from 5 mg/ml solution of diphytanoylphosphatidylcholine (DPhPC) (Avanti Polar Lipids, Inc., Alabaster, AL) in pentane. VDAC was kept in 0.2 ± 0.1 μg/μl concentration in a solution containing 10 mm Tris, pH 7.0, 50 mm KCl, 1 mm EDTA, 15% DMSO, 2.5% Triton X-100. Channel reconstitution was achieved by adding 0.1–0.5 μl of this solution to the 1.2-ml aqueous phase in the cis compartment while stirring. After channel conductance and voltage gating characteristics at pH 7.4 were established, pH was decreased by addition of 0.1 n HCl to the membrane-surrounding solutions at the cis, trans, or both sides of the membrane while stirring to record channel currents at different pH values ranging from pH 7.4 to pH 3. pH was monitored directly during experiments using a pH electrode. Finally, pH was restored to neutral by the addition of 0.1 n KOH.

The potential was defined as positive when it was greater at the cis side. Current recordings were performed as described previously (17) using an Axopatch 200B amplifier (Axon Instruments, Inc., Foster City, CA) in the voltage clamp mode. Single channel currents were filtered by the amplifier low pass Bessel filter at 10 kHz and directly saved into the computer memory with a sampling frequency of 50 kHz.

VDAC ion selectivity was determined from the measurements of the reversal potential that is defined as the voltage corresponding to zero current in a salt gradient. The reversal potential and corresponding open channel conductance were measured on single channels in a 1 m KCl cis versus 0.2 m KCl trans gradient, initially buffered with 5 mm HEPES at pH 7.4 followed by symmetrical addition of 0.1 n HCl or KOH as described above. The channel conductance was calculated as the slope of the I/V plot, which proved to be linear at the applied voltages within the range of ±25 mV.

VDAC voltage-dependent properties were assessed following the protocol devised by Colombini and co-workers (1, 25) in which gating is inferred from the response of multiple channels to slowly changing periodic voltage waves. A symmetrical 5 mHz triangular voltage wave with ±60 mV amplitude from a function waveform generator 33120A (Hewlett Packard) was used. Data were acquired with Digidata 1322A (Axon Instruments Inc.) at a sampling frequency of 1 Hz and analyzed with pClamp 10.2 software (Axon Instruments, Inc.). In each experiment, current traces were recorded in response to 5–10 periods of triangular voltage waves, and only the parts of the wave during which the channels were reopening (from ±60 to 0 mV) were used in subsequent analyses. The approach separately considers current responses to the voltages changing from positive to negative and from negative to positive.

Relative multichannel conductance and open probability plots were calculated using an algorithm developed in-house based on a previously described approach to gating analysis (1, 17). In particular, the probability of the channel to be open, P_open, was defined as the ratio given in Equation 1,

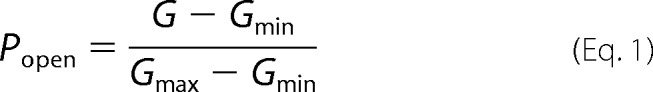where G_max and G_min are the maximum and minimum conductances, corresponding to the channels mostly open at small voltages and the channels mostly closed at high voltages, respectively. Open probability (P_open) plots were fit according to the Boltzmann Equation 2 (see explanations in Refs. 1, 17).

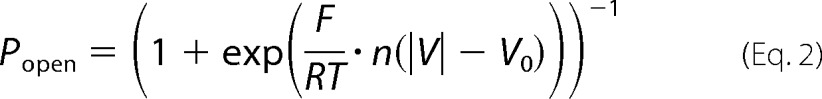where V₀ is the voltage at which half of the channels are open; n is the effective gating charge, and R, T, and F have their usual meanings of the gas constant, absolute temperature, and Faraday constant, respectively.

Molecular Dynamic Simulations

Structures of murine VDAC1 (Protein Data Bank code 3EMN) (26) were taken from the x-ray coordinates. The simulation systems for VDAC1 and the VDAC1/membrane/solvent system were built using the web-based CHARMM-GUI membrane builder (27). The complex was equilibrated at 303.15 K with a constant pressure, temperature, and membrane area ensemble for 10 ns using periodic boundary conditions and Particle Mesh Ewald summation for long range electrostatic interactions. This was followed with production runs of 240 ns. The temperature was maintained using a Lowe-Anderson thermostat. MD simulations were performed with the program suite NAMD2.9 (28). Subsequent analysis of the system was performed using the CHARMM program suite (35b1r1) (29). The CHARMM-27 force field with cross-term map (CMAP) corrections was used for the protein residues, and CHARMM-36 lipid force field was used to model the lipid bilayer (30). The rigid TIP3P model represented the solvent (31). The distances between the residues were computed with the coordinates module of CHARMM using the minimum distance between the heavy atoms of the residue side chain as the criteria for salt bridging.

RESULTS

Acidification Increases Voltage Sensitivity of VDAC

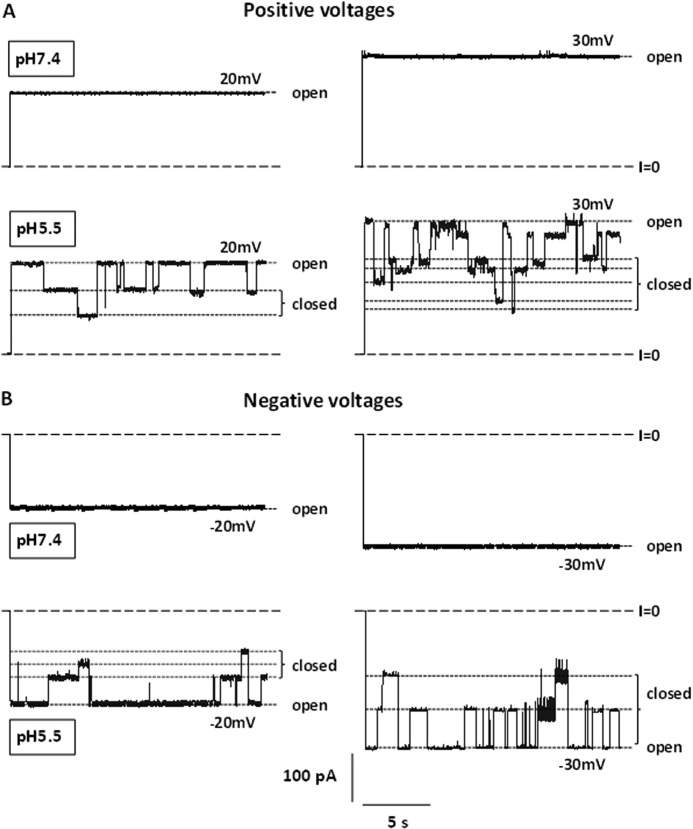
As reported previously (32), VDAC's voltage sensor bears positive charges with a net charge around +3 e, and neutralization of these charges by titration at high pH reduces the voltage sensitivity of the channel (1, 10). Correspondingly, neutralization of acidic charges leads to the increase of voltage-induced channel closure (11, 14, 32). A representative experiment illustrated by Fig. 1 demonstrates a dramatic difference in VDAC behavior between pH 7.4 and 5.5, with the pH symmetrically modified on both, cis and trans, sides of the membrane. Typical current traces of two VDAC channels at pH 7.4 and 5.5 are shown for two positive (Fig. 1A) and negative (Fig. 1B) applied voltages. At pH 7.4, VDAC remains in a high conducting open state of G = 4.1 ± 0.1 nanosiemens at both ± 20 and ± 30 mV (Fig. 1, A and B, upper traces). The voltage sensitivity of the channel increases significantly at pH 5.5 showing a number of transitions to the multiple low conducting or closed states, even at potentials as low as ± 20 mV (Fig. 1, A and B, lower traces).

FIGURE 1.

Acidification promotes VDAC closure. Representative current traces of two VDAC channels at positive (A) and negative (B) potentials at pH 7.4 (upper traces) and pH 5.5 (lower traces). Here and elsewhere, long-dashed lines indicate the zero current level. Short-dashed lines indicate the high conducting state (open) and the multiple lower conducting states (closed). The membrane-bathing solution contained 1 m KCl in both sides of the chamber. Records were digitally filtered at 10 Hz using Bessel algorithm.

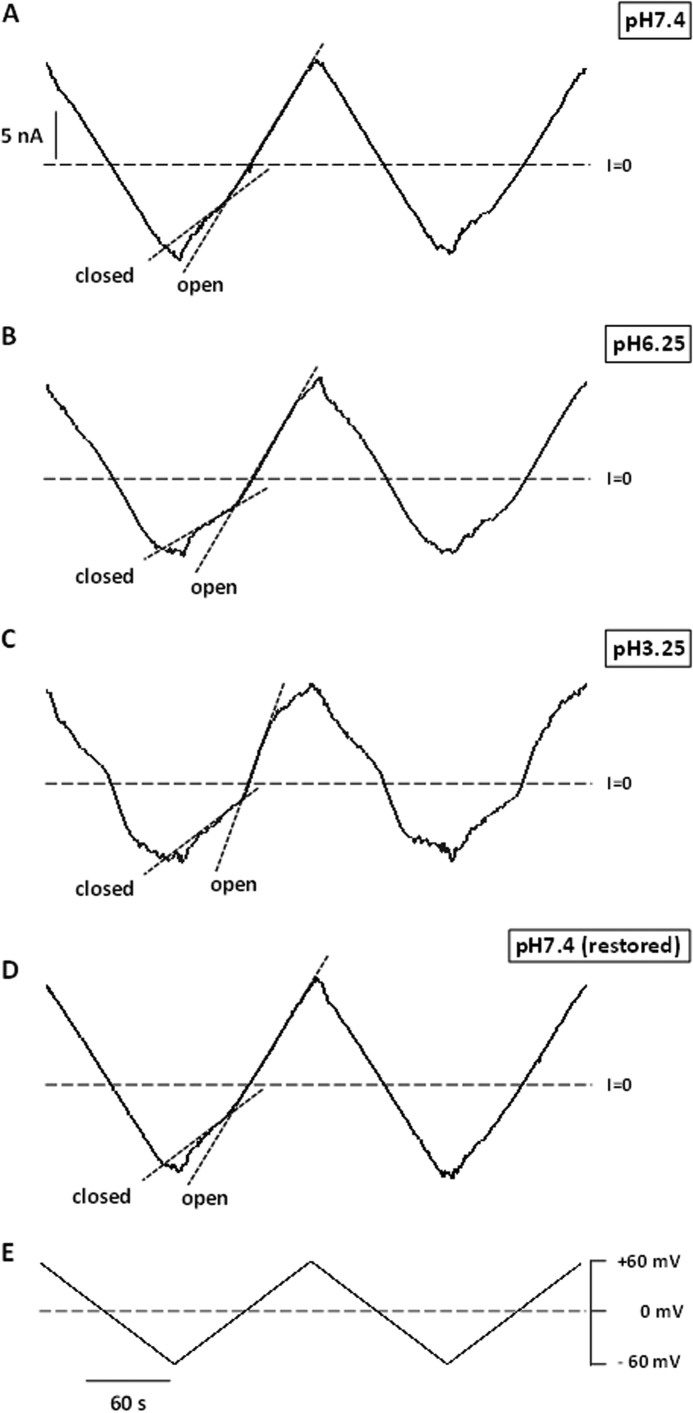
To quantify voltage-gating parameters upon acidification, we used a previously described approach (1, 17, 25, 33). Fig. 2, A–D, shows the current responses of the membranes containing multiple VDAC channels to the slow 5 mHz triangular voltage waves of ±60 mV amplitude (Fig. 2E) at different pH values at symmetric acidification. The steeper slopes correspond to the open channels, whereas the irregular lower slopes correspond to the lower conductance of multiple closed states. Similarly to the single channel responses at low pH (Fig. 1), conductance of the multichannel membrane also started to decrease at the lower potentials as pH was reduced from 7.4 to 3.25. These results show that acidification increases the voltage sensitivity of the majority of the reconstituted channels. Importantly, when the pH was restored back to neutral for the same set of channels that were subjected to an acidic environment, the voltage sensitivity of the channels returned to that observed initially at pH 7.4 (compare traces in Fig. 2, D and A). This demonstrates that the effect of acidification on VDAC voltage gating is reversible.

FIGURE 2.

VDAC closure induced by low pH is reversible. Traces of ion currents through the same membrane containing multiple VDAC channels in response to triangular voltage waves (5 mHz, ±60 mV, shown in E) at pH 7.4 (A), pH 6.25 (B), pH 3.25 (C), and after the pH was restored back to pH 7.4 (D). Steep slopes at low potentials correspond to the high conductance of open channels, whereas the reduced irregular slopes at higher potentials correspond to the lower conductance of closed states (short-dashed lines in A–D). Membrane-bathing solution contained 1 m KCl.

Acidification Causes an Increase of Anion Selectivity and Single Channel Conductance of the VDAC Open State

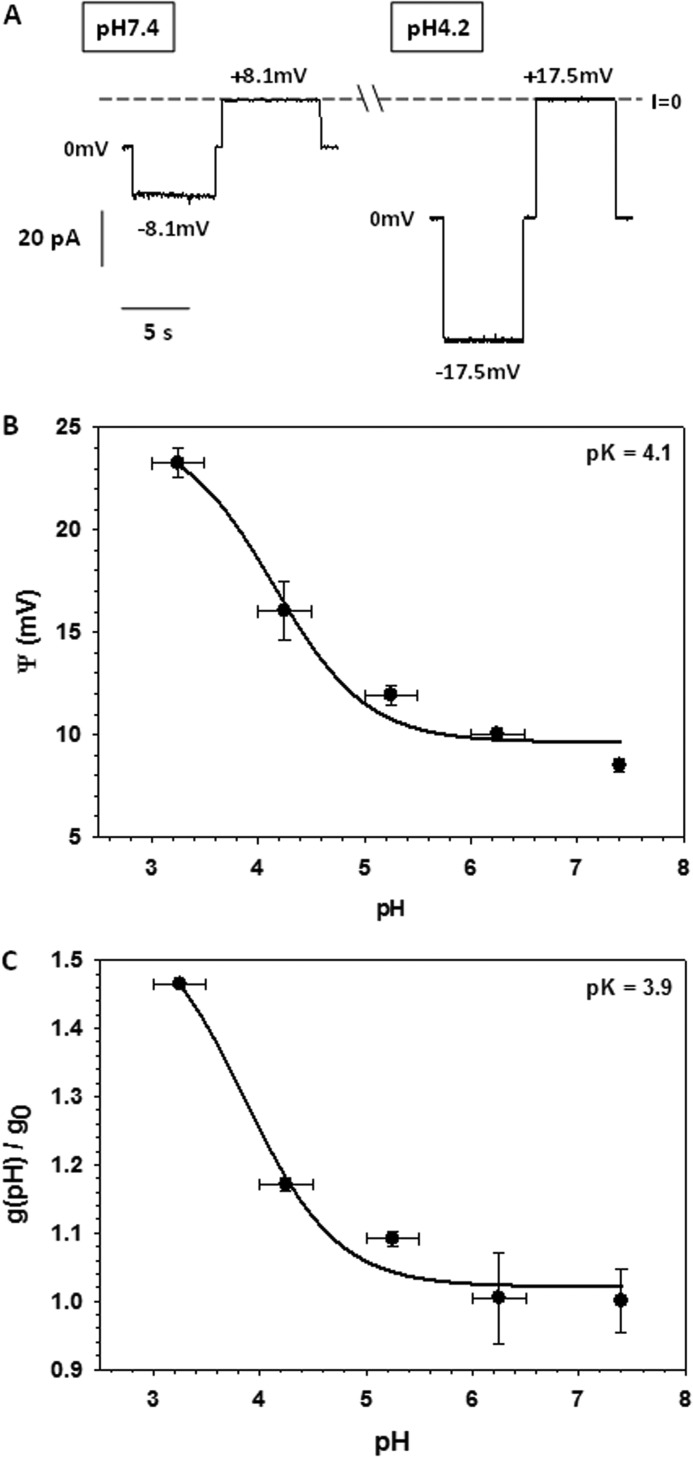
VDAC selectivity was measured on single channels in a 1 m/0.2 m (cis/trans) KCl gradient. Fig. 3A shows representative single channel current traces obtained in this KCl gradient at pH 7.4 and 4.2. The reversal potential, which is the voltage corresponding to zero current, increased significantly at pH 4.2. The summary of selectivity experiments obtained on different channels is shown in Fig. 3B. The reversal potential increased gradually from 8.5 ± 0.3 mV at pH 7.4 to a nearly 3-fold larger value of 23.3 ± 0.7 mV at pH 3.5 (Fig. 3B). This means that the anion/cation permeability ratio, P_Cl⁻/P_K⁺, increased from 1.65 ± 0.03 at pH 7.4 to 4.5 ± 0.3 at pH 3.5. Correspondingly, the single channel conductance at the same KCl gradient increased upon acidification (Fig. 3C). The largest increase of the reversal potential and conductance was observed at pH <5 where Asp and Glu residues are expected to be partially neutralized, depending on their location in the channel. Together with His titration, this should increase the net positive charge inside the channel lumen, which affects both its selectivity and conductance. The dependence of the reversal potential, Ψ(pH), and the relative open channel conductance, h(pH), on pH were fit with Equations 3 and 4,

and

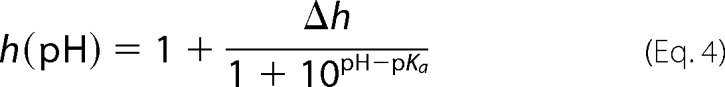where h(pH) is the normalized conductance g(pH)/g₀, with g₀ equal to the conductance of a single open channel at pH 7.4 and g(pH) equal to the open channel conductance obtained at given pH, g(pH); and Ψ_min is the minimum value of the reversal potential; ΔΨ = Ψ_max − Ψ_min and Δh = h_max − 1. The best fits (solid lines in Fig. 3, B and C) provided values of pK_a = 4.1 and 3.9 for the reversal potential and relative conductance, respectively. These values are close to the pK_a for Asp and Glu in aqueous solution. In addition, pK_a values for each residue were calculated using the protein pK_a predictor Propka 3.1 and the effective pK_a value of acidic residues for mouse VDAC1 was found to be around 4.0, which is consistent with the calculated pK_a based on our experimental data.

FIGURE 3.

Anion selectivity and conductance of the VDAC open state increase at low pH. Representative single VDAC current traces obtained in a gradient of 1 and 0.2 m KCl (cis/trans) at pH 7.4 (left panels) and pH 4.2 (right panels). The reversal potentials, which are the voltages corresponding to zero current (I = 0), are indicated (A). The reversal potential (B) and normalized single channel conductance (C) were obtained in the salt gradient as functions of pH, with pH kept the same on the both sides of the membrane. The normalized conductance, g(pH)/g₀, is a ratio of the open single channel conductance obtained at given pH, g(pH), to the open channel conductance at pH 7.4, g₀. The reversal potential and conductance were fit to Equations 3 and 4, respectively (solid lines). Data are mean values of 4–7 experiments ± S.D.

Response of VDAC Gating to Acidification Is Pronouncedly Asymmetric

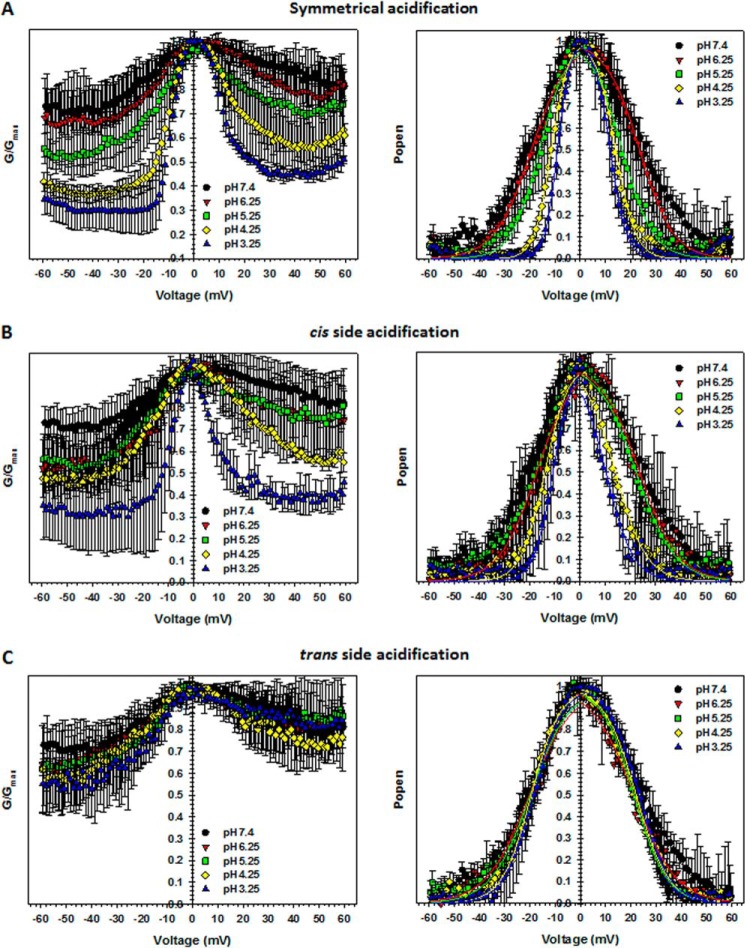
VDAC voltage gating has been known to be inherently asymmetric with respect to the sign of applied potential, which revealed the existence of at least two different closed states observed at positive or negative polarities (1). It was also shown that the degree of voltage-gating asymmetry depends on the existence of a salt gradient, the type of salt ions (25, 34), and the membrane lipid composition (1, 17). This asymmetry permits one to distinguish between channel orientations (cis versus trans) in the planar membrane. In this study, we use planar membranes from DPhPC, where the voltage-gating asymmetry is quite pronounced. The plots in Fig. 4 were obtained from the analysis of the multichannel current traces, examples of which are presented in Fig. 2. The left panels in Fig. 4 show the normalized conductance, G/G_max, versus voltage as a function of pH, where G_max is the maximum conductance of the multichannel membrane at potentials near 0 mV. Conductance was normalized due to the variable number of channels reconstituted in each experiment. According to these plots, VDAC closure at negative potentials is more pronounced than that at positive potentials, and this asymmetry is maintained upon pH changes.

FIGURE 4.

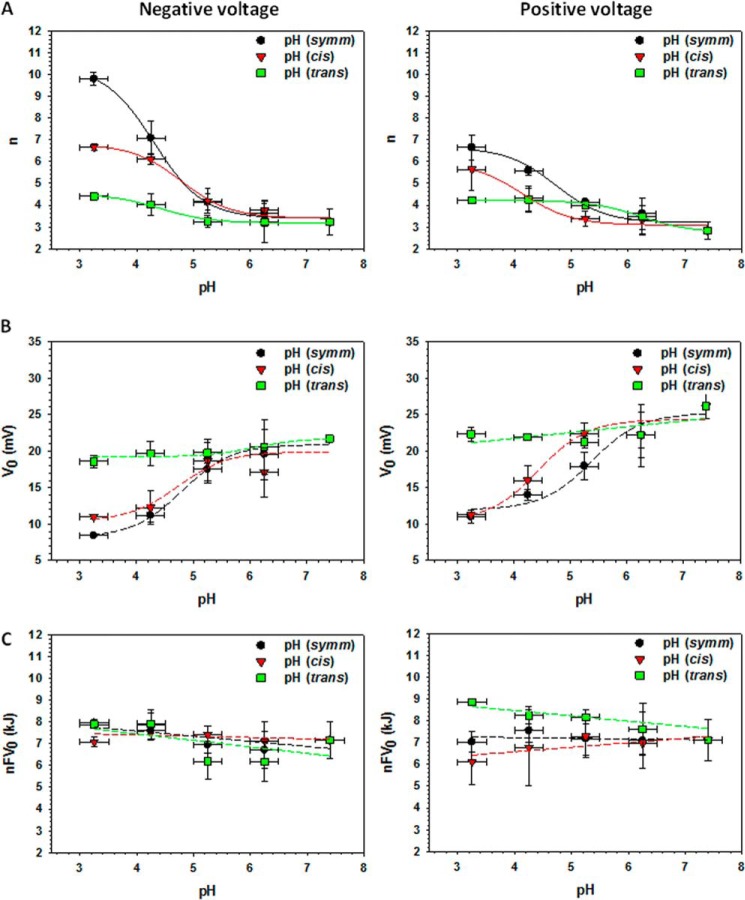
VDAC voltage gating responds asymmetrically to acidification. Characteristic bell-shaped plots of the normalized average conductance (left panels) and probability to be open (right panels) obtained on multichannel membranes as functions of applied potentials at different pH values. pH was either decreased symmetrically at both sides of the membrane (A) or at the cis (B) or trans (C) sides only. Normalized average conductance is defined as G/G_max, and the open probability is expressed in Equation 1. Open probabilities were fit with the Boltzmann equation (Equation 2) (solid lines) with V₀ and n as fitting parameters, which are presented in Fig. 5. Here and in Fig. 5, the data are means of 3–6 independent experiments ± S.D.

When acidification was applied symmetrically at both sides of the membrane, both the voltage required to close the channels and the minimum conductance were gradually reduced (Fig. 4A, left panels). G/G_max versus V plots can also be presented as voltage dependences of the open probability, P_open (Fig. 4, right panels). Symmetrical acidification induced a clear shift in the voltage-dependent closure toward smaller voltages and also an increase of the steepness of the bell-shaped open probability plots (Fig. 4A, right). As shown in Fig. 2, such pH dependence obtained on a multichannel system was reversible.

To gain information about the distribution of the charges involved in voltage sensitivity, we performed experiments at pH gradients by changing pH at either the cis (pH cis) or trans (pH trans) sides of the membrane only. Interestingly, the response of VDAC to pH turned out to be highly dependent on the side of the membrane exposed to the lower pH. Reducing the pH at only the cis side caused an increase of voltage gating similar to that observed for symmetrical pH changes (Fig. 4B). Conversely, acidification at only the trans side barely affected the voltage-gating behavior of the channels (Fig. 4C). Thus, the cis-facing side of VDAC is much more sensitive to acidification.

Open probability plots were fit by the Boltzmann equation (Equation 2) with the fitting parameters of the effective gating charge n and the voltage V₀ at which half of the channels are closed (solid lines in Fig. 4, right panels). These calculated gating parameters as functions of pH are plotted in Fig. 5, A and B, at negative (left panels) and positive (right panels) voltages. The largest increases in n (Fig. 5A) were observed when the pH was modified at both sides of the membrane (black circles) or at the cis side only (red triangles), whereas pH modifications at only the trans side did not appreciably affect the n values (green squares). Similarly to the reversal potential or single channel conductance, the major effect on n occurred at pH ≤ 5.0, except when the pH was changed only at the trans side of the membrane at positive applied potentials (green squares in Fig. 5A, right panels). The plots shown in the Fig. 5A were fit with Equation 5,

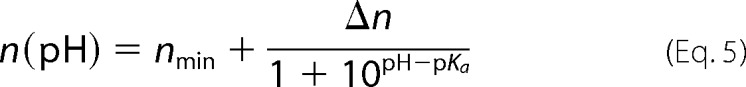where n_min is the minimum n value at pH 7.4 and Δn = n_max − n_min. The pK_a values obtained from the best fit for the negative and positive voltages at symmetrical pH changes (Fig. 5A, solid lines through black circles) were 4.3 and 4.7, respectively; for pH changes at the cis side (solid lines through red triangles) they were 4.8 and 4.1; and when the pH was changed on the trans side (solid lines through green squares) the pK_a values were 4.4 and 6.2.

FIGURE 5.

VDAC gating parameters depend on pH. Effective gating charge, n (A), the voltage at which half of the channels are open, V₀ (B), and the voltage-independent component of the free energy difference between the open and closed states, nFV₀ (C) as functions of pH changes at both sides of the membrane (black circles) and at the cis (red triangles) or trans (green squares) sides only. Gating parameters calculated for negative potentials are shown in the left panels and for positive potentials in the right panels. Solid lines in A represent the fitting of the n values by Equation 5, whereas dashed lines are eye-guiding lines.

The voltage required to close half of the channels, V₀, decreased significantly (by ∼15 mV) upon symmetrical or cis side acidification from pH 7.4 to 3.5 (Fig. 5B, black circles and red triangles, respectively), whereas trans side acidification barely changed V₀ (Fig. 5B, green squares). The voltage-independent component of the free energy change was calculated as nFV₀ (1). Upon acidification, n values increased, and V₀ decreased, which resulted in nearly constant energy at different pH values (Fig. 5C).

Stable Salt Bridges Along VDAC1 Pore Demonstrate Asymmetric Distribution

The asymmetric sensitivity to pH variation at the cis- versus trans-facing sides of the VDAC pore suggests an asymmetric distribution of titratable residues along the channel lumen. Considering that VDAC1 is the most abundant VDAC isoform in rat liver mitochondria, we used the mouse VDAC1 structure in the following analysis of charged residues. It turns out that the distribution of titratable residues across murine VDAC1 (26) is quite symmetric and therefore could not account for the more pronounced voltage-gating sensitivity to pH variation for the cis side titration. Calculated pK_a values suggest that at pH <3.5, all Asp or Glu are fully protonated. Our explanation of the observed pH-dependent gating asymmetry relies on the relative stability of salt bridges formed between key acidic and positive residues and on the distribution of such salt bridges along the channel. To test the stability and spatial distribution of salt bridges in VDAC1, we performed equilibrium MD simulations and analyzed salt bridging in VDAC1 from the last 50 ns of the MD trajectory. The resulting distribution of the average number of salt bridges in VDAC1 is shown in Fig. 6. If we define “side residues” as those positioned at less than 1 nm from the end of β-strand, salt bridge stability and the number of salt bridges for the cis and trans sides of VDAC1 were found to be quite different. The protein surface corresponding to the cis side of VDAC1 has stable salt bridges Glu-158/Lys-161 (with partial involvement of Arg-163), Asp-132/Lys-109, and Asp-78/Lys-53, Glu-189/Arg-218, and Glu-130/Lys-113, whereas the trans side shows only two stable salt bridges Glu-121/Arg-120 and Glu-40/Lys-32 (with a partial involvement of Lys-34). The center of the pore displays three stable salt bridges involving Asp-16 and a triad of basic residues Lys-12/Lys-20/Lys-224, Asp-280/Asp-30 pairing with Lys-32, and Asp-128 pairing with Lys-115 (Fig. 6).

FIGURE 6.

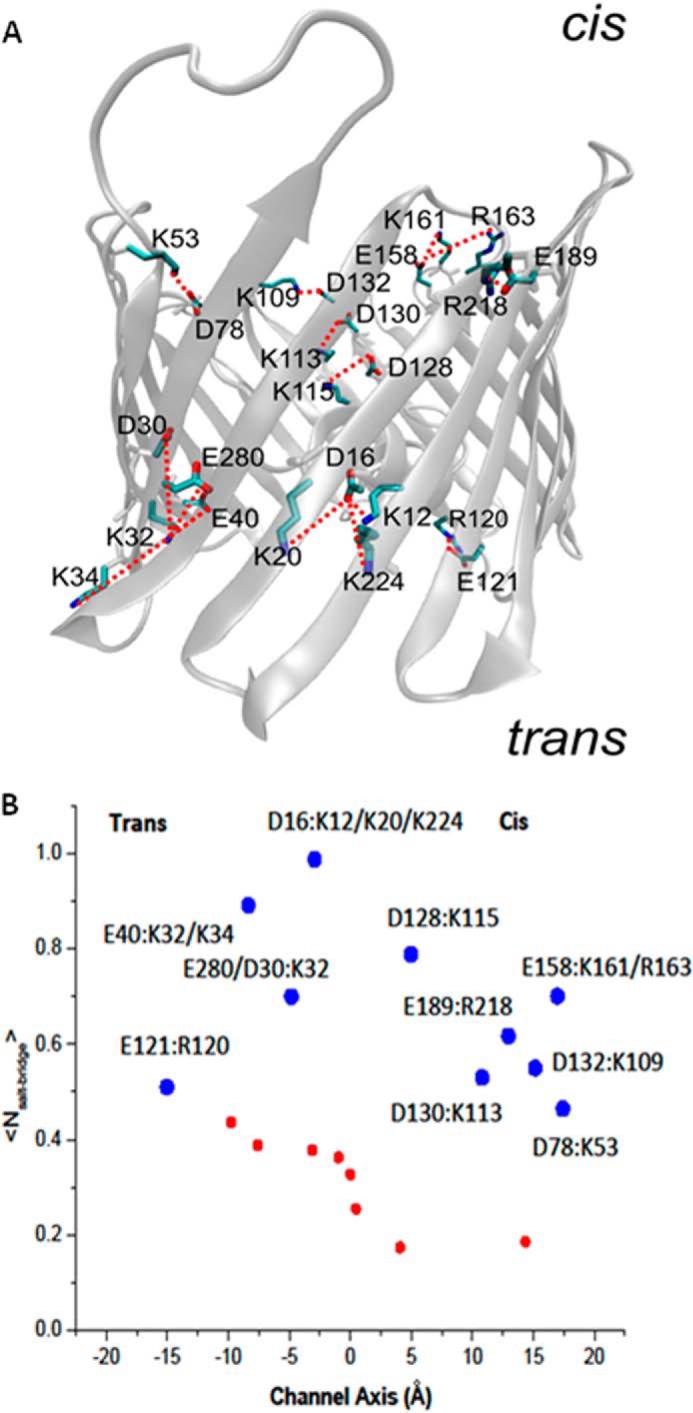
Salt bridges are asymmetrically distributed across VDAC1 structure. A, three-dimensional model of the open state of murine VDAC1 (26) showing the distribution of salt bridges in the cis (presumably cytosol-facing) and trans (presumably intermembrane space-facing) sides. B, average number of salt bridges per acidic residue evaluated from the last 50 ns of equilibrium MD simulations. The large blue circles display stable pairing (including bifurcating salt bridges) presented in >50% of frames from equilibrium MD trajectory. The smaller red circles correspond to short living salt bridge contacts in the channel. The z axis position corresponds to the center of mass for residue backbone.

Simulations reveal that many of the negatively charged residues, namely Asp-30, Glu-280, Glu-40, Asp-16, and Glu-158, are engaged in classic bifurcating salt bridges. As Fig. 6 shows, there is a disproportionate number of titratable residues on the cis side of the pore that are accessible to the solution. It is also notable that all of these salt-bridge residues are present in the β-sheets forming the walls of the pore, and the majority of salt bridges occurs between neighboring β-strands. Therefore, a possible explanation for the asymmetric sensitivity of VDAC gating to acidification might be related to the more pronounced effect of the cis side titration on the stability of the open VDAC state because more salt bridges are susceptible to disruption at low pH.

DISCUSSION

It has been demonstrated in a number of studies (3, 23, 35, 36) that different charged residues could be responsible for the channel gating, conductance, and ion selectivity. In agreement with these results, we found that the effective gating charge gradually increased in response to acidification (Fig. 5A) with the highest n values at pH <5.0. At such low pH values, acidic charges are being neutralized, which increases the net effective positive charge involved in gating. Indeed, the involvement of many positive as well as negative charges in VDAC gating has been suggested previously (14). When pH was reduced symmetrically at both sides of the membrane, the pK_a values calculated for n (Fig. 5A) were 4.3 and 4.7 at negative and positive voltages, respectively. These values are within the range of pK_a values obtained for Asp and Glu residues of VDAC computed using the Propka 3.1 protein pK_a prediction calculator. Another gating parameter, V₀, decreased upon acidification (Fig. 5B) in parallel with the increase of n, which resulted in a pH-independent free energy difference, nFV₀ (Fig. 5C).

To compare our data obtained over the pH range 7.4 to 3.5 with the previously published experiments performed over the pH range 6–11 by Colombini and co-workers (1, 10), we normalized the obtained gating parameters, n and V₀, at pH 6.1 ± 0.2 and plotted them together with those previously reported by Colomini and co-workers versus pH in the range of 3 < pH < 11 (Fig. 7). Combination of the data from the previous (Fig. 7, red squares) and present (black circles) studies gives the wide pH range curves with a region at pH >9.5 where titration of positive charges leads to a decrease in voltage gating (1, 10) and a region at pH <5.5 where titration of negative charges by acidification increases voltage gating. At pH >9.5, a decrease in the effective gating charge was accompanied by a parallel increase of V₀, reducing voltage sensitivity even more. Correspondingly, acidification at pH <5.5 led to an increase in voltage sensitivity. Both n and V₀ were constant for the two sets of data between pH 6.0 and 9.5. The voltage-independent component of the free energy change (nFV₀) also appears to be pH-independent for the whole range of 3 < pH < 11, with a shift of ∼2 kJ between the two sets of data (Fig. 7C). It is worth noting that there is a quite satisfying agreement between the previously published gating parameters (1, 10) and those obtained here over a wide range of pH values, despite the significant difference in experimental conditions. Specifically, in the previous work, VDAC was reconstituted into planar membranes made from a different lipid, soybean phospholipid, and bathed by 1 m LiCl with 5 mm CaCl₂, instead of DPhPC membranes in 1 m KCl aqueous solutions used in this work. The difference in experimental conditions could account for the difference in the absolute nFV₀ values between the two sets of data.

FIGURE 7.

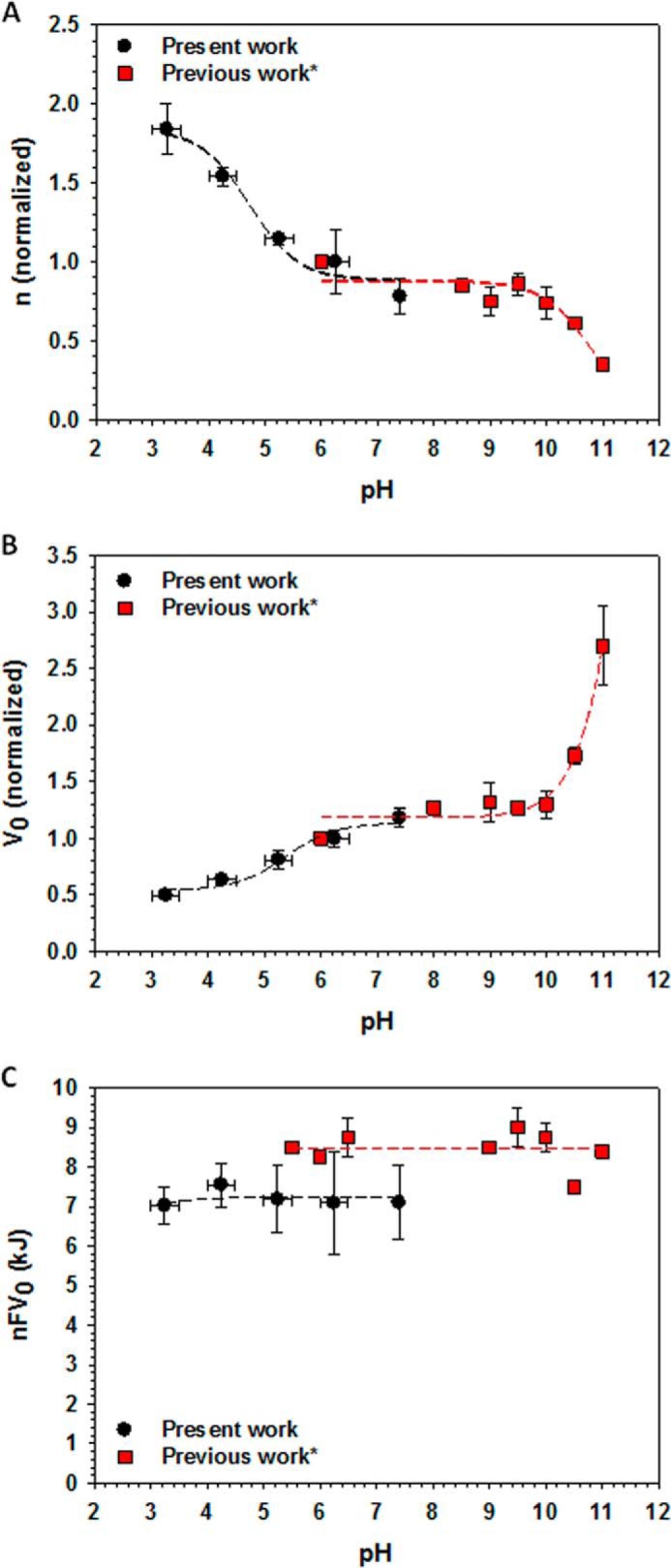
Voltage sensitivity of VDAC changes at pH <6.5 and pH >9.5. Combined data of the pH dependences of gating parameters n (A), V₀ (B), and nFV₀ (C), obtained in this study (black circles) and in previous work* by Colombini (1) and Bowen et al. (10) (red squares). Each data point in A and B gives parameters normalized over the corresponding values obtained at pH 6.1 ± 0.2 for each set in both studies. Gating parameters in Refs. 1, 10 were obtained on VDAC isolated from rat liver mitochondria and reconstituted into planar membranes made from soybean phospholipid and bathed in 1 m LiCl with 5 mm CaCl₂. Dashed lines represent eye-guiding lines.

To estimate the increase of n as a function of pH reduction from pH 7.4 to 3.5, the plots in Fig. 5A could be presented as Δn versus pH, where Δn is the difference between n at given pH and at pH 7.4 (Fig. 8). Because n is associated with the effective number of charges that move down the electric field upon gating, Δn should reflect how many of those charges are protonated when pH is lowered from 7.4 to 3.5. This representation clearly shows that the Δn values at symmetrical pH changes (black circles in Fig. 8) nearly correspond to the sum of Δn values obtained in the “cis and trans only” pH change experiments (blue diamonds in Fig. 8). This suggests that symmetrical pH titration of VDAC is the result of the additive effects of titration at both sides of the channel. The pH dependences of Δn were fit with Equation 5 (solid lines in Fig. 8) with the fitting parameters pK_a presented in Table 1 that appear to be very close to the pK_a values obtained by fitting the pH dependences of n (Fig. 5).

FIGURE 8.

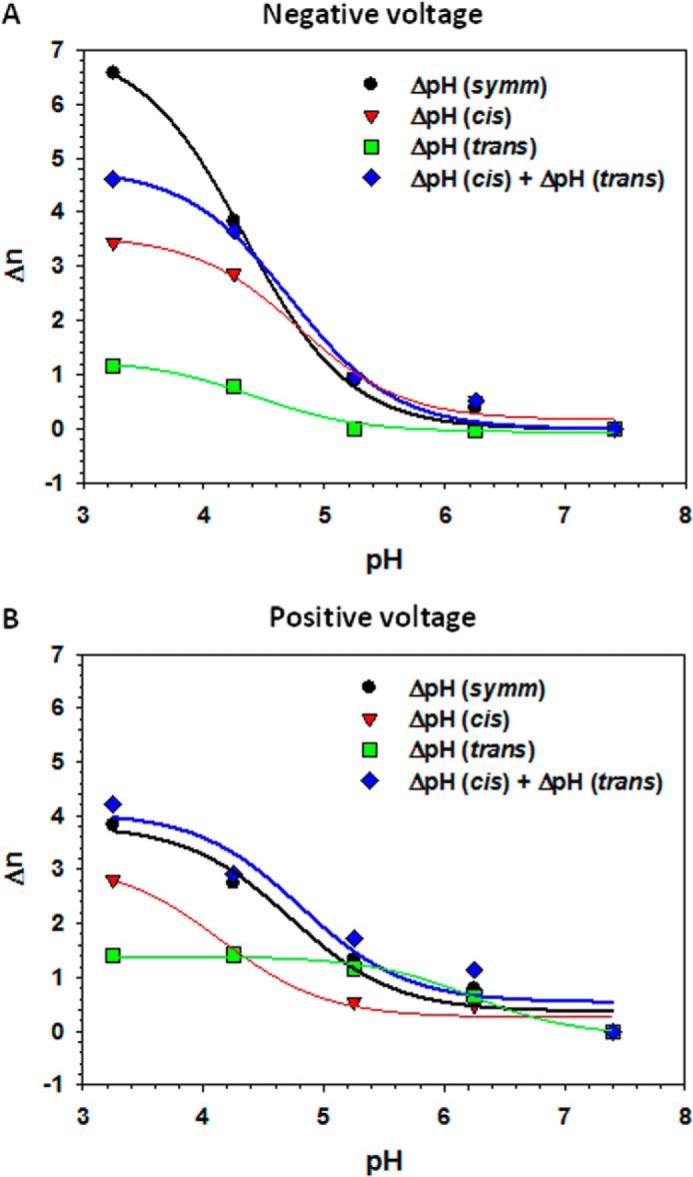
Effect of acidification on the effective gating charge is additive. Δn is the difference between n at a given pH, n(pH), and n at pH 7.4, i.e. Δn(pH) = n(pH) − n(pH 7.4). The Δn values at negative (A) and positive (B) applied voltages were calculated from the n values shown in Fig. 5. Plots show Δn dependence on symmetrical pH changes at both sides of the membrane (black circles) and pH changes at the cis (red triangles) or trans (green squares) sides only. The sum of Δn obtained in “the cis or trans sides only” experiments is shown by blue diamonds. Solid lines represent the fits by Equation 5 with pK_a values as fitting parameters (Table 1).

TABLE 1.

The pK_a values obtained as fitting parameters to Eq. (5) of the pH dependences of the effective gating charge, Δn in Fig. 8

pKa	Δn(symmetrical pH)	Δn (pH cis)	Δn (pH trans)	Δn(pH cis + trans)
Positive voltage	4.7	4.1	6.2	4.8
Negative voltage	4.3	4.8	4.4	4.3

Two other important channel parameters, ion selectivity and single channel conductance, were also affected by acidification (Fig. 3). The effect of pH on VDAC ion selectivity and conductance was previously assessed on VDAC isolated from Neurospora crassa (37), and an increase of the reversal potential of 2.5 mV between pH 6.6 and pH 5.3 suggested the titration of one His residue (23, 37). In this study, we were interested in the effects of titration of all titratable residues, i.e. His, Asp, and Glu, and for this reason, we studied a wider pH range, including acidic, far beyond physiological pH. In accordance with the previous observations (23, 37), we also found a shift of the reversal potential of ∼2 mV between pH 6.25 and 5.25. However, the most dramatic increase of VDAC anionic selectivity occurred at pH < 5.0 (Fig. 3B), most likely due to the titration of Asp and Glu residues.

Concomitantly with the increase in anion selectivity, the conductance of single open channels also increased upon acidification (Fig. 3C). It should be noted that the effect of pH on conductance and selectivity was measured for the open VDAC state only. The pH titration of the negative charges together with titration of His results in a total increase of the net positive charge inside the open channel, which apparently leads to an increase in anion selectivity of the open state. The pH-induced change of the electrostatic potential profile inside the channel lumen causes an increase of ion current carried by the electrolyte (KCl) (38, 39). The pK_a values around 4.0, obtained by fitting pH dependences of channel selectivity and conductance (Fig. 3, B and C, solid lines), are also consistent with the expected pK_a values for Asp and Glu. Notably, we obtained similar pK_a values by fitting pH dependences of voltage-gating parameters n (Fig. 5A) and Δn (Table 1) obtained in independent multichannel experiments.

An important observation is that the increase of voltage sensitivity of the channel upon acidification is reverted when pH is restored to neutral (Fig. 2). This is in agreement with the previous data on titration of VDAC gating charge at high pH (1, 10). Additionally, CD data indicate a large conformational rearrangement occurs for VDAC exposed to a low pH (<pH 5) environment (15, 16). These results suggest that restoration of the physiological pH is accompanied by the structural rearrangements of VDAC that totally reverse the effect of acidification.

Considering that insertion of channel-forming proteins into the planar membrane is a spontaneous and poorly controlled process, verification of channel orientation in the bilayer is always an issue. This is especially important when asymmetrical conditions, such as a pH gradient, are used in experiments. Evidence of VDAC unidirectional insertion in DPhPC membranes lies in its distinct gating asymmetry with respect to the polarity of the applied voltage when all conditions for both the cis and the trans sides of the membrane are the same except for the asymmetrical VDAC addition. This is demonstrated by the asymmetrical G versus V plots in Fig. 4A.

Our data show that the cis side of the reconstituted channel is the most sensitive to acidification, whereas the trans side is barely affected by pH changes (Fig. 4, B and C). When pH is modified on the cis side only, the voltage-gating parameters of VDAC are changed in a similar manner as those obtained under symmetrical acidification. The characteristic pK_a values ranged from 4.1 to 4.8 (Table 1), which corresponds to titration of Asp and Glu residues. Although the trans side of the channel does not show strong sensitivity to acidification, it cannot be neglected. Indeed, it is interesting to see how well the summation of separate titration curves from the cis and trans sides fit to the curve corresponding to symmetrical pH titration (Fig. 8).

Recently, it was reported that the two sides of phosphorylated VDAC reconstituted into planar membrane show distinctly different responses to tubulin addition (19). This permitted the identification of the reconstituted VDAC orientation in the planar lipid membrane and suggested that the extra-membrane loops opposite the C terminus are facing the cytosolic side of the channel (Fig. 6A) and are exposed at the cis side of the bilayer. This conclusion was supported by Tomasello et al. (18) who reported that the C terminus is not accessible to cleavage by cytosolic caspases in permeabilized HeLa cells expressing human VDAC1.

The pronounced asymmetry in VDAC sensitivity to pH changes suggests that the cis side has more residues sensitive to pH titration or that accessibility of those residues is greater on that side of the channel. However, this explanation is not supported by the observation that charged residues are distributed quite symmetrically across VDAC1's structure (26). MD simulations and analysis of the relative stability of salt bridges in VDAC1 provide a more plausible explanation. Surprisingly, we observed a very significant asymmetry in the number and stability of salt bridges between the cis and trans sides (Fig. 6). The cis side of VDAC1 has five stable salt bridges between the negative and positive residues in its β-strands, whereas the trans side shows only two stable salt bridges. Many of the salt bridges on the cis side were found between different β-strands of the channel, reminiscent of the between-helices salt bridges found in the voltage sensor of the K⁺ channel (40) that are responsible for the cooperative transition in gating. A similar mechanism was proposed recently for gating in Mg²⁺-selective CorA channel, where formation of inter-protamer salt bridges stabilizes different gating states of the system (41). Thus, we propose that salt bridging is essential for stabilization of the channel open state and that this large asymmetry in the number of salt bridges might explain the higher sensitivity of the VDAC1 cis side to acidification compared with that observed for the trans side (Figs. 4 and 5).

Fig. 9 shows a simplified schematic that helps to explain how an asymmetrical distribution of salt bridges along the channel could account for the pH-dependent gating asymmetry. We propose that formation of salt bridges between charge residues located on adjacent β-strands stabilizes the open state of VDAC and that large conformational changes implicated in transition to the closed states (2, 42) require breakage of these salt bridges (Fig. 9A). Acidic pH at the cis side of the pore may neutralize up to five negatively charged residues (Glu-158, Asp-132, Asp-78, Glu-189, and Asp-130, Fig. 6), which prevents formation of salt bridges and consequently shifts the open-close equilibrium toward the closed state (Fig. 9B). On the trans side there are only two residues, Glu-121 and Glu-40 (Fig. 6), that can be neutralized at low pH (Fig. 9C), thus making the trans side less sensitive to pH. It is important to note that charged residues involved in salt-bridge formation are distributed throughout the pore and that these salt bridges may be created and destroyed upon gating. This suggests that the gating mechanism cannot be explained solely by movement of a single helical region of the N terminus (26, 43–45) or a particular domain (3) but rather by an extensive, coherent, and simultaneous movement of a number of regions throughout the pore. Note that the asymmetrical distribution of stable salt bridges between the cis and trans sides accounts for the asymmetry in V₀ shift; analysis of the asymmetry in the gating charge might require additional structural information on VDAC's closed state.

FIGURE 9.

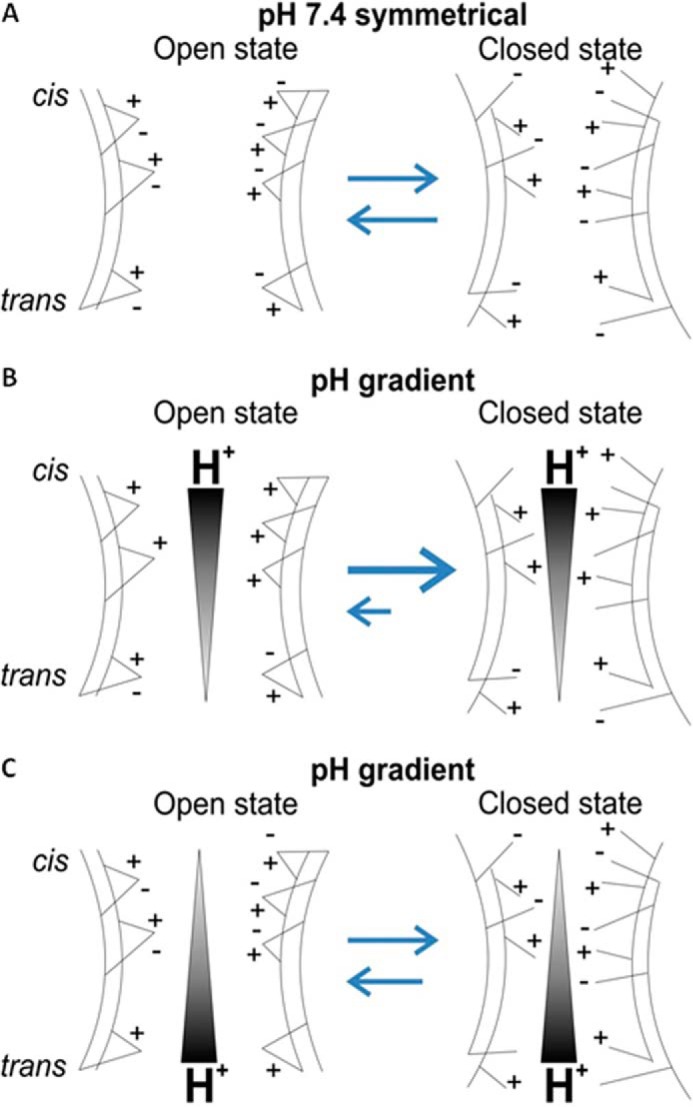
Model of the asymmetrical sensitivity of VDAC gating to acidification. An asymmetric distribution of stable salt bridges between the cis and trans sides of VDAC is shown. The reversible break of the salt bridges biases the conformational equilibrium of the channel toward the closed state (A). As the majority of titratable salt bridges are located at the cis side of the channel, a higher concentration of H⁺ at this side leads to the preferential closure of the channel (B), whereas the trans-titrated VDAC remains more stable because the number of salt bridges is significantly lower at that side (C).

There is a general agreement that in the open state of VDAC, the N-terminal region resides inside the pore. However, its position in the closed state remains under debate. It is interesting that the three charged residues, Lys-12, Asp-16, and Lys-20, located on the N terminus form salt bridges with β-strand residues (Fig. 6). This finding together with NMR studies demonstrating the rigidity of the N terminus (46–48) and with the recent evidence on N-terminal cross-linking to the β-barrel (49) support the idea of the localization of this region inside the pore in both open and closed states. However, several studies performed in cells suggest accessibility of the N-terminal region to antibodies (18, 50, 51).

The asymmetry in VDAC gating sensitivity to acidification could be physiologically relevant. Indeed, large pH changes in certain pathologies related to oxygen deprivation, such as ischemia and reperfusion injury, occur in the cytosol (20–22). Cytosolic acidification during ischemia protects cells from death (21, 52–56) by an as of yet poorly understood mechanism. Ischemia is followed by re-oxygenation or reperfusion where the pH is restored leading to cell death (21, 52–58). Although we observed the most dramatic effects of acidification on VDAC gating at a pH range well beyond physiological (pH <6.0), the revealed asymmetry may be amplified by the cell environment in vivo. For example, VDAC permeability in cells is also shown to be modulated by cytosolic proteins (4, 59–71), which might induce a more dramatic VDAC blockage at the physiologically low pH range observed during ischemia. Hypothetically, the increased VDAC gating upon acidification might be protective during ischemia by limiting the flow of respiratory substrates across VDAC that could be harmful to the mitochondria during anoxia. In addition, the reversibility of the effect of acidification on VDAC gating could lead to a reestablishment of VDAC permeability after reperfusion. Thus, returning to neutral pH would enhance the flux of respiratory substrates into the mitochondria thus boosting reactive oxygen species production and cell death.