Abstract
Background and Aims
Leaf transpiration is a key parameter for understanding land surface–climate interactions, plant stress and plant structure–function relationships. Transpiration takes place at the microscale level, namely via stomata that are distributed discretely over the leaf surface with a very low surface coverage (approx. 0·2–5 %). The present study aims to shed more light on the dependency of the leaf boundary-layer conductance (BLC) on stomatal surface coverage and air speed.
Methods
An innovative three-dimensional cross-scale modelling approach was applied to investigate convective mass transport from leaves, using computational fluid dynamics. The gap between stomatal and leaf scale was bridged by including all these scales in the same computational model (10−5–10−1 m), which implies explicitly modelling individual stomata.
Key Results
BLC was strongly dependent on stomatal surface coverage and air speed. Leaf BLC at low surface coverage ratios (CR), typical for stomata, was still relatively high, compared with BLC of a fully wet leaf (hypothetical CR of 100 %). Nevertheless, these conventional BLCs (CR of 100 %), as obtained from experiments or simulations on leaf models, were found to overpredict the convective exchange. In addition, small variations in stomatal CR were found to result in large variations in BLCs. Furthermore, stomata of a certain size exhibited a higher mass transfer rate at lower CRs.
Conclusions
The proposed cross-scale modelling approach allows us to increase our understanding of transpiration at the sub-leaf level as well as the boundary-layer microclimate in a way currently not feasible experimentally. The influence of stomatal size, aperture and surface density, and also flow-field parameters can be studied using the model, and prospects for further improvement of the model are presented. An important conclusion of the study is that existing measures of conductances (e.g. from artificial leaves) can be significantly erroneous because they do not account for microscopic stomata, but instead assume a uniform distribution of evaporation such as found for a fully-wet leaf. The model output can be used to correct or upgrade existing BLCs or to feed into higher-scale models, for example within a multiscale framework.
Keywords: Stomata, boundary layer, transpiration, microscale, computational fluid dynamics, leaf, droplet, multi-scale model, microclimate, boundary layer conductance, turbulence, convective mass transfer coefficient, functional–structural modelling
INTRODUCTION
Leaves are key players in the plant hydrological cycle as they regulate water loss to the environment, by transpiration via the stomata (Berry et al., 2010). Leaf transpiration is considered one of the most important moisture sources in the plant canopy (Schuepp, 1993) and is thus a critical determinant not only for water and energy budgets, affecting the earth's biosphere and atmosphere (Bauerle and Bowden, 2011a), but also for global agricultural production (Rijsberman, 2006).
A proper understanding of the underlying mechanisms affecting leaf transpiration is thus imperative, amongst others, for assessing land–climate interactions (Henderson-Sellers et al., 2008), plant stress (Leigh et al., 2012), photosynthesis (Shibuya et al., 2006), plant structure–function relationships (Bergmann, 2006; Maricle et al., 2007; Picotte et al., 2007; Lake and Woodward, 2008), precision agriculture (Roy et al., 2002; Boulard et al., 2004), and urban heat islands and mitigation strategies thereof (Santamouris, 2013). Transpiration rate is governed mainly by stomatal conductance (Roth-Nebelsick, 2007), which is regulated by its aperture, but as well by convective water vapour transfer from the stomata to the environment, which is often represented by boundary-layer conductance (BLC). An accurate quantification of this vapour transfer through the boundary layer is a key determinant for assessing leaf transpiration (Smith et al., 1997; Smith and Jarvis, 1998; Nobel, 2005; Bauerle and Bowden, 2011b), as reflected by recent research efforts in this area (see Roth-Nebelsick et al., 2009; Defraeye et al., 2013a).
Convective heat and mass transfer through the leaf boundary layer has been investigated by means of field tests and laboratory (wind-tunnel) experiments, using real or artificial leaves (e.g. Gurevitch & Schuepp, 1990; Daudet et al., 1998; Stokes et al., 2006; Roy et al., 2008). An overview is given by Defraeye et al. (2013b). Also, numerical modelling with computational fluid dynamics (CFD) has been applied (Roth-Nebelsick, 2001; Roy et al., 2008). This research focused particularly on bulk convective transfer from an entire leaf. Water vapour transfer, however, occurs predominantly over a small portion of the leaf surface, namely at the stomata, as the cuticle is quasi impermeable. These local elliptical perforations in the epidermis have sizes of a few tens of micrometres and only occupy one to a few per cent of the leaf surface area (Nobel, 2005). In conventional convective transfer studies on leaves, the impact of the very heterogeneous (non-uniform) nature of these mass exchange processes at the leaf surface, namely at discrete point sources at microscale level (stomata approx. 10−5 m), on total leaf transpiration is normally not considered or quantified explicitly. It is, however, obvious that stomatal size, aperture and density on the leaf surface will affect convective vapour transfer through the boundary layer, and thus the transpiration rate. Knowledge on the impact of these stomatal parameters on the overall transpiration rate of a single leaf is essential for a better understanding of plant–atmosphere interactions.
A few studies have looked at the impact of microscopic discretely distributed moisture sources, such as microscopic droplets but also stomata, on convective mass transfer using analytical or experimental methods for simplified flat-plate configurations (Cannon et al., 1979; Schlünder, 1988). They identified an influence of source size and density (surface coverage) on the evaporation/transpiration rate. Only the total convective transfer from the surface was evaluated here as an assessment of the boundary-layer flow and of the local transfer processes therein, which determine the microclimate around droplets/stomata, was not possible with the techniques used. However, such convective vapour transfer needs to be dealt with down to the level of individual stomata to identify the spatial variation of the BLC over the leaf surface. Similarly, stomatal conductance also varies spatially across the leaf surface, and a collective behaviour within different patches on the leaf surface was identified (Mott and Buckley, 2000). In addition, such a microscale assessment is essential for analysing the local boundary-layer microclimate around individual stomata or groups of stomata, as this boundary layer serves as a microhabitat for insects, bacterial and fungal pathogens (Boulard et al., 2002; Vidal et al., 2003), or bioinsecticides (Fargues et al., 2005; Roy et al., 2008). Quantification of water vapour transfer rates at individual stomata, whilst simultaneously quantifying the total transfer rate from the leaf, is considered virtually impossible experimentally. In such complex cases, a numerical modelling approach could be used to tackle the problem (DeJong et al., 2011).
Numerical methods have been used recently to model microscopic stomata in a discrete way. Roth-Nebelsick et al. (2009) modelled stomata arranged inside a single stomatal crypt (chamber in the leaf) and investigated the effect of stomatal aperture and trichomes in the crypt on the transpiration rate. Defraeye et al. (2013a) modelled transpiration from stomata (and evaporation of microscopic droplets) with CFD using a two-dimensional (2-D) model of a leaf, subjected to developed boundary-layer flow. A cross-scale modelling approach was used, reaching from leaf level (10−1 m) down to the stomatal scale (10−5 m), thus covering a very large spatial range. Evidence was provided that the convective vapour transfer was dependent on stomatal size, aperture and density (surface coverage), and on the boundary-layer microclimatic conditions around the stomata (air speed). Such cross-scale modelling provided new insights into the vapour transfer processes at the microscale level at these discrete sources, and the added value of numerical modelling was clearly demonstrated. However, this study was two-dimensional, thus implying that all stomata were in line with each other, and assumed developed boundary-layer approach flow, therefore representing a leaf mounted on a (wind-tunnel) wall instead of a freestanding leaf.
In this study, we investigate the effect of stomatal surface density and air speed on the convective vapour transfer from leaf surfaces via discretely distributed stomata for a more realistic case of a 3-D freestanding (still) leaf. This implies capturing the impact of strong boundary-layer development, including edge effects and a 3-D stomatal distribution. A 3-D cross-scale CFD modelling approach is used, which implies that all scales from leaf level down to the stomatal scale are explicitly included in the computational model, including individual stomata. Such 3-D cross-scale modelling is one of the novelties of this study and implies a very high computational cost. As such, the mass exchange at the air–leaf interface at individual stomata can be determined and high spatial resolution information is available on the (boundary-layer) flow field and the mass transport therein. A systematic study is undertaken to identify the effect of stomatal surface density and air speed on convective transfer, and thus on BLC. As such, this study aims at taking a next step towards bridging the gap between convective transfer at the stomatal scale and at the leaf scale. Such knowledge should improve modelling accuracy of evapotranspiration of leaves, related heat transfer processes and higher-scale models on tree or canopy level (Bauerle and Bowden, 2011b; Gromke, 2011; Saudreau et al., 2011; Leigh et al., 2012). Particular issues that we are able to address in this study, by using modelling, are: how the spatial distribution of the BLC over a leaf looks like down to a stomatal resolution and how it depends on stomatal surface density and air speed; how important edge effects are here; and how the boundary-layer microclimate (temperature and relative humidity) looks like and how it changes with varying stomatal surface coverage, for example.
MATERIALS AND METHODS
Numerical model
Computational domain
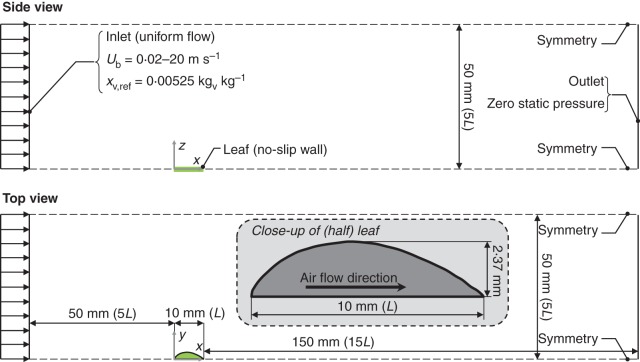
A simplified model of a single leaf was used to study leaf transpiration down to the stomatal level. A generic leaf shape was used as a model system, based on that of Laurus nobilis, with a length (L) of 10 mm, a maximal width (W) of 4·73 mm and a surface area of 33 mm2. Only half of the leaf was modelled, by assuming symmetry along the midrib. The leaf was of such small size to keep the computational cost within limits and to facilitate the associated meshing of the model (see below), as stomata were modelled discretely. The leaf surface was flat and still (not moving), and was placed parallel to the uniform low-turbulent approach flow. The 3-D computational domain is presented in Fig. 1, together with the imposed boundary conditions. The domain dimensions and the computational grid were based on best practice guidelines (Franke et al., 2007) and a grid sensitivity analysis. Upstream (5L), downstream (15L) and side (5L) sections avoid any influence of the imposed boundary conditions at inlet, outlet and lateral boundaries on the momentum and mass transfer in the vicinity of the leaf. The hybrid grid was composed of hexahedral, tetrahedral and prismatic computational cells and contained 5·88 × 106 3-D cells. From grid sensitivity analysis, the spatial discretization error was estimated by means of Richardson extrapolation (Roache, 1994; Franke et al., 2007) and is below 0·1 % for both leaf drag force and mass flux at the wall.
Fig. 1.
Computational domain and boundary conditions for leaf simulations, including close-up of the (half) leaf shape.
Computational grid: microscopic sources on the leaf surface
Stomata are elliptical and typically have an aperture of a few tens of micrometres when fully open (long axis approx. 20 µm, short axis approx. 5–15 µm, Nobel, 2005) and a resulting surface area of one to a few hundred square micrometres. However, differences can be large between species (Eckerson, 1908; Jones, 1992). To model such microscopic stomata discretely on the leaf surface, very small (2-D) triangular computational cells with a quasi uniform size were used on the entire leaf surface, namely with an average surface area of 215 µm2 and a standard deviation of 5 %. This stomatal area corresponds to equilateral triangles with sides of 22·3 µm or to a circle of 16·5 µm diameter. The stomatal size used in the computational model is thus realistic but, for meshing purposes, the stomatal shape was represented by triangular cells instead of elliptical shapes.
Different stomatal surface densities (called coverage ratios, CRs) were evaluated, which are typically very low (approx. 0·2–5 % for open stomata, Cannon et al., 1979; Jones, 1992; Nobel, 2005), namely CR = 0·1, 0·25, 0·5, 1, 2, 5 and 10 %, as well as a hypothetical CR of 100 %. All stomata were distributed in a random way over the leaf surface. The CR is defined as the ratio of the area occupied by the stomata (Aeff, m2) to the total leaf area (A, m2), i.e. CR = Aeff/A. A CR of 100 % corresponds in this study to a uniform water vapour pressure at the entire leaf surface (see below), which is often used to determine the BLC for flat plates or leaves, and its correlation with air speed (Defraeye et al., 2013b). The distribution of stomata on the leaf surface is shown for all CRs in Supplementary Data Fig. S1. The corresponding number of stomata and stomatal densities are given in Table 1.
Table 1.
Surface coverage ratio of stomata on a leaf surface, the corresponding number of stomata (on a leaf model, i.e. half a leaf) and stomatal surface density
| Coverage ratio ( %) | No. of stomata | Stomatal density (mm−2) |
|---|---|---|
| 0·1 | 79 | 5 |
| 0·25 | 193 | 12 |
| 0·5 | 366 | 22 |
| 1 | 783 | 48 |
| 2 | 1560 | 95 |
| 5 | 3849 | 234 |
| 10 | 7741 | 470 |
The small scale of the leaf surface cells is the main reason for the high number of computational cells in the computational model (7·68 × 104 2-D triangular cells on the surface of half a leaf). This cross-scale modelling approach, which implies that a large range of spatial scales are included in the same computational model (10−5 m for stomata to 10−1 m for the entire computational domain), is particularly challenging with respect to grid generation and implies a large computational cost. Details of the grid are shown in Supplementary Data Fig. S2 (details of grid sensitivity analysis are given in Fig. S3). Several transition regions were applied away from the leaf surface to reduce the number of cells in the computational model and to avoid very elongated or skewed cells. Despite the small scale of the computational cells at the surface (approx. 10–20 µm), the use of continuum models to calculate gas transport, based on Navier–Stokes equations with no-slip boundary conditions, is a valid assumption, as determined by Knudsen number evaluation (see Defraeye et al., 2013a).
Computational grid: boundary-layer modelling
Apart from modelling individual stomata discretely, the high number of computational cells in the computational model is also related to the way in which the flow in the boundary layer was modelled. Two modelling methods are commonly applied in CFD to model flow in the boundary layer: wall functions and low Reynolds number modelling (LRNM). Wall functions calculate the flow quantities in the boundary-layer region using semi-empirical functions (Launder and Spalding, 1974). LRNM, by contrast, explicitly resolves transport in the boundary layer, which is inherently more accurate. Grids for LRNM of the boundary layer require a high grid resolution (i.e. high cell density) in the wall-normal direction, particularly at high Reynolds numbers, to resolve the flow throughout the entire boundary layer. The dimensionless wall distance, i.e. y+ value, in the wall-adjacent cell centre point P (yP+) should ideally be below 1 for LRNM, whereas wall functions require 30 < yP+ < 500. Here, yP+ is defined as [(τw/ρg)1/2yP]/νg, where yP is the distance (normal) from the cell centre point P of the wall-adjacent cell to the wall (4 µm in this study), ρg is air density (1·225 kg m−3 in this study), νg is the kinematic viscosity of air (1·461 × 10−5 m2 s−1 in this study) and τw is the shear stress at the wall [Pa], which increases with the Reynolds number. The wall-adjacent cells are those computational cells (control volumes) that lie on the leaf surface (i.e. the wall). As such, wall functions can have much larger computational cells in the boundary-layer region as their yP can be much larger. The grid resulted in yP+ values, at the highest evaluated air speed (20 m s−1), below 1 for 99 % of the leaf surface and a maximum yP+ value of 1·9 in a limited number of computational cells.
Boundary conditions for air flow
Multiple low-turbulence, uniform free-stream air speeds (Ub) were imposed at the inlet of the computational domain, namely 0·02, 0·2, 2 and 20 m s−1, resulting in Reynolds numbers based on Ub and leaf length (L) varying from 14 to 1·37 × 104 (Reb = UbL /νg). These are relatively low, due to the small leaf size, but are representative for real leaves. The turbulence intensity (TIref) at the inlet of the domain was taken as low (0·02 %), which is representative for low-turbulence wind tunnels. The specific dissipation rate [ω, s−1; required for the shear stress transport (SST) k-ω turbulence model, see below] was determined from ω = k½/(Cμ1/4Ls) (ANSYS Fluent 13, 2010), where k is the turbulent kinetic energy [m2 s−2], Cμ is a turbulence model constant (0·09) and Ls is a length scale which was taken as small (arbitrarily) and equal to L/4 (0·0025 m). Air flow with a temperature of 15 °C (Tref) and a relative humidity of 50 % (RHref) was imposed at the inlet, resulting in a water vapour pressure of 853 Pa (pv,ref) and a corresponding mass fraction of 0·00525 kgv kg−1 (xv,ref), where the subscript ‘v’ indicates water vapour.
Zero static pressure was imposed at the outlet, which is advised in best practice guidelines (e.g. Franke et al., 2007). Symmetry boundary conditions were used for all lateral boundaries, which assume that the normal velocity component and the normal gradients at the boundary are zero. This implies that transpiration is assumed to occur at both abaxial and adaxial sides of the leaf. For the case considered here, such a symmetry assumption does not affect the mass flow results significantly, as flow is parallel to the leaf, by which the boundary-layer transport on one side is quasi independent of that on the other side. Note, however, that some effects will be present at the edges (see Results), and that more water vapour will be present in the air downstream of the leaf, compared with a leaf single side transpiring. The leaf surface was modelled as a no-slip wall with zero roughness as surface roughness values cannot be specified when LRNM is used in ANSYS Fluent 13 (2010). Although surface roughness (e.g. trichomes, wax structures, lobes or venation) may alter the flow field around the leaf to some extent and thereby enhance but also decrease (e.g. densely packed hairs) water vapour transfer rates, such effects were not included here.
Boundary conditions for heat and mass transfer at the leaf surface
Previous numerical studies on convective transfer from leaves (Roth-Nebelsick, 2001; Roy et al., 2008) or experiments on artificial leaves mostly imposed homogeneous (uniform) boundary conditions on the leaf surface, e.g. a constant scalar or flux condition (Defraeye et al., 2013b). To model the heterogeneous boundary conditions at the leaf surface found in reality (i.e. discretely distributed stomata) and to determine the resulting convective vapour transfer through the boundary layer, a specific type of boundary condition was imposed in the present study: a constant water vapour pressure (pv,w = 1705 Pa or xv,w = 0·0105 kgv kg−1, i.e. RHw = 100 % at 15 °C) at discrete locations on the leaf surface, i.e. at the computational cells which represent stomata; the rest of the surface was assumed to be impermeable for water vapour (no-flux condition), and thus a zero wall-normal gradient was present in the wall-adjacent cells. This dual boundary condition is representative for convective vapour exchange at discretely distributed stomata: only at these locations does water vapour transfer occur as (quasi) no water vapour transfer from/to the leaf surface is possible through the waxy cuticle. This type of boundary condition was implemented in the CFD software by means of user-defined functions. Such a boundary condition is a simplification in the sense that (1) an interaction with the transport inside the leaf (from sub-stomatal cavities through stomata) is not accounted for, so only the boundary-layer flow affects the transfer rate; and (2) all stomata are assumed to be at the same vapour pressure, i.e. the saturation water vapour pressure in this case. As mentioned before, stomatal CRs ranging from 0·1 to 10 % were evaluated, as well as a hypothetical CR of 100 %. The latter corresponds to a fully wet leaf as a RHw of 100 % was assumed.
There will be some dependency of the resulting mass flow (and thus BLC) on the specific distribution of the stomata over the leaf surface at a certain CR, which was chosen randomly. The impact of the introduced randomness on the vapour exchange was quantified by evaluating ten different distributions at a CR of 10 % and at a high Reynolds number (Ub = 2 m s−1). A standard deviation below 0·3 % on the average leaf vapour flow of these ten distributions is found, indicating a very small variation with coverage distribution. Due to this low sensitivity, only a single coverage distribution was evaluated for a specific CR.
Numerical simulation
The CFD simulations were performed with the commercial software ANSYS Fluent 13 (ANSYS Inc., Canonsburg, PA, USA), which uses the control volume method. The accuracy of CFD simulations depends to a large extent on the turbulence-modelling and boundary-layer modelling approaches that are used, and has to be quantified by means of validation simulations based on experiments. In this study, steady Reynolds-averaged Navier–Stokes (RANS) equations were used in combination with the SST k-ω turbulence model (Menter, 1994). LRNM was applied to resolve the transport in the boundary-layer region. LRNM was actually included in the SST k-ω model (ANSYS Fluent 13, 2010), i.e. the SST k-ω model was used as an LRNM and did not require additional damping functions in the vicinity of the wall. The good performance of this RANS turbulence model combined with LRNM has been demonstrated for several complex flow problems by detailed validation studies (e.g. Defraeye et al., 2010a, b, 2012), amongst others for flow around a sphere. Based on the aforementioned validation studies performed by the authors, the SST k-ω model was considered sufficiently accurate for the more simple flow problem of the present study, i.e. developing boundary-layer flow on a flat surface. A comparison with BLCs obtained from field and laboratory experiments is provided in the Results.
With respect to water vapour transport modelling, the air properties, and thus also airflow, are inherently a function of the water vapour mass fraction in the air (xv), as moist air can be considered as a mixture of dry air and water vapour, and of temperature (e.g. the saturation vapour pressure at the surface). In the present study, however, water vapour transfer was modelled as a passive scalar, which implies that it does not influence the flow field. This is a realistic assumption due to the low mass fractions of water vapour in air (xv ≈ 0·005–0·01 kgv kg−1 in this study). The main reason for assuming passive vapour transfer was that the computational cost to evaluate different boundary conditions (i.e. stomatal densities) decreased significantly, as air properties (e.g. density) were taken as being constant and thus independent of mass fraction. As such, the flow field had to be solved only once for each air speed because only the water vapour field had to be recalculated for different CRs. Thus, by disabling the solution of air flow and turbulence equations after flow-field convergence, the different water vapour boundary conditions could be evaluated more quickly.
The passive (turbulent) water vapour transport was implemented by means of a user-defined scalar (UDS = xv) in the CFD software. The following equation was solved:
| (1) |
where xv is the mass fraction of water vapour in the air [kgv kg−1], v is the air velocity vector [m s−1] and the subscript g represents moist air (dry air and water vapour). Dva,eff represents the effective diffusion coefficient of water vapour in (dry) air [m2 s−1], which is defined as the sum of the molecular diffusion coefficient (Dva) and the turbulent diffusion coefficient (Dva,t):
| (2) |
where Sct is the turbulent Schmidt number (0·85 in this study) and μt is the turbulent viscosity [kg m−1s−1]. The turbulent diffusion coefficient accounts for the influence of turbulence on water vapour transport and is proportional to μt, which is calculated by the (SST k-ω) turbulence model.
All air properties were assumed to be constant (ρg = 1·225kg m−3, Dva = 2·545 × 10−5 m2 s−1) and isothermal conditions were assumed, mainly because the aim was to focus on the general transport mechanism of a passive scalar, in this case water vapour. Buoyancy effects and radiation were also not taken into account. These assumptions imply forced convective flow and the validity of the heat and mass transfer analogy. As such, the vapour transport in the boundary layer and corresponding BLCs can easily be translated to transport of other species (O2, CO2) or to heat. To keep the discussion more general, we will also use the term ‘mass’ instead of ‘vapour’ below.
The conductance, i.e. (inverse) resistance, of water vapour transfer in the boundary layer can be quantified from the simulations, which is usually done by means of a convective mass transfer coefficient (CMTC, s m−1) or a BLC (m s −1). They both relate convective vapour flux normal to the wall (gv,w [kg s−1m−2]), i.e. at the air–material interface, to the difference between the water vapour pressure/mass fraction at the wall (pv,w or xv,w) and a reference vapour pressure or mass fraction (pv,ref or xv,ref), which can be taken, for example, to be equal to the approach flow conditions:
| (3) |
| (4) |
where Gv,w,avg [kg s−1] is the surface-averaged vapour flow over the leaf. The fluxes are assumed to be positive away from the leaf surface.
Second-order discretization schemes were used throughout. The SIMPLE algorithm was used for pressure–velocity coupling. Pressure interpolation was second order. A double-precision solver was required due to the very large range of spatial scales in the computational domain. Iterative convergence of the numerical simulation was assessed by monitoring the velocity, turbulent kinetic energy and temperature at the outlet, and the drag force and heat fluxes at the leaf surface. The simulations were stopped when these monitors no longer changed with an increasing number of iterations, as this indicated convergence of the simulation. In particular at low CRs and low Reynolds numbers, the convergence behaviour for water vapour (UDS) was quite slow.
Background
The impact of microscopic water vapour sources (e.g. stomata or droplets), which are distributed heterogeneously over a surface at a certain CR, on the convective water vapour transfer (and thus BLC and CMTC) was investigated previously down to the microscale level, both analytically (Schlünder, 1988: droplets on surfaces) and numerically (Defraeye et al., 2013a: stomata on leaves, 2-D; Defraeye et al., 2012: droplets and lenticels on spherical horticultural products, 3-D). The surface-averaged water vapour flows at a certain CR (Gv,w,avg,CR), and thus the BLCs, were found not to scale linearly with a reduced area for water vapour transfer (Aeff), compared with the flow at a CR of 100 % (Gv,w,avg,100 %). Instead, relatively high mass transfer rates could be maintained for a partially wetted surface and the surface actually acted very similar to a uniformly wetted surface (CR = 100 %), such as a fully wet leaf. The reasoning behind this is that, for small sources (with respect to the boundary-layer thickness) that are distributed homogeneously across the surface, the concentration contours quickly equalize within the viscous sub-layer in the wall-normal direction (become parallel to the wall) away from the sources. Thereby, about the same concentration is found in the wide proximity of these sources, and not only directly above the sources. This results in a high mass transfer rate, even for a reduced wet surface area (Schlünder, 1988; Defraeye et al., 2013a, b).
Apart from the CR, the characteristic size of the sources on the surface (d, e.g. stomata) and the thickness of the viscous sublayer δVSL (i.e. the lower part of the boundary layer where laminar transport occurs and where large velocity and water vapour gradients are found, e.g. Defraeye et al., 2010b; [m]) were found to be relevant parameters that influenced the total mass flow from the surface (Gv,w,avg,CR). Both length scales are combined into the d/δVSL ratio in this study, which is also called the microscopic Sherwood number (see Schlünder, 1988; Defraeye et al., 2013a). Here, d was taken to be equal to the equivalent circular diameter of the stomata (16·5 µm, see above) and δVSL (for turbulent boundary layers) was defined as the region where y+ < 5, which is approximately the upper y+ limit of the viscous sub-layer in turbulent boundary layers (e.g. Cebeci and Bradshaw, 1984). From the definition of y+ given above, this results in δVSL = 5νg (τw/ρg)−½. δVSL is thus inversely proportional to the square root of the shear stress at the wall. As the shear stress increases with air speed (Ub), the boundary-layer thickness (and thus also δVSL) will decrease. The present study aims to shed more light on the impact of CR, d and δVSL on the BLC for leaves, particularly for stomata, and thus for very low CRs.
RESULTS
Uniform coverage
Before assessing the influence of partial (stomatal) coverage of the leaf surface on mass transfer (next section), this section focuses on both air flow and mass transfer for a uniform coverage (CR 100 %), for example for a fully wet leaf. For this, the surface-averaged boundary-layer thickness over the leaf surface (δVSL,avg) is shown in Fig. 2, as a function of the Reynolds number (Reb), where δVSL,avg varies between 5·0 × 10−5 and 5·7 × 10−3 m. In addition, the microscopic Sherwood numbers (d/δVSL,avg) are given, as well as the surface-averaged mass flux over the leaf (i.e. at CR 100 %, gv,w,avg,100 %), which varies between 9·3 × 10−5 and 1·3 × 10−3 kg s−1m−2. Due to the developing boundary layer, both the boundary-layer thickness and the mass flux varied significantly over the leaf surface. In Fig. 3, the local wall shear stress (τw) and mass flux distribution over the leaf surface (CR 100 %, gv,w,100 %), scaled with the surface-averaged values (τw,avg and gv,w,avg,100 %), are shown at different Reynolds numbers (Reb) as a function of the distance from the leading edge (x/L). These local values (τw and gv,w,100 %) are actually the average values over individual 0·1-mm segments (in the x-direction) on the leaf surface. As the surface areas of these segments differ (Fig. 1), not each segment will contribute in the same way to the surface-averaged values (τw,avg and gv,w,avg,100 %). The reported mass fluxes are directly proportional to the BLC (and CMTC, eqns 3 and 4), due to the imposed constant mass fraction difference (xv,w – xv,ref).
Fig. 2.
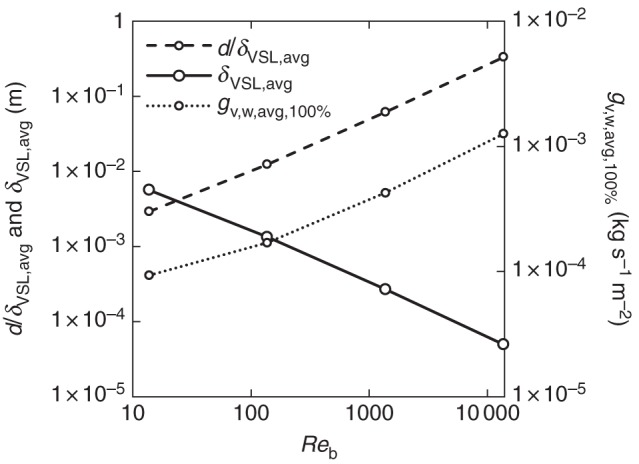
Leaf surface-averaged viscous sublayer thickness δVSL,avg, microscopic Sherwood numbers (d/δVSL,avg) and surface-averaged vapour flux (for CR = 100 %) as a function of the Reynolds number (Reb). Logarithmic scaling is used for both axes.
Fig. 3.
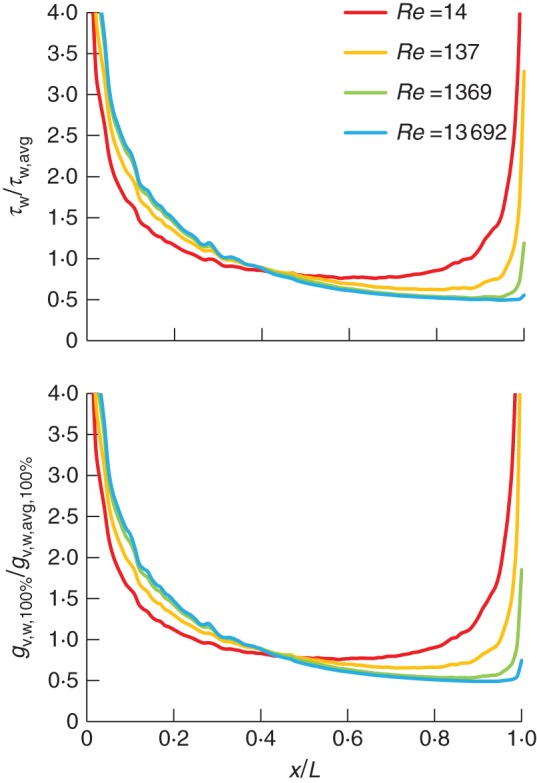
Local wall shear stress and vapour flux distribution over the leaf surface (τw and gv,w,100 %, averaged over 0·1-mm leaf segments along the streamwise direction x), scaled with the surface-averaged values over the leaf (τw,avg and gv,w,avg,100 %) as a function of the distance from the leading edge (x/L) for different Reynolds numbers (Reb) for a leaf with uniform coverage (CR = 100 %).
The distributions of shear stress and mass flux are quite similar, i.e. high values at the leading edge due to the (mass and momentum) boundary-layer development, and lower values further downstream. At low speeds, a clear increase in τw and gv,w,100 % is found towards the end of the leaf. This increase is due to edge effects at the trailing edge, caused by strong velocity and water vapour gradients here. Particularly at low air speeds, this effect manifests itself upstream of the trailing edge in an increased τw and gv,w,100 %. This means that at the edges, a clearly increased convective transfer rate (and thus BLC) is present, which will also have an impact on the local fluxes at stomata located in these regions, particularly at low speeds. The edge effect is also manifested at the leaf sides, and is partially held responsible for the fact that streamwise gradients (with x/L) in the proximity of the leading edge at low speeds are larger than at high speeds (Fig. 3), which is opposite to what is found for (2-D) flat plates (Defraeye et al., 2013a). This edge effect is indicated in Fig. 4 for the shear stress. Figure 4 is also representative for the mass flux due to the similarity between the two, as reflected in the shear stress and mass flux distributions (Fig. 3). This similarity was expected as the conditions for the mass and momentum analogy are fulfilled (Cebeci and Bradshaw, 1984), amongst others similar boundary conditions at the leaf surface, resulting in a developing boundary layer. When verifying the validity of the analogy, a very good agreement between momentum and mass transfer was found (results not shown).
Fig. 4.
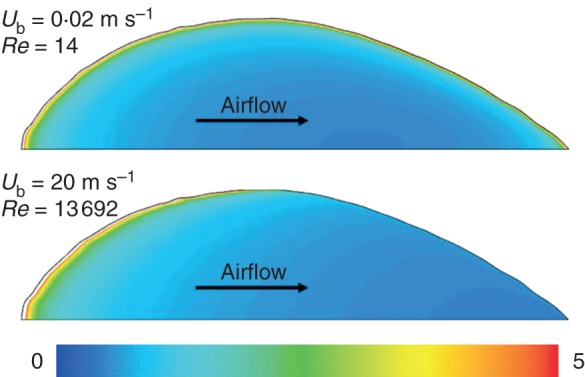
Contours of wall shear stress distribution over the leaf surface (τw), scaled with the surface-averaged value over the leaf (τw,avg) at high and low air speeds to indicate the edge effects. Due to similarity, these contours are also representative for the mass flux distribution (gv,w,100 %).
Finally, the BLCs obtained in the present study (for 100 % coverage) at different air speeds are compared with results from several laboratory and field experiments on real and artificial leaves, taken from the review of Defraeye et al. (2013b). For this, the Sherwood number is given as a function of the Reynolds number in Fig. 5. The Sherwood number is defined here as Sh = BLC × Lref/Dva, where Lref is a reference length (leaf length in this study, 0·01 m) and Dva is the diffusivity of water vapour in air [m2 s−1]. A correlation for laminar flow over a flat plate is also presented (Lienhard and Lienhard, 2006). Most of these Sherwood numbers were converted from Nusselt numbers or from heat and mass BLCs (from Defraeye et al., 2013b). The observed variability between the correlations is attributed to differences in approach-flow turbulence intensity, leaf morphology (shape, thickness, venation) and associated edge effects, leaf orientation relative to the wind, surface roughness and the scalar boundary conditions at the leaf surface (e.g. a stomatal distribution or a uniform boundary condition, such as a constant flux or scalar value), amongst others. Furthermore, correlations are often expressed as a function of different air speeds (e.g. free stream, above the canopy, local value within canopy) or characteristic lengths. As such, comparison with other studies is not always feasible or justified. The present study resulted in rather low BLC values, as compared with the other correlations, because a rather idealized case of parallel flow over a smooth, flat leaf surface was considered. Below we identify the impact of partial coverage, i.e. to what extent the aforementioned BLCs for uniform boundary conditions (CR of 100 %, e.g. fully wet leaf) are reduced when applying more realistic boundary conditions, i.e. low, stomatal CR.
Fig. 5.
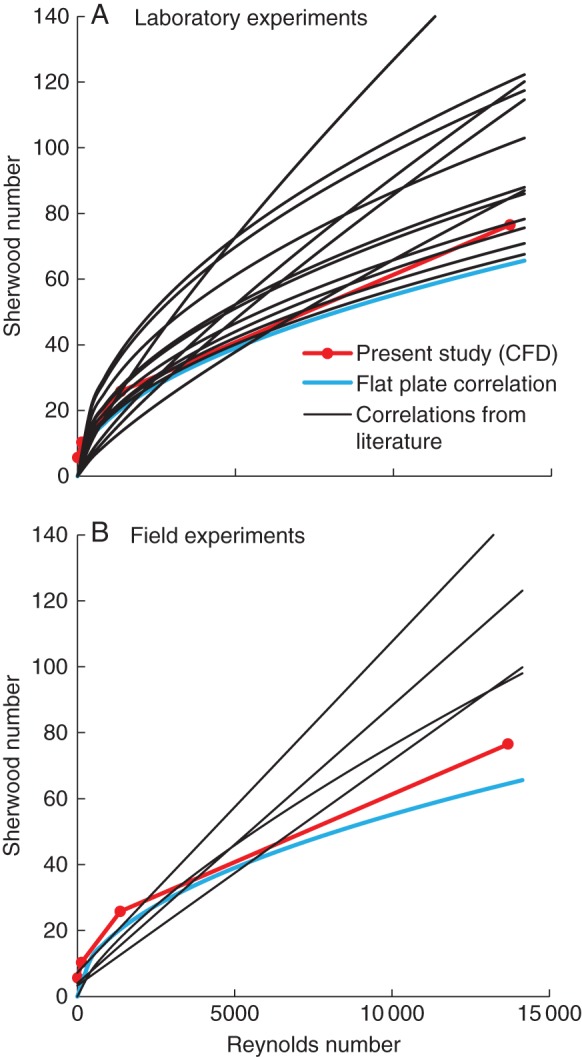
Correlations of Sherwood number with Reynolds number (Reb) for laboratory (A) and field (B) experiments presented by Defraeye et al. (2013b). A correlation for laminar flow over a flat plate (from Lienhard and Lienhard, 2006) is indicated with a blue line. The CFD results of the present study for a CR of 100 % are also included (at four air speeds).
Partial coverage
Surface-averaged mass flow from leaf surface
The impact of a reduced area for mass transfer, i.e. only at discretely distributed microscopic mass sources (stomata), on the convective transfer from the leaf surface is quantified here. The surface-averaged convective mass flows from the leaf (Gv,w,avg) are shown in Fig. 6 as a function of the CR, for CR = 0–10 %. Results at different air speeds (Ub), and thus d/δVSL ratios, are presented. These mass flows are scaled with the surface-averaged mass flow for a CR of 100 % (Gv,w,avg,100 %). As these mass flows are directly proportional to the BLC (and CMTC), when defined according to eqns (3) and (4), their results are equivalent to the ratio BLCavg/BLCavg,100 %, which is also indicated in Fig. 6.
Fig. 6.
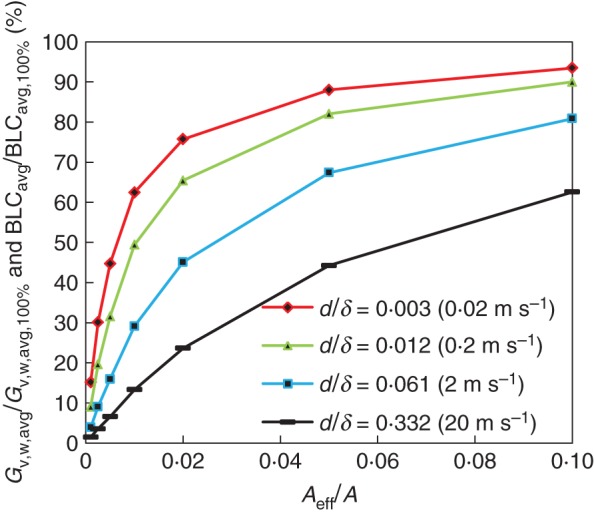
Surface-averaged convective mass flows and BLCs at the leaf surface as a function of CR (0–10 %) for different air speeds (Ub, i.e. d/δVSL ratios). The flows and BLCs are scaled with the surface-averaged values for a CR of 100 % (Gv,w,avg,100 % or BLCavg,100 %).
From Fig. 6, relatively high mass flows at the leaf surface are found (for all d/δVSL ratios), even at these low CRs, and thus they clearly do not vary linearly with the CR. This means that even though the leaf only has a limited number of moisture sources (i.e. stomata), the total mass flow (transpiration) from the leaf can still be considerable. This effect is particularly pronounced at low microscopic Sherwood numbers (d/δVSL), implying low air speeds (Fig. 6). These findings agree with Defraeye et al. (2013a), who identified a strong correlation between scalar flow from a 2-D leaf surface and the microscopic Sherwood number: for a certain CR, the scalar flow increased with decreasing d/δVSL ratio, irrespective of the specific source size or air speed at which it was evaluated. Although the impact of source size was not identified in the present study, it is most probable that lower microscopic Sherwood numbers, induced by smaller stomata, will also lead to higher mass flows at a certain CR. The results shown in Fig. 6 are obviously more realistic and representative for real leaves, compared with the 2-D study of Defraeye et al. (2013a), as the present (3-D) study includes edge effects and a 3-D stomatal distribution.
The lowest values for mass flows and BLCs are found at high microscopic Sherwood numbers (d/δVSL), compared with 100 % coverage. For example, the BLCavg of a leaf with stomata with a CR of 1 % is only 13 % of that of a leaf with a CR of 100 % at high air speeds (at 20 m s−1, d/δVSL = 0·332, Fig. 6). BLCs (or CMTCs) for leaves, and their correlations with air speed, are, however, often determined using homogeneous boundary conditions (CR 100 %, BLCavg,100 %) by experiments or simulations on plates or leaf models (Defraeye et al., 2013b). Such conventional BLCavg,100 % (or CMTC), as presented in Fig. 5, can thus result in a significant overprediction of the convective exchange for real leaves, particularly at high air speeds, as stomata have a much lower CR. As such, corrections are required for such conventional BLCavg,100 %. The impact of this mismatch between fully covered (uniform) and partially covered boundary conditions on BLC should be acknowledged by users of such BLC–Ub correlations. By means of relationships between the BLC and the CR, like those obtained in the present study (Fig. 6), a correction of BLCavg,100 % could be determined.
The largest decrease (or gradient) of mass flow with CR seems to occur in the CR range under study (CR = 0–10 %), namely between 63 and 93 % of Gv,w,avg,100 % in the present study. This decrease is larger for low microscopic Sherwood numbers (d/δVSL), i.e. low air speeds (or small source sizes). As such, small variations in stomatal density on the leaf surface between different leaves, e.g. due to biological variability, will have a large impact on the convective exchange, and thus on the BLC. This implies that within a single tree or plant, there is large variability on the BLCs of its individual leaves. From the present study, the BLCavg of a leaf with different stomatal densities (CR = 0·25–5 %) at a Reynolds number of 137 (Ub = 0·2 m s−1) will vary between 20 and 82 % of that of a leaf with a CR of 100 % (see Fig. 6). We also expect a similar impact of variations in CR, as induced by stomatal opening and closure, on the BLC. Quantifying this effect is less straightforward based on the profiles in Fig. 6 as also d, and thus d/δVSL ratio, changes. Ideally, a 3-D surface profile between BLCavg, CR and d/δVSL would be required for this purpose.
Local mass fluxes at stomata
As the mass flows do not scale linearly with a reduced surface area for mass transfer (Fig. 6), the local fluxes at the individual stomata (gv,w) should become higher at lower CRs. In Fig. 7, the local mass fluxes at the stomata are indicated by presenting the effective mass flux (gv,w,avg,eff), averaged only over all stomata on the leaf (Aeff), as a function of the CR. This implies averaging gv,w at the stomata only over Aeff (area occupied by the stomata) instead of A. These fluxes are scaled with the surface-averaged flux for a leaf with a uniform coverage (gv,w,avg,100 %). These fluxes all increase by a factor 5 or more, and at low microscopic Sherwood numbers even up to a factor above 100. This implies that stomata (of a certain size) induce higher mass transport into the boundary layer at lower CRs. So for a leaf with fewer stomata, these stomata will be able to transpire more via the boundary layer. This CR-dependent transpiration will also add complexity to the way in which the stomatal CR affects water transport inside the leaf.
Fig. 7.
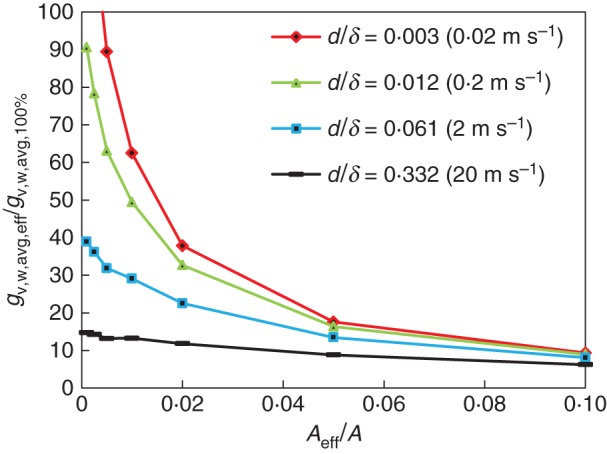
Effective convective mass fluxes at the leaf surface (gv,w,avg,eff), averaged only over the stomata on the leaf, and thus over Aeff, as a function of CR (0–10 %) for different air speeds (Ub, i.e. d/δVSL ratios). The flows are scaled with the surface-averaged mass flux for a CR of 100 % (gv,w,avg,100 %).
In Fig. 8, the distribution of the local mass fluxes at the stomata (gv,w,eff) is given for different surface CRs as a function of the distance from the leading edge (x/L) at a Reynolds number of 1369 (Ub = 2 m s−1). These values are the surface-averaged values over individual 0·1-mm segments (in the x-direction), where gv,w at the stomata is averaged only over the area of the segment that is occupied by stomata (Aeff,S). As such, at very low CRs, no mass fluxes could be reported in Fig. 8 for some segments because the local CR of these segments is zero. Two types of scaling are applied in Fig. 8: (1) Fig. 8A uses the surface-averaged mass flux of the entire leaf for a CR of 100 % (gv,w,avg,100 %). For a CR of 100 %, this curve is the same as that in Fig. 3 at the respective Reynolds number; (2) Fig. 8B uses the local average mass flux of each segment for a CR of 100 % (gv,w,100 %, see Fig. 3). In Fig. 8B, the δVSL/δVSL,avg distribution is also included.
Fig. 8.
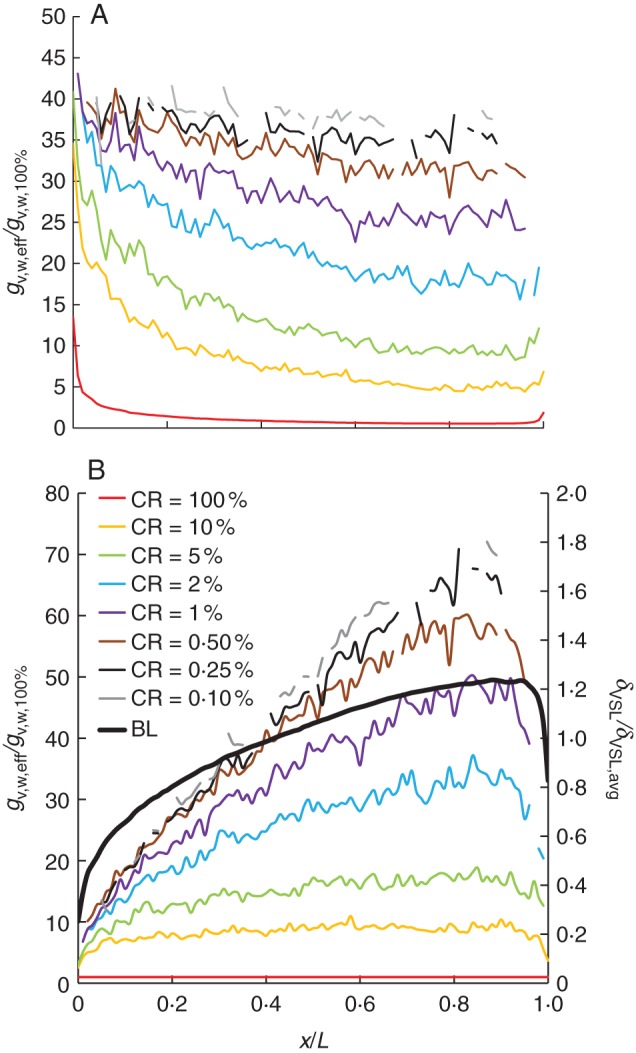
Local mass fluxes at the stomata (gv,w,eff) as a function of the distance from the leading edge (x/L) at an air speed of 2 m s−1 (Reb = 1369) for different surface CRs: (A) this mass flux is scaled with the surface-averaged value over the leaf for a CR of 100 % (gv,w,avg,100 %); (B) this mass flux is scaled with the local mass flux of each leaf segment of 0·1 mm for a CR of 100 % (gv,w,100 %). BL (boundary layer) indicates the relative viscous sub-layer thickness distribution (δVSL/δVSL,avg) over the surface.
Figure 8A confirms that the local mass fluxes at the stomata increase with decreasing CR everywhere at the leaf surface. Low CRs enhance the mass exchange locally at these sources, as the boundary layer surrounding these sources is at a lower vapour pressure. Figure 8B represents the difference, locally, of a partially covered surface with an entirely covered surface. The largest (local) differences between gv,w,eff and gv,w,100 % are predominantly found at locations with high δVSL values (i.e. low d/δVSL values). This finding corresponds to the previous findings of Schlünder (1988) and Defraeye et al. (2013a) and of Fig. 6 for surface-averaged values: the relative mass flow from the surface at partial coverage is the largest at low d/δVSL ratios. This is now confirmed also in a local manner in Fig. 8B.
Mass transport in the boundary layer
In Fig. 9, typical vapour concentration isocontours, i.e. xv at a constant value, are shown in the boundary layer above the leaf surface for a CR of 1 % at an air speed (Ub) of 2 m s−1 (Reb = 1369). These isocontours are coloured according to air speed and one isocontour is presented in each separate image. In addition, the air speed in a horizontal and vertical centreplane (also symmetry planes) is also shown. From the value of the water vapour mass fraction of the isocontour (xv,iso), a dimensionless isocontour value Iv was also determined, which is defined as: Iv = (xv,iso – xv,ref)/(xv,w – xv,ref). This value is 100 % at the leaf surface and 0 % in the free stream. Four different isocontour values are presented in Fig. 9. From Fig. 9, the vapour boundary-layer growth can clearly be observed, which becomes more saturated from leading edge to trailing edge. The individual sources are visible, particularly near the leading edge, due to the lower concentration in the boundary layer here. These results also indicate that the microclimatic conditions for organisms that reside within the boundary layer vary considerably across the leaf surface, and preferential positions exist for some of them, e.g. away from leaf edges and in the proximity of stomata.
Fig. 9.
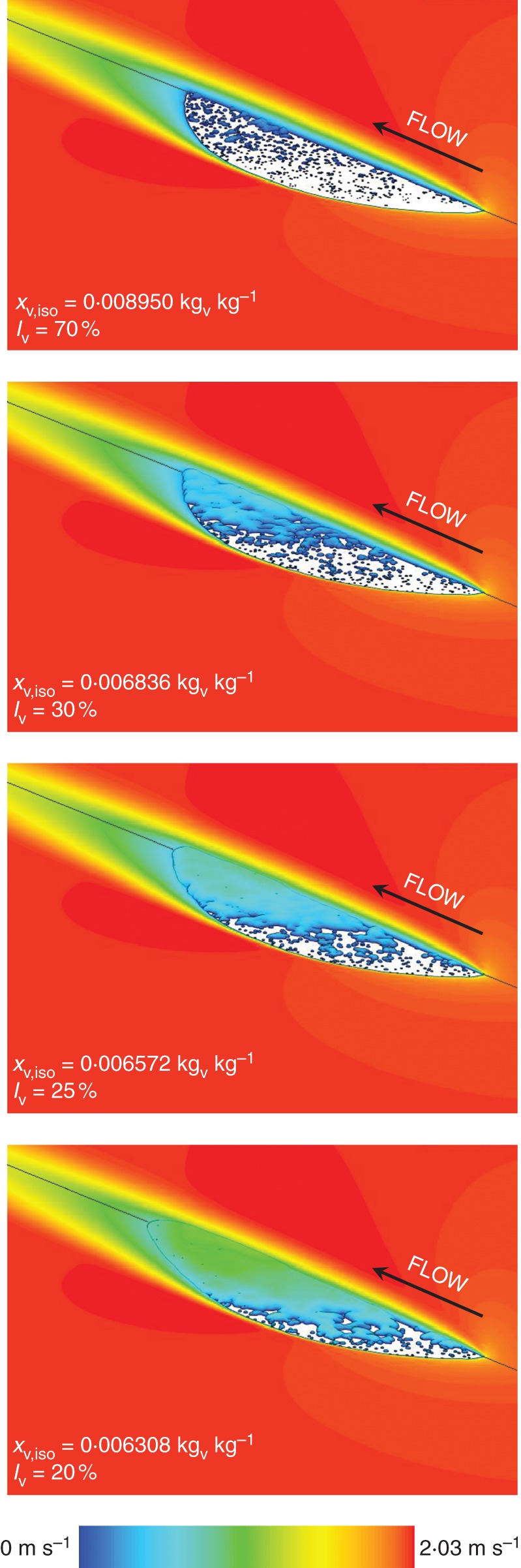
Typical water vapour concentration isocontours (i.e. of constant xv) in the boundary layer above the leaf surface for Ub = 2 m s−1 at a CR of 1 %. The dimensionless isocontour value (Iv) is also given. These isocontours are coloured according to air speed. One isocontour is shown per image. In addition, air speeds in a horizontal and vertical centreplane are also shown. The cross-section between these planes is indicated by the black line. The white area indicates the leaf surface. The colour scale includes the entire air speed range.
In Fig. 10, similar isocontours are shown (Ub = 2 m s−1), coloured according to air speed. Here, results at four different CRs are presented. For each CR, an arbitrary isocontour value (Iv) was chosen in such a way that the vapour boundary-layer thickness was roughly similar, so differences in the boundary-layer structure and development could be identified. The structure of the vapour boundary layer is clearly much more homogeneous at high CRs. The numerical approach used in this study made such detailed analysis of the boundary-layer microclimate possible, which is virtually not feasible experimentally, due to the small scale and related accessibility issues with respect to sensors to measure humidity concentrations very close to the leaf surface. The resulting (quantitative) visualizations (Figs 9 and 10) are thus one of the main merits of modelling, compared with experiments.
Fig. 10.

Water vapour concentration isocontours (i.e. of constant xv) in the boundary layer above the leaf surface for Ub = 2 m s−1 at different CRs (0·25, 1, 5 and 10 %). The dimensionless isocontour value (IV) is also given. These isocontours are coloured according to air speed. One isocontour is shown per image. In addition, air speeds in a horizontal and vertical centreplane are also shown. The cross-section between these planes is indicated by the black line. The white area indicates the leaf surface. The colour scale includes the entire air speed range.
DISCUSSION
An important step was taken in this study towards a better understanding of leaf transpiration via the boundary layer through cross-scale modelling, by explicitly including individual stomata. The findings of the present study can easily be transferred to BLCs of other scalars, such as CO2, but also to evaporation of microscopic droplets on leaf surfaces (see Defraeye et al., 2013a).
The developed numerical model allows us to study the transport mechanisms involved, but is still simplified in some aspects (e.g. a flat, smooth leaf surface). Future model developments are briefly listed below.
(1) Convective transfer in the boundary layer was not coupled to transport inside the leaf, i.e. from the mesophyll cells (RH ≈ 100 %) via the intercellular spaces through the stomata to the leaf surface. To quantify the actual transpiration rate, these resistances should also be accounted for in the model. In addition, this would allow us also to assess boundary-layer interference between stomata, i.e. the impact of stomatal transpiration on the concentration at the surface of the stomata further downstream (Cannon et al., 1979). In the present study, however, the surface concentration at the sources was taken to be constant (see ‘Boundary conditions for air flow’). Furthermore, the mass transport inside the leaf should also be coupled to heat transfer since the latent heat effect has a large impact on leaf temperature as transpiration cools the leaf. Modelling both heat or mass transport inside the leaf and in the air is called conjugate modelling, and has been shown to increase accuracy for convective exchange predictions (Defraeye et al., 2012).
(2) The geometric model of the leaf can be made more realistic to include leaf curvature and surface roughness (veins, hairs, lobes, guard cells of stomata).
(3) Mixed and natural convective flows can be considered, driven also by air density differences caused by variations in air temperature and moisture content. Such (partially) buoyancy-driven flows are particularly important as then the BLC is rather low, due to low air speeds, implying a large impact of the BLC on the transpiration rate, next to that of the stomatal aperture, and because for these conditions leaves are more prone to be under stress (less convective cooling) and lethal leaf temperatures can occur.
(4) More realistic environmental boundary conditions can be applied to mimic field conditions, such as atmospheric (high-turbulent) approach flow and strong solar radiation.
(5) Leaf flutter occurs in reality but implies modelling fluid–structure interactions, which would increase the computational cost tremendously.
The cross-scale modelling approach used in the present study implied that all scales from leaf level down to stomatal scale were explicitly included in the computational model. Such an approach was possible given that only one small leaf was considered. Even in this case, the computational model for half a leaf was extensive, i.e. approaching 6 million cells, and creating a high-quality mesh was very challenging. Including details at a lower scale (e.g. hairs, guard cells of stomata) by downscaling even more is considered too computationally demanding at present. When downscaling, modelling only a part of the leaf with a limited amount of stomata is advised (e.g. Roth-Nebelsick et al., 2009). Furthermore, upscaling the current cross-scale model to an entire plant, let alone a plant canopy, is also not feasible. Thus, complementary to cross-scale modelling, future research efforts should also be directed towards a multiscale modelling approach (Ho et al., 2011, 2012). For leaf transpiration, such a multiscale approach would imply calculating convective transfer at different scales, by separate simulations, and linking the information from the smaller scales to the higher scales to increase accuracy of higher scale models. The inherent problem of coupling between the scales remains, however, and should be explored in detail.
The developed numerical modelling approach has several distinct advantages for studying convective exchange processes, by which it complements experimental research on transpiration. First, a detailed analysis of the transport in the boundary layer is possible down to the stomatal level (microscale, see Figs 9 and 10). Such information on the boundary-layer microclimate could prove useful, amongst others, to study this microhabitat for organisms such as insects (e.g. whitefly), bacterial and fungal pathogens (Boulard et al., 2002; Vidal et al., 2003), or bioinsecticides (Fargues et al., 2005; Roy et al., 2008). This can help to identify more favourable positions for development and growth of such organisms as the microclimatic conditions (temperature and relative humidity) very close to the surface are known, even around individual stomata. Second, modelling could help in improving the accuracy of (existing) BLC predictions. Previous laboratory experiments in wind tunnels on artificial leaves and numerical simulations with CFD applied predominantly homogeneous (uniform) boundary conditions for simplicity (Defraeye et al., 2013a; e.g. uniform vapour pressure, CR = 100 %, e.g. full-wet leaf model, see Fig. 5). Such homogeneous conditions are, however, not realistic for leaf transpiration as transport only occurs via microscopic stomata, which are distributed heterogeneously over the leaf surface at very low CRs. The present modelling study provides relationships between CR, source size (d) and air speed (δVSL). Such relationships may be used to correct some of the existing correlations by including stomatal size, aperture or surface density. This can easily be achieved by using the relationships in Fig. 6, which quantify the BLC at a specific CR as a function of the BLC at a CR of 100 %, for which several existing correlations, i.e. of BLC with air speed, are available. Third, implementing BLC relationships that include stomatal information (e.g. size) in numerical leaf/plant/tree/canopy models for plant–atmosphere interactions (e.g. Dauzat et al., 2001; Tanaka, 2002; Tanaka et al., 2002; Hiraoka, 2005; Maricle et al., 2007) can improve the accuracy of such models, as stomatal aperture is a critical model parameter in these models. To date, the BLC is taken only as a function of air speed, but not as a function of stomatal parameters. The general applicability of such relationships should be verified however, for example with respect to wind direction or inter-leaf interference, prior to feeding them into higher-scale models. The present results also allow us to incorporate and quantify the impact of small variations in stomatal surface density between individual leaves in a tree or plant, on the BLC of these leaves, as a large impact of small variations in CR on BLC was identified.
To conclude, the innovative cross-scale modelling approach presented here shows promising perspectives to increase our understanding of transpiration at sub-leaf level, with respect to the influence of stomatal size, aperture and density but also the flow field (e.g. air speed, turbulence), edge effects and the boundary-layer microclimate. Such analysis is currently not considered to be feasible experimentally. This is the first time that such a cross-scale modelling approach has been applied for an entire leaf in 3-D for realistic stomatal surface coverages. The present study identified, amongst others, a strong dependency of BLC on stomatal surface coverage and air speed as well as significant differences between BLCs obtained by assuming actual heterogeneous coverage of the leaf surface by stomata with those assuming homogeneous boundary conditions at the leaf surface (CR = 100 %).
SUPPLEMENTARY DATA
ACKNOWLEDGEMENTS
T.D. is a postdoctoral fellow of the Research Foundation – Flanders (FWO) and acknowledges its support. This work was supported by the Research Foundation – Flanders (grant no. FWO-12C9712N to T.D.).
LITERATURE CITED
- ANSYS Fluent 13. Ansys Fluent 13·0 User's Guide & Theory Guide. Canonsburg, PA: Ansys Inc; 2010. [Google Scholar]
- Bauerle WL, Bowden JD. Predicting transpiration response to climate change: insights on physiological and morphological interactions that modulate water exchange from leaves to canopies. HortScience. 2011a;46:163–166. [Google Scholar]
- Bauerle WL, Bowden JD. Separating foliar physiology from morphology reveals the relative roles of vertically structured transpiration factors within red maple crowns and limitations of larger scale models. Journal of Experimental Botany. 2011b;62:4295–4307. doi: 10.1093/jxb/err156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergmann D. Stomatal development: from neighborly to global communication. Current Opinion in Plant Biology. 2006;9:478–483. doi: 10.1016/j.pbi.2006.07.001. [DOI] [PubMed] [Google Scholar]
- Berry JA, Beerling DJ, Franks PJ. Stomata: key players in the earth system, past and present. Current Opinion in Plant Biology. 2010;13:233–240. doi: 10.1016/j.pbi.2010.04.013. [DOI] [PubMed] [Google Scholar]
- Boulard T, Mermier M, Fargues J, Smits N, Rougier M, Roy JC. Tomato leaf boundary layer climate: implications for microbiological whitefly control in greenhouses. Agricultural and Forest Meteorology. 2002;110:159–176. [Google Scholar]
- Boulard T, Fatnassi H, Roy JC, et al. Effect of greenhouse ventilation on humidity of inside air and in leaf boundary-layer. Agricultural and Forest Meteorology. 2004;125:225–239. [Google Scholar]
- Cannon JN, Krantz WB, Kreith F, Naot D. A study of transpiration from porous flat plates simulating plant leaves. International Journal of Heat and Mass Transfer. 1979;22:469–483. [Google Scholar]
- Cebeci T, Bradshaw P. Physical and computational aspects of convective heat transfer. 1st edn. New York: Springer; 1984. [Google Scholar]
- Daudet FA, Silvestre J, Ferreira MI, Valancogne C, Pradelle F. Leaf boundary layer conductance in a vineyard in Portugal. Agricultural and Forest Meteorology. 1998;89:255–267. [Google Scholar]
- Dauzat J, Rapidel B, Berger A. Simulation of leaf transpiration and sap flow in virtual plants: model description and application to a coffee plantation in Costa Rica. Agricultural and Forest Meteorology. 2001;109:143–160. [Google Scholar]
- Defraeye T, Blocken B, Koninckx E, Hespel P, Carmeliet J. Computational fluid dynamics analysis of cyclist aerodynamics: performance of different turbulence-modelling and boundary-layer modelling approaches. Journal of Biomechanics. 2010a;43:2281–2287. doi: 10.1016/j.jbiomech.2010.04.038. [DOI] [PubMed] [Google Scholar]
- Defraeye T, Blocken B, Carmeliet J. CFD analysis of convective heat transfer at the surfaces of a cube immersed in a turbulent boundary layer. International Journal of Heat and Mass Transfer. 2010b;53:297–308. [Google Scholar]
- Defraeye T, Herremans E, Verboven P, Carmeliet J, Nicolai B. Convective heat and mass exchange at surfaces of horticultural products: a microscale CFD modelling approach. Agricultural and Forest Meteorology162–163. 2012:71–84. [Google Scholar]
- Defraeye T, Verboven P, Derome D, Carmeliet J, Nicolai B. Stomatal transpiration and droplet evaporation on leaf surfaces by a microscale modelling approach. International Journal of Heat and Mass Transfer. 2013a;65:180–191. [Google Scholar]
- Defraeye T, Verboven P, Ho QT, Nicolai B. Convective heat and mass exchange predictions at leaf surfaces: applications, methods and perspectives. Computers and Electronics in Agriculture. 2013b;96:180–201. [Google Scholar]
- DeJong TM, Da Silva D, Vos J, Escobar-Gutiérrez AJ. Using functional–structural plant models to study, understand and integrate plant development and ecophysiology. Annals of Botany. 2011;108:987–989. doi: 10.1093/aob/mcr257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckerson SH. The number and size of the stomata. Botanical Gazette. 1908;46:221–224. [Google Scholar]
- Fargues J, Smits N, Rougier M, et al. Effect of microclimate heterogeneity and ventilation system on enthomopathogenic hyphomycetes infection of Trialeurodes vaporariorum (Homoptera: Aleyrodidae) in Mediterranean greenhouse tomato. Biological Control. 2005;32:461–472. [Google Scholar]
- Franke J, Hellsten A, Schlünzen H, Carissimo B. Best practice guideline for the CFD simulation of flows in the urban environment. 2007 Hamburg: COST Action 732: Quality assurance and improvement of microscale meteorological models. [Google Scholar]
- Gurevitch J, Schuepp PH. Boundary layer properties of highly dissected leaves: an investigation using an electrochemical fluid tunnel. Plant Cell and Environment. 1990;13:783–792. [Google Scholar]
- Gromke C. A vegetation modeling concept for building and environmental aerodynamics wind tunnel tests and its application in pollutant dispersion studies. Environmental Pollution. 2011;159:2094–2099. doi: 10.1016/j.envpol.2010.11.012. [DOI] [PubMed] [Google Scholar]
- Henderson-Sellers A, Irannejad P, McGuffie K. Future desertification and climate change: the need for land-surface system evaluation improvement. Global and Planetary Change. 2008;64:129–138. [Google Scholar]
- Hiraoka H. An investigation of the effect of environmental factors on the budgets of heat, water vapor, and carbon dioxide within a tree. Energy. 2005;30:281–298. [Google Scholar]
- Ho QT, Verboven P, Verlinden BE, et al. A 3-D multiscale model for gas exchange in fruit. Plant Physiology. 2011;155:1158–1168. doi: 10.1104/pp.110.169391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ho QT, Carmeliet J, Datta AK, et al. Multiscale modeling in food engineering. Journal of Food Engineering. 2012;114:279–291. [Google Scholar]
- Jones HG. Plants and microclimate: a quantitative approach to environmental plant physiology. 2nd edn. New York: Cambridge University Press; 1992. [Google Scholar]
- Lake JA, Woodward FI. Response of stomatal numbers to CO2 and humidity: control by transpiration rate and abscisic acid. New Phytologist. 2008;179:397–404. doi: 10.1111/j.1469-8137.2008.02485.x. [DOI] [PubMed] [Google Scholar]
- Launder BE, Spalding DB. The numerical computation of turbulent flows. Computer Methods in Applied Mechanics and Engineering. 1974;3:269–289. [Google Scholar]
- Leigh A, Sevanto S, Ball MC, et al. Do thick leaves avoid thermal damage in critically low wind speeds. New Phytologist. 2012;194:477–487. doi: 10.1111/j.1469-8137.2012.04058.x. [DOI] [PubMed] [Google Scholar]
- Lienhard JH, IV, Lienhard JH., V . A heat transfer textbook. 3rd edn. Cambridge, MA: Phlogiston Press; 2006. [Google Scholar]
- Maricle BR, Cobos DR, Campbell CS. Biophysical and morphological leaf adaptations to drought and salinity in salt marsh grasses. Environmental and Experimental Botany. 2007;60:458–467. [Google Scholar]
- Menter FR. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA Journal. 1994;32:1598–1605. [Google Scholar]
- Mott KA, Buckley TN. Patchy stomatal conductance: emergent collective behaviour of stomata. Trends in Plant Science. 2000;5:258–262. doi: 10.1016/s1360-1385(00)01648-4. [DOI] [PubMed] [Google Scholar]
- Nobel PS. Physicochemical and environmental plant physiology. 3rd edn. London: Elsevier Academic Press; 2005. [Google Scholar]
- Picotte JJ, Rosenthal DM, Rhode JM, Cruzan MB. Plastic responses to temporal variation in moisture availability: consequences for water use efficiency and plant performance. Oecologia. 2007;153:821–832. doi: 10.1007/s00442-007-0794-z. [DOI] [PubMed] [Google Scholar]
- Rijsberman FR. Water scarcity: fact or fiction? Agricultural Water Management. 2006;80:5–22. [Google Scholar]
- Roache PJ. Perspective: a method for uniform reporting of grid refinement studies. Transactions of the ASME: Journal of Fluids Engineering. 1994;116:405–413. [Google Scholar]
- Roth-Nebelsick A. Computer-based analysis of steady-state and transient heat transfer of small-sized leaves by free and mixed convection. Plant Cell and Environment. 2001;24:631–640. [Google Scholar]
- Roth-Nebelsick A. Computer-based studies of diffusion through stomata of different architecture. Annals of Botany. 2007;100:23–32. doi: 10.1093/aob/mcm075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roth-Nebelsick A, Hassiotou F, Veneklaas EJ. Stomatal crypts have small effects on transpiration: a numerical model analysis. Plant Physiology. 2009;151:2018–2027. doi: 10.1104/pp.109.146969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy JC, Boulard T, Kittas C, Wang S. PA—Precision Agriculture: convective and ventilation transfers in greenhouses, Part 1: the greenhouse considered as a perfectly stirred tank. Biosystems Engineering. 2002;83:1–20. [Google Scholar]
- Roy JC, Vidal C, Fargues J, Boulard T. CFD based determination of temperature and humidity at leaf surface. Computers and Electronics in Agriculture. 2008;61:201–212. [Google Scholar]
- Santamouris M. Cooling the cities – A review of reflective and green roof mitigation technologies to fight heat island and improve comfort in urban environments. Solar Energy. 2013 in press. doi:10.1016/j.solener.2012.07.003. [Google Scholar]
- Saudreau M, Marquier A, Adam B, Sinoquet H. Modelling fruit-temperature dynamics within apple tree crowns using virtual plants. Annals of Botany. 2011;108:1111–1120. doi: 10.1093/aob/mcr054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlünder EU. On the mechanism of the constant drying rate period and its relevance to diffusion controlled catalytic gas phase reactions. Chemical Engineering Science. 1988;43:2685–2688. [Google Scholar]
- Schuepp PH. Tansley Review No. 59: Leaf boundary layers. New Phytologist. 1993;125:477–507. doi: 10.1111/j.1469-8137.1993.tb03898.x. [DOI] [PubMed] [Google Scholar]
- Shibuya T, Tsuruyama J, Kitaya Y, Kiyota M. Enhancement of photosynthesis and growth of tomato seedlings by forced ventilation within the canopy. Scientia Horticulturae. 2006;109:218–222. [Google Scholar]
- Smith DM, Jarvis PG. Physiological and environmental control of transpiration by trees in windbreaks. Forest Ecology and Management. 1998;105:159–173. [Google Scholar]
- Smith DM, Jarvis PG, Odongo JCW. Energy budgets of windbreak canopies in the Sahel. Agricultural and Forest Meteorology. 1997;86:33–49. [Google Scholar]
- Stokes VJ, Morecroft MD, Morison JIL. Boundary layer conductance for contrasting leaf shapes in a deciduous broadleaved forest canopy. Agricultural and Forest Meteorology. 2006;139:40–54. [Google Scholar]
- Tanaka K. Multi-layer model of CO2 exchange in a plant community coupled with the water budget of leaf surfaces. Ecological Modelling. 2002;147:85–104. [Google Scholar]
- Tanaka K, Kosugi Y, Nakamura A. Impact of leaf physiological characteristics on seasonal variation in CO2, latent and sensible heat exchanges over a tree plantation. Agricultural and Forest Meteorology. 2002;114:103–122. [Google Scholar]
- Vidal C, Fargues J, Rougier M, Smits N. Effect of air humidity on the infection potential of Hyphomycetous fungi as mycoinsecticides for Trialeurodes vaporariorum. Biocontrol Science and Technology. 2003;13:183–198. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.