Simulation of the evolution of root water foraging strategies in dry and shallow soils

Abstract

Background and Aims

The dynamic structural development of plants can be seen as a strategy for exploiting the limited resources available within their environment, and we would expect that evolution would lead to efficient strategies that reduce costs while maximizing resource acquisition. In particular, perennial species endemic to habitats with shallow soils in seasonally dry environments have been shown to have a specialized root system morphology that may enhance access to water resources in the underlying rock. This study aimed to explore these hypotheses by applying evolutionary algorithms to a functional–structural root growth model.

Methods

A simulation model of a plant's root system was developed, which represents the dynamics of water uptake and structural growth. The model is simple enough for evolutionary optimization to be computationally feasible, yet flexible enough to allow a range of structural development strategies to be explored. The model was combined with an evolutionary algorithm in order to investigate a case study habitat with a highly heterogeneous distribution of resources, both spatially and temporally – the situation of perennial plants occurring on shallow soils in seasonally dry environments. Evolution was simulated under two contrasting fitness criteria: (1) the ability to find wet cracks in underlying rock, and (2) maximizing above-ground biomass.

Key Results

The novel approach successfully resulted in the evolution of more efficient structural development strategies for both fitness criteria. Different rooting strategies evolved when different criteria were applied, and each evolved strategy made ecological sense in terms of the corresponding fitness criterion. Evolution selected for root system morphologies which matched those of real species from corresponding habitats.

Conclusions

Specialized root morphology with deeper rather than shallower lateral branching enhances access to water resources in underlying rock. More generally, the approach provides insights into both evolutionary processes and ecological costs and benefits of different plant growth strategies.

INTRODUCTION

An important function of plant structures, both above- and below-ground, is to acquire the limited resources available in the plant's environment, such as light, nutrients and water. The pattern of structural development of a plant can thus be seen as a strategy for exploiting these resources. The efficacy of different strategies of structural development will depend on the temporal and spatial patterns in the availability of the resources sought by the plant. The efficiency of different strategies of structural development will also depend on the cost of producing and maintaining the structures, along with the way that structure affects water transport, biomechanical support, resistance to wind and herbivory, fertilization and dispersal of pollen and seed (Fitter, 1987; Küppers, 1989; Gartner, 1995). Therefore, to understand why plants have evolved different strategies of structural development, we need to understand the various costs and benefits of different growth strategies, and how these depend on resource distribution through time and space (Farnsworth and Niklas, 1995; Lynch, 1995).

Modelling has been extensively used to address questions about the costs, benefits and optimality of both above- and below-ground plant structures, by allowing the costs and benefits of different plant structures to be quantified in different ways and at different levels of detail (e.g. Shinozaki et al., 1964; Honda and Fisher, 1979; Johnson and Thornley, 1987; Niklas, 1999; West et al., 1999; Schwinning and Ehleringer, 2001; Takenaka et al., 2001; Van Wijk and Bouten, 2001; Zhi et al., 2001; Falster and Westoby, 2003; King et al., 2003). However, the modelling used to investigate the optimality of plant structures has often ignored at least some of the following aspects: the explicit spatial geometry of the plant structure; the dynamic ontogeny of plant structural development; dynamic feedbacks between plant structure, function and environment; spatial and temporal heterogeneity in the distribution of resources within a plant's environment; and competition between individuals.

Functional–structural plant models (FSPMs) or ‘virtual plants’ represent the interaction between a plant's structure, the processes occurring within that structure and the surrounding environment (Sievänen et al., 2000; Prusinkiewicz, 2004; Yan et al., 2004; Godin and Sinoquet, 2005; Fourcaud et al., 2008; Hanan and Prusinkiewicz, 2008; Vos et al., 2010). FSPMs usually represent the dynamic development of the plant structure with explicit topology and geometry, as well as the dynamic processes occurring within and between the structure and its environment. The interactions between functional processes and structural development can be represented at a detailed mechanistic level (Allen et al., 2005; Costes et al., 2008; Lopez et al., 2008), or in simpler more empirical ways (Renton et al., 2005a, b, 2007). Moreover, FSPMs usually represent the dynamic feedbacks between function and structure; for example, as more roots are added, more water may be taken up, more photosynthesis occurs, more biomass is added and the root structure extends. Furthermore, because they are dynamic and spatially explicit, they can account for spatial and temporal heterogeneity in resource distribution and competition. Models that could be described as FSPMs have been used to explore costs and benefits of different structures and growth strategies both above and below ground (e.g. Pearcy and Yang, 1996; Colasanti and Hunt, 1997; Dunbabin et al., 2003; Pearcy et al., 2005; Sterck et al., 2005; Clark and Bullock, 2010; Pagès, 2011). However, because of their relative complexity, large number of parameters and dynamic nature, exploring all possible parameter combinations to identify optimal growth strategies is a computational challenge. Thus, these studies have mostly been limited to evaluating a number of specific strategies.

Evolutionary optimization algorithms (Fogel, 1994; Ashlock, 2006) provide a potential means of addressing this challenge by exploring the range of possibilities in search of optimal solutions in a computationally efficient way, and linking evolutionary algorithms with FSPMs would also seem to be an ideal way to analyse optimal plant design from an evolutionary perspective and gain insights into the relationships between genes, individual plants, ecosystems and evolution (Prusinkiewicz, 2000). Evolutionary algorithms and plant structural models have been used to simulate the evolution of above-ground plant form based on aesthetic criteria (McCormack, 1993, 2004; Jacob, 1994; Traxler and Gervautz, 1996), and explore multicriteria fitness landscapes (Niklas, 1994, 1999). More recently the combination has been used for addressing questions of ecological theory and above-ground plant competition at the level of individual plants and plant populations, at a relatively abstract level (Bornhofen and Lattaud, 2006, 2007, 2008, 2009; Kennedy, 2010), and assessment of uncertainty in FSPMs (Ford and Kennedy, 2011). However, to our knowledge, evolutionary algorithms have not been combined with models of below-ground plant structural development and resource acquisition, nor has the combination of evolutionary algorithms and FSPMs been used to explore the effect of heterogeneous resource distribution on optimal structural development.

In this study, we linked a dynamic FSPM with an evolutionary optimization algorithm in order to explore below-ground plant structural optimality. The tool we developed, linking the FSPM to the evolutionary algorithm to represent the evolution of rooting strategies, is referred to as the Tool for Analysis of Root Structures Incorporating Evolution of Rooting Strategies (TARSIERS). We applied TARSIERS to investigate evolution of root structures in a case study habitat with a highly heterogeneous distribution of resources, both spatially and temporally – the situation of perennial plants occurring on shallow soils in seasonally dry environments such as in the Mediterranean climate of south-west Australia. Several species restricted to these types of habitats have been shown to have a specialized root system morphology that has been hypothesized to enhance access to water resources in the underlying rock (Poot and Lambers, 2003a, b, 2008; Poot et al., 2008, 2012). The aim of the study was to explore whether an approach combining evolutionary algorithms and a root FSPM would be able to predict the evolution of these specialized root systems in these particular conditions, and whether this novel approach would provide insights into evolutionary processes regarding plant architecture and the ecological costs and benefits of plant growth strategies.

MATERIALS AND METHODS

Case study

The south-west of Australia is an area of high floral diversity, where plant species have evolved a wide range of ecological strategies to cope with a variety of different climates and environments. One of the harshest situations is faced by perennial plants that grow in shallow soil overlying rocky hills and ridges (e.g. Mishio, 1992; Groom and Lamont, 1995). In the Mediterranean climate of this region, these plants usually germinate during the wet winter but then face a long summer drought in shallow soils that have very limited capacity to hold and provide water.

In this region, as well as many others throughout the world, plant species that are found in these harsh, shallow-soil, rocky habitats tend to be restricted to these environments (Kruckeburg and Rabinowitz, 1985; Baskin and Baskin, 1988; Médial and Verlaque, 1997; Porembski and Barthlott, 2000). This would suggest that these species have evolved specializations that enable them to persist in these environments, but limit their ability to survive and reproduce successfully in other nearby habitats. A number of hypotheses have been formulated regarding the specialization driving this restriction, with experimental work suggesting that shade intolerance is the most likely hypothesis to date (Baskin and Baskin, 1988; Lavergne et al., 2004). However, a recent study argues that the strong habitat specificity of many shallow-soil endemics is related to the degree of below-ground specialization that is needed to establish and survive in these relatively extreme habitats, and the incompatibility of these adaptations with deeper soil environments (Poot et al., 2012). This specialization is likely to be particularly marked for perennial species in shallow soils with limited water-holding capacity in seasonally dry or otherwise water-limited environments.

This argument is based on the fact that there is growing evidence that, during the dry season, water held within the underlying bedrock is essential for meeting the transpiration demands of shrubs and trees (Rose et al., 2003; Querejeta et al., 2007). Therefore, obtaining root or mycorrhizal (Bornyasz et al., 2005) access to the water stored in the weathered bedrock via cracks, fissures and micropores is probably essential for the survival of many rock endemics. Indeed there is ample evidence of roots of woody species growing through the bedrock (Zwieniecki and Newton, 1994, 1995; Witty et al., 2003; Bornyasz et al., 2005; Schenk, 2008).

Previous research has shown that species endemic to shallow-soil ironstone communities in south-west Australia have a specialized root morphology that enhances their chance to access fissures in the underlying rock (Poot and Lambers, 2003a, b, 2008; Poot et al., 2008). This has been corroborated by seedling transplant studies in these communities which showed that the shallow-soil endemics had much higher survival rates than common congeners (Poot and Lambers, 2008). A more recent study tested the generality of these findings for species that are confined to a shallow-soil habitat that is of much greater global significance: granite outcrops (Poot et al., 2012). These studies showed that the shallow-soil endemics mostly differed in a predictable way from their congeners from deeper soils; they generally invested a larger portion of their biomass in roots, and distributed their roots more rapidly and more evenly over the container. Interestingly, the shallow-soil specialists achieved their apparent advantage by a different combination of the aforementioned traits. These results provide a possible explanation for the narrow endemism of many shallow-soil endemics because their root system traits seem to be adaptive in their own shallow-soil habitat in terms of obtaining access to fissures and water in the underlying rock, but are likely to be maladaptive in deeper soils.

Description of functional–structural plant model

Overview

Our TARSIERS tool is based on a functional–structural computational simulation model that aims to capture the important processes involved in the growth and development of root structures in a range of situations where water is the key limiting resource. The model was motivated by the experimental studies described above, but was constructed with the intention that it would form the basis of a flexible tool that could address questions about optimal structural rooting strategies in other conditions and plant species as well. An important requirement of the model was that it be flexible enough to allow a wide range of strategies to be represented and explored, but simple enough that the application of an evolutionary optimization algorithm would be computationally feasible. The model runs on a daily time step and simulates the growth of a single plant's root structure through the soil following germination at the start of a seasonal wet rainy period through to the start of a seasonal dry drought period. The model is implemented in the R programming language (R Development Core Team, 2013) and is freely available on request to the authors. For simplicity, only the primary and secondary roots are represented, since we assume that these are the most important in defining the overall architecture of the root system and its access to water, during both the initial wet period and the subsequent drought period. Shoot and fine roots are represented non-geometrically. An earlier version of the model is described in Renton et al. (2012), but the model was subsequently improved on the basis of further testing; here we present a full description of the updated model. The overall dynamics of the model are summarized and different aspects of the model illustrated in Fig. 1, and Fig. 2 provides an illustration of how the simulated structure develops over time.

Fig. 1.

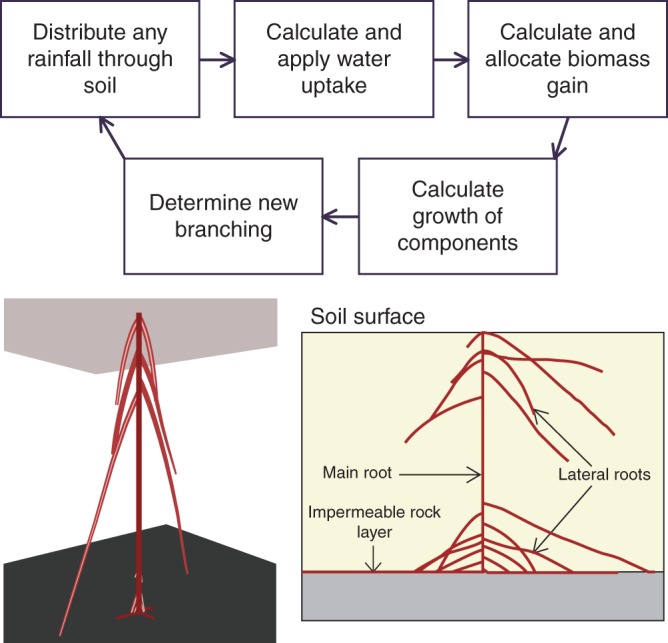
General features of the TARSIERS functional–structural model. Processes of water uptake and growth are simulated on a daily time step (top) leading to the dynamic emergence of a three-dimensional root structure that is usually represented in two dimensions for convenience (bottom).

Fig. 2.

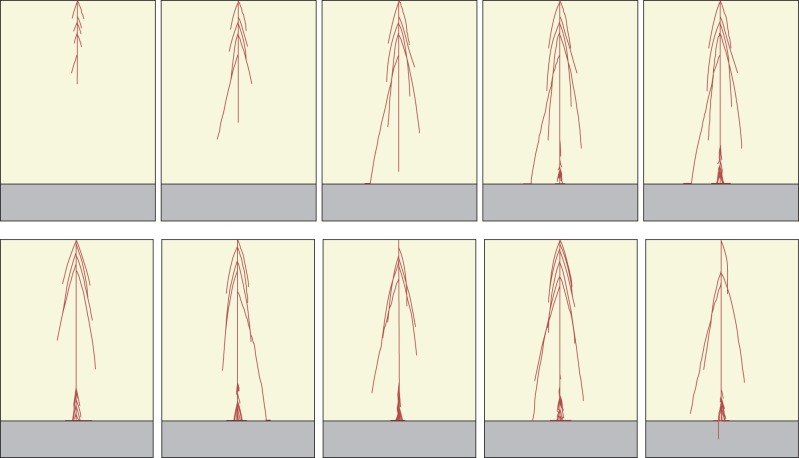
Phenotypic root structure realizations of the single TARSIERS genotype that was used as the starting point to generate the initial population for each of the four evolutionary runs. The top row shows selected ‘snapshots’ from a time series of one realization of a root structure generated from this genotype developing over the full wet season growing period (after day 36, 72, 108, 144 and 180, respectively). The bottom row shows different phenotypic root structure realizations generated from the same genotype, all at the end of the growing period only (day 180). Note that one single genotype can produce different phenotypes; in these examples, just one of the six illustrated phenotypic realizations of the one genotype has successfully found a wet crack (the final one at bottom right). Soil depth is 25 cm in all cases.

The model contains a number of parameters that define various characteristics of the soil, water uptake and biomass, and others that determine the dynamic development of root architecture and thus control the plant's rooting strategy (Tables 1 and 2). The parameters in Table 1 define various characteristics of the rainfall, soil, water uptake and biomass, and are known as fixed parameters, since they are assumed to be fixed for a particular environment. The parameters in Table 2 control how the root structure develops over time and are known as the strategy parameters, since they define the plant's growth strategy. Strategy parameters are fixed for the lifetime of an individual plant, but can evolve over multiple generations.

Table 1.

Fixed parameters: model parameters determining characteristics of soil, water uptake and biomass, with description, units (where relevant) and the value used in this study; these parameters are kept fixed during evolutionary simulations

Model parameter	Description*	Units	Value
dsoil	Soil depth	mm	250
cwater	The volume of water that can be held in a cubic millimetre of soil that is available for uptake by the roots	mm3	0·1
pwc	Probability of a given voxel at the top of the impermeable layer containing the entrance to a wet crack		0·005
umax	Maximum water uptake per root length	mm3 d−1 mm−1	10
etrans	Water transport efficiency of roots per cross-sectional root area	mm3 d−1 mm−2	0·002
kbm	Root biomass per volume	g mm−3	0·001
econ	Water to biomass conversion efficiency	g mm−3	0·00001
lwatervoxel	Edge length of cubic voxels used for water calculations	mm	25
tsim	Time represented in simulation, i.e. the length of the wet growing season	days	180
dwu	Implementation parameter controlling resolution of water uptake calculation	mm	0·5
Pmroot	Potential main root elongation rate	mm d−1	5

*Further details in text.

Table 2.

Strategy parameters: model parameters determining dynamic development of root structure, with description, units (where relevant) and the value used in this study to define the base genotype from which the initial population is generated; these parameters ‘evolve’ during evolutionary simulations

Model parameter	Description*	Units	Value
wt0	The initial lateral root growth weighting	–	0·1
wtΔ	The rate at which the lateral root growth weighting changes down the main root	–	0·05
wtvar	The random variability in lateral root growth weighting	–	0·001
θgr	Gravitropism parameter	–	0·99
θvar	Variability in vertical growth direction	radians	0·02
pdownmax, bdown, adown	Parameters determining probability of normal lateral root branching	See text	0·5; –0·1; 50
delay	Delay before lateral branching begins	days	10
pupmax, bup, aup	Parameters determining probability of lateral root branching triggered by main root encountering impermeable layer	See text	0·8; –0·1; 50
θbranch	Branching angle of lateral roots	radians	π/4
φph	Phyllotactic angle	radians	π/2
pshbmb, pshbma	Proportion of biomass allocated to shoot before/after a wet crack is encountered	–	0·1; 0·1

*Further details in text.

Soil and rainfall

The soil is represented as a three-dimensional grid of cubic voxels. Each voxel is defined to be either soil with a fixed available water-holding capacity, or impermeable rock, into which roots and water cannot penetrate. In a typical simple case, we could define the soil to be of a fixed depth d_soil, with all voxels less than this depth having an available fixed water-holding capacity c_water, and all voxels greater than this depth being impermeable (Fig. 1). This corresponds to a situation where there are no cracks in the underlying rock layer. In case we wish to simulate cracks, as we do in this study, we define some of the voxels at the top of the impermeable layer to be the entrance to cracks. For this study, these voxels are chosen at random with a frequency p_wc (Table 1). These are treated differently in the simulation from other soil voxels, as explained later. The edge length of the voxels is defined by the model parameter l_watervoxel which approximates the distance through the soil over which water is accessible to a root (Table 1; more details in Supplementary Data 1). For this study, we assumed a relatively simple rainfall pattern, where rainfall occurs once every 2 weeks during the simulated rainy period, starting on day 1, and that the amount of rainfall is sufficient to fill the shallow soil profile completely and replenish any cracks in the underlying rock.

Water uptake

We assume that through its associated finer root structures, each unit length of main or lateral root has the potential to take up the same amount of water, determined by the parameter u_max (Table 1). The assumption that finer root structures emerge uniformly along the major roots may be reasonable, given that we only simulate the first few months of the plant's growth, in a period where soil moisture is relatively high and consistent. Roots are able to access the water within the voxel in which they are located, and no other voxel's water. Roots take up water at their maximum potential rate until the total water available in the voxel falls to zero. Roots within a wet crack always take up water at the maximum rate. This may be a reasonable assumption during the simulated period of the wet season where there is regular rain and replenishment of water stored in rock cracks. For details of the algorithm used to calculate water uptake, see Supplementary Data 1.

Root and shoot growth

The total possible biomass growth of the plant for the day is simply the total water taken up, multiplied by the conversion efficiency parameter e_con (Table 1). This is first allocated between root and shoot according to the strategy parameters p_shbmb and p_shbma (Table 2). The shoot is simulated only as a single biomass pool with no structure. If a wet crack has not yet been encountered by the plant, then the proportion allocated to the shoot is p_shbmb; if it has, then the proportion is p_shbma. The remainder is allocated to the roots according to the relative growth weightings of the different roots, defined when they are created, as explained below in the ‘Branching’ section. The proportion allocated to a particular root is simply its own relative growth weighting divided by the sum of the relative growth weightings for all roots (main root and all laterals). The length increment of each root is then calculated based on the assumption that the ‘cost’ of constructing a root is proportional to the square of its length. This assumption correspond to da Vinci's rule and the pipe model commonly used in tree modelling (Shinozaki, 1964; Mandelbrot, 1983; Zimmerman, 1983; Prusinkiewicz and Lindenmayer, 1990) and ensures that roots grow faster when the plant is taking up more water, and that longer roots cost proportionally more than shorter roots due to their need to transport greater volumes of water (for details, see Supplementary Data 2). The direction of the new segment is calculated as follows. Every root has a current heading direction, defined by a vertical angle θ and a horizontal angle φ. When θ = 0 the root is heading directly down, and when θ = 90 ° the root is heading horizontally. The heading direction of the main root is always directly down (θ = φ = 0), unless it has hit an impermeable voxel, in which case it behaves like a lateral, as described below. The direction of a new lateral root segment is based on the current heading direction, with some stochastic variability, plus some gravitropism. The new vertical angle θ of the heading angle is the current vertical angle multiplied by a random variable drawn from a normally distributed distribution with mean of θ_gr and standard deviation θ_var, where θ_gr is a strategy parameter that determines the degree of gravitropism and θ_var is a strategy parameter that determines the stochastic variability in the vertical dimension (Table 2).

Effects of impermeable layers

When a new root segment is added to the end of the main or lateral root, as described in the previous section, a check is made of whether the segment has passed into an impermeable voxel. If it has, then an adjustment is made to the final position. The end of the new segment is set to be on the impermeable layer. If it is the main root, then it is effectively converted to a horizontally growing lateral, with θ set to zero and φ generated at random. If it is a lateral root, then it is set to grow horizontally (θ is set to zero and φ remains unchanged). If a root segment is found to have passed into a voxel defined to be the entrance of a wet crack then it continues its growth but the direction and spatial position of this growth are no longer simulated, as it is now assumed to be following along the crack.

Branching

Lateral branching may occur at two different times, when the main root is growing vertically down before it encounters an impermeable surface, and when the main root encounters an impermeable surface. The probability of branching during initial growth follows a logistic function of the distance from the top of the main root, and there may be a delay before the lateral starts to grow. The probability of branching after the main root encounters an impermeable surface follows a logistic function of the distance from the point of contact with the impermeable surface, and growth of any laterals produced proceeds immediately. The shape of the logistic curves defining branching probabilities, and the length of delay, are defined by strategy parameters, which allows a wide range of possible branching strategies (Table 2; for details see Supplementary Data 3).

The initial vertical heading angle is set to be θ_branch and its initial horizontal heading angle φ is set to be n × φ_ph, where n is the number of the potential lateral branching point counting down from the top, and φ_ph is a strategy parameter defining the rotational angle, analogous to the phyllotactic angle in leaves and above-ground branches (Table 2).

The main root and each of the lateral roots are also assigned a relative growth weighting when they are created that does not change with time; this represents the sink strength of the root. For the main root, this is set to be equal to 1, while for each lateral root this relative growth weighting is set stochastically at the time that the root is created using the strategy parameters wt₀, wt_Δ and wt_var (Table 2). Specifically, the weight is drawn from a normal distribution with mean equal to wt₀ × exp(wt_Δ × d_down) and standard deviation equal to wt_var times the mean. This relative growth weighting affects the allocation of biomass between roots, as describe above in the ‘Root and shoot growth’ section.

Model outputs

The model produces both graphical and numerical outputs. Graphical outputs enable the effects of the different model parameters determining the dynamic development of the root structure to be visualized using three-dimensional rendering or simpler two-dimensional representations (Figs 1 and 2). Numerical outputs allow some measure of the success of the strategy of the plant. For example, if the plant has not accessed any wet crack entrances by the start of the drought season, then it is deemed to have failed to establish and reproduce. If the plant has accessed a crack, then its relative success could be defined to be the number of cracks accessed or the total shoot biomass achieved, since these are likely to be important determinants of future growth and reproductive output. Other numerical outputs summarize important characteristics of the root structure, including the total root length and maximum radial root distance in different soil layers (Renton et al., 2012).

Evolutionary optimization algorithm

The complete TARSIERS links the model described above with a heuristic evolutionary optimization algorithm (Fogel, 1994) that iterates over a number of steps in each ‘generation’ (Fig. 3). First, values for the fixed parameters in Table 1 are specified; these are assumed to identify hard constraints representing aspects of the environment or plant physiology not able to be altered by evolution. A measure for relative reproductive potential or evolutionary fitness is defined. A population of plants is generated, with each individual plant defined by a set of values for the strategy parameters in Table 2. The growth of each individual over its first seasonal wet period is simulated as described, and the numerical outputs of the model are then used to calculate the relative reproductive potential of the individual, according to the defined measure. The reproductive potential of an individual is thus estimated based on its growth within its first wet season, which is reasonable for perennials in seasonal environments where initial establishment is key to ultimate success, particularly plants that must find a wet crack within that first season in order to survive. Once the plant has accessed a permanent water supply, its ultimate success is almost guaranteed. The first population now becomes the parent population. A new population of plants is then generated, of the same size as the first generation. The parents of each individual in the new population are selected at random from the individuals in the parent population, from a multinomial distribution with weightings equal to the parents' relative reproductive potential. The set of values for the parameters in Table 2 for each individual in the new population is the average of that of its two parents, with a small amount of random noise added to allow evolution to occur (more details below). The new population now becomes the parent population and this process is continued for a set number of populations or until a stopping criterion indicating stabilization of the evolutionary process is achieved. The resulting set of values for the parameters in Table 2 in the final population can then be considered a possible ‘solution’ or optimal ecological strategy given the constraints defined by the parameter values in Table 1. The whole evolutionary simulation can be repeated a number of times, to see whether a similar ‘solution’ is reached each time. It is possible, of course, that in any given evolutionary simulation the population may become extinct (reproductive potential of all individuals in any generation is equal to zero); if this happens repeatedly over many evolutionary simulations, then it may indicate that there is no suitable ecological strategy that achieves a positive reproductive potential with the given model parameter values, or that all individuals in the starting population are too different from any individual with a suitable ecological strategy.

Fig. 3.

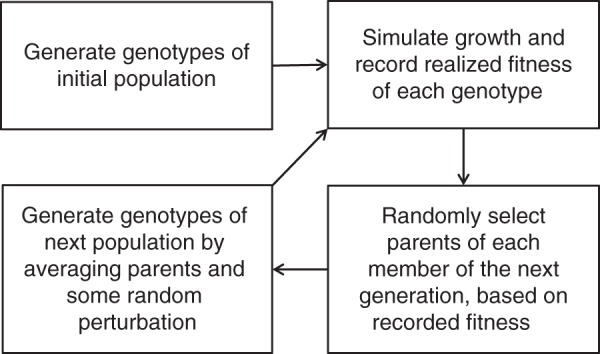
Summary of the steps involved in each iteration or ‘generation’ of the TARSIERS evolutionary algorithm.

The random perturbation to the strategy parameters applied after averaging the values for parents is an important part of the evolutionary algorithm. To ensure that parameter values stay within logical bounds, transformed scales are used. All parameters constrained to lie between 0 and 1, such as probabilities, are represented on a logistic scale, while all parameters constrained to be >0, such as relative growth weightings, are represented on a log scale. In this study, the perturbed value of each new parameter value (on the transformed scale if relevant) was drawn from a random distribution, with mean equal to the unperturbed value (the mean of the parents' values) and a fixed standard deviation. This fixed standard deviation was defined separately for each parameter with the aim of making it approx. 1 % of the range we expected to be a viable possible range for the parameter.

Simulations for this study

To test the TARSIERS approach of linking an FSPM with an evolutionary algorithm, four full evolutionary simulations were conducted. Initial testing based on around 100 generations showed that while evolution appeared to be occurring within this time frame, larger time frames would be needed to explore evolutionary potential more fully. The initial testing also indicated that small population sizes tended to become extinct, but populations of 100 individuals were sufficient to persist across generations and maintain ‘genetic diversity’ to an extent that allowed evolution to occur. Furthermore, the testing indicated that with a population size of 100 individuals, 2000 generations would be able to be conducted within a reasonable time using the computing resources available (several days on a desktop PC with six cores). Therefore, for this study, we set population size at 100 individuals and simulated evolution across 2000 generations.

Values for the fixed parameters (Table 1) were chosen to represent a possible plant and environment from our case study. The parameters are not meant to represent any particular soil or plant species, and for some parameters it was difficult to specify values based on available knowledge. We therefore followed a philosophy of specifying parameter values where we did have indications of values from previous studies (Poot and Lambers, 2003a, b, 2008; Poot et al., 2008, 2012) and then calibrating the remaining parameter values to ensure that overall growth rates and realized root sizes matched those observed in those studies.

We chose two clearly contrasting scenarios to explore. The first scenario (Crack Scenario) was based on our case study of plants growing in shallow soils that become totally dry at the end of the wet season, but where there are occasional cracks in the underlying substrate that allow access to more permanent water supply enabling survival over the drought season. In this scenario, the fitness of the individual plants (its relative reproductive potential) was simply defined to be 1 if at least one wet crack was encountered by the roots of the plant, and to be 0 if no wet crack was encountered. The second scenario (Biomass Scenario) was chosen to contrast with the first scenario, by representing a less extreme environment where overall growth might be the main ‘objective’ of a plant in its first growing season; here the fitness of the individual plants was defined to be their shoot biomass achieved at the end of the first wet season. Evolution across 2000 generations was independently simulated twice for each of the scenarios to investigate whether parallel evolutionary runs would be likely to lead to similar or different evolutionary trajectories and results. For both scenarios, a wet crack frequency of 0·005 was assumed (Table 1).

The initial population for all four evolutionary runs was generated in the same way. First a set of strategy parameter values (a ‘genotype’) was identified that lead to some phenotypes finding wet cracks (Table 2). A set of 100 different individual genotypes was then created by perturbing the first genotype in the standard way described previously, 100 separate times. This initial population of 100 individuals was based on the same first genotype but generated separately for each evolutionary run.

Analysis of simulation results

Each of the four evolutionary runs produced a large amount of results: 2000 populations, one for each generation, each including 100 genotypes (100 sets of values for each of the strategy parameters). Each of these 200 000 genotypes had its corresponding phenotypes, consisting of a realized root structure and shoot biomass, and the corresponding realized relative reproductive potential achieved by this phenotype. The results thus included 800 000 genotypes, phenotypes and measures of realized relative reproductive potential. To summarize these data, the mean and 5, 25, 50, 75 and 95 % percentiles were calculated for the relative reproductive potential and each of the strategy parameters at each generation. Linear regression was used to identify significant trends in the means over time. Using all recorded means would have involved temporal pseudo-replication, because values at one generation are not independent of values at the previous generation. Theoretically, dependence is limited to a lag of one generation, since a new generation is constructed only from the previous one, and indeed the R autocorrelation function (acf) (R Development Core Team, 2013) showed that empirically temporal autocorrelation was limited to a few generations at most. However, to be conservative, we avoided any chance of temporal pseudo-replication by taking the mean of the values across 50 year periods (40 values in all) and ran a linear regression on these values vs. their index to test for temporal trends over the full period. We also split the data into four separate periods of 500 generations each (with ten values per period) and similarly used linear regression to test for temporal trends over each of these periods.

We also conducted additional testing of the final populations. For each of the 100 genotypes in the final populations from the four evolutionary runs, we ran the FSPM 100 times and recorded the relevant measure of relative reproductive success (shoot biomass for the Biomass Scenario and probability of finding a crack for the Crack Scenario). We then used a proportion test (Crack Scenarios) and an analysis of variance (ANOVA) (Biomass Scenarios) to test whether the 100 individuals in the population had different fitness. Note that a given genotype produces a different phenotype and thus a different measure of relative reproductive success each time the model is run, just as real genetically identical seeds will produce different phenotypes. For these runs on the final populations, we also recorded the non-relevant measure of relative reproductive success (shoot biomass for Crack Scenario and probability of finding a crack for Biomass Scenario) to enable comparison.

RESULTS

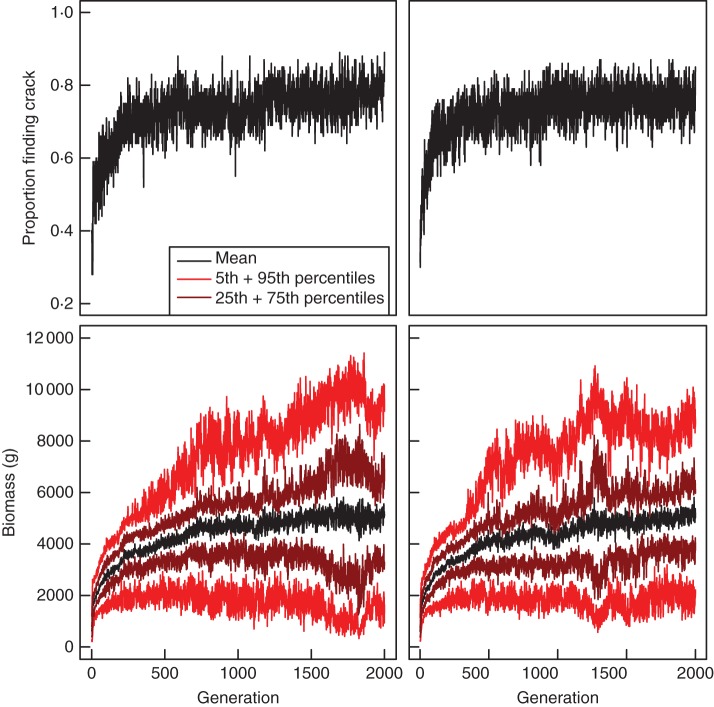
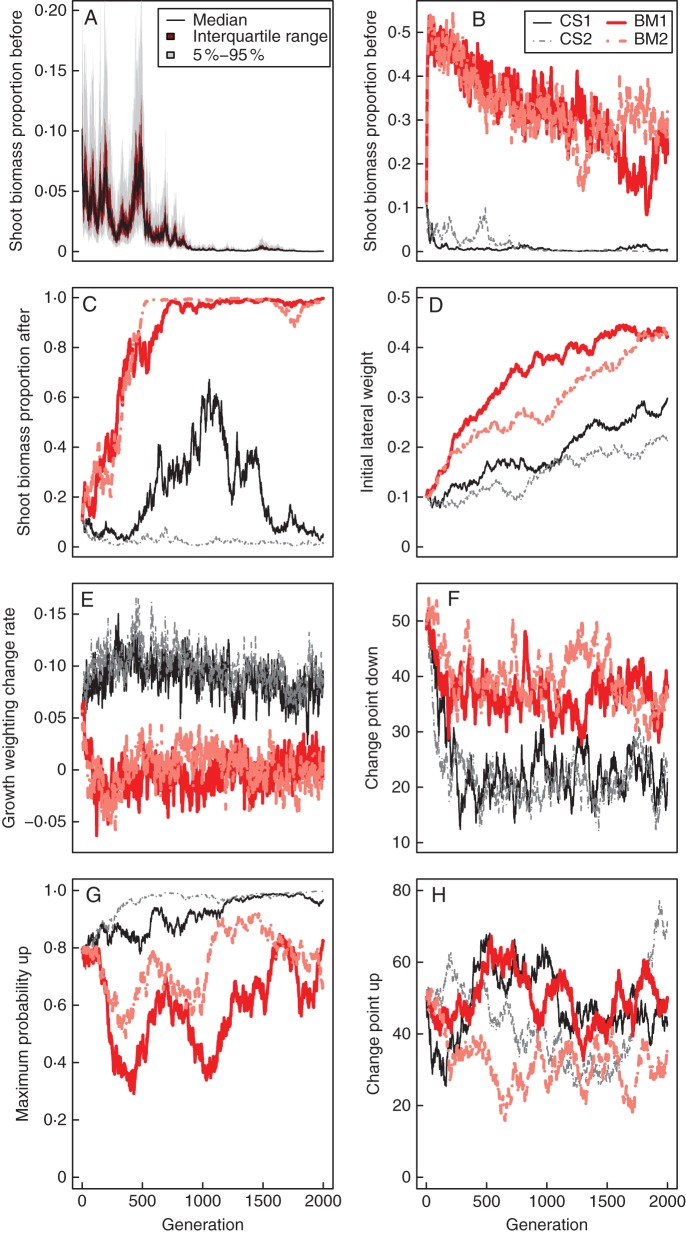
In each of our four evolutionary simulations, selection of genotypes towards improved fitness over time was clearly evident and significant (Fig. 4; last line of Tables 3 and 4), despite a large amount of variability in the fitness of individuals within a population at any given time (Fig. 4). It is interesting to note that for both runs of the Biomass Scenario and the second run of the Crack Scenario, there is some evidence that a maximum average fitness may have been achieved (no significant increase over the final 500 generations) whereas for the first run of the Crack Scenario there is no evidence of such a plateau at the end (significant increase over the final 500 generations) but instead some indication of evolution ‘getting stuck’ temporarily for a period with no significant increase over the second 500 generations.

Fig. 4.

Mean relative reproductive success or fitness over 2000 generations for the Crack Scenario (top) and Biomass Scenario (bottom) for two evolutionary runs (left and right). For the Biomass Scenarios, the 5th and 95th, and 25th and 75th percentiles are shown in addition to the mean (see key) to give an indication of variability within populations. Similar indications of variability within populations were not informative for the Crack Scenario as the recorded measure was binary (a given individual either found a crack, or did not), and both outcomes occurred in every single generation.

Table 3.

Results of linear regression tests for significant trends in mean of strategy parameter values and fitness over all generations (All) and over the first, second, third and fourth period of 500 generations for the first Crack Scenario evolutionary run and the first Biomass Scenario evolutionary run, showing the significance of the trend, and, where significant, whether the trend is increasing (inc) or decreasing (dec)

	Crack scenario					Biomass scenario
	All	First	Second	Third	Fourth	All	First	Second	Third	Fourth
pdownmax	inc***	inc***	inc***	n.s.	inc**	inc***	inc**	inc***	dec**	n.s.
adown	dec*	dec***	inc†	n.s.	n.s.	dec†	dec*	n.s.	n.s.	n.s.
bdown	dec***	dec**	n.s.	inc*	dec***	dec***	dec***	dec**	n.s.	n.s.
Delay	n.s.	dec***	inc***	n.s.	dec***	dec***	n.s.	dec***	n.s.	n.s.
pupmax	inc***	n.s.	n.s.	inc***	dec**	inc*	dec***	n.s.	inc***	n.s.
aup	n.s.	inc**	n.s.	dec†	n.s.	n.s.	inc*	dec***	dec**	n.s.
bup	dec***	n.s.	n.s.	n.s.	inc†	dec***	dec***	n.s.	n.s.	n.s.
wt0	inc***	inc***	n.s.	inc***	inc**	inc***	inc***	inc***	inc**	n.s.
wtΔ	dec***	inc**	n.s.	n.s.	n.s.	inc†	dec†	dec**	n.s.	inc**
wtvar	inc***	n.s.	inc***	inc***	n.s.	dec***	dec†	n.s.	n.s.	n.s.
pshbmb	dec*	dec*	n.s.	dec*	n.s.	dec***	dec***	dec†	dec†	n.s.
pshbma	n.s.	n.s.	inc***	dec**	dec*	inc***	inc***	inc**	inc**	n.s.
θgr	n.s.	dec*	inc†	n.s.	n.s.	inc***	n.s.	inc†	inc**	inc***
θvar	dec***	dec†	dec*	dec***	inc***	dec**	inc**	dec†	dec***	n.s.
θbranch	dec***	n.s.	n.s.	inc**	inc†	n.s.	inc*	inc*	n.s.	n.s.
φph	n.s.	inc†	n.s.	dec**	n.s.	n.s.	dec**	dec†	inc†	n.s.
Fitness	inc***	inc***	n.s.	inc**	inc**	inc***	inc***	inc***	inc***	n.s.

***P < 0·001; **P < 0·01; *P < 0·05; ^†P < 0·1; n.s. P > 0·1.

Table 4.

Results of linear regression tests for significant trends in mean of strategy parameter values and fitness over all generation (All) and over the first, second, third and fourth period of 500 generations for the second Crack Scenario evolutionary run and the second Biomass Scenario evolutionary run, showing the significance of the trend, and, where significant, whether the trend is increasing (inc) or decreasing (dec)

	Crack scenario					Biomass scenario
	All	First	Second	Third	Fourth	All	First	Second	Third	Fourth
pdownmax	inc***	inc**	n.s.	inc**	n.s.	inc***	inc**	inc***	n.s.	n.s.
adown	n.s.	dec**	n.s.	n.s.	n.s.	dec**	dec*	n.s.	n.s.	dec*
bdown	n.s.	dec***	n.s.	inc***	n.s.	dec***	dec***	dec***	n.s.	n.s.
Delay	dec***	dec***	n.s.	n.s.	dec**	dec***	n.s.	n.s.	n.s.	n.s.
pupmax	inc***	inc***	n.s.	n.s.	inc***	inc***	dec**	dec**	inc**	dec***
aup	n.s.	n.s.	n.s.	dec*	inc***	dec**	dec*	n.s.	n.s.	n.s.
bup	dec**	dec**	n.s.	n.s.	inc*	dec***	n.s.	n.s.	n.s.	n.s.
wt0	inc***	inc**	n.s.	inc**	inc*	inc***	inc***	n.s.	inc***	inc***
wtΔ	dec***	inc**	n.s.	n.s.	n.s.	n.s.	n.s.	n.s.	dec**	n.s.
wtvar	n.s.	dec**	inc***	n.s.	dec**	dec***	dec***	inc**	n.s.	dec***
pshbmb	dec***	n.s.	dec***	n.s.	dec***	dec***	dec***	dec*	n.s.	n.s.
pshbma	dec***	dec*	dec*	n.s.	n.s.	inc***	inc***	inc*	n.s.	n.s.
θgr	inc***	n.s.	n.s.	inc***	dec**	dec***	n.s.	inc**	dec***	dec*
θvar	dec***	n.s.	n.s.	dec**	inc***	dec***	dec***	dec**	dec*	dec**
θbranch	n.s.	inc*	n.s.	n.s.	n.s.	n.s.	inc*	dec**	inc*	dec*
φph	n.s.	n.s.	n.s.	n.s.	n.s.	dec***	dec**	n.s.	dec***	inc**
Fitness	inc***	inc**	inc*	inc*	n.s.	inc***	inc***	n.s.	inc**	inc***

***P < 0·001; **P < 0·01; *P < 0·05; ^†P < 0·1; n.s. P > 0·1.

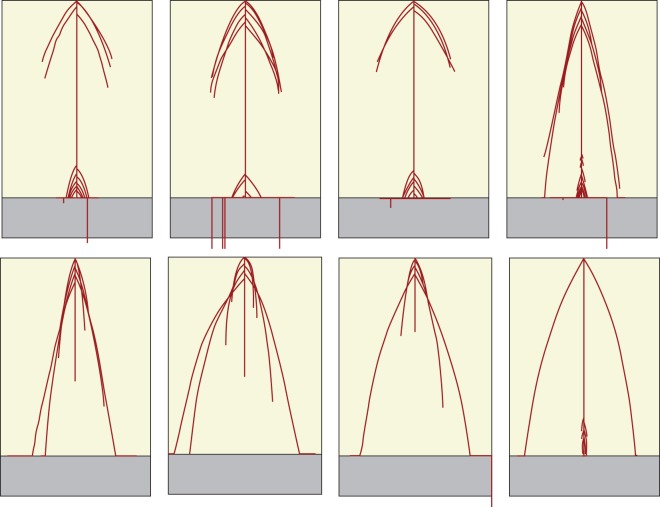
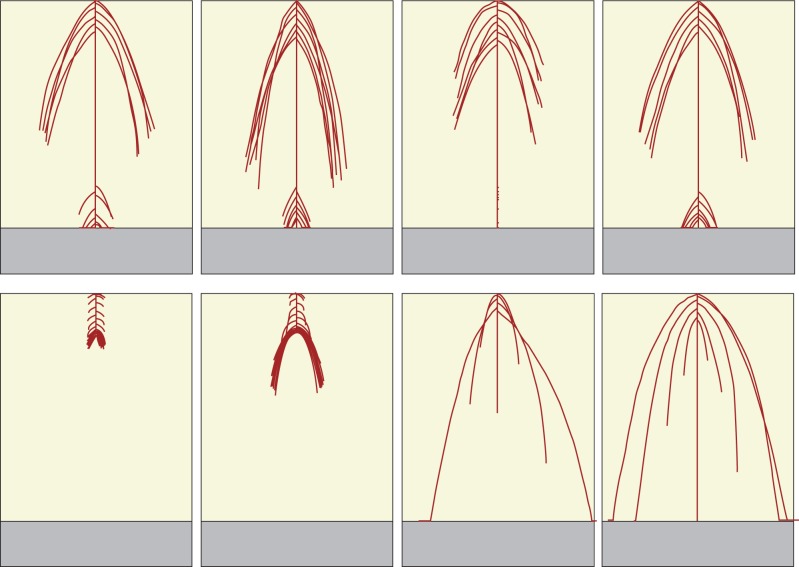
There was a wide variability in the phenotypes observed within the final populations (Figs 5 and 6), and differences between genotypes in terms of average relative reproductive success were highly significant (P < 0·001 in all four populations). Adaptations that made biological sense could be observed in the plants that had the highest average relative reproductive success (top rows in Figs 5 and 6); proliferation of relatively long roots close to the substrate in the Crack Scenario and proliferation of relatively long roots close to the soil surface in the Biomass Scenario. The populations also contained some relatively unfit genotypes (bottom rows in Figs 5 and 6), whose phenotypes clearly differed from the more fit phenotypes in the same populations. Overall final populations were definitely adapted to their defined fitness criteria. The average shoot biomass achieved by plants in the final populations in the Biomass Scenarios was 5029 g, while for plants in the final populations in the Crack Scenarios it was just 0·2 g. The mean probability of finding a crack for plants in the final populations in the Biomass Scenarios was 0·50 while for plants in the final populations in the Crack Scenarios it was 0·85.

Fig. 5.

Realized phenotypes of genotypes selected from the final population of 100 individual plants from the first Crack Scenario evolutionary run, based on additional testing of the final population. The top row shows realized phenotypes from the four most successful genotypes under the additional testing; each of these genotypes succeeded in finding a wet crack in exactly 97 out of 100 phenotypic realizations. The bottom row shows realized phenotypes from the four least successful genotypes under the additional testing; each of these genotypes succeeded in finding a wet crack in <50 out of 100 phenotypic realizations (specifically 33, 41, 43 and 43 times from left to right). Soil depth is 25 cm in all cases.

Fig. 6.

Realized phenotypes of genotypes selected from the final population of 100 individual plants from the first Biomass Scenario evolutionary run, based on additional testing of the final population. The top row shows realized phenotypes from the four most successful genotypes under the additional testing; each achieved a mean final shoot biomass of >7750 g over 100 phenotypic realizations (specifically 7750, 7770, 8773 and 8882 g from left to right). Note that the laterals at the bottom of the profile here are much shorter than those in Fig. 4. The bottom row shows realized phenotypes from four of the least successful genotypes under the additional testing; each achieved a mean final shoot biomass of >4800 g over 100 phenotypic realizations. Soil depth is 25 cm in all cases.

All parameter values showed some significant trends of change over time, at least for some of the periods tested (Tables 3 and 4; Figs 7 and 8). There was variability in parameter values within all generations of the evolving populations. Similarly, there was variation in the trajectories of parameter values across generations between evolutionary runs with the same fitness criterion. However, the trajectories of evolution of parameter values usually differed more between evolutionary runs with contrasting fitness criteria, as shown for some selected parameters in Figs 7 and 8. In the Crack Scenario, evolution led to a fast increase in relative allocation to roots vs. shoots (Fig. 7A–C) and a moderate increase in the initial allocation to lateral roots (i.e. basal laterals) vs. the main root (Fig. 7D; also see Fig. 8 top panels). Also, the inflection point for the probability of branching moving down the main root greatly decreased, suggesting an advantage for fewer but possibly longer basal laterals (Fig. 7F). Once the main root had reached the rock layer, there was an increase in the maximum probability of branching (Fig. 7G; also see Fig 8 bottom panels) and in the relative allocation to deep vs. superficial laterals (Fig. 7E). In contrast, plants in the Biomass Scenario invested much more biomass in shoots, showed a larger increase in the initial allocation to laterals, and did not show an increased probability of branching once the main root reached the rock layer or a preferential allocation of biomass to deep laterals. For some parameters, such as the rate of change of the probability of branching moving up the main root following its first encounter with the impermeable surface (a_up) for example, there appeared to be no consistent evolutionary trajectory, and variation over time seemed to be a result of stochastic drift rather than selection pressure (Fig. 7H). In addition, trajectories of evolution of some parameters showed phases where evolution of parameter values seemed to ‘get stuck’ for a while before continuing again (Figs 7 and 8; Tables 3 and 4).

Fig. 7.

Change in selected strategy parameters over generations, including the proportion of biomass allocated to shoot before a wet crack is encountered, p_shbmb, in the first Crack Scenario run (A, quantile ranges shown to illustrate variability within a single population at given generations; and B, only means shown to allow clear comparison of four different evolutionary runs; CR1, first Crack Scenario run; CR2, second Crack Scenario run; BM1, first Biomass Scenario run; BM2, second Biomass Scenario run), the proportion of biomass allocated to shoot after a wet crack is encountered p_shbma (C), the initial growth weighting of the lateral roots wt₀ (D), the rate at which growth weighting of the laterals changes with depth wt_Δ (E), the inflection point for probability of branching moving down the main root b_down (F), the maximum probability of branching moving up the main root following its first encounter with the impermeable surface p_upmax (G) and the inflection point for probability of branching moving up the main root following its first encounter with the impermeable surface b_up (H), for all four evolutionary runs (key in B also applies to C–H).

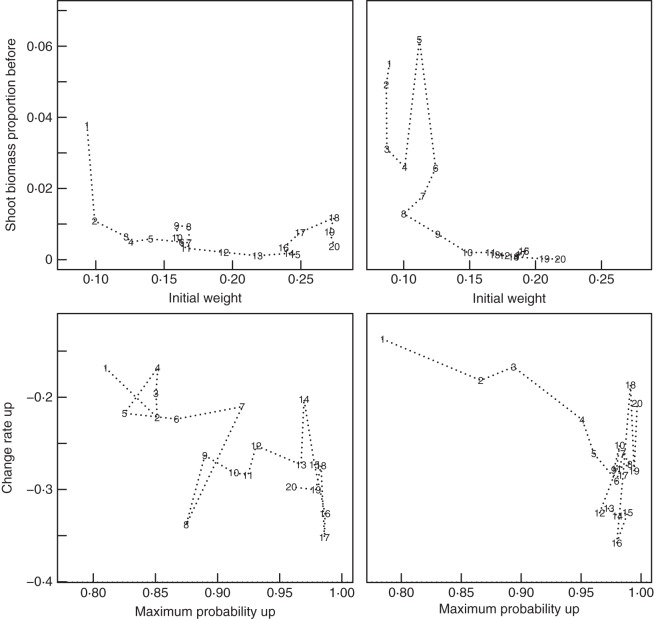
Fig. 8.

Two-dimensional representation of how selected strategy parameters covary over generations for the first Crack Scenario run (left) and the second Crack Scenario run (right). The proportion of biomass allocated to shoot before a wet crack is encountered, p_shbmb, is plotted against the initial growth weighting of the lateral roots, wt₀ (top), and the rate of change of the probability of branching moving up the main root following its first encounter with the impermeable surface, a_up, is plotted against the maximum probability of branching moving up the main root following its first encounter with the impermeable surface p_upmax (bottom). Points represent the average value of the parameter over a 100 generation period (1, first 100 generations; 2, second 100 generations, etc.). For the top sub-plots, note how the trajectory seems to ‘get stuck’ between approximately the 600th and 1100th generations and again between the 1400th and 1600th generations in the first run, while in the second run it similarly stalls between the 1100th and 1800th generations and temporality regresses towards initial values around the 500th generation. Nonetheless, the two trajectories follow generally similar paths, although the second is lagging behind the first by a few hundred generations. Similar patterns, differences and overall similarities can be observed in the lower sub-plots, although there is more indication that evolution has stabilized by the 2000th generation, in the sense that parameter values are not changing as fast or as systematically as in earlier generations.

DISCUSSION

The approach developed in TARSIERS of linking a dynamic FSPM with an evolutionary optimization algorithm was able successfully to simulate evolutionary dynamics of root structures, leading to improved fitness under two contrasting criteria: short-term accumulation of biomass and the ability for roots to find a wet crack in order to access long-term water supplies in an underlying substrate. The most successful structural phenotypes in the final generations correspond well to what might be expected and what has been observed in the field, in terms of the position of lateral branches at different soil depths. Under the Crack Scenario, the most successful phenotypes exhibited a strong response of induced lateral branching at depth upon hitting the impermeable rock substrate (Fig. 5), just as has been observed and suggested for real species endemic to these kinds of environments in south-west Australia (Poot and Lambers, 2003b, 2008; Poot et al., 2012).

Also, very little biomass is allocated to the shoot until a wet crack is found. Although allocation to the shoot was unrealistically low as a result of our simplifying assumptions (see discussion later), this result emphasizes the importance of a high allocation to roots in species from seasonally dry environments (e.g. see Walck et al., 1999; Poot and Lambers, 2003b; Poot et al., 2012). It greatly increases the probability of acquiring access to alternative water sources inside the rock before the onset of the dry season. Under the Biomass Scenario (Fig. 6), the most successful phenotypes exhibited quite a different behaviour, with strong early lateral root branching, fewer and much shorter induced lateral branches at depth upon hitting the impermeable rock substrate, and a significant allocation of biomass to the shoot from the onset of growth. This makes sense as an ecological strategy as early investment in the shoot, under a relatively ample water supply, would lead to the highest fitness (defined in the model as shoot biomass at the end of the wet period). Also, their relatively large investment in superficial laterals as opposed to more distal ones is logical as the former are cheaper to construct and thus confer a growth advantage under ample water supply. Thus, the first results of coupling a FSPM based on relatively few parameters, with an evolutionary optimization algorithm, seem logical and predict evolution of several root traits in a direction that has been observed in plant species confined to shallow-soil habitats.

Some parameter variables showed clear trends over evolutionary time. The clear decreasing trend in the initial proportion of biomass allocated to shoot (p_shbmb), in the Crack Scenarios, makes obvious sense, as without access to cracks in the underlying rocks at the onset of the dry season plants would die. Similarly, the clear increasing trend in the proportion of biomass allocated to shoot after the wet crack is found (p_shbma), in the Biomass Scenarios, is logical. However, the decreasing trend in p_shbmb in the Biomass Scenarios after a very quick and large initial increase is more puzzling (see Fig. 7B), and probably indicates that much larger allocation to biomass was a quick solution to increasing fitness, but as other solutions were found (greater root mass for greater water uptake) it became more effective to allocate less biomass to shoot early in the growing season and grow roots instead as an early investment for later gain. The clear increasing trend in initial allocation to laterals in favour of the main root (wt₀) shows that fast growing basal laterals were important in both scenarios as a means of quickly establishing root mass for water uptake. This trend was particularly strong in the Biomass Scenario, but also evident in the Crack Scenario, indicating that initial lateral growth was still important to establish root mass to drive later growth in search of the wet crack, but main root growth was also important. The need to establish early lateral root mass is also the reason for the increasing trend in the maximum probability of branching before hitting the rock substrate (p_downmax), particularly in the Biomass Scenarios. The parameter determining the maximum probability of branching induced from hitting the substrate (p_upmax) increased steadily towards a maximum in the Crack Scenarios, but showed little clear trend in the Biomass Scenarios; this is what drives the concentrated induced lateral branching that explores the substrate surface and increases the chance of finding the wet crack. The parameter controlling the rate at which the relative growth weighting of laterals changed going down the main root (wt_Δ) increased in the Crack Scenarios, in clear contrast to the Biomass Scenarios; this meant that in the Crack Scenarios lateral growth at the bottom of the profile dominated growth at the top, once the lower roots had been created following the hitting of the substrate. The point at which branching began to ‘turn off’ as the main root grows down (a_down) decreased for both scenarios, indicating that producing fewer roots at the beginning of growth conferred an advantage, probably because these fewer roots then each received a larger portion of the allocated biomass and thus grew faster and explored more space. This trend was particularly marked in the Crack Scenarios, because the reduced competition from the early laterals also allowed the main root to grow faster towards the substrate, and the laterals at the bottom of the profile to grow faster in search of wet cracks. Some parameters, such as a_up, changed significantly in one direction in one period of 500 generations, but in another direction in another period, showing little consistent trend overall (Tables 3 and 4; Fig. 7H). This would appear to be because for a certain combination of other parameter values at one time there was a positive selection pressure on this variable, but for a different set of other parameter values reached at a later time, there was a negative selection pressure on this variable (functional correlation between parameters). It may also be because an overall strategy was relatively successful for some period, but then was ultimately outcompeted by another.

There was high variability between individuals within populations at one time, in terms of fitness and traits (strategy parameter values), as illustrated by the examples of phenotypes from the final populations. Even after 2000 generations of evolution and a clear increase in average fitness, there were still some very unfit individuals within the populations. This was partly due to the differences between phenotypes of the same genotype (Fig. 2). For the Crack Scenario in particular, the measure of fitness (finding a crack) was dependent on chance as well as genotype, since the location of cracks was randomly generated for each run. Another reason for the large variation in phenotypes at the end of the evolutionary run may have been that a number of different strategies were present in populations at the same time (increasing variability in traits) and crosses between individuals with different strategies could have inherited incompatible trait combinations that lead to relatively poor fitness (increasing variability in fitness). A third reason may have been the size of the perturbations we used to generate some random variation in the strategy parameters between generations. Even when a particular individual in a new generation inherited a compatible combination of strategy parameter values from its parents, and thus would have been quite fit, the random perturbation of its strategy parameter values could have resulted in a much less compatible combination of strategy parameter values, and a much lower degree of fitness. To investigate further this variability in future, we could track the parenthood of every individual, as well as its fitness and trait values, and look for cases where high fitness parents produce low fitness offspring.

Although the current study has demonstrated the great potential of combining an FSPM with an evolutionary algorithm, reflection on the results suggests a number of possible changes to improve the approach for future investigations. The measure of relative reproductive success used for the Biomass Scenario and the Crack Scenario were purposely chosen to give contrasting results, which was appropriate for this initial exploration of the TARSIERS system. However, the measure used in the Crack Scenario should be made more realistic. Rather than all plants finding a crack being assigned the same maximum relative reproductive success, a plant that does find a crack could be assigned a relative reproductive success proportional to the shoot biomass it achieves, as a representation of its capacity to compete, and to produce and disperse pollen and seed in future years. All plants not finding a crack could still be assigned a zero fitness measure, since they would be assumed to die before reaching reproductive maturity. This would help avoid the unrealistic result found here, where plants selected for crack-finding ability lost all allocation of biomass to shoot over time. Another way to address this and further improve realism would be to ensure that both water uptake and shoot biomass (representing leaf area) can act to limit photosynthesis and thus new biomass production.

Other possible improvements concern trait inheritance, the size and distribution of the perturbations used to generate variation and introducing the option for trait change during the growing season instead of only between generations. Rather than the value for a trait for a new individual being the mean of the values for the two randomly selected parents, it could be calculated as a weighted mean with weightings generated randomly. This might better represent real qualitative inheritance, as offspring would resemble one parent more than the other in regard to each trait, thus leading to less homogenous blending and the retaining of more variability. We also suspect that using smaller perturbations for the random component of evolution would lead to different and possibly more realistic patterns of evolution. The use of a fat-tailed distribution, such as the Cauchy distribution, to generate variability instead of the normal distribution may also be preferable, as it would produce many relatively small perturbations, with occasional much larger ones. Also, most of the traits (strategy parameter values) are fixed for the whole growing season in the current model, with only shoot biomass allocation being allowed to have a discrete step change triggered by finding a wet crack; while increasing model complexity, it would be interesting and maybe more realistic to allow parameters to change over the growth period, either with time itself, or with the total biomass of the plant. For example, it may be unrealistic for a plant to ‘know’ and thus adapt its behaviour when it has found a crack, since in the wet season soil both above and within the crack is likely to be equally wet; it may be more realistic for the plant to vary its proportional allocation to root vs. shoot as a function of its total biomass. After implementing such improvements, TARSIERS could be used to investigate further our case study, addressing how the optimal rooting strategy changes with (1) soil depth and the frequency of wet cracks (with an infinite number of cracks reflecting a deep soil); (2) the duration of the wet season; (3) varying wet season rainfall patterns (including actual ones from different locations that vary from year to year); and (4) introduced variability in soil water-holding capacity and supply. Most of the above are also highly relevant in the context of climate change and it would be interesting to explore how projected changes in climate would influence the success of previously optimal strategies.

The functional–structural root development simulation model in TARSIERS is designed specifically for evolutionary investigation of ecological rooting strategies. In order to allow evolutionary algorithms to be applied, the model needed to have a relatively simple representation of the dynamic root structure, and a relatively small number of parameters. In this way it contrasts with more detailed root simulation models (e.g. Diggle, 1988; Lynch et al., 1997; Bidel et al., 2000; Pagès et al., 2004; Draye et al., 2010; Dupuy et al., 2010; for a recent review, see Dunbabin et al., 2013) which are not designed for use within global optimization investigations and which are generally aimed at representing quite specific situations (Pagès et al., 1989; Doussan et al., 1998; Ge et al., 2000; Lynch and Brown, 2001; Rubio et al., 2001; Dunbabin et al., 2002a, b, 2007). However, the TARSIERS FSPM also needed to have enough parameters and structural detail to give sufficient flexibility to represent a wide variety of possible dynamic structural development, and the figures in this paper show that this has been achieved. Nonetheless, in future we would consider adding more biological realism and other features to the model. The current model of water extraction and uptake is relatively simple and could probably be improved without overcomplicating the model by allowing some movement of water through the soil between soil water voxels. Higher root orders could be added to the model, and/or explicit representation of spatial heterogeneity in finer root structures. Costs associated with maintaining root and shoot components could also be explicitly included in the model, and the function defining the cost of root construction adapted to account for empirical observations or theoretical rules regarding hydraulic conductance that do not agree with da Vinci's rule (Tyree and Zimmerman, 2002; McCulloh et al., 2003; Lintunen and Kalliokoski, 2010). More complex root–shoot allocation strategies that vary with time could be represented, as could a capacity to store resources for later remobilization. Competition could be modelled more explicitly by simulating the growth of multiple individuals in the same soil competing for the same water and access to cracks. Additional limiting resources could be included; for example, how does including a limited supply of available soil P in the top soil layers affect the optimal root strategy? Also, there is no plasticity in the rooting strategies as currently implemented; while adding additional complexity, it would be very interesting to add phenotypic plasticity by allowing strategies to change depending on the current state of individual roots and their local environment, or of the plant as a whole, and then investigate the costs and benefits of such adaptive strategies relative to fixed ones. For example, the ability to follow water gradients would presumably increase fitness.

The variability and complexities in the results raise questions about the relationships between genotype and phenotype, and how they both contribute to and are acted upon by evolution (Watson et al., 2003), and how the selected genotypes and phenotypes represent trade-offs between different evolutionary goals (Fitter, 1987; Noor and Milo, 2012; Shoval et al., 2012); a tool such as TARSIERS could be used for further investigation of such evolutionary issues. The wide range of phenotypes in the populations and the indications that these represent alternative strategies suggest that TARSIERS could also be used to address related issues such as speciation (Turelli et al., 2001; Servedio and Noor, 2003). TARSIERS could also be used to address more applied issues in conservation management and planning, restoration, and possibly horticulture and agriculture. For example, by investigating how plants that have evolved strategies for particular combinations of edaphic and climatic conditions, such as those in our case study, are likely to be affected by predicted changes in climate, we may better address planning for conservation reserve prioritization, evaluation of mining proposals and restoration following mining in such particular shallow soil environments (e.g. Conservation Council of Western Australia, 2007), or manage livestock grazing pressure in rangelands across such sensitive areas.

The results presented in this paper show that the TARSIERS tool is capable of simulating the evolution of ecological strategies regarding root structural development. The underlying FSPM achieves its goal of being flexible enough to represent a wide range of root structural development strategies, but simple enough to have an evolutionary algorithm applied to it. The results of our case study application of TARSIERS to perennials growing in shallow seasonally dry soils provides support for ecological hypotheses that (1) early lateral root branching improves the water/carbon investment trade-off; (2) high branching frequencies may reduce space exploration and thus water uptake; and (3) high branching frequencies at greater depths close to underlying rocky layers increase the chance of finding cracks in these layers. More generally, these results suggest that the combination of FSPM and evolutionary algorithms can be a valuable tool in providing insights into the relationships between the ecological optimality and efficiency of different structures in contrasting environments. It can also provide insights into the evolutionary dynamics of phenotype–genotype relationships.

SUPPLEMENTARY DATA

Supplementary data providing additional model details are available online at www.aob.oxfordjournals.org and consist of the following. 1: details of water uptake algorithm. 2: details of rooting economics. 3: details of branching.