Architecting the Finite Element Method Pipeline for the GPU

Abstract

The finite element method (FEM) is a widely employed numerical technique for approximating the solution of partial differential equations (PDEs) in various science and engineering applications. Many of these applications benefit from fast execution of the FEM pipeline. One way to accelerate the FEM pipeline is by exploiting advances in modern computational hardware, such as the many-core streaming processors like the graphical processing unit (GPU). In this paper, we present the algorithms and data-structures necessary to move the entire FEM pipeline to the GPU. First we propose an efficient GPU-based algorithm to generate local element information and to assemble the global linear system associated with the FEM discretization of an elliptic PDE. To solve the corresponding linear system efficiently on the GPU, we implement a conjugate gradient method preconditioned with a geometry-informed algebraic multi-grid (AMG) method preconditioner. We propose a new fine-grained parallelism strategy, a corresponding multigrid cycling stage and efficient data mapping to the many-core architecture of GPU. Comparison of our on-GPU assembly versus a traditional serial implementation on the CPU achieves up to an 87 × speedup. Focusing on the linear system solver alone, we achieve a speedup of up to 51 × versus use of a comparable state-of-the-art serial CPU linear system solver. Furthermore, the method compares favorably with other GPU-based, sparse, linear solvers.

1. Introduction

The finite element method (FEM) is a numerical technique for finding approximate solutions of partial differential equations (PDEs). FEM naturally handles complex geometries through the use of unstructured meshes and because of this and other provable numerical properties, FEM is widely used for the simulation of physical phenomena in many disciplines such as continuum mechanics, fluid dynamics, and biophyisics. In general, the FEM is implemented as a pipeline consisting of three computationally intensive tasks: computation of the elemental local operators, assembly of the local operators into a system of linear equations for the global unknown degrees of freedom, and solving of the system of equations [1, 2]. In this paper we refer to these tasks as the element computation step, the assembly step and the linear solve step, respectively. The element computation step is application dependent and, in general, embarrassingly parallel. Correspondingly, this step will be mentioned but not highlighted in this paper. The other two steps, however, require careful consideration when attempting to optimize their corresponding algorithms for parallel architectures. The assembly step uses the mesh topology information to gather information from multiple elements to form the FEM linear system representing the relationship between the global degrees of freedom. This system is then solved using computational linear algebra techniques that are appropriate for the type of the matrix formed.

In many of FEM applications, the FEM method is part of a much larger scientific or engineering undertaking. In many cases, the FEM solve is done multiple times on very large datasets in order to explore parameters spaces, fit measured data, or solve an inverse problem. One way to accelerate the FEM pipeline is by exploiting advances in modern computational hardware. In recent years, the rapid advancement of many-core processors, and in particular graphical processing units (GPUs), has sparked a broad interest in porting numerical methods to these architectures, thanks to their low cost and very high computing capacity. With appropriate numerical algorithms, modern GPUs demonstrate very strong computational performance comparable to supercomputers of just a few years ago.

The single instruction multiple thread (SIMT) architecture used in GPUs places particular constraints on both the design and implementation of algorithms and data structures, making the porting of existing numerical strategies often difficult, inefficient, or even impossible. The architecture provides a large number of parallel computing units (up to several hundred cores) with a hierarchical data-sharing structure. For example, current NVIDIA GPUs are composed of up to 16 streaming multiprocessors (SMs) each containing a number of streaming processor cores (SPs) and on-chip memory. All SMs have access to global memory, the off-chip memory (DRAM), which has a high latency of several hundred clock cycles. The on-chip memory of each SM includes a space partitioned into registers for individual threads, shared memory which can be accessed by multiple threads and general data cache which is not user controllable. The on-chip memory have very low latencies of only 20–30 clock cycles [3]. These architectural features place important restrictions on algorithms if one wants them to run efficiently on such hardware. Addressing these constraints in the context of the finite element method is one important aspect of this paper.

Another reason for the increasing popularity of GPU computing is the emergence of consistent, relatively simple GPU computing models, such as the Compute Unified Device Architecture (CUDA) and the Open Computing Language (OpenCL), and associated APIs compatible with several general purpose programing languages. In this paper, we use CUDA extensions to C for our GPU implementation. In CUDA a CPU program instantiates a collection of kernels, each of which runs as a SIMT computation that is executed in parallel. Kernels are organized into blocks, and each block of threads in the grid is executed on a single streaming multiprocessor on the GPU. Threads in the same block may communicate via shared memory and synchronization primitives, with low latency. Alternatively, threads between blocks must communicate via global memory, which has high latency. When sequentially numbered threads access sequential data in global memory, the memory access of up to 128 bytes may be performed as a single transaction, a process referred to as coalescing. Since global memory accesses have high latency, global memory coalescing is important for performance optimization if the kernel is memory bound. Access to shared memory is banked, and if two threads executing the same instruction attempt to access different words of data from the same bank, a conflict will occur and the accesses must be performed sequentially in conflict-free subsets. In summary, the most optimized kernels minimize global memory transactions, avoid shared memory bank conflicts, and minimize register and shared memory usage to fully occupy the arithmetic logic and floating point units.

For experimental results in this paper, we use a standardized prototypical problem—the elliptic Helmholtz equation solved over a nontrivial domain—to demonstrate the algorithmic and data structure modifications that must be made in order to gain efficiency of the FEM pipeline on the GPU. In particular, we focus our attention on the two nontrivial tasks: the global assembly step and the global linear solve step. Because the local matrices are already formed in the element computation step, the global assembly step usually includes first allocating and initializing a memory space for the global matrix, then finding the location in the global matrix for each local matrix value and finally assembling (summing) these values to the location in the global matrix. A number of strategies [4, 5, 6, 7, 8] have been proposed to port this step to the GPU (e.g. graph coloring and reduction lists) in a way that one gains the benefits of fine-grain parallelism. However, these strategies need significant preprocessing that does not easily port to the GPU. We propose an alternative method that minimizes the preprocessing and at the same time achieves great performance on GPU.

For solving the global linear system that comes as a consequence of FEM assembly, numerous methods have been proposed in the literature. The most popular group of methods within the FEM community are the (iterative) Krylov subspace methods such as the conjugate gradient method [9, 10]. The number of iterations of the method is bounded by the rank of the matrix; the particular convergence rate with respect to a given linear system is determined by the eigenspace structure of the operator (often expressed in terms of the condition number of the matrix). Thus a preconditioner that improves the structure of the eigenspace often helps accelerate the convergence rate of these methods. The global linear system that we seek to solve is both symmetric and positive definite. Considering this and the need for a preconditioning method that maps effectively to the GPU, we propose a solver that used the conjugate gradient method (CGM), preconditioned with a geometry-informed, algebraic multigrid (AMG) method.

In this paper, we present the algorithms and data structures necessary to execute on the GPU the full FEM pipeline as a PDE solver over unstructured tessellations. Our proposed GPU global assembly step requires very little preprocessing and shows a significant performance boost compared to an optimized CPU implementation. For the solving of the global linear system, we propose a geometry-informed algebraic multigrid method and present novel fine-grained parallelism strategies and corresponding data structures to suit GPU architecture. GPU-based MG methods typically use the Jacobi or polynomial methods for the relaxation as these are based on easily parallelizable sparse matrix vector multiplication (SPMV) [11, 12]. However, these methods do not make full use of GPU computing power, because SPMV is generally a memory bound operation with low computational density. In this paper we propose a relaxation method that operates on a novel data structure and has higher computational density and demonstrates better performance. We also analyze the performance of our strategy and data structures in different problem scenarios, compared against state-of-the-art GPU and CPU linear solvers. In our AMG method the set-up stage needs extra work compared to typical AMG implementations so its performance is slightly worse than the setup of other state-of-the-art GPU implementations, but our solving stage is significantly faster. This makes our method particularly suitable for some applications, such as in bidomain problems [13], where the mesh is fixed and the linear system solving needs to be performed many times or for ill-conditioned problems where linear solving takes a long time compared to the assembly and AMG set-up.

The remainder of this paper is organized as follows. In Section 2 we describe the related previous work from the literature. In Section 3 we introduce the problem definition that we have selected as the canonical problem for this work, and will present the basics of the finite element method discretization methodology. In Section 4 we present our GPU-based computing strategy for the FEM assembly step. In Section 5, we present the details of how we solve the global linear system on the GPU – namely, we present our GPU-focused mesh-informed algebraic multigrid method used to precondition a conjugate gradient linear system solver. In Section 6 we show numerical results related to several different engineering scenarios. We analyze different GPU implementation strategies and data structures and explain the optimizations that were required to achieve performance under the austere constraints of the GPU. For completeness, we compare our performance against other alternative GPU and CPU linear solvers. In Section 7 we summarize the paper and discuss future research directions related to this work.

2. Previous work

In the past decade, there have been a multitude of studies that have the explicit goal of porting part or all of the finite element pipeline to many-core architectures. In our review, we will focus on the two compute-intense and challenging components of the pipeline: the global linear system assembly step and the global system solve step.

For the assembly step, early works [14, 15] present relatively simple assembly strategies designed in light of their specific applications. They compute in parallel each nonzero value in the global linear system independently, which suits many-core architectures very well. However, these methods are based on special characteristics of their applications which allow them to derive simple expressions for the nonzero values not available for use in the general FEM context.

Some more general, but more complicated, GPU assembly strategies have recently been proposed. For instance, [16, 17] employ graph coloring to partition elements into non-overlapping sets so that all elemental matrices of one set can be accumulated to the global matrix in parallel without conflicts. Similarly, graph partitioning and reduction list strategies are proposed in [8] to optimize the assembly performance on GPU. These strategies, however, need significant preprocessing such as the generation of a graph coloring, graph partitioning, and/or a reduction list based upon the graph induced by the mesh being used. Information derived from this preprocessing is used in the generation of the data-structured used on the GPU. Many of these preprocessing steps in and of themselves are not easily parallelizable; in addition, their serial implementations take significant running time.

Recently, Markall et al. [4] compare several different assembly strategies on different architectures; they propose a local matrix approach for their assembly and demonstrate that this approach is efficient on many-core architectures for 2D meshes. Their method stores all the local matrices of the elements in a large block matrix instead of storing an assembled global matrix. The matrix vector multiplication is performed in three stages: a spreading operation, a local matrix vector-multiplication, and a gather operation as done in high-order finite element methods [18]. The local matrices typically have the same size and use the same data structure for their storage, so the local matrix vector-multiplication has a regular memory access pattern amenable to GPUs. In addition, this method requires very little preprocessing to accomplish the assembly operation. The authors in [19] introduce a similar approach for GPU-based FEM which computes the local matrices on the fly. The local matrices, however, need much more memory space than the fully assembled global matrix, especially for 3D meshes. Our experiment shows the matrix operations using this approach perform worse than using assembled global matrix in 3D meshes, consistent with the CPU study in [20]. Some recent studies [6, 7], conducted in parallel to this paper, propose to assembly the global matrix into a Coordinate list (COO) format and then convert the matrix to compressed sparse row (CSR) format by removing duplicate non-zero entries. We propose an agglomeration strategy for the assembly step. The proposed strategy decreases the memory footprint by removing data duplication which, when combined with a novel compact sparse matrix data structure, enables the method to avoid the preprocessing used by others, which rely on search operations and atomic addition operations in the fast on-chip memory.

The linear system of equations that comes from the use of the finite element methodology is often sparse, symmetric and positive definite [1]. Consequently, Krylov subspace methods such as the conjugate gradient method are amongst the most widely used numerical linear algebra techniques used with FEM analysis. In practice, the conjugate gradient methods are almost always preconditioned to help improve their convergence rate [9, 10]. The simplest pre-conditioner is the diagonal preconditioner which is very simple to apply but is usually of marginal benefit, because it takes as the approximate inverse merely the inverse of the diagonal of the original matrix.

Incomplete LU factorization (ILU) is a widely used preconditioning method which computes a sparse lower triangular matrix L and sparse upper triangular matrix U such that A = LU + R. When the system satisfies certain conditions, the matrix M = LU can be used as an effective preconditioner for conjugate gradient [21]. ILU however depends on triangular solves which are sequential in nature and hence particularly difficult to parallelize/optimize for large sparse matrices because of the fill-in of nonzero elements. Thus, ILU preconditioning is not particularly well-suited to GPUs [22]. Another popular preconditioner is the block Jacobi preconditioner, which is easy to parallelize and implement on GPU. In the block Jacobi preconditioner, one partitions the domain into blocks on which one does Jacobi iterations independent of the other blocks with some timed synchronization strategy. The problem with this kind of precon-ditioner is that it usually requires a large number of iterations to be effective (e.g. converge), so the benefits of improved parallelism may be outweighed by the increased work in iterations [22]. We have elected to use the a variant of the multigrid method [23, 24] as the preconditioner for our conjugate gradient solver. The multigrid method is a widely used preconditioner and has been shown to be very effective on systems resulting from FEM. Multigrid methods, by employing grids of different mesh sizes (levels), provide rapid convergence rates by reducing low frequency error through coarse grid correction and removing high frequency error via fine grid smoothing. Research has shown that multigrid methods scale very well when applied to parallel computing and are very fast for many practical problems [14, 12, 25, 11, 26, 27, 28, 29].

Recently, some effort has been made to port the preconditioned Krylov subspace method with multigrid preconditioner to many-core architectures. Representative works include [12] and [11]. In [12], the authors present a GPU implementation of a preconditioned conjugate gradient method with a multi-grid preconditioner. They use an algebraic multigrid similar to boomerAMG [25] and the interleaved compressed sparse row (ICSR) data structure for sparse matrix storage in an attempt to coalesce the global memory accesses. As pointed out in [30], however, ICSR (the same as the Ellpack data structure described in [30]) is not suitable for unstructured meshes where their nodes have highly variable valance. The authors of [11] also presents a parallel algebraic multigrid method which exposes substantial fine-grained parallelism in both the construction of the multigrid hierarchy as well as the cycling or solve stage. In both works, the Jacobi method is used in the most expensive multigrid step, the relaxation at each resolution. This method is easy to parallelize but is not very effective as the relaxation step [28]. Additionally, the Jacobi method depends on the sparse matrix-vector multiplication operation, which has low computational density and is generally memory bandwidth bounded. In [31, 32, 33], the authors introduce GPU-based linear solvers with multigrid methods. The solvers use the ELLpack sparse matrix data structure for their specific problems, which is not efficient when number of non-zero entries per row varies largely. Their proposed approach also rely on sparse matrix-vector multiplication which has low computational density as previously mentioned. In this paper, we propose to combine a geometry-informed algebraic multigrid solver as the preconditioner to the Krylov-based conjugate gradient method. To better exploit GPU hardware, we will employ block Jacobi relaxation as part of our preconditioner.

3. Problem Definition and FEM Discretization

We use as our canonical problem the generalized elliptic Helmholtz problem, given in the strong form as:

$$-\nabla ·(\sigma (\mathbf{x})\nabla u(\mathbf{x}))+\lambda u(\mathbf{x})=f(\mathbf{x})\mathbf{x}\in \mathrm{\Omega }$$ (1)

with zero Neumann (i.e. natural) boundary conditions on the boundary of the domain Ω. In Equation 1, u(x) is the solution over a domain Ω, f(x) is a (given) right-hand-side forcing function, σ(x) is a symmetric, positive definite matrix and λ is a strictly positive constant. This problem has been chosen as it is representative of the type of system found in many engineering applications such as solid and fluid mechanics [1, 2]. Although Neumann conditions have been selected for simplicity, nothing presented in this paper strongly depends on this choice; Dirichlet or mixed (Robin) conditions could equally have been chosen.

In traditional finite element analysis, the weak form of Equation 1 is formed through integration by part and the resulting equation then discretized. Let us define our approximation space based upon a piecewise tessellation of Ω denoted Ω_T, which contains E elements and N nodes. We seek to find an approximation ũ ∈ 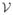such that for all v ∈ :

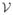$$(\nabla v,\sigma \nabla u)+\lambda (v,u)=(v,f)$$ (2)

where (·, ·) denotes the L₂ inner product over the domain. Following [1], we express our function space in terms of a basis of global piecewise linear tent functions ϕ_i(x) where i denotes a vertex index within our triangulation of the computational domain. In this work, we use piecewise linear finite elements for all experiments. With this choice of the discretizing trial and test functions, we arrive at the following system of equations:

$$\sum _{j=1}^N(\nabla {\varphi }_i,\sigma \nabla {\varphi }_j){\stackrel{\sim }{u}}_j+\lambda \sum _{j=1}^N({\varphi }_i,{\varphi }_j){\stackrel{\sim }{u}}_j=({\varphi }_i,f),$$ (3)

where ũ_j denotes the approximation of u on node v_j and i ranges from 1, …, N. We can rewrite the above equation in matrix form:

$$\{\begin{array}{l}\mathbf{A}\underset{\_}{u}=\underset{\_}{b},\hfill \\ \mathbf{A}=\mathbf{S}+\lambda \mathbf{M},\hfill \end{array}$$ (4)

where b is the forcing vector formed from the right-hand-side of Equation 3, S is the stiffness matrix given by S_ij = (∇ϕ_i, σ∇ϕ_j) and M is the mass matrix given by M_ij = (ϕ_i, ϕ_j). Given λ > 0, A is a symmetric, positive-definite matrix.

In practice, each entry A_ij of the matrix A is assembled from all elements that contain both nodes v_i and v_j and similarly each entry b_i of the vector b is assembled from all elements that contain v_i.

A standard approach (e.g. following [2]) used to form the global mass and stiffness matrices is to form the local mass and stiffness matrices associated with each element and to assemble them based upon the mesh topology. For a triangulated 2D domain Ω ⊂ 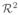, considering a triangle e ∈ Ω_T, the local matrix A^e is computed as $A_{kl}^e=S_{kl}^e+\lambda M_{kl}^e$ where k and l denote the local indices of the vertices v_i and v_j in triangle e (i.e. i = i(e, k) and j = j(e, l)) and the entries of S^e and M^e are computed by $S_{kl}^e={(\nabla {\varphi }_i,\nabla {\varphi }_j)}_e$ and $M_{kl}^e={({\varphi }_i,{\varphi }_j)}_e$ respectively. The integrals are computed with numerical quadrature over the triangle (using a mapping and Gaussian integration [2]). The matrix entries $A_{kl}^e$ can then be accumulated to the i^th row and j^th column of the global matrix A, i.e., $A_{ij}+=A_{kl}^e$. The forcing vector can be computed in a similar manner. The entry b_i of b is the integral of the basis function at v_i and the forcing function, i.e, b_i = (ϕ_i, f). The integral over each element is computed first and then accumulated to its corresponding location in b as done in the formation of A. The serial algorithm for the general assembly step to compute A is show in Algorithm 3.1.

Algorithm 3.1.

Assembly(Ω_T)

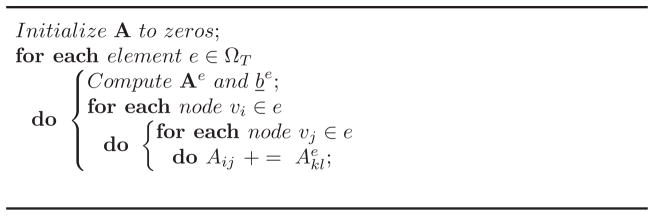
Once the global matrix A and the forcing vector b are formed, a linear solver is used to solve the system Au = b for u. Of the three steps main steps within the finite element method, the elemental computation step is embarrassingly parallel once the data is ready. To save memory access, this step is combined with the assembly step in our FEM pipeline. In the sections to follow, we focus on the details of our assembly and linear system solution strategies and the elemental computation step outlined above will be mentioned in the assembly step description.

4. FEM Assembly On The GPU

Generally, a parallel assembly algorithm would proceed as follows. First, one forms the empty global matrix according to the given mesh, using a sparse matrix representation (e.g, CSR storage), and sets all entries of the matrix to zeros. One then loads the data needed for the elemental computation (node indices and coordinates) from global memory and performs all elemental computations in parallel. Finally, one accumulates the local matrix entry values to the proper locations in the precomputed empty matrix. To find the proper locations, one needs to perform the searching operations before the accumulation.

This algorithm is simple and needs minimal preprocessing, but it is not, in this direct form, well-suited to GPU architectures. This is because the global memory accesses of the nodal coordinates and the loading of needed data for each element are not coalesced. Also, each node’s coordinates are shared by multiple elements so the coordinates, residing in global memory, are accessed redundantly. When a thread is trying to accumulate the computed element matrix to the global matrix, it needs to search for the memory location. This search operation is expensive to accomplish using global memory. Finally, the accumulation operations are done in parallel which can cause race conditions. This requires that atomic add operation be used to do the accumulation; such operations are also expensive when accomplished using global memory.

To address these challenges, we propose a patch-based hierarchical assembly strategy. With the proposed strategy, global memory accesses are coalesced, redundant global memory loads are avoided, and the global matrix entry accumulation is performed in a hierarchical way. Binary search and accumulation are done in shared memory, and the accumulated values are written back to global memory as a block. The details of the algorithm for this strategy are described as follows.

The algorithm begins with a data preparation step. Given a mesh including a node coordinate list, an element list and an adjacency (neighboring nodes) information, we first partition the node set of the mesh into mutually disjoint subsets that we call patches. We assign the elements to the patches based on the patch assignments of their first nodes. In this way, each patch consists of a set of elements that do not overlap with other patches (as demonstrated in Figure 1).

Figure 1.

Non-overlapping patches.

We then rearrange the node coordinate list and element list according to this decomposition. The node indices are changed after rearrangement so that the node indices of each element and the adjacency information of the mesh are also changed accordingly. The x, y, z coordinates of the node list are, in practice, stored in three separate arrays for coalesced global memory access. For the same reason, the node indices of the element list are also stored in separate arrays. For instance, we use four arrays to store the node indices of the tetrahedral elements with array i storing the indices of the i^th node of each element (as shown in Figure 2).

Figure 2.

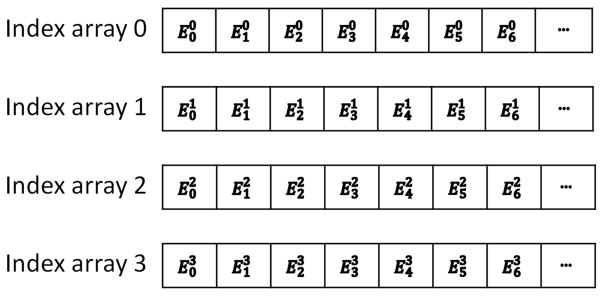
Element list data structure. $E_j^i$ denotes the index of the i^th node of element j.

This decomposition operation does not add to the total running time of the FEM solve, because this decomposition is also used by the linear system solver in subsequent parts of the algorithm.

Next, we form the global empty matrix from the adjacency information of the mesh as the nonzero entry column indices of row i corresponds to the index of node v_i (diagonal entry) and the indices of v_i’s neighbors. Because the global matrix is symmetric, we build and store only the upper half (including the diagonal) of the matrix. We choose to use the compressed sparse row (CSR) format to store this matrix. CSR consists of three arrays: row_of f sets, column_indices and values where values is an array of the (left-to-right, then top-to-bottom) non-zero values of the matrix; column_indices is the column indices corresponding to the values; and row_of f sets is the list of indices where each row starts. We then fill the row_of f sets and column_indices arrays according to the mesh adjacency information and all entries of the values with zero.

With the node coordinate list, the element list and an empty global matrix prepared, the assembly process consists of the following six steps:

1. The coordinate data for each patch are loaded into shared memory (the details concerning the matching of patch sizes to shared memory size is discussed in the subsequent section). Specifically, assuming that patch i has N_i nodes, we use each of the first N_i threads to load the coordinates of one node. By this procedure the global memory accesses are coalesced.

2. Assuming that patch i has E_i elements, each thread loads the coordinates needed by an element and stores them (based upon the compiler) into registers. For the elements on the boundary of a patch, some of their nodes are outside of the patch. In this case, the node indices are not available in shared memory so data has to be loaded from global memory.

3. Each thread executes the elemental computation to construct the local (elemental) matrices (4 by 4 symmetric matrices for linear finite element).

4. The column_indices and values arrays of the CSR global matrix are loaded into shared memory, overwriting the shared memory space used for node coordinates in the first step. Shared memory has a limited size which is not enough to store all the data (i.e. coordinates, column_indices and values) for our typical patch size so the shared memory for coordinates is overwritten to save shared memory. In this situation, preserving the ordering in which data is loaded into shared memory is essential to guarantee correctness, i.e, the loading of column_indices and values must be accomplished after the coordinates are loaded into local storage (registers or local memory) for all elements of this patch. The values array in shared memory is initialized to zero.

5. Local matrix entries are accumulated (with atomic add being used on variables stored in shared memory) to the proper location in the values array in shared memory. The proper location is found by a binary search on the column_indices array in the shared memory. Specifically, considering an element e (processed by the e^th thread in kernel function), $A_{kl}^e$ must be accumulated to row i(e, k) and column j(e, l) in the global matrix. Array segment column_indices [row_of f sets [i]] to column_indices [row_of f sets [i + 1]] contains all the column indices of the nonzero entries of row i. However, it is not known where index j is inside this segment. We use a binary search to find the location of index j, which is also the location in values where we should accumulate $A_{kl}^e$ to a patch boundary element. A patch boundary elements is an element where one of its nodes is outside of the patch. In such a case, a binary search and atomic add have to be used on global memory.

6. The values array in shared memory, which holds the values of the nodes inside a patch, is written into global memory in a coalesced manner. Note that the shared memory values array write back can conflict with other patches that are processing boundary elements as the inside nodes of a patch can be the boundary nodes of other patches. Because of this, a temporary values_B array in global memory is used to store the boundary element accumulation. After the whole assembly kernel function has completed, values_B is added to values array.

5. Solution of the FEM Linear System

In this section, we present our GPU-aware conjugate gradient solver preconditioned with a geometrically-informed algebraic multigrid solver used for the solution of the linear system produced through the FEM method described previously.

5.1. Method Description

The matrix from our canonical problem, discretized using the finite element method, produces a sparse, symmetric positive-definite matrix. Therefore, we choose a preconditioned conjugate gradient (PCG) algorithm to solve the linear system Au = b, as shown in Algorithm 5.1.

Algorithm 5.1.

Preconditioned Conjugate Gradient(A, b, u₀)

We use a geometry-informed algebraic multigrid (AMG) solver as a precon-ditioner for the conjugate gradient method (PCG-AMG), in order to achieve an efficient and robust linear system solver for finite element problems. In this section, we describe in detail our parallelism scheme and data structures used to adapt our PCG-AMG to the GPU architecture. The proposed AMG solver is based on the smoothed aggregation multigrid (SAMG) method described in [26]. As in most other AMG methods, SAMG constructs the graph corresponding to the interconnectivity of the degrees of freedom from the matrix. The proposed AMG method constructs (on the GPU) the graph and corresponding meshes (the primary mesh and coarsened structure) directly from the mesh, and therefore we call it geometry-informed. In this way, we can save the computation that converts a mesh to a graph and use the geometry information to measure the quality of the aggregation or patches that are used in our AMG method.

The PCG-AMG method consists of two stages: the set-up stage and the iteration stage. The set-up stage includes the following steps: grid construction, prolongator generation and coarse-level operator generation. This stage prepares the data for the multigrid method and is executed only once. The iteration stage includes the CG iteration, as shown in Algorithm 5.1. A multigrid V-cycle is performed once as the preconditioner for each CG iteration. In the following subsections, we describe in detail the proposed GPU-based PCG-AMG method.

5.1.1. Set-up Stage

The set-up stage begins with the construction of the AMG meshes from the mesh. This construction starts with the decomposition of the nodes into small mutually disjoint subsets. This decomposition process is called aggregation and the node subsets are called aggregates. The aggregation, as in [27] and [29], relies on a maximal independent set (MIS) of mesh nodes to define roots of aggregates and then groups each root and its neighbors into one aggregate. After this process, any ungrouped nodes are assigned to the nearest aggregate. After the aggregation of one level, the algorithm builds an induced graph from the aggregation by treating each aggregate as a node in the coarser level and adding an edge between two aggregates (nodes in the coarser level) if any of their nodes are connected in the finer level. Then the algorithm performs the aggregation again on the coarser level graph. The algorithm continues until the number of nodes in the graph is smaller than a certain threshold. In practice, because our relaxation method requires the graphs of each level be partitioned into larger patches, we propose the double partitioning strategy which will be described in Section 5.2.

With the meshes constructed, the i^th row and j^th column of the tentative prolongator matrix at level l, P̃^l, is given by:

$${\stackrel{\sim }{P}}_{ij}^l=\{\begin{array}{ll}1\hfill & ifi\in C_j^l\hfill \\ 0\hfill & \mathit{otherwise},\hfill \end{array}$$ (5)

where $C_j^l$ denotes the aggregate to which node j belongs in level l. The actual prolongator is a smoothed version of the P̃. We choose the weighted Jacobi method as the smoother, thus yielding a prolongator matrix given by:

$$P^l=(I-\omega D^{-1}{A}^l){\stackrel{\sim }{P}}^l,$$ (6)

where ω is a positive constant (scaling), I is the identity matrix, D is the matrix given by the diagonal of A^l, which is the grid operator matrix of level l. Given the prolongator at the level l, its coarser level l + 1 operator (matrix) is formed variationally. Firstly, we compute the restrictor which is the transpose of the prolongator: R^l = P^lT and then compute the coarser-level operator by A^l+1 = R^lA^lP^l.

5.1.2. Iteration Stage

The iteration stage includes the PCG-AMG iterations as shown in Algorithm 5.1. In each iteration, one AMG V-cycle is performed as the preconditioner. From the computational point of view, in this stage, the AMG V-cycle is actually the bulk of the work. Here describe our V-cycle algorithm in detail.

A V-cycle is generally composed of these steps: prerelaxation to smooth the values, computation of the residual, restriction of the residual to higher level, recursively calling the V-cycle procedure until the coarsest level is reached, solution of the coarsest level linear system, prolongation of the value to finer level and post-relaxation to smooth the value again. The detailed algorithm is as follows:

Algorithm 5.2.

V-cycle(A^k, R^k, P^k, b^k, u^k)

The relaxations (pre-relax and post-relax) are the most time-consuming parts of all the V-cycle steps, so a suitable relaxation method and optimized implementation are essential for overall performance. In our case, a good relaxation method should effectively smooth out the high frequency errors and be easily parallelized for GPU. The relaxation is usually implemented as a Jacobi smoothing (See Equation 7) since it is very easy to implement for parallel architectures. Indeed, both [11] and [12] use this method in their respective AMG GPU implementations.

$$u=u+\omega D^{-1}(b-Au).$$ (7)

However, the Jacobi method is not ideal for multigrid relaxation in terms of convergence rate [28]. Its implementation depends on the matrix-vector multiplication, which generally has low computational density and does not efficiently use resources on the GPU. In this paper, we propose to use a variant of weighted block Jacobi method for relaxation. This method gives significantly better convergence rate than the Jacobi method and can achieve fine-grained parallelism and high computational density by taking advantage of the hierarchical memory layout on GPU.

The standard weighted block Jacobi is defined as follows. Let 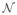= {1, …, n} be the set of all the nodes in the domain and consider decomposing 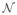into p non-overlapping patches,

$$\mathcal{N}=\underset{1}{\overset{p}{\cup }}{\mathcal{N}}_k.$$

Let A be partitioned into blocks A_ij of size n_i × n_j where the rows of A_ij are in 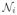and the columns are in . The weighted block Jacobi method takes the matrix form:

$$u=u+\omega M^{-1}(b-Au),$$ (8)

where ω is a positive constant (scaling), M is a block diagonal matrix with M = diag{A_kk} with diag{A_kk} denoting the block diagonal matrix with blocks A_kk.

Because $M^{-1}=\mathit{diag}\{A_{kk}^{-1}\}$, block Jacobi computes $g_k=A_{kk}^{-1}$ in parallel with each processor (e.g. a CPU core or a GPU streaming multiprocessor) solving for one of the g_k either directly or iteratively. We do not precisely compute M⁻¹, but instead we use multiple weighed Jacobi iterations to approximate g_k. That is, we iterate ${\stackrel{\sim }{g}}_k^{n+1}={\stackrel{\sim }{g}}_k^n+\omega D_{kk}^{-1}{r}_k$ multiple times. D_kk is the diagonal matrix of A_kk and r_k denotes the residual values corresponding to . With this method, we can use low-latency GPU memories (shared memory and registers) to store the diagonal matrices and do the weighted Jacobi iterations on these fast memory spaces to achieve high performance. Our experiments (see Section 6) show that this method is very effective as the relaxation for multigrid in terms of overall convergence rate.

5.2. Implementation and Data structures

We now present the implementation details and data structures needed to effectively use the GPU’s streaming multiprocessors.

5.2.1. Set-up Stage

The block Jacobi method requires that the domain be partitioned into patches with each patch containing a group of connected nodes. This task is challenging for the several reasons. First, we want to map the patches to the CUDA blocks, thus the patches should be small enough so that they can fit into limited hardware resources. Second, the patches should be large enough so that patch partitioning does not result in too many edge cuts, because this increases interactions between patches and undermines the effectiveness of the Jacobi updates. Third, the SAMG that we are mimicking needs a finer partition of the mesh into aggregates as mentioned in Section 5.1. It is important that the patch partition does not cut through aggregates in order to achieve the best convergence rate.

We propose the bottom-up double partitioning strategy to generate the aggregates and patches. The double partitioning strategy includes three steps: (1) generation of the aggregates (aggregate partition), (2) building an induced graph from the aggregates, and (3) generation of the patches by partitioning the induced graph again (patch partition).

Both of the partitions rely on maximal independent sets (MIS) or k-MIS, an extension of MIS where k specifies the radius of independence of the set. An MIS is a set of nodes in the graph no two of which are connected by an edge, a k-MIS is a set of nodes in the graph no two of which are connected by a path of length k or less. Both MIS and k-MIS have the property that no node in the graph can be added to the set without violating the independence property. Since regularity of aggregate size is important to the convergence of the solver, we have found it necessary to take steps to control the aggregate sizes to improve the distribution.

Our partition method takes as input the graph representation of the mesh and produces the permutation necessary to re-order the nodes of the input graph according to their patch and aggregate membership, the indices for the start of each aggregate and partition in the permuted graph, and the graph representation of the next coarser mesh. The aggregate partition is performed as follows:

1. Find a k-MIS for the graph, where the value of k is chosen to control the number and size of generated aggregates. Higher values of k result in sparser sets of root nodes and therefore larger aggregates.

2. Number the nodes in the k-MIS sequentially to index the aggregates.

3. Add other nodes to aggregates iteratively. Each node in the graph checks its neighbors to see which aggregate they are in. If all neighbors are in the same aggregate, the current node will add itself to the same aggregate. If the neighbors are members of more than one aggregate, the node selects the aggregate with which it shares the highest adjacency. This repeats until all nodes are allocated.

4. After the initial allocation is completed, find the number of nodes in each aggregate, remove aggregates below a certain size (typically nine) by labeling all nodes in these aggregates as unallocated, and then re-index the remaining aggregates.

5. Repeat the allocation process to add the nodes from eliminated aggregates to remaining aggregates.

The patch partition consists of performing the partition defined above on the induced graph, which includes a weight for each node that is the number of nodes in the corresponding aggregate. The size control mechanisms applied therefore use the total weight of nodes rather than their count.

To control the size of patches, we remove patches below a threshold weight and re-allocate their aggregates as detailed above. Then we iteratively exchange nodes between patches to improve the size distribution. The patches exchange aggregates as follow:

1. Compute the weighted size for each patch.

2. Each aggregate that could move to another patch calculates the most desirable exchange for itself.

3. Every patch for which it is desirable to give up a node(s) performs the most desirable exchange (This limit is to damp oscillations of patch size that could be caused by multiple exchanges).

4. Recalculate the weighted sizes for each patch, and if the largest patch is smaller than the threshold value (typically 400) the process terminates, otherwise another iteration begins.

Our experiments show that for 3D tetrahedral meshes, k = 2 is best for the aggregate partition and k = 1 for the patch partition, as the resulting aggregates and patches generated are of the appropriate size. Our parallel k-MIS algorithm is similar to [34, 29, 11] and implemented on GPU. We know of one other k-MIS implementation in the publicly available CUSP library, which according to our experiments has comparable performance (in terms of computing time) to our implementation.

The partitions described above form a permutation array that maps the indices of the nodes in the original mesh (graph) to a re-ordered index list in which nodes belonging to the same patch are grouped together and within each patch, nodes belonging to the same aggregate are grouped together. In this way, patches contain aggregates. Once the partitions are done, we permute the matrix of each multigrid level according to the permutation array and the tentative prolongator P̃ is constructed according to Equation 5. Then P̃ is smoothed with one weighed Jacobi iteration as described in Equation 6. P̃ is a sparse matrix with a special sparse pattern that each row has only one non-zero value which is set to one. We use a special version of parallel sparse matrix-matrix multiplication as described in [11] to compute AP̃ needed in the prolongator smoothing process. Lastly, the restrictor and the matrix for the next level is computed as described in the previous section. We use the matrix transpose and matrix-matrix multiplication functions in the CUSP library to compute the restrictor and the matrix for next level.

5.2.2. Iteration Stage

The iteration stage performs the PCG iterations. As depicted in Algorithm 5.1, one iteration of PCG consists of a preconditioning step (one V-cycle), a matrix vector multiplication and some vector operations. Of all these operations, the preconditioning step (V-cycle) is the most expensive. As mentioned above, the V-cycle consists of prerelaxation, residual computation, restriction, coarsest level solution, prolongation, error correction and postrelaxation. The prerelaxation, residual computation and postrelaxation steps are the bulk of the work since each of them needs to access the operator matrix of a level. Our proposed V-cycle pipeline combines the prerelaxation and residual computation steps to save one costly matrix access. Next, we will describe the data structures we propose for our AMG preconditioner and the V-cycle pipeline in detail.

An appropriate data structure is essential to fully harness the potential computing power of the GPU. The GPU has limited fast memory space (shared memory and registers) in addition to global memory. When local data of a kernel is too large to fit in the fast memory space, the data spills over to the local memory, which is as slow as global memory. So a compact data structure is desired to save storage and memory accesses. The data structure determines also the memory access pattern which is particularly important for global memory accesses because of their high latency. Block Jacobi requires domain decomposition (patches) and the matrix is permuted accordingly to bear a blocked pattern. Each edge in the domain corresponds to a non-zero value in the matrix.

We propose a novel sparse matrix data structure specially designed for the block Jacobi method, which we call patch sparse matrix format (patchSPM). This proposed data structure is composed of three parts: the patch inside A_I, the patch boundary A_B, and the diagonal A_D. Thus, A = A_I + A_B + A_D. A_I is composed all the entries A_ij of A such that i and j belong to the same patch. A_B is defined as the opposite and A_D stores the diagonal values in an array. Matrix A_I is a diagonally blocked matrix, and all the matrix blocks are symmetric, sparse matrices. These matrix blocks are concatenated in the GPU global memory with each of them in a sparse matrix format. An integer array is used to store the beginning offset for each matrix block.

The patch inside matrix A_I is typically much denser than A_B, and each of its matrix blocks is loaded into shared memory and accessed many times during the block Jacobi inner updates, as described in Section 5.1.2. Therefore, the data format of its matrix blocks has a significant impact on the performance. We considered three potentially appropriate sparse matrix formats: Ellpack (ELL), CSR, Symmetric Coordinate list (SymCOO). ELL format stores a M by N matrix nonzero values in a dense M by K array values, where K is the maximum number of nonzeros entries per row. Similarly, the corresponding column indices are stored in another M by K array indices. The rows that have fewer than K nonzero values are padded with a sentinel value. ELL format is regular resulting in coalesced global memory accesses, but it stores sentinel data to pad the unstructured matrix to be rectangular, which wastes bandwidth and undermines GPU performance. In addition, due to the sentinel padding data, ELL data structure is not compact enough to fit into the fast memory space (shared memory and registers). For many meshes where the maximum valence is high, the data spills over into slow local memory and inner Jacobi iterations become very expensive. CSR, as describe in Section 4, is compact but irregular, which leads to uncoalesced global memory access. The SymCOO format is a variant of COO for symmetric matrices. It consists of three arrays: row_indices, column_indices and values. The row_indices and column_indices arrays store the row index and column index of each non-zero entry of the upper half of the matrix. The values array stores the values of those non-zero entries. SymCOO is the most compact data structure since it stores only half of the matrix and it is regular. The drawback of SymCOO is that it typically requires atomic operations in the relaxation step. We alleviate this drawback by performing the atomic operation in the faster GPU memory space (shared memory space). Our experiments show that using SymCOO format for the matrix blocks of A_I has the best overall performance. The boundary matrix A_B is very sparse and stored in general COO format. Figure 3 shows the patchSPM data structure.

Figure 3.

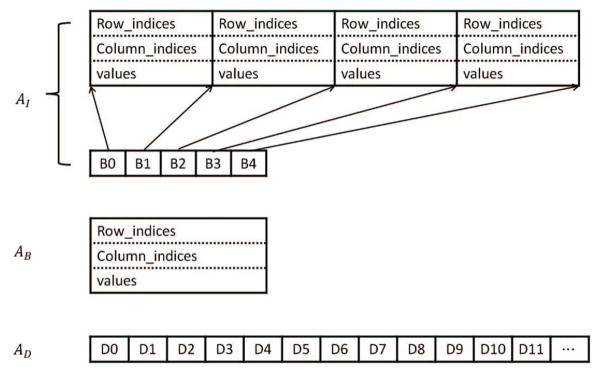
The patchSPM data structure consists of three parts: A_I, A_B and A_D. A_I includes a concatenated list of SymCOO formats and an integer array indicating the beginning and ending of each matrix block in the list, A_B is in COO format, and A_D is an array of diagonal values.

In our V-cycle pipeline, as mentioned before, we combine the prerelaxation and residual steps, i.e, we use only one CUDA kernel function, which we call prerelax-residual, for these two steps. We now describe this kernel in detail as follows.

1. Each CUDA block loads a segment of A_D, b and a matrix block of A_I (corresponding to a patch) into the shared memory and registers.

2. The kernel allocates two arrays s-Ax and s-u in shared memory and initializes their elements to zeros. These arrays are used to store the block matrix vector multiplication result and the temporary result after each inner Jacobi iteration respectively. The kernel synchronizes here to make sure the matrix block of A_I is loaded and s-Ax is initialized within a CUDA block before execution of the next instruction.

3. The kernel performs multiple inner Jacobi iterations in the shared memory registers to obtain the final u result now in s-u and the final result is written back to global memory after synchronization.

4. One more block matrix vector multiplication is performed to compute the partial residual r̃.

Here the computed residual is incomplete because the computation takes into account only the values of the inside matrix A_I and the diagonal matrix A_D, i.e, the computed residual from this kernel is r̃ = b − (A_I + A_D)u. The real residual should be r = b − Au so after this kernel call, we need to “compensate” the residual by subtracting A_Bx from r̃, and then the real residual is r = r̃ − A_Bu. Similarly, before the post-relaxation, A_B x should be subtracted from b to get the real right hand side for the block Jacobi iteration as described in Equation 8. The post-relax kernel is quite similar to the prerelax-residual, but it does not have the residual computation step. Since A_B is relatively sparse compared to A_I, the running time needed to compute A_Bu is relatively short. On the whole, we have a different V-cycle pipeline (Algorithm 5.3) for our multigrid method from the typical pipeline shown in Algorithm 5.2.

Algorithm 5.3.

V-cycle-new ( $A_I^k,A_B^k,A_D^k$, R^k, P^k, b^k, u^k)

5.3. Mixed-Precision Computation

In numerical computing on the GPU, there is a fundamental performance advantage in using single precision floating point data format over double precision. Due to a more compact representation, twice the number of single precision data elements can be stored at each level of the memory hierarchy including the register file, caches, and main memory. By the same token, handling single precision values consumes less bandwidth between different memory levels. In addition, many modern processor architectures, including GPUs, have much better throughput for single precision operations than for double precision operations. For example, NVIDIA’s Fermi GPUs’ single precision operations are around twice as fast as double precision [35]. Thus, researchers have been trying to find ways to use single precision operations as much as possible without sacrificing the overall accuracy. [36] and [37] point out that for a preconditioned Krylov-subspace method, the preconditioner can be single precision without affecting the accuracy. This is important for our proposed solver since we are trying to load the matrices associated with the multigrid levels into fast, but limited size, local memory spaces. In our implementation, the multigrid associated matrices and floating point vector are in single precision while all other floating point numbers are in double precision. We store an extra copy of the finest level matrix A_fine in double precision, and this matrix is used for the matrix vector multiplication in the PCG iteration. A_fine is not used for any blocked operation so it is stored in a general sparse matrix data structure called Hybrid which is particularly efficient for unstructured sparse matrix (e.g. [30]). Due to the extra copy of the finest level matrix, this approach requires more memory storage. Assuming the number of non-zero entries in the finest level matrix is M, the memory footprint for storing the matrices is X = MF * 2S if we use double precision for all matrices, where S = size of (float) and $F={\sum }_{k=0}^{L-1}\frac{1}{R^k}$ with L denoting the number of levels and R denoting the size ratio of the i^th level matrix and the (i + 1)^th (coarser) level matrix. With mixed precision, the require memory storage for the matrices is Y = MF * S + 2MS = (F + 2)MS. So $\frac{Y}{X}=\frac{F+2}{2F}$. In practice, F is approximately 1.1, so $\frac{Y}{X}\approx 1.41$. That is, the mixed precision requires around 41% more memory.

6. Numerical Results

To show the characteristics of our proposed method and the performance of the implementation, we conduct a set of systematic experiments with various unstructured meshes and numerical set-ups. We compare our implementation against our optimized serial CPU version for the assembly step and compare our linear system solver against the state-of-the-art multigrid-based GPU and CPU solvers, namely the CUSP [38] and Hypre [39] libraries. We refer to these solvers as CUSP-PCGAMG and Hypre-PCGAMG respectively, and we call our solver patchPCGAMG. All experiments are executed on a Linux (OpenSuse 11.4) computer equipped with an Intel i7 965 Extreme CPU running at 3.2 GHz and a NVIDIA GeForce GTX 580 GPU. The GPU is equipped with 1.5 GBytes of memory and 16 streaming multiprocessors, where each multiprocessor consists of 32 SIMD computing cores that run at 1.544 GHz. Each streaming multiprocessor has configurable 16 or 48 KBytes of on-chip shared memory for quick access to local data. Computation on the GPU means running a kernel with a batch process of a large group of fixed size thread blocks. NVCC 4.0.1 and gcc 4.3 are used to compile the CUDA and CPU codes respectively and -O3 flag is used in the compiling. We use the CPU results barely for benchmarking, and all CPU results are measured using only one thread.

The unstructured meshes we use in our tests are listed in Table 1. The Regular mesh is generated by the following process: subdivide a 4 × 4 × 4 cube into 512 0.5 × 0.5 × 0.5 small cubes and then cut each small cube into six tetrahedra resulting in an initial tetrahedral mesh containing 729 nodes and 3072 elements. We then subdivide each tetrahedron of this initial tetrahedral mesh into eight smaller tetrahedra by connecting the midpoints of the edges. We perform this midpoint subdivision three times to produce the final Regular mesh shown in Table 1. In this process, a series of tetrahedral meshes is generated with each finer mesh doubling the resolution of the coarser mesh. This series of meshes is used in our scalability experiment in Section 6.2.2. The Irregular mesh is generated by tetrahedralizing a 4 × 4 × 4 cube. The Heart and Brain meshes are visualized in Figure 4. The Blobs mesh has two regions, inside of the blobs (taking around 20% of the total volume) and outside of the blobs, which are color coded differently in Figure 5. This mesh is used in the heterogeneous domain experiment in Section 6.2.4 where the two regions have different coefficients (σ in Equation 4).

Table 1.

The meshes used in our experiments.

mesh names	node number	element number	min valance	max valance	NNZ(million)
Regular	274,625	1,572,864	3	18	5.1
Irregular	197,561	1,122,304	3	25	4.1
Heart	437,355	2,306,717	5	36	9.4
Brain	322,497	1,805,242	6	34	8.7
Blobs	277,657	1,650,105	5	46	4.2

Figure 4.

Surface rendering of the exterior surfaces of the Heart and Brain meshes.

Figure 5.

A cross section and the volume visualization of the Blobs mesh.

The proposed assembly and linear system solution methods extend naturally to 2D triangular meshes with some parameter tuning. Therefore, we only report the 3D tetrahedral mesh result in this section.

6.1. Assembly performance

We show the performance of our GPU assembly by assembling for the linear system of the Helmholtz equation (Equation 1 with λ = 1) from all the meshes mentioned above and comparing the running time against our optimized serial CPU implementation which is based on Algorithm 3.1. Both implementations compute the global matrix A as in Equation (4) using double precision. The results are shown in the table (Table 2) below. Our GPU implementation of the assembly step is up to 87 time faster than the CPU implementation.

Table 2.

Assembly performance (double precision): GPU and CPU running time (in seconds) comparison.

meshes	GPU	CPU	speedup
Regular	0.0298	1.080	36
Irregular	0.0229	1.010	44
Heart	0.0465	3.114	67
Brain	0.0355	3.077	87
Blobs	0.0319	2.525	79

6.2. Linear system solution numerical experiments

We conduct a series of experiments to show the properties of our method and the performance of our implementation. We compare the result against the state-of-the-art GPU and CPU multigrid based linear solver: CUSP-PCGAMG and Hypre-PCGAMG. For Hypre-PCGAMG, hybrid Gauss-Seidel method is used for the relaxation and PMIS is chosen for coarsening. We use mixed precision strategy for patchPCGAMG and CUSP-PCGAMG and double precision for Hypre-PCGAMG as our experiment shows that single precision and double precision performance difference is very small on CPU. The CUSP-PCGAMG uses the same smoothed aggregation multigrid method as ours while the Hypre library uses BoomerAMG based multigrid preconditioner. For all the experiments, the solution is considered converged if the relative error ε = ||r||/||b||< 1e − 8, where r is the residual and b is the right hand side of the linear system whose all entries are set to one, i.e, (ϕ_i, f) = 1 in Equation (3). ||x|| denotes the l² norm of a vector x. We show the result of tolerance 1e − 8 but the trend is the same for smaller tolerances.

6.2.1. Multigrid set-up stage performance

Table 3 shows the running time of the multigrid set-up stage for all meshes with the result compared to the set-up stages of CUSP-PCGAMG and Hypre-PCGAMG. S1 and S2 are the speedups in contrast with Hypre-PCGAMG and CUSP-PCGAMG respectively, and numbers are in parentheses when patch-PCGAMG is slower.

Table 3.

Multigrid set-up stage running time in seconds. S1 and S2 are the speedups comparing patchPCGAMG to Hypre-PCGAMG and CUSP-PCGAMG. Speedup number is in parentheses when patchPCGAMG is slower.

meshes	patchPCGAMG	Hypre-PCGAMG	S1	CUSP-PCGAMG	S2
Regular	0.519	1.10	2.0	0.420	(1.2)
Irregular	0.385	0.665	1.7	0.292	(1.3)
Heart	0.813	2.51	3.2	0.604	(1.3)
Brain	0.591	1.68	2.9	0.451	(1.3)
Blobs	0.569	1.27	2.1	0.431	(1.3)

Compared to CUSP-PCGAMG, our AMG set-up stage has an extra partitioning step as described in Section 5.2.1 and hence its performance is worse. As shown in the table above, patchPCGAMG is 1.2× to 1.3× slower. On the other hand, patchPCGAMG achieves up to 3.2× speedup for the set-up stage when compared with Hypre-PCGAMG.

6.2.2. Scalability with problem size

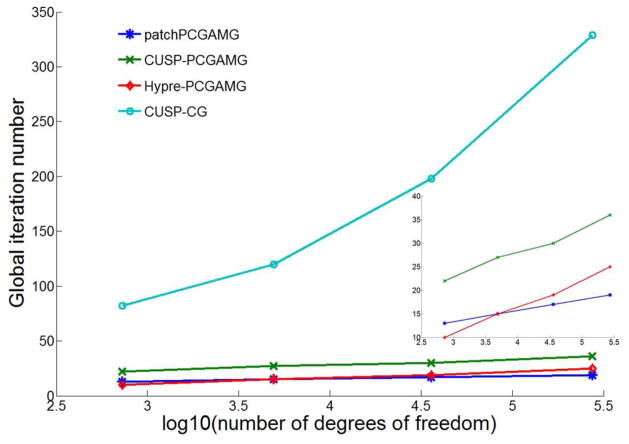
Multigrid-preconditioned Krylov subspace methods are known to have linear scalability with the matrix size for structured problems, and thus the convergence rate (number of CG iterations) should not change with the matrix size [27, 28, 29]. In this section, we show how our AMG preconditioned CG linear system solver scales when the mesh resolution increases using the series of regular tetrahedral meshes mentioned before. FEM is used to solve the Helmholtz equation with natural boundary condition on these meshes. We solve the associated linear system with our AMG preconditioned CG linear solver and show the scalability of the solver by measuring the number of global (PCG) iterations needed to converge. The result is compared to the other two AMG preconditioned CG linear solvers(CUSP-PCGAMG and Hypre-PCGAMG) and a pure CG solver (CUSP-CG) (See the plot in Figure 6).

Figure 6.

The plot for number of degrees of freedom against global iteration number: the inset plot is the zoom in of the three PCGAMG methods. Three inner iterations are performed for the patchPCGAMG.

As shown in Figure 6, our solver demonstrates good scalability with problem size although not perfectly linear. It is slightly better than the other two PCG-AMG solvers. In addition, our solver needs only about half the number of iterations to converge compared to CUSP-PCGAMG. This difference is mainly due to the difference of the relaxation method since both are using SAMG method and the aggregate partition strategy is similar. The inexact block Jacobi relaxation we use shows clear advantage over the Jacobi method used by CUSP-PCGAMG. We can also see from the plot that all three PCG-AMG solvers scale much better than the pure CG solver which confirms the claim that MG generally has good scalability with problem size.

6.2.3. Inner iteration influence on convergence rate

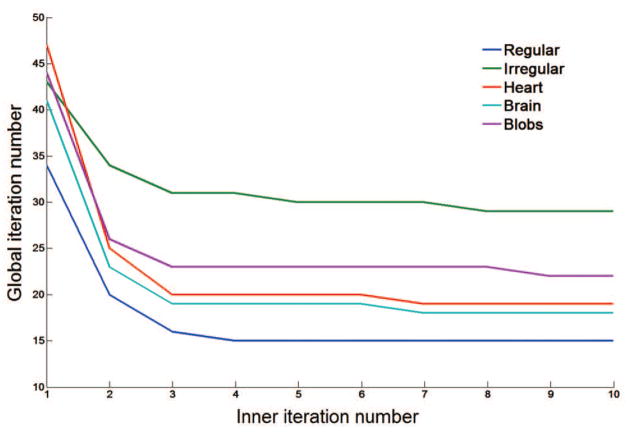
As mentioned earlier, we use the inexact weighted block Jacobi method for the relaxation step in the multigrid method. Multiple inner Jacobi iterations are performed to approximate the inverse of the matrix block A_ii according to patch i. The reasons why we compute the inverse inexactly are two-fold: first, the inverse computation for the matrix blocks are different if we compute exactly which leads to imbalanced work loads for the CUDA blocks. Second, we are using the block Jacobi as the relaxation to smooth out the high frequency error and there is no need to compute the inverse exactly. Figure 7 shows how the number of inner iterations is related to the global (PCG) iteration number needed to converge for the meshes. It can be seen from the plot that larger inner iteration number generally lead to less global iterations but after around three inner iterations, the global iteration number does not change any more or changes very little. Although the inner iteration is relatively cheap as we load the matrix blocks into fast memory space (registers or shared memory), it is not totally free. Larger inner iteration number leads to poorer per-iteration relaxation performance. Our experiments show that a choice of three inner iteration is generally the sweet spot for overall performance.

Figure 7.

Plot of inner iteration number against global iteration number for patchPCGAMG.

6.2.4. Heterogeneous media influence on convergence rate

This experiment shows how the method performs when the domain is heterogeneous, i.e., the coefficients of the Laplacian operator in Equation (2) σ = σ (x) are not the same for all x. This happens when a simulation is done on a multimaterial domain as the σ is usually different in different materials. Table 4 shows how the method performs when the meshes have two different materials and one of the material has σ = 1 and the other material’s σ is 1, 10, 100 respectively and compares to CUSP and Hypre and the unpreconditioned conjugate gradient method from CUSP library which we call CUSP-CG. As shown in the table, all methods converge slower with increased heterogeneity. The patchPCGAMG and CUSP-PCGAMG are becoming worse at roughly the same rate (the convergence rate ratio of the two is roughly the same with different heterogeneity). This means the patch partition used in patchPCGAMG is not affecting the performance for heterogeneous problem.

Table 4.

Heterogeneous media performance comparison for the Blobs mesh: (m,n) means the σ values for the two materials in the domain are m and n respectively. The numbers reported are the global iteration numbers.

Methods	(1,1)	(1,10)	(1,100)
patchPCGAMG	23	31	60
CUSP-PCGAMG	50	60	122
Hypre-PCGAMG	28	30	40
CUSP-CG	1048	2419	7071

6.2.5. Running times for all meshes comparison

Table 5 compares the running times and (number of iterations) for our linear solver along with CUSP-PCGAMG and Hypre-PCGAMG. We also include two pure (unpreconditioned) conjugate gradient implementations: a GPU implementation from the CUSP libraray (CUSP-CG) and a CPU implementation in Hypre (Hypre-CG). S1 and S2 are the speedups of patchPCGAMG compared to Hypre-PCGAMG and CUSP-PCGAMG. S3 is the speedup of the CUSP-CG compared to the Hypre-CG.

Table 5.

Running times in seconds (global iteration number) for all meshes: S1 and S2 are the speedups of patchPCGAMG compared to Hypre-PCGAMG and CUSP-PCGAMG. S3 is the speedup of the CUSP-CG compared to the Hypre-CG.

meshes	patch PCGAMG	Hypre-PCGAMG	S1	CUSP-PCGAMG	S2	CUSP-CG	Hypre-CG	S3
Regular	0.139 (19)	3.86 (25)	28	0.175 (36)	1.3	0.680 (329)	3.73 (329)	5
Irregular	0.167 (31)	3.02 (29)	18	0.216 (56)	1.3	2.43 (1639)	14.8 (1639)	6
Heart	0.218 (20)	11.2 (31)	51	0.631 (46)	2.9	4.64 (1148)	33.8 (1131)	7
Brain	0.165 (19)	7.78 (27)	47	0.432 (45)	2.6	8.15 (1838)	60.4 (1810)	9
Blobs	0.172 (23)	5.70 (28)	33	0.409 (50)	2.4	3.34 (1048)	16.0 (1030)	5

Also shown in Table 6, the patchPCGAMG achieves up to 51× speedup compared to the state-of-the-art CPU PCG-AMG implementation Hypre-PCGAMG while porting the pure CG method to GPU gains only up to 9× speedup. This is indicative that CG is not particularly well-suited for the GPU many-core architectures. Although adding AMG as the preconditioner makes the solver much more complicated than pure CG, it is worth the extra effort considering the performance improvement on the GPU. In addition, the patchPCGAMG achieves 1.3× to 2.9× speedup comparing to the CUSP-PCGAMG on the same GPU. The global iteration numbers in the table demonstrate that our block Jacobi relaxation greatly improve the convergence rate compared to Jacobi method used in CUSP-PCGAMG. Table 6 shows the per global iteration performance of the three PCGAMG methods. Comparing to the CUSP-PCGAMG, the per iteration running time of the patchPCGAMG is comparable although the block Jacobi relaxation used in the patchPCGAMG performs much more computation than the Jacobi method. This confirms our claim that our relaxation method increases the computational density and better balances the memory bandwidth and computations. It can also be noted from Table 6 that for the simpler meshes, Regular and Irregular, where the valance is relatively not variable, the CUSP has better per iteration performance because it uses the Hybrid sparse matrix data structure that performs better when the matrix is regular ([11]). For the other meshes, which are more representative of real life data, the patchPCGAMG performs similarly or even better. As expected, both GPU implementations have much better per iteration performance than the Hypre-PCGAMG.

Table 6.

Per global iteration running times in milliseconds for all meshes: S1 and S2 are the speedups of patchPCGAMG compared to Hypre-PCGAMG and CUSP-PCGAMG. Speedup number is in parentheses when patchPCGAMG is slower.

meshes	patch PCGAMG	Hypre-PCGAMG	S1	CUSP-PCGAMG	S2
Regular	7.31	154	21	4.68	(1.6)
Irregular	5.40	104	19	3.86	(1.4)
Heart	10.9	361	33	13.7	1.3
Brain	8.71	288	33	9.60	1.1
Blobs	7.49	204	27	8.18	1.1

7. Conclusions and Future Work

In this paper, we present the complete pipeline of a parallel FEM solver for unstructured meshes that performs very well on the many-core parallel processors. The proposed GPU assembly performs up to 87× better than an optimized CPU implementation, and the proposed multigrid preconditioned CG solver achieves a speedup of up to 51× compared to the state-of-the-art CPU implementations. These speed ups compare very favorably against other attempts at GPU-accelerated linear solvers, many of which report lackluster results [40]. The algorithms and data structures need not be changed to run on newer generation hardware (e.g. Kepler GPU) efficiently. However, some parameter might need to be tuned to obtain the best performance, such as the patch size and inner iteration number.

We choose to use a geometry-informed AMG as the preconditioner for the CG method to solve the linear system from the FEM. The proposed AMG pre-conditioner dramatically speeds up the convergence rate of the CG method and changes the computational bulk of the work from the CG iteration to the AMG preconditioner—a solver methodology which adapts very well to the many-core parallel architecture with proposed parallelism scheme and data structures. This is juxtaposed with the typical CG implementation on the GPU, which suffers from excessive communication and low computational density. This is borne out in the experimental data, which shows dramatically better speed ups for AMG on the GPU vs the CPU. Thus, the corresponding improvements in AMG performance on the GPU make it a particularly attractive option for taking advantage of the significant compute power offered by these devices.

Unfortunately, AMG presents some challenges, particularly in the aggregation, restriction, and prolongation methods, that are sometimes problem dependent; thus, it is more difficult to imagine a completely general software solution for the linear solve, as one would typically expect with a CG solver. We have included some preliminary results for the heterogeneous media and those results are very encouraging, but further investigation is needed to fully understand how the heterogeneity influences the performance when the partitions (aggregate and patch) do not align with the heterogeneity. Anisotropy is likely to present further challenges. In this paper, we focused on solving the FEM problems with a single GPU. However, there are circumstances that single GPU is not enough for a given problem, either because the problem size is too large to fit into the memory of a single GPU, or the performance of the problem on a single GPU is not satisfactory. Therefore, an important area of future work would be solvers that use an out-of-core paradigm for memory handling/shuffling to the GPU or solvers that scale across multiple GPUs or GPU clusters.