Extension of DNA in a Nanochannel as a Rod-to-Coil Transition

Abstract

DNA confinement in nanochannels is emerging as an important tool for genomics and an excellent platform for testing the theories of confined wormlike polymers. Using cutting-edge, large scale Monte Carlo simulations of asymptotically long wormlike chains, we show that, in analogy to the rod-to-coil transition for free wormlike polymers, there exists a universal, Gauss-de Gennes regime that connects the classic Odijk and de Gennes regimes of channel-confined chains. For DNA in a nanochannel, this Gauss-de Gennes regime spans practically the entire experimentally relevant range of channel sizes, including the nanochannels used in an incipient genome mapping technology.

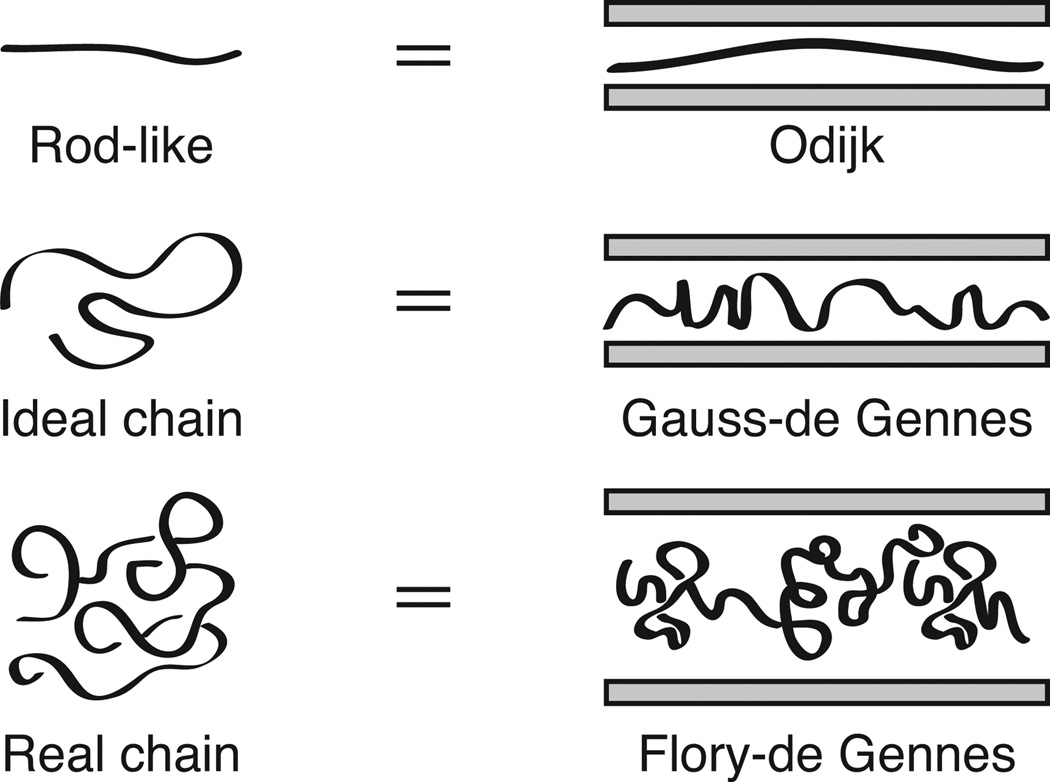
When a wormlike polymer such as DNA is confined in a long channel whose width is smaller than the polymer's free solution radius of gyration, steric interactions with the walls cause the polymer to extend along the channel axis. The classical theories describing this phenomenon, sketched in Fig. 1, were described by Odijk [1] and de Gennes [2], respectively, over 30 years ago. However, these theories are only valid in the impractical cases of very strong (D ≪ l_p) or very weak (D ≫ l_p) confinement, respectively, where D is the channel size and l_p is the persistence length of the chain. In this Letter, we establish that the relevant intermediate regime for DNA extension in a nanochannel is a universal de Gennes-like regime with ideal blobs. We arrived at this conclusion by recognizing the connection with the rod-to-coil transition for free wormlike polymers [3–5] illustrated in Fig. 1. In addition to describing the experimentally relevant phenomena for DNA, this connection leads to a complete description of the universal regimes for all long channel-confined wormlike chains that we validated using large-scale Pruned-Enriched Rosenbluth Method (PERM) simulations [6, 7].

FIG. 1.

Illustration of the analogy between free solution and confined configurations of a wormlike chain. The classical theories renormalize the chain into a series of subchains, where these subchains are either rod-like (Odijk) or excluded volume blobs (de Gennes). We demonstrate here the existence of a universal Gauss-de Gennes regime in confinement that connects the (rod-like) Odijk and (excluded volume) de Gennes regime. For clarity, we refer to the classic de Gennes regime as the “Flory-de Gennes” regime to highlight its excluded volume nature.

To understand the analogy in Fig. 1, let us first recall the regimes of chain conformations in free solution. Three regimes characterize the normalized end-to-end distance of a wormlike chain, ρ ≡ 〈R²〉^1/2/l_p. This distance depends on two dimensionless numbers: N ≡ L/l_p, the number of persistence lengths in a chain of length L, and an anisotropy parameter ε ≡ w/l_p, which measures the relative strength of the excluded volume interactions (quantified by the effective chain width w) to the bending energy. In the limit of negligible excluded volume interactions [8], z ≡ εN^1/2 ≪ 1, the Benoit-Doty equation for a continuous wormlike chain gives [5]

$${\rho }^2/2=N-1+\text{exp}(-N)$$ (1)

This model predicts a stiff chain with ρ ~ N for N ≲ 1 and Gaussian statistics with ρ ~ N^1/2 for 1 ≲ N ≲ ε⁻². For a sufficiently long chain N ≳ ε⁻², excluded volume interactions are important and ρ ~ ε^2ν−1N^ν, where ν = 0.5877 is the modern value of the Flory parameter [9]. As evident in Fig. 2, the scaling in the Gaussian regime is not exactly that for an ideal chain due to finite excluded volume effects. Moreover, weakly anisotropic chains ― such as DNA, which is only a moderately stiff biopolymer (ε ≈ 0.1) [10] ― have a very narrow Gaussian regime. However, in the limit ε → 0, the Gaussian regime spans an infinite amount of chain length and is thus a universal regime. Accordingly, many biopolymers [11] are stiff enough to exhibit broad Gaussian regimes.

FIG. 2.

(color online) The normalized mean-square end-to-end distance of a wormlike chain in free solution as a function of normalized chain length from Eq. 1 (ε = 0, - -), renormalization group theory [4] with (descending from top to bottom in the figure) ε = 2, 0.5, 0.2, 0.1 (DNA), 0.05, 0.01, and PERM simulations for ε = 0.05 (□, L_max/w = 2 × 10⁴). The most flexible chain corresponds to an upper bound ε = 2, where the Kuhn length of the chain equals its width [12].

We will demonstrate, via simulations, that three similar regimes characterize the confinement free energy of an asymptotically long wormlike chain confined in channel. Following Odijk [1] and de Gennes [2, 13], the chain is renormalized into N/g units containing g persistence lengths per unit. This in turn implies that the chain properties (confinement free energy and extension) are extensive, as has been shown many times [1, 2, 13, 14] for an infinite chain in a quasi-1D geometry.

The Odijk regime [1] in Fig. 1 corresponds to rod-like behavior over the length scale D. For channel sizes δ ≡ D/l_p ≲ 1 [1], the stiff chain projects a distance of λ ~ (D²l_p)^1/3 before deflecting off of the walls. This makes the number of persistence lengths in the correlation volume

$$g=\lambda /l_p~{\delta }^{2/3}$$ (2)

Assuming an energy of k_BT per independent segment [1] gives the dimensionless confinement free energy,

$$ℱ\equiv \frac{\mathrm{\Delta }{F}_c}{N{k}_{B}T}~1/g~{\delta }^{-2/3}$$ (3)

The extension is given by the projection of the deflection segment length onto the channel axis X = (N/g)λ cos θ [1] which simplifies to

$$\langle X/L\rangle =1-\alpha {\delta }^{2/3}$$ (4)

where the prefactor α = 0.18274 for a square nanochannel is given by high resolution simulations [15]. Analogous to the rod-like behavior in free solution, the thermodynamics of the Odijk regime is independent of the width of the chain.

Continuing with the analogy, the de Gennes regime [2] in Fig. 1 corresponds to real chain statistics, which leads us to call it the “Flory-de Gennes” regime. Here, as was the case for real chains in free solution, we need to account for the finite chain width. To do so, we use the concept of a “blob” to denote a section of the chain with g persistence lengths that has a correlation length equal to the channel size D. Recalling that the Flory radius for a chain in a good solvent is R_F/l_p ≈ ε^2ν−1N^ν [8], the blobs have the size

$$\delta \approx {\epsilon }^{2\nu -1}{g}^{\nu }$$ (5)

With the assumption that the free energy scales as k_BT per blob [2], we have ℱ ~ 1/g, or

$$ℱ~{(\delta {\epsilon }^{1-2\nu })}^{-1/\nu }$$ (6)

Following the same reasoning, the extension 〈X〉 is also extensive in the number of blobs, 〈X〉 ≅ (N/g)D. Substituting Eq. (5) in the latter gives the scaling

$$\langle X/L\rangle \cong {\delta }^{1-1/\nu }{\epsilon }^{2-1/\nu }$$ (7)

Since the Flory-de Gennes regime corresponds to the onset of excluded volume interactions [16], we would expect this regime to start when the excluded volume parameter for a blob reaches

$$Z_{\text{blob}}\equiv \epsilon g^{1/2}\approx 1$$ (8)

We thus find that g ≳ ε⁻² corresponds to the Flory-de Gennes regime. Recall that the excluded volume scaling in free solution begins when N ≳ ε⁻². We thus infer that g in confinement is the analogue of N in free solution. Additionally we note that by combining Eqs. (5) and (8), we can find the boundary of the Flory-de Gennes regime limit in terms of the channel size, δ ≳ ε⁻¹, which proves more useful since the channel size is an experimental observable.

For intermediate channel sizes 1 ≲ δ ≲ ε⁻¹, the g persistence lengths inside D³ exhibit approximately Gaussian statistics. The derivation of the confinement free energy follows that for the Flory-de Gennes regime with ν = 1/2, leading

$$ℱ~{\delta }^{-2}$$ (9)

Since this regime consists of blobs with Gaussian statistics, we refer to it as the “Gauss-de Gennes” regime. This free energy scaling is the same as that of a channel-confined phantom chain originally derived by Cassassa [2, 14]. As is the case in free solution, the scaling of ℱ for chains with a finite value of ε will not be exactly equal to Eq. (9). This arises from the weakness (rather than absence) of excluded volume at the persistence length scale.

In the Gauss-de Gennes regime, the intra-polymer correlations are screened at the channel wall [13, 17], which gives g ~ δ² persistence lengths per correlation length, D. Since the extended chain consists of N/g such correlation lengths, the corresponding fractional extension is

$$\langle X\rangle /L~{\delta }^{-1}$$ (10)

The latter scaling has been observed in a number of previous simulations (see [10, 18–20] and supporting Fig. S6), but its origin and universal nature (or lack thereof) have been elusive until now because DNA is not an especially stiff biopolymer. Given this fact one may be tempted to dismiss the regime as unimportant, but consider the case of DNA in a high ionic strength buffer (ε = 0.1) which is highlighted in Fig. 3. Although the Gauss-de Gennes regime spans less than a decade in dimensionless channel size, these sizes encompass the typical channels used in experiments [17, 21–24]. Morover, the Flory-de Gennes regime corresponds to ≲ 20% extension and the Odijk regime corresponds to ≳ 90% extension, leaving the Gauss-de Gennes regime to span a significant portion of the practically relevant range of fractional extensions for genomic mapping. However, this regime is not in principle limited to a small range of channel sizes. For stiff enough chains, the range of applicable channel sizes 1 ≲ δ ≲ ε⁻¹ will span many decades, showing the existence of a universal regime.

FIG. 3.

(color online) Comparison of the fractional extension of the chain predicted by Odijk [1] and de Gennes [2] and simulations of an asymptotically long DNA chain (⌂, l_p = 50 nm, w = 5 nm, ε = 0.1) using the Pruned-Enriched Rosenbluth Method (PERM). The extent of the Gauss-de Gennes regime increases for more filamentous chains (+, l_p = 50 nm, w = 0.5 nm, ε = 10⁻²). The shading corresponds to the regimes for ε = 0.1.

We have tested this scaling theory in square channels using Pruned-Enriched Rosenbluth Method (PERM) simulations of asymptotically long chains that are long enough to suppress any end effects. PERM is a biased chain-growth Monte Carlo algorithm originally introduced for lattice chains by Grassberger [6]. In the algorithm, “tours” of chains are grown and the Rosenbluth weight of the chain is controlled by selective pruning and enrichment, thus overcoming the attrition problem for the Rosenbluth-Rosenbluth chain growth algorithm [25] for long self-avoiding chains. Choosing efficient parameters for executing the original PERM algorithm is somewhat of an art, and we have followed a parameterless version by Prellberg [7] that simplified the calculation considerably. Our optimized implementation of PERM (see supporting information) allowed us to sample long chain lengths (typically 2 × 10⁴ touching beads of size w) while spanning four decades in the dimensionless channel size δ and three decades in the anisotropy ε. For DNA with w = 5 nm, our data typically correspond to contour lengths of 100 µm, a full order of magnitude longer than traditional Markov chain Monte Carlo techniques [10, 17–20, 33]. This combination of asymptotically long chains, a thorough exploration of the (δ,ε) phase space (see supporting information), and the large range of confinement free energies allowed us to draw meaningful conclusions about universality. In addition to providing the chain conformational properties shown in Fig. 2 and Fig. 3, PERM can provide thermodynamic properties like the confinement free energy.

To clearly see the analogy with the rod-to-coil transition in free solution, we also need the equivalent of Eq. (1) for the confinement free energy of an ideal wormlike chain (ε = 0). To a good approximation, the confinement free energy of a chain in a channel is equal to twice the confinement free energy of a chain confined to a slit [14, 26]

$$ℱ=(2/3){\pi }^2{\delta }^{-2}$$ (11)

Additionally, extensive computational work on strongly confined wormlike chains has yielded an accurate prefactor to the Odijk expression for square channels [15]

$$ℱ=2.2072{\delta }^{-2/3}$$ (12)

Following Chen and Sullivan [27] we propose an interpolation formula of the form

$$ℱ=\frac{(2/3){\pi }^2{\delta }^{-2}}{{(5.147{\delta }^{-2}+3.343{\delta }^{-1}+1)}^{2/3}}$$ (13)

Taking the limit δ → ∞ yields Eq. (11) and δ → 0 matches Eq. (12). The remaining constant for the δ⁻¹ term is used to fit the shape of the crossover region obtained from PERM simulations in the absence of excluded volume (see supporting information).

The similarity between Fig. 2 and Fig. 4 confirms the analogy between bulk and confinement, and the plateau in Fig. 4 validates the presence of a Gauss-de Gennes regime in confinement that connects the Odijk and Flory-de Gennes regimes. Compared to free solution, the Gauss-de Gennes regime in confinement is less prominent than the Gaussian regime in free solution because (i) the upper bound is lower in confinement (ε⁻¹ versus ε⁻²) and (ii) it is challenging to simulate extremely long chains with small ε at very high spatial resolution. Nevertheless, Fig. 4 clearly demonstrates the three regimes, including the scaling exponent predicted by Eq. (9).

FIG. 4.

(color online) The normalized free energy of confinement as a function of normalized channel width, δ_eff = (D − w)/l_p from Eq. 13 (ε = 0, - -) and PERM simulations for ε = 2 × 10⁻³ (△), 5 × 10⁻³ (▽), 0.01 (+), 0.02 (◇), 0.05 (×), 0.1 (⌂, DNA), and 0.2 (×̶).

The close agreement here between the scaling theory and simulations has parallels with DNA confined in a sphere [28], but calls into question previous theories for the thermodynamics of a channel-confined chain between the Odijk and the Flory-de Gennes regimes. Most treatments apply Flory theory for a confined chain [16, 29–31] notwithstanding the fact that the accuracy of Flory theory predictions in free solution relies on a serendipitous cancellation of errors that are not a priori applicable in confinement. For example, the scaling ℱ ~ δ^−4/3 predicted by Flory theory [22] for the “extended de Gennes” regime [10, 16, 29, 31] is not evident in our simulations. Other theories have attempted to incorporate backfolding of the chain to explain the transition between the Odijk and Flory-de Gennes regime [17, 19, 20, 29, 32]. The analogy between free solution and confinement makes the role of backfolding clear ― it is simply the transition from rod-like to ideal statistics in the correlation volume.

Our results provide not only a complete description of the universal regimes of any long, channel-confined wormlike chain, but also have practical implications for genomic mapping in nanochannels [23, 24]. Our simulations predict that the Odijk regime is valid for an effective channel size δ_eff ≡ (D − w)/l_p ≤ 0.3 and the Flory-de Gennes regime begins at δ_eff ≥ (2ε)⁻¹ (see supporting information). For DNA in a nanochannel, the Odijk extension [1, 15] applies for channels smaller than 20 nm, whereas the Flory-de Gennes extension [2] only starts to apply for channels larger than around 200 nm, where stretching is insubstantial. Since almost all experiments [22] and the commercial nanochannel technology [23] operate between these limiting cases, it is unsurprising that the experimental data are not described by the Odijk or de Gennes theories. Additionally, the Gauss-de Gennes regime certainly has implications for dynamics, which have recently been shown to be very sensitive to the anisotropy ε over similar ranges of extension [33]. Future device design, as well as fundamental work, will need to account for the nature of the rod-to-coil transition of the subchains comprising nanoconfined polymers.