The role of mechanics during brain development

Abstract

Convolutions are a classical hallmark of most mammalian brains. Brain surface morphology is often associated with intelligence and closely correlated to neurological dysfunction. Yet, we know surprisingly little about the underlying mechanisms of cortical folding. Here we identify the role of the key anatomic players during the folding process: cortical thickness, stiffness, and growth. To establish estimates for the critical time, pressure, and the wavelength at the onset of folding, we derive an analytical model using the Föppl-von-Kármán theory. Analytical modeling provides a quick first insight into the critical conditions at the onset of folding, yet it fails to predict the evolution of complex instability patterns in the post-critical regime. To predict realistic surface morphologies, we establish a computational model using the continuum theory of finite growth. Computational modeling not only confirms our analytical estimates, but is also capable of predicting the formation of complex surface morphologies with asymmetric patterns and secondary folds. Taken together, our analytical and computational models explain why larger mammalian brains tend to be more convoluted than smaller brains. Both models provide mechanistic interpretations of the classical malformations of lissencephaly and polymicrogyria. Understanding the process of cortical folding in the mammalian brain has direct implications on the diagnostics of neurological disorders including severe retardation, epilepsy, schizophrenia, and autism.

1. Introduction

For more than a century, the unique surface morphology of the mammalian brain has fascinated scientists across all disciplines [39]: Why does the brain have this complex convoluted structure, and, more importantly, to which extent is brain structure correlated to brain function [66]? From a mechanics point of view, these questions naturally translate into the quest for a basic understanding of brain morphology [7]: What are the underlying mechanisms of brain folding?

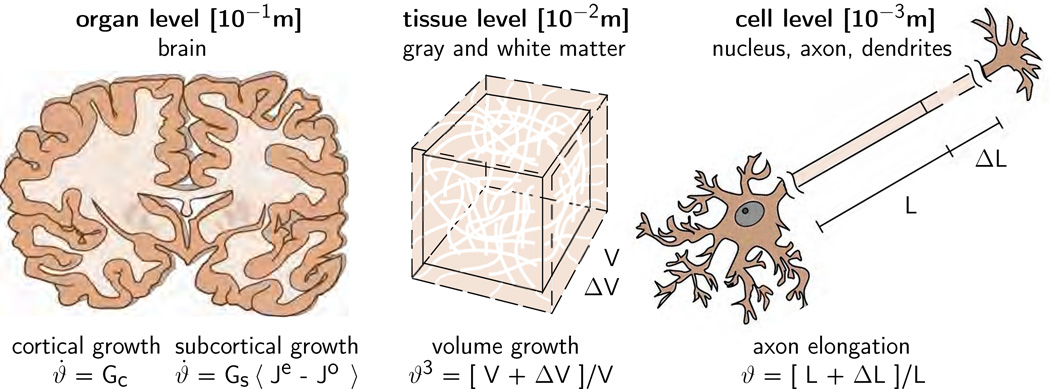
The mammalian brain is composed of an outer cortical layer of gray matter, consisting primarily of cell bodies, and an inner subcortical core of white matter, consisting primarily of axons. Within the limited space inside the skull, gyrification, the folding of the cortical layer, is viewed as a process to maximize the number of cell bodies and minimize the distance between them [70]. The total number of neurons, the number of connections, and the signaling speed are directly correlated with the capacity of information processing. It is thus not surprising that not only the total brain volume, but also the brain surface area, are viewed as strong indicators of intelligence [56]. The ratio between brain surface area and brain volume, and with it the degree of gyrification, can vary significantly between species [32]. With 86 billion neurons, 0.15 quadrillion connections, and a mass of 1,500 g, the human brain is often considered the most developed mammalian brain [30].

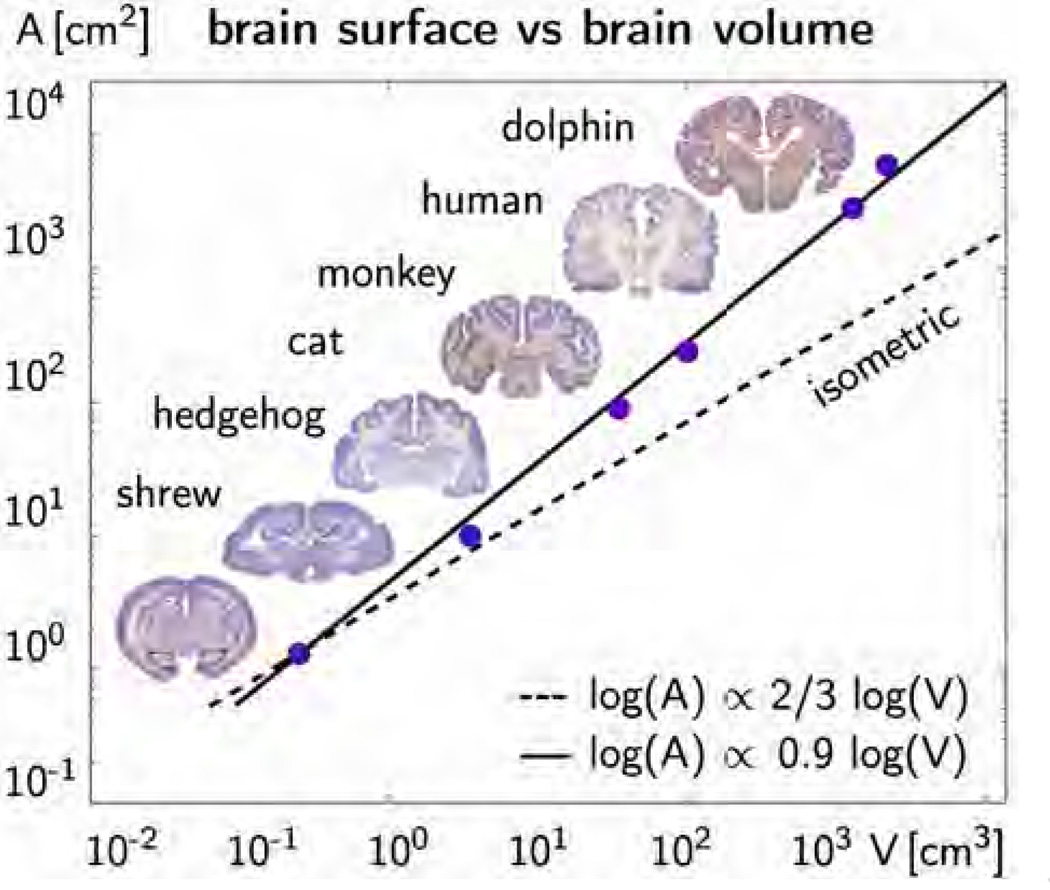
Figure 1 illustrates the average surface-to-volume relation of shrew, hedgehog, cat, monkey, human, and dolphin brains [32]. The graph confirms our intuition that larger mammals generally tend to have larger brains [65]. However, surprisingly, the surface area of the mammalian brain increases disproportionally faster than its volume [56]. In the log-log plot, the surface-to-volume ratio scales with a slope of 0.9, which is significantly larger than the slope of 2/3 for isometric scaling: Larger mammals not only have larger, but also more convoluted brains. This naturally raises the question [28]: What is the evolutionary advantage of a folded brain?

Figure 1.

Surface to volume ratio of the mammalian brain. Larger mammals have larger brains [65]. The dashed line with a slope of 2/3 indicates isometric scaling for which brain surface area would scale proportionally with brain volume. The solid line with a slope of 0.9 indicates that the mammalian brain surface area increases disproportionally faster than brain volume [32]. The degree of gyrification increases with brain size.

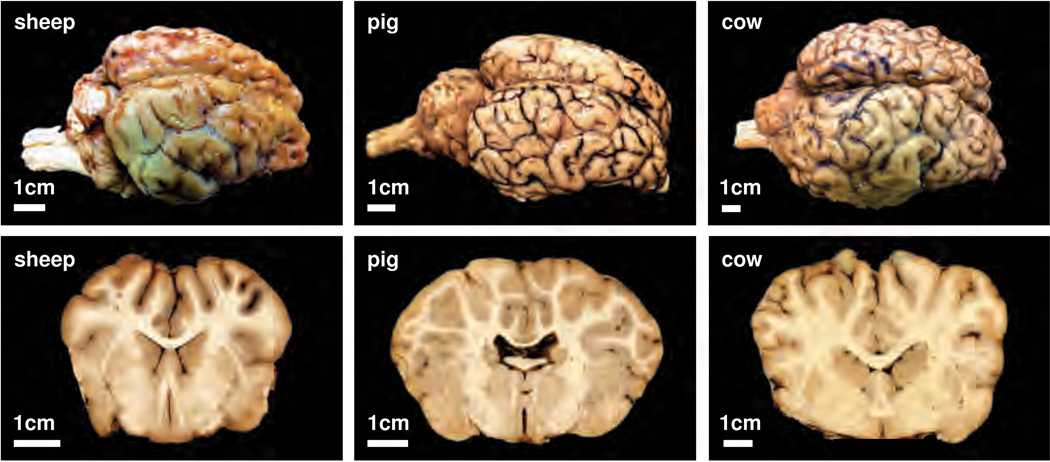
Figure 2 shows three explanted mammalian brains, which reconfirm that larger mammals tend to have larger brains [61]: The cow brain is larger than the pig brain, which in turn is larger than the brain of the sheep. Frontal coronal sections of the three brains illustrate that the degree of gyrification increases with brain size: The surface of the cow brain seems more folded than the surface of the pig brain, which seems more folded than the brain of the sheep [70]. The cortical thickness, however, seems to vary only marginally between the different species [66]. Studies of mammalian brains indicate that brain size is not the only contributing factor to gyrification [69]. This motivates our hypothesis that rather than brain size, other anatomical features like cortical thickness, cortical stiffness, and cortical growth during brain development play a crucial role in pattern formation.

Figure 2.

Surface morphology of the mammalian brain. Larger mammals have larger brains: The cow brain, right, is larger than the pig brain, middle, which is larger than the sheep brain, left. Photographs of the entire brain, upper row, and a frontal coronal brain section, lower row, illustrate the characteristic folding pattern: The surface of the cow brain, right, is more folded than the surface of the pig brain, middle, which is more folded than the sheep brain, left. The degree of gyrification increases with brain size.

The development of the mammalian brain takes place in two distinct stages, which are crucial for cortical folding [56]: First, progenitor cells located around the ventricles divide symmetrically into two new progenitor cells to increase the total number of cells. Then, these newly created cells divide asymmetrically into a progenitor cell and a neuron [61]. Neurons migrate toward the surface along radial glial cells to form the cortical layer [31]. According to the radial unit hypothesis, all neurons of the same progenitor cell stack up on top of one another to form a cortical column [49]. Symmetric division is therefore primarily responsible for an increase in brain surface area, while asymmetric division is primarily responsible for an increase in cortical thickness [56]. Irregularities in cell division or cell migration can evoke abnormalities in surface area or thickness [31]. Those range from polymicrogyria, a malformation associated with an increased surface area and an excessive number of small folds [62], to lissencephaly, a malformation associated with an increased cortical thickness and a reduced number of shallow folds [38]. Severe malformations are often correlated to neurological disorders, including developmental delay, epilepsy, schizophrenia, and autism [53]. Despite its pathophysiological importance, the phenomenon of cortical folding remains barely understood [57].

Cytological studies alone fail to explain the process of cortical folding [59] and seem to indicate that mechanical factors could play a crucial role [6]. Two competing hypotheses suggest that cortical folding is either driven by axonal tension [63] or by differential growth [54]. There is no direct evidence for either of these theories. Axonal tension, a mechanism to bring functionally related units topographically closer together, can explain folding irrespective of tissue stiffness, but disagrees with dissection experiments, which reveal significant tangential tension in the outer layers but not inside the developing gyri [64]. Differential growth, a mechanism to release residual stresses by surface buckling, agrees well with dissection experiments, but relies on unrealistic stiffness differences between cortex and subcortex [7]. From other biological systems we know that differential growth is capable of generating sufficient compressive stresses to induce structural instabilities [45]. Different geometric constraints, stiffness ratios, and growth rates may evoke different types of instabilities like buckles, wrinkles, creases, or folds [41]. Soft materials are especially susceptible to surface folding because of their low material stiffness [40]. Unfortunately, experiments to characterize the stiffness of the brain are rare and measured stiffness values span several orders of magnitude [25]. Virtual experiments and systematic parameter studies provide a powerful alternative to explore the developing mammalian brain.

Here we model brain development using the continuum theory of finite growth [55]. We model the cortex as a morphogenetically growing outer layer of cell bodies and the subcortex as a strain-driven growing inner core of axons. Motivated by experiments of axon elongation [11], we assume that chronic axonal overstretch activates mechanotransduction pathways, which collectively result in a gradual increase in axonal length [20]. This approach combines the two popular hypotheses of cortical folding, axonal tension and differential growth [6]. Using this model, we explore the effect of three key players in cortical folding: cortical thickness, stiffness, and growth. Since the absolute cortical stiffness and growth rate are poorly characterized [26], we explore the role of the relative cortical stiffness, and growth rate with respect to the subcortical properties.

The remainder of this manuscript is organized as follows: In Section 2, we present our analytical model for cortical folding to establish analytical estimates for the critical time, the critical pressure, and the critical wavelength at the onset of folding. In Section 3, we introduce our continuum model for finite growth to predict brain surface morphologies beyond the onset of folding. In Section 4, we summarize its computational solution within a nonlinear finite element setting. In Section 5, we utilize our model and perform systematic sensitivity studies of cortical thickness, stiffness and growth to understand the origin of pathological malformations. We close by a critical discussion of our results and their potential impact on understanding brain development in Section 6.

2. Analytical model

To establish analytical estimates for the brain surface morphology, we approximate cortical folding as the instability problem of a confined, layered medium subjected to growth-induced compression. We adopt the Föppl-von-Kármán theory [24, 35], and model the cortical deflection w using the classical fourth order plate equation [21],

$$\frac{E_{\mathrm{c}}}{1-{\nu }_{\mathrm{c}}^2}\frac{t_{\mathrm{c}}^3}{12}\frac{{\mathrm{d}}^{4}w}{\mathrm{d}{x}^4}+P{t}_{\mathrm{c}}\frac{{\mathrm{d}}^{2}w}{\mathrm{d}{x}^2}=q.$$ (1)

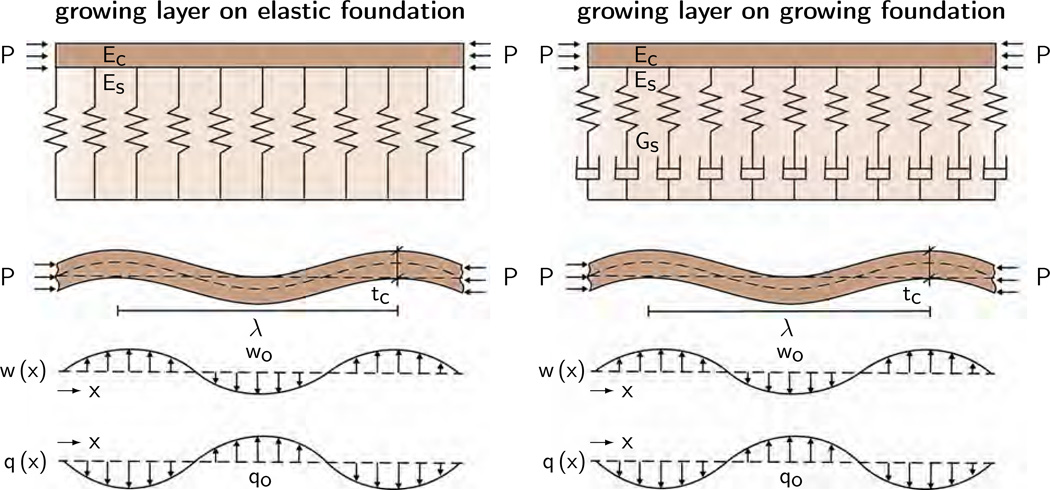
Figure 3 illustrates the analytical model with the cortical deflection w, Young’s modulus of the cortex E_c, Poisson’s ratio of the cortex ν_c, the cortical thickness t_c, the cortical pressure P, and the deflection-induced transverse force of the subcortical foundation q. We adopt a sinusoidal ansatz for the cortical deflection,

$$w(x)=w_0\text{cos}(nx)\text{with}n=2\pi /{\lambda }^{\text{crit}},$$ (2)

where the amplitude w₀ represents the sulcal depth, the wavenumber n represents the number of gyri and sulci, and the wavelength λ^crit represents the distance between two neighboring gyri. With this ansatz, the fourth order equation for cortical folding (1) takes the general form [10],

$$\frac{E_{\mathrm{c}}}{1-{\nu }_{\mathrm{c}}^2}\frac{t_{\mathrm{c}}^3}{12}{n}^4{w}_0\text{cos}(nx)-P{t}_{\mathrm{c}}{n}^2{w}_0\text{cos}(nx)=q(x),$$ (3)

where the transverse force q depends on the nature of the subcortical foundation. In the following, we illustrate analytical estimates for the critical pressure P^crit and the critical wavelength λ^crit for both an elastic foundation [9] as shown in Figure 3, left, and a growing foundation [10] as shown in Figure 3, right.

Figure 3.

Analytical model of confined, layered medium subjected to growth-induced compression. Growing layer on an elastic foundation, left, and on a growing foundation, right. We model cortical folding using the classical fourth order Föppl-von-Kármán plate theory and adopt a sinusoidal ansatz for the deflection w, which generates a sinusoidal transverse force q. This provides analytical estimates for the critical cortical pressure P^crit and for the wavelength λ^crit parameterized in terms of the cortical thickness t_c, the cortical and subcortical Young’s moduli E_c and E_s, and the cortical and subcortical growth rates G_c and G_s.

2.1. Growing cortex on elastic subcortex

To establish analytical estimates for cortical folding on an elastic subcortical foundation, we interpret the subcortex as an infinite half-space and impose a sinusoidal deflection w(x) = w₀ cos(nx) with a wavelength n and an amplitude w₀ on the upper boundary. This deflection evokes a transverse force q(x) with the same wavelength n,

$$q(x)=q_0\text{cos}(nx)\text{with}{q}_0=-\frac{E_{\mathrm{s}}}{2[1-{\nu }_{\mathrm{s}}^2]}n{w}_0.$$ (4)

Its amplitude q₀ depends on the amplitude of the deflection w₀, and, through the analytical solution of the elastic half space in terms of the Airy stress function, on Young’s modulus of the subcortex E_s, on Poisson’s ratio of subcortex ν_s, and on the wavenumber n [9]. Inserting this ansatz (4) into the Föppl-von-Kármán plate equation (3) yields the following equation for the cortical pressure P,

$$P=\frac{1}{12}\frac{E_{\mathrm{c}}}{1-{\nu }_{\mathrm{c}}^2}{t}_{\mathrm{c}}^2{n}^2+\frac{1}{2}\frac{E_{\mathrm{s}}}{1-{\nu }_{\mathrm{s}}^2}\frac{1}{t_{\mathrm{c}}n}.$$ (5)

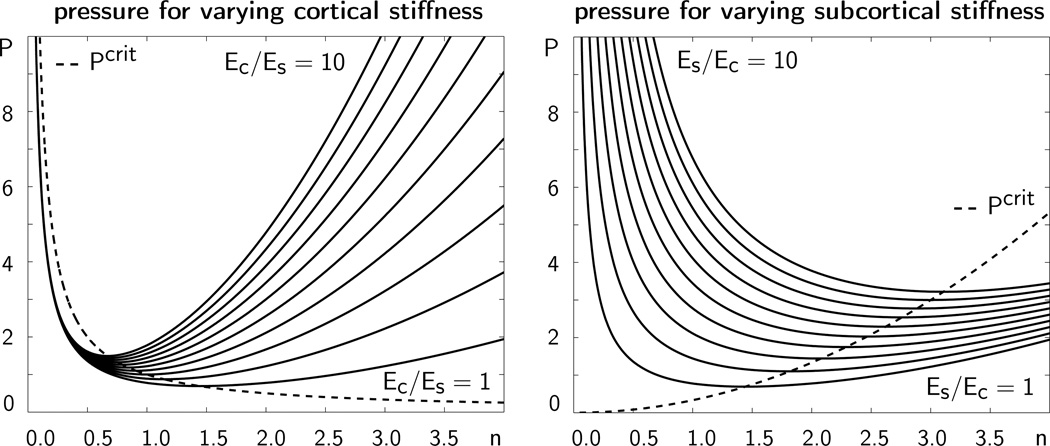
Figure 4 illustrates the growth-induced cortical pressure P as a function of the wavenumber n for varying cortical and subcortical stiffnesses. The minimum of each curve corresponds to the critical pressure P^crit at which folding occurs. The corresponding value of n is the critical wavenumber. The dotted line illustrates the critical pressure for varying wavenumbers.

Figure 4.

Growth-induced cortical pressure P as a function of the wavenumber n for varying cortical stiffnesses E_c, left, and varying subcortical stiffnesses E_s, right. The dotted line characterizes the critical pressure P^crit at which folding occurs. The corresponding wavenumber n characterizes the critical folding pattern.

To determine the critical wavenumber n, we elaborate the minimization problem P(n) → min, or, equivalently,

$$\frac{\mathrm{d}P}{\mathrm{d}n}=\frac{1}{6}\frac{E_{\mathrm{c}}}{1-{\nu }_{\mathrm{c}}^2}{t}_{\mathrm{c}}^{2}n-\frac{1}{2}\frac{E_{\mathrm{s}}}{1-{\nu }_{\mathrm{s}}^2}\frac{1}{t_{\mathrm{c}}{n}^2}\doteq 0\text{thus}n=\frac{1}{t_{\mathrm{c}}}\sqrt[3]{3\frac{1-{\nu }_{\mathrm{c}}^2}{1-{\nu }_{\mathrm{s}}^2}\frac{E_{\mathrm{s}}}{E_{\mathrm{c}}}}.$$ (6)

We can then immediately obtain estimates for the critical pressure P^crit and the critical wavelength λ^crit as functions of the cortical thickness t_c, the cortical and subcortical Young’s moduli E_c and E_s, and the cortical and subcortical Poisson’s ratios ν_c and ν_s [1],

$$P^{\text{crit}}=\frac{3}{4}\frac{E_s}{1-{\nu }_{\mathrm{s}}^2}\sqrt[3]{\frac{1}{3}\frac{1-{\nu }_{\mathrm{s}}^2}{1-{\nu }_{\mathrm{c}}^2}\frac{E_{\mathrm{c}}}{E_{\mathrm{s}}}}\text{and}{\lambda }^{\text{crit}}=2\pi t_{\mathrm{c}}\sqrt[3]{\frac{1}{3}\frac{1-{\nu }_{\mathrm{s}}^2}{1-{\nu }_{\mathrm{c}}^2}\frac{E_{\mathrm{c}}}{E_{\mathrm{s}}}}.$$ (7)

The Poisson’s ratios of biological tissue are typically within the same range, i.e., ν_c ~ ν_s. The most important observation is thus that the critical wavelength, the distance between two neighboring gyri, is directly proportional to the cortical thickness, λ^crit ∝ t_c, and to the third root of the ratio of the cortical and subcortical stiffnesses, ${\lambda }^{\text{crit}}\propto \sqrt[3]{E_{\mathrm{c}}/E_{\mathrm{s}}}$.

Remark 1 (Special case of incompressibility). If we assume that the cortex and subcortex are incompressible, ν_c = 0.5 and ν_s = 0.5, the analytical estimates for the critical pressure and wavelength reduce to the following expressions,

$$P^{\text{crit}}=E_{\mathrm{s}}\sqrt[3]{\frac{1}{3}\frac{E_{\mathrm{c}}}{E_{\mathrm{s}}}}\mathit{\text{and}}{\lambda }^{\text{crit}}=2\pi t_{\mathrm{c}}\sqrt[3]{\frac{1}{3}\frac{E_{\mathrm{c}}}{E_{\mathrm{s}}}}.$$

These are common estimates in materials sciences to characterize the buckling of a thin polymeric film on a thick polymeric substrate [16]: The wavelength of the buckling pattern is proportional to the thin film thickness, λ^crit ∝ t_c, and to the third root of the ratio of the film-to-substrate stiffness, ${\lambda }^{\text{crit}}\propto \sqrt[3]{E_{\mathrm{c}}/E_{\mathrm{s}}}$.

2.2. Growing cortex on growing subcortex

To establish analytical estimates for cortical folding on a growing foundation, we again interpret the subcortex as an infinite half-space and impose a sinusoidal deflection w(x) = w₀ cos(nx) on its upper boundary. Yet, now we assume that this deflection is the sum of an elastic subcortical deflection $w_0^e$ and subcortical growth $w_0^g$, such that $w_0=w_0^{\mathrm{e}}+w_0^{\mathrm{g}}$. Similarly, we can additively decompose the deflection rate ẇ₀ into an elastic part ${ẇ}_0^e$ and a growth part ${ẇ}_0^g$ [42],

$${ẇ}_0={ẇ}_0^{\mathrm{e}}+{ẇ}_0^{\mathrm{g}}\text{with}{ẇ}_0^{\mathrm{e}}=-\frac{2[1-{\nu }_{\mathrm{s}}^2]}{E_{\mathrm{s}}n}{\mathrm{q̇}}_0\text{and}{ẇ}_0^{\mathrm{g}}=G_{\mathrm{s}}{w}_0^{\mathrm{e}}=-G_{\mathrm{s}}\frac{2[1-{\nu }_{\mathrm{s}}^2]}{E_{\mathrm{s}}n}{q}_0.$$ (8)

The elastic deflection, $w_0^{\mathrm{e}}=-2[1-{\nu }_{\mathrm{s}}^2]/[E_{\mathrm{s}}n]q_0$, and its rate, ${ẇ}_0^{\mathrm{e}}=-2[1-{\nu }_{\mathrm{s}}^2]/[E_{\mathrm{s}}n]{\mathrm{q̇}}_0$, follow from inverting the elastic half-space relation in equation (4). The growth deflection rate ${ẇ}_0^g$ represents the growing subcortex. We assume that subcortical growth is stretch-induced, proportional to the elastic subcortical deflection $w_0^e$, scaled by the subcortical growth rate G_s. Combining all three equations yields an equation for the transverse force q₀ as a Maxwell-type viscoelastic response to the deflection w₀,

$${\mathrm{q̇}}_0+G_{\mathrm{s}}{q}_0=-\frac{E_{\mathrm{s}}}{2[1-{\nu }_{\mathrm{s}}^2]}n{ẇ}_0.$$ (9)

We introduce a sinusoidal representation of the transverse force q(x) and adopt a convolution type solution for the amplitude q₀,

$$q=q_0\text{cos}(nx)\text{with}{q}_0(t)=-\frac{E_{\mathrm{s}}}{2[1-{\nu }_{\mathrm{s}}^2]}n{\int }_{-\infty }^t\text{exp}(-G_{\mathrm{s}}[t-s])\frac{\mathrm{d}{w}_0}{\mathrm{d}s}\mathrm{d}s.$$ (10)

We choose an exponential ansatz for the deflection amplitude, w₀(t) = W₀ exp (G t), such that dw₀/ds = Gw₀(t), where G is the characteristic time constant of cortical folding. We insert equation (10) into the Föppl-von-Kármán plate equation (3) to eventually obtain the equation for the cortical pressure,

$$P=\frac{1}{12}\frac{E_{\mathrm{c}}}{1-{\nu }_{\mathrm{c}}^2}{t}_{\mathrm{c}}^2{n}^2+\frac{1}{2}\frac{E_{\mathrm{s}}}{1-{\nu }_{\mathrm{s}}^2}\frac{G}{G+G_{\mathrm{s}}}\frac{1}{t_{\mathrm{c}}n}.$$ (11)

Similar to the elastic foundation, we evaluate the minimization problem P(n) → min to determine the critical wavenumber n,

$$\frac{\mathrm{d}P}{\mathrm{d}n}=\frac{1}{6}\frac{E_{\mathrm{c}}}{1-{\nu }_{\mathrm{c}}^2}{t}_{\mathrm{c}}^{2}n-\frac{1}{2}\frac{E_{\mathrm{s}}}{1-{\nu }_{\mathrm{s}}^2}\frac{G}{G+G_{\mathrm{s}}}\frac{1}{t_{\mathrm{c}}{n}^2}\doteq 0\to n=\frac{1}{t_{\mathrm{c}}}\sqrt[3]{3\frac{1-{\nu }_{\mathrm{c}}^2}{1-{\nu }_{\mathrm{s}}^2}\frac{E_{\mathrm{s}}}{E_{\mathrm{c}}}\frac{G}{G+G_{\mathrm{s}}}}.$$ (12)

The estimates for the critical pressure P^crit and the wavelength λ^crit then follow immediately as functions of the cortical thickness t_c, the cortical and subcortical Young’s moduli E_c and E_s, the cortical and subcortical Poisson’s ratios ν_c and ν_s, the subcortical growth rate G_s, and the characteristic time constant of cortical folding G,

$$P^{\text{crit}}=\frac{3}{4}\frac{E_{\mathrm{s}}}{1-{\nu }_{\mathrm{s}}^2}\frac{G}{G+G_{\mathrm{s}}}\sqrt[3]{\frac{1}{3}\frac{1-{\nu }_{\mathrm{s}}^2}{1-{\nu }_{\mathrm{c}}^2}\frac{E_{\mathrm{c}}}{E_{\mathrm{s}}}\frac{G+G_{\mathrm{s}}}{G}}\text{and}{\lambda }^{\text{crit}}=2\pi t_{\mathrm{c}}\sqrt[3]{\frac{1}{3}\frac{1-{\nu }_{\mathrm{s}}^2}{1-{\nu }_{\mathrm{c}}^2}\frac{E_{\mathrm{c}}}{E_{\mathrm{s}}}\frac{G+G_{\mathrm{s}}}{G}}.$$ (13)

Again, we can assume that the Poisson’s ratios of the cortex and subcortex are of the same order, ν_c ~ ν_s. From the remaining parameters, we conclude that the critical wavelength, the distance between two neighboring gyri, is directly proportional to the cortical thickness, λ^crit ∝ t_c, to the third root of the ratio of the cortical and subcortical stiffnesses, ${\lambda }^{\text{crit}}\propto \sqrt[3]{E_{\mathrm{c}}/E_{\mathrm{s}}}$, and to the subcortical growth rate, ${\lambda }^{\text{crit}}\propto \sqrt[3]{(G+G_{\mathrm{s}})/G}$. At the onset of folding, we assume that the growth-induced pressure in the cortical layer is equivalent to the elastic modulus of the cortex, $E_{\mathrm{c}}/[1-{\nu }_{\mathrm{c}}^2]$, multiplied by the amount of cortical growth. In the simplest case, we can represent cortical growth as the product of the cortical growth rate G_c and the critical folding time t^crit [6],

$$P^{\text{crit}}=\frac{E_{\mathrm{c}}}{1-{\nu }_{\mathrm{c}}^2}{G}_{\mathrm{c}}{t}^{\text{crit}}.$$ (14)

By combining the critical pressure P^crit at the onset of folding (13.1) with the cortical pressure generated by growth (14), we obtain a critical condition at the onset of folding, expressed in terms of the critical folding time t^crit and the characteristic time constant for cortical folding G.

$$\frac{E_{\mathrm{c}}}{1-{\nu }_{\mathrm{c}}^2}{G}_{\mathrm{c}}{t}^{\text{crit}}\doteq \frac{3}{4}\frac{E_{\mathrm{s}}}{1-{\nu }_{\mathrm{s}}^2}\frac{G}{G+G_{\mathrm{s}}}\sqrt[3]{\frac{1}{3}\frac{1-{\nu }_{\mathrm{s}}^2}{1-{\nu }_{\mathrm{c}}^2}\frac{E_{\mathrm{c}}}{E_{\mathrm{s}}}\frac{G+G_{\mathrm{s}}}{G}}$$ (15)

To further evaluate this condition, we choose G = 1/t^crit [6], to obtain a quintic equation for the critical folding time,

$${(t^{\text{crit}})}^5+\frac{2}{G_{\mathrm{s}}}{(t^{\text{crit}})}^4+\frac{1}{G_{\mathrm{s}}^2}{(t^{\text{crit}})}^3-\frac{9}{64}\frac{{[1-{\nu }_{\mathrm{c}}^2]}^2}{{[1-{\nu }_{\mathrm{s}}^2]}^2}\frac{E_{\mathrm{s}}^2}{E_{\mathrm{c}}^2}\frac{1}{G_{\mathrm{c}}^3{G}_{\mathrm{s}}^2}\doteq 0.$$ (16)

For given cortical and subcortical Young’s moduli E_c and E_s, cortical and subcortical Poisson’s ratios ν_c and ν_s, and cortical and subcortical growth rates G_c and G_s, we solve this equation for the folding time t^crit and then determine the critical pressure P^crit from equation (14) and the critical wavelength λ^crit from equation (13.2).

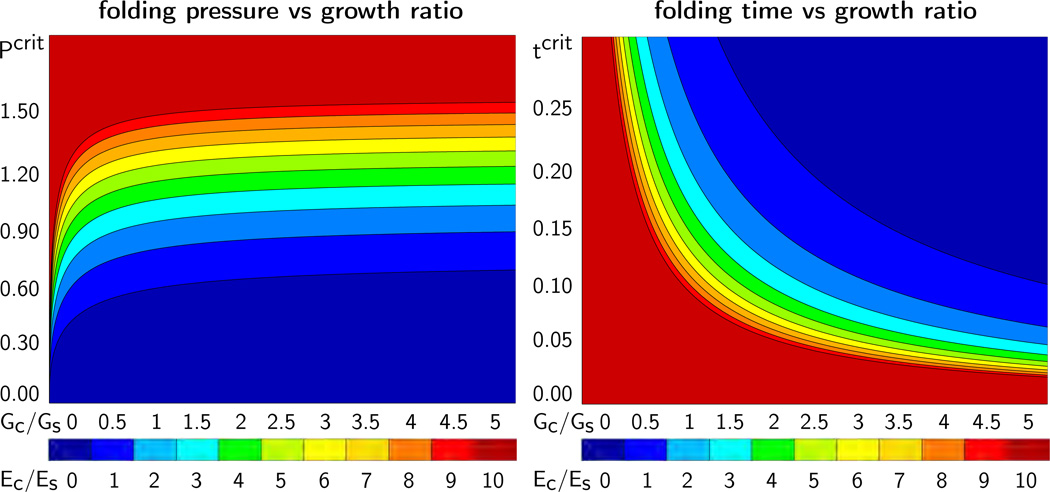
Figure 5 illustrates the critical folding pressure P^crit, left, and the critical folding time t^crit, right, for varying growth ratios G_c/G_s and stiffness ratios E_c/E_s. For simplicity, we have assumed that cortex and subcortex have identical Poisson’s ratios, ν_c = ν_s. The graphs agree with our intuition: The larger the cortical stiffness, the larger the required folding pressure P^crit and the smaller the folding time t^crit.

Figure 5.

Critical folding pressure P^crit, left, and critical folding time t^crit, right, for varying growth ratio G_c/G_s and varying stiffness ratio E_c/E_s. The folding pressure P^crit increases with increasing cortical growth G_c and increasing cortical stiffness E_c. The folding time t^crit decreases with increasing cortical growth G_c and increasing cortical stiffness E_c.

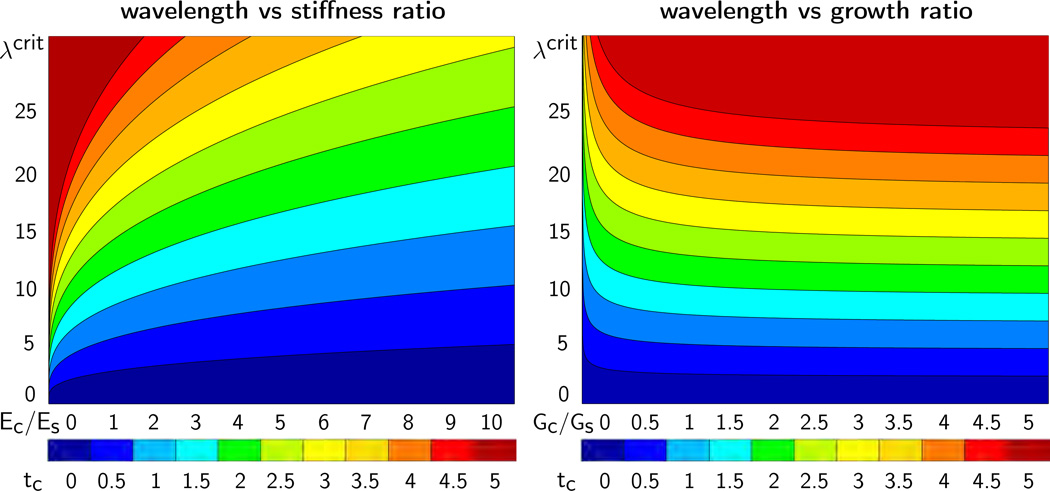
Figure 6 illustrates the critical wavelength λ^crit for varying stiffness ratios E_c/E_s and varying cortical thicknesses t_c, left, and for varying growth ratios G_c/G_s and varying cortical thicknesses t_c, right. The graphs visualize our analytical estimates: The wavelength increases linearly with increasing cortical thickness t_c, increases with increasing stiffness ratio E_c/E_s, and decreases with increasing growth ratio G_c/G_s.

Figure 6.

Critical wavelength λ^crit for varying stiffness ratios E_c/E_s and varying cortical thicknesses t_c, left, and for varying growth ratios G_c/G_s and varying cortical thicknesses t_c, right. The wavelength λ^crit increases with increasing cortical stiffness E_c, with increasing subcortical growth rate G_s, and with increasing cortical thickness t_c.

Remark 2 (Special case of incompressibility). If we assume that the cortex and subcortex are incompressible, ν_c = 0.5 and ν_s = 0.5, the analytical estimates for the critical pressure and wavelength reduce to the following expressions,

$$P^{\text{crit}}=E_{\mathrm{s}}\frac{G}{G+G_{\mathrm{s}}}\sqrt[3]{\frac{1}{3}\frac{E_{\mathrm{c}}}{E_{\mathrm{s}}}\frac{G+G_{\mathrm{s}}}{G}}\mathit{\text{and}}{\lambda }^{\text{crit}}=2\pi t_{\mathrm{c}}\sqrt[3]{\frac{1}{3}\frac{E_{\mathrm{c}}}{E_{\mathrm{s}}}\frac{G+G_{\mathrm{s}}}{G}}.$$

This simplification agrees with findings in the literature [6]: The wavelength of cortical folding is proportional to the cortical thickness, λ^crit ∝ t_c, to the third root of the ratio of the cortical-to-subcortical stiffness, ${\lambda }^{\text{crit}}\propto \sqrt[3]{E_{\mathrm{c}}/E_{\mathrm{s}}}$, and to the subcortical growth rate ${\lambda }^{\text{crit}}\propto \sqrt[3]{G+G_{\mathrm{s}})/G}=\sqrt[3]{1+G_{\mathrm{s}}{t}^{\text{crit}}}$.

Remark 3 (Special cases of solid- and fluid-like subcortex). As indicated in Figure 3, we have modeled the growing subcortex as Maxwell type viscoelastic solid with ${\mathrm{q̇}}_0+G_{\mathrm{s}}{q}_0=-E_{\mathrm{s}}/[2[1-{\nu }_{\mathrm{s}}^2]]$ n ẇ₀ in equation (9). This implies that the subcortex will behave solid-like and fluid-like in the two extreme cases,

$$G_{\mathrm{s}}\ll G\text{solid-like subcortex with}{\lambda }^{\text{crit}}=2\pi t_c\sqrt[3]{\frac{1}{3}\frac{1-{\nu }_{\mathrm{s}}^2}{1-{\nu }_{\mathrm{c}}^2}\frac{E_{\mathrm{c}}}{E_{\mathrm{s}}}}{G}_{\mathrm{s}}\gg G\text{fluid-like subcortex with}{\lambda }^{\text{crit}}\to \infty .$$

For small subcortical growth rates G_s ≪ G, we immediately recover the solution for the elastic subcortex from Section 2.1. In Figure 5, left and right, and Figure 6, right, small subcortical growth rates correspond to large growth ratios G_c/G_s. We recover the special case of a solid-like subcortex as the asymptotic behavior for G_c/G_s → ∞. Increasing the subcortical growth rate increases the wavelength λ^crit. For large enough subcortical growth rates G_s ≫ G, we can suppress folding entirely. We recover the special case of a fluid-like subcortex as the asymptotic behavior for G_c/G_s → 0 with t^crit → ∞and λ^crit → ∞. These extreme cases agree with the literature of a wrinkling layer on a viscous substrate [34]: The solid-like subcortex corresponds to the extreme case of a glassy substrate; The fluid-like subcortex corresponds to the extreme case of a rubbery substrate.

3. Continuum model

To explore the folding pattern beyond the onset of folding, we model growth using the nonlinear field theories of mechanics supplemented by the theory of finite growth. This results in a set of five equations, which define the kinematics, the constitutive behavior, the mechanical equilibrium, the growth kinematics, and the growth kinetics.

Figure 7 illustrates our multiscale continuum model for cortical and subcortical growth in the developing mammalian brain. To characterize the kinematics of finite deformation, we introduce the deformation map ϕ, which maps points X from the undeformed configuration to their new positions x = ϕ (X, t) in the deformed configuration. We then introduce the deformation gradient, which we decompose multiplicatively into an elastic part F^e and a growth part F^g [27],

$$\mathit{F}={\mathrm{\nabla }}_{\mathit{X}}\phi ={\mathit{F}}^{\mathrm{e}}·{\mathit{F}}^{\mathrm{g}}\text{and}J=\text{det}(\mathit{F})=J^{\mathrm{e}}{J}^{\mathrm{g}}.$$ (17)

Figure 7.

Multiscale continuum model for cortical and subcortical growth. The cortex, the gray matter, grows morphogenetically at a constant rate G_c. Cortical growth induces subcortical deformation, which triggers subcortical growth. The subcortex, the white matter, grows at a stretchdependent rate as G_s 〈 J^e − J⁰ 〉, where G_s mimics the axon elongation rate and 〈 J^e − J⁰ 〉 activates growth only, if the elastic volume stretch J^e exceeds its baseline value J⁰.

A similar multiplicative decomposition holds for the Jacobian J, which we decompose into an elastic part J^e and a growth part J^g. To define the growth kinematics, for simplicity, we assume that growth is purely isotropic, parameterized in terms of a single scalar-valued growth multiplier ϑ,

$${\mathit{F}}^{\mathrm{g}}=\vartheta \mathit{I}\text{and}{J}^{\mathrm{g}}=\text{det}({\mathit{F}}^{\mathrm{g}})={\vartheta }^3.$$ (18)

This implies that the grown volume J^g is identical to the growth multiplier cubed ϑ³. In the initial ungrown state, the growth multiplier is one, ϑ = 1, such that ϑ > 1 and ϑ < 1 characterize volume growth and shrinkage. The elastic tensor F^e and its Jacobian J^e then take the following explicit forms,

$${\mathit{F}}^{\mathrm{e}}=\mathit{F}/\vartheta \text{and}{J}^{\mathrm{e}}\text{det}({\mathit{F}}^{\mathrm{e}})=J/{\vartheta }^3.$$ (19)

For simplicity, we assume that both cortex and subcortex are isotropic and elastic. We characterize their constitutive behavior through the following Neo-Hookean free energy parameterized exclusively in terms of the elastic tensor F^e and its Jacobian J^e, for example as

$$\psi ({\mathit{F}}^{\mathrm{e}})=\frac{1}{2}\lambda {\text{ln}}^2(J^{\mathrm{e}})+\frac{1}{2}\mu [{\mathit{F}}^{\mathrm{e}}:{\mathit{F}}^{\mathrm{e}}-3-2\text{ln}(J^{\mathrm{e}})],$$ (20)

where λ and µ are the Lamé constants. This implies that only the elastic part of the deformation induces stress. For the following considerations, it proves convenient to reparameterize the free energy (20) in terms of the total deformation gradient F and the growth factor ϑ,

$$\psi (\mathit{F},\vartheta )=\frac{1}{2}\lambda {\text{ln}}^2\left(\frac{J}{{\vartheta }^3}\right)+\frac{1}{2}\mu [\frac{1}{{\vartheta }^2}\mathit{F}:\mathit{F}-3-2\text{ln}(\frac{J}{{\vartheta }^3}\left)\right].$$ (21)

Following standard arguments of thermodynamics, the Piola stress P follows as energetically conjugate to the deformation gradient F,

$$\mathit{P}=\frac{\partial \psi (\mathit{F},\vartheta )}{\partial \mathit{F}}=\frac{1}{{\vartheta }^2}\mu \mathit{F}+\left[\lambda \text{ln}\right(\frac{J}{{\vartheta }^3})-\mu ]{\mathit{F}}^{-\mathrm{t}}.$$ (22)

The Piola stress enters the standard balance of linear momentum, the equation of mechanical equilibrium. In the absence of volume forces, the balance of linear momentum reduces to the vanishing divergence of the Piola stress,

$$\text{Div}(\mathit{P})\doteq \mathbf{0}.$$ (23)

It remains to define the kinetics of growth, the equations that characterize the evolution of the growth multiplier in time [43]. Since the cortex consists primarily of cell nuclei whereas the subcortex consists primarily of axons, we assume different growth kinetics for the cortex and subcortex.

3.1. Cortical growth

For the cortex, we assume that growth is purely morphogenetic [8], independent of mechanical stress or strain [2], characterized exclusively by the growth rate G_c,

$$\mathrm{\vartheta ̇}=G_{\mathrm{c}}.$$ (24)

The cortical growth rate G_c may vary in time and space, depending on the current stage of development and on the regional location. For simplicity, here we let the cortex grow linearly in time and homogeneously in space, G_c = const.

3.2. Subcortical growth

For the subcortex, we assume that growth is stretch-induced [37]. Cortical growth induces extreme deformations in the subcortex. The subcortex is primarily populated by axons, which lengthen gradually when subject to chronic stretch [11]. We make the following ansatz,

$$\mathrm{\vartheta ̇}=G_{\mathrm{s}}\langle J^{\mathrm{e}}-J^0\rangle =G_{\mathrm{s}}\langle J/{\vartheta }^3-J^0\rangle ,$$ (25)

where G_s is the subcortical growth rate. With 〈 J^e − J⁰ 〉 = J^e − J⁰ for J^e > J⁰ and 〈 J^e − J⁰ 〉 = 0 otherwise, the term in the Macaulay brackets activates growth only if the elastic volume stretch J^e exceeds its baseline value J⁰, i.e., when axons are stretched beyond their physiological limit [20].

Remark 4 (Stresses). To provide a more intuitive illustration of the Piola stress, we re-evaluate the thermodynamic stress definition P = ∂ψ/∂F of equation (22), yet now, formulated in terms of the elastic deformation F^e, using the Neo-Hookean free energy (20),

$$\mathit{P}=\frac{\partial \psi ({\mathit{F}}^{\mathrm{e}})}{\partial \mathit{F}}=\frac{\partial \psi ({\mathit{F}}^{\mathrm{e}})}{\partial {\mathit{F}}^{\mathrm{e}}}:\frac{\partial {\mathit{F}}^{\mathrm{e}}}{\partial \mathit{F}}={\mathit{P}}^{\mathrm{e}}·{\mathit{F}}^{\mathrm{g}-\mathrm{t}}=\frac{1}{\vartheta }{\mathit{P}}^{\mathrm{e}}.$$ (26)

This indicates that the Piola stress in equation (22) is nothing but the growth-weighted classic elastic Piola stress,

$${\mathit{P}}^{\mathrm{e}}=\frac{\mathrm{d}\psi ({\mathit{F}}^{\mathrm{e}})}{\mathrm{d}{\mathit{F}}^{\mathrm{e}}}=\mu {\mathit{F}}^{\mathrm{e}}+{\lambda }^{\text{crit}}[\text{ln}(J^{\mathrm{e}})-\mu ]{\mathit{F}}^{\mathrm{e}-\mathrm{t}}.$$ (27)

For the special case of isotropic growth, growth-weighting simplifies to dividing the elastic Piola stress by the growth factor ϑ.

4. Computational model

To solve the nonlinear equations for brain development, we adopt a finite element discretization in space and a finite difference discretization in time. We introduce the growth multiplier ϑ as an internal variable, and solve its evolution equation for cortical growth (24) and subcortical growth (25) locally at the integration point level. We approximate the growth rate ϑ̇ through a finite difference ansatz,

$$\mathrm{\vartheta ̇}=[\vartheta -{\vartheta }_{\mathrm{n}}]/\mathrm{\Delta }t,$$ (28)

where ϑ is the current growth multiplier, ϑ_n is the growth multiplier of the previous time step, and Δt = t − t_n denotes the current time increment.

4.1. Cortical growth

For the cortex, we determine the new growth multiplier ϑ explicitly through a linear update of the previous growth multiplier ϑ_n using equations (24) and (28) as

$$\vartheta ={\vartheta }_{\mathrm{n}}+G_{\mathrm{c}}\mathrm{\Delta }t.$$ (29)

To solve the global set of equations, we determine the tangent moduli of the cortex through the total derivative of the Piola stress P from equation (22) with respect to the deformation gradient F and fix the current growth multiplier ϑ,

$$\mathbf{A}=\frac{\mathrm{d}\mathit{P}}{\mathrm{d}\mathit{F}}={\frac{\partial \mathit{P}}{\partial \mathit{F}}|}_{\vartheta }={\mathbf{A}}^{\mathrm{e}}.$$ (30)

Since the growth multiplier is independent of the current deformation, the tangent moduli simply consist of the growth-weighted classical elastic tangent moduli [48],

$${\mathbf{A}}^{\mathrm{e}}=\frac{1}{{\vartheta }^2}\mu \mathit{I}\otimes ̅\mathit{I}+[\mu -\lambda \text{ln}(\frac{J}{{\vartheta }^3}\left)\right]{\mathit{F}}^{-\mathrm{t}}\otimes ̲{\mathit{F}}^{-1}+\lambda {\mathit{F}}^{-\mathrm{t}}\otimes {\mathit{F}}^{-\mathrm{t}}.$$ (31)

Here, we have used the following abbreviations, {•⊗̅◦}_ijkl = {•}_ik {◦}_jl and {•⊗̲◦}_ijkl = {•}_il {◦} _jk, for the non-standard fourth order products.

4.2. Subcortical growth

For the subcortex, we apply an implicit time integration scheme and reformulate the evolution equation (25) with the help of the finite difference ansatz (28). This introduces the discrete residual 𝖱 in terms of the unknown growth multiplier ϑ,

$$𝖱=\vartheta -{\vartheta }_{\mathrm{n}}-G_{\mathrm{s}}\langle \frac{1}{{\vartheta }^3}J-J^0\rangle \mathrm{\Delta }t\doteq 0.$$ (32)

To solve this nonlinear equation, we adopt a local Newton iteration. For each iteration step, we calculate the linearization of the residual 𝖱 with respect to the current growth multiplier ϑ,

$$𝖪=\frac{\mathrm{d}𝖱}{\mathrm{d}\vartheta }=1+3G_{\mathrm{s}}\frac{1}{{\vartheta }^4}J\mathrm{\Delta }t\mathscr{H}(J/{\vartheta }^3-J^0).$$ (33)

The Heaviside step function ℋ is one during growth, J/ϑ³ − J⁰ > 0, and zero otherwise. Within each iteration step, we update the unknown growth multiplier,

$$\vartheta \leftarrow \vartheta -𝖱/𝖪,$$ (34)

until we achieve local convergence, i.e., until the absolute value of the growth update |𝖱/ 𝖪 | is smaller than a user-defined convergence threshold. To solve the global set of equations, we determine the tangent moduli of the subcortex through the total derivative of the Piola stress P from equation (22) with respect to the deformation gradient F,

$$\mathbf{A}=\frac{\mathrm{d}\mathit{P}}{\mathrm{d}\mathit{F}}={\frac{\partial \mathit{P}}{\partial \mathit{F}}|}_{\vartheta }+\frac{\partial \mathit{P}}{\partial \vartheta }\otimes {\frac{\partial \vartheta }{\partial \mathit{F}}|}_F={\mathbf{A}}^{\mathrm{e}}+{\mathbf{A}}^{\mathrm{g}}.$$ (35)

The first term, the Hessian of the free energy function for constant growth, ϑ = const., defines the growth-weighted classical elastic tangent moduli similar to the case of cortical growth (31),

$${\mathbf{A}}^{\mathrm{e}}=\frac{\partial \mathit{P}}{\partial \mathit{F}}=\frac{1}{{\vartheta }^2}\mu \mathit{I}\otimes ̅\mathit{I}+[\mu -\lambda \text{ln}(\frac{J}{{\vartheta }^3}\left)\right]{\mathit{F}}^{-\mathrm{t}}\otimes ̲{\mathit{F}}^{-1}+\lambda {\mathit{F}}^{-\mathrm{t}}\otimes {\mathit{F}}^{-\mathrm{t}}.$$ (36)

The second term is specific to the constitutive equation (20) and characterizes the sensitivity of the Piola stress P with respect to the growth multiplier ϑ,

$$\frac{\partial \mathit{P}}{\partial \vartheta }=-\frac{1}{{\vartheta }^3}[2\mu \mathit{F}+\lambda {\mathit{F}}^{-\mathrm{t}}].$$ (37)

The third term is specific to both the kinetic equation for growth (25) and its algorithmic solution (33),

$$\frac{\partial \vartheta }{\partial \mathit{F}}=\frac{\partial \vartheta }{\partial \mathrm{\vartheta ̇}}\frac{\partial \mathrm{\vartheta ̇}}{\partial \mathit{F}}=\frac{1}{{\vartheta }^3}\frac{G_{\mathrm{s}}\mathrm{\Delta }t}{𝖪}J{\mathit{F}}^{-\mathrm{t}},$$ (38)

where ∂ ϑ̇/∂ϑ = 𝖪 and ∂ ϑ̇/∂F = G_s J F^−t/ϑ³. The Hessian of the free energy function for constant deformation, F = const., defines the correction of the constitutive moduli due to growth,

$${\mathbf{A}}^{\mathrm{g}}=-\frac{1}{{\vartheta }^6}\frac{G_{\mathrm{s}}\mathrm{\Delta }t}{𝖪}J[2\mu \mathit{F}+\lambda {\mathit{F}}^{-\mathrm{t}}]\otimes {\mathit{F}}^{-\mathrm{t}}.$$ (39)

The fourth-order tangent moduli for the cortex (30) and for the subcortex (35) enter the iteration matrix for the global Newton iteration. Upon convergence of the global Newton iteration, we store the current growth multiplier ϑ locally at the integration point level.

Remark 5 (Tangent moduli). Again, we can reformulate the definition of the elastic tangent operator A^e = ∂P/∂F in terms of the elastic deformation F^e to obtain a more intuitive interpretation of its terms,

$${\mathbf{A}}^{\mathrm{e}}({\mathit{F}}^{\mathrm{e}})=\frac{\partial \mathit{P}({\mathit{F}}^{\mathrm{e}})}{\partial \mathit{F}}=\frac{\partial \mathit{P}({\mathit{F}}^{\mathrm{e}})}{\partial {\mathit{F}}^{\mathrm{e}}}:\frac{\partial {\mathit{F}}^{\mathrm{e}}}{\partial \mathit{F}}=[\mathit{I}\otimes ̅{\mathit{F}}^{\mathrm{g}-1}]:\frac{\mathrm{d}\mathit{P}({\mathit{F}}^{\mathrm{e}})}{\mathrm{d}{\mathit{F}}^{\mathrm{e}}}:[\mathit{I}\otimes ̅{\mathit{F}}^{\mathrm{g}-\mathrm{t}}]=\frac{1}{{\vartheta }^2}\frac{\mathrm{d}{\mathit{P}}^{\mathrm{e}}({\mathit{F}}^{\mathrm{e}})}{\mathrm{d}{\mathit{F}}^{\mathrm{e}}}.$$ (40)

This indicates that the elastic tangents in (31) and (36) are nothing but the growth-weighted standard tangent operator,

$$\frac{\mathrm{d}{\mathit{P}}^{\mathrm{e}}({\mathit{F}}^{\mathrm{e}})}{\mathrm{d}{\mathit{F}}^{\mathrm{e}}}=\frac{{\mathrm{d}}^2\psi ({\mathit{F}}^{\mathrm{e}})}{\mathrm{d}{\mathit{F}}^{\mathrm{e}}\otimes \mathrm{d}{\mathit{F}}^{\mathrm{e}}}=\mu \mathit{I}\otimes ̅\mathit{I}+[\mu -\lambda \text{ln}(J^{\mathrm{e}})]{\mathit{F}}^{\mathrm{e}-\mathrm{t}}\otimes ̲{\mathit{F}}^{\mathrm{e}-1}+\lambda {\mathit{F}}^{\mathrm{e}-\mathrm{t}}\otimes {\mathit{F}}^{\mathrm{e}-\mathrm{t}}.$$ (41)

For the special case of isotropic growth, this growth-weighting simplifies to dividing the tangent by the growth factor squared ϑ².

5. Results

To illustrate the features of our computational model, we expand the analytical study in Section 2 beyond the onset of folding, which is difficult to assess analytically and has only been addressed recently by a few groups [4, 15]. During brain development, constrained growth of the cortical layer induces compressive stresses P. Once these stresses reach a critical value P^crit, the brain surface buckles into a wavy pattern to partially release the growth-induced stress. In analogy to the analytical estimates in Section 2 and Figure 6, we explore the role of the three main contributors to the folding pattern: the cortical thickness t_c, the stiffness ratio between cortex and subcortex E_c/E_s, and the growth ratio between cortex and subcortex G_c/G_s.

5.1. Sensitivity of surface morphology with respect to cortical thickness

To explore the effect of the initial cortical thickness t_c on the folding pattern, we explore constrained growth in a regular rectangular slice of 2 × 1 × 0.05 cm³ of a transverse brain section. We discretize the slice with 80 × 40 × 1 = 3, 200 tri-linear Q1 elements and 19,926 degrees of freedom and assume a plane strain state. To constrain growth, we fix the left, bottom, and right boundary nodes orthogonal to the boundary, but allow them to slide freely along the edge.

We model the cortex as Neo Hookean elastic with Lamé constants λ_c = 34.2 kPa and µ_c = 3.3 kPa [60] and assume that the subcortex is three times softer with λ_s = 11.4 kPa and µ_s = 1.1 kPa [12]. We fix the cortical growth rate to G_c = 2.0, the subcortical growth rate to G_s = 0.003, and the physiological limit for axonal growth to J⁰=1.0 [17]. Since a perfectly regular rectangular domain would not fold in the computational simulation, we trigger an initial imperfection by selectively increasing the subcortical growth rate G_s by 10% in a 0.05 cm thin vertical band in the center of the rectangle [6]. We gradually increase the initial cortical thickness from t_crit = 0.125mmto t_crit = 1.000mm in eight equal steps of Δt_crit = 0.125 mm.

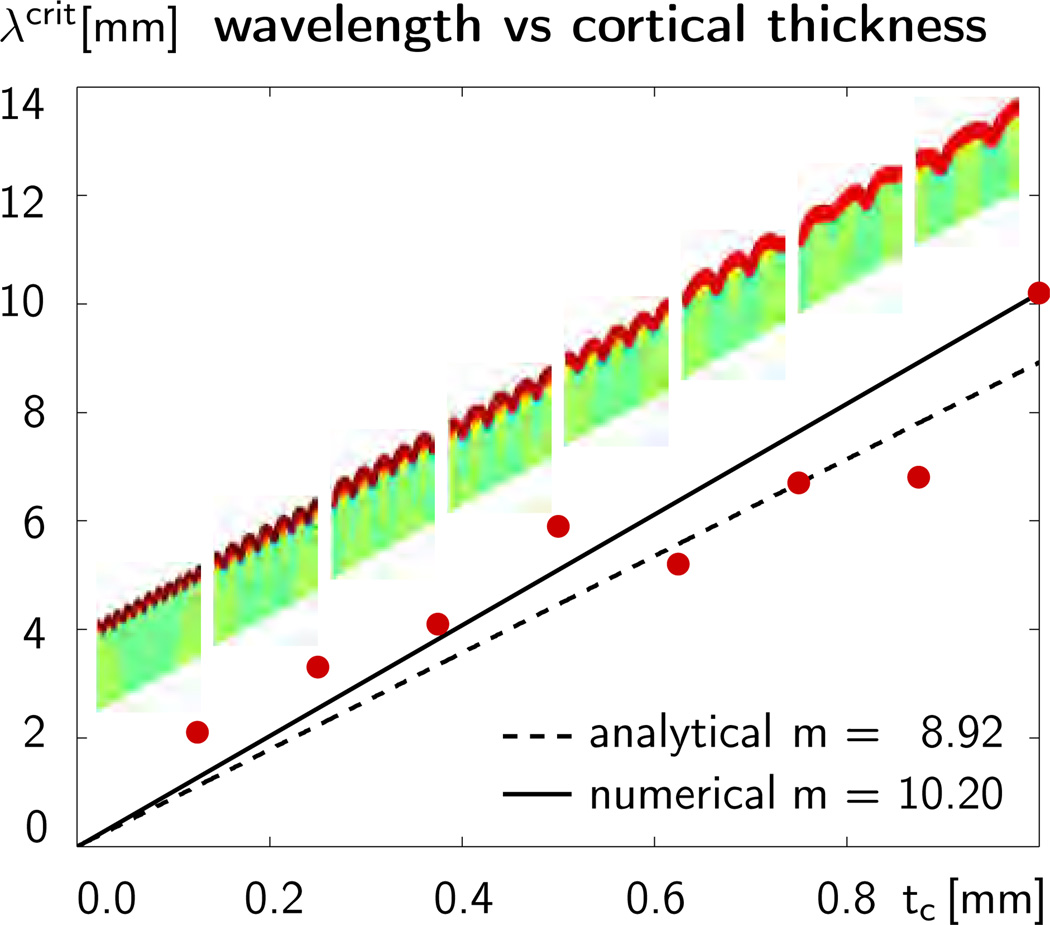
Figure 8 illustrates the sensitivity of the wavelength λ^crit with respect to the initial cortical thickness t_c. The eight dots indicate the computationally predicted wavelengths for the eight different cortical thicknesses. The eight figures inside the graph additionally illustrate the corresponding folding patterns. Simulations with coarser and finer meshes and with smaller and larger perturbations predicted similar folding patterns and similar wavelengths. This indicates that the computationally predicted surface morphology is relatively insensitive to the underlying discretization and to the imposed mode of perturbation. The dashed line shows the analytical wavelength-thickness relation for a growing cortical layer on a growing subcortical foundation according to Section 2. According to equation (8), the analytical solution is based on the additive decomposition of the rate of deformation into elastic and growth parts. It follows from evaluating equation (13), the equation to estimate the critical wavelength, ${\lambda }^{\text{crit}}=2\pi t_{\mathrm{c}}\sqrt[3]{1+G_{\mathrm{s}}/G}$, as a function of the characteristic time scale of folding G, which we obtain from iteratively solving the quintic equation (16) as $G^5-64G_{\mathrm{c}}^3{[G_{\mathrm{s}}+G]}^2\doteq 0$. The solid line shows the averaged computational wavelength-thickness relation for a morphogenetically growing cortex on a stretch-driven growing subcortex according to Sections 3 and 4. According to equation (17), the computational prediction is based on the multiplicative decomposition of the deformation gradient into elastic and growth parts. Figure 8 suggests that the analytical estimate with the additive decomposition and the computational prediction with the multiplicative decomposition agree well in the small deformation limit [40, 42]. Their direct comparison confirms that the wavelength increases linearly with the initial cortical thickness, λ^crit ∝ t_c. The slope of m=10.20 of the computational model is slightly higher than the slope of m=8.92 of the analytical model, which indicates that the computational prediction is slightly stiffer than the analytical estimate. This discrepancy is in agreement with the well-known overly stiff response of tri-linear finite elements, in particular in bending-dominated problems. In addition, the chosen homogeneous Neumann boundary conditions at the lateral sides enforce symmetric folding patterns for which the computationally predicted wavenumbers are always multiples of one half. Aside from these limitations, the analytically and computationally predicted surface morphologies are in excellent quantitative and qualitative agreement. Yet, additional discrepancies might arise between the wavelength-to-thickness relation on initially flat geometries as studied here and initially curved geometries [40] of real mammalian brains.

Figure 8.

Sensitivity of surface morphology with respect to initial cortical thickness for constrained growth in a rectangular domain. The dots illustrate the computationally predicted wavelengths λ^crit for varying cortical thicknesses t_c. The solid line shows the averaged computational wavelength-thickness relation for a morphogenetically growing cortex on a stretch-driven growing subcortex. The dashed line shows the analytical wavelength-thickness relation for a growing cortical layer on a growing subcortical foundation.

5.2. Sensitivity of surface morphology with respect to stiffness ratio

To explore the effect of the stiffness ratio E_c/E_s on the folding pattern, we simulate growth of an elliptic brain slice to mimic an idealized transverse brain section during early development. While the cortical thickness t_c is a parameter that is easy to measure experimentally, the cortical and subcortical stiffnesses E_c and E_s are relatively difficult to determine. On the one hand, in vivo experiments on living brain tissue seem virtually impossible. On the other hand, it remains questionable to which extent ex vivo experiments can provide useful estimates for the material properties of the living brain in vivo. Some effort has been made to identify the elastic material parameters of the human brain [26], yet, the reported values deviate considerably: Young’s modulus was found to vary four orders of magnitude, from 0.5 kPa to 500 kPa, and even Poisson’s ratio was reported to range from 0.2 to 0.5 [25]. Due to the structural difference between neuronal cell bodies and neuronal axons, it seems reasonable to assume that the stiffness is not even uniform across the brain, and that cortical and subcortical stiffnesses are inherently different.

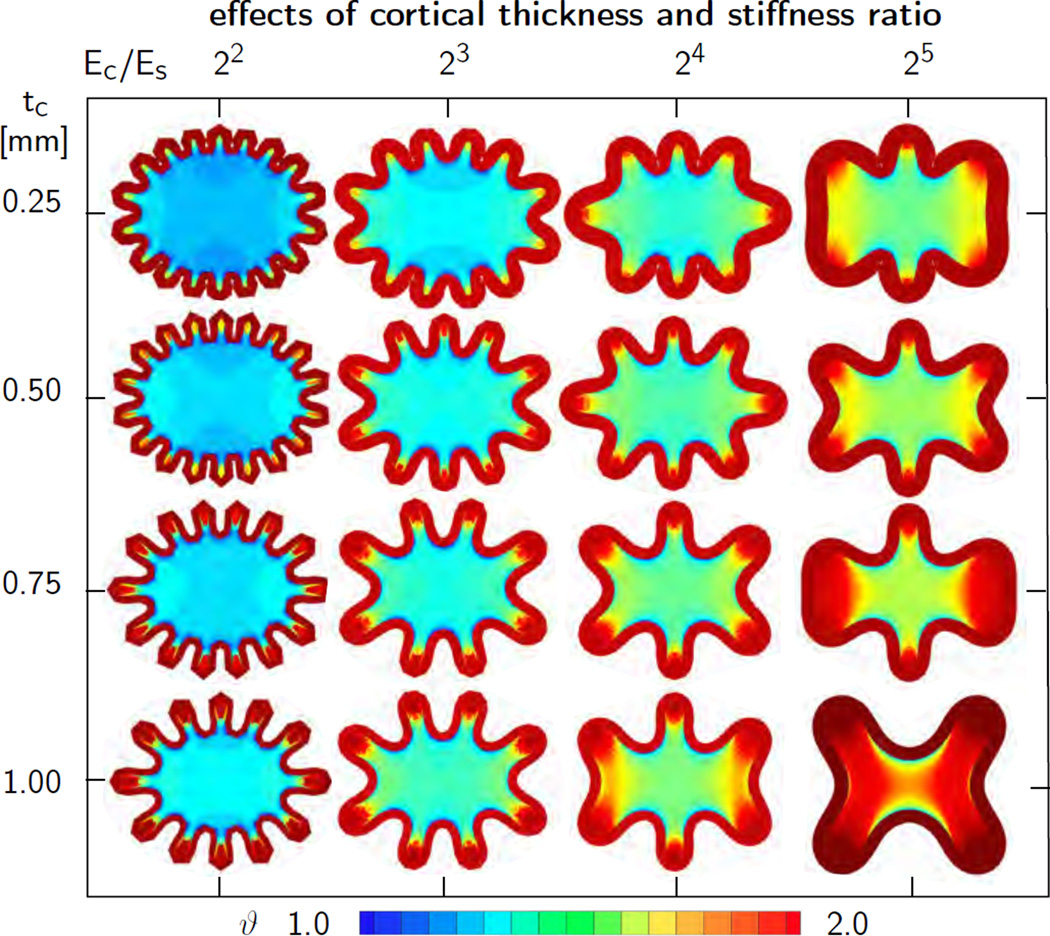
Although there is no general agreement of the absolute stiffness values of cortex and subcortex, we can still perform a sensitivity study of the cortical-to-subcortical stiffness ratio E_c/E_s. To this end, we simulate growth of an elliptic brain slice of an area of 4 cm², an ellipticity ratio of 1.15, and a thickness of 0.005 cm. We discretize the ellipse with 3,328 tri-linear Q1 elements and 20,358 degrees of freedom and assume a plane strain state. This discretization introduces 128 nodes on the outer boundary, which implies that it can capture a folding pattern with 16 folds at a resolution of eight notes per wavelength. We model the cortex as Neo Hookean elastic with Lamé constants λ_c = 34.2 kPa and µ_c = 3.3 kPa and systematically double the cortical-to-subcortical stiffness ratio E_c/E_s from 2² to 2⁵ in four subsequent steps by adjusting the subcortical Lamé constants λ_s and µ_s. We fix the cortical growth rate to G_c = 2.0, the subcortical growth rate to G_s = 0.003, and the physiological limit for axonal growth to J⁰=1.0 [17]. In addition, we gradually vary the initial cortical thickness from t_crit = 0.25mm to t_crit = 1.00mm in four equal steps of Δt_crit = 0.25 mm. In contrast to the perfectly regular rectangular domain, the elliptic domain possesses an inherent imperfection because of its varying curvature, and we do not need to impose additional artificial imperfections to trigger folding.

Figure 9 illustrates the sensitivity of the wavelength λ^crit with respect to the initial cortical thickness t_c and the stiffness ratio E_c/E_s. Snapshots of each column have the same stiffness ratio E_c/E_s and are displayed at the same stage of cortical growth ϑ, the stage of first self contact within the corresponding column. Snapshots of each row have the same cortical thickness t_c and are displayed for subsequent stages with increasing cortical growth ϑ as the stiffness ratio increases. The computational simulation agrees well with the analytical estimates in Section 2: The wavelength λ^crit increases with increasing cortical thickness t_c, from top to bottom, and with increasing stiffness ratio, E_c/E_s, from left to right. In all cases, folding started first in the region of lowest curvature, on the shorter symmetry axis, and gradually propagated outwards to the regions of highest curvature. While cortical growth is identical in all sixteen cases, and homogeneously distributed across the entire cortex, subcortical growth varies significantly across the sixteen simulations and displays pronounced regional heterogeneities. In general, larger cortical wavelengths induce larger subcortical stretch resulting in larger subcortical growth. As the wavelength increases, the individual folds become deeper. As a consequence, subcortical growth is largest in the gyri and smallest in the sulci.

Figure 9.

Sensitivity of surface morphology with respect to initial cortical thickness and stiffness ratio for elliptic geometry. The wavelength λ^crit increases with increasing cortical thickness t_c, from top to bottom, and with increasing stiffness ratio, E_c/E_s, from left to right. Larger wavelengths induce larger subcortical stretch resulting in larger subcortical growth.

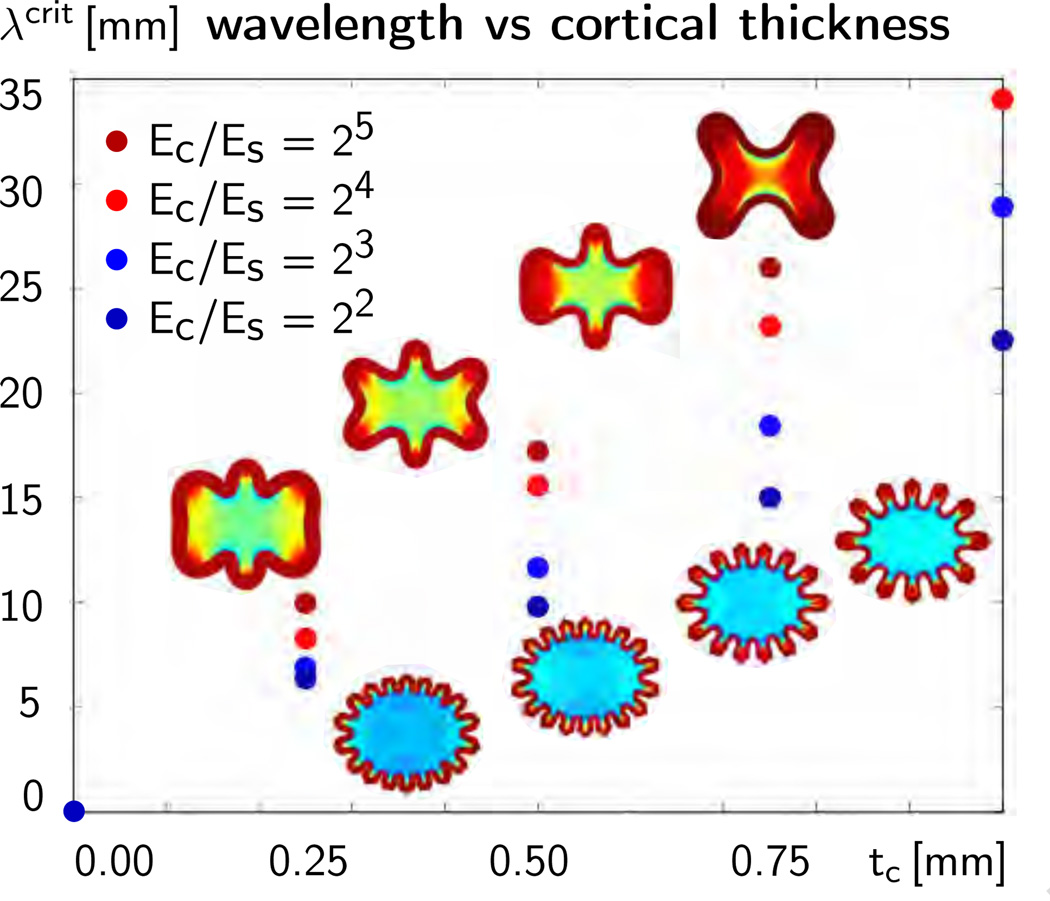
Figure 10 summarizes the computationally predicted average wavelength λ^crit, i.e., the elliptical circumference divided by the number of folds n, for the four varying cortical thicknesses and the four varying stiffness ratios. In agreement with the analytical estimates in Section 2, the average wavelength increases linearly with increasing cortical thickness t_c, from left to right. Also in agreement with the analytical estimates, the average wavelength increases with increasing stiffness ratio E_c/E_s, from lower blue dots to upper red dots.

Figure 10.

Sensitivity of surface morphology with respect to initial cortical thickness and stiffness ratio for elliptic geometry. The dots illustrate the computationally predicted average wavelengths λ^crit for varying cortical thicknesses t_c and varying stiffness ratios E_c/E_s. The average wavelength increases with increasing cortical thickness t_c, from left to right, and with increasing stiffness ratio, E_c/E_s, from lower blue dots to upper red dots.

5.3. Sensitivity of surface morphology with respect to growth ratio

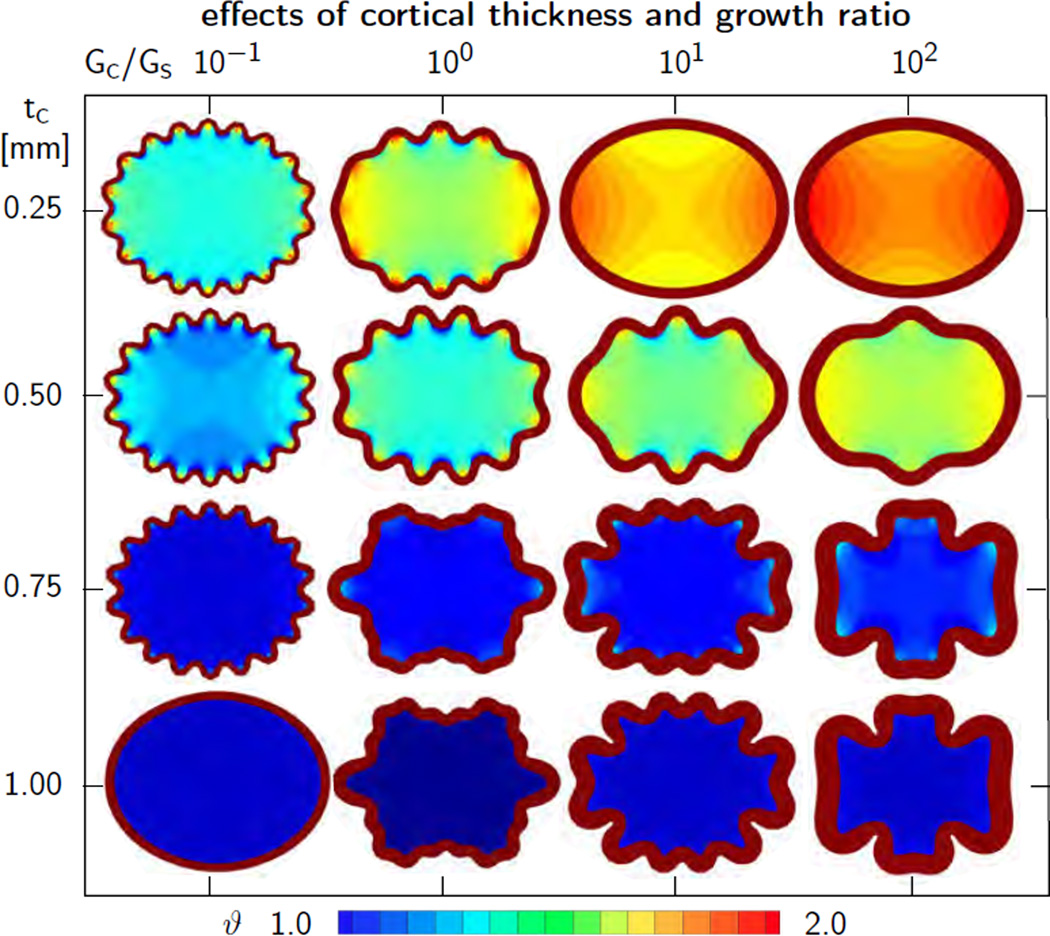
To explore the effect of the growth ratioG_c/G_s on the folding pattern, we simulate the same idealized elliptic transverse brain section as in Section 5.2 with an elliptic area of 4 cm², an ellipticity ratio of 1.15, and a thickness of 0.005 cm. Again, we discretize the ellipse with 3,328 tri-linear Q1 elements and 20,358 degrees of freedom and assume a plane strain state. We model the cortex as Neo Hookean elastic with Lamé constants λ_c = 34.2 kPa and µ_c = 3.3 kPa [60] and assume that the subcortex is three times softer with λ_s = 11.4 kPa and µ_s = 1.1 kPa [12]. We fix the subcortical growth rate to G_s = 0.003 and fix the physiological limit for axonal growth to J⁰ = 1.0. We systematically increase the cortical-to-subcortical growth ratio G_c/G_s from 10⁻¹ via 10⁰ and 10¹ to 10². Similar to the previous example, we also vary the initial cortical thickness from t_crit = 0.25mm to t_crit = 1.00mm in four equal steps of Δt_crit = 0.25 mm.

Figure 11 illustrates the sensitivity of the wavelength λ^crit with respect to the initial cortical thickness t_c and the growth ratio G_c/G_s. All snapshots correspond to the stage of cortical growth, at which the final folding pattern of all sixteen ellipses had fully developed. Again, folding started first in the region of lowest curvature, on the shorter symmetry axis, and gradually propagated outwards to the regions of highest curvature. Cortical growth is identical in all sixteen cases and homogeneously distributed across each slice, whereas subcortical growth varies significantly across the sixteen simulations and displays pronounced regional heterogeneities. The left column indicates that slow cortical growth rates G_c allow for balanced cortical and subcortical growth, which keeps the wavelength uniform and generates simple sinusoidal folding patterns. In contrast, large cortical growth rates G_c scale down subcortical growth. This generates higher compression in the cortex, which initiates the formation of secondary folds. According to the analytical estimates from Section 2, shorter critical wavelengths require a larger critical pressure before buckling is induced. For instance, in the bottom, left corner of Figure 11, growth has not yet generated sufficient compression to induce folding. If the cortex keeps on growing, this ellipse will buckle at a shorter wavelength than any of the other shown ellipses. The concurrence of slow growth rates and thick cortices prevents reaching a load high enough to initiate buckling.

Figure 11.

Sensitivity of surface morphology with respect to initial cortical thickness and growth ratio for elliptic geometry. The wavelength of primary folding λ^crit increases with increasing cortical thickness t_c, from top to bottom. The overall wavelength increases with increasing growth ratios G_c/G_s, from left to right.

6. Discussion

Despite its tremendous significance, little is known about the origin of cortical folding in the developing mammalian brain [7]. Two popular but competing hypotheses suggest that cortical folding originates either in the subcortex, driven by axonal tension [63], or in the cortex, driven by differential growth [54]. Here we have combined both hypotheses into a bilayered material model for cortical folding, in which we represent the cortex as a morphogenetically growing outer layer [33], and the subcortex as a strain-driven growing inner core [12].

To gain first insight into these competing mechanisms [6], we have established analytical estimates for the critical time, pressure, and wavelength at the onset of folding by modeling cortical folding by means of the instability problem of a confined, layered medium under growth-induced compression [10]. We have shown that the critical wavelength λ^crit, the distance between two neighboring gyri, is directly proportional to the cortical thickness, λ^crit ∝ t_c, proportional to the third root of the cortical-to-subcortical stiffness ratio, ${\lambda }^{\text{crit}}\propto \sqrt[3]{E_{\mathrm{c}}/E_{\mathrm{s}}}$, and proportional to the third root of the subcortical growth rate, ${\lambda }^{\text{crit}}\propto \sqrt[3]{(G+G_{\mathrm{s}})/G}$.

To explore the evolution of surface morphologies beyond the onset of folding, we have proposed a continuum model for finite growth, which we have solved computationally within a nonlinear finite element setting [3]. In regular rectangular geometries, we had to apply a small perturbation to trigger the formation of instabilities [48]. In agreement with the literature [15], we observed that the computationally predicted surface morphology was relatively insensitive to the imposed mode of perturbation. In elliptic geometries, the heterogeneity in curvature was sufficient to initiate folding [23]. The instability originated at the center of the long axis and then spread symmetrically outward.

We have systematically varied cortical thickness, stiffness, and growth and predicted folding patterns that were in excellent agreement with our analytical estimates. As expected, our computational model predicted a much wider variety of surface morphologies than the analytical solutions. In some cases, it even predicted the formation of secondary folds [16]. In general, folding patterns deviated from the symmetric sinusoidal ansatz towards morphologies with larger gyri and smaller sulci. This asymmetry reflects the impact of chronic axon elongation in gyral regions with positive stretch [11], which induces subcortical growth. As a natural consequence, the subcortical growth multiplier ϑ displays significant regional variations with maxima of ϑ > 2.0 in the gyral centers and minima of ϑ = 1.0 indicating no growth at the sulcal base. This confirms that analytical modeling can provide valuable first insight into regular folding patterns [10], but computational modeling is mandatory to explore irregular brain surface morphologies [12].

6.1. Sensitivity of surface morphology with respect to cortical thickness

Of all parameters, our model seems to be most sensitive to variations in cortical thickness. Our simulations suggest that the intersulcal distance increases linearly with increasing cortical thickness [9]. A considerably thickened cortex can even suppress the formation of folds entirely [53]. This tendency is consistent with clinical pictures of diseased human brains: Lissencephaly, a malformation with a markedly thickened cortex, is characterized by a smooth brain surface [38]; Polymicrogyria, a malformation with a regionally thinned cortex, is characterized by a highly convoluted brain surfaces with many small and superficial folds [62]. Thin cortices and decreased gyrification are associated with epilepsy, attention deficit hyperactivity disorder, dementia, mental retardation, and dyslexia; Thick cortices and increased gyrification are associated with Williams syndrome, autism, and schizophrenia [70]. We conclude that the cortical thickness directly influences the gyral wavelength and is a key parameter to control surface morphology and primary folding.

6.2. Sensitivity of surface morphology with respect to stiffness ratio

The stiffness ratio between cortex and subcortex has a similar effect as the cortical thickness, however, only when scaled by its third root. Controlling surface morphology through the stiffness ratio has been discussed intensely in the materials sciences community [14], where thin stiff films on compliant substrates with stiffness ratios of up to four orders of magnitude play a major role [5]. As the cortex with its neuronal cell bodies and synapses is much denser packed than the subcortex with its myelinated axons, it is intuitive that it may have a larger mechanical stiffness. Yet, experiments have shown that the cortical stiffness is less than an order of magnitude larger than the subcortical stiffness [22]. Some studies only found a stiffness difference of 50% [18]. This has, in fact, been the major criticism of the first mechanical model for cortical folding based on the hypothesis of differential growth [54]. We conclude that the stiffness ratio may influence surface morphology, but because of its small variation, it can not be the single main driving force to explain cortical folding and morphological abnormalities.

6.3. Sensitivity of surface morphology with respect to growth ratio

Of all parameters, the growth ratio between cortex and subcortex seems to be the least well understood. Yet, it is probably the most important parameter to control the formation of secondary folds [67]. In the continuum model, cortical and subcortical growth are introduced constitutively through the kinetics of growth in equations (24) and (25). Eventually, we hope to tie these equations to cellular mechanisms such as axon elongation [11]. In the analytical model, we have made a critical assumption to evaluate the relation between the critical wavelength, the time constant of growth, and the subcortical growth rate, namely that G = 1/t^crit [6]. At this point, this is a plain assumption, yet it provides some insight into the two extreme cases of abnormally slowly and abnormally fast growing cortices. Abnormally slowly growing cortices create an almost fluid-like behavior of the subcortex: Axons are capable of responding almost instantaneously to growth-induced subcortical deformation and, in extreme cases, folding is suppressed entirely. Abnormally fast growing cortices create an elastic solid-like behavior of the subcortex: Axons are incapable of responding to stretch, the pressure in the cortical layer raises quickly, and provokes the formation of secondary folds [41]. In the human brain, for example, primary folding begins at 22 weeks gestation and secondary folding takes place between weeks 25 and 30 [53]. In the materials science community, these two types of folds are associated with kinematically induced instabilities, controlled by thickness and stiffness, and dynamically induced instabilities, controlled by growth rates [34]. The interplay of kinematic and dynamic instabilities generates a wide variety of surface morphologies, in which secondary folding serves as a mechanism to release large compressive stresses in the outer layer [16]. We conclude that the growth ratio is a key parameter to control irregular surface morphologies and secondary folding.

6.4. Mechanical modeling explains surface morphologies of mammalian brains

From the explanted mammalian brains in Figure 2, we conclude that brain size increases with increasing animal size [32] from 140g in sheep via 180g in pigs to 450g in cows [47]. Yet, the average cortical thickness in the frontal coronal sections in Figure 2 varies only marginally from 0.23 cm in the sheep via 0.22 cm in the pig to 0.22 cm in the cow brain. This is in line with the common understanding that the average cortical thickness varies marginally across mammalian species and is independent of brain size [56]. Similarly, the average gyral wavelength in Figure 2 varies marginally from 0.61 cm in the sheep via 0.53 cm in the pig to 0.90 cm in the cow brain. According to our model, increasing the brain size at a constant cortical thickness does not affect the absolute gyral wavelength; yet, it increases the relative gyral wavelength when scaled by brain size. This is in agreement with a recent review, which reported the gyrification index, the ratio between the total brain surface area and the exposed surface area, to be 1.94 in sheep and 2.18 in pig [70]. Our model can thus explain why the surface-to-volume ratio of mammalian brains in Figure 1 increases disproportionally faster than predicted by isometric scaling and why the degree of gyrification tends to increase with brain size.

6.5. Limitations

Both our analytical and our computational model provide valuable insight into the development of the mammalian brain. Yet, they have a few limitations, which could be addressed to make the models more realistic:

First, in our current model, we have neglected the geometric constraint by the skull. Our results indicate that the skull is not necessary to trigger gyrification; yet, it might be an important regulator of cortical folding [46]. In our model, folding is constrained exclusively by the subcortical layer underneath the growing cortex. Adding a stiff skull above the growing cortex would certainly influence the final folding pattern, for example, by flattening out the gyral ridges. Yet, the impact if the skull on the initial gyral wavelength at the onset of folding might be rather minor [6].

Second, here, we have assumed the constitutive behavior as quasi-incompressible with a Poisson’s ratio of ν = 0.458 in the linear regime [60]. Other studies suggest that brain tissue is nearly incompressible with ν = 0.496 [25] or entirely incompressible [50, 51]. Our analytical model in Section 2 is generally valid for both compressible and incompressible materials. Our continuum model in Section 3 would require a different strain energy function in equation (20) to capture incompressibility exactly. Imposing incompressibility in the computational model in Section 4 would require additional modifications both on the constitutive level and on the element level, since the overall response would alternate between compressible during growth and incompressible during purely elastic phases [52, 58].

Third, within this study, we have simplified the elastic response of the brain as Neo Hookean isotropic [60]. Although the microstructure of both cortex and subcortex is clearly anisotropic, their anisotropic material behavior remains poorly characterized. The microstructure of the cortex is relatively regular and closely correlated to the radial direction r₀, which defines the orientation of the cortical columns [49]. The microstructure of the subcortex is rather irregular and closely correlated to the axon orientation a₀, which needs to be identified through diffusion tensor imaging [44] or other novel imaging techniques [19]. Detailed measurements of the cortical stiffness, along and perpendicular to the cortical columns, supplemented by measurements of the subcortical stiffness, along and perpendicular to the axon orientation, would be tremendously valuable. To improve the elastic module of our model, we are currently performing a series of nano-indentation tests [68] to characterize cortical and subcortical stiffnesses, the degree of cortical and subcortical anisotropy, and the stiffness variation across different species.

Fourth, we have not only simplified the elastic behavior bout also the growth response as isotropy. For cortical growth, we are currently working on replacing the isotropic growth tensor, F^g = ϑ I, in equation (18) by an anisotropic growth tensor, F^g = ϑ^⊥ I + [ϑ^‖ − ϑ^⊥] r₀ ⊗ r₀, where r₀ characterizes the radial direction [52]. In this setup, the radial growth multiplier ϑ^‖ characterizes cortical thickening along radial direction [29], and the surface growth multiplier ϑ^⊥ characterizes area growth perpendicular to it [13]. This allows us to replace the single phenomenological evolution of cortical growth, ϑ̇ = G_c, in equation (24) by two independent equations for cortical thickening and surface growth. We can then mechanistically link surface growth, ${\mathrm{\vartheta ̇}}^{\perp }=G_{\mathrm{c}}^{\perp }$, to the symmetric cell division of progenitor cells into two new progenitor cells, and thickness growth, ${\mathrm{\vartheta ̇}}^{\Vert }=G_{\mathrm{c}}^{\Vert }$ to the asymmetric cell division into a progenitor cell and a neuron [56]. For subcortical growth, we could replace the growth tensor F^g = ϑ I, in equation (18) by an anisotropic growth tensor, F^g = I + [ϑ^‖ − 1] a₀ ⊗ a₀, where a₀ characterizes the axon orientation [71]. The growth multiplier ϑ^‖ characterizes the chronic axon elongation in response to overstretch [20]. We could then replace elastic volume change 〈 J^e − J⁰ 〉 as the driving force for subcortical growth, ϑ̇‖| = G_s 〈 J^e − J⁰ 〉, in equation (25) by the elastic axonal stretch 〈 λ^e − λ⁰ 〉 with λ^e = [a₀ · F^t · F · a₀]^1/2, to correlate the model parameters to experimentally measured axon elongation rates [11].

Finally, growth is neither homogeneous in space nor constant in time. To functionally correlate cellular and molecular events to cortical and subcortical growth [36], we could turn different growth rates on and off to better represent the sequence of events during gyrogenesis, including neuronal proliferation, differentiation, apoptosis, dendrogenesis, synapsogenesis, glial proliferation, lamination, and cellular rearrangement [53].

7. Concluding remarks

Mechanical modeling of brain development can explain variations in surface morphology of the mammalian brain. Variations in cortical and subcortical thickness, stiffness, or growth can generate variations in pattern formation. A thinner, softer, or slower growing layer of gray matter generally enhances cortical folding and reduces the gyral wavelength. A thicker, stiffer, or faster growing layer of gray matter reduces cortical folding and increases the gyral wavelength. Larger mammals tend to have larger brains, but similar cortical thicknesses. Our model predicts that the absolute gyral wavelength in mammals is almost constant across different species, while the relative gyral wavelength increases with brain size. This explains why the surface-to-volume ratio of mammalian brains increases disproportionally faster than predicted by isometric scaling. Our model can also explain the pathological malformations of polymicrogyria, associated with a thin and overly convoluted cortex, and lissencephaly, associated with a thick and poorly convoluted cortex. Understanding the mechanisms of cortical folding during brain development may have direct implications on the diagnostics of neurological disorders, including severe retardation, epilepsy, schizophrenia, and autism.