Conformational entropy in molecular recognition by proteins: A first example from the calmodulin system

Abstract

Molecular recognition by proteins is fundamental to almost every biological process, particularly the protein associations underlying cellular signal transduction. Understanding the basis for protein-protein interactions requires the full characterization of the thermodynamics of their association. Historically it has been virtually impossible to experimentally estimate changes in residual protein entropy, a potentially important component of the change in the free energy of protein association. However, solution NMR spectroscopy has recently emerged as a powerful tool for characterizing the dynamics of proteins and has thereby gained access to their residual entropy¹. Here we show that the change in internal dynamics of the protein calmodulin varies significantly upon binding a variety of target domains. Surprisingly, the apparent change in the corresponding residual entropy is linearly related to the change in the overall binding entropy. These results indicate that changes in residual protein conformational entropy can contribute significantly to the free energy of protein-ligand association. It seems evident that protein entropy can be exploited in the maturation of high affinity interactions either by biological evolution or by human intervention such as in the design of protein-targeted pharmaceuticals.

Numerous structural studies have revealed that protein-protein interfaces often involve dozens of amino acids and thousands of Ų of contact area ². It has also become apparent that a non-uniform contribution of individual residues to the free energy of binding can exist and that static structural analyses can mask important factors underlying the high affinity interactions between proteins³. Of particular interest here is the role of the residual protein conformational entropy in modulating the free energy of the association of a protein with a ligand, i.e.

$$\begin{array}{l}\mathrm{\Delta }{G}_{\mathit{binding}}=\mathrm{\Delta }{H}_{\mathit{binding}}-T\mathrm{\Delta }{S}_{\mathit{binding}}\\ =\mathrm{\Delta }{H}_{\mathit{binding}}-T\left(\mathrm{\Delta }{S}_{\mathit{binding}}^{\mathit{protein}}+\mathrm{\Delta }{S}_{\mathit{binding}}^{\mathit{ligand}}+\mathrm{\Delta }{S}_{\mathit{binding}}^{\mathit{solvent}}\right)\end{array}$$ (1)

The trivial decomposition made in Equation 1 emphasizes the fact that the entropy of binding (ΔS_binding ), obtainable by calorimetric methods, is comprised of contributions associated with the ligand, solvent and the protein. It is well-established that gross disorder-order transitions of a ligand can profoundly influence the entropy of macromolecular associations⁴. It is also well-established that burial of hydrophobic surface area and the consequent release of hydration waters to the bulk solvent can also contribute significantly to the thermodynamics of binding ⁵. What is less understood is the potential entropic contributions from a structured protein ( $\mathrm{\Delta }{S}_{\mathit{binding}}^{\mathit{protein}}$), which includes changes in its internal residual conformational entropy ( $\mathrm{\Delta }{S}_{\mathit{conf}}^{\mathit{protein}}$) as well as changes in rotational and translational entropy^6–8. Here we focus on $\mathrm{\Delta }{S}_{\mathit{conf}}^{\mathit{protein}}$. As is obvious from Equation 1, the measurement of total system thermodynamic parameters does not resolve contributions from internal protein conformational entropy. The estimation of changes in conformational entropy due to protein-protein association from molecular dynamics simulations remains a considerable challenge⁹. Direct measurement of the residual conformational entropy of the protein in its free and complexed states is therefore required. Recent developments in NMR relaxation methods and analysis now make this feasible.

We have employed calmodulin as a model system to investigate the role for changes in protein conformational entropy in the high affinity association of proteins. Calmodulin is a central participant in the calcium-mediated signal transduction pathways of eukaryotes¹⁰. It interacts with and regulates the activity of approximately three hundred proteins¹¹. In principle, the characterization of calmodulin’s internal dynamics should facilitate measurement of conformational entropy changes through a “counting of states” implicit in molecular motion¹. Previously, using NMR relaxation methods, we have shown that calcium-saturated calmodulin itself is an unusually dynamic protein, which is characterized by a broad, non-uniform multi-modal distribution of the amplitude of fast side chain dynamics¹². Binding of a target domain to calcium-saturated calmodulin causes a significant redistribution of the fast side chain dynamics in calmodulin¹². This raises the possibility that CaM employs its internal residual entropy to “tune” its affinity for ligands.

Here we explore this question by using NMR methods to determine the dynamical response of CaM to the binding of six target domains. Peptides representing the calmodulin-binding domains of the smooth muscle myosin light chain kinase (smMLCKp)¹³, the neuronal and endothelial nitric oxide synthases (nNOSp and eNOSp)¹⁴, the calmodulin kinase kinase (CaMKKαp)¹⁵, the calmodulin kinase I (CaMKIp)¹⁶, and the phosphodiesterase (PDEp)¹⁷ have been employed. All have a basic amphiphillic character and form alpha-helical structure when bound to calmodulin (Figure 1a). Four of the peptides have been found previously by isothermal titration calorimetry to have roughly the same affinity for calmodulin but with widely different thermodynamic parameters defining the free energy of association¹⁸. We have repeated the ITC measurements at a temperature (35 °C) that is more optimal for solution NMR spectroscopy and have characterized the binding of the two additional domains (Figure 1b). In the case of the CaMKKαp and smMLCKp domains, binding is driven by a large favourable change in system enthalpy overcoming a large unfavourable change in system entropy. At the other extreme, nNOSp binding is driven by a large favourable change in system enthalpy accompanied by a small favourable change in system entropy. The PDEp, CaMKIp, and eNOSp calmodulin-binding domains represent intermediate cases. The entropy of binding of these domains varies by 90 kJ/mole and changes sign.

Figure 1. Calmodulin-binding peptides.

a, Sequence alignment of the six calmodulin-binding peptides. Note that CaMKKαp binds in opposite orientation to CaM relative to the other five peptides. For PDEp, a C15S mutation has been used to avoid complications with oxidation. b, Thermodynamic parameters. The Gibbs free energy (ΔG), enthalpy (ΔH) and entropy (−TΔS) for the formation of the six calcium-saturated CaM-peptide complexes at 35 °C. Values are tabulated in the Supplementary Information.

Titration of CaM with each of the peptides reveals that all six of the resulting complexes have a 1:1 stoichiometry and are in slow exchange with their dissociated components on the NMR ¹H chemical shift time scale (not shown). The CaM-smMLCKp, CaM-PDEp and CaM-CaMKKαp complexes show very little conformational heterogeneity, as judged by ¹⁵N- and ¹³C-HSQC spectra, while the CaM-nNOSp, CaM-eNOSp and CaM-CaMKIp complexes show limited heterogeneity at a small number of locations in the calmodulin molecule. This was found to largely arise from populations of minor rotameric orientations of methyl bearing side chains. These results indicate a range of localized conformational heterogeneity in calmodulin across the six calmodulin complexes. This heterogeneity represents classical conformational entropy.

The sub-ns dynamics of the polypeptide backbone of calmodulin in the six complexes were probed using ¹⁵N dipolar relaxation by its attached hydrogen¹⁹ and by transverse cross-correlated relaxation between ¹³CO chemical shift anisotropy and the ¹³CO-¹³Cα dipolar interactions ²⁰. The sub-ns dynamics of methyl groups of calmodulin side chains were characterized using ²H spin relaxation methods²¹. The degree of spatial restriction of each motional probe was assessed via the squared model-free generalized order parameter (O²)²². Values of the O² parameter can vary from 0 to 1, corresponding to isotropic disorder and a fixed orientation in the molecular frame, respectively. We denote the O² parameters for motion of the amide N-H bond, C_α-C′ bond and methyl symmetry axis as $O_{NH}^2,O_{C\alpha CO}^2$ and $O_{\mathit{axis}}^2$, respectively.

The dynamics of the backbone of calmodulin are invariant across the complexes, as indicated by the average $O_{NH}^2$ and $O_{C\alpha CO}^2$ parameters (Supplementary Information). In contrast, the motion of methyl-bearing amino acid side chains varies significantly with the nature of the target domain. There are 56 methyl-bearing amino acids providing 80 methyl groups as probes distributed across the primary sequence of calmodulin and include nine methionines that line the target domain binding sites formed in the various complexes.

To project the change in internal protein dynamics in terms of residual protein entropy, we follow Karplus and co-workers and describe the protein as a disjoint multidimensional harmonic well⁸:

$$S_{\mathit{conf}}^{\mathit{protein}}=\sum _{i=1}^N{p}_i{S}_i^h-k_B\sum _{i=1}^N{p}_{i}ln{p}_i$$ (2)

where $S_i^h$ represents the entropy manifested by fast intra-well motion and the second term corresponds to the classical conformational entropy arising from the N distinct conformations. Here $S_i^h$ is obtained from interpretation of local order parameters, which is model-dependent. We choose a simple harmonic oscillator treatment²³. Differences in entropy calculated from changes in O²are fairly insensitive to the model used²⁴. Calcium-saturated calmodulin is used as the reference state for obtaining $\mathrm{\Delta }{S}_{\mathit{conf}}^{\mathit{protein}}$. The second term of Equation 2 represents classical entropy from the local heterogeneity of side chain conformers. This can be manifested on a range of time scales. Some methyl sites exhibited slowly interconverting conformational heterogeneity on the chemical shift time scale. This was interpreted as classical entropy with the population of each state (p_i ) estimated from the intensity of cross peaks. This contributed less than 2% of the estimated change in conformational entropy due to binding. It has also been shown that fast motion between rotamer wells contributes significantly to low $O_{\mathit{axis}}^2$ parameters²⁴. This also represents conformational entropy and was estimated using a previously described model²⁴. This resulted in a roughly constant 15% of the total conformational entropy.

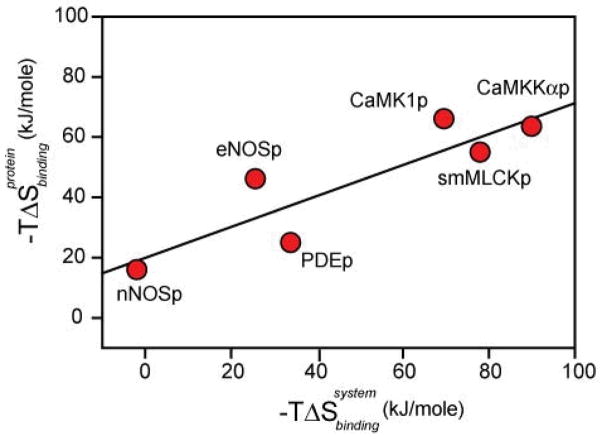
Notwithstanding the limitations imposed by correlated motion²⁴, the changes in the residual entropy of calmodulin upon binding to the six peptides, obtained by simple summation of the individual local entropies, shows a linear correlation (R² = 0.78) with the corresponding entropy of binding (Figure 2). Taken at face value, half of the binding entropy is reflected in the motion of the methyl-bearing amino acid side chains. There is no a priori reason for such a correlation. However, the linearity of the correlation implies that either the change in the residual entropy of calmodulin upon binding a target domain is a major contribution to the binding entropy or that the various sources of entropy change in concert (see Equation 1). Regardless, it appears that the residual entropy of calmodulin can vary sufficiently to impact the free energy changes arising from high affinity protein associations. Therefore the commonly held view that high affinity interactions are necessarily energetically dominated by specific structural (enthalpic) interactions must be relaxed to include the structural dynamics and heterogeneity that contributes to residual protein entropy.

Figure 2. Correlation of the change in residual conformational entropy of calmodulin with the change in the total entropy of binding of a target domain.

The change in conformational entropy was estimated using Equation 2 as described in the Methods and Supplementary Information. Propagation of measurement error in fitted order parameters results in uncertainties in conformational entropy less than the size of the symbols used. The fitted linear correlation coefficient (R²) of conformational entropy versus the entropy of binding is 0.78 with a slope of 0.51.

The binding of target domains to CaM results in a distribution of $O_{\mathit{axis}}^2$ parameters that is remarkable for its distinct clustering into three apparent classes of motion (Figure 3). The relative populations of these motional classes in calmodulin vary considerably across the six complexes. Although the distinctive grouping of order parameters, seen across all six complexes studied here, is often obscured in other proteins²⁵, the motional origin of these classes is clear. In the case of calmodulin, two fundamental types of motion occurring on the sub-ns time scale are involved: motion within a rotamer well and motion between rotamer wells of side chain torsion angles²⁴. It has been shown that the class of motion centred on a $O_{\mathit{axis}}^2$ value of ~0.35 generally involves a significant contribution from rotameric interconversion on the nanosecond or faster time scale as it leads to a significant averaging of scalar coupling (J) constants²⁴. More recent experimental results²⁶ and theoretical simulations²⁷ suggests this to be general. The distribution of motion at the other extreme is centred on a $O_{\mathit{axis}}^2$ value of ~0.8, which represents highly restricted motion within a rotamer well. The class of motion centred on a $O_{\mathit{axis}}^2$ value of ~0.6 involves little detectable rotamer interconversion and is restricted to motion within a single rotamer well. The precise value reflects intra-well motion and the effects of superposition of similar motion about connected torsion angles. We have termed these groupings the J-, ω- and α-classes of motion, respectively¹. The distributions of $O_{\mathit{axis}}^2$ parameters in each of the six physiologically-relevant calmodulin complexes are satisfactorily described by a sum of three Gaussians (Figure 3 and Supplementary Information).

Figure 3. Distribution of the amplitude of methyl-bearing side chain motion of calmodulin in complex with target domains and correlation with the change in total entropy of binding.

Shown are histograms of the squared generalized order parameters for calmodulin methyl group symmetry axes obtained at 35 °C. The solid lines represent fitted 3-Gaussian distributions centred on $O_{\mathit{axis}}^2$ values of 0.35 (J-class, red), 0.58 (α-class, green) and 0.78 (ω-class, blue). The relative populations of each class were derived from the fitted 3-Gaussian distributions for each complex. The change in population of the J, α and ω classes with the $-T\mathrm{\Delta }{S}_{\mathit{binding}}^{\mathit{system}}$ have fitted linear correlation coefficients (R²) of −0.83, +0.74 and +0.70, respectively. Correlation of the number of sites assigned to each class by simple binning, as colour-coded, yielded similar results (see Supplementary Information). Error bars reflect the variation of the population of each motional class that results from an increase or decrease in the measured $O_{\mathit{axis}}^2$ values by two standard deviations (see Figure 2).

There exists a surprising correlation between the populations of the three classes of motion and the change in total system entropy for binding (Figure 3). The population of the J-class is negatively correlated with the entropic contribution (−TΔS) to the free energy of binding. The populations of the ω- and α-classes are positively correlated. The correlations are remarkably linear for all three classes. This is a direct, relatively model-insensitive indication that the residual entropy of calmodulin changes in concert with the change in the entropy of binding and that this variation can, in part, be identified with the motional class of the involved side chains.

In summary, we have employed a battery of NMR methods to characterize the dynamical response of calmodulin to the binding of six target regulatory domains. This view has been interpreted in terms of the changes in conformational entropy of calmodulin upon binding. The behaviour of the six physiologically relevant interactions indicates that the residual entropy of structured proteins can enter very significantly into high affinity interactions between proteins. It will therefore be of great interest to determine how prevalent this is across the universe of protein-protein interactions in biology. Finally, the results presented here suggest that residual protein entropy can indeed play a significant role in more complex protein functions such as allostery⁷.

METHODS

Sample preparation & isothermal titration calorimetry

Calmodulin and synthetic peptides and complexes were prepared as described previously²⁸. All solutions were prepared in 20 mM imidazole (pH 6.5), 100 mM KCl, 6 mM CaCl₂ and 0.02 % (w/v) NaN₃. For isothermal titration calorimetry, calcium-saturated calmodulin (200 μM) was used to titrate dilute solutions of peptide (10–20 μM) in order to avoid artefacts arising from peptide aggregation. ITC measurements were performed with a VP-ITC (Microcal) thermostatically regulated at 35 °C. Data were analyzed with Origin (v.5) software. NMR samples were slightly (~10%) over-titrated with peptide to ensure full complex formation.

NMR methods

$O_{\mathit{axis}}^2$ parameters were determined from T₁ and T_1ρ deuterium relaxation²¹ measured at two magnetic fields. Rotational correlation times and $O_{NH}^2$ were determined by ¹⁵N relaxation measurements¹⁹ obtained at two magnetic fields. $O_{CO-C\alpha }^2$ parameters were determined by transverse cross-correlated relaxation between ¹³CO chemical shift anisotropy and the ¹³CO-¹³Cα dipolar interactions as described elsewhere²⁰. All measurements were made at 35 °C. Model free parameters²² were determined using a comprehensive grid search approach²⁹. The average error of $O_{\mathit{axis}}^2,O_{NH}^2$ and $O_{CO-C\alpha }^2$ parameters across all complexes were estimated by Monte Carlo sampling to be 0.016, 0.011 and 0.024, respectively. The squared generalized order parameters and effective correlation times have been deposited in the Biological Magnetic Resonance Data Bank (http://www.bmrb.wisc.edu/).

Data interpretation

The summed distribution of $O_{\mathit{axis}}^2$ parameters of all six complexes was fitted to a random distribution and to one, two and three Gaussian distribution models. The bin size for this analysis was determined from a well-established formula for optimal bin width³⁰ and was found to be 0.05. Only the three Gaussian model could satisfactorily describe the data (p < 0.0001). The fitting procedure is described in the Supplementary Information. The summed distribution yielded fitted 3-Gaussian distributions centred on $O_{\mathit{axis}}^2$ values of 0.35 (J-class), 0.58 (α-class) and 0.78 (ω-class). These centres were fixed in subsequent fitting of the $O_{\mathit{axis}}^2$ distributions of the individual complexes from which the relative populations of each motional class were obtained. Uncertainties in the fitted populations were estimated by varying the $O_{\mathit{axis}}^2$ parameters by two standard deviations. This results in asymmetric error bars. The total change in conformational entropy of calmodulin upon binding a target domain was calculated as the sum of three terms: $\mathrm{\Delta }{S}_{\mathit{conf}}^{\mathit{protein}}=\mathrm{\Delta }{S}^{\mathit{harm}}+\mathrm{\Delta }{S}_{\mathit{rotamer}}^{\mathit{fast}}+\mathrm{\Delta }{S}_{\mathit{rotamer}}^{\mathit{slow}}$. Changes in conformational entropy (ΔS^harm) expressed as changes in motion within a rotameric well on the fast time scale (sub-ns) were obtained from the experimentally determined $O_{\mathit{axis}}^2$ parameters using a simple harmonic oscillator model.²³ To calculate changes in entropy derived from motion of the same oscillator, site-to-site comparison to free calcium-saturated calmodulin was used as the reference state. The change in the entropy reflected by the change in the motion of each methyl symmetry axis was estimated using $\mathrm{\Delta }S=-18\times \mathrm{\Delta }{O}_{\mathit{axis}}^2\mathrm{J}{\text{mol}}^{-1}{\mathrm{K}}^{-1}$. See Li et al.²³ for further details of the model. A classical entropy term ( $\mathrm{\Delta }{S}_{\mathit{rotamer}}^{\mathit{fast}}$) was added to represent minor conformers that are sampled due to fast rotameric interconversion that also contributes to the generalized order parameter²⁴. For the small number of methyl sites having multiple conformations in slow exchange on the NMR chemical shift time scale, an additional classical entropy contribution ( $\mathrm{\Delta }{S}_{\mathit{rotamer}}^{\mathit{slow}}$) was calculated based on the measured intensities. See Supplementary Information for additional details and results.