NPEST: a nonparametric method and a database for transcription start site prediction

Abstract

In this paper we present NPEST, a novel tool for the analysis of expressed sequence tags (EST) distributions and transcription start site (TSS) prediction. This method estimates an unknown probability distribution of ESTs using a maximum likelihood (ML) approach, which is then used to predict positions of TSS. Accurate identification of TSS is an important genomics task, since the position of regulatory elements with respect to the TSS can have large effects on gene regulation, and performance of promoter motif-finding methods depends on correct identification of TSSs. Our probabilistic approach expands recognition capabilities to multiple TSS per locus that may be a useful tool to enhance the understanding of alternative splicing mechanisms. This paper presents analysis of simulated data as well as statistical analysis of promoter regions of a model dicot plant Arabidopsis thaliana. Using our statistical tool we analyzed 16520 loci and developed a database of TSS, which is now publicly available at www.glacombio.net/NPEST.

INTRODUCTION

The accurate and reliable determination of transcription start sites (TSS) in eukaryotic genes is an important problem that has yet to be resolved. Many of the promoter motif-finding methods rely on the correct identification of upstream regions and TSS. It was previously reported that the position of the transcription factor binding site with respect to the TSS plays a key role in the specific programming of regulatory logic within noncoding regions [1,2]. This highlights the importance of determining the precise location of TSS for motif discovery. In order to reliably predict TSS, it is essential to have a good quality assembled genome and a comprehensive collection of Expressed Sequence Tags (ESTs) per locus mapped to the potential promoter regions. An EST is a short fragment (typically about 200–500 nucleotides) of a transcribed cDNA sequence, commonly used for gene identification. By 2013 over 75 million ESTs had been accumulated in the NCBI GenBank database. One of the problems with the 5′ ESTs is that even in the best libraries; only 50%–80% of the 5′ ESTs extend to the TSSs [3–5]. The traditional approach to predict the position of the TSS was based on finding the position of the longest 5′ transcripts (for overview of eukaryotic promoter prediction methods see Fickett and Hatzigeorgiou [6]). It has been demonstrated that the quality of TSS prediction can be improved when combining data from multiple sources, such as collections of 5′ EST and conserved DNA sequence motifs [4,5].

Down and Hubbard [7] developed a machine-learning approach (Eponine) to build useful models of promoters; their method uses weight matrices for the most significant motifs around the TSS (e.g., TATA box and CpG island) to predict the position of the TSS. Eponine was tested on human chromosome 22 and detected 50% of experimentally validated TSS, but in several cases it did not predict the direction of transcription correctly. In 2003, King and Roth reported the use of a non-parametric model aimed at the improved prediction of transcription factor binding sites in gene promoters [8]. Abeel et al. [9] presented the EP3, a promoter prediction method based on the structural large-scale features of DNA, including bendability, nucleosome position, free energy, and protein-DNA twist. EP3 identifies the region on a chromosome that is likely to contain TSS, but it does not predict the direction of a promoter. Over several years, Solovyev and colleagues developed maximum likelihood approaches to bacterial [10] and plant [11] promoter prediction. This work resulted in the TSSP algorithm which, in addition to predictions, provides novel measures of confidence for these predictions. TSSP produced the most accurate results when compared with four other plant promoter identification programs [12]. In 2009 Troukhan et al. [13] proposed to predict TSS considering positional frequency of 5′ EST matches on genomic DNA together with the gene model. Troukhan et al. showed that such a statistical approach, implemented as the TSSer algorithm, outperforms deterministic methods. TSSer considers positional frequency of 5′ EST matches on genomic DNA together with the gene model, which allows an accurate determination of the TSS.

Most current methods choose only one TSS per locus; however, it was demonstrated (for example, by Joun et al. [14] and Tran et al. [15]) that some genes contain several alternative TSSs that direct tissue specific expression and the production of multiple protein isoforms via alternative splicing of transcripts. Rach et al. [16] published a method for TSS identification based on hierarchical clustering of ESTs mapping onto a genome. This approach grouped ESTs by positions and hence allowed identification of alternative TSS. Rach et al. [16] presented a comprehensive map of fruit fly TSSs and the conditions under which they are utilized. They found genomic similarities of usage of alternative TSSs across species.

In this paper we present a sophisticated probabilistic treatment of the TSS prediction problem. We propose a nonparametric approach for analysis of TSS. This approach expands recognition capabilities to multiple TSS per locus and therefore can aid in understanding of alternative splicing mechanisms. Our nonparametric approach is computationally efficient, sensitive and reliable. In addition to producing estimates for the number of TSS, it also estimates the probability distribution of EST positions on the genome.

MATERIALS AND METHODS

Materials

Genome annotation files and sequences for 3000 nucleotides upstream from ATG were obtained from The Arabidopsis Information Resource (TAIR) [17]. We used the TAIR10 version of the genome. The sequences were truncated based on the position of the nearest upstream locus. 290085 EST sequences were obtained from NCBI and TAIR and mapped onto the 27199 upstream sequences using nucleotide BLAST + [18] (minimum identity percent: 95%; maximum query start of alignment: 5; only plus strand alignments were used). Using the text search we removed ESTs annotated as 3′ or partial.

Methods

The positions of the 5′ end of ESTs can be considered as noisy experimental evidence of the location of TSS. If the total number of ESTs for a given locus is N, then any genomic position can have from zero to N ESTs mapped to it. In the case when all N ESTs are mapped to the same position, we have a single and reliable prediction of the TSS. Other cases are more complex. Since each locus may have one or more real TSS, we have a mixture model with an unknown number of components, corresponding to an unknown number of TSS per locus. For illustration, we used the well annotated genome of Arabidopsis thaliana whose loci may have thousands of ESTs per locus mapped to any given promoter region. In our application we assumed that the length of the promoter-containing region is at most 3000 nucleotides and a TSS can be located in any position in the promoter-containing region. The true positions of the TSS are determined by an unknown parameter θ. The task is to determine the probability distribution of θ based on the positions of 5′ ESTs on the genome.

Theory

We used nonparametric maximum likelihood (NPML [19],) framework to develop NPEST, an algorithm for estimating the unknown probability distribution F given the data Y. Consider the following statistical model:

$$\begin{array}{c}\hfill Y_i~p_i(Y_i\mid {\theta }_i),i=1,\dots ,N,\hfill \\ \hfill {\theta }_i~F\hfill \end{array}$$

Where Y_i is a vector of independent but not necessarily identically distributed measurements with known density p_i(Y_i|θ_i), θ_i is a vector of unknown parameters defined on a space Θ in finite dimensional Euclidean space, F is an unknown probability distribution on Θ. Assume that given the probability distribution F, parameters {θ_i} are independent and identically distributed random vectors with common (but unknown) probability distribution F on Θ. Our goal is to estimate F based on the data Y^N=(Y₁,…,Y_N). In the next section we provide a brief explanation of the mathematical foundations of NPEST.

Nonparametric maximum likelihood (NPML)

In statistics, maximum likelihood estimation (MLE) is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum likelihood estimation provides estimates for the model's parameters. NPML produces an estimate of an unknown distribution F given the data set and a statistical model without assuming anything about the shape or the structure of it. The NPML method is applicable to many well-known estimation problems in statistics. For example, consider a population of adult halibut. One may be interested in measuring the distribution of the length of the halibut. It is known in general that male halibut are longer than female halibut. But there are short males and long females. The NPML estimate of the distribution of lengths would then be bimodal (two peaks). This would say that there are “hidden” covariates in the data. For example, it can be the gender of a halibut (which is not easy to determine), or something else.

The log likelihood function of F is a function of an unknown distribution F which is formed as a log of joint distribution of the data set given F and can be written as follows

$$l\left(F\right)=\log \left(p\right(Y^N\mid F\left)\right)=\sum _{i=1}^N\log \left(p_i\right(Y_i\mid F\left)\right)$$

where

$$p_i(Y_i\mid F)=\int p_i(Y_i\mid \theta )\mathrm{d}F\left(\theta \right)$$

We call F^ML a maximum likelihood estimate of F if it maximizes the likelihood function of F over all possible distributions of θ. As shown by Mallet [20], the ML estimator F^ML of F is a discrete distribution with no more than N support points where N is the number of objects in the population. The positions and weights of the support points are unknown. If we assume that K is a number of support points, then the ML estimator can be written as follows:

$$F^{\mathrm{ML}}=w_1{\delta }_{{\phi }_1}+\cdots +w_K{\delta }_{{\phi }_K}=\sum _{k=1}^K{w}_k{\delta }_{{\phi }_k},K\le N$$

Where {φ_k} are the support points in Θ and {w_k} are the weights such that w₁≥0,…,w_k≥0 and ${\sum }_{k=1}^K{w}_k=1$ The terms δ_φ represents the delta distribution on ta with the defining property that it is equal to 1 at φ and zero everywhere else. Positions and weights of the support points are unknown and the likelihood maximization problem is now to find the set of θ₁,…,θ_K and w₁,…,w_K that maximize log-likelihood function, where

$$l\left(\lambda \right)=\sum _{i=1}^N\log \left(\sum _{k-1}^K{w}_k{p}_i(Y_i\mid {\phi }_k)\right)$$ (1)

We implemented an algorithm based on the expectation-maximization (EM) method to determine F^ML [21]. The algorithm works as follows:

Initialization: Let λ = (φ₁,…,φ_K, w₁,…,w_K) and fix some K ≤N,

• Step 1.

  Initiate: λ = λ⁽⁰⁾

• Step 2.
  E-step: compute the conditional expectation

  $$Q(\lambda ,{\lambda }^{\left(n\right)})=E\left[l\right(\lambda )\mid Y_1,\cdots ,Y_N,{\lambda }^{\left(n\right)}]$$
• Step 3.

  M-step: find λ⁽ⁿ⁺¹⁾ that maximizes Q(λ,λ⁽ⁿ⁾)

• Step 4.

  If |λ⁽ⁿ⁾-λ⁽ⁿ⁺¹⁾|<ε, where ε is a small pre-set number, then stop. Otherwise, go to Step 2.

Note that λ⁽ⁿ⁺¹⁾ that maximizes Q(λ,λ⁽ⁿ⁾)) can be found as follows:

$${\phi }_k^{(n+1)}=\mathrm{argmax}\left\{\sum _{i=1}^{N}p({\phi }_k^{\left(n\right)}\mid Y_i,{\phi }^{\left(n\right)})\log \left(p_i\right(Y_i\mid \phi \left)\right):\phi \in ϴ\right\}$$ (2)

for all k = 1,…, K, and

$$w_k^{(n+1)}=\frac{1}{N}\sum _{i=1}^{N}p({\phi }_k^{\left(n\right)}\mid Y_i,{\lambda }^{\left(n\right)})$$ (3)

where

$$p({\phi }_k^{\left(n\right)}\mid Y_i,{\lambda }^{\left(n\right)})=\frac{w_k^{\left(n\right)}{p}_i(Y_i\mid {\phi }_k^{\left(n\right)})}{\sum _{m=1}^K{w}_m^{\left(n\right)}{p}_i(Y_i\mid {\phi }_m^{\left(n\right)})}$$ (4)

for all i = 1,…, N.

The derivations of these formulas together with the proof of the fact that the EM algorithm increases the value of the likelihood function can be found in Schumitzky [21]. However, it is well known that the EM algorithm does not always converge to a global maximum. Therefore we used so-called directional derivatives to check if the distribution that we found using our iterative scheme is in fact the global maximum of the likelihood function. Let

$$D(\phi ,F)=\sum _{i=1}^N\frac{p(y_i\mid \phi )}{p(y_i\mid F)}-N$$

Then the following theorem holds:

Theorem 1 [22]. F^ML is the distribution that maximizes l (F) if and only if max{D(φ,F^ML):φ∈Θ} = 0. Moreover, the support points of F^ML are contained in the set of zeros of the function D(φ,F^ML), when {φ:D(φ,F^ML) = 0}.

The way we check if the set of φ₁,…,φ_K and w₁,…,w_K that we found using the EM algorithm gives us a global maximum of the log-likelihood function is as follows. Calculate D(φ,F^ML) for a large set of values of h_i in Θ. If D(φ,F^ML)≤0, then accept the results. If this is not the case, we choose a different K and repeat the procedure. We now only have to determine the right number of components, K. It is also not difficult; we have to determine the minimum K that satisfies the conditions of the Theorem 1. However, NPML gives only a point estimate of the distribution F (i.e., if for some reason you say that a probability of a fair coin landing heads is $\frac{1}{3}$, it will be a point estimate of the true probability of heads, but it may be far from it). In the case of a finite-dimensional parameter there are methods to estimate the accuracy of such point estimates, but in our case F is an infinitely dimensional parameter and there are no standard methods of estimating the accuracy of such parameters. However, it is possible to get bootstrapped confidence intervals for NPML which can be thought of as an approximation of accuracy of the estimates.

Postprocessing: determination of the number of peaks in the mixture

There is an optional post processing step of the algorithm. The goal of this step is to obtain smoothed versions of F^ML, find the number of peaks, and remove peaks that are supported by less than the preset fraction of ESTs.

A smoothed version of F^ML(φ) is obtained by fitting normal distributions around support points φ_k. The value of standard deviation for these normal distributions is selected to keep the distance between alternative TSS to be at least 100 nucleotides, as suggested by Rach et al. [16]. The R routine findpeaks from the package pracma is applied to this smoothed distribution of F^ML(φ) to identify the number and positions of peaks.

RESULTS

The validity and utility of the NPML approach to nonlinear mixture models in pharmacokinetics have been described by Tatarinova et al. [19]. NPEST is a logical extension of this framework to the problem of analysis of EST distribution. Since the number of EST per locus varies from none to several thousand, prediction of TSS may be either a data rich or a data poor problem. NPEST is suitable for both large and small number of ESTs per locus. We utilize the following model:

$$\begin{array}{c}\hfill Y_i~p_i(Y_i\mid {\theta }_i),i=1,\dots ,N,\hfill \\ \hfill {\theta }_i~F\hfill \end{array}$$

where p_i(Y_i|θ_i) is a Binomial distribution:

$$(y\mid n,p)=\left(\begin{array}{c}\hfill n\hfill \\ \hfill y\hfill \end{array}\right)p^y{(1-p)}^{n-y}$$ (5)

where n is the length of the upstream region, N is the number of ESTs corresponding to a given locus, and values of probability p are specific for each locus, and θ = n × p. The bigger the values of probability p, the larger distance between TSS and ATG. A binomial model provides a convenient description of the TSS-prediction problem by considering each position Y_i as the number of successes in p Bernoulli trials. p is the probability of success, where success is considered to be a presence of EST at a given nucleotide of the n nucleotide-long promoter.

NPEST on simulated data

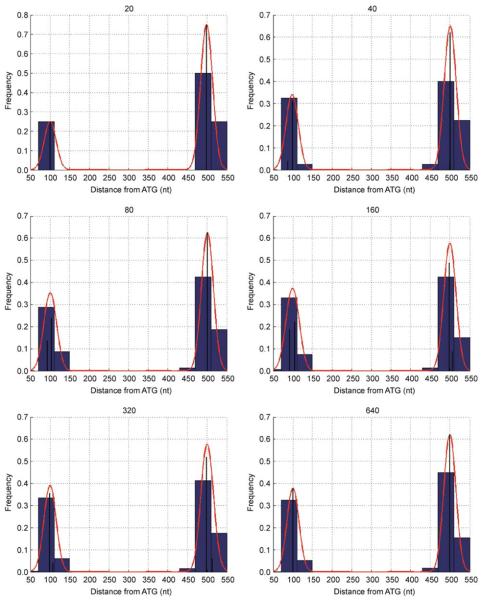
We have conducted a simulation study using Eq. 5. We simulated six datasets, varying the total number of ESTs, N = 20,40,80,160,320,640. The length of the upstream region was assumed to be 1000. Two alternative transcription start sites were placed at 100 and 500 nucleotides upstream from the start of translation. 60% of ESTs corresponded to the 100 nt TSS and 40% to the 500 nt TSS. Positions of ESTs are taken from the mixture of Binomial distributions with parameters n = 1000 and p = x/n, where x was 100 with probability 0.6 or 500 with probability 0.4. Variability of simulated EST positions provided by Binomial distribution represents combined biological and experimental noise. The model in Eq. 5 was implemented using Matlab [23]. Results are shown in Figure 1. NPEST was able to predict the correct number of peaks and appropriate relative strength of alternative transcription start sites.

Figure 1. Simulated dataset with N = 20,40,80,160,320,640 ESTs attributed to two alternative TSS at positions 100 and 500 nucleotides upstream from the start of translation.

The blue histogram shows the distribution of EST positions, black lines correspond to the NPEST output, F^ML(θ), and red lines correspond to the smoothed distribution of TSS positions.

Next, we applied NPEST to a real dataset of ESTs of Arabidopsis thaliana. We compared our TSS predictions to a number of previously annotated datasets. Using NPEST, we predicted TSS for 16520 loci in Arabidopsis. Genome-wide analysis was conducted on the USC high performance computer cluster (HPCC, USC Center for High-Performance Computing and Communications). The predicted TSSs and promoter sequences can be downloaded from www.glacombio.net. Below we present a comparison of NPEST annotations to TAIR, PlantProm DB, PlantPromoter Database and Pol II occupancy data. Since the four databases contain different numbers of promoters, for each comparison we extracted a new subset of NPEST predictions.

We used well-known statistical features of core promoter regions to compare performance of TSS-prediction methods. For example, the TATA-box motif, located around position − 30 from the TSS, is the most over-represented sequence pattern [24,25]. Another conserved feature is the initiator (Inr), located at TSS, commonly containing the dinucleotide sequence CA [1,26].

Comparison between NPEST and TAIR annotations

We compared the performance of NPEST and TAIR annotations. To make this comparison we used the main prediction by TAIR release 10 (using version .1 of each locus) and the main prediction made by NPEST (the highest peak of the distribution function). For the set of 15875 promoters predicted by both methods 11304 (71%) were predicted within 50 nucleotides of each other and 7192 (45%) within 10 nucleotides of each other.

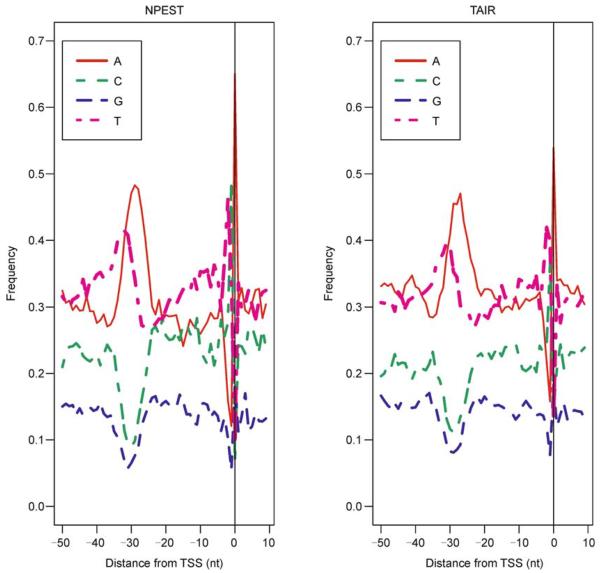
Next, we have selected only those “reliable” promoters that had at least 5 ESTs mapped to the mode of the EST distribution. We compared the frequencies of canonical TATA-box 4-nucleotide sequence (“TATA”) in promoters predicted by TAIR and by NPEST. We found that 30% of TAIR-predicted promoters contain “TATA” in the interval [− 40, − 20] nucleotides upstream from the TSS, as compared to 44% of NPEST-predicted promoters (Table 1). Counting less common 4-nucleotide forms of the TATA-box (such as “TAAA” and “CTAT”) are also more prevalent in NPEST-predicted promoters (61% vs. 55%). In addition, there is a stronger nucleotide consensus at TSS (46% of T and 49% of C followed by 65% of A) for NPEST then for TAIR (43% of T and 35% of C followed by 53% of A) (see Figure 2). Both methods produce the TSS consensus which is in agreement with the core promoter model described by Lenhard et al. [26].

Table 1.

Comparison of promoters predicted by TAIR and NPEST algorithms.

Annotation method	TATA	TATA + TAAA	TATA + TAAA + CTAT
TAIR	0.30	0.52	0.55
NPEST	0.44	0.59	0.61

Frequency of TATA-box in the interval [−40,−20] nucleotides upstream from the TSS

Figure 2. Comparison between NPEST (left) and TAIR (right).

Nucleotide consensus around the predicted TSS is more pronounced for the NPEST algorithm than for the TAIR annotations. There are 45% of T and 44% of C followed by 63% of A for NPEST and for TAIR: 43% of T and 35% of C followed by 53% of A.

An example

Figure 3 shows an example (locus AT1G72610) of TSS prediction by NPEST. According to TAIR, the 5′ UTR is 116 nucleotides long; according to NPEST, there are two peaks. The major peak is 55 nucleotides (as supported by 64% of the ESTs mapped to this locus) and the minor peak 116 nucleotides upstream from ATG. To compare the two predictions, we have extracted 60 nucleotides (50 upstream and 10 downstream) around the transcription start sites. For the TSS at 55 nt, the sequence has a very strong canonical TATA-box (“CTATATAAA”) at − 37 nt upstream from the TSS:

Figure 3. Example of the distribution of EST positions in an upstream region and NPEST prediction of TSS.

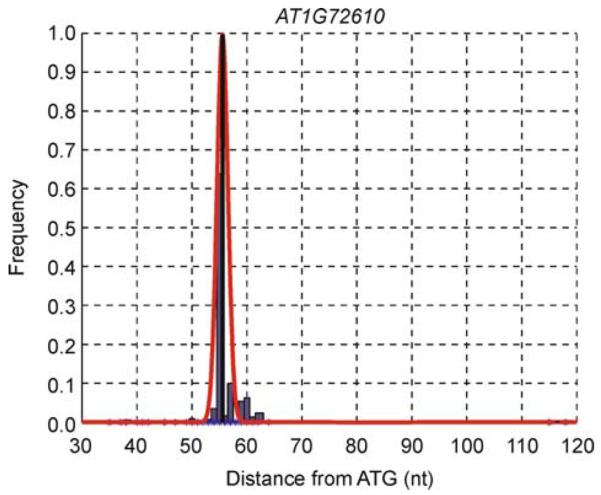
Histogram of the data is shown in blue, NPEST predictions are shown as black lines, and smoothed distributions are shown as red curves. There are 460 EST sequences mapped to the position −55, and 2 EST sequences are mapped to positions −115 nt and −117 upstream from the ATG.

This example illustrates that NPEST ranks TSS supported by multiple expressed sequence tags higher than those with less EST support. It also shows that since NPEST reports multiple TSSs per locus, and the main one does not necessarily agree with the TAIR prediction, the overlap between the two methods is actually higher than the one reported above. For example, locus AT1G72610 will be reported as mismatching, since the distance between the main TSS reported by NPEST (at 55 nt) and the TSS reported by TAIR (at 116 and agreeing with the minor TSS prediction by NPEST) is above 50 nucleotides. Note that the minor TSS will disappear during the post-processing step.

Comparison between NPEST and PlantProm DB

Next, we used a collection of Arabidopsis promoters from PlantProm DB [27], containing positions of TSS for 3503 genes, to assess the performance of NPEST. Of those genes, 3216 have NPEST prediction as well as PlantProm DB ones. Of those, 2521 (78%) PlantProm DB predictions agree with the main NPEST predictions within 50 nucleotides. Furthermore, 1609 (50%) loci agree within 10 nucleotides. Using promoters predicted by both methods we computed frequency of TATA-box in NPEST and PlantProm DB predictions.

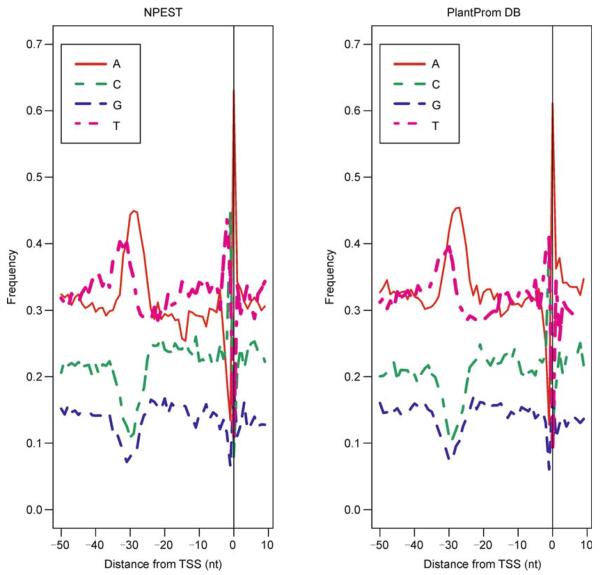
Arabidopsis promoters predicted by NPEST contain the “TATA” motif within the interval [−40, −20] in 36% of cases, contain the “TAAA” motif in 41% of cases and “CTAT” motif in 20% of cases. Arabidopsis promoters in PlantProm DB contain the “TATA” motif within the interval [−40, −20] in 35% of cases, contain the “TAAA” motif in 37% of cases and the “CTAT” motif in 16% of cases. Nearly 6% of promoters contain all three versions of the TATA-box (“TATA”, “CTAT” and “TAAA”). One of the examples is locus AT1G72610 discussed above, where all four motifs overlap and form a long composite motif “CTATATAAA”. We observed that promoters equipped with multiple copies and/or versions of the “TATA” box on average have twice more EST sequences mapped to them as compared to promoters with the canonical “TATA” box only. Therefore, we speculate that “TATA”-like motifs have multiplicative effect. Next, we examined nucleotide consensus at the TSS. There are 44% of T and 45% of C followed by 63% of A for NPEST and for PlantProm DB: 39% of T and 40% of C followed by 61% of A (see Figure 4).

Figure 4. Comparison between NPEST(left) and PlantProm DB (right).

Nucleotide consensus around the predicted TSS is more pronounced for the NPEST algorithm than for the PlantProm DB annotations. There are 44% of T and 45% of C followed by 63% of A for NPEST and for PlantProm DB: 39% of T and 40% of C followed by 61% of A.

Comparison between NPEST and PlantPromoter DB data

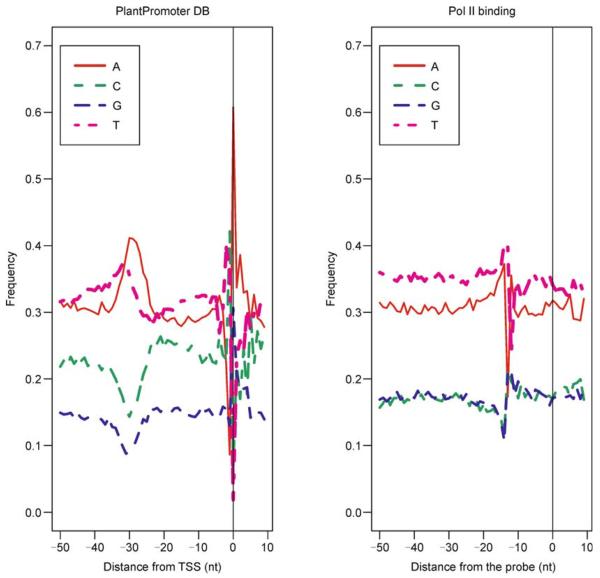
We have obtained results of the CT-MPSS experiment, a combination of the cap-trapper and massively parallel signature sequencing methods [28]. We mapped positions of TSS tags onto the upstream sequences from TAIR; 8583 of the upstream sequences have transcription start sites predicted by the CT-MPSS technique. Of those, the TSS positions of 6817 (79%) loci are located within 50 nucleotides of the main NPEST prediction and 4511 (53%) within 10 nucleotides. Comparing to the NPEST predictions that have at least five ESTs mapped to the mode of EST distribution, we find that 31% of PlantPromoter DB sequences contain “TATA” motif, 35% contain “TAAA”, and 14% contain “CTAT” in the interval [−40, −20] nucleotides upstream from TSS. At the TSS, are 40% of T, followed by 42% of C, and then 61% of A (see Figure 5).

Figure 5.

Comparison between PlantPromoter DB (left) and RNA polymerase II binding data (right)

Comparison between NPEST and RNA polymerase II binding data

Nucleosomes present a barrier to RNA polymerase II (Pol II) transcription. We used Pol II occupancy data from Chodavarapu et al. [29]. Although the dataset does not have the resolution to define positions of TSS, nonphosphorylated Pol II CTD are expected to be enriched in promoters, and the dataset provides a useful indication of transcription initiation region. We mapped Pol II occupancy data onto the upstream sequences from TAIR; 4589 of the upstream sequences are covered by the Pol II experimental data. As expected, Pol II occupancy data moderately agree with NPEST predictions: only 1496 (33%) of loci have positions of Pol II and NPEST at the distance under 50 nucleotides from each other; 1056 (23%) are within 10 nucleotides. There is also a weak agreement between Pol II binding data and CTMPSS-predicted transcription start sites: in only (33%) of loci the distance is below 50 nucleotides. Since Pol II occupancy data cannot point to the exact start of transcription, nucleotide consensus is weaker than in obtained by other methods. “TATA” motif was detected only in 12% of promoters in the interval [−40, −20]; “TAAA” was detected in 16% of promoters; and “CTAT” was detected in 7% of promoters.

DISCUSSION

NPEST uses the distribution of ESTs to predict positions of transcription start sites. The most reliable prediction is attained for those loci where there are a large number of ESTs mapped to the upstream region. We have investigated how the number of mapped ESTs affect the number of predicted TSS per locus. Using EST library annotation information, we have assigned each EST to one of the 40 categories based on the library (e.g., “Shoots”, “Roots”, “Drought” etc.). A separate category was reserved for ESTs without library information. There are 7549 loci that have one category of EST assigned to them and 5281 with two categories. On average, one-category loci have 1.43 alternative TSSs and 3.69 ESTs mapped to the promoter region. Two-category loci have 2.43 TSSs and 9.65 ESTs.

What is the relationship between the number of ESTs and the number of predicted TSS? In order to answer this question we use a partial correlation coefficient. Partial correlation coefficient p_XY·Z measures the degree of association between the number of alternative TSSs (Y) and the number of ESTs per locus (Z), with the effect of number of EST categories (X) removed. Pearson's correlation between the number of categories and the number of TSS is 0.55, between the number of categories and the number of ESTs is 0.29, and between the number of ESTs and number of TSS is 0.14. Resulting partial correlation coefficient is p_XY·Z = −0.02. Therefore, we believe that loci with ESTs from different libraries have more alternative transcription start sites than loci from one library, regardless of the total amount of mapped ESTs.

When compared to the other methods, NPEST predictions have an increased number of TATA-like sequences in promoters and a stronger “TCA” consensus at the TSS. We need to point out that the TATA box motif is especially over-represented in promoters of stress-related or tissue-specific genes [13,30]. Analyzing fruit fly promoters, Rach et al. [16] distinguished two initiation patterns: “peaked” TSSs, and “broad” TSS cluster groups. Broad initiation regions are more common in constitutively expressed genes and peaked TSS are more prevalent in stress- and tissue-specific genes. Yamamoto et al. [28] classified Arabidopsis core promoter elements into two types: the “TATA-type” and the “GA-type”. Yamamoto et al. also pointed out that genes with the “TATA-type” promoters have high expression with sharp-peak TSS clusters. In contrast, the “GA-type” produces broad TSS clusters. Therefore, enrichment of TATA boxes and strong nucleotide consensus at TSS in NPEST-predicted promoters (evident from Figures 2, 4, and 5 and Table 1) indicates that NPEST may perform better for promoters of stress- and tissue-specific genes.

In the near future we will combine the 5' EST analysis discussed in this paper with other indicators of the TSS position, such as: over-representation of known transcription factor binding sites, DNA methylation, characteristic UTR length, nucleosome positioning, investigated by a number of researchers [1,29,31,32]. We also plan to extend our approach to other plant and animal species.

CONCLUSIONS

We present a novel nonparametric method called NPEST, which has been devised for the more accurate and reliable analysis of EST distributions. The method was applied to the genome of Arabidopsis thaliana, and predicted promoters were compared to TAIR predictions. The method is organism-independent and can be applied to a wide range of experimental evidence for TSS positions. Our proposed method expands recognition capabilities to multiple TSS per locus and enhances the understanding of alternative splicing mechanisms for production of multiple products from a single structural gene. Using our statistical tools we analyzed the promoters and have developed a database of TSS for 16520 loci, which is publicly available at www.glacombio.net. Promoter sequences shorter than 100 nucleotides were removed from the database. The method is organism- and data-type independent and can be efficiently used to analyze large data sets. Reliable prediction of TSSs will improve performance of motif-finding tools, such as cisExpress [30] and TSSer [13] that rely on availability of accurately identified promoter sequences.