PIGEONS' DELAY DISCOUNTING FUNCTIONS ESTABLISHED USING A CONCURRENT-CHAINS PROCEDURE

Abstract

Several studies have examined discounting by pigeons and rats using concurrent-chains procedures, but the results have been inconsistent. None of these studies, however, has established that discounting functions derived from estimates of indifference points can be obtained with a concurrent-chains procedure, so their validity remains in doubt. The present study used a concurrent-chains procedure within sessions combined with an adjusting-amount procedure across sessions to determine the present, subjective values of food reinforcers to be obtained after a delay. Discounting was well described by the hyperbolic discounting function, suggesting that the concurrent-chains procedure and the more typical adjusting-amount procedure are measuring the same process. Consistent with previous studies with rats and pigeons using adjusting-amount procedures, no significant effect of the amount of the delayed reinforcer on the degree of discounting was observed, suggesting that the amount effect may be unique to humans although consistent with the view that animals' choices are controlled by the relative, rather than the absolute, value of reinforcers.

Humans and nonhuman animals are constantly making choices: where to forage, what food to eat, what route to take to get home, etc. In some situations, choices are relatively easy to make, and it is relatively easy to predict what will be chosen. For example, when the choice is between two otherwise identical rewards that differ only in amount, there is a tendency to choose the larger over the smaller; when choosing between rewards of the same amount that differ only in when they can be received, the tendency is to choose the one that can be received sooner over the one that would be received later. Choices are not as easy to predict, however, when the alternatives vary along more than one dimension, as is the case when the alternatives are a smaller reward that could be received immediately and a larger reward that could be received later. This is because the present, subjective value of a reward decreases as the delay to the reward's receipt increases, a phenomenon known as delay discounting (for reviews, see Frederick, Loewenstein, & O'Donoghue, 2002; Green & Myerson, 2004). Delay discounting describes the fact that although a smaller, immediate reward might be chosen over a larger, delayed reward, if the delay were decreased, the immediate amount decreased, or the delayed amount increased, then the opposite choice might be observed, and the larger, delayed reward might be the one that is chosen.

Such effects of delay and reward amount on choice may be represented mathematically. Both human and nonhuman discounting data have been shown to be well described by a hyperboloid discounting function of the form:

$$V=A∕{(1+kD)}^s,$$ (1)

where V is the present, subjective value of a delayed reward of amount A, D is the delay to the receipt of that reward, k is a parameter that represents the rate of discounting, with larger values representing steeper discounting, and s is a parameter that reflects the nonlinear scaling of amount and delay (Myerson & Green, 1995). When s = 1.0, Equation 1 reduces to a simple hyperbola (Mazur, 1987), which provides a good fit to data from nonhuman animals (e.g., Green, Myerson, Holt, Slevin, & Estle, 2004; Oliveira, Calvert, Green, & Myerson, 2013), whereas with human data, an s parameter less than 1.0 typically provides a significantly better fit (Green & Myerson, 2004).

Another aspect of delay discounting that suggests a difference between humans and nonhuman choices is referred to as the amount effect (also known as the magnitude effect). Numerous studies have shown that humans discount larger delayed rewards less steeply than smaller delayed rewards. For example, Green, Myerson, and McFadden (1997) presented subjects with choices between a larger amount ($100, $2,000, $25,000, or $100,000) to be received after a delay (ranging between 3 months and 20 years) and a smaller amount to be received immediately. Results showed that the rate of discounting decreased as the amount of the delayed reward increased, at least up to the $25,000 amount, after which it leveled off.

The amount effect has been observed in numerous studies, not only with hypothetical monetary rewards (e.g., Benzion, Rapoport & Yagil, 1989; Green, Myerson, Oliveira, & Chang, 2013; Kirby, 1997; Thaler, 1981), but also with other types of hypothetical outcomes, including consumable rewards like beer, soda, and candy (Estle, Green, Myerson, & Holt, 2007), medical treatments (Chapman, 1996), heroin (Giordano et al., 2002), cigarettes (Baker, Johnson, & Bickel, 2003), and vacation time (Raineri & Rachlin, 1993). The amount effect also has been observed in studies in which real money (Johnson & Bickel, 2002; Kirby, 1997) and consumable liquids (Jimura, Myerson, Hilgard, Braver, & Green, 2009) were the rewards.

Using adjusting-amount procedures similar to those typically used with humans, several animal studies have failed to observe the amount effect. Richards, Mitchell, de Wit, and Seiden (1997, Experiment 3) studied the discounting by rats of different amounts of water at different delays. Although a small tendency for steeper discounting of larger amounts (opposite to what is typically observed in humans) was observed, this effect was not significant. Similarly, Green et al. (2004) failed to find an effect of amount on the degree of discounting of food reinforcers by either pigeons or rats.

In a study comparing the discounting of qualitatively as well as quantitatively different reinforcers, Calvert, Green, and Myerson (2010) first assessed rats' degree of preference for different food and water reinforcers, and then compared the rates at which different amounts of each reinforcer were discounted, as well as the discounting rates of differentially preferred reinforcers (highly preferred vs. less-preferred reinforcers of the same amount). Consistent with previous findings with nonhuman animals, no systematic differences in degree of discounting as a function of reinforcer amount were observed. Importantly, there also were no differences in degree of discounting as a function of quality (i.e., differentially preferred reinforcers). Finally, Freeman, Nonnemacher, Green, Myerson, and Woolverton (2012) extended these findings to nonhuman primates employing a procedure typically used in behavioral pharmacology for establishing dose-effect functions. Freeman et al. compared the rates at which rhesus monkeys discounted 10% and 20% concentrations of delayed sucrose, and found no systematic differences in the discounting of the two sucrose concentrations.

Other studies have investigated whether nonhuman animals show an amount effect using a concurrent-chains procedure. For example, Grace (1999) used a two-component concurrent-chains procedure. In both components, the initial-links were associated with an independent, concurrent VI 30-s VI 30-s schedule. In the “small amount” component, the keys were transilluminated with red light in the initial link, and both terminal links were associated with relatively brief access to food, whereas in the “large amount” component, the keys were transilluminated with green light in the initial link and both terminal links were associated with access to food for 2.5 times longer. The terminal links of both components were associated with different pairs of VI schedules across different experimental conditions (10 s and 20 s; 20 s and 10 s; 6 s and 24 s; and 24 s and 6 s). Sensitivity to terminal-link delay was evaluated by examining how response allocation in the initial link varied across conditions, with more extreme preference for the briefer terminal-link schedule taken as evidence of greater sensitivity to delay. No systematic differences were observed in pigeons' sensitivity to delay between the “small amount” and “large amount” components.

Ong and White (2004) repeated Grace's (1999) study with modifications aimed at enhancing discrimination between the “small amount” and “large amount” components. Specifically, in their Experiment 1, Ong and White used a larger ratio between the two reinforcer durations (4.5-s vs. 1-s access to grain) and reversed the terminal-link delays between components so that the delay to the smaller and larger amounts was conditional on the color of the initial-link keys. Their results suggested that pigeons' delay sensitivity was greater for the larger amount, although this was not true in their Experiment 2 where they replicated the procedure used by Grace. More recently, Orduña, Valencia-Torres, Cruz, and Bouzas (2013) conducted a study with rats in which they replicated Ong and White's first experiment, and again found greater sensitivity to delay in the component with the larger reinforcer. It is important to note that the direction of this effect is the opposite of that typically observed with humans, whose sensitivity to delay is consistently greater with smaller amounts (i.e., smaller rewards are discounted more steeply than larger rewards).

To our knowledge, only Grace, Sargisson, and White (2012) have reported an effect of reinforcer amount in nonhuman animals (specifically, pigeons) that is consistent with that observed with human subjects. Like Orduña et al. (2013) and Ong and White (2004), Grace et al. used a two-component concurrent-chains procedure, but in this case each terminal link was associated with a different amount of food (1-s vs. 4.5-s access to wheat). In the component in which the initial-link keys were red, the delay to the smaller amount of food in the terminal link was always 2 s and the delay to the larger amount of food was varied between 2 and 28 s across conditions. In the component in which the initial-link keys were green, the delay to the larger amount in the terminal link was always 28 s and the delay to the smaller amount was varied between 2 and 28 s across conditions. Grace et al. compared the rate at which preference for the larger reinforcer decreased as its delay increased across conditions in the red component with the rate at which preference for the smaller reinforcer decreased as its delay increased across conditions in the green component. They reported that relative preference for the larger amount, a measure of its relative value, decreased more slowly with increasing delay than did relative preference for the smaller reinforcer amount, which they interpreted as indicating steeper discounting of smaller rewards, a result similar to that observed with humans.

The findings regarding amount effects obtained with concurrent-chains procedures have been inconsistent, although procedural differences appear to play a role (Ong & White, 2004). Furthermore, none of the studies using a concurrent-chains procedure assessed the present value of the delayed reinforcers directly by estimating indifference points between the smaller, sooner and the larger, more delayed reinforcer, although Grace et al. (2012) did present their group mean data in the form of a discounting function in which a transform of the logarithm of the ratio of the response rates in the initial links was plotted as a function of the delay in the terminal links. In the absence of discounting functions based on indifference points, however, the validity of this approach and its relation to the results of adjusting-amount procedures used with humans remains uncertain.

Accordingly, the goal of the first phase of the current investigation was to determine whether the data obtained with concurrent-chains procedures, like those obtained with adjusting-amount procedures, are well described by a simple hyperbola (i.e., Eq. 1 with s set equal to 1.0). The novel approach we developed for this purpose combined the concurrent-chains and the adjusting-amount procedures. Specifically, response allocation in the initial link of the concurrent chains was used to assess pigeons' preference between a smaller, immediate reinforcer and a larger, delayed reinforcer; across sessions, the amount of the smaller reinforcer in the terminal links was adjusted based on the preference until indifference between the smaller and the larger amounts was reached at each of five delays to the larger reinforcer. This allowed us to plot out individual discounting functions and evaluate whether the simple hyperbola provided a good description of the data.

The second phase of the experiment was designed as a systematic replication of the first that would allow us to evaluate whether an amount effect was observed when the amount of the delayed reinforcer was changed. The same pigeons were studied in the second phase using the same procedure and delays as in the first phase, but with the amount of the delayed reinforcer reduced by half (from 32 pellets in Phase 1 to 16 pellets in Phase 2). If the degree of discounting increased when the amount of the delayed reinforcer was reduced to 16 pellets, such a finding would be evidence for an amount effect similar to that observed with humans.

Method

Subjects

Ten male White Carneau pigeons (Columba livia), all of whom had previous experience with discounting procedures, served as subjects. The pigeons were maintained at 85% of their free-feeding weight. Deprivation level was maintained by providing postsession feeding when necessary. The pigeons were housed in individual home cages where they had continuous access to water and grit and were maintained on a 12:12-h light:dark cycle.

Apparatus

Two experimental chambers (Med Associates, Inc.), each measuring 29 cm long by 25 cm wide by 28.5 cm high, were located within sound- and light-attenuating enclosures each equipped with a ventilation fan. Two response keys, spaced 16 cm apart center to center, were mounted on the front panel of the chamber, 23.5 cm above the grid floor and 3.5 cm from the side walls of the chamber, and could be transilluminated with white, red, and green light. A clicker was used to provide auditory feedback for all key pecks during a trial. A triple-cue light, centered on the panel and equipped with a green, yellow, and red bulb, was located 26.5 cm above the grid floor. A food magazine was mounted on the center of the panel, 4 cm above the grid floor, and equipped with a 7-W white light that was illuminated during reinforcement. A pellet dispenser (Med Associates, Inc.), situated behind the front panel, delivered 20-mg precision food pellets (TestDiet®) at the rate of one pellet every 0.3 s. Pellet dispensers were tested daily and on those rare occasions when a pellet dispenser became jammed during a session, the respective data were not used. A 7-W houselight was mounted centrally on the ceiling of the chamber. Med-PC™ software (Med-Associates, Inc.) was used to control experimental events and record responses.

Procedure

The study consisted of two control conditions followed by the two experimental phases (each involving five delay conditions) which differed in the number of delayed food pellets. A concurrent-chains procedure was used in all control and experimental conditions. During the initial link of the chain, both keys were illuminated with white light. In the terminal link, red and green keys were associated with either the smaller, immediate reinforcer or the larger, delayed reinforcer. For half the pigeons, the smaller, immediate reinforcer was associated with the left, red key, and the larger, delayed reinforcer was associated with the right, green key. For the other half of the pigeons, the smaller, immediate reinforcer was associated with the right, green key, and the larger, delayed reinforcer was associated with the left, red key. However, for ease of exposition, all conditions will be described according to the former arrangement.

Each trial began with the illumination of the houselight and both initial-link keys being lit with white light. The schedule associated with the initial link was a non-independent VI 30-s schedule to ensure that daily sessions ended with an equal number of left and right terminal-link outcomes (Alsop & Davison, 1986; Stubbs & Pliskoff, 1969). A 2-s changeover delay was used to prevent the pigeons from constantly switching between the two response keys (Shahan & Lattal, 1998). Each session consisted of 40 trials, half of which resulted in the smaller, sooner reinforcer, and half of which resulted in the larger, delayed reinforcer. The specific intervals associated with the VI schedule were derived using the exponential progression method described in Fleshler and Hoffman (1962).

On smaller–sooner trials, once the VI had timed out (and the changeover delay completed), a peck on the left white key turned both white keys off and illuminated the left red key. A fixed-ratio 3 (FR 3) schedule was associated with the terminal links. After three pecks, the red key would turn off, the red cue light would flash once (for 0.3 s), after which the small reinforcer was delivered. On larger–later trials, once the VI had timed out, a peck on the right white key turned both white keys off and illuminated the right green key. Three pecks on this key would turn it off, and the large reinforcer (16 or 32 pellets in different phases) was delivered after a delay (1, 3, 6, 10, or 20 seconds in the different conditions). The green cue light flashed (0.3 s on, 0.3 s off) for the duration of the delay. Preference for the smaller–sooner or larger–later outcome was measured using the relative number of responses on each of the white keys during the initial link.

Control conditions

Prior to the experiment proper, two control conditions were conducted in order to ensure that the pigeons were sensitive to the amounts of and delays to reinforcement to be used in the experiment. In the first control condition, the pigeons chose between 32 pellets to be delivered immediately (from the left, red key) and 32 pellets to be delivered after a 10-s delay (from the right, green key). In the second control condition, the pigeons chose between 16 pellets (left, red key) and 32 pellets (right, green key), both of which were delivered immediately.

Each of the control conditions ran for a minimum of 14 sessions, and until stability was achieved. For stability, the last nine sessions were divided into three 3-session blocks. Behavior was considered stable when (a) the median relative rate of each of these blocks did not show a trend (i.e., neither Md₁>Md₂>Md₃, nor Md₁< Md₂< Md₃), and (b) there was no visual trend in relative rate during the final five sessions. The pigeon was considered to be sensitive to the difference in delay to and the amount of the reinforcers if its mean relative rate of responding in the initial link on the key associated with the shorter delay (control condition 1) and the key associated with the larger amount (control condition 2), was greater than .55 during the final five sessions.

Experimental conditions

The experiment proper consisted of two phases, each consisting of five conditions. In the first phase, the delayed reinforcer was 32 food pellets, and in the second phase the delayed reinforcer was 16 food pellets. Each of the two delayed amounts was studied at five delays (1, 3, 6, 10, and 20 s), and in both phases, each pigeon experienced the five delays in a different order.

At the beginning of each condition, the pigeons chose between the larger reinforcer (16 or 32 pellets) and a smaller reinforcer that was half that of the larger reinforcer (i.e., 8 or 16 pellets). The pigeon's preference was assessed via the relative number of pecks made on the left white key during the initial link (the key associated with the smaller, immediate reinforcer terminal link). If the percentage of pecks made on the left, initial-link white key was more than 55% of the total number of pecks made during the initial link of the session, the pigeon was said to prefer the smaller, immediate outcome. If less than 45% of the total number of pecks in the initial link were to the left, initial-link white key, the pigeon was said to prefer the larger, delayed outcome. If the pigeon made between 45% and 55% of its initial-link responses to the left, white key, then it was considered to be indifferent between the two terminal-link outcomes.

In each condition, an adjusting-amount procedure was used to obtain an estimate of the amount of immediate reinforcer that was equivalent in value to the delayed reinforcer (for details, see Du, Green, & Myerson, 2002). If the pigeon preferred the immediate reinforcer, the amount of the smaller reinforcer was decreased; if the pigeon preferred the larger reinforcer, the amount of the smaller reinforcer was increased; if the pigeon showed no preference, the condition was terminated and the last smaller amount used was considered to be the indifference point or present subjective value of the larger, delayed reinforcer.

The size of the adjustment (i.e., the decrease or increase in the immediate reinforcer) decreased throughout the condition. The first adjustment was half of the difference between the immediate and the delayed reinforcers, and each subsequent adjustment was half that of the preceding adjustment, down to a 2-pellet adjustment. For example, in the condition where the pigeon chose between 8 immediate pellets and 16 pellets to be received in 10 s, if the pigeon preferred the 16 pellets, then the smaller reinforcer would be increased to 12 pellets. If then the pigeon showed a preference for the 12 pellets, the amount of the smaller reinforcer would be decreased to 10 pellets (the final, 2-pellet adjustment). The preference shown by the pigeon at this value determined the final subjective value estimated for that condition: If the pigeon preferred the 10 pellets, the final subjective value was estimated to be 9 pellets; if the pigeon preferred the 16 pellets, the final subjective value was estimated to be 11 pellets; and if the pigeon was indifferent between 10 and 16 pellets, the final subjective value was 10 pellets. It is to be noted that with this procedure, indifference points could be obtained down to a single pellet for both delayed amounts.

A condition ended when the pigeon was indifferent between the two amounts (i.e., the percentage of responses to the left key in the initial link was between 45 and 55%), or when preference was considered to be stable at the 2-pellet adjustment point. For stability, several criteria had to be met. First, there had to have been a minimum of seven sessions completed at each adjusting amount. Second, the percentage of responses made to the left initial-link key had to be within one of three ranges (< 45%, 45–55%, or > 55%) for the final five sessions. Finally, the last three sessions could not show an upward or downward trend (with the exceptions of a trend towards 0% when preference was below 45% or towards 100% when preference was above 55%). The mean number of sessions was 24.9 (SD = 10.8; range 7–51) for the 16-pellet conditions and 27.9 (SD = 15.2; range 7–62) for the 32-pellet conditions.

Results

Because all the pigeons had extensive experience with discounting procedures (but not a concurrent-chain procedure), no training was required. Of the ten pigeons exposed to the two control conditions, two did not meet the delay and amount sensitivity criteria and therefore were not run in the experiment proper. Mean relative rates of responding for the last five sessions of both control conditions for the eight pigeons that met criteria are shown in Table 1.

Table 1.

Mean relative preference for the sooner reinforcer (Control Condition 1) and for the larger reinforcer amount (Control Condition 2).

Pigeon	Control 1	Control 2
33	.73	.62
36	.79	.60
38	.75	.59
39	.66	.56
82	.80	.60
83	.59	.60
84	.72	.58
86	.61	.65

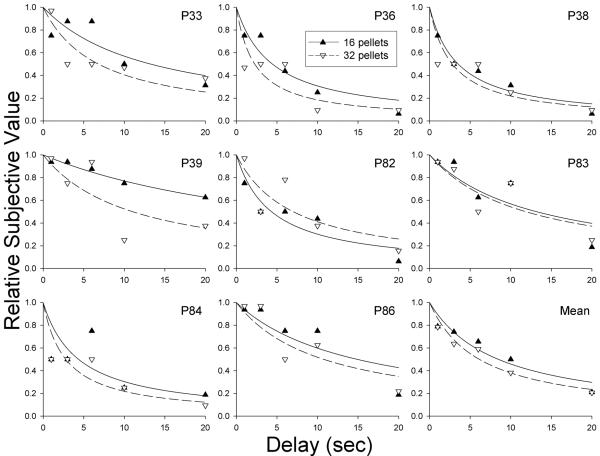
Figure 1 shows the relative subjective value of the delayed reinforcer (i.e., the amount of the immediate reinforcer at the indifference point as a proportion of the amount of the delayed reinforcer) plotted as a function of delay. Filled symbols represent data from Phase 1 in which the delayed amount was 16 pellets, and the open symbols represent data from Phase 2 in which the delayed amount was 32 pellets. As may be seen, in all cases the relative subjective value of the delayed reinforcer decreased systematically as the delay to its receipt increased. In most cases, the simple hyperbola (Eq. 1 with s = 1.0) provided a good fit to the data, with median R²s of .77 and .65 for the 16- and 32-pellet phases, respectively; the fits to the group mean data (shown in the lower right panel) were very good, with R²s for the two phases of .88 and .93. Table 2 presents the estimates of the discounting rate parameter (k) and the R² values for each pigeon at each amount.

Fig. 1.

Relative subjective value of the 16- and 32-pellet reinforcers plotted as a function of delay. Symbols represent the estimated indifference points (subjective values), and curves represent the best-fitting hyperbolic discounting functions (Eq. 1 with s set equal to 1.0) for each pigeon and for the group means. The 16-pellet delayed amount is represented by solid curves and filled circles; the 32-pellet delayed amount is represented by dashed curves and open circles.

Table 2.

Proportions of variance accounted for (R²), discounting rate parameters (k in s⁻¹ units), and root mean square error (RMSE) for the 16- and 32-pellet phases for each pigeon.

Pigeon	Amount	R 2	k	RMSE
33	16	.66	0.076	0.129
	32	.69	0.147	0.116
36	16	.88	0.225	0.095
	32	.39	0.442	0.152
38	16	.93	0.284	0.059
	32	.35	0.357	0.135
39	16	.96	0.030	0.023
	32	.62	0.091	0.181
82	16	.79	0.231	0.100
	32	.71	0.143	0.155
83	16	.75	0.076	0.139
	32	.72	0.084	0.135
84	16	.00	0.229	0.209
	32	.35	0.357	0.135
86	16	.76	0.067	0.136
	32	.79	0.093	0.132

In addition to the proportion of variance accounted for (R²), Table 2 presents the root mean square error (RMSE) for fits of the simple hyperbola to the data from each subject in each amount condition. As Johnson and Bickel (2008) noted, the R²s for fits of hyperbolic discounting functions tend to be correlated with estimates of the k parameter because R² depends on the ratio of the variance in the residuals to the variance in the data, and steep discounting tends to be associated with greater variance in the data than shallow discounting. The RMSE does not have this property because it is equivalent to the standard deviation of the residuals and is independent of the variance in the data. It also is independent of the number and range of the delays studied, and if the data are expressed in proportions (relative subjective value), it is independent of the amount of the delayed reward, as well. Thus, the RMSE, which may be thought of as a weighted average deviation from predictions, provides a good basis for comparing fits for different subjects as well as different conditions and studies.

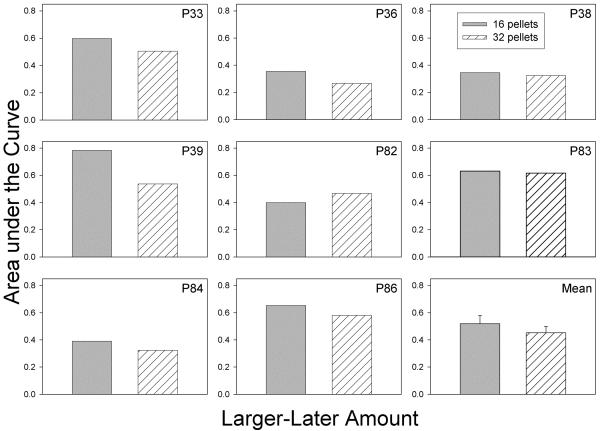
Inspection of Figure 1 and Table 2 suggests that if anything, the degree of discounting of the larger amount was greater than for the smaller amount, opposite to what is found in humans. However, there was no significant difference between the logarithms of the k values for the two amounts, t(14) = 1.02, p = .33. Moreover, there also was no statistically significant difference between the area under the curve (AuC) for the 16-pellet phase and the AuC for the 32-pellet phase, t(14) < 1.0. AuCs are calculated based on the obtained indifference points rather than a fitted curve, and thus represent a theoretically neutral measure (Myerson, Green, & Warusawitharana, 2001) that can vary between 0.0, indicating maximal discounting, and 1.0, indicating no discounting (see Fig. 2). Thus, regardless of whether one uses the AuC or the k parameter estimates, no significant difference was observed between the discounting of 16 and 32 food pellets.

Fig. 2.

Area under the Curve for the 16- and 32-pellet phases for each pigeon and the group means.

Discussion

The present study used a novel procedure that combines concurrent-chains and adjusting-amount procedures in order to establish discounting functions based on indifference points obtained at various delays until reinforcement. The purpose of the study was two-fold: first, to determine whether a simple hyperbola (i.e., Eq. 1 with s set equal to 1.0) would provide a good description of the results using this novel procedure, and second, to investigate whether, as in humans, larger amounts of delayed reinforcement are discounted less steeply than smaller amounts.

Eight pigeons discounted 16 and 32 food pellets at five delays (1, 3, 6, 10, and 20 seconds). Results showed that as the delay to a reinforcer increased, its present subjective value decreased, and the data were well-fitted by a hyperbolic discounting function (Mazur, 1987). This result validates the use of the combination of concurrent-chains with an adjusting-amount procedure as appropriate for studying delay discounting.

It is to be noted that the pigeons produced shallower discounting functions (as indicated by lower discounting rate parameters) in the current study vis-à-vis other pigeon studies that used an adjusting-amount procedure (Green et al., 2004; Oliveira et al., 2013). Across pigeons and amounts, the mean k value was 0.183 (SD = 0.125) in the current study, 0.523 (SD = 0.266) in Green et al., and 0.614 (SD = 0.456) in Oliveira et al. This difference might be related to the fact that in the previous studies, on each trial the pigeons chose between the two outcomes via a single peck, whereas in the current study the pigeons begin choosing between the outcomes at the onset of the initial links, that is, earlier in time relative to the receipt of the reinforcer than with the typical adjusting-amount procedure. The addition of a common delay to both alternatives has been shown to increase self-control in pigeons (Calvert, Green, & Myerson, 2011), which would be evidenced by a lower value of k.

The amount effect is a robust finding in the human discounting literature: Larger delayed amounts are consistently discounted less steeply than smaller delayed amounts. The effect has been observed in a variety of scenarios, with different types of rewards (e.g., both monetary and directly consumable rewards), with both real and hypothetical rewards, and in different populations (e.g., Estle et al., 2007; Jimura et al., 2009; for a review, see Green & Myerson, 2004). In contrast, there have been repeated failures to find an amount effect in nonhuman animals (see Table 3). Studies that have used the more typical adjusting-amount procedure and have established discounting functions based on indifference points, as in human studies, have found no systematic differences between the discounting of different amounts of reinforcement. In addition, studies that have employed a concurrent-chains procedure, evaluating sensitivity to delay but not establishing discounting functions, have reported either no amount effect or a reverse amount effect. One such study (Grace et al., 2012) did report an amount effect and discounting functions, although they were not based on indifference points. However, the present study, which used a hybrid concurrent-chains adjusting-amount procedure to establish discounting functions based on indifference points (in which changes in the amount of the smaller-sooner reinforcer were made between sessions based on preferences determined within sessions) also revealed no evidence of an amount effect when evaluated either by the log k parameter or by AuC.

Table 3.

Summary of pigeon and rat studies investigating the amount effect.

Author	Species	Procedure*	Amounts	Result
Richards et al. (1997)	Rat	AA	100, 150, 200 μL	No amount effect
Grace (1999)	Pigeon	CC	Food duration varies; 2.5:1 ratio	No amount effect
Green et al. (2004)	Pigeon, Rat	AA	5, 12, 20, 32 pellets for pigeons; 5, 12, 20 pellets for rats	No amount effect
Ong and White (2004) Expt. 1	Pigeon	CC	1, 4.5 sec of access	Reverse amount effect
Ong and White (2004) Expt. 2	Pigeon	CC	1, 4.5 sec of access	No amount effect
Calvert et al. (2010)	Rat	AA	10, 30 pellets; 100, 500 μL	No amount effect
Grace et al. (2012)	Pigeon	CC	1, 4.5 sec of access	Amount effect
Orduña et al. (2013)	Rat	CC	1, 4 pellets	Reverse amount effect
Present study	Pigeon	AA/CC combination	16, 32 pellets	No amount effect

^*AA = Adjusting-amount procedure; CC = concurrent-chains procedure

Although it is conceivable that the failure to observe an amount effect in the present study was because the order of the amount phases was not counterbalanced, this seems highly unlikely given the many other failures in the literature. Moreover, although experience can increase self-control in pigeons, the effect of experience asymptotes after relatively brief exposure to choice procedures (Logue, Rodriguez, Peña-Correal, & Mauro, 1984). In contrast, the pigeons in the present study had been run in an experiment using the adjusting-amount procedure for more than one year prior to the current study, and thus had extensive experience with discounting.

How might one account for the difference between human and nonhuman animals regarding the effect of amount? Orduña et al. (2013) noted that the ratios between the different amounts and the types of reward typically used in human and animal studies vary substantially. Indeed, the highest ratio of the largest to the smallest delayed amounts in animal studies was 6.4:1 (Green et al., 2004), whereas with humans, the ratios are often much higher. It is to be noted, however, that Johnson and Bickel (2002) observed consistent amount effects with both real and hypothetical monetary rewards and with ratios between the monetary amounts as low as 2.5:1. Moreover, Jimura et al. (2009) also observed an amount effect in humans using a primary reinforcer (real liquid rewards) and a ratio of 2:1.

Orduña et al. (2013) and Grace et al. (2012) pointed out that in human studies, participants usually experience all of the delayed amounts being studied over the course of a single experimental session. In the present study and in animal studies that used the adjusting-amount procedure, subjects often run under the same standard amount for several weeks at a time. However, other animal studies using concurrent-chains procedures have varied amounts within a single session (Grace, 1999; Ong & White, 2004; Orduña et al., 2013) and have observed either no amount effect or a reverse amount effect.

It is important to note that the finding that animals' discounting is not affected by the amount of delayed reinforcement is consistent with the view, exemplified by the matching law (Herrnstein, 1970), that choices are controlled by the relative, rather than the absolute, value of reinforcers. Other evidence consistent with this view is the finding that when rats chose between immediate and delayed amounts of the same reinforcer, the degree to which they discounted was the same regardless of the quality of the reinforcers involved (Calvert et al., 2010). That is, the rats in the Calvert et al. study strongly preferred saccharin-flavored water to quinine-flavored water, but their choices between immediate and delayed liquids were the same, regardless of whether both were saccharin flavored or quinine flavored. In addition, Oliveira et al. (2013) reported that the degree to which pigeons discounted delayed food reinforcers was not affected by the level of deprivation. If amount, quality, and deprivation result in proportionally equivalent changes in the value of alternative reinforcers, leaving preference between the alternatives unchanged, then it would be expected that manipulations of these independent variables would not affect discounting rates. Thus, the question is not why do animals not show an amount effect, but why humans do.

Regardless of the explanation for the apparent species difference in the effects of amount on discounting, the point we would stress is that there appears to be no discrepancy between results obtained with adjusting-amount and concurrent-chains procedures: In neither case is a reliable amount effect observed in nonhuman animals. Further, what we have shown in the present study, in which the two procedures were combined so that concurrent chains were in effect within sessions, and the amount of immediate reinforcer was adjusted between sessions, is that the effect of delay on subjective value is at the very least highly similar in both cases, with discounting following the same hyperboloid form. This similarity is important because there may be cases (e.g., probability discounting) where concurrent-chains procedures have distinct advantages, and the present findings suggest that in such cases, researchers can use these procedures without worrying that any novel results will necessarily be attributed to their use of a different procedure from those more typically used in studies of discounting.