Abstract
An important question in the evaluation of an additional risk prediction marker is how to interpret a small increase in the area under the receiver operating characteristic curve (AUC). Many researchers believe that a change in AUC is a poor metric because it increases only slightly with the addition of a marker with a large odds ratio. Because it is not possible on purely statistical grounds to choose between the odds ratio and AUC, we invoke decision analysis, which incorporates costs and benefits. For example a timely estimate of the risk of later non-elective operative delivery can help a woman in labor decide if she wants an early elective cesarean section to avoid greater complications from possible later non-elective operative delivery. A basic risk prediction model for later non-elective operative delivery involves only antepartum markers. Because adding intrapartum markers to this risk prediction model increases AUC by 0.02, we questioned whether this small improvement is worthwhile. A key decision-analytic quantity is the risk threshold, here the risk of later non-elective operative delivery at which a patient would be indifferent between an early elective cesarean section and usual care. For a range of risk thresholds, we found that an increase in the net benefit of risk prediction requires collecting intrapartum marker data on 68 to 124 women for every correct prediction of later non-elective operative delivery. Because data collection is non-invasive, this test tradeoff of 68 to 124 is clinically acceptable, indicating the value of adding intrapartum markers to the risk prediction model.
Keywords: AUC, cesarean section, decision curves, receiver operating characteristic curves, relative utility curves
1. Introduction
Many statisticians evaluate an additional marker for risk prediction using the change in the area under the receiver operating characteristic (ROC) curve, often denoted AUC [1]. An important issue is how to interpret a small change in AUC. For example an estimate of the risk of later non-elective operative delivery (instrumental vaginal delivery or cesarean section) can help a woman in labor decide if she wants an early elective cesarean section to avoid greater complications from possible later non-elective operative delivery. Schuit et al.[2] constructed two risk prediction models for later non-elective operative delivery. Model 1 was a baseline model involving only antepartum markers (maternal age, parity, previous cesarean section, diabetes, gestational age at delivery, gender, and ultrasonic estimated fetal weight). Model 2 was an extended model that added to the antepartum markers a set of intrapartum markers (induction of labor, oxytocin augmentation, fever, rupture of membranes after 24 hours, epidural analgesia, meconium-stained amniotic fluid, and the use of ST-analysis). In our evaluation, the use of Model 2 instead of Model 1 increased the AUC from 0.73 to 0.75. We questioned whether this small improvement in AUC with Model 2 versus Model 1 is worth the “cost” in time and money of increased data collection on intrapartum markers.
1.1 Why decision analysis
In recent years many researchers have criticized the use of change in AUC for evaluating the performance of an additional marker for risk prediction. As noted by Biswas et al., [3] “The area under the ROC curve (AUC) has been the standard for evaluating the discrimination ability of a risk prediction model. However, in the past few years, it has been increasingly recognized that changes in AUC are not sensitive when few potentially useful factors (such as biomarkers) are added to a model that already comprises standard risk factors”. Similarly, Spitz et al. [4] wrote “The receiver operating characteristics curve may not be sensitive to differences in probabilities between models and, therefore, may be insufficient to assess the impact of adding new predictors. A very large independent association of the new marker is required for a meaningful improvement in AUC, and a substantial gain in performance may not yield a substantial increase in AUC.” The following syllogism summarizes the aforementioned viewpoint.
A risk prediction marker has a large odds ratio after adjustment for other markers.
The addition of the risk prediction marker increases AUC only slightly.
Therefore the increase in AUC is a poor metric for evaluation.
The flaw in the syllogism is the unsupported assumption that a large odds ratio trumps a small increase in AUC for deciding if the addition of the risk prediction marker is worthwhile. As Pencina et al. [5] note, “the fact that markers with very large effect sizes are needed to increase the AUC does not automatically imply that small increases are sufficient and likely to translate into meaningful gains in clinical performance. “Because the odds ratio and AUC are both purely statistical and measuring different quantities, it is not possible to decide which is more informative. A way out of this dilemma is a decision analytic approach that includes costs and benefits. Along these lines Pencina et al. [5] compared change in AUC to the change in the decision-analytic metrics of net benefit and relative utility. Here we discuss the interpretation of a decision-analytic metric, the test tradeoff, which can be derived from a difference in net benefits or relative utilities and is used in a sensitivity analysis.
1.2 Decision and relative utility curves
The net benefit, a term commonly used in public policy analyses, is the total benefit minus the total costs [6]. In a biostatistical framework, the net benefit is an expectation that incorporates probabilities of events and is sometimes discussed in terms of value of information [7, 8]. “Benefit” in the context of heath care evaluation is the value associated with a health outcome, for example the value of avoiding later obstetric complications or the value of preventing cancer incidence. “Costs” in the context of health care evaluation can include risks, harms, and inconvenience, as well as economic costs. Because costs and benefits are difficult to specify, the key to a good decision analytic approach is a simple sensitivity analysis involving the ratio of costs to benefits. As will be discussed, a convenient summary of this ratio of costs to benefits is the risk threshold. Two widely used decision-analytic approaches for evaluating an additional risk prediction marker via a simple sensitivity analysis involving risk thresholds are decision-curves [9, 10] and relative utility curves [11–13]. Although these two approaches generally rank net benefits of different risk prediction models identically, they differ in two ways: scaling and decision-analytic underpinnings.
In terms of scaling, decision curves plot a scaled version of net benefit (called simply net benefit in the decision curve literature) versus risk threshold while relative utility curves plot relative utility versus risk threshold. The net benefit in decision curves is scaled because it sets the benefit of correct prediction equal to one. Relative utility is the maximum net benefit of prediction (over different cutpoints) divided by the net benefit of perfect prediction; it varies from 0 (no predictive value) to 1 (perfect prediction). Ignoring differences arising from different decision-analytic underpinnings, the net benefit in decision curves equals the relative utility multiplied by the probability of the event.
In terms of decision analytic underpinnings, relative utility curves, unlike decision curves, arise from a classic result in decision analysis for finding the optimal slope of a concave (sloping downward) ROC curve. For this reason the literature on relative utility curves discusses a maximum net benefit of risk prediction and concave ROC curves, while the literature on decision curves discusses net benefit of risk prediction and does not mention maximization of the net benefit or concavity of ROC curves. Because we wish to present the decision analytic underpinnings with the aforementioned optimality result, we discuss relative utility curves rather than decision curves. However, both curves generally lead to similar conclusions via the test tradeoff [11–13].
As will be discussed, the test tradeoff is the minimum number of persons receiving a test for an additional marker that needs to be traded for one correct prediction to yield an increase in net benefit with the additional marker. Other names for the test tradeoff are number needed to test [14] and test threshold [11] We prefer the name “test tradeoff” because number needed to test is easily confused with number needed to treat and test threshold is easily confused with risk threshold.
1.3 Risk intervals for estimation
A simple and appealing nonparametric method to estimate the concave ROC curve (for relative utility curves) is to group risks by interval, create a piecewise constant preliminary ROC curve, and then create the final ROC curve as the concave envelope of the preliminary ROC curve. Importantly the concave envelope is not simply a curve-fitting exercise but is rooted in a decision-analytic optimization. More details are provided later. This estimation procedure is a reasonable approach that is relatively easy to understand and implement. There are also three other appealing aspects of a risk interval approach to estimation. First investigators can report the data by interval (as we do) when they cannot report the individual-level data due to confidentiality concerns [15]. There is a growing recognition of the importance of presenting the data so others can reproduce the results [16]. Also sometimes only count data is published and available for re-analysis [14]. Second, risk intervals make explicit the coarseness of estimation inherent in calibration plots that compare predicted and observed risks in various intervals. Such calibration plots are widely used with individual-level data without appreciation that their coarseness implies a “tolerance” at the level of the intervals. Third, the extension to survival data is simple because risk intervals do not overlap, unlike the case with individual-level data. Overlapping intervals require a complicated adjustment with censored survival data to avoid inconsistencies in estimation [17].
2. Decision analysis underpinning of relative utility curves
Our convention is that the event is unfavorable. In our obstetrics example the event is harmful complications associated with later non-elective operative delivery. Let Tr0 denote the treatment that would be given to all persons in the absence of risk prediction. In our example Tr0 is usual care. Let Tr1 denote a treatment thought, in comparison to Tr0, to reduce the probability of the unfavorable event but at a cost of detrimental effects unrelated to the event. In our example Tr1 is early elective cesarean section, which has fewer complications than later non-elective operative delivery. Persons at sufficiently high risk for the unfavorable event would opt for Tr1 instead of Tr0.
We define a marker as single baseline variable or set of baseline variables used in the risk prediction model. The ascertainment of marker data, which can involve answering a questionnaire, collecting non-invasive measurements, or performing an invasive test, has a cost or harm. Our question is whether the collection of additional markers to improve the risk prediction model is worthwhile. To answer this question we compute the test tradeoff which involves ROC curves, utilities, and the net benefit of risk prediction.
2.1 ROC curve
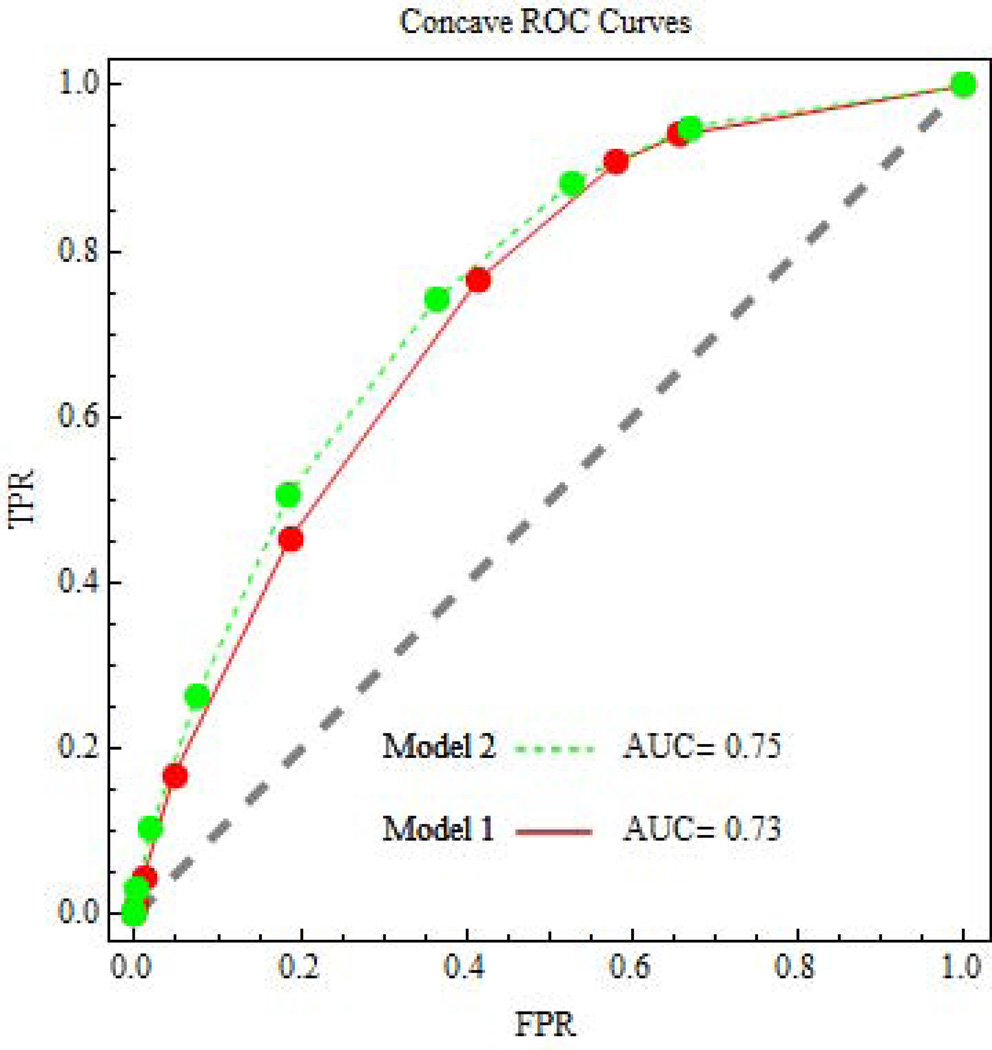
Let J= j index risk intervals. We use the convention that larger values of the risk score indicate higher risk. We classify persons with J ≥ j as positive, which means they would receive Tr1. We classify persons with J< j as negative, which means they would receive Tr0. Let D =1 if persons experience the event under Tr0, and D=0 if they do not experience the event under Tr0. We write the risk in interval j as Rj = pr(D=1| J=j). Let Wj = pr(J = j). The probability of the event under Tr0 is P = pr(D=1) = Σj Rj Wj. The true positive rate for risk interval j, TPRj = pr(J ≥ j | D=1) = Σj≥s Rs Ws / P, is the probability of a positive classification among persons who experience the event under Tr0. The false positive rate at risk interval j, FPRj = pr(J ≥ j | D=0) = Σj≥s (1–Rs) Ws / (1–P), is the probability of a positive classification among persons who experience the event under Tr0. The ROC curve is a plot of TPRj versus FPRj for various values of j. See Figure 1.
Figure 1.
ROC curves for risk prediction involving later non-elective operative delivery.
2.2 Utilities
Some decision-analytic papers in the statistics literature discuss only costs of false positives and false negatives [18, 19]. Here we discuss the full utility formulation. The four basic utilities are as follows:
UTr0:NoEvent|Tr0 = utility of Tr0 when the unfavorable event would not occur under Tr0,
UTr1:NoEvent|Tr0 =utility of Tr1 when the unfavorable event would not occur under Tr0,
UTr0:Event|Tr0 = utility of Tr0 when the unfavorable event would occur under Tr0,
UTr1:Event|Tr0 = utility of Tr1 when the unfavorable event would occur under Tr0.
In the obstetric example
UTr0:NoEvent|Tr0 = utility of usual care that does not lead to later non-elective operative delivery,
UTr1:NoEvent|Tr0 = utility of unnecessary early elective cesarean section when usual care would not lead to later non-elective operative delivery,
UTr0:Event|Tr0 = utility of usual care that leads to later non-elective operative delivery,
UTr1:Event|Tr0 = utility of early elective cesarean section when usual care lead to later non-elective operative delivery.
We assume utilities do not depend on the risk of the event. This assumption holds for UTr0:NoEvent|Tr0 and UTr0:Event|Tr0 because the treatment is Tr0 and the event status under Tr0 is given. The assumption also holds for UTr1:NoEvent|Tr0 because the harm from Tr1 depends on side effects unrelated to the event. However the assumption could fail for UTr1:Event|Tr0 because the effect of Tr1 in reducing the risk of the event could depend on the risk of the event under Tr0. Because the ultimate goal is a sensitivity analysis, a violation of this assumption may have little effect on conclusions. In any case, the assumption holds for UTr1:Event|Tr0 in the obstetrics example because the effect of cesarean section is no later non-elective operative delivery regardless of the risk of later non-elective operative delivery.
If we set UTr0:NoEvent|Tr0 at a reference value of zero, UTr10:NoEvent|Tr0 is negative because it involves costs associated with unnecessary Tr1, UTr0:Event|Tr0 is negative because the unfavorable event occurs, and UTr1:Event|Tr0 is positive because the unfavorable event may not occur. There is also a cost of marker testing or ascertainment, denoted CTest, which we treat as a positive because it will be subtracted in the formula for net benefit of risk prediction.
2.3 Net benefit of risk prediction
We define the net benefit of risk prediction as the expected benefit of risk prediction minus the expected benefit of no treatment,
| (1) |
Equation (1) simplifies to
| (2) |
| (3) |
| (4) |
The quantity B is the benefit of Tr1 instead of Tr0 in a person who would experience the unfavorable event under Tr0. B is positive because it equals a negative utility subtracted from a positive utility. The quantity C is the cost or harm of side effects from Tr1 instead of Tr0 in a person who would not experience the unfavorable event under Tr0. C is positive because it equals a negative utility subtracted from a reference utility of zero. In 1884 in the context of tornado prediction, Peirce [20] proposed a simpler version of equation (2), without the subscript or underlying utility differences. Only in recent years has the article by Peirce received widespread attention [21].
2.4 Risk threshold
Although the cost-benefit ratio C/B may be used for a sensitivity analysis, its large range makes plotting problematic. As an alternative we use the risk threshold,
| (5) |
The name “risk threshold” comes from the interpretation of T as the event rate at which a person is indifferent between treatments Tr0 and Tr1 [22]. More precisely, the risk threshold is the value of T such that the expected utility of Tr1, T UTr1:Event|Tr0 + (1−T) UTr1:NoEvent|Tr0, equals the expected utility of Tr0, T UTr0:Event|Tr0 + (1−T) UTr0:NoEvent|Tr0.
2.5 Maximum net benefit of risk prediction
Let ROCSlopej = (TPRj − TPRj+1) / (FPRj − FPRj+1) denote the slope of the ROC curve associated with risk interval j. By definition, for a concave ROC curve, ROCSlopej increases as j increases. If the ROC curve is concave, the maximum net benefit of risk prediction occurs at risk interval j such that the change in the net benefit of risk prediction over adjacent intervals is zero (analogous to find the maximum of a function when the slope is zero). Mathematically this condition is
| (6) |
Solving equation (6) gives the classic result in decision theory [23] that the maximum net benefit of risk prediction for a given risk threshold T occurs at risk interval j= j(T) such that
| (7) |
This maximum net benefit of risk prediction equals
| (8) |
Because we can write
| (9) |
an equivalent solution to equation (6) is j= j(T) such that Rj = T [24]. As discussed later, for this risk interval framework we use linear interpolation when Rj ≤ T ≤ R(j+1).
2.6 Relative utility curve
Relative utility is the maximum net benefit of risk prediction divided by the net benefit of perfect prediction when the cost of marker ascertainment is zero. The net benefit of perfect prediction equals equation (2) with TPRj = 1, FPRj = 0, and CTest = 0 to yield P B. Mathematically, relative utility is
| (10) |
The appeal of relative utility is that it is a meaningful function of utilities (excluding marker ascertainment cost) only through T, thereby leading to a simple and informative sensitivity analysis. A relative utility curve is a plot of RU(T) versus T. See Figure 2. Because the ROC curve is concave, the relative utility curve monotonically decreases as T increases and is always greater than or equal to zero. The leftmost point of the relative utility curve is T=P. The proof follows. Because Tr0 is the treatment in the absence of risk prediction, the expected utility of Tr0 in the absence of risk prediction must be greater than the expected utility of Tr1 in the absence of risk prediction. The former expected utility is UNoTreat = (1−P) UNoTreat:NoEvent + P UNoTreat,Event. The latter expected utility is UTreat = (1−P) UTreat:NoEvent + P UTreat:Event. Setting UNoTreat > UTreat gives T ≥ P. The maximum relative utility at T=P corresponds to ROCSlopej(P) = 1 and hence equals the Youden index at risk interval j(P), namely RU(P) = TPRj(P) − FPRj(P).
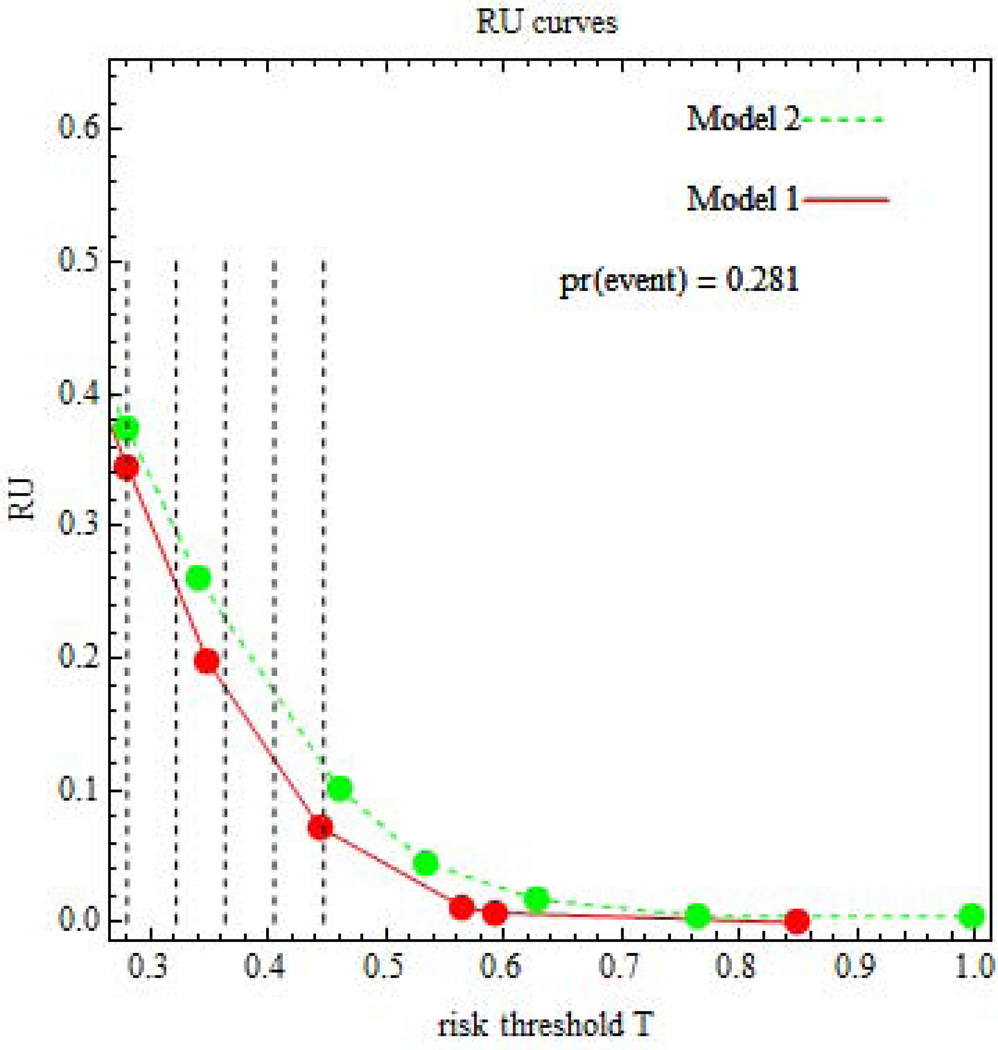
Figure 2.
Relative utility (RU) curves for risk prediction involving later non-elective operative delivery. Vertical lines indicate risk thresholds
2.7 Test tradeoff
For evaluating the addition of a marker to the risk prediction model, a key quantity is the change in relative utility between Models 1 and 2, namely
| (11) |
Let CMarker = CTest(Model2) – CTest(Model1)denote the cost of ascertaining the additional marker. For an additional marker to be worthwhile, the maximum net benefit of risk prediction for Model 2 must be greater than the maximum net benefit of risk prediction for Model 1, namely,
| (12) |
Equation (12) implies
| (13) |
The quantity RU(T) P is called the maximum acceptable testing harm [12]. When the maximum acceptable testing harm is positive, a more intuitive quantity to consider is the test tradeoff,
| (14) |
Equation (12) also implies
| (15) |
Thus the test tradeoff is the minimum value for B/ CMarker. In other words the test tradeoff is the minimum number of persons receiving a test for an additional marker that needs to be traded for one correct prediction to yield an increase in net benefit with the additional marker. (To understand how this interpretation arises, suppose that B were the price of apples and CMarker were the price of oranges; then B/ CMarker would be the number of oranges traded for an apple). If the test tradeoff is acceptable over a wide range of risk thresholds, then risk prediction with the additional marker is recommended.
3. Estimation
We focus on the situation in which investigators fit the risk prediction model to data in a training sample and evaluate the risk prediction model in an independent test sample. This procedure is a simple way to avoid overfitting bias in evaluation. (Although Schuit et al. [2] used the same sample for both fitting and evaluation, they reduced overfitting bias by shrinking the regression parameters using a bootstrap approach). Furthermore, if the training sample is from a different population than the test sample, the evaluation in the independent test sample provides support for generalizability. For a rare event, investigators may wish to create the test sample by random sampling from persons who experience or do not experience the event in a target population.
3.1 Risk stratification tables
An appealing aspect of the risk interval approach is that we can present the data in the form of two risk stratification tables that cross-classify risk intervals for Model 1 (rows) and Model 2 (columns). One risk stratification table corresponds to persons who experience the event (Table 1), and the other corresponds to persons who do not experience the event (Table 2). For Model 1 risk interval i and Model 2 risk interval j, let xij denote the number of persons who experienced the event and yij denote the number who did not experience the event. The following calculations use Model 2 as an example but would also apply to Model 1. For risk interval j let xj = Σi xij denote the number of persons who experienced the event and let yj = Σi yij denote the number who did not experience the event. The total number in risk interval j is xj + yj = nj. The estimated risk in risk interval j is rj = xj / nj. The fraction in risk interval j is wj = nj / n, where n=Σj nj is the size of the sample. The event rate in the sample is p = Σj rj wj.
Table 1.
Risk stratification table for women experiencing later non-elective operative delivery.
| Model 1 risk intervals |
Model 2 risk intervals | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.00– 0.10 |
0.10– 0.20 |
0.20– 0.30 |
0.30– 0.40 |
0.40– 0.50 |
0.50– 0.60 |
0.60– 0.70 |
0.70– 0.80 |
0.80– 0.90 |
Total | ||
| j = 1 | j = 2 | j = 3 | j =4 | j =5 | j = 6 | j =7 | j =8 | j = 9 | |||
| 0.00– 0.10 | i = 1 | 78 | 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 95 |
| 0.10– 0.20 | i = 2 | 2 | 31 | 18 | 1 | 0 | 0 | 0 | 0 | 0 | 52 |
| 0.20– 0.30 | i = 3 | 0 | 49 | 82 | 75 | 19 | 0 | 0 | 0 | 0 | 225 |
| 0.30– 0.40 | i = 4 | 0 | 9 | 105 | 188 | 162 | 32 | 1 | 0 | 0 | 497 |
| 0.40– 0.50 | i = 5 | 0 | 0 | 18 | 94 | 166 | 137 | 37 | 0 | 0 | 452 |
| 0.50– 0.60 | i = 6 | 0 | 0 | 2 | 14 | 37 | 70 | 56 | 17 | 0 | 196 |
| 0.60– 0.70 | i = 7 | 0 | 0 | 0 | 0 | 1 | 18 | 21 | 16 | 1 | 57 |
| 0.70– 0.80 | i = 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 9 | 6 | 15 |
| 0.80– 0.90 | i = 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| Total | 80 | 106 | 225 | 372 | 385 | 257 | 115 | 42 | 8 | 1590 | |
Table 2.
Risk stratification table for women not experiencing later non-elective operative delivery.
| Model 1 risk intervals |
Model 2 risk intervals | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.00– 0.10 |
0.10– 0.20 |
0.20– 0.30 |
0.30– 0.40 |
0.40– 0.50 |
0.50– 0.60 |
0.60– 0.70 |
0.70– 0.80 |
0.80– 0.90 |
Total | ||
| j = 1 | j = 2 | j = 3 | j =4 | j =5 | j = 6 | j =7 | j =8 | j = 9 | |||
| 0.00– 0.10 | i = 1 | 1295 | 110 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1405 |
| 0.10– 0.20 | i = 2 | 59 | 204 | 38 | 3 | 0 | 0 | 0 | 0 | 0 | 304 |
| 0.20– 0.30 | i = 3 | 0 | 222 | 276 | 163 | 20 | 0 | 0 | 0 | 0 | 681 |
| 0.30– 0.40 | i = 4 | 0 | 41 | 262 | 387 | 203 | 32 | 2 | 0 | 0 | 927 |
| 0.40– 0.50 | i = 5 | 0 | 1 | 88 | 145 | 180 | 130 | 23 | 0 | 0 | 567 |
| 0.50– 0.60 | i = 6 | 0 | 0 | 2 | 21 | 46 | 49 | 27 | 6 | 0 | 151 |
| 0.60– 0.70 | i = 7 | 0 | 0 | 0 | 2 | 3 | 14 | 14 | 6 | 0 | 39 |
| 0.70– 0.80 | i = 8 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 2 |
| 0.80– 0.90 | i = 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| Total | 1354 | 578 | 666 | 721 | 452 | 225 | 68 | 13 | 0 | 4077 | |
3.2 Estimating the preliminary ROC curve
We first estimate a preliminary ROC curve based on the initial set of risk intervals. The preliminary ROC curve is a plot of fprj versus tprj, where fprj = Σj≥s (1–rs) ws / (1–p) and tprj = Σj≥s rs ws / p. See Table 3 for these calculations applied to our example involving the risk prediction for later non-elective operative delivery.
Table 3.
Estimates for the preliminary ROC curve for Model 1. Using rj and wj, we compute fprj and tprj and hence ROCSlopej. The preliminary ROC curve is not concave because ROCSlopej decreases from j=8 to j=9 (from right to left on the ROC curve).
| Model 1 risk interval |
xj | nj | wj | rj | fprj | tprj | ROCSlopej | |
|---|---|---|---|---|---|---|---|---|
| 0.00–0.10 | j = 1 | 95 | 1500 | 0.2647 | 0.0633 | 1 | 1 | 0.1734 |
| 0.10– 0.20 | j = 2 | 52 | 356 | 0.0628 | 0.1461 | 0.6554 | 0.9403 | 0.4386 |
| 0.20– 0.30 | j = 3 | 225 | 906 | 0.1599 | 0.2483 | 0.5808 | 0.9075 | 0.8472 |
| 0.30– 0.40 | j = 4 | 497 | 1424 | 0.2513 | 0.3490 | 0.4138 | 0.7660 | 1.3747 |
| 0.40– 0.50 | j = 5 | 452 | 1019 | 0.1798 | 0.4436 | 0.1864 | 0.4535 | 2.0441 |
| 0.50– 0.60 | j = 6 | 196 | 347 | 0.0612 | 0.5648 | 0.0473 | 0.1692 | 3.3283 |
| 0.60– 0.70 | j = 7 | 57 | 96 | 0.0169 | 0.5938 | 0.0103 | 0.0459 | 3.7476 |
| 0.70– 0.80 | j = 8 | 15 | 17 | 0.0030 | 0.8824 | 0.0007 | 0.0101 | 19.2311 |
| 0.80– 0.90 | j = 9 | 1 | 2 | 0.0004 | 0.5000 | 0.0002 | 0.0006 | 2.5642 |
| 0 | 0 | |||||||
3.3 Why a concave envelope of ROC points
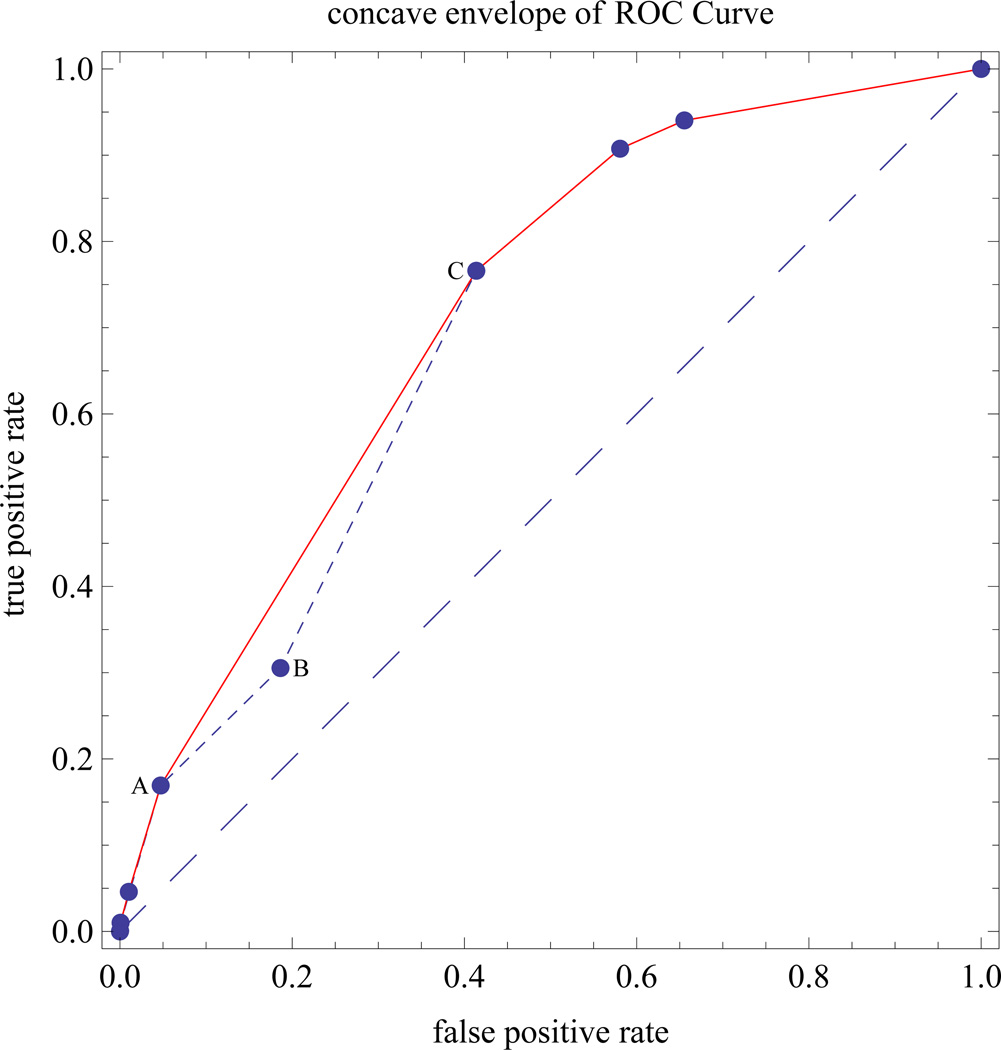
If the preliminary ROC curve is not concave, we construct a concave ROC curve using the concave envelope of discrete points on the ROC curve, which is optimal from a decision-analysis standpoint [25, 26]. To understand this optimality property, consider the preliminary non-concave ROC curve in Figure 3, which connects points A, B, and C. For the concave envelope of ROC points, line segment AC replaces line segments AB and BC. The true positive rate on line segment AC is higher than the true positive rates on line segments AB and BC, so AC is preferred to the union of AB and BC. Line segment AC corresponds to mixed decision rule defined as follows. Let (FPRA, TPRA) denote coordinates of point A and let (FPRC, TPRC) denote the coordinates of point C. The line segment from A to C has true positive rate (1–θ) TPRA + θ TPRC corresponding to false positive rate (1–θ) FPRA + θ FPRC, for 0 ≤ θ ≤ 1, where θ is the probability of selecting a cutpoint corresponding to point C and (1–θ) is the probability of selecting a cutpoint corresponding to point A.
Figure 3.
Example showing construction of a concave envelope of ROC points
3.4 Estimating the concave ROC curve and the relative utility
Starting with the leftmost point on the ROC curve, we successively select the next ROC point on the right whose line segment from the previously selected point has the largest slope. For risk interval u associated with the concave ROC curve, we denote the false and true positive rates by fprCu and tprCu, respectively, where subscript “C” denotes concave. Using the slope of the concave ROC curve, rocslopeCu = {tprCu – tprC(u+1)} / {fprCu – fprC(u+1)}, we estimated the risk and relative utility in risk interval u by
| (16) |
| (17) |
See Table 4 for an example of these calculations.
Table 4.
Estimates for the concave ROC curve and relative utility curve for Model 1. From the concave ROC curve, {fprCu, tprCu}, we compute ROCSlopeCu from which we compute rCu and ruCu. In this case rPOPCu equals rCu because the event rate is the same in the test sample and the target population.
| Model 1 risk interval | fprCu | tprCu | ROCSlopeCu | rCu | rPOPCu | ruCu | |
|---|---|---|---|---|---|---|---|
| 0.00–0.10 | u= 1 | 1 | 1 | 0.1732 | 0.0633 | 0.0633 | 0.8268 |
| 0.10– 0.20 | u = 2 | 0.6554 | 0.9403 | 0.4397 | 0.1464 | 0.1464 | 0.6521 |
| 0.20– 0.30 | u = 3 | 0.5808 | 0.9075 | 0.8473 | 0.2484 | 0.2484 | 0.4154 |
| 0.30– 0.40 | u = 4 | 0.4138 | 0.766 | 1.3742 | 0.3489 | 0.3489 | 0.1973 |
| 0.40– 0.50 | u = 5 | 0.1864 | 0.4535 | 2.0439 | 0.4435 | 0.4435 | 0.0725 |
| 0.50– 0.60 | u = 6 | 0.0473 | 0.1692 | 3.3324 | 0.5651 | 0.5651 | 0.0116 |
| 0.60– 0.70 | u = 7 | 0.0103 | 0.0459 | 3.7292 | 0.5926 | 0.5926 | 0.0075 |
| 0.70– 0.90 | u = 8 | 0.0007 | 0.0101 | 14.4286 | 0.8491 | 0.8491 | 0.0000 |
| 0 | 0 | ||||||
3.5 Adjusting for different event rates in test sample and target population
When the estimated event rates in the test sample and target population, p and P, differ due to random sampling of persons with and without the event, we adjust the estimated risk as follows [12]. We write the risk of the event among the target population as
| (18) |
The random sampling implies pr(U=u | D=d, test sample) = pr(U =u | D=d, pop) which implies
| (19) |
| (20) |
Substituting equations (19) and (20) into equation (18) and simplifying gives the estimated risk in the target population,
| (21) |
3.6 Estimating the relative utility curve
The estimated relative utility at risk threshold T is
| (22) |
The estimated relative utility curve is a plot of ru(T) versus T.
3.7 Small bias with non-predictive additional markers
When the additional marker has no effect on risk, estimates of the change in relative utility should be centered near zero. Using simulation, Pepe et al [27] showed that the continuous net reclassification index (NRI) [28] was substantially biased in this situation. Using a similar simulation (Appendix A) with sample size 400, 2000 iterations and 10 risk intervals, we obtained the following medians for various simulated distribution: 0.11 for continuous NRI, −0.002 for categorical NRI, and −0.011 for the change in relative utility at T=P; this suggests little bias for the change in relative utility with non-predictive additional markers.
3.8 Extensions to survival outcomes
With survival data, for each cell in the risk stratification table we compute a Kaplan-Meier estimate of the probability of surviving to a pre-specified time, from which we compute an estimated count. We then proceed as if the estimated counts were observed counts [29]. See Appendix B for a justification.
3.9 Estimating the test tradeoff
We computed the maximum acceptable testing harm, ru(T) P, and test tradeoff, 1/{ru(T) P}, at five equally spaced risk thresholds over a range of risk thresholds (Figure 2). The lowest bound of the range is the minimal risk threshold for the relative utility curve, here T= P =0.28. However it is difficult to specify the upper bound of the range. For an upper bound we chose the risk threshold of T= 0.45, corresponding to a relative utility for Model 1 of 0.10. We presume that a patient whose relative utility is less than 0.10 would opt for Tr0.
Before computing test tradeoff, investigators should compute the maximum acceptable testing harm (Table 5). If the maximum acceptable testing harm is negative for any risk threshold (not the case here), investigators can conclude that adding the marker can lead to more harm than good, as could arise with overfitting. Otherwise the next step is to compute the test tradeoffs for the range of risk thresholds.
Table 5.
Maximum acceptable testing harms and test tradeoffs over a range of risk thresholds.
| Maximum acceptable testing harm |
||||
|---|---|---|---|---|
| Risk threshold |
Estimate | Lower bound |
Test tradeoff | |
| Model 1 versus Chance | 0.28 | 0.097 | 0.091 | 10 |
| 0.32 | 0.072 | 0.065 | 14 | |
| 0.36 | 0.05 | 0.042 | 20 | |
| 0.41 | 0.034 | 0.026 | 29 | |
| 0.45 | 0.02 | 0.014 | 50 | |
| Model 2 versus Model 1 | 0.28 | 0.008 | 0.003 | 124 |
| 0.32 | 0.011 | 0.006 | 88 | |
| 0.36 | 0.015 | 0.008 | 68 | |
| 0.41 | 0.014 | 0.008 | 69 | |
| 0.45 | 0.013 | 0.006 | 74 | |
For Model 1 versus Chance the test tradeoff for antepartum markers ranged from 10 to 50 (Table 5). In other words, for an increase in the net benefit from risk prediction with antepartum data, it is necessary to collect antepartum data from at least 10 to 50 women for every correction prediction of later non-elective operative delivery –an acceptable tradeoff. For Model 2 versus Model 1, the test tradeoff for the addition of intrapartum markers ranged from 68 to 124 (Table 5). In other words, for an increase in the net benefit from the addition of intrapartum data, it is necessary to collect intrapartum data from at least 68 to 124 women for every correction prediction of later non-elective operative delivery—also an acceptable test tradeoff.
Our application of the test tradeoff methodology to obstetrics is unusual in that there is a temporal component to the collection of additional marker data. Consequently even though the test tradeoff for the addition of intrapartum markers is acceptable, clinicians may prefer to use a risk prediction model based only on antepartum markers, because data collection for antepartum markers occurs earlier and their test tradeoff versus chance was also acceptable.
Even if point estimates of test tradeoff are acceptable, some clinicians may require reasonable confidence that the results are not due to chance before committing time and resources to ascertain additional marker data. This requirement translates into a lower bound for the 95% confidence intervals for maximum acceptable testing harm that is greater than zero for all risk thresholds considered, as was the case here (Table 5). We computed these confidence intervals using percentiles from 10000 multinomial bootstrap replications drawn separately from persons with and without the event in the test sample. These confidence intervals, which treat the risk prediction model and the probability of event (which is sometimes specified for the target population) as fixed, summarize sampling variability in the test sample.
3.10 Applying the risk prediction model to patients
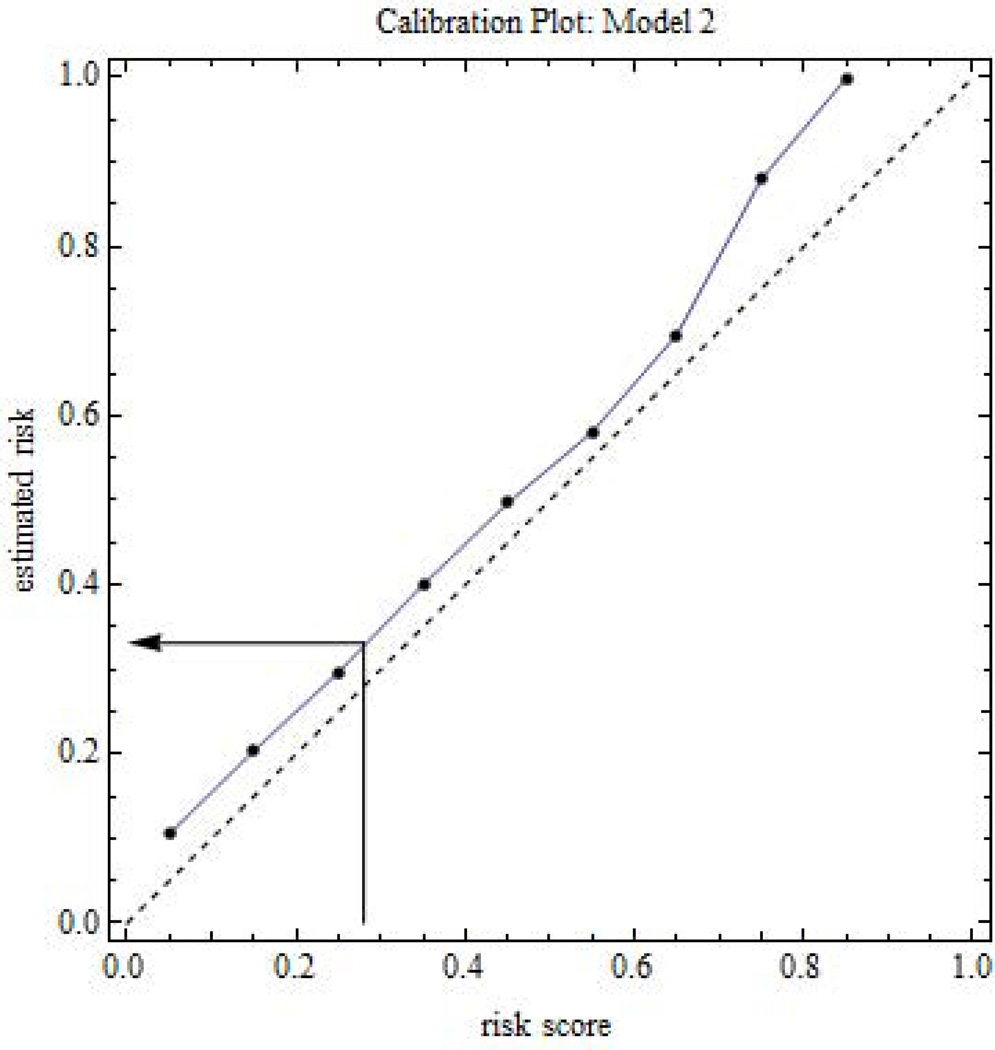
To apply a risk prediction model to patients, the clinician applies the risk prediction model to the patient’s marker values to compute a risk score for the patient. The risk score may be biased due to overfitting or because it involves a different population than in the test sample. To convert the risk score to an unbiased estimated risk, the clinician can use a test sample calibration plot that compares the estimated risk in an interval versus the average risk score in an interval (Figure 4). Using visual interpolation or appropriate software, the clinician finds the estimated risk corresponding to a patient’s risk score. The clinician discusses the estimated risk and anticipated benefits and harms of treatment with the patient, so that the patient can make an informed decision about treatment.
Figure 4.
Calibration plot involving risk prediction for later non-elective operative delivery. The dashed line is the 45 degree line reference for no bias. The arrow shows an example of converting a risk score to an estimated risk via interpolation.
4. Discussion
To circumvent the dilemma of choosing between the odds ratio and AUC to measure the value of an additional marker for risk prediction, we use decision analytic approach, which incorporates costs and benefits. Our key metric is the test tradeoff computed over a range of risk thresholds. In essence the test tradeoff reduces a complicated net benefit involving five utilities to a range of test tradeoffs, thereby greatly simplifying the sensitivity analysis. Admittedly two aspects of computing the test tradeoff have a subjective component: deciding if a test tradeoff is acceptable and selecting the upper bound of the range of risk thresholds. However these subjective aspects are minor compared with the subjective interpretation of purely statistical measures such as odds ratio and AUC.
With evaluation of markers for risk prediction, generalizability is a challenge. If a comparison of risk prediction models yields acceptable test tradeoffs in a variety of populations, then generalizability is supported. Of course the ideal situation is computing test tradeoffs in a random sample (perhaps with different sampling from events and non-events) from a target population, but we recognize that such data are often not available.
Using the risk stratification tables, investigators can perform all calculations in a spreadsheet format with the exception of finding the concave envelope of the ROC curve, if needed. Freely available software written in Mathematica [31] is available at http://prevention.cancer.gov/programs-resources/groups/b/software/rufit.
Appendix A
To investigate bias when additional markers have no effect on risk prediction we perform the following simulation. Let expit(x) = exp(x)/{1+exp(x)}. Each replication involves the following four steps.
Step 1 Generate the training sample
Let z index persons in training sample. Let xTRAINz denote the baseline marker that determines the true risk. Let mTRAINkz for k=1,2,3,4 denote additional markers with no impact on the true risk. We generate independent normally distributed markers with mean 0 and variance 1. We generate random binary events, yTRAINz, from a Bernoulli distribution with probability expit(θ0 + θX xTRAINz), where θ0 = logit(0.1/0.9) and θX =1.7.
Step 2 Generate the test sample
Let v index persons in training sample. Let xTESTv denote the marker determining true risk and mTESTkv for k=1,2,3,4 denote additional markers. We generate independent normally distributed marker variables with mean 0 and variance. We generate random binary events in the test samples, yTESTv, from a Bernoulli distribution with probability expit(θ0 + θX xTESTv).
Step 3: Fit the risk prediction model to the training sample
Using the data from the training sample, {xTRAINv, mTRAINkv, yTRAINz,}, we fit Model 1, pr(YTRAINv =1) = expit(α0 + αX xTRAINv), and Model 2, pr(YTRAINv =1) = expit(β0 + βX xTRAINv + Σk βMk mTRAINkv). Let a0, aX, b0, bX, and bMk denote the estimates of α0, αX, β0, βX, and βMk, respectively.
Step 4 Compute risk scores in the test sample
For each person in the test sample we compute a risk score using {xTESTv, mTESTkv} and parameter estimates from the training sample. For Model 1 the risk score is expit(a0 + aX xTESTv). For Model 2 the risk score is expit(b0 + bX xTESTv + Σk bMk mTESTkv). We compute relative utility as a function of these risk scores and {yTESTv}. The computation of categorical NRI uses the same risk intervals as with relative utility curves.
Appendix B
This appendix provides a rationale for substituting expected counts from a Kaplan-Meier estimate for observed counts in a risk stratification table and treating them like observed counts in the analysis. Consider a prospective study of N persons. For the risk stratification table for persons with D=d, we can write the observed counts as N fd|ij wij, where fd|ij is the fraction estimating pr(D=d | I=i, J=j) and wij is the fraction estimating pr(I=i, J=j). If the expected counts have the form N sd|ij wij , where sd|ij has the same distribution as that of a fraction estimating pr(D=d | I=i, J=j), it is appropriate to treat the expected counts as observed counts when computing estimates and variances of functions of the counts. This is the case when s0|ij is a Kaplan-Meier estimate of pr(D=0 | I=i, J=j), denoting the probability of surviving no event to a pre-specified time. Following Peto’s formula [30], the estimated variance of s0|ij is (s0|ij)2 (1– s0|ij) / kij, where kij is the observed number at risk. Approximating kij by the expected number at risk, namely N s0|ij wij; gives an estimated variance of s0|ij (1– s0|ij) / N wij, which is the same variance as if s0|ij were a fraction estimating pr(D=0 | I=i, J=j).
References
- 1.Tzoulaki I, Liberopoulos G, Ioannidis JP. Assessment of claims of improved prediction beyond the Framingham risk score. Journal of the American Medical Association. 2009;302:2345–2352. doi: 10.1001/jama.2009.1757. [DOI] [PubMed] [Google Scholar]
- 2.Schuit E, Kwee A, Westerhuis ME, Van Dessel HJ, Graziosi GC, Van Lith JM, Nijhuis JG, Oei SG, Oosterbaan HP, Schuitemaker NW, Wouters MG, Visser GH, Mol BW, Moons KG, Groenwold RH. A clinical prediction model to assess the risk of later non-elective operative delivery. BJOG : an International Journal of Obstetrics and Gynaecology. 2012;119:915–923. doi: 10.1111/j.1471-0528.2012.03334.x. [DOI] [PubMed] [Google Scholar]
- 3.Biswas S, Arum B, Parmigiani G. Reclassification of predictions for uncovering subgroup specific improvement. Statistics in Medicine. 2014 doi: 10.1002/sim.6077. **Early View. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Spitz MR, Amos CI, D'Amelio A, Jr, Dong Q, Etzel C. Discriminatory accuracy from single-nucleotide polymorphisms in models to predict breast cancer risk. Journal of the National Cancer Institute. 2009;101:1731–1732. doi: 10.1093/jnci/djp394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Pencina MJ, D'Agostino RB, Massaro JM. Understanding increments in model performance metrics. Lifetime Data Analysis. 2013;9:202–218. doi: 10.1007/s10985-012-9238-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Stokey E, Zeckhauser R. A Primer for Policy Analysis. New York: WW Norton and Company; 1978. [Google Scholar]
- 7.Weinstein MC, Fineberg HV, Elstein AS, Frazier HS, Neuhauser D, Neutra RR, McNeil BJ. Clinical Decision Analysis. Philadelphia: WB Saunders Company; 1980. [Google Scholar]
- 8.Chen MH, Willan AR. Value of information methods for assessing a new diagnostic test. Statistics in Medicine. 2014 doi: 10.1002/sim.6085. **Early View. [DOI] [PubMed] [Google Scholar]
- 9.Vickers AJ, Elkin EB. Decision curve analysis: a novel method for evaluating prediction models. Medical Decision Making. 2006;26(6):565–574. doi: 10.1177/0272989X06295361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Vickers AJ, Cronin AM, Elkin EB, Gonen M. Extensions to decision curve analysis, a novel method for evaluating diagnostic tests, prediction models and molecular markers. BMC Medical Informatics and Decision Making. 2008;8:53. doi: 10.1186/1472-6947-8-53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Baker SG, Cook NR, Vickers A, Kramer BS. Using relative utility curves to evaluate risk prediction. Journal of the Royal Statistical Society Series A. 2009;172:729–748. doi: 10.1111/j.1467-985X.2009.00592.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Baker SG. Putting risk prediction in perspective: relative utility curves. Journal of the National Cancer Institute. 2009;101:1538–1542. doi: 10.1093/jnci/djp353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Baker SG, Van Calster B, Steyerberg EW. Evaluating a new marker for risk prediction using the test tradeoff: An update. International Journal of Biostatistics. 2012;8:5. doi: 10.1515/1557-4679.1395. [DOI] [PubMed] [Google Scholar]
- 14.Baker SG, Kramer BS. Evaluating a new marker for risk prediction: Decision analysis to the rescue. Discovery Medicine. 2012;14:181–188. [PubMed] [Google Scholar]
- 15.Baker SG, Darke AK, Pinsky P, Parnes HL, Kramer BS. Transparency and reproducibility in data analysis: the Prostate Cancer Prevention Trial. Biostatistics. 2010;11:413–418. doi: 10.1093/biostatistics/kxq004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Laine C, Goodman SN, Griswold ME, Sox HC. Reproducible research: moving toward research the public can really trust. Annals of Internal Medicine. 2007;146(6):450–453. doi: 10.7326/0003-4819-146-6-200703200-00154. [DOI] [PubMed] [Google Scholar]
- 17.Heagerty PJ, Lumley T, Pepe MS. Time dependent ROC curves for censored survival data and diagnostic markers. Biometrics. 2000;56:337–344. doi: 10.1111/j.0006-341x.2000.00337.x. [DOI] [PubMed] [Google Scholar]
- 18.Cai T, Tian L, Lloyd-Jones DM. Comparing costs associated with risk stratification rules for t-year survival. Biostatistics. 2011;12:597–609. doi: 10.1093/biostatistics/kxr001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Briggs WM, Zaretzki R. The Skill Plot: a graphical technique for evaluating continuous diagnostic tests. Biometrics. 2008;64(1):250–256. doi: 10.1111/j.1541-0420.2007.00781_1.x. [DOI] [PubMed] [Google Scholar]
- 20.Peirce CS. The numerical measure of the success of predictions. Science. 1884;4:453–454. doi: 10.1126/science.ns-4.93.453-a. [DOI] [PubMed] [Google Scholar]
- 21.Van Calster B. It takes time: A remarkable example of delayed recognition. Journal of the American Society for Information Science and Technology. 2012;63:2341–2344. [Google Scholar]
- 22.Pauker SG, Kassirer JP. The threshold approach to clinical decision making. New England Journal of Medicine. 1980;302:1109–1117. doi: 10.1056/NEJM198005153022003. [DOI] [PubMed] [Google Scholar]
- 23.Metz CE. Basic principles of ROC analysis. Seminars in Nuclear Medicine. 1978;8:283–298. doi: 10.1016/s0001-2998(78)80014-2. [DOI] [PubMed] [Google Scholar]
- 24.Gail MH, Pfeiffer RM. On criteria for evaluating models for absolute risk. Biostatistics. 2005;6:227–239. doi: 10.1093/biostatistics/kxi005. [DOI] [PubMed] [Google Scholar]
- 25.Provost F, Fawcett T. Robust classification for an imprecise environment. Machine Learning. 2001;42:203–231. [Google Scholar]
- 26.Hand DJ. Measuring classifier performance: a coherent alternative to the area under the ROC curve. Machine Learning. 2009;77:103–123. [Google Scholar]
- 27.Pepe MS, Janes H, Li C. Net risk reclassification p-values: valid or misleading? Journal of National Cancer Institute. 2014;106(4) doi: 10.1093/jnci/dju041. **dju041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Leening MJG, Vedder MMJ, Witteman JCM, Pencina MJ, Steyerberg EW. Net reclassification improvement: computation, interpretation, and controversies: a literature review and clinician's guide. Annals of Internal Medicine. 2014;160 doi: 10.7326/M13-1522. 122-131-131. [DOI] [PubMed] [Google Scholar]
- 29.Steyerberg EW, Pencina MJ. Reclassification calculations for persons with incomplete follow-up. Annals of Internal Medicine. 2010;152:195–196. doi: 10.7326/0003-4819-152-3-201002020-00019. [DOI] [PubMed] [Google Scholar]
- 30.**Mathematica version 8.0. Champaign IL USA: Wolfram Research, Inc.; 2010. [Google Scholar]
- 31.Peto R, Pike MC, Armitage P, Breslow NE, Cox DR, Howard SV, Mantel N, McPherson K, Peto J, Smith PG. Design and analysis of randomized clinical trials requiring prolonged observation of each patient: II analysis and examples. British Journal of Cancer. 1972;35:1–39. doi: 10.1038/bjc.1977.1. [DOI] [PMC free article] [PubMed] [Google Scholar]