The Mechanism of Collapse of Heterogeneous Lipid Monolayers

Abstract

Collapse of homogeneous lipid monolayers is known to proceed via wrinkling/buckling, followed by folding into bilayers in water. For heterogeneous monolayers with phase coexistence, the mechanism of collapse remains unclear. Here, we investigated collapse of lipid monolayers with coexisting liquid-liquid and liquid-solid domains using molecular dynamics simulations. The MARTINI coarse-grained model was employed to simulate monolayers of ∼80 nm in lateral dimension for 10–25 μs. The monolayer minimum surface tension decreased in the presence of solid domains, especially if they percolated. Liquid-ordered domains facilitated monolayer collapse due to the spontaneous curvature induced at a high cholesterol concentration. Upon collapse, bilayer folds formed in the liquid (disordered) phase; curved domains shifted the nucleation sites toward the phase boundary. The liquid (disordered) phase was preferentially transferred into bilayers, in agreement with the squeeze-out hypothesis. As a result, the composition and phase distribution were altered in the monolayer in equilibrium with bilayers compared to a flat monolayer at the same surface tension. The composition and phase behavior of the bilayers depended on the degree of monolayer compression. The monolayer-bilayer connection region was enriched in unsaturated lipids. Percolation of solid domains slowed down monolayer collapse by several orders of magnitude. These results are important for understanding the mechanism of two-to-three-dimensional transformations in heterogeneous thin films and the role of lateral organization in biological membranes. The study is directly relevant for the function of lung surfactant, and can explain the role of nanodomains in its surface activity and inhibition by an increased cholesterol concentration.

Introduction

Due to their amphiphilic nature, lipid molecules act as surfactants: they adsorb at polar-apolar interfaces, such as an air-water interface, to form a monolayer and reduce the surface tension (1, 2). Lipid monolayers, with a thickness (∼nm) much smaller than its in-plane (lateral) dimension (∼μm), are thin films with two-dimensional phase behavior. The monolayer phase state at a given temperature depends on the surface density, which in turn determines the surface tension, γ_m, at the interface according to

$${\gamma }_m\left(A_L\right)={\gamma }_0-\Pi \left(A_L\right),$$

where γ₀ is the surface tension at the pure interface, A_L is the area per lipid molecule, and Π(A_L) is the surface pressure arising from the interactions between the molecules. An increase in monolayer surface density, achieved via surfactant adsorption or monolayer lateral compression, generally results in formation of phases that are more ordered and a decrease in surface tension (3, 4). Reduction of surface tension is possible until a certain threshold, below which the monolayer becomes unstable at the interface and collapses into the third dimension. This threshold is called the “minimum surface tension” or “collapse pressure”.

Collapse of viscoelastic (5, 6) thin films proceeds via an established pathway (7, 8). The film develops periodic out-of-plane (bending) deformations, or wrinkling, in response to confining its area. This Euler buckling instability is related to strong compression forces versus weak bending forces due to the small thickness of the film. The characteristic length scale, i.e., the wavelength of wrinkling, λ, is set by the rigidities of the film, K_b, and the subphase/substrate, Ks:

$$\lambda \sim {\left(K_b/K_s\right)}^{1/4}.$$

As compression continues, the wrinkles grow in amplitude; at a certain degree of confinement, the distribution of deformation energy becomes nonuniform and focuses (9) into several wrinkles. Increasing the amplitude of these wrinkles is followed by symmetric or antisymmetric folding of the film to produce a bilayer or a trilayer, respectively (10). The folds thus formed can undergo further transformations (11); collapse of surfactant monolayers results in a variety of three-dimensional structures, depending on the material properties of the monolayer. Monolayers in the liquid phase typically collapse near the equilibrium spreading pressure to form vesicles, tubes, or micelles, whereas monolayers in the solid phase can sustain higher pressures (lower surface tensions) and produce (giant) folds, ridges/crumpling, or fractures upon collapse (see, e.g., Lee (12), Oppenheimer et al. (13), and Lipp et al. (14) for review).

This pathway describes collapse transformations for homogeneous monolayers. Lateral heterogeneity, such as domains of coexisting phases, alters the material properties of the monolayer and introduces an additional length scale related to domain size and defects at domain boundaries.

Different scenarios have been proposed to explain the stability of heterogeneous monolayers. They include enhanced elasticity and cohesiveness of the liquid matrix with embedded solid domains, two-dimensional composite alloys of solid nanodomains, percolation of rigid clusters, and initiation of buckling or budding by curved regions or compositional modulations (14, 15, 16, 17, 18, 19, 20). Yet a unified view on the effect of domains on monolayer stability is lacking. Uncertainties also remain regarding the distribution of phases between the monolayer and bilayers on collapse. Fold nucleation is theoretically predicted to occur at domain boundaries (21, 22); experimental studies reported fold formation both at the edge of a solid phase and in a liquid phase (23, 24). The squeeze-out hypothesis (25, 26, 27, 28) describes collapse of multicomponent monolayers via preferential ejection of unsaturated lipids forming liquid phases. Different experimental studies support (29, 30) or contradict this hypothesis (14, 31, 32). In experiments, individual events of fold nucleation are difficult to capture. Quantitative analysis of phase behavior is complicated by the presence of three-dimensional bilayer structures connected to the two-dimensional monolayer, as well as by irreversible loss of lipids to the subphase. As a result, the mechanism of collapse of heterogeneous monolayers is still not fully understood.

Collapse of lipid monolayers separated into coexisting phases is important for understanding two-to-three-dimensional transformations of heterogeneous thin films in general. This process is also essential in the regulation of surface tension at the gas exchange interface in the lungs (26, 33). This interface is covered by a monolayer of lung surfactant, separated into domains of coexisting phases, which undergoes collapse to transfer lipids to the associated bilayer reservoirs (34, 35, 36, 37, 38, 39). The mechanism of lung surfactant function in general and the role of monolayer domains in particular have not been elucidated in detail. Phase behavior of lipid monolayers is also of fundamental interest for understanding lipid-lipid interactions underlying lateral organization in biological membranes (40, 41). Nanoscale dynamic domains in cell membranes, or rafts (42, 43), are believed to be vital for intracellular transport, signal transduction, and entry of pathogens (44, 45); yet the driving forces for raft formation remain controversial (46, 47, 48).

In this work, we used molecular dynamics simulations to investigate collapse of lipid monolayers in the presence of coexisting phases. We employed the MARTINI coarse-grained force field (49) to simulate monolayer patches with a lateral dimension of ∼80 nm on a timescale of tens of microseconds, while retaining near-atomic detail and chemical specificity. In simulations, we can follow directly the monolayer-bilayer transformations upon collapse. We reproduce the coexistence of liquid-expanded (LE) and liquid-condensed (LC) phases, as well as liquid-ordered (Lo) and liquid-disordered (Ld) phases. These two cases are of general interest, because they represent solid-liquid and liquid-liquid coexistence, respectively, and are directly relevant for biological membranes. Phase separation of both mixtures has been previously simulated in the MARTINI model in either monolayers or bilayers (50, 51, 52, 53, 54, 55, 56). Collapse of homogeneous (one-phase) monolayers in earlier simulations was in agreement with the theoretically predicted pathway (11). Here, we characterized the mechanisms of collapse of monolayers with phase coexistence. We investigated the effect of domains on the stability of the monolayer, the sites of fold formation, the preferential transfer of components upon collapse, and the distribution of phases between the monolayer and bilayer folds in equilibrium.

Methods

We performed molecular dynamics simulations with the MARTINI coarse-grained model (49) using the GROMACS software package (Ver. 4) (57). The system setup consisted of a water slab in vacuum with two symmetric monolayers at the two water/vacuum interfaces. The lipids included DPPC (dipalmitoyl-phosphatidylcholine), DOPC (dioleoyl-phosphatidylcholine), POPG (palmitoyloleoyl-phosphatidylglycerol), and cholesterol. Two different lipid mixtures, in ratios DPPC/POPG/DOPC 3:1:1, and DPPC/DOPC/cholesterol 5:3:4, were simulated. These mixtures separated into LC/LE and Lo/Ld phases (56). Additional mixture of POPG/DOPC 1:1 and pure DOPC were used to mimic the LE and Ld phases. The monolayers were simulated at surface tensions from −3 to +25 mN/m and temperatures between 270 and 310 K. Starting structures were chosen from Baoukina et al. (56) such that the monolayer phase behavior did not change substantially at near-zero surface tensions. Near-zero surface tensions were applied to induce initial collapse of the monolayers from the interface and formation of bilayer folds (11).After collapse, selected structures were simulated at a constant interfacial area to equilibrate lipids between the monolayer and the bilayer folds. Surface tensions below equilibrium were applied to these structures to investigate the rates of collapse of the monolayer connected to bilayers. Distribution of phases between the monolayer and bilayers were analyzed for temperatures at which the monolayer remained phase-separated between near-zero and equilibrium surface tensions. Each monolayer contained 9216 lipids (corresponding to an in-plane size of ∼80 × 80 nm) and ∼500,000 water particles. The water contents varied slightly with lipid composition; at 270 K, ∼5% of the water particles were substituted by antifreeze water particles to prevent water crystallization. Na⁺ ions were added to compensate for the charge of anionic POPG lipids, and make the system electrically neutral. A summary of all simulations is given in Table S1 in the Supporting Material.

In the MARTINI force field, molecules are represented by particles that group approximately four heavy atoms together. DPPC and DOPC are standard components of this force field. For the POPG lipid, the glycerol group was represented by a polar particle (P4) as in previous simulations (11, 58). The unsaturated chains were modified as in Baoukina et al. (56); note that this modification is similar to the model of DLiPC lipids in Risselada and Marrink (52). For nonbonded interactions, the standard cutoffs for the MARTINI force field were used: the Lennard-Jones potential was shifted to zero between 0.9 and 1.2 nm, and the Coulomb potential was shifted to zero between 0 and 1.2 nm with a relative dielectric constant of 15. The time step was 20 fs with neighbor-list updates every 10 steps. Lipids and water were coupled separately to a target temperature using the velocity rescaling thermostat (59) with a time constant of 1 ps. The surface tensions were maintained using the surface-tension coupling scheme and Berendsen barostat (60) with a time constant of 4 ps and a compressibility of 5 × 10⁻⁵ bar⁻¹ in the lateral direction; the compressibility in the normal direction was set to zero to prevent box contraction. Constant interface area was maintained using constant volume simulations. The monolayer collapse simulations were 10 μs in length; the monolayer-bilayer equilibration simulations were 5–10 μs for mixed monolayers and 25 μs for demixed monolayers. Initial structures of monolayers with phase coexistence were used from Baoukina et al. (56), where they were the final structures after 25 μs of equilibration.

To quantify domains in monolayers, we used a MATLAB-based program (The MathWorks, Natick, MA), with parameters previously described in Baoukina et al. (56). Briefly, a Voronoi tessellation is performed to calculate the areas occupied by individual lipids. The lipids are then assigned to the coexisting phases based on a connectivity matrix with a specific cutoff, the chain order parameter, and a domain size cutoff. Lipid concentrations were calculated based on averaging over the last 500 ns of the trajectories and combining the data from two monolayers in the simulation box. The monolayer curvature was calculated using a MATLAB-based program as in Baoukina et al. (56) and Mendez-Villeundas et al. (61). The coordinates of the glycerol-ester groups of phospholipids (GL1, GL2 sites) and the hydroxyl group of cholesterol (ROH site), averaged over 1 ns, were fitted to a surface using a binomial filter in two dimensions to remove the noise. This convoluted surface was converted to an equally spaced grid (0.4 nm) for which partial derivatives were calculated to find the curvature matrix, the trace of which is the mean curvature, H(61). The rate of collapse

$$c=1/A_0\times dA/dt$$

was calculated as the change of monolayer area A over time t relative to its initial area A₀. At the point of the rate change, lipid concentrations were calculated and averaged over the two monolayers.

Results

Monolayer morphology

The monolayers of 3:1:1 DPPC/POPG/DOPC formed a roughly homogeneous LE phase at 310 K at all surface tensions studied. At 290 K, dropletlike domains of LC phase in the LE matrix were observed (Fig. 1 a) at low surface tensions (<9 mN/m); at higher surface tensions, the monolayer formed an LE phase. At 270 K, coexistence of LC and LE phases was observed between near-zero and equilibrium (∼25 mN/m) surface tensions; LC domains had a networklike shape (Fig. 1 b).

Figure 1.

Monolayer morphologies at low surface tensions, view from air (top panel), and side view (bottom panel). The mixture of 3:1:1 DPPC/POPG/DOPC at 290 K and 0 mN/m (a), at 270 K and 0 mN/m (b), and the mixture of 5:3:4 DPPC/DOPC/cholesterol at 290 K and 5 mN/m (c); final structures are shown. The following color scheme is used: (green) DPPC, (yellow) POPG, (orange) DOPC, and (purple) cholesterol; water not shown. To see this figure in color, go online.

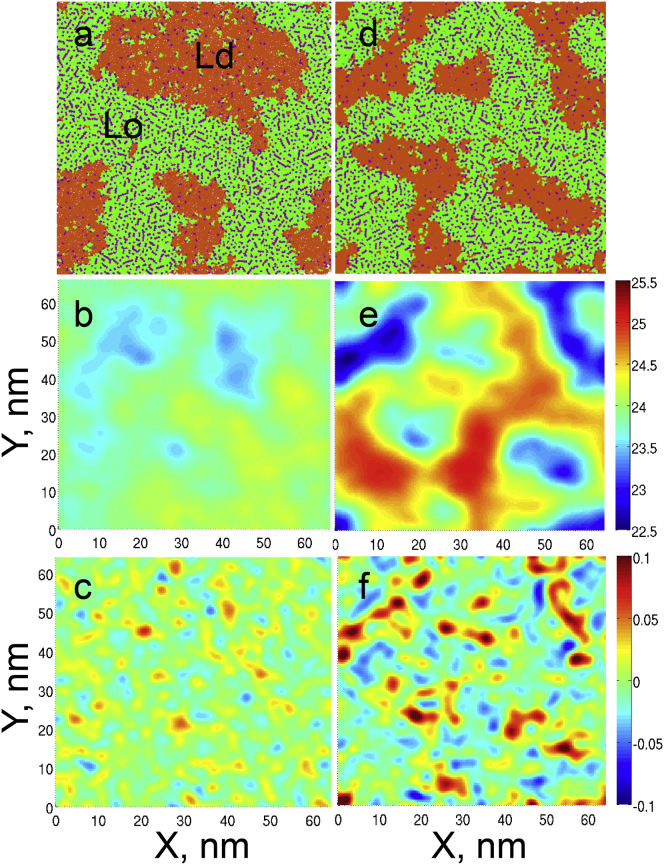
The monolayers of 5:3:4 DPPC/DOPC/cholesterol at 290 K formed networklike Lo domains separating Ld-phase regions (Fig. 1 c). This monolayer had a nonflat surface, which can be clearly seen in the side view in Fig. 1 c. The out-of-plane deformations (bending) were negligible at the equilibrium (22 mN/m) surface tension (Fig. 2, a–c), and increased noticeably as the surface tension was reduced to the minimum value (5m/N/m, Fig. 2, d–f). This is expected because the surface tension counteracts the increase of monolayer area associated with its bending. At low surface tensions, the out-of-plane deformation of the monolayer matched the distribution of the phases (compare Fig. 2, d and e). The Lo domains had a persistent concave shape as viewed from the air subphase, whereas the Ld domains fluctuated between flat and convex shapes. Lo domains have a spontaneous-curvature value of ∼−0.06 nm⁻¹ at 5 mN/m. It originates from the high concentration of cholesterol (with a fraction of 0.43 in the Lo phase), which is known to induce negative spontaneous curvature (62).

Figure 2.

The mixture of 5:3:4 DPPC/DOPC/cholesterol at 290 K at the equilibrium surface tension of 22 mN/m (a–c) and minimum surface tension of 5 mN/m (d–f). Monolayer view from air (a and d), surface profile (nm) obtained with a binary filter (b and e), and mean curvature (nm⁻¹) (c and f) are shown. Color scheme for panels a and d as in Fig. 1. To see this figure in color, go online.

Monolayer stability

To understand the effect of phase separation on monolayer stability, we compared the minimum surface tensions for monolayers with and without domains. To this end, we performed several simulations at low surface tensions for the monolayers separated into the LC/LE or Lo/Ld phases, and for homogeneous monolayers forming a LE or a Ld phase of a similar composition (56) (see Table S1).The minimum surface tension was determined as the lowest surface tension at which the monolayers did not collapse on the simulation timescale. The results show (Table 1) that the presence of the LC domains increased the monolayer stability compared to monolayers forming the LE phase. Interestingly, the networklike percolated LC domains allowed sustaining lower tensions compared to dropletlike domains. In contrast, the presence of the Lo domains in the Ld phase reduced the monolayer stability compared to a homogeneous Ld phase. The difference in minimum surface tensions between the monolayers with phase coexistence and homogeneous monolayers was 2–3 mN/m. This difference increased with increasing the size of the simulated monolayers, and was 1 mN/m for a monolayer of 2304 lipids with a lateral size of ∼40 nm. Below minimum surface tensions, the monolayers collapsed from the interface.

Table 1.

Minimum surface tensions

C	T, K	Phase	γmin, mN/m	C∗	T, K	Phase	γmin,mN/m
DPPC/POPG/DOPC 3:1:1	290	LC + LE	1	POPG/DOPC 1:1	290	LE	3
	270	LC + LE	0		270	LE	2
DPPC/DOPC/cholesterol 5:3:4	290	Lo + Ld	5	DOPC	290	Ld	2

C is the monolayer composition, C^∗ is the composition of homogeneous monolayers used for comparison, T is temperature, and γ_min is the minimum surface tension (see text).

Monolayer collapse

Monolayer collapse initiated with out-of-plane deformation in response to lateral compression. At negative surface tensions, compression resulted in steady buckling, as reported in Baoukina et al. (11). Buckling was not correlated with the distribution of phases/domain boundaries. At positive surface tensions, the monolayers developed bending undulations, which increased in amplitude as the surface tension approached low values. Monolayer bending/buckling was followed by folding into a bilayer in water.

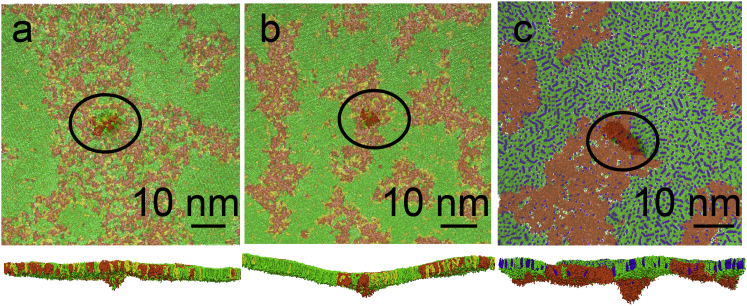
Folds nucleated in the more disordered phase (LE or Ld) in all cases. In the 3:1:1 DPPC/POPG/DOPC monolayers at 290 K, folding occurred in the LE phase away from the domain boundaries (Fig. 3 a). At 270 K, the LE domains were smaller in size than at 290 K, and were separated by networklike LC domains; folds formed in the bent monolayer in the LE phase between the LC domains (Fig. 3 b). In the 5:3:4 DPPC/DOPC/cholesterol monolayers at 290 K, folds formed in the Ld phase close to the phase boundary with the Lo phase (Fig. 3 c).

Figure 3.

Formation of bilayer folds for different monolayer morphologies. The mixture of 3:1:1 DPPC/POPG/DOPC at 290 K and 0 mN/m (a), at 270 K and −1 mN/m (b), and the mixture of 5:3:4 DPPC/DOPC/cholesterol at 290 K and 2 mN/m (c). View from air (top panel), and side view (bottom panel); (semitransparent, top view) monolayer in the top view; (opaque) bilayer fold; (black ellipses) folds. Color scheme as in Fig. 1. To see this figure in color, go online.

Once formed, fold transformation proceeded via the previously described pathway (11): a bilayer initially assumed a flat semielliptical shape, which grew in size (see Fig. 4), and then bent and closed into a semivesicle, connected to the monolayer (see Figs. 5 and 6). The more disordered phase (LE or Ld) was always preferentially ejected from the monolayers, with greater compression leading to a partial ejection of the more ordered phase (LC or Lo). At a similar degree of monolayer compression, characterized by the relative reduction of monolayer area, a larger fraction of the LC phase compared to the Lo phase was transferred to bilayers. The Lo domains due to their liquid nature rearranged during collapse to facilitate ejection of the Ld domains. The flow of lipids, accompanied by the increasing surface tension, continued until the monolayer compression was stopped by fixing the interfacial area.

Figure 4.

Fold growth for the 3:1:1 DPPC/POPG/DOPC mixture at 290 K and 0 mN/m (a–c) and for the 5:3:4 DPPC/DOPC/cholesterol mixture at 290 K and 2 mN/m (d–f). Once the folds are formed (images a and d correspond to Fig. 3, a and c), they grow in amplitude (b and e) and bend (c and f) to form a semivesicle. Upside-down view from water (folds grow into water); folds are sliced for clarity, with color scheme as in Fig. 1. To see this figure in color, go online.

Figure 5.

Monolayer in equilibrium with bilayers. The 3:1:1 DPPC/POPG/DOPC mixture at 270 K at the equilibrium surface tension for smaller (a–c) and larger (d–f) monolayer compression is shown; top view (a and d), cross-section view (b and e), and upside-down view (c and f) with sliced bilayers. Color scheme as in Fig. 1. To see this figure in color, go online.

Figure 6.

Monolayer in equilibrium with bilayers. The 5:3:4 DPPC/DOPC/cholesterol mixture at 290 K at the equilibrium surface tension for smaller (a–c) and larger (d–f) monolayer compression is shown; top view (a and d), cross-section view (b and e), and upside-down view (c and f) with sliced bilayers. Color scheme as in Fig. 1. To see this figure in color, go online.

Monolayer in equilibrium with bilayers

At a constant interfacial area, the monolayers and bilayers reached equilibrium. In this state, collective lipid transfer completed (within hundreds of nanoseconds; see Fig. S1 in the Supporting Material), bringing the monolayer surface tension to the equilibrium value. Diffusion of individual lipids between the monolayer and bilayers was still possible via their connection. The calculated equilibrium surface tension (see Table S2) was somewhat higher in the cases when the bilayers were demixed. This can be related to several differences in monolayer composition as described below. The distribution of phases and lipid components between the monolayer and the bilayers is summarized in Table 2.

Table 2.

Distribution of phases between the monolayer and bilayers

C	T, K	Structure	Monolayer phase	Bilayer phase	γm, mN/m	Cm	Cdisordered	Cconnection	Am/Aeq	Aordered/Am
DPPC/POPG/DOPC 3:1:1	270	Monolayer	LE + LC	—	23	0.20:0.20	0.29 ± 0.01:0.43 ± 0.01	—	1	0.458 ± 0.004
			LE + LC	—	20	0.20:0.20	0.29 ± 0.01:0.46 ± 0.01	—	0.99	0.490 ± 0.005
		Monolayer + bilayer	LE + LC	LE	21	0.19 ± 0.01:0.17 ± 0.02	0.30 ± 0.01:0.43 ± 0.01	0.28 ± 0.01:0.60 ± 0.03	0.88	0.518 ± 0.002
			LE + LC	LE + LC	25	0.19 ± 0.01:0.18 ± 0.01	0.30 ± 0.01:0.41 ± 0.01	0.30 ± 0.01:0.58 ± 0.01	0.56	0.50 ± 0.01
DPPC/DOPC/cholesterol 5:3:4	290	Monolayer	Lo + Ld	—	22	0.33:0.25	0.15 ± 0.01:0.75 ± 0.01	—	1	0.557
			Lo + Ld	—	20	0.33:0.25	0.15 ± 0.01:0.74 ± 0.01	—	0.99	0.555
		Monolayer + bilayer	Lo + Ld	Ld	21	0.35 ± 0.01:0.19 ± 0.01	0.17 ± 0.01:0.71 ± 0.01	0.20 ± 0.01:0.76 ± 0.01	0.87	0.632 ± 0.001
			Lo + Ld	Lo + Ld	23	0.38 ± 0.01:0.12 ± 0.02	0.24 ± 0.01:0.60 ± 0.01	0.19 ± 0.01:0.69 ± 0.01	0.58	0.718 ± 0.004

C is the mixture composition, T is temperature, γ_m is the monolayer surface tension; C_m, C_disordered, and C_connection are the fractions of non-DPPC components (POPG and DOPC, or cholesterol and DOPC, in this order) in the monolayer, the disordered phase (LE or Ld), and the monolayer-bilayer connection, respectively; A_eq is the monolayer area at the equilibrium surface tension, A_m is the monolayer area at a given surface tension, and A_ordered is the area occupied by the ordered phase (LC or Lo) in the monolayer.

In the 3:1:1 DPPC/POPG/DOPC mixture at 270 K and lower compression (with area reduction <20%), only the LE but not the LC domains were transferred to bilayers (Fig. 5, a–c). This resulted in an increase of the fraction of the LC phase, and a decrease of the concentration of unsaturated lipids in the monolayer. At greater compression (with area reduction >20%), both the LE and LC domains were transferred to bilayers (see Fig. 5, d–f). In either case, formation of bilayer folds changed the fractions of the coexisting phases in the monolayer. The monolayer-bilayer connection region differed in composition from the LE phase, and was highly enriched in the unsaturated DOPC lipid (see Table 2).

In the 5:3:4 DPPC/DOPC/cholesterol mixture at 290 K, only the Ld phase was transferred to the bilayer (Fig. 6, a–c) at low compression. Compared to the LC/LE mixture, much greater monolayer compression (with area reduction > 30%) was necessary to transfer both the Ld and Lo phases in the bilayers (Fig. 6, d–f). With increasing compression, the fraction of DOPC lipids decreased significantly in the monolayer in total, and also became smaller in the Ld phase, whereas the fraction of the Lo phase increased. The content of DOPC in the monolayer-bilayer connection was somewhat larger than in the Ld phase.

Collapse rates

The monolayers connected with bilayers underwent further collapse at surface tensions below equilibrium. The rates of collapse, characterized by the normalized reduction of the monolayer area with time, depended on the applied surface tension (see Table 3). Interestingly, for biphasic monolayers the rates of collapse changed with time. Notably, the rate of collapse dropped by 2–3 orders of magnitude in the 3:1:1 DPPC/POPG/DOPC mixture at 270 K, even at low surface tensions. The crossover was observed as the LC domains formed an interconnected network, and the area fraction (as well as the fractions of lipids) forming the LC phase increased above ∼0.6. In the 5:3:4 DPPC/DOPC/cholesterol monolayer at 290 K, the crossover occurred only at higher surface tensions, with most of the Ld phase ejected into the bilayers.

Table 3.

Rates of monolayer collapse

C	T, K	γm, mN/m	Phase	c, ns−1	Aordered/A0	Cordered
DPPC/POPG/DOPC 3:1:1	270	20	LC + LE	10−4–5 10−6	0.57 ± 0.02	0.61 ± 0.02
		15	LC + LE	3 10−4–5 10−6	0.61 ± 0.03	0.65 ± 0.02
		10	LC + LE	10−3–10−6	0.61 ± 0.03	0.66 ± 0.02
		5	LC + LE	3 10−4–4 10−6	0.71 ± 0.03	0.76 ± 0.03
	290	15	LE	7 10−4	0	0
		10	LE	2 10−3	0	0
DPPC/DOPC/cholesterol 5:3:4	290	15	Lo + Ld	2 10−4–7 10−6	0.86 ± 0.02	0.89 ± 0.02
		10	Lo + Ld	8 10−4–10−5	—	—
		5	Lo + Ld	2 10−3	—	—

C is the monolayer composition, T is temperature, γ_m is the monolayer surface tension, c is the rate of monolayer collapse (varying values are separated by dash), A₀ is the total monolayer area, A_ordered is the area occupied by the ordered phase (LC or Lo) at which the rate of collapse changes, and C_ordered is the fraction of lipids in the ordered phase (LC or Lo) in the monolayer at which the rate of collapse changes.

Discussion

We investigated the mechanism of collapse of lipid monolayers separated into LE and LC, and Ld and Lo phases. We have previously characterized the properties of these phases in monolayers, as well as in bilayers (56, 63). On lateral compression, monolayer collapse proceeds via wrinkling of the monolayer, followed by folding into a bilayer in the water subphase (8, 11). Wrinkling can originate from either steady buckling or thermally induced bending undulations (capillary waves) (64). Folding into a bilayer in water is favorable over a bilayer in air or a trilayer, because it reduces the surface free energy of the hydrocarbon chains exposed to air. This two-to-three-dimensional transition occurs when the compression forces exceed the bending forces. In lipid monolayers, the characteristic wavelength, λ, of wrinkling is estimated to be ∼1 μm (8, 64). In simulations, the box size of 80 nm limits the monolayer wrinkling wavelength. Smaller wavelengths are associated with higher bending energies, which increase the energy barrier for monolayer collapse. In addition, the imposed periodicity of the simulation box increases monolayer ordering, lowering the entropy of the liquid (disordered) phase. These factors generally enhance the monolayer stability in simulations (i.e., provide lower minimum surface tensions) compared to experimental systems.

In biphasic monolayers, wrinkling and folding are more likely to develop in a liquid (disordered) phase, because it is less rigid, and bending is associated with weaker forces. Monolayer folding always initiates in the LE or Ld phase in our simulations. It should be noted that the MARTINI model, although coarse-grained, reproduces the elastic properties of LE/Ld, Lo, and LC phases (11, 50, 65). The bending wavelength is then limited by the size of liquid domains (∼20 nm). This can explain lower minimum surface tensions in the presence of LC domains compared to a homogeneous LE phase in our simulations. We expect that in macroscopic monolayers the effect of phase separation is determined by the ratio of the wrinkling wavelength and the domain size: formation of ordered domains (with negligible spontaneous curvature) enhances monolayer stability if liquid domains become smaller than the wrinkling wavelength.

Spontaneous curvature of domains induces monolayer bending at low surface tensions. Monolayer roughness producing budding at low tensions has been observed experimentally (19, 64, 66). This roughness was suggested to originate from packing defects at the boundary of LC domains (19). Grain boundaries in crystalline membranes were theoretically shown to serve as defects and initiate buckling (22). Theoretical models predict that spontaneous curvature reduces monolayer stability against buckling (20). Alternative models predict an inflection at domain boundaries, which destabilizes the monolayer if the spontaneous curvatures of the two phases differ (21). In our simulations, spontaneous curvature of Lo domains increases the minimum surface tension compared to a homogeneous Ld phase, and folding occurs in the Ld phase close to domain boundaries. These results suggest that spontaneous curvature facilitates monolayer collapse by creating wrinkle precursors, and domain boundaries do not serve as fold formation sites if elastic properties of the two phases differ.

Fold formation in the liquid (Ld or LE) domains initiates the flow of the liquid phase enriched in unsaturated lipids from the monolayer. This result supports the squeeze-out hypothesis, which suggests selective ejection of unsaturated lipids on collapse of multicomponent monolayers (25, 26, 27, 28). Our results also show that the more-ordered (Lo or LC) domains enriched in saturated components can flow into bilayers following the liquid domains. The amount of the ordered phase transferred depends on the degree of monolayer compression, and in turn affects the distribution of components and phases between the monolayer and bilayers. The composition and phase ratios thus become different due to the partial collapse of the monolayer, compared to a flat monolayer at the same surface tension. The monolayer-bilayer connection, due to its high negative curvature, leads to additional lipid demixing; it has an increased concentration of unsaturated lipids (compared to the Ld or LE phases), which makes the connecting region softer and reduces the free energies of bending and stretching. Because bilayer folds have a significant fraction of unsaturated lipids, their bending into a vesicle is favorable; tubes could possibly be observed for larger systems.

Monolayers connected to bilayers collapse at surface tensions below the equilibrium value. Bilayers serve as preexisting nuclei of the three-dimensional phase, and the two-to-three-dimensional transformations occur without a free energy barrier. The rates of collapse decrease by several orders of magnitude as the fraction of LC domains approaches the percolation threshold (15). The LC domains form an interconnected network, which provides the rigid support for monolayers under compression. The rates of collapse in simulations are much higher compared to experimental values (67). We have previously shown that the rates of monolayer compression in simulations are much higher than experimental rates (11). At the same time, the length scales in simulations are much smaller compared to experimental length scales; this allows a faster response of the system to the applied perturbation. Because the monolayer surface viscosity in simulations is lower than experimental values (56, 68, 69), lipid transfer occurs on a much shorter timescale. In experimental studies, it was reported that high compression rates can lead to monolayer supercompression, which significantly lowers the minimum surface tension by trapping the monolayer in an amorphous state (70, 71). Amorphous phases were not observed in our simulations. Due to the setup of monolayer compression in simulations (see Methods), the rate of compression cannot exceed the rate of collapse.

Our results have direct implications for the function of lung surfactant. Lung surfactant maintains the surface tension at the gas-exchange interface at low values during the breathing cycle (72, 73). It contains a significant fraction of unsaturated lipids (74, 75), which typically collapse at equilibrium surface tensions and do not sustain near-zero tensions. Domains of coexisting phases undergo restructuring from micro- to nanoscale upon reduction of surface tension in vitro (24, 39). If the size of the liquid domains becomes lower than the wrinkling wavelength, it can explain enhanced stability of lung surfactant at low surface tensions. Percolation of solid domains could slow the transfer of lipids to bilayer reservoirs and thus allow reaching low tensions, but it would require a significant depletion of the liquid phase/unsaturated lipids in the monolayer. Finally, an elevated concentration of cholesterol, which was shown to inhibit lung surfactant function (76, 77), could induce spontaneous curvature of (Lo) domains, which would destabilize the monolayer.

Conclusions

We characterized the mechanism of collapse of lipid monolayers at the air-water interface separated into LE and LC, and Ld and Lo phases. The main conclusions can be summarized as follows:

• 1.The presence of flat ordered domains in the liquid (disordered) phase enhances monolayer stability, if the size of liquid domains is smaller than the characteristic bending wavelength.
• 2.The presence of domains with spontaneous curvature induces monolayer bending at low surface tensions, and facilitates monolayer collapse.
• 3.Fold formation occurs in the liquid (disordered) phase; curved domains shift fold-formation sites toward the phase boundaries.
• 4.On collapse, the liquid (disordered) phase enriched in unsaturated lipids is preferentially transferred to the bilayers, which supports the squeeze-out hypothesis.
• 5.Percolation of solid domains decreases the rate of monolayer collapse by several orders of magnitude.
• 6.The monolayer-bilayer connection region has an increased concentration of unsaturated lipids compared to the liquid (disordered) phase.
• 7.Monolayers in equilibrium with bilayers have a modified composition and distribution of phases compared to flat monolayers at the same surface tension.

We believe that these conclusions can be generalized to surfactant monolayers with liquid-liquid and solid-liquid phase coexistence. These findings provide important insights into the effect of lateral heterogeneity on the mechanism of two-to-three-dimensional transformation in thin films.

Editor: Reinhard Lipowsky.