Abstract
The aggregation of proteins with expanded polyglutamine (polyQ) tracts is directly relevant to the formation of neuronal intranuclear inclusions in Huntington’s disease. In vitro studies have uncovered the effects of flanking sequences as modulators of the driving forces and mechanisms of polyQ aggregation in sequence segments associated with HD. Specifically, a seventeen-residue amphipathic stretch (N17) that is directly N-terminal to the polyQ tract in huntingtin decreases the overall solubility, destabilizes nonfibrillar aggregates, and accelerates fibril formation. Published results from atomistic simulations showed that the N17 module reduces the frequency of intermolecular association. Our reanalysis of these simulation results demonstrates that the N17 module also reduces interchain entanglements between polyQ domains. These two effects, which are observed on the smallest lengthscales, are incorporated into phenomenological pair potentials and used in coarse-grained Brownian dynamics simulations to investigate their impact on large-scale aggregation. We analyze the results from Brownian dynamics simulations using the framework of diffusion-limited cluster aggregation. When entanglements prevail, which is true in the absence of N17, small spherical clusters and large linear aggregates form on distinct timescales, in accord with in vitro experiments. Conversely, when entanglements are quenched and a barrier to intermolecular associations is introduced, both of which are attributable to N17, the timescales for forming small species and large linear aggregates become similar. Therefore, the combination of a reduction of interchain entanglements through homopolymeric polyQ and barriers to intermolecular associations appears to be sufficient for providing a minimalist phenomenological rationalization of in vitro observations regarding the effects of N17 on polyQ aggregation.
Introduction
Aggregation and phase separation of polyQ tracts contribute directly to pathological processes that underlie neurodegeneration in Huntington’s disease (1). Insoluble inclusions that accumulate within neuronal nuclei encompass the exon 1-encoded portion of the huntingtin protein (2). This block copolymeric sequence includes a 17-residue amphipathic segment (N17), a homopolymeric polyQ tract (Qn), and a 38-residue proline-rich segment (C38). The amino acid sequences of N17 and C38 are MATLEKLMKAFESLKSF and P11-QLPQPPPQAQPLLPQPQ-P10, respectively. Exon 1 spanning sequences can be generated either by proteolysis of mutant huntingtin (3) or by translation of aberrantly spliced mutant mRNA transcripts with expanded CAG repeats (4).
Systematic studies have investigated the synergy between polyQ length and sequence context on various properties. These include the conformational properties of monomeric forms of exon 1 spanning fragments (5, 6, 7, 8, 9, 10, 11), temperature dependent solubilities (12, 13), rates of loss of monomers into growing aggregates (14, 15, 16, 17, 18, 19, 20, 21, 22, 23), rates of growth of fibrillar aggregates (24, 25), and morphologies of aggregates in insoluble inclusions (26, 27). Of particular relevance are the recent in vitro studies of Thakur et al. (18) and Crick et al. (12). The latter used a combination of methods to uncover the effects of N17 and C38 as modulators of driving forces for and mechanisms of polyQ aggregation. Although N17 has high intrinsic solubility, it lowers the overall solubility of N17-Qn-(Lys)2 constructs vis-à-vis Qn-(Lys)2 (Qn-K2). Conversely, the high intrinsic solubility of C38 causes an enhancement of the solubility of Qn-C38 vis-à-vis Qn-K2. Experiments to probe the intrinsic aggregation mechanisms of polyQ tracts and the modulation of these mechanisms by N17 and C38 were performed under conditions where the magnitudes of driving forces for aggregation are equivalent for all constructs, i.e., the solutions were equivalently supersaturated.
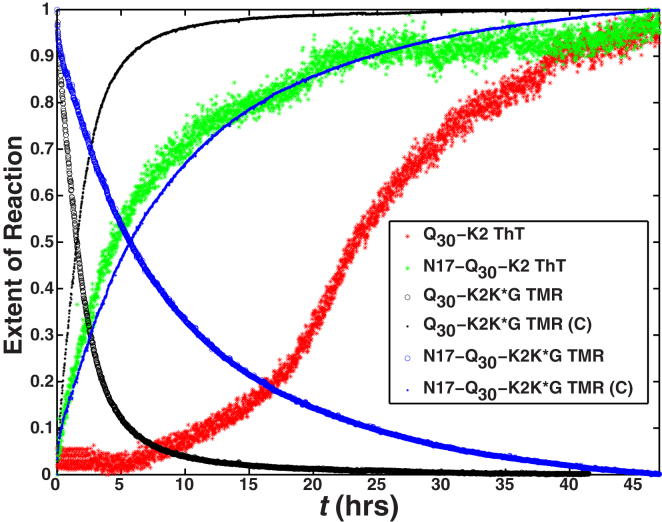
Aggregation mechanisms were probed using two assays, viz., the rate of loss of tetramethyl rhodamine (TMR) fluorescence and the rate of gain of thioflavin T (ThT) fluorescence (see Fig. 1). In the TMR assay (28), disaggregated molecules with covalently attached TMR labels are incorporated into growing aggregates. Their fluorescence is quenched only when TMR dimers form within the aggregates. The loss of fluorescence depends on the formation of aggregates, and it appears to be agnostic regarding aggregate morphologies or specific structures formed within the aggregates (28). The TMR assay affords enhanced temporal and spatial resolution (12, 28). In contrast, the gain in ThT fluorescence measures the rate of growth of fibrillar species.
Figure 1.
Summary of the overall rates of aggregation for polyQ constructs with and without N17. The data are from the work of Crick et al. (12). The rate of loss of TMR fluorescence for Q30 peptides with and without the N17 module is quantified by the blue and black open circles, respectively. The blue and black stars plot the complement of these data, which provide an assessment of the rates of growth of aggregates as monitored by the TMR assay. These data are to be compared to the green and red stars that quantify the rate of increase in ThT fluorescence for Q30 peptides with and without the N17 module. The rate of loss of TMR fluorescence and the rate of gain in ThT fluorescence are plotted in normalized units and depict the rates of the change of reactions that are being monitored by the distinct probes. Here, K∗ refers to the lysine residue that is covalently modified by attachment of the TMR dye.
Based on the data in Fig. 1, we make the following observations. The rate of loss of TMR fluorescence is slowed by the presence of N17, as shown by the comparison of data for Q30-K2K∗G to those for N17-Q30-K2K∗G. Aggregates detected by the TMR assay, which were shown to be spherical clusters using electron microscopy for Q30-K2K∗G, form early and on distinct timescales when compared to the slow fibril formation observed from the gain in ThT fluorescence for Q30-K2. In the presence of N17, aggregates monitored in the TMR assay form on timescales equivalent to that for the formation of fibrillar aggregates as monitored by the ThT assay. It appears that N17 destabilizes nonfibrillar states and accelerates the formation of fibrils. The effect of N17 as an accelerator of fibril formation is also observed in exon 1-mimicking fragments such as N17-Qn-C38, yielding equivalent fibril growth rates as compared to N17-Qn-K2 for similar degrees of supersaturation (12).
The effects of N17 on the conformational properties of monomeric forms of polyQ and the frequencies of intermolecular associations have been investigated in atomistic simulations by Williamson et al. (29). These simulations were based on the ABSINTH implicit solvation model and forcefield paradigm (30). The physical underpinnings of the ABSINTH paradigm have been detailed in previous publications (30, 31, 32). It has been used successfully—as judged by comparisons to experimental data—in simulations of intrinsically disordered proteins (33, 34, 35, 36, 37, 38, 39), proline-rich systems (31), protein unfolded states (40), and polyQ-containing systems (7, 8, 29, 41). Williamson et al. compared the conformational properties and intermolecular associations of N17-Qn peptides to that of Qn. The helical propensity of N17 increases for short polyQ tracts (n < 10). It decreases sharply for 10 < n < 20, and becomes negligibly small as the polyQ length increases (n > 20). N17 unfolds and adsorbs by forming an intramolecular, interdomain interface with the surface of the globular polyQ. The latter mimics a high local concentration of urea, thus denaturing N17. A similar proposal has been put forth for the effect of polyQ on cytosolic proteins (42). N17-Qn peptides form patchy-colloid-like architectures (43, 44) for n > 20 (see Fig. S1 in the Supporting Material). This weakens the effective surface tension, as well as the effective favorable energy that is associated with interactions between glutamine residues. Williamson et al. (29) also quantified the comparative frequency of forming dimers for Qn versus N17-Qn for n = 15, 25, and 35. N17 diminishes the frequency of dimer formation by up to a factor of 3 in the temperature range 298–315 K. By imparting directionality and specificity to intermolecular associations, N17 helps reduce the random associations characteristic of the uniformly sticky, intrinsically disordered homopolymeric polyQ globules.
Here, we develop a phenomenological model that provides a conceptual framework to bridge the observations regarding N17-modulated polyQ aggregation as quantified in vitro and in simulations. We seek to understand how N17 diminishes the frequency of random intermolecular associations while simultaneously destabilizing small, nonfibrillar aggregates and accelerating fibril formation. The physics of flexible homopolymers in poor solvents provides the conceptual lynchpin. Intermolecular associations of homopolymers in poor solvents, such as polyQ in aqueous milieus, promote entanglements between pairs of molecules (45, 46). Within dimers or higher-order clusters, the polymers are likely to have liquidlike organization, and chains can become entangled with each other because the intrachain and interchain interactions are equivalent for homopolymers (47, 48). Our reanalysis of the simulation results of Williamson et al. (29) shows clear evidence for entanglements between polyQ domains. We also find that N17 reduces interchain entanglements between polyQ domains. Therefore, N17 diminishes intermolecular associations between globular polyQ while reducing interchain entanglements through these domains.
Coarse-grained models provide access to large spatial scales and morphologies (49, 50, 51). Here, we introduce an ultra-coarse-graining approach (52) that leverages the information gleaned from analysis of atomistic simulation results to develop a phenomenological (as opposed to transferrable) coarse-grained model that resembles efforts often deployed in studies of colloidal particles. We model globule-forming polyQ molecules as spherical colloidal particles. The effects of N17 that include a barrier to interparticle interactions and the quenching of interparticle entanglements are modeled using suitable pair potentials. The remainder of the narrative is organized as follows: First, we present the methodological details of our Brownian dynamics (BD) simulations. This is followed by a presentation of the results obtained from BD simulations designed to study the aggregation of colloidal particles that interact via distinct classes of pair potentials. We show that the phenomenological pair potentials provide a minimalist framework for understanding the effects of the N17 module on polyQ aggregation kinetics and morphologies.
Materials and Methods
We performed three-dimensional BD simulations composed of 2 × 104 spherical particles in a cubic box of length L = 256Rg with periodic boundary conditions. Here, Rg corresponds to the particle radius. We set Rg = 1 unit, and all distances are measured in units of Rg. The volume fraction is fv = 0.005, which is in accord with a supersaturated system of polyQ molecules (12). The equation of motion for each particle i is given by
| (1) |
Here, Γ is the monomer friction coefficient and Wi is the random force on each particle i, defined as a Gaussian white noise that satisfies the fluctuation-dissipation relation. In our simulations, Γ = 0.5 and Δt = 0.005 in reduced time units of Rg(m/kT)1/2, where m = 1. Accordingly, t = 1 is the time it takes to diffuse a distance of Rg.
Developing a suitable set of phenomenological models
In the ultra-coarse-grained model, each molecule (Qn or N17-Qn) is modeled as a spherical particle. This is justified by the observation that monomeric polyQ forms compact globules in aqueous solvents, and this property is preserved for N17-Qn molecules providing n > 20 (29) (see Fig. S2). Therefore, the early stages of aggregation in supersaturated solutions will most likely involve the diffusion and collision of globules that can coalesce through their polyQ domains. We use reduced units and normalize all lengthscales by the radius of gyration (Rg) of the molecule in question. Accordingly, an interparticle distance, R, quantified as the distance between the centers of particles, is normalized and denoted by X, where . X = 1 implies that R = Rg and X = 2 implies that R = 2Rg. Therefore, X is a normalized interparticle separation, i.e., it is R normalized by Rg. We stipulate that X = 1 corresponds to the fully entangled state, because values of X < 1 are rarely observed in atomistic simulations of monomer-dimer equilibria, indicating a significant excluded volume barrier below X = 1; X = 2 corresponds to the docking state, and X > 2 corresponds to dissociated particles.
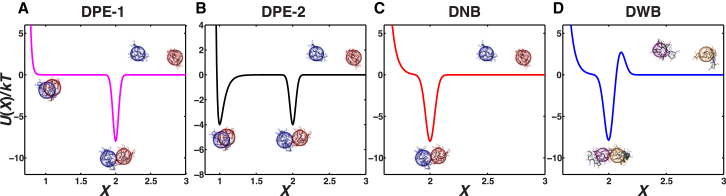
The results presented in the main text are based on four different interparticle potentials, U(X) (Fig. 2, A–D). We use two potentials to model different archetypes of docking plus entanglement (DPE) and these are designated DPE-1 and DPE-2. A potential with a single well and a featureless entangled state is shown in Fig. 2 A for 1 < X < 2. For this potential (DPE-1), different degrees of entanglement are energetically equivalent, and the realization of entangled states arises purely due to entropic considerations. Alternatively, the fully entangled state can be of equivalent stability to the docked state, because interchain contacts can be maximized in fully entangled states. Accordingly, DPE-2 (Fig. 2 B) shows a bistable double-well potential with two minima, one at X = 1 and one at X = 2, implying that a pair of particles can either dock (X = 2) or entangle (X = 1).
Figure 2.
Phenomenological pair potentials designed to model the effective interactions in coarse-grained simulations of Qn and N17-Qn globules. To see this figure in color, go online.
Fig. 2 C shows a single-well potential with no docking barrier (docking with no barrier (DNB)). This pair potential is designed to capture one of the effects of the N17 module, quenching of interchain entanglements. Finally, Fig. 2 D shows a single-well potential with a barrier to docking (docking with a barrier (DWB)). This pair potential is designed to capture the two effects attributed to N17, namely, minimization of interchain entanglements and creation of a barrier that limits intermolecular associations. Note that the DNB and DWB potentials are designed to accommodate some degree of interchain entanglement, as evidenced by the location of the steep excluded-volume wall at values of X < 2 rather than at X = 2.
Functional forms for DPE-1, DPE-2, DNB, and DWB
The interparticle interaction potentials for DPE-1, DPE-2, DNB, and DWB are linear combinations of three terms, UM, UD, and UB, that are pair potentials written in terms of the normalized interparticle distance, X. The term UM is a 2n − n Mie potential and is written as
| (2) |
Here, n = 18, εM is the well depth of the potential, and Xm corresponds to the location of the minimum of the Mie potential. We use the Mie potential instead of a Lennard Jones potential because we wish to have precise control over the location of minima, and because this potential is used in simulations of particles that are agglomerations of atoms, i.e., colloidal particles. The Mie potential provides a useful way to model a steeply rising excluded-volume wall and short-range attractions that allow us to incorporate additional terms to capture specific effects such as entanglements or docking. The term UD is an inverted Gaussian written as
| (3) |
Here, εD is the depth of the potential well and δD controls the width of the well. In all cases, δD = 0.04. The term UB is a Gaussian written as
| (4) |
Here, εB corresponds to the height of the barrier and δB controls the width of the barrier. In all cases, δB = 0.04.
The DPE-1, DPE-2, DNB, and DWB models take the forms shown in Eqs. 5–8 below, with all well depths and barrier heights written in units of kT, where k is Boltzmann’s constant and T is the simulation temperature.
| (5) |
| (6) |
| (7) |
| (8) |
The cutoff for the range of interparticle interactions was set to 2.2Rg for the DPE and DNB models and to 2.3Rg for the DWB model. The slightly larger cutoff for the latter is to accommodate the inclusion of a barrier beyond X = 2. All contributions to the interparticle forces beyond the respective cutoffs are neglected. Each simulation starts from a random configuration and is run for 4 × 106 time steps, corresponding to a simulation time of t = 2 × 104. This is sufficient for the achievement of steady-state behavior. All simulation results are averaged over five runs for each model.
Parameterization of the pair potentials
We used a single-well potential based on Eq. 2 and varied the depth of the well in this potential until we achieved the steady-state behavior of spherical clusters coexisting with large, aspherical fractal aggregates (see Figs. S3–S5). In addition, the crossover lengthscale between spheres and clusters was required to reach a saturation value. Based on these considerations, we converged on an energy scale of 8kT for the system of interacting particles. Accordingly, for the DPE-1, DNB, and DWB systems, the well depth was set to 8kT, and for the DPE-2 system, the two wells were each set to 4kT, such that the overall energy scale for interparticle interactions remains 8kT, except that it is now split between the docked and entangled states. The overall energy scale 8kT is set to control the extent of aggregation. This energy scale does not distinguish aggregation that yields small spherical aggregates versus aggregation that yields large linear species. Instead, setting the overall energy scale is equivalent to fixing the degree of supersaturation, and this should be the same for all four models. If the stability of the entangled state is to be increased, then there has to be a concordant weakening of the stability of the docking state. This feature allows us to mimic the experimental approach of assessing aggregation mechanisms at equivalent degrees of supersaturation as opposed to equivalent concentrations. Finally, the barrier for interparticle interactions in the DWB system was parameterized to yield a slower convergence toward smaller spherical aggregates than is seen for the DPE systems. This choice reflects the mapping of the DWB potential to systems with the N17 module, whereas the DPE potentials map to the polyQ system.
Results
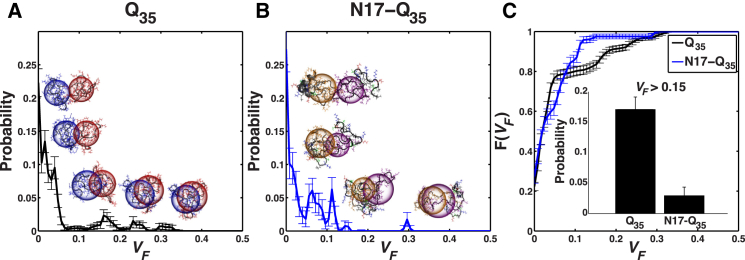
Reanalysis of atomistic simulation results shows evidence for interchain entanglements between polyQ domains and modulation of these entanglements by N17. We analyzed the simulation results of Williamson et al. (29) for dimers of Q35 and N17-Q35. The chain-length-normalized radii of gyration are equivalent for monomeric forms of Qn and N17-Qn (n = 30 and 35, respectively) (see Fig. S2). This implies that their densities are equivalent, and therefore, we use the simulation results for Q35-containing systems as proxies for Q30-containing systems. For each of the associated molecules in the simulated ensembles, we calculated theintersected volume fraction as . Here, SSI corresponds to the sphere-sphere intersection and is defined as
where dcom is the distance between the centers-of-mass of two interacting Q35 domains and Rg,m1 and Rg,m2 correspond to the radii of gyration of the Q35 domains in molecules 1 and 2, respectively. In addition, Vm1 and Vm2 are the volumes of the spheres with radii Rg,m1 and Rg,m2, respectively. Unlike other measures of size, the radius of gyration is a formal order parameter in polymer physics theories and it provides a direct assessment of chain density, which is altered by aggregation via docking and/or entanglement.
If dimers form strictly through the docking of undeformed surfaces, then VF = 0. Conversely, VF increases as the degree of entanglement between polyQ domains increases. Fig. 3, A and B, shows comparative assessments of the probability densities of realizing conformations for dimers with specific degrees of entanglements between polyQ domains, as observed in simulations of Q35 (Fig. 3 A) versus N17-Q35 (Fig. 3 B) molecules. Fig. 3 C provides a quantitative summary of these comparisons. Here, we calculated the cumulative distribution function, which allows us to compute the probability of realizing dimer conformations that have values of VF greater than a specific threshold. It can be seen that the N17 module diminishes the degree of entanglement through polyQ domains, such that the probability of realizing conformations with VF > 0.15 is an order of magnitude higher for Q35 than for N17-Q35 (Fig. 3 C, inset).
Figure 3.
Quantifying the degree of entanglement between polyQ domains (T = 315 K) as observed for Q35 peptides in atomistic simulations for Q35 and N17-Q35. (A and B) Probability density distributions using a bin width of 0.008. This quantifies the likelihood of observing conformations of dimers that have intersection volume fractions, VF, that lie within specific intervals. These intersected volumes are computed over the polyQ domains alone, as described in the main text. Shown are two sets of representative conformations corresponding to distinct values of VF. The radius of each translucent sphere corresponds to the Rg of each Q35 domain for the corresponding conformation. (C) Cumulative distribution functions for Q35 (black) and N17-Q35 (blue). The bumpiness evident in the probability distribution functions is the result of finite-sized artifacts, which are intrinsic to quantifying entanglements from simulations of monomer-dimer equilibria as opposed to monomer-oligomer equilibria. The latter simulations were not performed using atomistic descriptions, because these are computationally prohibitive at this juncture. F(VF) quantifies the probability of finding dimer conformations where the intersected volume fraction is less than or equal to a particular value for VF. (Inset) Probability of finding entangled conformations for Q35 versus N17-Q35 at volume fractions of VF > 0.15. To see this figure in color, go online.
How to analyze steady-state and kinetics profiles to distinguish aggregation mechanisms
Our goal is to achieve a comprehensive analysis of the contributions of all of the particles in the system and analyze the aggregation process using theories that yield precise predictions in terms of the overall structure factor. Further, we avoid analyses that are ad hoc in nature, because the results can depend on nuances such as the definitions of aggregate sizes and criteria for deciding on aggregation. The experimental data (Fig. 1) suggest that a class of models based on diffusion-limited aggregation (53, 54, 55, 56, 57) and diffusion-limited cluster aggregation (58, 59, 60, 61) have relevance to the early phases of polyQ aggregation. Guided by theories for the kinetics of gelation and aggregation, we analyzed the temporal evolution and steady-state properties of the structure factor S(q), for a system of spherical particles (62, 63, 64). S(q) provides information regarding the structures that form across distinct lengthscales. Here, q has units of inverse wavelength. High-q values provide information regarding structures at small lengthscales and low-q values provide structural information regarding those at larger lengthscales. In the early stages of aggregation, spherical clusters can form, and according to Porod’s law (65), the presence of spherical clusters is detectable, because S(q) should scale as q–4. This would imply a straight line with a slope of –4 in a log-log plot of S(q) versus q. Spherical clusters form during the early phases, but these spheres do not grow into macroscopic aggregates. If the arrival time of new clusters is faster than the rearrangement timescales within the aggregates, then the spherical structures that form on small lengthscales give way to large, aspherical, and extended structures (66) such that S(q) scales as q–1.8. In this work, these large, open aspherical structures will serve as proxies for linear, fibrillar morphologies that form in the postelongation phase of protein aggregation.
At steady state, the log-log plots of S(q) versus q will have two linear regimes, one with a slope of ∼–4 and the other with a slope of ∼–1.8. The former corresponds to spherical aggregates that form across small lengthscales (high-q) and the latter to those that form across large lengthscales (low-q). The q-regime at which the slopes cross over reflects the joint contributions of the average aggregate sizes and shapes. If large aggregates form in solution, then the crossover lengthscale, qc shifts to lower values. In a similar way, if aspherical aggregates form in the high-q regime, then qc also shifts to lower values. Section S1 in the Supporting Material summarizes our formal approach for detecting the two linear regimes for steady-state structure factors. Once we identify the corresponding linear regimes, we monitor the temporal evolution of the slopes within each region, and this helps us analyze aggregation kinetics across distinct lengthscales.
Analysis of structure factors
The preceding paragraphs set the expectations for our analysis of the steady-state structure factors and their temporal evolution. We first present a summary of the observations extracted from the steady-state structure factors and their temporal evolutions for each of the four models. For a system of N particles, the structure factor at time t is written in terms of the q-vectors as
| (9) |
Here, and are the position vectors of particles i and j, respectively. The relevant results are shown in Figure 4, Figure 5, Figure 6.
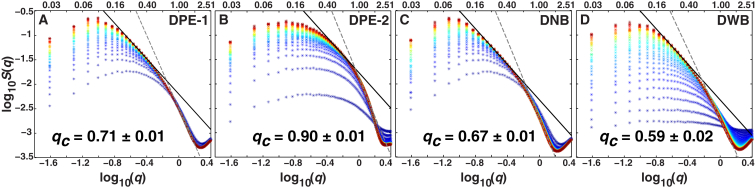
Figure 4.
Log-log plots of the temporal evolution of the structure factor for aggregation modeled using the DPE-1, DPE-2, DNB, and DWB pair potentials. The structure factors plotted with cooler-colored symbols correspond to early time points and those plotted with hotter-colored symbols correspond to the later times and include steady-state behavior. The structure factors were calculated between t = 500 and t = 20,000 in increments of 500. Solid black lines correspond to the line of best fit to the low-q regime of the steady-state structure factor and dashed lines to that of the high-q regime. The crossover lengthscale, qc, is calculated from the steady-state structure factor for each potential as the point where the two lines intersect.
Figure 5.
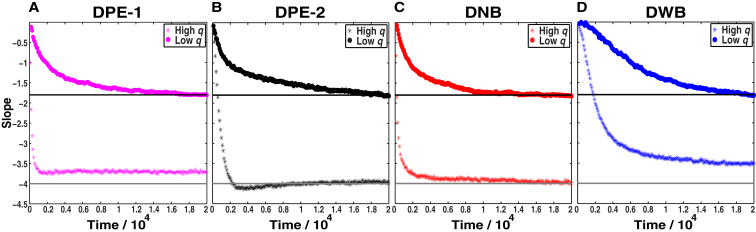
Temporal evolution of the slopes in the high- and low-q regimes for each of the four models. (A) The DPE-1 model, the formation of small, nearly spherical aggregates is detected by monitoring the evolution of the slope of the straight line in the high-q region (1.18 ≤ q ≤ 1.40) and the formation of linear aggregates is detected by monitoring the temporal evolution of the slope of the straight line in the low-q region (0.22 ≤ q ≤ 0.44). (B) The corresponding analysis for the DPE-2 model analyzes the evolution of slopes in the regimes 1.08 ≤ q ≤ 1.30 and 0.44 ≤ q ≤ 0.66, respectively. (C) For the DNB model, the evolution of slopes is followed in the regimes 0.96 ≤ q ≤ 1.18 and 0.20 ≤ q ≤ 0.42. (D) The same analysis for the DWB model by monitoring the slopes in the regimes 0.98 ≤ q ≤ 1.20 and 0.17 ≤ q ≤ 0.39, respectively. To see this figure in color, go online.
Figure 6.
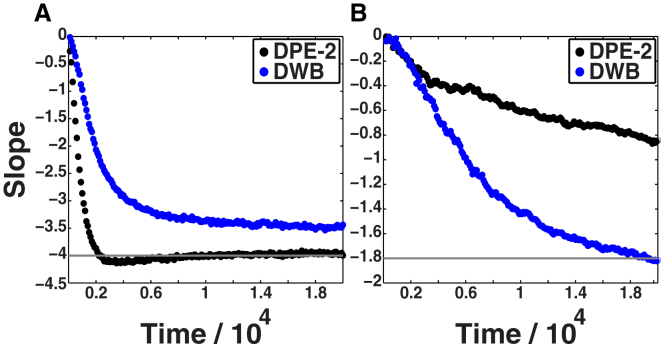
Comparative assessments of the rates of aggregation in the high-q (A) and low-q (B) regimes for DPE-2 and DWB models. We choose the high-q regime (1.08 ≤ q ≤ 1.30) (A) and the low-q regime (0.17 ≤ q ≤ 0.39) (B) from the steady-state structure factors for the DPE-2 and DWB models, respectively. These choices are made to quantify comparative kinetics on equivalent lengthscales. Accordingly, we note that stable entanglements arrest the ability to form large linear aggregates, as evidenced by the inability of the DPE-2 system to achieve a slope of –1.8 on lengthscales corresponding to the steady-state low-q regime for the DWB system (B). To see this figure in color, go online.
Fig. 4, A–D, shows the temporal evolution of S(q) for particles interacting via the DPE-1, DPE-2 DNB, and DWB potentials, respectively. These are shown as log-log plots. For each model, we analyzed the long-time steady-state structure factors to uncover the model-specific high-q and low-q regions that yield slopes of ∼–4 and ∼–1.8, respectively (Fig. 4). The steady-state structure factors were also analyzed to extract the crossover lengthscale between the two regimes. The resultant values for qc are 0.71 ± 0.01, 0.90 ± 0.01, 0.67 ± 0.01, and 0.59 ± 0.02 for the DPE-1, DPE-2, DNB, and DWB systems, respectively. These values show a shift toward higher q values for DPE-1 and DPE-2 vis-à-vis DNB and DWB. Therefore, the steady-state aggregates are smaller in the presence of entanglements and are largest when entanglements are quenched and there is a barrier to interparticle association.
Having identified the high-q and low-q regimes that yield distinct slopes for each steady-state structure factor, we quantify the evolution of the slopes in these regimes as a function of time for each of the models (Fig. 5, A–D). The regimes within which these slope evolutions are calculated are different for each model because of the different qc values (see summary in Table S1). As noted in Materials and Methods, we use reduced units for time by calibrating the simulation time against the average time it takes for a single particle to traverse a distance Rg via translational diffusion. For the DPE-1 model, the energetic equivalence between different entangled states leads to slightly aspherical aggregates as steady-state species in the high-q regime—note the convergence toward a slope of –3.73 as opposed to –4. The timescales for converging on steady-state slopes corresponding to the high-q and low-q regimes are an order of magnitude different from each other for DPE-1, and this is true for DPE-2 as well. Inasmuch as either model mimics the behavior of polyQ sans the N17 module, the results show qualitative agreement with expectations based on in vitro experiments, because distinct types of aggregates form on distinct timescales. Clearly, interchain entanglements engender a separation of timescales, and this separation is more pronounced for the DPE-2 model.
The results for DPE-1 and DPE-2 are to be contrasted with results from equivalent analyses for the DNB and DWB models (Figure 4, Figure 5, C and D, respectively). The DNB and DWB systems mimic the ability of N17 to reduce interchain entanglements. Fig. 5 C shows that the temporal gap between the formation of early spherical clusters and the cluster-cluster associations that lead to structures that yield the q–1.8 scaling behavior is narrowed considerably in the absence of entanglements. Thus, the formation of spherical clusters and large aspherical/linear aggregates is temporally synchronized in congruence with the observations of Fig. 1. In the DWB system, entanglements are quenched, this leads to overall synchrony between the aggregation timescales across the two distinct lengthscales. However, the presence of a barrier to interparticle interactions slows down the overall timescales for aggregation compared to that of the DNB system. Further, the smaller aggregates are relatively aspherical, as evidenced by the slope of –3.5 as opposed to –4 for the steady-state value of the slope in the high-q regime. Therefore, the DWB system that incorporates both effects of N17 from atomistic simulations leads to overall aggregation kinetics that agrees with in vitro observations.
Based on the preceding analysis, we take the DPE-2 and DWB models as the optimal approximations for the aggregation mechanisms of Qn versus N17-Qn molecules, respectively. In Fig. 6, we show comparative kinetics for the evolution of the slopes corresponding to the high-q and low-q regimes extracted from the steady-state structure factors for DPE-2 and DWB, respectively. The presence of N17 should reduce the frequency of intermolecular associations and hence slow down the kinetics of early aggregation. This behavior was observed when comparing the rates of loss of TMR fluorescence with and without the N17 module (Fig. 1, A and B, respectively), and it is reproduced in the coarse-grained model (Fig. 6 A). This plot compares the rate of convergence to the steady-state value for the slope in the high-q regime for DPE-2 and DWB. In accordance with the experimental data, Fig. 6 A shows that the presence of a barrier slows the early stages of aggregation such that the lack of entanglement is sufficient to synchronize the timescales for aggregation on small and large scales, whereas the presence of entanglements leads to significant slow-down in the growth of larger, linear aggregates (see Fig. 6 B and Fig. 5, A–D). Fig. S6 shows a plot of the rate of loss of monomers into aggregates for each of the four models, and Fig. S7 shows plots equivalent to those in Fig. 6 for all four models. These plots support the overall conclusions summarized above.
Fig. 7 shows representative snapshots for the DPE-2 and DWB models drawn from the steady-state ensembles. Fig. S8 shows an equivalent plot for all four models. The aggregates are colored based on the number of particles within each aggregate. This provides a visual depiction of the prevalence of numerous small, mostly spherical aggregates for the DPE-2 system. This highlights how interchain entanglements suppress growth into large aspherical aggregates. Conversely, for the DWB system, the snapshots reveal a variety of large aspherical aggregates and few small spherical aggregates. Indeed, for the DWB system, even the small aggregates are mildly aspherical and this shows that the reduction of entanglements promotes the formation of large aspherical aggregates through enhanced cluster-cluster associations.
Figure 7.
Representative snapshots of the steady-state aggregates that result from the simulations based on DPE-2 and DWB (left and right, respectively). Molecules in the snapshots are colored according to the size of the corresponding aggregates, i.e., the number of molecules, n, within the aggregate to which they belong. The scheme is as follows: black, n ≤ 10; blue, 10 < n ≤ 50; green, 50 < n ≤ 100; red, 100 < n ≤ 400; purple, n > 400. The snapshots were generated using the Visual Molecular Dynamics package (67).
Discussion
We have introduced a phenomenological coarse-grained model designed to connect the observations from the small lengthscales accessible to atomistic simulations to those from considerably larger lengthscales in in vitro experiments. The structure factors provide a concise and complete analysis of the structures that form on all lengthscales and have the advantage of enabling direct connections to multiangle dynamic light-scattering experiments (5, 9, 14, 68, 69, 70).
Results from the coarse-grained BD simulations demonstrate that small spherical clusters and large aspherical aggregates form on distinct timescales for particles interacting via the DPE potentials. Further, the overall aggregate sizes, characterized by the crossover lengthscale are smallest for the DPE-2 system. In contrast, eliminating entanglements (DNB) synchronizes the timescales for forming small/spherical aggregates and large aspherical/linear aggregates, whereas the introduction of a docking barrier in the DWB system slows the overall aggregation kinetics while further destabilizing small spherical aggregates. It appears that the observations regarding the incipient interactions between pairs of molecules can be used to extract insights regarding the coarse-grained morphologies and dynamics that develop on larger lengthscales.
Explanations for the coarse-grained simulation results
In diffusion-limited cluster aggregation, which is captured by the DNB system, the spherical clusters do not grow isotropically, because the arrival times of the monomers and clusters at the growing front are faster than the rearrangement times required to achieve a macroscopic spherical aggregate. Conversely, thermal fluctuations set up deformations on the surfaces of spherical clusters, and the size scale of these deformations can be commensurate with the sizes of the spherical clusters (56). The deformations are akin to instabilities, and these grow through diffusion-limited cluster aggregation, which gives rise to open, aspherical structures that generate a distribution of voids around them, thus making these aggregates fundamentally different from densely packed, spherical macroscopic aggregates.
We find that entanglements destabilize the growth into large, aspherical structures. The result is a distribution of spherical aggregates that coexist with shorter aspherical aggregates and this seems to be consistent with the recent electron microscopy data of Crick et al. for peptides that approximate homopolymeric polyQ. In addition, the quantum yield for ThT fluorescence is an order of magnitude smaller for Q30-K2 vis-à-vis N17-Q30-K2 and is suggestive of smaller, less fibrillar species forming for homopolymeric polyQ.
Entanglements are the result of the homopolymeric nature of polyQ and reflect the intrinsic conformational heterogeneity and degeneracy of interchain interaction possibilities through polyQ domains. The presence of entanglements offsets the deformation of spherical clusters, because the particles have an additional lengthscale to explore. Therefore, unlike the DNB and DWB systems, where rearrangements within spherical clusters are quenched by design, the presence of entanglements allows for rearrangements, thus arresting the molecules within long-lived spherical aggregates. In the DPE-2 case, these cannot grow into macroscopic sizes because the entangled and docked states are equivalent in energy for a pair of particles. This leads to energetic frustration and local intracluster rearrangement, which can interfere with cluster-cluster associations.
Connecting the results to polyQ biology
Experiments highlight the importance of heterogeneous distributions of small, spherical, and diffuse aggregates for polyQ toxicity in living cells and model organisms (71, 72). In direct contrast, large, well-ordered aggregates are thought to protect cells against polyQ toxicity. Within the framework of our model, it would appear that enhanced interchain entanglements that derive from the absence of flanking sequence modules or increased polyQ length could give rise to a long-lived distribution of smaller, spherical aggregates that contribute to cellular toxicity. Inasmuch as this is a prediction, it should be possible to design sequences that modulate the degree of entanglement and assess the effects of this modulation on in vitro aggregation as well as cellular toxicities.
Making the models transferrable and development of multiresolution models
The models introduced here are purely phenomenological as opposed to being transferrable. It should be possible to design transferrable potentials based on quantitative statistics extracted from atomistic simulations of varying polyQ lengths and different sequence contexts, such as amphipathic-flanking sequences from other polyQ-disease-related proteins. We expect that the overall energy scale for aggregation will be governed by the decrease in saturation concentrations with increased polyQ length (12). Further, we expect that the precise nature of the entangled state, i.e., whether it is featureless or whether it allows for one or more minima, will be governed by the nature of the interface between the flanking sequence and the polyQ globule. It is worth emphasizing that the framework developed here applies only for flanking sequences and polyQ lengths where the overall density is akin to that of polyQ globules. Accordingly, the modeling of molecules as spherical particles will not apply for constructs with the C38 module, because this semiflexible, proline-rich region behaves differently from N17 in atomistic simulations (K. Ruff and R. Pappu, unpublished).
The ultra-coarse-graining method has limitations in that it lacks the necessary internal structure to enable the distinction between fractal-like structures and fibrillar, β-sheeted aggregates or other amorphous higher-order aggregates. Systematic coarse-graining methods that interpolate between the atomistic simulations and the ultra-coarse-grained description used here might provide an attractive multiscale, renormalizable description of aggregation and phase-ordering processes.
Acknowledgments
We are grateful to Dr. Scott Crick for helpful discussions and for the use of his data for Fig. 1. We thank the anonymous reviewers for their constructive criticisms and comments.
This work was supported by grant 5R01NS056114 from the National Institutes of Health.
Editor: Michael Feig.
Footnotes
Kiersten Ruff and Siddique Khan contributed equally to this work.
Eight figures and one table are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(14)00737-1.
Supporting Material
References
- 1.Walker F.O. Huntington’s disease. Semin. Neurol. 2007;27:143–150. doi: 10.1055/s-2007-971176. [DOI] [PubMed] [Google Scholar]
- 2.Becher M.W., Kotzuk J.A., Ross C.A. Intranuclear neuronal inclusions in Huntington’s disease and dentatorubral and pallidoluysian atrophy: correlation between the density of inclusions and IT15 CAG triplet repeat length. Neurobiol. Dis. 1998;4:387–397. doi: 10.1006/nbdi.1998.0168. [DOI] [PubMed] [Google Scholar]
- 3.Landles C., Sathasivam K., Bates G.P. Proteolysis of mutant huntingtin produces an exon 1 fragment that accumulates as an aggregated protein in neuronal nuclei in Huntington disease. J. Biol. Chem. 2010;285:8808–8823. doi: 10.1074/jbc.M109.075028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sathasivam K., Neueder A., Bates G.P. Aberrant splicing of HTT generates the pathogenic exon 1 protein in Huntington disease. Proc. Natl. Acad. Sci. USA. 2013;110:2366–2370. doi: 10.1073/pnas.1221891110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chen S., Berthelier V., Wetzel R. Polyglutamine aggregation behavior in vitro supports a recruitment mechanism of cytotoxicity. J. Mol. Biol. 2001;311:173–182. doi: 10.1006/jmbi.2001.4850. [DOI] [PubMed] [Google Scholar]
- 6.Crick S.L., Jayaraman M., Pappu R.V. Fluorescence correlation spectroscopy shows that monomeric polyglutamine molecules form collapsed structures in aqueous solutions. Proc. Natl. Acad. Sci. USA. 2006;103:16764–16769. doi: 10.1073/pnas.0608175103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Vitalis A., Wang X., Pappu R.V. Atomistic simulations of the effects of polyglutamine chain length and solvent quality on conformational equilibria and spontaneous homodimerization. J. Mol. Biol. 2008;384:279–297. doi: 10.1016/j.jmb.2008.09.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Vitalis A., Lyle N., Pappu R.V. Thermodynamics of β-sheet formation in polyglutamine. Biophys. J. 2009;97:303–311. doi: 10.1016/j.bpj.2009.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Walters R.H., Murphy R.M. Examining polyglutamine peptide length: a connection between collapsed conformations and increased aggregation. J. Mol. Biol. 2009;393:978–992. doi: 10.1016/j.jmb.2009.08.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Thakur A.K., Wetzel R. Mutational analysis of the structural organization of polyglutamine aggregates. Proc. Natl. Acad. Sci. USA. 2002;99:17014–17019. doi: 10.1073/pnas.252523899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Caron N.S., Desmond C.R., Truant R. Polyglutamine domain flexibility mediates the proximity between flanking sequences in huntingtin. Proc. Natl. Acad. Sci. USA. 2013;110:14610–14615. doi: 10.1073/pnas.1301342110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Crick S.L., Ruff K.M., Pappu R.V. Unmasking the roles of N- and C-terminal flanking sequences from exon 1 of huntingtin as modulators of polyglutamine aggregation. Proc. Natl. Acad. Sci. USA. 2013;110:20075–20080. doi: 10.1073/pnas.1320626110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chen S., Wetzel R. Solubilization and disaggregation of polyglutamine peptides. Protein Sci. 2001;10:887–891. doi: 10.1110/ps.42301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chen S., Ferrone F.A., Wetzel R. Huntington’s disease age-of-onset linked to polyglutamine aggregation nucleation. Proc. Natl. Acad. Sci. USA. 2002;99:11884–11889. doi: 10.1073/pnas.182276099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bhattacharyya A.M., Thakur A.K., Wetzel R. polyglutamine aggregation nucleation: thermodynamics of a highly unfavorable protein folding reaction. Proc. Natl. Acad. Sci. USA. 2005;102:15400–15405. doi: 10.1073/pnas.0501651102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bhattacharyya A., Thakur A.K., Wetzel R. Oligoproline effects on polyglutamine conformation and aggregation. J. Mol. Biol. 2006;355:524–535. doi: 10.1016/j.jmb.2005.10.053. [DOI] [PubMed] [Google Scholar]
- 17.Wetzel R. Kinetics and thermodynamics of amyloid fibril assembly. Acc. Chem. Res. 2006;39:671–679. doi: 10.1021/ar050069h. [DOI] [PubMed] [Google Scholar]
- 18.Thakur A.K., Jayaraman M., Wetzel R. Polyglutamine disruption of the huntingtin exon 1 N terminus triggers a complex aggregation mechanism. Nat. Struct. Mol. Biol. 2009;16:380–389. doi: 10.1038/nsmb.1570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Jayaraman M., Thakur A.K., Wetzel R. Assays for studying nucleated aggregation of polyglutamine proteins. Methods. 2011;53:246–254. doi: 10.1016/j.ymeth.2011.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kar K., Jayaraman M., Wetzel R. Critical nucleus size for disease-related polyglutamine aggregation is repeat-length dependent. Nat. Struct. Mol. Biol. 2011;18:328–336. doi: 10.1038/nsmb.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Jayaraman M., Kodali R., Wetzel R. Slow amyloid nucleation via α-helix-rich oligomeric intermediates in short polyglutamine-containing huntingtin fragments. J. Mol. Biol. 2012;415:881–899. doi: 10.1016/j.jmb.2011.12.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Jayaraman M., Mishra R., Wetzel R. Kinetically competing huntingtin aggregation pathways control amyloid polymorphism and properties. Biochemistry. 2012;51:2706–2716. doi: 10.1021/bi3000929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wetzel R. Physical chemistry of polyglutamine: intriguing tales of a monotonous sequence. J. Mol. Biol. 2012;421:466–490. doi: 10.1016/j.jmb.2012.01.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Walters R.H., Jacobson K.H., Murphy R.M. Elongation kinetics of polyglutamine peptide fibrils: a quartz crystal microbalance with dissipation study. J. Mol. Biol. 2012;421:329–347. doi: 10.1016/j.jmb.2012.03.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tam S., Spiess C., Frydman J. The chaperonin TRiC blocks a huntingtin sequence element that promotes the conformational switch to aggregation. Nat. Struct. Mol. Biol. 2009;16:1279–1285. doi: 10.1038/nsmb.1700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ignatova Z., Thakur A.K., Gierasch L.M. In-cell aggregation of a polyglutamine-containing chimera is a multistep process initiated by the flanking sequence. J. Biol. Chem. 2007;282:36736–36743. doi: 10.1074/jbc.M703682200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Caron N.S., Hung C.L., Truant R. Live cell imaging and biophotonic methods reveal two types of mutant huntingtin inclusions. Hum. Mol. Genet. 2014;23:2324–2338. doi: 10.1093/hmg/ddt625. [DOI] [PubMed] [Google Scholar]
- 28.Garai K., Frieden C. Quantitative analysis of the time course of Aβ oligomerization and subsequent growth steps using tetramethylrhodamine-labeled Aβ. Proc. Natl. Acad. Sci. USA. 2013;110:3321–3326. doi: 10.1073/pnas.1222478110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Williamson T.E., Vitalis A., Pappu R.V. Modulation of polyglutamine conformations and dimer formation by the N-terminus of huntingtin. J. Mol. Biol. 2010;396:1295–1309. doi: 10.1016/j.jmb.2009.12.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Vitalis A., Pappu R.V. ABSINTH: a new continuum solvation model for simulations of polypeptides in aqueous solutions. J. Comput. Chem. 2009;30:673–699. doi: 10.1002/jcc.21005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Radhakrishnan A., Vitalis A., Pappu R.V. Improved atomistic Monte Carlo simulations demonstrate that poly-L-proline adopts heterogeneous ensembles of conformations of semi-rigid segments interrupted by kinks. J. Phys. Chem. B. 2012;116:6862–6871. doi: 10.1021/jp212637r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Vitalis A., Pappu R.V. Methods for Monte Carlo simulations of biomacromolecules. Annu. Rep. Comput. Chem. 2009;5:49–76. doi: 10.1016/S1574-1400(09)00503-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Mao A.H., Crick S.L., Pappu R.V. Net charge per residue modulates conformational ensembles of intrinsically disordered proteins. Proc. Natl. Acad. Sci. USA. 2010;107:8183–8188. doi: 10.1073/pnas.0911107107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Vitalis A., Caflisch A. Micelle-like architecture of the monomer ensemble of Alzheimer’s amyloid-β peptide in aqueous solution and its implications for Aβ aggregation. J. Mol. Biol. 2010;403:148–165. doi: 10.1016/j.jmb.2010.08.003. [DOI] [PubMed] [Google Scholar]
- 35.Wuttke R., Hofmann H., Schuler B. Temperature-dependent solvation modulates the dimensions of disordered proteins. Proc. Natl. Acad. Sci. USA. 2014;111:5213–5218. doi: 10.1073/pnas.1313006111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Das R.K., Crick S.L., Pappu R.V. N-terminal segments modulate the α-helical propensities of the intrinsically disordered basic regions of bZIP proteins. J. Mol. Biol. 2012;416:287–299. doi: 10.1016/j.jmb.2011.12.043. [DOI] [PubMed] [Google Scholar]
- 37.Das R.K., Pappu R.V. Conformations of intrinsically disordered proteins are influenced by linear sequence distributions of oppositely charged residues. Proc. Natl. Acad. Sci. USA. 2013;110:13392–13397. doi: 10.1073/pnas.1304749110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lyle N., Das R.K., Pappu R.V. A quantitative measure for protein conformational heterogeneity. J. Chem. Phys. 2013;139:121901–121912. doi: 10.1063/1.4812791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Mittal A., Lyle N., Pappu R.V. Hamiltonian Switch Metropolis Monte Carlo simulations for improved conformational sampling of intrinsically disordered regions tethered to ordered domains of proteins. J. Chem. Theory Comput. 2014 doi: 10.1021/ct5002297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Meng W., Lyle N., Pappu R.V. Experiments and simulations show how long-range contacts can form in expanded unfolded proteins with negligible secondary structure. Proc. Natl. Acad. Sci. USA. 2013;110:2123–2128. doi: 10.1073/pnas.1216979110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Halfmann R., Alberti S., Lindquist S. Opposing effects of glutamine and asparagine govern prion formation by intrinsically disordered proteins. Mol. Cell. 2011;43:72–84. doi: 10.1016/j.molcel.2011.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.England J.L., Kaganovich D. Polyglutamine shows a urea-like affinity for unfolded cytosolic protein. FEBS Lett. 2011;585:381–384. doi: 10.1016/j.febslet.2010.12.023. [DOI] [PubMed] [Google Scholar]
- 43.Sacanna S., Pine D.J., Yi G.R. Engineering shape: the novel geometries of colloidal self-assembly. Soft Matter. 2013;9:8096–8106. [Google Scholar]
- 44.Sciortino F., Zaccarelli E. Reversible gels of patchy particles. Curr. Opin. Solid State Mater. Sci. 2011;15:246–253. [Google Scholar]
- 45.Semenov A.N. Dynamic correlation-function of polymer density-fluctuations in concentrated solutions. Physica A. 1990;166:263–287. [Google Scholar]
- 46.Raos G., Allegra G. A cluster of chains can be smaller than a single chain: new interpretation of kinetics of collapse experiments. Macromolecules. 1996;29:8565–8567. [Google Scholar]
- 47.Raos G., Allegra G. Macromolecular clusters in poor-solvent polymer solutions. J. Chem. Phys. 1997;107:6479–6490. [Google Scholar]
- 48.Pappu R.V., Wang X., Crick S.L. A polymer physics perspective on driving forces and mechanisms for protein aggregation. Arch. Biochem. Biophys. 2008;469:132–141. doi: 10.1016/j.abb.2007.08.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Wang Y., Voth G.A. Molecular dynamics simulations of polyglutamine aggregation using solvent-free multiscale coarse-grained models. J. Phys. Chem. B. 2010;114:8735–8743. doi: 10.1021/jp1007768. [DOI] [PubMed] [Google Scholar]
- 50.Marchut A.J., Hall C.K. Side-chain interactions determine amyloid formation by model polyglutamine peptides in molecular dynamics simulations. Biophys. J. 2006;90:4574–4584. doi: 10.1529/biophysj.105.079269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Marchut A.J., Hall C.K. Effects of chain length on the aggregation of model polyglutamine peptides: molecular dynamics simulations. Proteins. 2007;66:96–109. doi: 10.1002/prot.21132. [DOI] [PubMed] [Google Scholar]
- 52.Dama J.F., Sinitskiy A.V., Voth G.A. The theory of ultra-coarse-graining. 1. General principles. J. Chem. Theory Comput. 2013;9:2466–2480. doi: 10.1021/ct4000444. [DOI] [PubMed] [Google Scholar]
- 53.Witten T.A., Sander L.M. Diffusion-limited aggregation, a kinetic critical phenomenon. Phys. Rev. Lett. 1981;47:1400–1403. [Google Scholar]
- 54.Meakin P., Witten T.A. Growing interface in diffusion-limited aggregation. Phys. Rev. A. 1983;28:2985–2989. [Google Scholar]
- 55.Witten T.A., Sander L.M. Diffusion-limited aggregation. Phys. Rev. B. 1983;27:5686–5697. [Google Scholar]
- 56.Sander L.M. Diffusion-limited aggregation: a kinetic critical phenomenon? Contemp. Phys. 2000;41:203–218. [Google Scholar]
- 57.Lapidus L.J. Understanding protein aggregation from the view of monomer dynamics. Mol. Biosyst. 2013;9:29–35. doi: 10.1039/c2mb25334h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Meakin P. Diffusion-limited aggregation in 3 dimensions: results from a new cluster cluster aggregation model. J. Colloid Interface Sci. 1984;102:491–504. [Google Scholar]
- 59.Meakin P., Majid I., Stanley H.E. Topological properties of diffusion limited aggregation and cluster cluster aggregation. J. Phys. A. 1984;17:L975–L981. [Google Scholar]
- 60.Meakin P. Structure of the active zone in diffusion-limited aggregation, cluster-cluster aggregation, and the screened-growth model. Phys. Rev. A. 1985;32:453–459. doi: 10.1103/physreva.32.453. [DOI] [PubMed] [Google Scholar]
- 61.Meakin P. Computer simulations of diffusion-limited aggregation processes. Faraday Discuss. Chem. Soc. 1987;83:113–124. [Google Scholar]
- 62.Honda K., Toyoki H., Matsushita M. A theory of fractal dimensionality for generalized diffusion-limited aggregation. J. Phys. Soc. Jpn. 1986;55:707–710. [Google Scholar]
- 63.Puertas A.M., Fernández-Barbero A., de Las Nieves F.J. Structure factor scaling in colloidal charge heteroaggregation. Eur. Phys. J. E Soft Matter. 2005;18:335–341. doi: 10.1140/epje/e2005-00036-7. [DOI] [PubMed] [Google Scholar]
- 64.Sandkühler P., Lattuada M., Morbidelli M. Further insights into the universality of colloidal aggregation. Adv. Colloid Interface Sci. 2005;113:65–83. doi: 10.1016/j.cis.2004.12.001. [DOI] [PubMed] [Google Scholar]
- 65.Porod G. Theory of the diffuse small angle x-ray scattering in colloidal systems. Z. Naturforsch. A. 1949;4:401–414. [Google Scholar]
- 66.Lin M.Y., Lindsay H.M., Meakin P. Universality in colloid aggregation. Nature. 1989;339:360–362. [Google Scholar]
- 67.Humphrey W., Dalke A., Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. 27–28. [DOI] [PubMed] [Google Scholar]
- 68.Lee C.C., Walters R.H., Murphy R.M. Reconsidering the mechanism of polyglutamine peptide aggregation. Biochemistry. 2007;46:12810–12820. doi: 10.1021/bi700806c. [DOI] [PubMed] [Google Scholar]
- 69.Smith M.I., Sharp J.S., Roberts C.J. Insulin fibril nucleation: the role of prefibrillar aggregates. Biophys. J. 2008;95:3400–3406. doi: 10.1529/biophysj.108.131482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Weiss W.F., 4th, Hodgdon T.K., Roberts C.J. Nonnative protein polymers: structure, morphology, and relation to nucleation and growth. Biophys. J. 2007;93:4392–4403. doi: 10.1529/biophysj.107.112102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Beam M., Silva M.C., Morimoto R.I. Dynamic imaging by fluorescence correlation spectroscopy identifies diverse populations of polyglutamine oligomers formed in vivo. J. Biol. Chem. 2012;287:26136–26145. doi: 10.1074/jbc.M112.362764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Arrasate M., Finkbeiner S. Protein aggregates in Huntington’s disease. Exp. Neurol. 2012;238:1–11. doi: 10.1016/j.expneurol.2011.12.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.