Abstract
We have previously introduced tethered fluorophore motion (TFM), a single-molecule fluorescence technique that monitors the effective length of a biopolymer such as DNA. TFM uses the same principles as tethered particle motion (TPM) but employs a single fluorophore in place of the bead, allowing TFM to be combined with existing fluorescence techniques on a standard fluorescence microscope. TFM has been previously been used to reveal the mechanism of two site-specific recombinase systems, Cre-loxP and XerCD-dif. In this work, we characterize TFM, focusing on the theoretical basis and potential applications of the technique. Since TFM is limited in observation time and photon count by photobleaching, we present a description of the sources of noise in TFM. Comparing this with Monte Carlo simulations and experimental data, we show that length changes of 100 bp of double-stranded DNA are readily distinguishable using TFM, making it comparable with TPM. We also show that the commonly recommended pixel size for single-molecule fluorescence approximately optimizes signal to noise for TFM experiments, thus enabling facile combination of TFM with other fluorescence techniques, such as Förster resonance energy transfer (FRET). Finally, we apply TFM to determine the polymerization rate of the Klenow fragment of DNA polymerase I, and we demonstrate its combination with FRET to observe synapsis formation by Cre using excitation by a single laser. We hope that TFM will be a useful addition to the single-molecule toolkit, providing excellent insight into protein-nucleic acid interactions.
Introduction
Single-molecule methods have enabled researchers to study biological processes free from the constraints of ensemble averaging (1). Along with this, combination methods have recently begun to allow single-molecule techniques to capture a wider range of information (2, 3). One single-molecule method is tethered particle motion (TPM). It is used for observing large-scale conformational changes in polymers, typically DNA. TPM experiments usually observe a long (> 400 bp) DNA molecule tethered to a surface with a bead (20 to 500 nm in diam.) attached to the surface-distal end of the DNA (4). By monitoring the Brownian motion of the bead, the apparent length of the DNA can be inferred (5). TPM has been used to study a variety of protein-DNA interactions including: lac repressor induced looping (6), transcription (4), restriction enzymes (7), and fundamental aspects of polymer dynamics governing DNA (8, 9).
Although reductions in bead size have enabled TPM measurements with a precision as low as 40 bp (10), TPM still has limitations. Beads introduce an entropic stretching force, which alters the probability distribution of bead excursions (11); beads also introduce a hydrodynamic drag, which systematically reduces enzymatic rates under investigation (12). More practically, the bead represents another surface that needs passivation and can attach to multiple DNA molecules simultaneously.
To combine TPM with single-molecule fluorescence techniques, we have recently introduced tethered fluorophore motion (TFM) (13). TFM replaces beads with single organic fluorophores, which are much smaller (e.g., Cy5, a commonly used fluorophore, has a backbone length of 1 nm (14)), thus minimizing entropic stretching and hydrodynamic drag. Attachment is achieved using a range of covalent chemistries that reliably attach one DNA per fluorophore. A distinguishing feature of TFM is that the fluorophore can be utilized for other fluorescence techniques simultaneously, such as Förster resonance energy transfer (FRET), allowing multiple length scales to be monitored simultaneously.
FRET, the nonradiative transfer of energy from donor to acceptor fluorophores, is sensitive to subnanometer distance changes in the 1 to 10 nm range and is used in the study of protein-nucleic acid interactions (15, 16). Because small-scale rearrangements of protein complexes can mediate larger-scale conformational changes, the straightforward combination of TFM and FRET should allow studies of such systems in increased detail (17). TFM and FRET can be combined on the simplest of FRET microscopes, using a single excitation laser, with the FRET donor as the TFM reporter.
Unlike TPM, because TFM relies on a single fluorophore to report on DNA conformation, TFM has a finite photon budget before photobleaching. Higher laser powers can be used to increase the photon detection rate and thus give more accurate measures of the DNA conformation; however, intense excitation causes the fluorophore to bleach, shortening the total observation time. We build on previous work (18, 19, 20) to derive an expression for the uncertainty in the width of a single fluorophore image (the main TFM observable). Using our uncertainty expression, we compare our model of the measurement noise with our experimental results and Monte Carlo simulations. We characterize the TFM observable of image width using worm-like chain (WLC) simulations of DNA, and use TFM to recover the persistence length of DNA under our conditions. Finally, we apply TFM to DNA polymerization by the Klenow fragment (KF) of DNA polymerase I (21), and synaptic complex formation by a site-specific recombinase, Cre (22). Experiments with Cre combine TFM and FRET, using a single excitation laser, to simultaneously measure large-scale DNA conformations and nanometer distances within nucleoprotein complexes.
Materials and Methods
DNA and protein preparation
Long DNA substrates were prepared by polymerase chain reaction (PCR) with one fluorophore labeled, one biotin, or biotin and fluorophore, labeled oligonucleotide primer, and a plasmid template, using a Phusion High-Fidelity DNA polymerase (NEB, Ipswich, MA). DNA sequences of the primers are shown (Fig. S1 in the Supporting Material). Oligonucleotides were synthesized, labeled and high performance liquid chromatography (HPLC) purified by ATDBio (Southampton, UK). Following PCR reactions, the product was gel-purified.
Cyanine dyes were chosen for their brightness and photostability (15), with Cy5 used for all singly labeled constructs because its emission was in a relatively background (from dirt or auto-fluorescence from optics) free spectral region.
KF was expressed and purified using standard methods (23). Our KF DNA substrate (Fig. S1 B) was produced using PCR, with a 20-fold excess of the labeled strand to produce an excess of single-stranded DNA (ssDNA), followed by binding of streptavidin (1 mg/ml) and gel purification. The gel was run after binding of streptavidin to retard double-stranded DNA (dsDNA). Single-stranded DNA, unaffected by streptavidin, was purified from the gel fragment. Fresh biotinylated oligonucleotides were then annealed to produce the final substrate (Fig. S2).
A mutant of Cre, A36V, previously shown to give stable synapses without complete recombination, was expressed and purified using standard methods (13). The Cre DNA substrate was 1000 bp long, with two antiparallel loxP sites. The surface proximal loxP site was labeled with Cy5, and the surface distal site was labeled with Cy3B (Fig. S1 C). Cy3B was chosen because its large spectral separation from Cy5 allowed separation of the two emission channels with little cross talk.
Instrumentation
Single-molecule total internal reflection fluorescence (TIRF) experiments were performed on a custom-built objective-type TIRF microscope. A green (532 nm Cobolt Samba, Cobalt, Solna, Sweden) and red (635 nm CUBE, Coherent, Santa Clara, CA) laser were combined using a dichroic mirror and coupled into a fiber optic cable. The output of the fiber was focused into the back focal plane of the objective (100× oil-immersion, NA 1.4, f/26.5, UPlanSApo, Olympus, Tokyo, Japan) and displaced perpendicular to the optical axis such that laser light was incident at the slide-solution interface at greater than the critical angle, creating an evanescent excitation field. Unless stated otherwise, illumination powers were set to 1 mW, which corresponds to an approximate power density of 0.4 μW/μm2 incident on the 50 × 50 μm field of view. Fluorescence emission was collected by the objective and separated from the excitation light by a dichroic (545 nm/650 nm, Semrock, Rochester, NY) and cleanup filters (545 nm LP, Chroma, Bellows Falls, VT; and 633/25 nm notch filter, Semrock). Emission signal was focused on a rectangular slit to crop the image and then spectrally separated, using a dichroic (630 nm DRLP, Omega, Brattleboro, VT), into two emission channels that were focused side by side onto an electron multiplying charge coupled device (EMCCD) camera (iXon 897, Andor, Belfast, UK). The EMCDD was set to an EM gain of 300, corresponding to an approximate real gain of 3.75 counts per photon. Each pixel on the EMCCD corresponded to a 96 × 96 nm region in the imaging plane. A CRIFF (ASI, Eugene, OR) autofocus system was used throughout the work to ensure focus stability over the course of data acquisition.
Data analysis
Extraction of fluorescence intensity signals from microscope images was performed using previously described twoTone software (24). An apparent FRET efficiency, , was calculated from the extracted fluorescence emission as follows:
| (1) |
where is the fluorescence emission from the acceptor under donor excitation and is the emission from the donor. The acceptor fluorophore image width (FIW) was obtained from the mean width of the fitted elliptical Gaussian.
DNA simulations
Discrete WLC simulations were performed according to the scheme originally implemented by Hagerman and Zimm (25) and applied in the specific case of TPM by others (5, 11). DNA molecules are modeled as being composed of discrete rigid segments, each of length = 3.4 nm. Under the assumption that twisting energy and interactions between distant sections of the DNA can be ignored, the flexibility of the DNA chain is described by the energy cost associated with bending. To simulate a single conformation of the DNA chain, we sequentially assign orientations to each segment in the chain relative to the previous one, defined by the axial and azimuthal bend angles and . Assuming no preferred bending axis, we can choose values for from a uniform distribution between 0 and 2π, and choose from the following distribution:
| (2) |
where is a normalization constant and is the persistence length (25). To validate this model, we generated many chain conformations and calculated the mean end-to-end distance, and observe good agreement between our simulations and the known analytical expression for the WLC.
For simulations of DNAs tethered to a surface, we discard any chain that crosses the plane, which corresponds to the slide surface. We consider the first linkage, of the DNA to the surface, to be completely free; we also do not take into account steric clashes of the chain with itself (Fig. S3 A).
We computed many (>106) fluorophore positions from independent DNA chain simulations to adequately sample from the space of accessible DNA conformations (Fig. S3 B). We then used the probability distributions of the fluorophore position in the sample volume to calculate the expected FIW observed on the camera as described in the next section.
We fit the persistence length, P, to experimental data by computing the mean square difference between predicted and observed FIWs over a range of P, obtaining an optimum value of P = 48 nm (Fig. S3 C). Although the simulations do not consider electrostatic interactions, steric clashes of the DNA with itself (excluded-volume effects) or defocusing, this value agrees with experimentally measured values under similar conditions (Table VIII in Lu et al., P = 35 – 55 nm) (26).
Camera simulations
The probability distributions described in the previous section were used in Monte Carlo simulations of EMCCD images, which included the effects of finite pixel size, shot noise, electron multiplying gain, and background noise. The response function of our microscope was generated using a method written in Python (python.org) by Kim Mortensen (19), assuming left-hand circularly polarized light incident at the maximum angle of incidence allowed by our objective NA (1.4). The response function was convolved with the fluorophore position probability distributions, weighted by the evanescent excitation profile of the TIRF illumination, to produce a theoretical image. We chose the image of a subdiffraction fluorescent bead as our theoretical response function, because the fluorescence anisotropy of our substrates, measured using a fluorimeter (Photon Technologies International, Edison, NJ), was near the limiting value of 0.4, e.g., the 1000 bp internally labeled substrate had an anisotropy of 0.35. This suggests that the fluorophore is approximately stationary during its emission lifetime, but free to be in any orientation over the course of a camera frame (100 to 500 ms). We found that the width of the image of a single fluorophore (defined as the width parameter of a fitted Gaussian) attached to a very short DNA was 150 nm rather than the 126 nm predicted using the work of Mortensen et al. (19) We attribute this to imperfections in our optics and alignment, combined with the effect of biotin-neutravidin and PEG linker lengths, and accounted for this additional width by convolving our theoretical image with a Gaussian kernel chosen to match the experimental image width. The properties of our camera (gain and read noise) were experimentally determined using the scheme described by Ulbrich et al. (27), choosing an empty region in a field of view at a given excitation intensity to determine our background count. The simulated images (> 104 per point plotted, using >100 different tether locations within a pixel), produced in MATLAB (The MathWorks, Natick, MA), were fit with a 2D-Gaussian using the same scheme as our data analysis software, twoTone (24).
Noise theory
To quantify the resolution of TFM, we derived an expression for the uncertainty in the fitted width of a Gaussian image. Previous work, which focused on using weighted least squares fitting, underestimated the noise by 57% (20). We consider ordinary least-squares (OLS) fitting because it is robust (24, 19), fast to implement, and commonly used ( e.g., as in the twoTone software used in our data analysis). We start by assuming that the image of the DNA is well approximated by a 2D-Gaussian with width characterized by its standard deviations and . Fitting is done by minimizing as follows:
| (3) |
with respect to the parameters being fit, where is the observed photon count at pixel and is the expected photon count at the same pixel for a fit image. Minimizing Eq. 3 with respect to obtains the following:
| (4) |
where . We can expand to first order in , the deviation from the true standard deviation of the image (i.e., the uncertainty in the fitted FIW), and define to obtain the following:
| (5) |
We can square Eq. 5 and average over to obtain the following:
| (6) |
where denotes the expectation value over many camera frames. Because the noise is uncorrelated between pixels, we can write , where is the photon count variance because of shot-noise, background, read noise, and electron multiplying gain, which gives the following:
| (7) |
with
| (8) |
where is the expected background photon count, is the standard deviation of the read-noise in digital units, and is the electron multiplying gain factor. The factor of 2 is approximately the square of the excess noise factor, which accounts for noise introduced by the electron multiplication process (24). For convenience, we can write , where captures the background and read noise. Equation 7 can be solved numerically, but we proceed analytically by approximating the sums in Eq. 7 as integrals. Unlike with weighted least-squares fitting (20), we do not need to interpolate between the high photon count and high background limits. Using the following photon distribution:
| (9) |
where is the total number of photons detected on average per frame attributable to the molecule; the effect of evanescent illumination is included implicitly here, because a DNA of a different length, or one imaged with a different TIRF angle, will have a different photoemission rate. We can approximate using the following:
| (10) |
where the pixel size has been introduced to match if we integrated over a single pixel. Hence, we arrive at the following:
| (11) |
Equation 11 can be modified to include the uncertainty in the detection position of a particular photon because of pixelation (18, 20), giving the result in Eq. 12 (see Results and Discussion).
Single-molecule experiments
DNA (∼ 200 pM) was incubated for 1 min at the surface of a polyethylene glycol or bovine serum albumin passivated cover slip, attaching by biotin-neutravidin interactions, and sealed using a silicone gasket (Grace Bio-labs) and a second cover slip. Imaging was performed in a buffer (50 mM Tris-HCl pH 7.5, 50 mM NaCl, 5 mM MgCl2, 100 μg/ml BSA, and 1mM UV-treated Trolox). An enzymatic oxygen scavenging system consisting of 1 mg/ml glucose oxidase, 40 μg/ml catalase, and 1.4% (w/v) glucose was added before sealing the sample before image acquisition.
Klenow fragment experiments
Single-molecule experiments were performed as previously outlined, in a buffer (50 mM Tris pH 7.5, 10 mM MgCl2, 1 mM DTT, 10% glycerol, 100 μg/ml BSA, and 1mM UV-treated Trolox). We added KF (24 nM) and nucleotides (10 μM each) during data acquisition and did not seal the wells. Data was collected at 2 Hz, until no further polymerization could be observed or the majority of fluorophores had photobleached.
To estimate the FIW response in our DNA polymerization experiments, we simulated DNA molecules at various stages of polymerization, i.e., 1087 base long DNAs, with varying fractions of dsDNA (Fig. S4). We used our optimal fitted persistence length for dsDNA of 48 nm and a literature value of 2 nm for ssDNA (28), along with a reduced segment length of 0.34 nm for the discretization of the WLC.
Cre experiments
The 532 nm laser was used to excite the Cy3B donor fluorophore, whose FIW reported on the effective length of the DNA. Cre was added to immobilized DNA at a concentration of 20 nM, and movies were acquired with an acquisition rate of 10 Hz.
Hidden Markov Modeling (HMM) was used to automate the extraction of dwell times as described previously (29). The dwells corresponding to synaptic complex formation were used to extract the corresponding values and the first and last frames of dwells were discarded as unreliable measures of FRET.
Results and Discussion
Principle of TFM
Imaging a single immobile emitter onto a camera produces an image much larger than the emitting molecule, which arises because of the diffraction of light through the optical system. The shape of this image depends on the emission spectrum and the orientation of the fluorophore, as well as the numerical aperture and any aberrations present in the optics of the microscope. Typical single-molecule imaging experiments observe fluorophores attached to biomolecules immobilized to a slide surface using biotin-neutravidin (or similar) interactions; such fluorophores (despite their ability to rotate locally) are well approximated by immobile emitters, and thus their observed image width corresponds to the diffraction limit. However, when the fluorophore is not immobilized (on scales > 10 nm), deviations can be observed in the width of the fluorophore image, which we term the FIW.
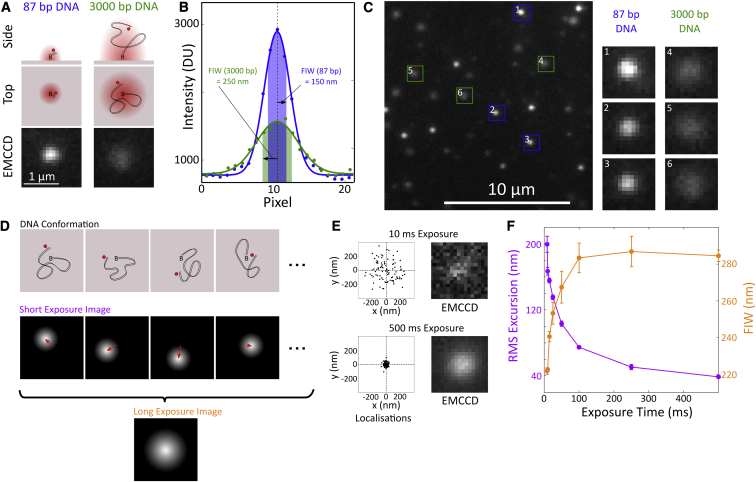
DNA strands typically used in single-molecule experiments (< 100 bp) have short end-to-end distances (< 35 nm) compared with their diffraction-limited images (∼ 150 nm FIW); hence, in the case of short DNAs (Fig. 1 A, left), we observe FIWs close to those of a diffraction-limited image. However, for DNAs with end-to-end distances longer than the FIW of a single immobile emitter (Fig. 1 A, right), diffusion of their free ends and attached fluorophores, about the tether point, increases the FIW significantly (Fig. 1 B and C).
Figure 1.
Principle of TFM. (A) Cartoon and images of single emitters. A Cy5 fluorophore, shown as a red circle was attached to DNA and tethered to a cover slip using a biotin-neutravidin interaction. An 87 bp DNA results in a diffraction limited image (red in the cartoons); but a 3000 bp DNA allows the fluorophore to diffuse about the tether point during a frame, causing the image to appear broader. The bottom panels show EMCCD data. (B) Gaussian fits to the pixel intensity values, in digital camera units (DU), from cross-sections through the EMCCD data shown in (A) demonstrate the difference in FIW (highlighted region and arrow). (C) Example regions of interest corresponding to 87 and 3000 bp DNA are shown in the right panels. A section of our field of view: 87 bp DNA appear as bright, narrow spots; and 3000 bp DNA appear as dimmer, broader spots. (D) Cartoon of two different imaging schemes. Using short exposures, we see a diffraction-limited FIW and the DNA length is apparent as a mean excursion (red arrows). Using long exposures, the averaging is done during the camera acquisition and we see an increased FIW, fixed in the image plane. (E) Single-molecule localizations from sequential frames of a 100-frame movie of 3000 bp DNA, taken with 10 or 500 ms exposure times. Localizations (i.e., the position of the peak of the fitted Gaussian) are shown in black, and the mean of all localizations is indicated by the dashed lines. Representative images at the two exposure times are shown. The brightness of the images has been adjusted because the 500 ms exposure gives a much brighter image. (F) FIW and root mean square (RMS) excursion for 3000 bp DNAs at frame times from 8.5 to 500 ms. There is a decrease in FIW and increase in mean excursion as the frame time becomes comparable with the DNA relaxation time. Error bars are the standard error in mean from five molecules at each exposure time. Localization error is less than 10 nm in all cases.
The properties of the images of fluorophore attached to long DNAs will depend on the relative timescales of DNA motion and camera integration. If the DNA does not move appreciably during a single camera frame, individual snapshots of the fluorophore position will be observed, and a mean excursion can be computed (Fig. 1 D, middle and Fig. 1 E, top). However, if the integration time is much longer than the relaxation time of the DNA, the diffusive motion of the fluorophore will be apparent as an increased FIW (Fig. 1 D, bottom and Fig. 1 F) and an average of the fluorophore position will be observed (Fig. 1 E, bottom, and Fig. 1 F) (5). In this work, we focus on the latter case, because of signal-to-noise considerations for the long observation times desired in our experiments.
In addition to FIW changes, fluorophores attached to long DNAs examined using TIRF microscopy experience reduced average excitation intensity because the fluorophores are (on average) further away from the surface. As a result, they show reduced intensities compared with ones tightly tethered to the surface.
Differentiating DNA lengths
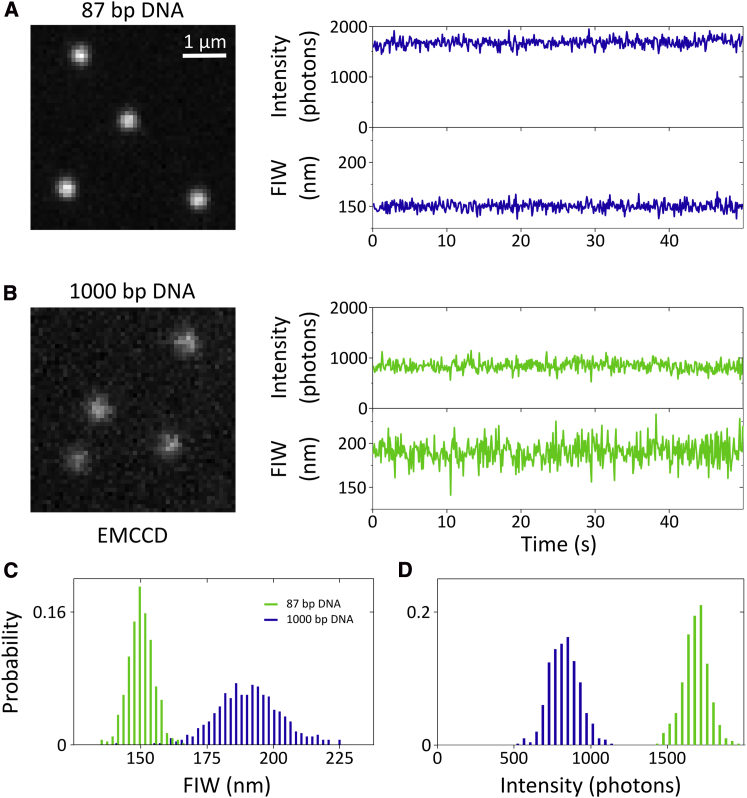
To quantify the changes in FIW and fluorescence intensity because of differences in the length of labeled DNA, we separately acquired movies of 87 and 1000 bp dsDNA molecules (Fig. 2). We observe many molecules in each field of view for 100 s movies (Fig. 2 A and B). Images from the camera clearly show differences in both the intensity and FIW, and time-traces for individual DNAs (Fig. 2 A and B, right) show mean FIWs of ∼ 150 nm and ∼ 190 nm for 87 and 1000 bp DNAs, respectively, indicating a broadening of ∼ 40 nm because of the motion of the longer DNA above the cover slip (Fig. 2 C). We see well-defined and reproducible FIWs over the course of repeated experiments (Fig. 3 A, error bars).
Figure 2.
Influence of DNA length. (A) Example camera image (left) of 87 bp DNA and timetrace (right) showing relatively high intensity, and narrow FIW. Data were taken with 1 mW illumination intensity and a 10 Hz frame rate. (B) Example camera image of 1000 bp DNA and timetrace showing lower intensity, and increased FIW. (C) Histogram of FIW showing the two populations are resolvable using FIW. (D) Histogram of intensities. The 87 and 1000 bp DNA are distinguishable by their intensities. To see this figure in color, go online.
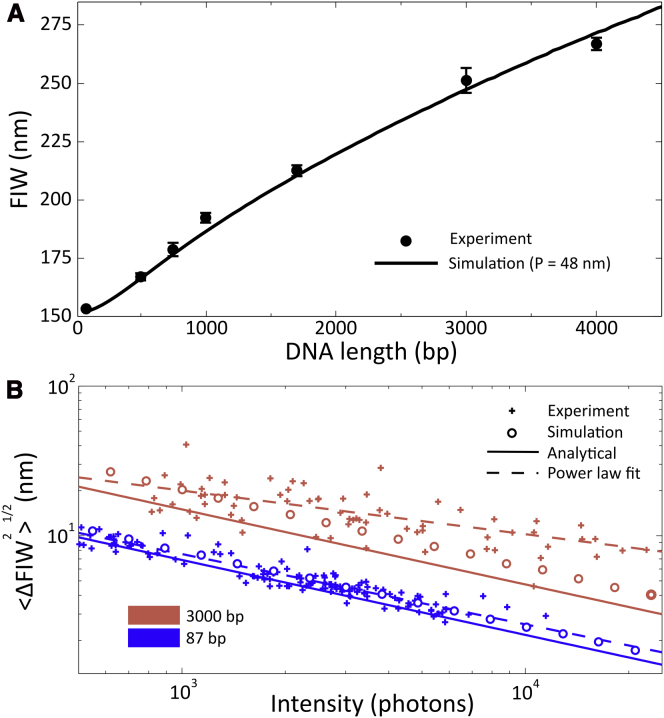
Figure 3.
Physical models of TFM. (A) Experimental measurements of the FIW for double stranded DNAs 87 to 4000 bp in backbone length. Data were acquired at 1 Hz, and error bars indicate the standard deviation of three independent measurements for each sample. The solid line is the best fit of persistence length to experimental data (P = 48 nm). We observe transient sticking of the DNA end to the surface in less than 1% of traces. (B) The resolution of TFM. Three methods were used to quantify the uncertainty in FIW for DNAs of 87 and 3000 bp. The experimentally determined uncertainties for individual molecules, from 100-frame movies recorded at 2 Hz with illumination powers in the range 1 to 50 mW, are shown as crosses. The intensity plotted is the photon count for a single molecule. Dashed lines are power-law fits as guides for the eye. Equation 12 was used to plot the analytical approximation (solid lines). A simulation, using the parameters of our microscope and the theoretical images of the DNA, generated as described in Materials and Methods, was used to produce the data shown as circles. We observe a good agreement between experiment, simulations, and our analytical expression, with the approximations made in deriving the analytical expression tending to underestimate the noise. For the 3000 bp DNA, deviations can be observed at intensities > 3000 photons, which we attribute to incomplete sampling of the conformations available to the DNA during a single camera frame. The background count in experiments was found to vary linearly with the observed photon count, with 5.3 × 10-3 background photons per recovered photon for the 87 bp DNA and 9.4 × 10-3 for the 3000 bp DNA; this was used in our simulations and in the plotting of the analytical approximation. To see this figure in color, go online.
We also observe differences in intensities between DNAs of different lengths, (Fig. 2 D). However, this intensity difference is sensitive to many factors, including the underlying intensity of the fluorophore, the excitation pattern across the field of view, and the TIRF angle. Hence, absolute intensity differences between molecules can arise separately to DNA length changes. Observations over time of individual molecules will not be subject to these factors, but the magnitude of observed intensity changes will still depend on the depth of the evanescent illumination field. In this work, we chose to concentrate on the FIW, which is not as sensitive to instrumental and alignment factors.
Noise in TFM
To calibrate the relation between FIW and DNA tether length, we measured the mean value of the FIW for DNAs with lengths between 87 and 4000 bp with surface-distal fluorophores, (Fig. S1 A). All lengths tested were clearly distinguishable on the basis of FIW, and the standard deviation from three independent measurements (of ∼ 10 molecules in separate fields-of-view) was consistently less than 10 nm (Fig. 3 A). The FIW responded approximately linearly to DNA length over the range of DNA lengths tested.
To ensure that our observed FIWs agree with a physical model of DNA, and to test our ability to predict TFM observables for future experiments, we performed discrete WLC simulations of our experimental system, similar to previous simulations of TPM experiments (5, 11). We obtained the static distributions of DNA conformations and related these distributions to FIWs (see Materials and Methods; Fig. S3 A and B). The measured FIWs agree well with our simulation using a persistence length of 48 nm (Figs. S3 C and 3 A). This broadly agrees with typically measured persistence lengths for dsDNA (26), although in our simulation we do not consider electrostatic interactions or steric clashes of the DNA with itself. These simulations give us confidence in the predictable nature of TFM.
To quantify the precision of TFM measurements and validate our understanding of the sources of noise in TFM, we measured the standard deviations of the FIW from many molecules over a range of excitation intensities for DNAs with lengths of 87 and 3000 bp (Fig. 3 B), and compared the measured FIWs with predictions from analytical theory (Eq. 12) and camera simulations (see Materials and Methods). Our analytical expression differs from the weighted least-squares expression (20) in the first term, as well as in that it is not an interpolation between the high-background and photon-shot-noise-dominated regimes. The spread of standard deviations in the experimental data at a given intensity is because of variations in FIW caused by defocusing across the field of view, and variations in background photon counts for each molecule.
| (12) |
Our results for the 87 bp DNA show agreement between the experimental data and the predictions from the analytical expression and the simulations. Over the range of photon counts investigated, the uncertainty is roughly a power law of the intensity, as indicated by straight lines on a logarithmic plot (Fig. 3 B, dashed lines). Standard deviations as low as 5 nm (corresponding to the ability to resolve a change from 87 to 237 bp in a single frame) can be obtained for photon counts of several thousand photons per frame, which are readily achieved experimentally (15). Closer inspection of the data shows that the analytical expression underestimates the noise by ∼ 10%, in part because of several approximations in our derivation (see Materials and Methods). On the other hand, the simulation is in excellent agreement with the data, showing that better approximations to the microscope response function and more detailed models of noise per pixel can account for the deviation between theory and data.
For the 3000 bp DNA, we observe broader FIWs, and as a result, greater uncertainty in FIWs. We also observe that the analytical expression underestimates the noise by ∼ 40%, with the deviation increasing because of most approximations used becoming less valid. However, the experimental data and the simulation agree well with the data below an intensity of ∼ 4000 photons, suggesting that the simulation captures the behavior of our system well. For photon counts of > 4000, the simulation underestimates the uncertainty, likely because of DNA dynamics on timescales similar to our exposure time, which leads to incomplete sampling of possible DNA conformations within the 500 ms frames of our experiment. The underestimation is only apparent at higher photon counts, because when the fitting noise (modeled by our simulation) diminishes, the incomplete sampling noise dominates. The decay of the TIRF field is taken into account in our simulations and analytical expression, because the models are parameterized by the observed photon count, and we input the experimental background count at each illumination intensity.
We now move to discussing the dependence of the uncertainty in the FIW on the microscope design, in particular on the effect of changing the magnification and the pixel size. For single-molecule tracking, there is a well-known optimum pixel size close to the FIW (18). We experimentally varied our pixel size between 96 and 384 nm by using binning on our EMCCD. For each pixel size we determined the camera parameters separately and found that the background photon count varies linearly with the pixel area (Fig. S5 A), and the read-noise and the gain remain approximately constant. This variation in background means that we cannot simply minimize Eq. 12 with respect to the pixel size to derive an analytical optimum pixel size, but we must evaluate it numerically. Numerically, our theoretical expression has a minimum at a pixel size of 45 nm, smaller than the simulated minimum at 100 nm (Fig. S5 C), which may be because of the finite fitting window of 24 pixels used in our simulations. The experimental data matches the simulation well, with a small underestimation, which we attribute to incomplete sampling of conformations by the DNA within the 500 ms frame. We suggest that a pixel size approximately equal to the FIW is optimum for TFM, despite different DNA lengths having different optima, because the shallow gradient (Fig. S5 C) of the uncertainty in this region allows a large range of FIWs to be studied with the same experimental setup.
The resolution of TFM
To give context to the resolution of TFM, we compared it with TPM. TPM is typically performed on a dark-field microscope using a camera capable of high-frame rates (8), whereas TFM is implemented on a fluorescence microscope with an EMCCD camera. We anticipate that when designing an experiment, the equipment available, the ease of performing TFM in combination with existing fluorescence techniques, and the observation time desired will be deciding factors. The temporal resolution of TPM is fundamentally limited by the relaxation time of the DNA being probed; even at a small bead size (20 nm), the relaxation time of a 400 bp DNA is almost doubled, giving a temporal resolution of 20 ms for a 400 bp looping event in an 800 bp molecule (9). In TFM, because the fluorophore is smaller than a bead, the drag exerted on the DNA is much smaller, and hence the DNA relaxation time will be shorter, leading to increased temporal resolution; however, photobleaching will limit our observation span. Using short (∼ 1 ms) exposures and computing the mean excursion (Fig. 1 D–F) from 10 consecutive frames in a 20 ms window, with a sufficiently high photon count of ∼ 1000 photons per frame (which corresponds to a localization precision of < 10 nm (18)), we expect to bleach a Cy3B fluorophore after ∼ 30 s of observation, while at least matching the temporal resolution of TPM.
In terms of spatial resolution, TPM typically can detect 200 bp changes in an 800 bp DNA using an averaging window of 4 s (30). To match this using FIW as the observable, we would need ∼ 2500 photons in 4 s (Eq. 12, Fig. 3 B). This is easily achievable, considering we currently have ∼ 1000 photons per 100 ms frame in our experiments (Fig. 2 A); such conditions allow observation times of several tens of minutes before photobleaching.
Polymerization by Klenow fragment
Having looked at the theoretical basis of TFM, we next used two model systems to demonstrate the utility of TFM. We studied DNA polymerization by Klenow fragment (KF), a fragment of Escherichia coli DNA polymerase I described previously (23), lacking the 5′-3′ nuclease domain, but retaining polymerase activity. We used TFM to monitor the change in persistence length of a single DNA molecule, as it was converted from predominantly single-stranded to fully double-stranded (Fig. 4 A).
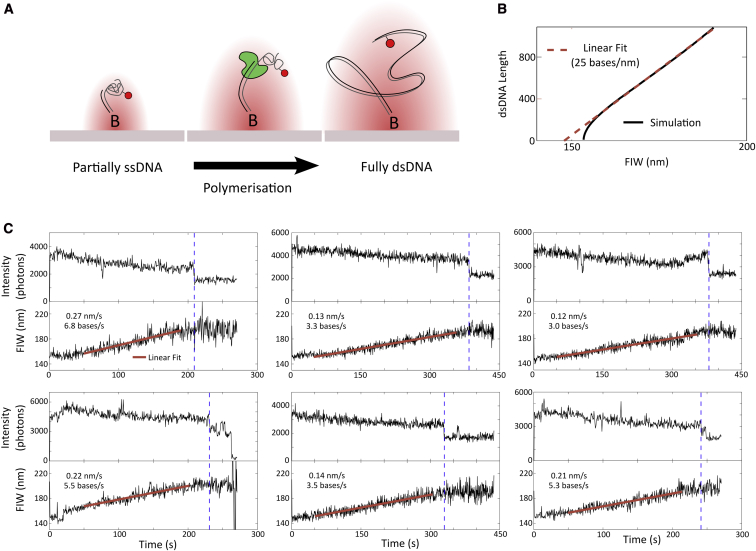
Figure 4.
KF DNA-polymerization assay. (A) Schematic. Initially the predominantly ssDNA substrate has a FIW close to that of the diffraction limit. As the DNA is converted to double stranded during polymerization, the mean persistence length increases, broadening the FIW until polymerization is complete. (B) Predicted FIW during polymerization. A linear fit to the region from 200 bp onward extracts an approximate conversion of 25 bases/nm. (C) Time traces from six polymerizing molecules. Dashed lines indicate the drop in fluorescence associated with the completion of polymerization, because of the conversion from single- to double-stranded of the DNA in the vicinity of the fluorophore. The straight lines are linear least squares fits to the actively polymerizing segments of the time traces, defined as from 50 s after the start of data acquisition until 20 s before the end of polymerization. The gradients of these fits can be used to extract a mean polymerization rate of 4.5 ± 0.7 bases/s. Molecules were selected to have not bleached before the end of the movie. In some (50%) of the time traces a small PIFE is evident before the completion of polymerization, which can be attributed to the proximity of KF to the fluorophore. To see this figure in color, go online.
Our substrate DNA consisted of a 55 bp double-stranded segment, which was tethered to the surface, followed by a 1032-base-long single-stranded segment (template) with an internal Cy5 label (Fig. S1 B). The initial substrate shows an FIW of ∼ 150 nm. Upon addition of KF and nucleotides, polymerization extended the double-stranded segment and thus increased the FIW (Fig. 4 A). Once polymerization was complete, the product DNA was fully double-stranded, with an FIW of ∼ 190 nm (Fig. 2 B). To establish a calibration between FIW and the degree of polymerization, we simulated DNAs at various stages of polymerization (Fig. S3) and found an approximately linear relation between the rate of change of FIW and the polymerization rate (Fig. 4 B). Thus, we multiplied the rate of change of FIW by 25 bases/nm to get the polymerization rate.
To analyze our data, we manually selected molecules that did not bleach during data acquisition and showed an increasing FIW consistent with polymerization initiating, progressing, and terminating (Fig. 4 C). We used linear least squares fitting in MATLAB to estimate the gradient, and hence the polymerization rate (Fig. 4 C, red lines). The end of polymerization was evident as a drop in fluorescence intensity (Fig. 4 C, dashed blue lines), which can be attributed to a change in the local environment of the fluorophore as the DNA in its vicinity is converted to double-stranded. We performed our linear fits from 50 s, which allows enough time for polymerization to initiate, to ∼ 20 s before the drop in fluorescence intensity. In 50% of the time traces, a small protein induced fluorescence enhancement (PIFE) (31) was evident before the drop in fluorescence. This is an established single-molecule observable, which occurs when a protein (here KF) reaches the proximity of a fluorophore that undergoes a cis-trans isomerization, such as Cy5. The presence of the protein reduces the rate of isomerization to the photo-inactive cis state. The PIFE may only be visible in some timetraces because our frame rate is too slow to resolve the shortest events, and because some events are obscured by noise.
With a nucleotide concentration of 10 μM, we measure a rate of polymerization of 4.5 ± 0.7 bases/s (mean ± standard error in mean, from six molecules). This is slower than the rate of six bases/s measured by Maier et al. using a 1 pN stretching force and 100 μM of each nucleotide (32); however, we note that, in our case, we measure polymerization under no force and at lower nucleotide concentration. Without an applied force, it is likely that transient secondary structure formed in the large portion of ssDNA serves to slow down action of KF. Our result is slower than the 14 bases/s, at 100 μM dNTPs, found by Schwartz et al. (33), because our method does not attempt to resolve short (of the order of 10 s) pauses and hence these get averaged into our rate. The longer pauses (∼ 1000 s), found by Maier et al., were not apparent in our data because our observation time was ∼ 400 s before photobleaching.
Although our KF experiments used a fluorophore attached to the DNA, a labeled protein can be used as the TFM reporter, enabling much longer observation times, as the turnover of protein binding to the DNA would continually replace bleached fluorophores. In this case, the second fluorophore on KF would allow direct measurement of KF processivity, and a FRET scheme such as in Santoso et al. (23), could be used to observe protein conformational changes and correlate them to the progress of polymerization.
DNA looping by Cre
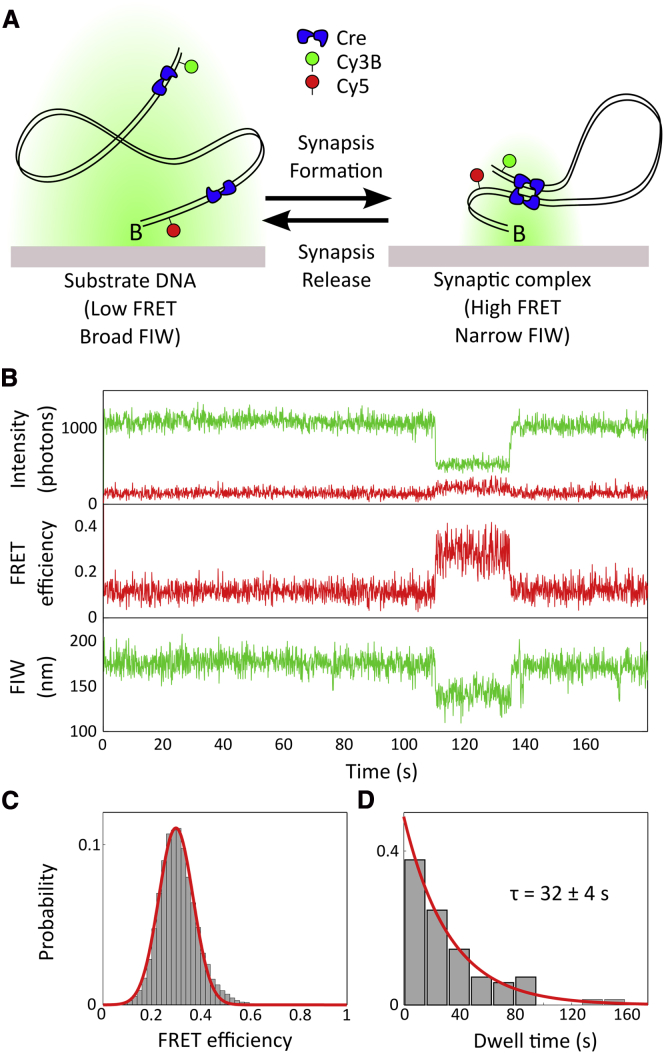
TFM can also be applied to observe step changes in DNA length, while simultaneously monitoring FRET between fluorophores. Previous work (13), using alternating laser excitation (ALEX) (34), has shown that Cre A36V is capable of forming stable synapses. We chose to use a single excitation laser to illustrate the simplicity of combining TFM and FRET, and to observe at a high temporal resolution. This combination allowed us to correlate large-scale loop formation in the DNA with a particular structural arrangement of the nucleoprotein complex (Fig. 5 A). Cre is a well-studied tyrosine recombinase of the bacteriophage P1 of Escherichia coli that forms synaptic complexes with two antiparallel loxP sites and four Cre monomers (22).
Figure 5.
Studying synaptic complex formation using TFM-FRET. (A) Cartoon. A 1 kb DNA is labeled with Cy5 and Cy3B, 10 bp and 990 bp from the biotin end, respectively. The substrate DNA displays a broad Cy3B FIW. Upon addition of Cre, synaptic complex formation between loxP sites located close to the labeling positions leads to a looping of the DNA and a decrease in FIW, as well as bringing the Cy3B and Cy5 fluorophores into close proximity, resulting in FRET. (B) Representative time trace of reversible synaptic complex formation in the presence of Cre, with the intensities corresponding to the emission of the donor, in green (light gray), and acceptor, in red (darker), under 532 nm continuous excitation. Synapsis is evident between 110 and 135 s. (C) Histogram of FRET efficiency, measured within the looped complex formed, with mean E∗ = 0.299 ± 0.004, determined using an unweighted least-squares fit to the data. (D) Histogram of dwell times of individual looping events, fit using maximum likelihood to a one parameter single exponential with a dwell time of 32 ± 4 s. The uncertainty in fit parameters is defined by the 1-σ confidence interval of the fit (n = 52). Movies were taken with a laser power of 1 mW and a frame rate of 10 Hz. To see this figure in color, go online.
We used a 1000 bp doubly labeled DNA substrate (Figs. S1 C and 5 A). While acting as the FRET donor, the FIW of the Cy3B also reported on the diffusional freedom of the free end of the DNA. The fluorophores were positioned such that synaptic complex formation would bring them close enough for FRET, allowing us to visualize the structure of individual synaptic complexes.
Synapsis was evident as a drop in the FIW of the donor, coincident with an increased (Fig. 5 B, 110 to 135 s). We used HMM based on to segment time traces, because showed superior signal-to-noise compared with FIW, and binned the from all frames acquired during synapsis, in all molecules (n = 51), in a histogram (Fig. 5 C) to recover for these complexes. The dwell times were fit with a single exponential using maximum likelihood parameter estimation in MATLAB, and a dwell time of 32 ± 4 s was extracted (Fig. 5 D), in broad agreement with previously measured time of 52.1 s (13).
Upon synapsis, the Cy3B intensity dropped by significantly more than the Cy5 intensity rose (Fig. 5 B, top). In part, this can be attributed to different quantum yields and detection efficiencies between the red and green channels. However, in simulations, we noticed that at smaller FIWs the OLS Gaussian fit underestimated the photon count more than at larger FIWs (Fig. S5 B) (24). Between this and the effect of the evanescent illumination field, we note that intensity and FIW are correlated in a nontrivial manner.
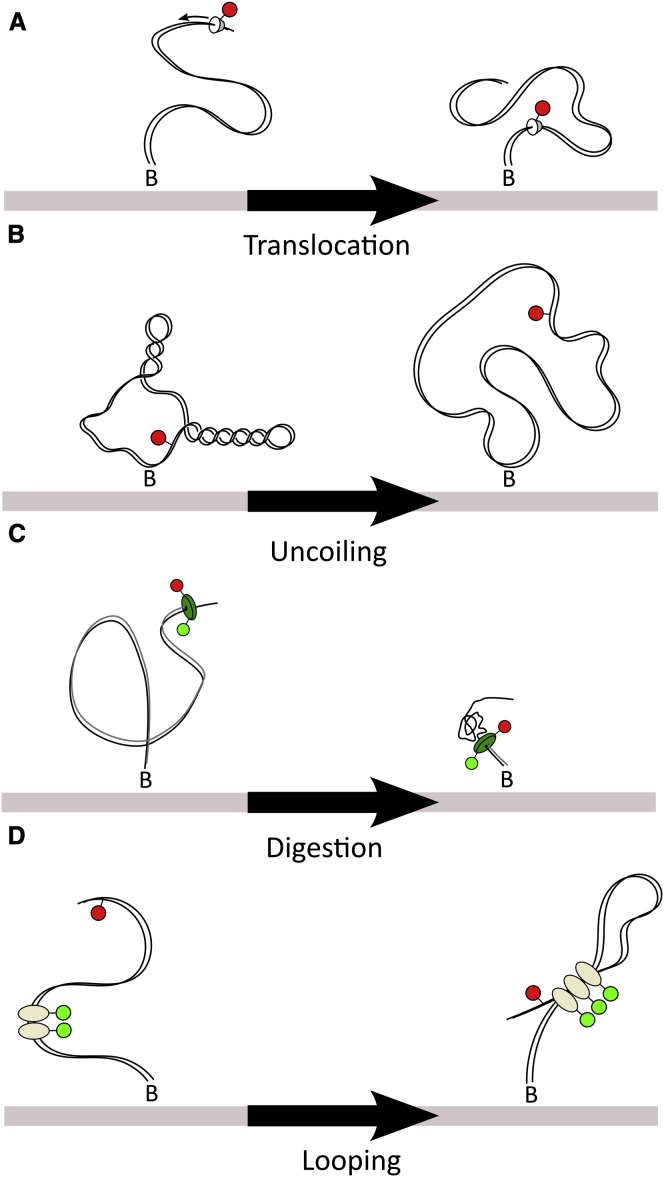
We have previously applied TFM to study another recombinase system, XerCD-dif (35). Recombination by XerCD is activated by the DNA translocase, FtsK, and the labeling of such accessory proteins offers another set of TFM experiments (Fig. 6 A) (17, 36). The FIW on translocase binding can be used to determine where along the DNA it binds; any motion along the substrate can be followed as changes in the FIW. Circular substrates also offer the possibility of watching topological simplification of DNA by topoisomerases (Fig. 6 B) (37). Plectonemes have lengths of several kb (38) and so their presence would be apparent as a reduced FIW. Analogously to polymerization, digestion by lambda exonuclease (39) could be monitored using TFM-FRET (Fig. 6 C). Multiple spectrally separate TFM probes can be attached to one DNA with minimal interference, to simultaneously measure the effective length at multiple sites along DNA (Fig. 6 D).
Figure 6.
Ideas for future TFM experiments. (A) Labeled translocase on a DNA track. As the translocase moves toward the surface the FIW decreases. (B) Topological simplification of DNA. Supercoiled, or knotted DNA, would show an increase in FIW as an enzyme simplifies their topology. (C) Digestion of DNA. An enzyme, such as lambda exonuclease, that digests DNA would reduce the effective persistence length, reducing the FIW. A FRET pair can be used as the TFM reporter while simultaneously monitoring protein conformation. (D) Looping by a protein of unknown stoichiometry. The FIW of one fluorophore can be used to determine where along the DNA the proteins are binding. Looping can be inferred by a decrease in the FIW of the DNA fluorophore. To see this figure in color, go online.
Conclusion
TFM uses the diffusional characteristics of a fluorophore tethered to a slide to report on the effective length of the polymer used as the tether. The use of a single fluorophore enables TFM to be combined with a variety of single-molecule fluorescence methods, such as FRET and PIFE. The absence of a large bead ensures that the motion of the DNA determines the dynamics of the system (9, 12) and eliminates the entropic stretching force exerted by the bead (11). Sample preparation is easy, because there is only one noncovalent attachment chemistry. TFM can be readily implemented on any existing single-molecule wide-field microscope: conveniently, the optimum signal-to-noise for TFM requires a pixel size very similar to that for single-molecule localization microscopy. Despite these advantages, TFM is limited in observation time to the photobleaching lifetimes of the fluorophores used, and signal-to-noise has to be traded against this lifetime. However, we have shown that in conditions typical for single-molecule experiments, length resolutions down to 100 bp are achievable. More photostable fluorophores, such as Atto647N (ATTO-TEC GmbH, Seigen, Germany) would allow longer observations. TFM can be used to address similar questions to TPM, while enabling combination measurements with existing single molecule fluorescence techniques. We hope that TFM will expand the possibilities available to the single-molecule community and that advances in combination techniques such as TFM-FRET, combining local and global information at the level of single biological reactions, will provide new and useful insight into the biochemistry of protein-DNA interactions.
Acknowledgments
P. F. J. M. was supported by The MathWorks (Cambridge, UK). J. N. M. P. was supported by the Engineering and Physical Sciences Research Council. Work in the A. N. K. laboratory was supported by the European Commission Seventh Framework Program (grant FP7/2007-2013 HEALTH-F4-2008-201418), the Biotechnology and Biological Research Council (grant BB/H01795X/1), and the European Research Council (starter grant 261227). Work in the D. J. S. laboratory was supported by a Wellcome Trust Senior Investigator Award (WT099204AIA).
Editor: David Rueda.
Footnotes
Peter F. J. May and Justin N. M. Pinkney contributed equally to this work.
Five figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(14)00742-5.
Supporting Material
References
- 1.Kapanidis A.N., Strick T. Biology, one molecule at a time. Trends Biochem. Sci. 2009;34:234–243. doi: 10.1016/j.tibs.2009.01.008. [DOI] [PubMed] [Google Scholar]
- 2.Lang M.J., Fordyce P.M., Block S.M. Simultaneous, coincident optical trapping and single-molecule fluorescence. Nat. Methods. 2004;1:133–139. doi: 10.1038/nmeth714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hohng S., Zhou R., Ha T. Fluorescence-force spectroscopy maps two-dimensional reaction landscape of the holliday junction. Science. 2007;318:279–283. doi: 10.1126/science.1146113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Schafer D.A., Gelles J., Landick R. Transcription by single molecules of RNA polymerase observed by light microscopy. Nature. 1991;352:444–448. doi: 10.1038/352444a0. [DOI] [PubMed] [Google Scholar]
- 5.Nelson P.C., Zurla C., Dunlap D. Tethered particle motion as a diagnostic of DNA tether length. J. Phys. Chem. B. 2006;110:17260–17267. doi: 10.1021/jp0630673. [DOI] [PubMed] [Google Scholar]
- 6.Finzi L., Gelles J. Measurement of lactose repressor-mediated loop formation and breakdown in single DNA molecules. Science. 1995;267:378–380. doi: 10.1126/science.7824935. [DOI] [PubMed] [Google Scholar]
- 7.Rusling D.A., Laurens N., Halford S.E. DNA looping by FokI: the impact of synapse geometry on loop topology at varied site orientations. Nucleic Acids Res. 2012;40:4977–4987. doi: 10.1093/nar/gks183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Brinkers S., Dietrich H.R.C., Rieger B. The persistence length of double stranded DNA determined using dark field tethered particle motion. J. Chem. Phys. 2009;130:215105. doi: 10.1063/1.3142699. [DOI] [PubMed] [Google Scholar]
- 9.Manghi M., Tardin C., Destainville N. Probing DNA conformational changes with high temporal resolution by tethered particle motion. Phys. Biol. 2010;7:046003. doi: 10.1088/1478-3975/7/4/046003. [DOI] [PubMed] [Google Scholar]
- 10.Yin H., Landick R., Gelles J. Tethered particle motion method for studying transcript elongation by a single RNA polymerase molecule. Biophys. J. 1994;67:2468–2478. doi: 10.1016/S0006-3495(94)80735-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Segall D.E., Nelson P.C., Phillips R. Volume-exclusion effects in tethered-particle experiments: bead size matters. Phys. Rev. Lett. 2006;96:088306. doi: 10.1103/PhysRevLett.96.088306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bai H., Kath J.E., Marko J.F. Remote control of DNA-acting enzymes by varying the Brownian dynamics of a distant DNA end. Proc. Natl. Acad. Sci. USA. 2012;109:16546–16551. doi: 10.1073/pnas.1203118109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Pinkney J.N.M., Zawadzki P., Kapanidis A.N. Capturing reaction paths and intermediates in Cre-loxP recombination using single-molecule fluorescence. Proc. Natl. Acad. Sci. USA. 2012;109:20871–20876. doi: 10.1073/pnas.1211922109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sindbert S., Kalinin S., Seidel C.A.M. Accurate distance determination of nucleic acids via Förster resonance energy transfer: implications of dye linker length and rigidity. J. Am. Chem. Soc. 2011;133:2463–2480. doi: 10.1021/ja105725e. [DOI] [PubMed] [Google Scholar]
- 15.Roy R., Hohng S., Ha T. A practical guide to single-molecule FRET. Nat. Methods. 2008;5:507–516. doi: 10.1038/nmeth.1208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gell, C., D. Brockwell, and A. Smith.2006. Handbook of Single Molecule Fluorescence Spectroscopy.
- 17.Mumm J.P. Single-molecule microscopy of Cre recombination. Proc. Natl. Acad. Sci. USA. 2012;109:20779–20780. doi: 10.1073/pnas.1218768110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Thompson R.E., Larson D.R., Webb W.W. Precise nanometer localization analysis for individual fluorescent probes. Biophys. J. 2002;82:2775–2783. doi: 10.1016/S0006-3495(02)75618-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mortensen K.I., Churchman L.S., Flyvbjerg H. Optimized localization analysis for single-molecule tracking and super-resolution microscopy. Nat. Methods. 2010;7:377–381. doi: 10.1038/nmeth.1447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.DeSantis M.C., DeCenzo S.H., Wang Y.M. Precision analysis for standard deviation measurements of immobile single fluorescent molecule images. Opt. Express. 2010;18:6563–6576. doi: 10.1364/OE.18.006563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Klenow H., Henningsen I. Selective elimination of the exonuclease activity of the deoxyribonucleic acid polymerase from Escherichia coli B by limited proteolysis. Proc. Natl. Acad. Sci. USA. 1970;65:168–175. doi: 10.1073/pnas.65.1.168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ghosh K., Guo F., Van Duyne G.D. Synapsis of loxP sites by Cre recombinase. J. Biol. Chem. 2007;282:24004–24016. doi: 10.1074/jbc.M703283200. [DOI] [PubMed] [Google Scholar]
- 23.Santoso Y., Joyce C.M., Kapanidis A.N. Conformational transitions in DNA polymerase I revealed by single-molecule FRET. Proc. Natl. Acad. Sci. USA. 2010;107:715–720. doi: 10.1073/pnas.0910909107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Holden S.J., Uphoff S., Kapanidis A.N. Defining the limits of single-molecule FRET resolution in TIRF microscopy. Biophys. J. 2010;99:3102–3111. doi: 10.1016/j.bpj.2010.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hagerman P.J., Zimm B.H. Monte Carlo approach to the analysis of the rotational diffusion of wormlike chains. Biopolymers. 1981;20:1481–1502. [Google Scholar]
- 26.Lu Y., Weers B., Stellwagen N.C. DNA persistence length revisited. Biopolymers. 2001-2002;61:261–275. doi: 10.1002/bip.10151. [DOI] [PubMed] [Google Scholar]
- 27.Ulbrich M.H., Isacoff E.Y. Subunit counting in membrane-bound proteins. Nat. Methods. 2007;4:319–321. doi: 10.1038/NMETH1024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Tinland B., Pluen A., Weill G. Persistence length of single-stranded DNA. Macromolecules. 1997;30:5763–5765. [Google Scholar]
- 29.McKinney S.A., Joo C., Ha T. Analysis of single-molecule FRET trajectories using hidden Markov modeling. Biophys. J. 2006;91:1941–1951. doi: 10.1529/biophysj.106.082487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Pouget N., Dennis C., Salomé L. Single-particle tracking for DNA tether length monitoring. Nucleic Acids Res. 2004;32:e73. doi: 10.1093/nar/gnh073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hwang H., Kim H., Myong S. Protein induced fluorescence enhancement as a single molecule assay with short distance sensitivity. Proc. Natl. Acad. Sci. USA. 2011;108:7414–7418. doi: 10.1073/pnas.1017672108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Maier B., Bensimon D., Croquette V. Replication by a single DNA polymerase of a stretched single-stranded DNA. Proc. Natl. Acad. Sci. USA. 2000;97:12002–12007. doi: 10.1073/pnas.97.22.12002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Schwartz J.J., Quake S.R. Single molecule measurement of the “speed limit” of DNA polymerase. Proc. Natl. Acad. Sci. USA. 2009;106:20294–20299. doi: 10.1073/pnas.0907404106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kapanidis A.N., Lee N.K., Weiss S. Fluorescence-aided molecule sorting: analysis of structure and interactions by alternating-laser excitation of single molecules. Proc. Natl. Acad. Sci. USA. 2004;101:8936–8941. doi: 10.1073/pnas.0401690101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zawadzki P., May P.F.J., Arciszewska L.K. Conformational transitions during FtsK translocase activation of individual XerCD-dif recombination complexes. Proc. Natl. Acad. Sci. USA. 2013;110:17302–17307. doi: 10.1073/pnas.1311065110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Grindley N.D.F., Whiteson K.L., Rice P.A. Mechanisms of site-specific recombination. Annu. Rev. Biochem. 2006;75:567–605. doi: 10.1146/annurev.biochem.73.011303.073908. [DOI] [PubMed] [Google Scholar]
- 37.Champoux J.J. DNA topoisomerases: structure, function, and mechanism. Annu. Rev. Biochem. 2001;70:369–413. doi: 10.1146/annurev.biochem.70.1.369. [DOI] [PubMed] [Google Scholar]
- 38.van Loenhout M.T.J., de Grunt M.V., Dekker C. Dynamics of DNA supercoils. Science. 2012;338:94–97. doi: 10.1126/science.1225810. [DOI] [PubMed] [Google Scholar]
- 39.Perkins T.T., Dalal R.V., Block S.M. Sequence-dependent pausing of single lambda exonuclease molecules. Science. 2003;301:1914–1918. doi: 10.1126/science.1088047. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.