Analytic 3D Imaging of Mammalian Nucleus at Nanoscale Using Coherent X-Rays and Optical Fluorescence Microscopy

Abstract

Despite the notable progress that has been made with nano-bio imaging probes, quantitative nanoscale imaging of multistructured specimens such as mammalian cells remains challenging due to their inherent structural complexity. Here, we successfully performed three-dimensional (3D) imaging of mammalian nuclei by combining coherent x-ray diffraction microscopy, explicitly visualizing nuclear substructures at several tens of nanometer resolution, and optical fluorescence microscopy, cross confirming the substructures with immunostaining. This demonstrates the successful application of coherent x-rays to obtain the 3D ultrastructure of mammalian nuclei and establishes a solid route to nanoscale imaging of complex specimens.

Introduction

Nanoscale three-dimensional (3D) structures greatly enhance our understanding of nanomaterials and biological systems (1) and facilitate the rational design of new functional nanostructures. In the last several decades, electron microscopy has played a key role in unveiling high-resolution structures (2, 3), but its application in imaging thick specimens has been hampered. As a promising alternative, coherent diffraction imaging (CDI) has demonstrated its potential for noninvasive, quantitative imaging of whole biological cells and nanomaterials, especially using x-rays, which generally penetrate deeper into the specimens than electrons (4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16). In particular, CDI may provide a more economic use of x-ray radiation by directly detecting signals from a specimen without the interference of a lens, where absorption is indispensible, which is essential to realize high-resolution and high-contrast imaging (17, 18, 19, 20, 21, 22).

Particularly in the last couple of years, investigators have employed CDI for paradigm-shifting applications in nanomaterials and biosystems by utilizing femtosecond x-ray laser pulses from x-ray free electron lasers (XFELs) (23, 24, 25, 26, 27, 28, 29, 30, 31, 32). Single-shot diffraction imaging with intense (∼mJ), ultrashort (∼10 fs) x-ray laser pulses from XFELs enables one to acquire intact structures by recording diffraction signals from specimens before the onset of x-ray radiation-induced sample deformation (known as diffraction before destruction) (23, 24, 25, 33, 34). Although XFEL single-shot imaging is expected to facilitate high-resolution imaging by overcoming the radiation-damage limit, it may not be directly applicable for 3D imaging of heterogeneous specimens at such radiation-unlimited resolution, since the same specimen may not be measured repeatedly while preserving intact structure (32, 35). The combined use of 3D imaging with synchrotron radiation and high-resolution 2D single-shot imaging with XFELs may provide a dexterous imaging modality (36), but requires a concrete establishment of each imaging technique. Despite the rapid progress that has been made in the last several years, however, analytical imaging of complex structures such as whole mammalian cells has remained challenging.

Here, we introduce the first (to our knowledge) successful application of analytic 3D imaging to multiorganelle mammalian nuclei, progressing beyond the level of proof-of-concept applications to rather simple structures. The cellular nucleus is the control tower of eukaryotic cells, where the essential biological functions of gene replication and transcription take place (37, 38, 39). The nucleus itself, enclosed by a lipid bilayer, is a composite organelle that contains functionally distinct substructures (nucleoli, chromatin structures, and several different nuclear bodies or speckles). They comprise the complex architecture of the nucleus, and intricate interactions occur to coordinate their functions. To understand the cellular functions of the nuclei and, in particular, the complex process of gene regulation (37, 40, 41, 42), it is essential to reveal the whole 3D ultrastructure of the nucleus.

Materials and Methods

Sample preparations

We prepared cells with micronuclei by treating A9 cells using nocodazole, an inhibitor of microtubule polymerization. When assembly of the mitotic spindle is interfered with, chromosomes are scattered in the cytoplasm in mitotic cells. When the cells eventually return to interphase, after a period of metaphase delay, the nuclear envelope is assembled around individual chromosomes or small groups of chromosomes to generate interphase micronuclei. The micronuclei largely preserve the morphological features of normal control nuclei, except for the size (43).

Mouse A9 cells were purchased from HSRRB (Osaka, Japan) and grown in Eagle’s minimum essential medium with 10% fetal calf serum in a humidified incubator at 37°C with 5% CO₂. The formation of micronuclei was induced by treating cells with 200 ng/ml nocodazole for 48 h. After cells that were still in mitosis were removed by shaking, the remaining cells were trypsinized, harvested, washed twice with serum-free medium, and suspended in ice-cold RSB (10 mM Tris, pH 7.5, 10 mM NaCl, and 1.5 mM MgCl₂). After 15 min incubation on ice, the cells were homogenized by 10 strokes with a stainless homogenizer to release nuclei. All subsequent procedures were performed at 4°C. After cellular debris was removed by centrifugation at 70 g for 10 min, the lysate was layered over a stepped sucrose gradient consisting of 60%/50%/40% sucrose in RSB, followed by centrifugation at 3920 g for 15 min using a JS13.1 rotor (Beckman). Fractions containing 50–60% sucrose were manually collected, diluted three times with RSB, supplemented with Triton X-100 to 0.5%, mixed well using a syringe attached to a 27-G needle, placed on a stepped sucrose gradient consisting of 60%/40% sucrose in RSB, and spun at 3920 g for 15 min in the JS13.1 rotor. Micronuclei that accumulated on the top of the 60% sucrose layer were collected and fixed with 0.5% glutaraldehyde. The chemically fixed interphase micronuclei were mounted and dried on 30 nm thin Si₃N₄ membranes for x-ray imaging experiments.

Immunofluorescence staining and imaging

Treated A9 cells were fixed with 3.7% formaldehyde in PBS for 10 min and processed for immunofluorescence staining using mouse monoclonal antibody against fibrillarin (clone 38F3; Abcam) and Alexa Fluor 488 goat anti-mouse IgG (Life Technologies). DNA was counterstained with Hoechst 33342. Images were acquired on a Deltavision (Applied Precision) equipped with a camera (CoolSNAPHQ2) using a zoom lens of 60× magnification (1.4 NA), PlanApo objective (Olympus), and softWoRx acquisition software (Applied Precision). Images with a focal step of 0.2 μm were collected and deconvoluted with softWoRx.

Phase retrieval and image reconstruction

Images were reconstructed after the phases of measured diffraction amplitude were retrieved through numerical iteration using the Guided Hybrid-Input-Output (GHIO) algorithm (44). The measured diffraction pattern was centro-symmetrized. Data with an array size of 1260 × 1260, equivalent to 41.7 μm⁻¹ in resolution, were used for reconstructions. The data were numerically binned by merging 3 × 3 pixel arrays, enhancing the signal/noise ratio by almost an order of magnitude. Numerical deconvolution was then carried out, resulting in an exactly oversampled diffraction pattern (45). The final array size used for the phase retrieval was 420 × 420, but still represented the same resolution of 41.7 μm⁻¹. The GHIO phase retrieval started with 16 independent sets of random phases using the Hybrid-Input-Output (HIO) algorithm (46). A rectangular boundary confining the image-containing area, or support, was estimated from the oversampling ratio (47). An image with the lowest R-value, R≡∑_i,j|F_calc(i.j)−F_meas(i.j)|/∑_i,jF_meas(i.j), among 16 reconstructions of 3000 iterations each was chosen as the best image by finishing the first generation of the reconstruction. Sixteen independent reconstructions for the next 3000 iterations were then started from 16 images generated by taking the geometrical means of the respective 16 images obtained from the previous generation’s reconstruction with the best image. These procedures were repeated up to the sixth generation. Finally, five images of low R-values were averaged to generate a tight support. The averaged image was smoothed over three to five pixels and the region with mass density higher than 7–9% of the average density was read to define a tight support. Using this tightened support, the GHIO was run again starting from fresh random phases and the same procedures were repeated up to the eighth generation, resulting in 16 images that were almost identical, ensuring the fidelity of our phase retrieval. The three best images were averaged to represent the reconstructed image of that diffraction pattern. The missed central portion of the data was acquired during phase retrieval by taking the values cast from the reconstructions. With all the data having the missing central part of the data within the central speckle of the measured pattern, we observed remarkable stability in the retrieved amplitude.

Results and Discussion

Coherent x-ray diffraction imaging

CDI experiments were carried out at beamline 29XU of SPring-8. Incident x-ray photon energy was fixed at 5 keV. To enhance the spatial coherence of the x-rays, we installed a circular aperture of 20 μm diameter at 1.0 m upstream of the sample (48, 49). The pinhole aperture enhanced illuminations of spatially coherent x-rays with the same phase (plane wave incidence) at the specimen. Two bevel-edged slits were placed in front of the sample to block parasitic scattering from the aperture and other optics components. X-ray diffraction patterns from the specimen were recorded on a liquid-nitrogen-cooled charge-coupled device (CCD) detector (Roper) mounted 1.23 m downstream of the sample. A beam stopper made of Tantalum and installed right in front of the CCD chip blocked the direct x-ray beam to avoid any damage to the CCD chip by intense x-rays. The x-ray beam stopper results in a missing portion at the center of the diffraction pattern. In general, this missing portion, when limited to the central speckle, does not influence phase retrieval. During the phase retrieval, this missing portion is left unbiased whereas other parts are constrained by measured data. When this missing central part is smaller than the central speckle, the retrieved amplitude usually converges rapidly and reliably (50).

2D imaging with the projection density of a nucleus

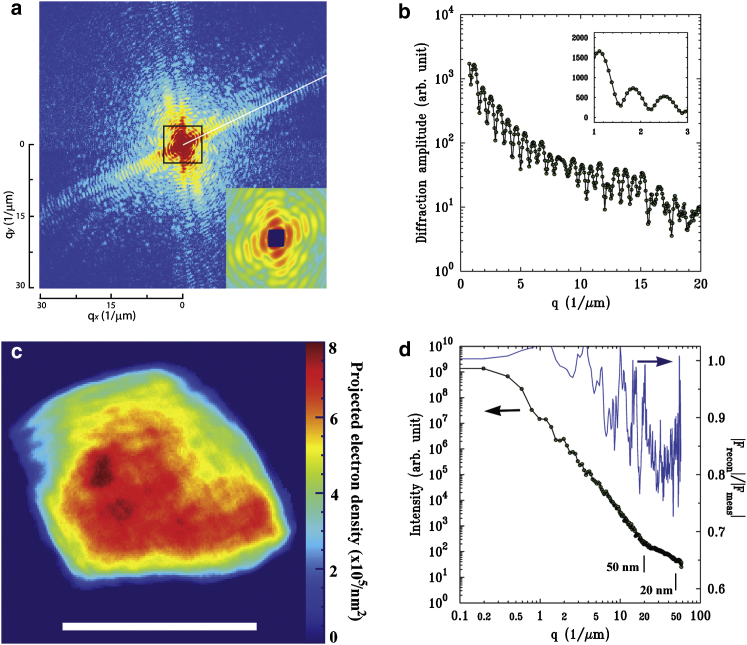
We obtained a 2D coherent diffraction pattern from a nucleus as displayed in Fig. 1 a. The missing portion of the data due to the beam stopper was confined within the central speckle as shown in the inset of Fig. 1 a. A line cut of the diffraction pattern in Fig. 1 b along the white line in Fig. 1 a displays clearly discernible fringes with an oscillation period of ∼1.5 μm, reflecting the size of the specimen. After the aforementioned phase retrieval process, we reconstructed the image from the diffraction pattern with the scale bar representing 1.0 μm in Fig. 1 c. The reconstructed image, a 2D projection density of the interphase nucleus, displays the planar morphology of the specimen with inhomogeneous local density variation resulting from the complex internal structures.

Figure 1.

Imaging 2D projection density. (a) The coherent diffraction pattern of the nucleus is displayed. The inset zooms in the data marked by the black square. (b) A line cut along the white line in a shows fringe oscillation reflecting the sample size of ∼1.5 μm. (c) The reconstructed image shows the projected electron density of the nucleus. The scale bar represents 1.0 μm. (d) The power spectral density of the diffraction pattern and PRTF were calculated. The diffraction pattern maintains good signal down to 20 nm. PRTF confirms that the image is reliably obtained up to 20 nm in full period. To see this figure in color, go online.

We calculated the quantitative value of the projected electron density directly from the intensity at the center of the CCD detector (dI(Q = 0)) and incident x-ray flux density (I_o) using the relation

$$dI\left(Q\right)=I_{\text{o}}{r}_{\text{e}}^2{N}_{\text{e}}^2{\left|f_N\left(Q\right)\right|}^{2}d\Omega ,$$ (1)

Here, dΩ is the solid angle spanned by the central pixel of the detector, dX × dY, located at a distance r from the sample with dΩ = (dX × dY)/r²; f_N(Q) is the normalized atomic form factor (f_N(Q = 0) = 1); r_e is the classical electron radius; and N_e is the total number of electrons. For the CCD detector used in this experiment, dX and dY have the same dimension of 20 μm. Using the relation in Eq. 1, we obtained the total number of electrons (N_e) explicitly, and we scaled the total electron density of the reconstructed image to be consistent with this value (N_e) to represent the actual electron density. The projected density is displayed quantitatively as a color map with the scale bar to the right in Fig. 1 c. The spatial resolution of the image is usually assessed by the signal/noise ratio of the measured diffraction patterns and consistency in retrieved phases. The diffraction pattern sustains good signal up to a spatial frequency corresponding to better than 20 nm image resolution, as inferred from the power spectral density Fig. 1 d. To further assess the resolution, we estimated the phase retrieval transfer function (PRTF). We determined the resolution-dependent fidelity of image reconstruction as shown in Fig. 1 d (26) by comparing the calculated speckle pattern (|F_calc(Q)|) of the reconstructed image with the measured value of (|F_meas(Q)|) as |F_calc(Q)|/|F_meas(Q)|. The PRTF scores higher than 0.6, implying that the projected density maps were obtained at better than 20 nm image resolution (see also Fig. S1 in the Supporting Material) (51).

3D coherent diffraction microscopy

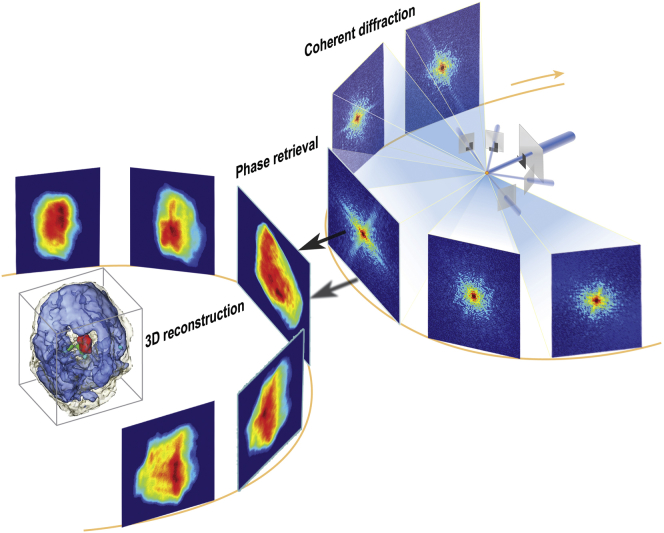
As the 2D image is limited to displaying a projection image with buried details of internal structures, we proceeded to carry out 3D imaging by acquiring multiple projection images. Fig. 2 displays the schematics of tomographic 3D CDI. We acquired a 3D density map of the mouse micronucleus in its interphase from multiple 2D images, which were plane-projected density maps of the nucleus with its orientation controlled by the rotation stage. By rotating the specimen from −76° to +76° with intervals allowing an equal angular slope, we recorded 29 diffraction patterns on the CCD detector. Each individual 2D diffraction pattern was first converted to an image corresponding to a plane-projected 3D density, as known from the Fourier slice theorem (52). We obtained the 3D structure using these 29 projection images via iterative equal-slope tomographic (EST) reconstruction (53). We first aligned all of the 29 projections to the same rotation center by employing the center-of-mass alignment scheme (54). This alignment scheme ascertains the self-consistency among all of the images, resulting in precise alignments. The EST allows consistent tomographic reconstruction via iterative refinements of the 3D structure while being consistent with the obtained projection images and diffraction patterns simultaneously. The EST method can achieve efficient tomographic reconstructions using a limited number of projections and thus is effective for radiation-damage-sensitive specimens (Figs. S2–S4). Technical details of the EST methods have been published elsewhere (51, 55, 56, 57).

Figure 2.

Coherent x-ray diffraction tomography. The schematics of 3D imaging via synchrotron coherent x-rays are displayed. A 3D density map was reconstructed using 29 projections of 2D density maps by rotating the same specimen along an axis perpendicular to the incident x-ray direction. To see this figure in color, go online.

Quantitative 3D architecture of the nucleus

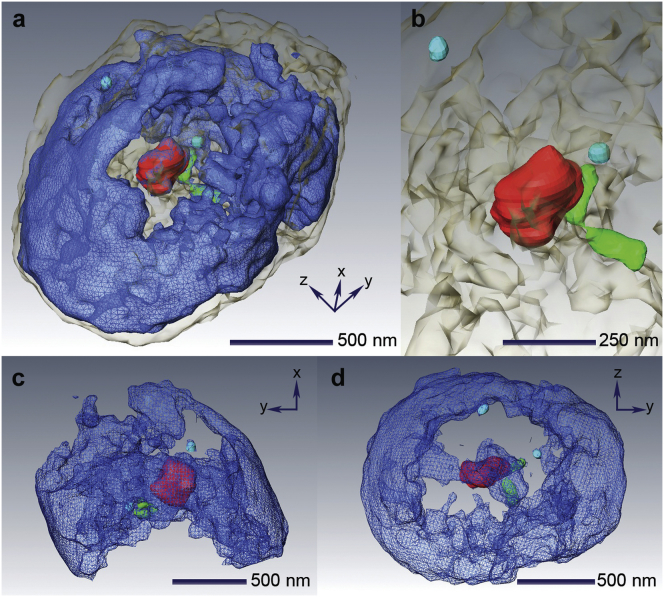
We revealed the quantitative 3D architecture of the interphase micronucleus noninvasively using coherent x-rays (Fig. 3; Movie S1). The direction of the incident x-rays was parallel to the z-axis at a tilting angle of 0° and the sample was tilted through rotation along the y-axis in Fig. 3. The volume-rendered density map is visualized in Fig. 3. The total volume of the nucleus was found to be 2.3 μm³, with an average density of 0.44 electrons/ų calculated from the total electron density according to the aforementioned procedure. The average density is similar to the nominal electron density of proteins (58).

Figure 3.

3D architecture of the nucleus. (a) Volume-rendered 3D image of a whole, unstained nucleus. (b) Nuclear substructures of chromatin region (blue), nucleolus (∼330 nm in red), condensed chromatin (∼340 nm in green), and nuclear bodies or speckles (∼80 nm in cyan). (c and d) Side and top views of the nucleus are shown. To visualize the nuclear substructures clearly, the nuclear envelope is not displayed. To see this figure in color, go online.

In Fig. 3, a and b, the internal density distributions of the 3D structure display the substructures directly from the reconstructed image. Different colors are used to distinguish each individual nuclear substructure (nuclear envelope in gray, chromatin in blue, nucleolus-reminiscent structure in red, heterochromatin-like highly condensed chromatin in green, and nuclear blobs in cyan). To visualize the internal structures, the nuclear envelope is displayed transparently in Fig. 3, c and d. Visualization of the substructures is aided by the segmentations in Fig. 3. The segmentation was carried out by identifying the connected equal density regions manually. The segmentation was employed to facilitate visualization only, and the actual quantitative analysis was performed using the raw data of the 3D density. The 3D density map readily reveals nuclear substructures in Fig. 3. The condensed chromatin appears to be ∼340 nm long, with each part being 170 nm in length. A small spherical object in the vicinity of a nucleolus-like structure implies a nuclear blob. Another object of similar size and shape is found at the periphery of the nucleus. Side and top views of the nucleus display the skeleton-like structure with the nucleolus-like structure and condensed chromatin near the center in Fig. 3, c and d (41, 42, 59).

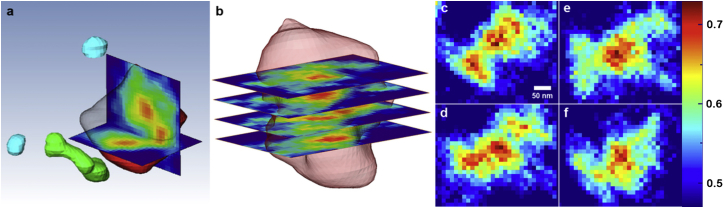
Located near the center of the nucleus is an isolated high-density substructure with a diameter of ∼330 nm, resembling a nucleolus (red) (59). The nucleolus is a nuclear substructure in which the synthesis and processing of preribosomal RNA, as well as the assembly of proteins into preribosomal structures, occur. Internal fine structures, such as fibrillar centers, present in nucleoli as characteristic features. Details regarding the functions and structures of nucleoli can be found elsewhere (59, 60, 61, 62). The volume of the nucleolus-reminiscent structure is 0.0044 μm³, representing ∼0.2% of the volume fraction of the whole nucleus. Its average electron density is estimated to be 0.62 electrons/ų, ∼1.5 times the average nucleus density obtained. Internal details of the nucleolus-like structure were observed directly from the 3D structure shown in Fig. 4 (39, 63). Cross sections of reconstructed density explicitly visualize inhomogeneous density distributions characterizing fine structures of the nucleolus in Fig. 4. These fine structures, which range between 40 nm and 60 nm in diameter, are shown in Fig. 4, a and b. The electron density inside the nucleolus was acquired directly from the reconstructed 3D image in Fig. 4, c–f. The density maps were obtained by numerically sectioning the nucleolus to display total densities contained in 36-nm-thick slabs. The position of the sectioned density maps in Fig. 4, c–f corresponds to the cross-sectional view in Fig. 4 b (bottom). The observed characteristic fine structures support the finding that the identified structure resembles the nucleolus (60).

Figure 4.

Quantitative density map of the nucleolus. (a) Cross-sectional views of the nucleolus, displaying characteristic fine structures of nucleoli with inhomogeneous density profiles. (b) The overall morphology of the nucleolus is displayed with actual densities inside shown via cross-sectional views. (c–f) The density distribution inside the nucleolus was obtained directly from the reconstructed 3D structure with 36-nm-thick slabs (three pixel layers) along the vertical direction. The images in c–f can be matched to a position from the bottom in the cross-sectional view in b. The electron density of the reconstructed image is directly displayed using a color map with the scale bar to the right (in electrons/ų). To see this figure in color, go online.

Internal structures displayed via numerical sectioning

The reconstructed 3D image was numerically sectioned to display the internal electron density distribution in Fig. 5. Three image pixel layers, corresponding to a 36-nm-thin slab, were added along the x direction in the visualization of the sectioned images in Fig. 5. The coordinate follows the same convention used in Fig. 3. An isolated high-density object, identified as the nucleolus, is apparent in the sectioned image of x:88–91 through x:103–105, supporting the interpretation in Figs. 3 and 4. Arrows mark the nucleolus (NO) in the sectioned images where it appears most conspicuously. The fine structures of the nucleolus are also observed within the nucleolus. Overall, a skeleton-like structure of chromatin regions is noted in the sectioned images (41).

Figure 5.

Density map obtained via numerical sectioning. A quantitative density map of the reconstructed 3D structure is explicitly visualized through 2D sectioned images. Three image pixel layers, corresponding to 36.3 nm in thickness, are added along the x direction in this visualization. The isolated high-density structure is marked by arrows denoting the nucleolus (NO). To see this figure in color, go online.

Fluorescent optical imaging

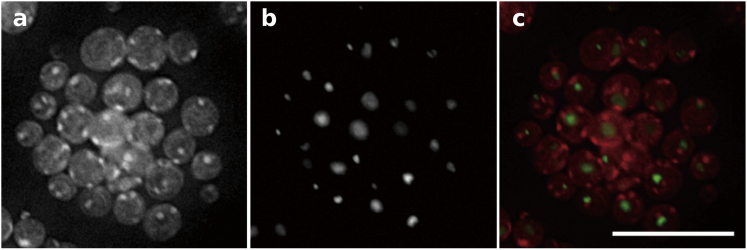
Next, we turn to fluorescent optical-microscope imaging to verify the nuclear substructures through multicolor labeling specific to each substructure, as shown in Fig. 6 (see also Figs. S5 and S6). The specimens with circular boundaries in Fig. 6 a correspond to individual micronuclei in the interphase. Chromatin structures were imaged by staining the DNA with Hoechst 33342 (Fig. 6 a). The bright spots represent heterochromatic regions in Fig. 6 a (see also Fig. S5). The heterochromatin structures identified by fluorescent optical-microscope imaging are consistent with the 3D architecture obtained using coherent x-rays (Fig. 3) in terms of size, shape, and distribution.

Figure 6.

Multicolor immunofluorescent optical-microscope images. (a) Chromatin structures in micronuclei were identified by staining of DNA. Specimens with a complete circular boundary show individual micronuclei. Bright spots represent heterochromatic regions. (b) Nucleoli are emphasized by immunostaining of fibrillarin. (c) The nucleolus (green) is overlaid with chromatin (red). Structures in the brighter red color indicate heterochromatins located close to nucleoli (green). The scale bar is 15 μm. To see this figure in color, go online.

Fig. 6 b displays nucleoli identified by staining fibrillarin using a mouse monoclonal antibody (clone38F3; Abcam) and Alexa Fluor 488 goat anti-mouse IgG (Life Technologies) (Fig. S6). Two images in Fig. 6, a and b, are overlaid, displaying the location of nucleoli (green) and chromatins (red) in the micronuclei shown in Fig. 6 c. We observed that the heterochromatin (shown in bright red with stronger staining by Hoechst3342) was often located near the fibrillarin in Fig. 6 c, similar to what was observed for the 3D structure from x-ray imaging in Fig. 3. This spatial proximity of heterochromatin to the nucleolus may indicate that the observed heterochromatin stems from the nucleolus-like structure (59). The observation of nucleoli, broadly distributed chromatins, and localized heterochromatins in the vicinity of nucleoli and the nuclear periphery in Fig. 6 further reveals the architecture of nuclei commonly noticed in the interphase (41, 59).

Conclusions

In this work, we unveiled the 3D architecture of mammalian nuclei quantitatively by using coherent x-ray diffraction tomography. Nuclear substructures were successfully obtained and confirmed independently by fluorescent optical microscopy after multicolor immunostaining. The combination of high-resolution x-ray imaging and multicolor fluorescence microscopy was able to reveal the quantitative 3D architecture of a whole mammalian nucleus, and can be readily extended to other complex structures that contain multiple components at a resolution of several tens of nanometers in 3D. The total x-ray radiation dose delivered to the specimen was estimated to be 4 × 10⁸ Gy, which is less than the maximum tolerable radiation dose at which structures at this scale remain intact under cryogenic conditions (64). In the x-ray experiments, we made an elaborate effort to maintain a lower radiation dose by reducing the number of projections and limiting the exposure time for recording each 2D diffraction pattern to avoid degrading the image resolution and contrast (see also Fig. S4). Although we remain cautious about the achieved image resolution, we were able to distinguish fine structures of ∼40 nm successfully. Imaging with cryocooling is essential, especially for 3D imaging using synchrotron x-rays, to better preserve the specimens with increased tolerance to the x-ray radiation dose. We expect that coherent x-ray diffraction tomography may achieve a 10 nm scale resolution for cryocooled specimens, which can tolerate a few hundred times higher x-ray doses (65, 66, 67). We believe our use of synchrotron coherent x-ray imaging to unveil the 3D architecture of complex mammalian nuclei together with optical multicolor fluorescence microscopy will greatly strengthen the analytic capability of such an imaging scheme.

Editor: Lois Pollack.

Supporting Material

Movie S1. 3D architecture of the micronucleus

The 3D structure of the A9 micronucleus is displayed. The density distribution of the chromatin territories is visualized via a 3D contour in different colors (gray, blue, and orange). A cross section of the nucleolus shows internal fine structures. The nuclear envelope is displayed in purple.