A critical appraisal of the use of microRNA data in phylogenetics

Significance

As progress toward a highly resolved tree of life continues, evolutionary relationships that defy resolution continue to be identified. Recently, the presence/absence of microRNA families has emerged as a potentially ideal source of information to resolve these difficult phylogenetic problems, and these data have been used to address several long-standing problems in the metazoan phylogeny. To our knowledge, this study performs the first rigorous statistical assessment of the phylogenetic utility of microRNAs and finds that a high incidence of homoplasy and sampling error renders published phylogenies based on microRNA data highly biased or uncertain. This study casts serious doubt on the central phylogenetic conclusions of several previous analyses of microRNA datasets.

Abstract

Recent progress in resolving the tree of life continues to expose relationships that resist resolution, which drives the search for novel sources of information to solve these difficult phylogenetic problems. A recent example, the presence and absence of microRNA families, has been vigorously promoted as an ideal source of phylogenetic data and has been applied to several perennial phylogenetic problems. The utility of such data for phylogenetic inference hinges critically both on developing stochastic models that provide a reasonable description of the process that give rise to these data, and also on the careful validation of those models in real inference scenarios. Remarkably, however, the statistical behavior and phylogenetic utility of microRNA data have not yet been rigorously characterized. Here we explore the behavior and performance of microRNA presence/absence data under a variety of evolutionary models and reexamine datasets from several previous studies. We find that highly heterogeneous rates of microRNA gain and loss, pervasive secondary loss, and sampling error collectively render microRNA-based inference of phylogeny difficult. Moreover, our reanalyses fundamentally alter the conclusions for four of the five studies that we reexamined. Our results indicate that the capacity of miRNA data to resolve the tree of life has been overstated, and we urge caution in their application and interpretation.

As genomic tools and affordable DNA sequencing have become widely available, our ability to leverage molecular sequence data to estimate species phylogeny has rapidly increased. The flood of molecular data has, in turn, witnessed brisk progress in resolving the tree of life (1, 2). Nevertheless, many relationships have resisted resolution despite repeated efforts using increasing amounts of sequence data. These challenging cases have motivated the search for new sources of molecular phylogenetic information, which places precedence on data that evolve by rare and nearly irreversible genomic changes. Patterns of gene rearrangement, duplication, insertion, and deletion, as well as positional information for retrotransposons, have all been promoted as candidate data with “ideal” phylogenetic properties (e.g., refs. 3–6). Although new types of phylogenetic data may hold promise in resolving difficult nodes in the tree of life, they require careful consideration to appropriately model the underlying evolutionary process by which they arose and to accommodate possible sampling biases associated with their collection.

One recently promoted class of putatively ideal phylogenetic data comprises the presence/absence of microRNA (miRNA) families (7, 8). MicroRNAs are small regulatory RNA molecules that play a pervasive role in gene regulation and are understood to influence a variety of biological processes both in normal physiological and pathological disease contexts (9, 10). Because of their widespread importance in regulating gene networks and their potential role in the evolution of complexity, miRNAs are currently the subject of considerable focus in developmental biology (11–13).

The justification for the phylogenetic utility of miRNA presence/absence data stems from the way that novel miRNA families arise. MicroRNAs originate from random hairpin sequences in intronic or intergenic regions (typically 60–80 bp in length) of the genome that become transcribed into RNA (14, 15). After transcription, the resulting primary miRNAs may fold into hairpins that serve as the substrate for a pair of enzymes—called Drosha and Dicer—involved in miRNA synthesis (16), culminating in a mature miRNA (typically 22 bp in length).

The odds that any individual hairpin structure will acquire the requisite mutations to form a novel miRNA are exceedingly slim; however, genomes contain many thousands of these structures, such that novel miRNAs are likely to accumulate over deep time (14). After the introduction of new functional miRNAs, strong purifying selection associated with their regulatory role can lead to both extraordinarily low rates of substitution within miRNA sequences and long-term preservation of miRNAs in the genome (14). This biological scenario is expected to lead to an evolutionary pattern wherein new miRNAs—over long time scales—continually arise in genomes and experience a low rate of secondary loss (15). Moreover, the origin of novel miRNAs involves the accumulation of random mutations to a relatively long sequence (60–80 bp in animals), rendering it highly improbable that identical miRNAs will evolve convergently (17). These considerations have led to the promotion of miRNAs as a new source of data that are ideal for parsimony inference of phylogeny: they should exhibit extraordinarily low levels of homoplasy (i.e., they are not expected to arise convergently or to be lost secondarily) and thus provide unambiguous synapomorphies (shared-derived character states), elevating miRNAs to “one of the most useful classes of characters in phylogenetics” (18).

The above reasoning has led to a recent proliferation of miRNA-based phylogenetic studies seeking to unequivocally resolve several recalcitrant relationships in the tree of life. At the time of our analysis, these included five formal phylogenetic analyses of miRNA data focused on identifying the phylogenetic position of turtles within amniotes (19), acoelomorph flatworms within animals (20), lampreys within vertebrates [hagfish and jawed vertebrates (18)], myzostomidan worms within bilaterians (21), and on establishing the monophyly of—and resolving relationships within—annelids (22). [Several additional studies discuss the phylogenetic implications of miRNA data, but do not subject these data to a formal phylogenetic analysis. Typically in these studies, the phylogeny is first estimated from some other source of data, and then the correspondence of the inferred tree to select miRNA families is discussed (e.g., refs. 23–27)].

These studies proceed by first identifying the set of miRNAs present in each study lineage using one of two general approaches: by searching for known or novel miRNAs either in existing genome assemblies or in novel data generated by sequencing small-RNA libraries. The identified miRNA families are then used to construct a data matrix in which each miRNA family is treated as an ordered binary character, where miRNA presence is the derived state. Finally, this data matrix is subjected to (Dollo or Wagner) parsimony analysis to estimate phylogenetic relationships.

Here, we critically examine the use of miRNA data for phylogeny estimation, focusing on three concerns: (i) the validity of claims related to the evolution of miRNA families (i.e., that secondary loss is exceptionally rare); (ii) limitations of parsimony methods used to infer phylogeny from miRNA presence/absence data; and (iii) problems associated with the detection of miRNA families. We demonstrate that these concerns collectively render published phylogenetic conclusions based on miRNA data uncertain (obscured by their reliance on nonstatistical methods) or strongly biased (because of problems in miRNA detection or inference method). We illustrate these concerns by reanalyzing five published phylogenetic studies of miRNA data.

Interpreting and Analyzing miRNA Data: Is miRNA Absence Evidence or Absence of Evidence?

To properly analyze and interpret miRNA presence/absence data, we must be explicit on the nature and meaning of “absence.” A microRNA family that is scored as absent in a particular lineage can, in principle, have one of three histories: (i) the miRNA family may have never arisen in or been inherited by that lineage (true absence); (ii) the miRNA family may have previously been present in the lineage but subsequently lost from the genome (secondary loss); or (iii) the miRNA family may actually be present in the genome but escaped detection during data collection (sampling error). If all (or nearly all) absences of miRNA families are true absences, then miRNA loss strictly does not occur (or occurs exceedingly rarely): this is the implicit assumption of miRNA studies. Accordingly, because the evolution of miRNA data involves minimal character change—miRNA families have a unique origin (bereft of convergence) with negligible/no secondary loss—the use of parsimony as an inference method might be justified.

In fact, nearly all published miRNA studies (including all five reexamined here) have used some variant of the parsimony method to estimate phylogeny. The miRNA study by Sperling et al. (22) used “standard” (Wagner) parsimony—in which gains and losses of miRNA families incur equal cost (28)—and the remaining four studies (18–21) used Dollo parsimony (29). Dollo parsimony allows for the unique evolution of a character and its subsequent loss (both with equal cost), but precludes reevolution of the same character (with effectively infinite cost) once it has been lost.

Secondary Loss of miRNA Families Is Common

Here we explore the claim that secondary loss of miRNA families is exceedingly rare (e.g., refs. 17, 24, and 25). We derived estimates of the prevalence of miRNA loss from analyses of published miRNA datasets. The prediction is quite simple: if loss of miRNA families is exceedingly rare, then the most parsimonious tree for a given miRNA dataset should be virtually free of homoplasy (implied secondary loss of miRNA families), given that Dollo parsimony does not permit convergent or parallel evolution.

To derive estimates of the implied prevalence of miRNA loss, we reanalyzed the miRNA datasets under Dollo parsimony with PAUP* v4b10 (30) by means of exhaustive searches, treating all characters as “Dollo.up,” which provides the parsimony score (i.e., the total number of implied miRNA gains and losses) for the optimal tree. We then tabulated the number of miRNA losses using the “dollop” function in Phylip v3.5c (31). Finally, we estimated the prevalence of miRNA secondary loss in each of the five formal miRNA phylogenetic studies, which is simply calculated as the number of implied losses divided by the parsimony score (total number of implied changes).

Our survey of published studies suggests that secondary loss of miRNA families is apparently quite common (Table 1). In all but the amniote study (19) (addressed below), secondary miRNA losses constitute between 27% and 54%, with an overall average of 38%, of the implied evolutionary changes. These phylogenetic results accord well with those of molecular evolutionary studies, in which prevalent secondary loss of miRNA families has been inferred for various taxa (14, 32–35).

Table 1.

Prevalence of miRNA loss inferred under Dollo parsimony and the stochastic Dollo model

miRNA study	Source	No. parsimony informative	Optimal parsimony score	No. implied miRNA losses	Proportion of secondary loss	Estimated rate of miRNA loss [mean, (HPD)]
Amniotes*	(19)	34	36	1	0.03	1.99 × 10−4, (3.48 × 10−6, 4.75 × 10−4)
Animals	(20)	115	158	43	0.27	2.01 × 10−4, (4.05 × 10−6, 4.79 × 10−4)
Annelids	(22)	71	113	42	0.37	1.99 × 10−4, (9.15 × 10−6, 4.75 × 10−4)
Bilaterians	(21)	71	147	79	0.54	2.01 × 10−4, (2.73 × 10−6, 4.82 × 10−4)
Vertebrates	(18)	172	249	84	0.34	2.04 × 10−4, (1.08 × 10−5, 4.87 × 10−4)

^*The number of implied miRNA losses calculated here (and reported in the original study) is an underestimate. The original study indicates that additional miRNAs were detected that entailed secondary losses [see supplementary table 1 in Lyson et al. (19)], but these data were excluded from the dataset.

Although we suspect that the degree of secondary loss in published studies is somewhat inflated by miRNA sampling errors (see Sampling Error in miRNA Detection and Its Phylogenetic Impact, below), the complex character histories of miRNA evolution nevertheless suggest that the use of parsimony—which effectively places all of the probability on the single character history with the absolute minimal amount of change—is not a suitable method with which to infer phylogeny from miRNAs.

Statistical Analysis of miRNA Data Exposes Considerable Phylogenetic Uncertainty

As discussed in the preceding section, the evolution of miRNA often appears to be complex, which raises concerns about the choice of parsimony as a method of inference. Stochastic models are available that are more appropriate for accommodating complex histories, as the likelihood of a given character (in this case, a miRNA family) is calculated by integrating all possible character histories (in this case, patterns of miRNA gain and secondary loss that could give rise to the observations), weighting each history by its probability under the model. Furthermore, stochastic models are available that may be appropriate for the analysis of miRNA presence/absence data. For example, the binary stochastic Dollo model (36, 37) appears to be well-suited for the analysis of miRNA presence/absence data. The stochastic Dollo model describes an immigration-death stochastic process for a set of observed binary characters where the origin of a character (miRNA family) is modeled as a homogeneous Poisson process with instantaneous rate λ, and its subsequent loss is modeled as a stochastic branching process (where the probability of loss is proportional to the branch length in which it persists toward the present) with an instantaneous rate of secondary loss, μ (37). Accordingly, this model allows a character to evolve once, with the possibility of subsequent loss (possibly independently in multiple lineages), but prohibits any secondary origin of the character once it has been lost within a lineage (37). Inference under stochastic models within a Bayesian statistical framework provides a natural means for assessing support and accommodating uncertainty in phylogenetic estimates. Because the majority of published miRNA studies to date have either ignored the issue of evidential support for estimates, or have relied on ad hoc support measures [such as the Bremer support index (38)] that have no clear statistical interpretation (39), the availability of an inference framework that explicitly assesses support is particularly attractive.

Markov chain Monte Carlo (MCMC) simulation is used to approximate the joint posterior probability distribution of the phylogenetic parameters. A Markov chain is specified that has state space comprising all possible values for the phylogenetic model parameters, which has a stationary distribution that is the distribution of interest (i.e., the joint posterior probability distribution of the model parameters). Samples drawn from the stationary Markov chain provide valid estimates of the joint posterior probability density, which can be queried marginally with respect to any parameter of interest. In the case of topology, the marginal posterior probability for a given clade is simply its frequency in the sampled trees.

Bayesian Inference of Phylogeny from miRNA Datasets.

These considerations motivated us to reanalyze previously published miRNA datasets within a Bayesian statistical framework using a stochastic binary Dollo model (37) to describe the gain and loss of miRNA families. For each of the five miRNA datasets, we treated all characters as “Dollo type” and approximated the joint posterior probability density via MCMC using BEAST v1.7.5 (40). We specified a prior for the rate of miRNA loss, μ, using an exponential distribution with a small rate parameter $\left(\overline{x}=1.0\times {10}^{-4}\right)$ and specified a prior on the tree topology and node heights using a stochastic birth-death branching process.

Molecular studies have alternatively characterized the evolution of miRNAs as a gradual process of continuous accumulation via mutation (14), or as an episodic process associated with major regulatory or developmental innovations (15). Accordingly, we explored an array of (relaxed) clock models to describe the variation in rates of miRNA evolution across the tree or through time that range from stochastically constant to episodic. Selection among these alternative clock models yields ultrametric phylogenies that give us insight into the pattern of miRNA accumulation and loss, as well as information about the placement of the root of the phylogeny. Specifically, for each dataset, we performed analyses under the strict-clock model, the random local clock model (41), and the uncorrelated log-normal and exponential relaxed-clock models (42). Inference of the joint posterior probability density for each composite phylogenetic model [i.e., the binary stochastic Dollo model + one of the (relaxed) clock models] involved at least three independent MCMC analyses, running each chain for 100 million cycles and sampling every 10,000^th cycle.

To compare fit of the data to these four alternative clock models, we performed additional analyses targeting the marginal likelihood of the data under each of the four composite phylogenetic models. For each dataset, this entailed running the MCMC through a series of 50 power posteriors spanning from the prior to the posterior, with the powers spaced along a β(0.3, 1.0) distribution. We then estimated the marginal likelihood from this chain using both path and stepping-stone sampling analyses (43–45). We performed at least three replicate MCMC simulations under each model to ensure stability of the marginal-likelihood estimates. We then compared support for the alternative clock models by calculating Bayes factors as the ratio of the marginal likelihoods for each pairwise combination of candidate models. We interpret Bayes factors (BF) following Kass and Raftery (46): viewing 2 ln BF values >10 as very strong support for the candidate model, between 6 and 10 as strong support, between 2 and 6 as positive evidence, and <2 as essentially equivocal regarding the alternative models. We performed model comparison only for models where the analyses performed very well, judged by the MCMC mixing efficiently across the power posteriors and highly stable estimates of the marginal likelihood across replicated analyses with both stepping-stone and path sampling.

In total, this analysis design entailed 180 MCMC analyses: each of the five miRNA datasets was analyzed under each of the four (relaxed) clock models, with three independent MCMC analyses under each model, and with analyses repeated to target first the joint prior probability, then the joint posterior probability, and finally the marginal-likelihood densities. We assessed the performance of each MCMC analysis for all parameters (including the topology) using Tracer and AWTY (“are we there yet?”) (47, 48), which suggested that the chains mixed well and had converged before ∼50 million cycles in nearly all cases. In the few instances where poor mixing or convergence was noted, we ran additional independent analyses until an adequate sample from the target density could be obtained, or it became clear that the MCMC could not adequately sample from the target distribution. Inferences under each model were based on the combined stationary samples from each of the independent chains, which provided adequate sampling for all parameters according to the effective sample size (40).

Finally, we assessed support for the key phylogenetic findings of each published miRNA study using Bayes factors. This assessment entailed a second round of analyses targeting the marginal likelihood for the best-fitting (relaxed) clock model (as judged by the Bayes factor model comparisons above), but with the topology constrained to the appropriate alternative hypothesis in each case (discussed in more detail below). These analyses allowed us to quantify the extent to which each miRNA dataset can decisively distinguish among alternative phylogenetic hypotheses.

Patterns and Rates of miRNA Evolution.

We used Bayesian model-comparison methods to assess the fit of the miRNA datasets to four (relaxed) clock models, which differ in their ability to accommodate rate variation across lineages. The strict-clock model makes the most stringent assumption of rate homogeneity, the random-local clock is intermediate, and the uncorrelated (exponential and log-normal) relaxed-clock models are able to capture the most extreme rate fluctuations across branches; rates on adjacent branches are modeled as independent and identically distributed random variables drawn from a common (exponential or log-normal) probability distribution (41, 42). Interestingly, the two uncorrelated relaxed-clock models had the highest marginal likelihood and therefore provided the best description of the process generating every single miRNA dataset (Table 2). We were unable to perform a few of these comparisons because of poor mixing of MCMC that prohibited stable estimation of a marginal likelihood for some of the data + model combinations (the uncorrelated log-normal in particular; see Table 2). However, the uncorrelated exponential model was very strongly preferred (2 ln BF > 10) to the strict-clock model for four datasets, and was preferred (2 ln BF > 4) for the fifth. These results, combined with the large estimated values for the coefficient of variation under the preferred model (Table 2), imply substantial heterogeneity in the rate of miRNA evolution across branches in these datasets, conditions in which parsimony inferences are more likely to be inconsistent (e.g., refs. 49–51). Finally, as in the case of the Dollo parsimony analyses, Bayesian estimates under the stochastic Dollo model indicate substantial rates of miRNA loss in all five miRNA datasets (Table 1).

Table 2.

Marginal likelihoods of miRNA datasets under four different clock models ranging from strictly clock-like to highly variable evolutionary rates

	Marginal likelihood†
miRNA Study	Strict	Random local	Uncorrelated exponential	Uncorrelated log-normal	CV‡
Amniotes	−128.44 (0.06)	−127.93 (0.14)	−124.00* (0.02)	−125.22 (0.53)	0.996
Animals	−649.83 (0.15)	−639.60 (0.36)	−605.37* (0.08)	—	1.117
Annelids	−454.75 (0.16)	—	−433.34* (0.21)	—	1.105
Bilaterians	−622.88 (0.25)	−602.47 (0.89)	−583.58* (0.31)	—	1.107
Vertebrates	−1107.98 (0.17)	−1054.95 (0.06)	−1034.07* (0.17)	−1037.44 (0.38)	1.043

^†The marginal log probability of miRNA datasets under the stochastic Dollo and (relaxed) clock models estimated using path sampling. Values are means and SE of three independent runs. The winning models are denoted with an asterisk. Empty cells denote the model-dataset combinations for which poor MCMC mixing prevented a stable estimate of the marginal likelihood.

^‡Coefficient of Variation in evolutionary rate among branches of the phylogeny for the winning model.

Evaluating Support for Key Phylogenetic Conclusions of Published miRNA Studies.

Bayesian analyses of miRNA data offered novel insight into several previously published studies. In three of the five cases, the Bayesian analysis recovers a result that disagrees in important respects from the parsimony result, but agrees with other published studies based on more traditional phylogenomic analyses of molecular sequence datasets. Parsimony and Bayesian analyses recover congruent conclusions for the two remaining studies, although both of these cases remain problematic because of large uncertainty or sampling error. We briefly discuss key results for each of these analyses below.

Annelid dataset.

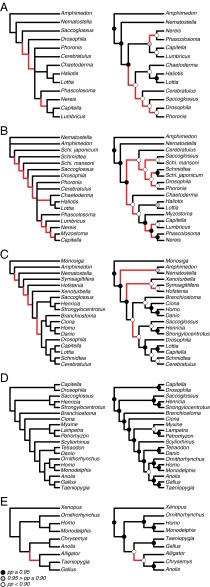
Sperling et al. (22) sought to evaluate the monophyly of and establish phylogenetic relationships within annelids. Based on the parsimony analysis of the miRNA dataset, they concluded that: (i) annelids are monophyletic (Nereis, Lumbricus, and Capitella form a clade); (ii) the sipunculan species, Phascolosoma, is the sister group of annelids; and finally, (iii) polychaete annelids are not monophyletic (Nereis and Capitella do not form a clade). Bayesian analysis of the miRNA data under the stochastic Dollo model infers the tree: ((Nereis, Phascolosoma), (Lumbricus, Capitella)) (Fig. 1A). Accordingly, these results neither support annelid monophyly nor a sister-group relationship between sipunculans and annelids. Our finding that sipunculids (represented by Phascolosoma) are included within annelids—and thus, that annelids are paraphyletic—is consistent with most recent molecular phylogenetic/omic studies (e.g., refs. 52–57).

Fig. 1.

Comparison of phylogenetic hypotheses for each dataset: (A) Annelids, (B) Bilaterians, (C) Animals, (D) Vertebrates, and (E) Amniotes. The left column is the originally published parsimony result and the right column is the maximum clade credibility tree from the stochastic Dollo reanalysis under the winning clock model. Red branches highlight topological differences between the trees, and dots on nodes signify nodal posterior probabilities for the Bayesian trees.

We assessed the decisiveness of support for these alternative topological models by performing analyses in which the topology was constrained alternatively to the parsimony estimate (Model M₁) (Table 3) and the Bayesian estimate (Model M₀) (Table 3) and compared the marginal likelihoods under the two models. A 2 ln BF of ∼12 in favor of the Bayesian topology suggests that the data very strongly prefer the Bayesian estimate relative to the parsimony estimate.

Table 3.

Selection of topology models (tests of phylogenetic hypotheses) for miRNA datasets based on Bayes factor comparisons of estimated marginal likelihoods

miRNA study	Topology model*	ln P(X|Mi)†	$2\ln B{F}_{ij}$‡	Description	Resulting from§
Amniotes	M0	−114.98 (0.03)	17.52	Lepidosaur hypothesis: turtles + lizards	B and P
	M1	−123.74 (0.14)		Archosaur hypothesis: turtles + archosaurs
Amniotes-corrected¶	M0	−126.21 (0.22)	5.17	Archosaur hypothesis: turtles + archosaurs	B and P
	M1	−128.80 (0.08)		Lepidosaur hypothesis: turtles + lizards
Animals	M0	−574.67 (0.44)	−11.69	(((Acoel 1, Acoel 2), Xenoturbella), (remaining Bilateria))	B
	M1	−568.83 (0.17)		(Acoel 1 (Acoel 2 (Xenoturbella (remaining Bilateria)))	P
Annelids	M0	−414.65 (0.11)	11.97	((Phascolosoma, Nereis), (Lumbricus, Capitella))	B
	M1	−420.64 (0.23)		(Phascolosoma (Nereis (Lumbricus, Capitella)))	P
Bilaterians	M0	−552.63 (0.02)	100.92	Myzostomids sister to annelids	B
	M1	−603.09 (0.26)		Myzostomids nested within annelids	P
Vertebrates	M0	−994.81 (0.14)	0.91	Cyclostome hypothesis: lampreys sister to hagfish	B and P
	M1	−995.26 (0.13)		Jawed vertebrate hypothesis: lampreys sister to jawed vertebrates

^*Topology models refer to various phylogenetic hypotheses corresponding to the description column; see text for details.

^†The marginal log probability of miRNA datasets (and SE) under the stochastic Dollo model and the preferred relaxed-clock model estimated using path sampling as described in the text.

^‡Two times the natural log of the Bayes factor is twice the difference between the natural log marginal likelihoods estimated under the alternative topological models. Our interpretation follows ref. 46.

^§An indicator for which unconstrained analysis type recovered each topological model. B, Bayesian stochastic Dollo; P, Parsimony.

^¶This is a version of the amniote miRNA dataset from the study of Lyson et al. (19) that has been corrected for sampling error; see text for details.

Bilaterian dataset.

Helm et al. (21) sought to resolve the phylogenetic affinity of myzostomid worms using an expanded version of the miRNA dataset from the Sperling et al. (22) study, testing alternative hypotheses that placed myzostomids within either annelids or platyzoans. Their parsimony analysis of the miRNA data “strongly confirms a phylogenetic position of Myzostomida” as “deeply nested within the annelid radiation, as sister to Capitella” (21). In contrast, Bayesian analysis of this miRNA dataset under the stochastic Dollo model implies that myzostomids are the sister group of annelids (with a clade probability of ∼0.97–0.99), which agrees with estimates based on recent analyses of phylogenomic data (e.g., ref. 55) (Fig. 1B).

We assessed the support for these alternative hypotheses by performing analyses in which the topology was constrained to the parsimony estimate (model M₁) (Table 3), and compared the marginal likelihood of this model to that from analyses constrained to the Bayesian estimate (model M₀) (Table 3). These analyses decisively reject the inclusion of Myzostoma within annelids (2 ln BF ∼100). It was not possible to perform a clear test of the alternative “platyzoan” hypothesis, as Platyzoa was not inferred to be monophyletic in our unconstrained analyses.

Animal dataset.

Philippe et al. (20) sought to establish the phylogenetic placement of acoels and xenoturbellids within animals using three independent datasets: a large number of mitochondrial genes, a phylogenomic dataset comprising 38,330 amino acid positions, and a microRNA dataset. The phylogeny inferred from their Dollo parsimony analysis of the miRNA dataset implied that acoels (Symsagittifera and Hofstenia) and xenoturbellids (Xenoturbella) form a paraphyletic grade near the base of bilaterians: (Symsagittifera, Hofstenia, (Xenoturbella, (remaining bilaterians))). The Bayesian analysis of this miRNA dataset under the stochastic Dollo model infers a very different tree in which acoels are monophyletic and sister to xenoturbellids: (((Symsagittifera, Hofstenia), Xenoturbella), remaining bilaterians) (Fig. 1C). We assessed support for these hypotheses by performing additional analyses in which the topology was alternatively constrained to the parsimony estimate (topological model M₁) (Table 3) and the Bayesian estimate (topological model M₀) (Table 3) and compared the marginal likelihoods. In contrast to all of the other studies, the Bayes factor suggests that the miRNA data favor the parsimony hypothesis in this case (2 ln BF ∼ −12). Thus, these contrasting results give no clear guidance on which alternative is the more reliable topology. However, the extensive phylogenomic analysis that was paired with the original miRNA analysis helps to clarify which topology is likely correct.

Notably, Philippe et al. (20) favored a hypothesis that disagreed with the miRNA parsimony result. The central phylogenetic finding in Philippe et al. is the close relationship between Xenoturbella and (a monophyletic) Acoela (Symsagittifera, Hofstenia). Although this result strongly conflicts with their parsimony analysis of miRNA data, Philippe et al. prefer it based on their rigorous Bayesian analyses of large-scale molecular datasets. In fact, in discussing the conflicting estimates based on their Bayesian analyses of the phylogenomic data and their parsimony analysis of the miRNA data, Philippe et al. were skeptical of the miRNA phylogeny, attributing this discrepancy to the effects of pervasive secondary loss of miRNA families in acoels. Interestingly, our Bayesian analysis of the miRNA dataset recovers the same monophyletic Acoela sister to Xenoturbella. However, both Bayesian and parsimony analyses of the miRNA data conflict with the preferred tree from Philippe et al. in other respects, suggesting that secondary loss has obscured phylogenetic relationships for these data.

Vertebrate dataset.

Heimberg et al. (18) sought to resolve the phylogenetic position of lampreys within vertebrates using miRNA data, testing alternative hypotheses that either placed lampreys as sister to hagfish (the “cyclostome” hypothesis) or to jawed vertebrates (the “vertebrate” hypothesis). Analysis of the vertebrate miRNA dataset using Dollo parsimony supported the cyclostome hypothesis: the two lampreys, Lampetra and Petromyzon, form a clade that is sister to the hagfish species, Myxine: ((Lampetra, Petromyzon), Myxine)). Bayesian analysis of the vertebrate miRNA dataset under the stochastic Dollo model also supported the cyclostome hypothesis, albeit weakly (i.e., with a clade probability of ∼0.79) (Fig. 1D).

We assessed the support for cyclostome monophyly by performing analyses in which the topology was constrained to the alternative phylogenetic hypothesis in which lampreys are sister to jawed vertebrates (model M₁) (Table 3), and compared the marginal likelihoods of the constrained and unconstrained (model M₀) (Table 3) analyses. Comparison of the marginal likelihoods under the constrained and unconstrained models suggests that the miRNA data are essentially equivocal regarding the phylogenetic affinity of lampreys (2 ln BF ∼1).

Amniote dataset.

Lyson et al. (19) sought to resolve the phylogenetic placement of turtles within amniotes, using a miRNA dataset to test whether turtles were either sister to lizards + tuatara (the “lepidosaur” hypothesis), or to birds + crocodilians (the “archosaur” hypothesis). Analysis of the miRNA dataset using Dollo parsimony supports the lepidosaur hypothesis, and this finding was also strongly supported by Bayesian analysis under the stochastic Dollo model (with a clade probability of ∼1.0) (Fig. 1E).

We further assessed support for the lepidosaur hypothesis by performing analyses of the amniote miRNA dataset in which the topology was constrained to the alternative phylogenetic hypothesis in which turtles are sister to archosaurs (model M₁) (Table 3), and compared the marginal likelihoods to those from the lepidosaur hypothesis (model M₀) (Table 3). In contrast to all other studies, comparison of the marginal likelihoods under the two models suggests that the miRNA data provide strong support for the originally published result (2 ln BF ∼17). However, we demonstrate below that this result is an artifact of sampling error in the detection of amniote miRNAs (see Sampling Error in miRNA Detection and Its Phylogenetic Impact).

Anomalous Results from miRNA Analyses.

Bayesian analysis of published miRNA datasets casts considerable doubt on the key phylogenetic conclusions of these previously published studies. In three of five cases (animals, annelids, and bilaterians), using a model that accounts for the uncertainty in character histories alters the key phylogenetic conclusion, often with strong support. In a fourth case (vertebrates), considering the uncertainty in character history leads to the conclusion that miRNAs are essentially silent on the relationship of interest. In only one case (amniotes) does accounting for uncertainty in character history leave the key conclusion unchanged, although this case reveals a second issue that we explore below. Moreover, our reanalyses of published miRNA datasets also supported some highly unusual phylogenetic results. For example, Bayesian analyses of the amniote miRNA dataset failed to support the (virtually incontrovertible) monophyly of archosaurs (Fig. 1E), whereas analyses of the animal miRNA dataset supported (the very odd placement of) chordates as the sister to all other bilaterians (Fig. 1C). We argue below that such remarkable findings likely have a more prosaic explanation.

Shortly after the present manuscript returned from an initial round of peer review, a paper appeared that further discussed the phylogenetic potential of miRNAs and demonstrated phylogenetic inference with miRNAs using the binary stochastic Dollo model (8). This report by Tarver et al. (8) assembled a dataset of miRNA presence/absence for 29 metazoan taxa from subsets of the data matrices developed in previous studies (including those that we reexamine here) and analyzed it using the stochastic Dollo model. The resulting phylogeny had high posterior probabilities on all nodes except one, with a topology that is congruent with other estimates based on more traditional phylogenetic and phylogenomic analyses. The Tarver et al. result therefore appears to strongly contradict our findings. However, this discrepancy appears to stem from the choice of taxa excluded from the Tarver et al. (8) dataset. Specifically, the dataset includes only a subset of the taxa reported in the original studies, whereas our analyses are based on the original complete datasets. Furthermore, the Tarver et al. (8) dataset is missing the critical taxa for all of the nodes of interest that we identify above. For example, we identify weak support and pervasive uncertainty associated with the relationship between the lamprey (Lampetra and Petromyzon) and the hagfish (Myxine), the focal taxa of the study by Heimberg et al. (18). In contrast, the Tarver et al. (8) study retains only one lamprey (and no hagfish) from the original dataset and thus cannot assess the support for this clade. Similarly, the acoels (Symsagittifera, Hofstenia) and Xenoturbella are central to the study by Philippe et al. (20). The relationships among these taxa strongly contradict relationships based on traditional phylogenetic analyses, but again were excluded from the Tarver et al. (8) study. Similarly, Tarver et al. (8) include the two bird species (Gallus and Taenopygia) and the lizard from the Lyson et al. (19) dataset, but exclude the critical turtle and alligator from their analysis. Likewise, the Tarver et al. (8) study excludes both the key taxon Myzostomida from Helm et al. (21), and also the key Nereis and Phascolosoma taxa from Sperling et al. (22). Tarver et al. (8) neither discuss the rationale for the taxon sampling in their analysis, nor justify their decision to exclude key taxa from the revised dataset. Because miRNAs have been strongly promoted for their purported ability to resolve particularly vexing phylogenetic relationships, it strikes us that including only nonproblematic taxa precludes demonstration of the potential of these data to resolve vexing relationships.

Sampling Error in miRNA Detection and Its Phylogenetic Impact

Sampling error can to lead to the (apparent) absence of miRNAs in phylogenetic datasets. This is of particular concern because most miRNA phylogenetic studies use a mixture of approaches to identify miRNAs in different lineages (namely, using a combination of bioinformatic scans of complete genomes and de novo sequencing of small-RNA libraries). If these approaches vary in their detection probabilities, then miRNAs are more likely to be discovered in some lineages than in others. As more and more data are collected under this biased detection scheme, certain lineages are likely to accumulate true presences, whereas the remaining lineages will accumulate apparent absences. Because the presence and absence of miRNAs are the direct source of phylogenetic information, this sampling artifact may lead to biased estimates of topology.

Here we demonstrate sources of sampling error in the detection of miRNA families, first focusing on the analysis of turtle relationships within amniotes as a detailed case study, and then assessing the generality of this sampling error by means of a more general survey.

Sampling Bias in the Detection of Amniote miRNAs.

Lyson et al. (19) used a mixture of miRNA detection methods in an attempt to resolve the phylogenetic position of turtles within amniotes. Specifically, their study searched for miRNAs using: (i) similarity searches against whole-genome assemblies for two birds—chicken (Gallus), zebra finch (Taeniopygia)—and four outgroup taxa; (ii) a combination of similarity searches against the genome assembly for the lizard (Anolis) and de novo sequencing of an Anolis RNA library; and (iii) de novo sequencing of RNA libraries for a turtle species—the painted turtle (Chrysemys)—and the American alligator (Alligator). At the time of their study, full genome assemblies for the painted turtle and alligator were not available. The authors identified 19 miRNA families unique to birds, one miRNA family unique to archosaurs (birds and crocodilians), but no miRNA families shared between archosaurs and turtles. Furthermore, the study identified four miRNA families that are shared between the anole and turtle. Taken at face value, these data appear to unequivocally support a turtle + lizard relationship, to the exclusion of archosaurs.

Draft genome assemblies for both the painted turtle and American alligator are now available (58, 59), which provide an independent check of the miRNAs detected—and the phylogenetic conclusions reached—in the Lyson et al. (19) study. We sought to confirm that each of the miRNA families that were identified by Lyson et al. as unique to birds (n = 19) were in fact absent from the turtle and alligator genomes, and that the single archosaur-specific miRNA was absent from the turtle genome. We also assessed whether each of the miRNA families that were identified as being shared exclusively by turtles and lizards were in fact present in the turtle genome and absent from the alligator genome.

We downloaded both the longer stem-loop sequence (60–80 bp) and the shorter mature sequence (22 bp) for each relevant miRNA from miRBase (60) for each appropriate reference taxon (Gallus for the 19 bird-specific and the single archosaur-specific miRNA families; Anolis for the four miRNA families uniquely shared by turtle + lizard). We constructed local BLAST databases from the turtle and alligator genome assemblies (v3.0.3 and 0.1d27, respectively) and searched against them with each of the relevant miRNA stem-loop sequences using BLASTN [v2.2.25, minimum word size = 11, e-value cutoff = 10–2 (61)]. We then predicted secondary structure for any putative miRNAs that we identified using mFold (62).

We scored a miRNA family as being present in the turtle or alligator genome if it met three criteria: (i) We observed a highly significant hit (i.e., with a minimum e-value of 10⁻²⁰) for the reference stem-loop sequence against the relevant genome assembly. (ii) The matching sequence in the genome contained a nearly perfect match to the mature ∼22-bp miRNA sequence (i.e., containing no more than one substitution in the mature miRNA sequence). (iii) The matching sequence in the turtle or alligator genome folded into the expected hairpin secondary structure and this structure was similar to the predicted secondary structure published for the reference sequence.

Our search confirmed that the single archosaur-specific miRNA (miRNA 1791) was present in the alligator genome, as expected. However, we discovered that this miRNA is also present in the turtle genome (for sequences and predicted secondary structure, see Fig. S1). Furthermore, we discovered three additional miRNA families present in both the alligator and turtle genomes that were reported by Lyson et al. (19) as being unique to birds (miRNA families 1641, 1743, and 2964). All four families exhibited very high sequence similarity with the known miRNA from the reference taxon, highly conserved stem-loop structures with similar free energies to that predicted from the reference taxon, and mature sequences that were identical (two families) or nearly identical (two families) to the reference (see Fig. S1 for sequence alignments and predicted structures). This sampling error may be inherent to miRNA-detection approaches that rely on RNA sequencing. For example, Sperling et al. (22) observed a similar pattern in the polychaete worm, Capitella. They discovered five additional miRNAs from the genome of this organism that were not detected in the sequences derived from an RNA library. MicroRNAs are frequently expressed only in certain tissues, at certain stages of development, or expressed at low levels (22, 63–66). In these cases, it is likely that miRNAs actually present in the genome will be missed because they are not being transcribed (or only being transcribed at low levels) in the tissue that was used to make the RNA library.

Finally, we sought to confirm that the four miRNA families identified by Lyson et al. (19) as uniting a lizard + turtle clade were, in fact, present in the turtle genome and absent in the alligator genome (miRNA families 5390, 5391, 5392, and 5393). Our search confirmed that all four miRNA families were absent from the alligator genome, as expected. However, we were only able to find one of the four reported miRNA families (miRNA 5391) in the turtle genome. We found no significant BLAST hits to any of the other three expected miRNAs, even under relaxed search settings (word size = 4, e-value cutoff = 10). We then assessed whether we could identify these miRNAs in the Anolis genome and found all four families, as expected. At present, the cause of this discrepancy is unclear. Our failure to detect these sequences could be a false-negative, indicating that the turtle genome assembly is incomplete and missing these three sequences. Alternatively, their previous detection could be a false-positive in the Lyson et al. (19) study, stemming from contamination between the Anolis and Chrysemys sequencing libraries or from another source of error. The turtle genome assembly has 18× coverage and is estimated to be 93% complete, which suggests that the former explanation is unlikely (59). Nevertheless, we cannot formally distinguish between these possibilities at present.

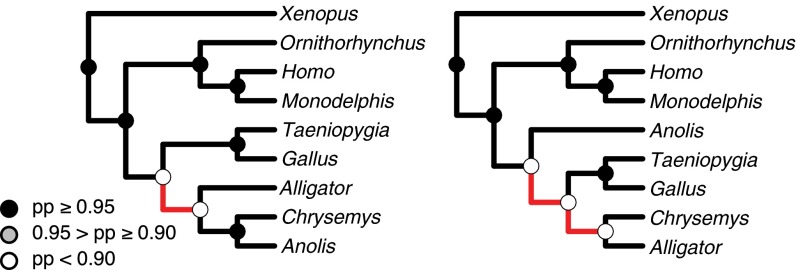
We then revised the Lyson et al. (19) data matrix to correct this sampling error and subjected the revised matrix to Bayesian phylogenetic analysis under the stochastic Dollo model (analyses performed as detailed above). Rather than supporting a strong relationship between lizards and turtles, the corrected miRNA dataset supports a relationship between turtles and archosaurs, albeit weakly (i.e., with a clade probability of ∼0.54) (Fig. 2). This result is consistent with several recently published studies that examine the phylogenetic placement of turtles using large DNA sequence datasets (59, 67–69).

Fig. 2.

The maximum clade credibility tree for the Amniote dataset before (Left) and after (Right) correcting for sampling error. Red branches highlight topological differences between the trees.

We assessed support for the archosaur hypothesis by performing analyses of the corrected amniote miRNA dataset in which the topology was constrained to the alternative archosaur and lepidosaur hypotheses (models M₀ and M₁ in Table 3, respectively). Comparison of the marginal likelihoods under the alternative models indicate that the miRNA data provide positive evidence in favor of the archosaur hypothesis (2 ln BF ∼5). This analysis illustrates that miRNA detection is prone to strong sampling error, to a degree that can fundamentally alter the conclusions of phylogenetic inferences based on these data.

General Survey of Sampling Bias in miRNA Detection.

Our ability to provide a detailed description of the miRNA detection bias in the amniote study largely rests on the serendipitous availability of two new genome assemblies. Accordingly, it is not possible to perform a comparably detailed analysis of the potential sampling errors in the other four published miRNA phylogenetic studies. However, we can make a more general comparison of alternative miRNA detection strategies. To do so, we compiled information from the literature of cases in which the total miRNA complement of various organisms had been estimated both by means of de novo sequencing of small-RNA libraries and also by means of bioinformatic searches of DNA sequence resources. If no sampling error exists, identical sets of miRNA families should be identified using alternative strategies. In stark contrast to this expectation, however, we see a high degree of variation in the miRNA complement identified under the two strategies (Table 4). Although this comparison does not directly replicate the alternative methods used in published phylogenetic studies, it clearly indicates the prevalence of variation in total miRNA complement detection and, as we have shown, this type of sampling error has the potential to impact estimates of phylogeny.

Table 4.

Comparison of empirical and computationally derived estimates of miRNA complements for selected taxa

Species	Number of miRNA orthologs obtained empirically (source)*	Number of miRNA orthologs accessioned in:
		miROrtho†	miRBase‡
Apis mellifera	267 (71)	52	222
Tribolium castaneum	203 (72)	35	430
Drosophila melanogaster	148 (73)	147	426
Caenorhabditis elegans	112 (74)	130	368
Schmidtea mediterranea	122 (75); 66 (76)	38	257
Schistosoma japonicum	227 (77)	—	78
Schistosoma mansoni	211 (78)	—	29
Petromyzon marinus	267 (15)	40	302
Branchiostoma floridae	152 (15); 32 (79)	—	187
Saccoglossus kowalevskii	90 (15)	—	115
Stronglylocentrotus purpuratus	58 (15)	12	70
Danio rerio	198 (80)	113	255
Oryzias latipes	599 (81)	—	146
Nematostella vectensis	40 (82)	—	78

^*miRNA counts in this column are derived from studies that used small RNA isolation followed by deep sequencing to estimate miRNA complements per species; see citations.

^†miRNA counts in this column were predicted by combining orthology with a vector support machine for each sequenced genome as described in Gerlach et al. (70).

^‡miRNA counts in this column are derived from the public repository for all published miRNA sequences and includes data from small RNA sequencing and computational predictions (60).

Conclusions

The current wealth of molecular data will continue to resolve relationships in the tree of life, but not all nodes will acquiesce with equal effort. Predictably, the variously recalcitrant, enigmatic, inscrutable, and impenetrable relationships will continue to be identified. Ultimately, resolution of these problematic cases may require the discovery of new and improved phylogenetic data (and the elaboration and careful application of more realistic models that better describe important aspects of the processes that give rise to conventional genomic data). Accordingly, it is predictable that the addition of a putative silver bullet—such as miRNA presence/absence data—to our phylogenetic arsenal will be greeted with enthusiasm. We would argue, however, that this enthusiasm should be tempered with careful consideration of how to appropriately accommodate the correspondingly novel processes by which these new data evolved and new procedures by which they are collected.

We have demonstrated that the evolution of miRNA families is complex. Contrary to repeated claims, secondary loss of miRNA appears to be quite prevalent, and miRNA evolution typically exhibits substantial variation in rate across branches through time. Consequently, the complex character histories associated with miRNA evolution suggest that parsimony—which effectively places all of the probability on the character history with the minimal change—is not a defensible method with which to infer phylogeny from these new data. We have demonstrated that, in principle, it is both possible and preferable to estimate phylogeny from miRNA data within a Bayesian statistical framework using stochastic evolutionary models. Adopting a statistical approach for estimating phylogeny from miRNA (or other) data confers many benefits: this approach allows us to choose objectively among models, to perform formal tests of competing hypotheses, promotes a richer study of the evolutionary process, and enables us to gauge and accommodate uncertainty in our estimates. We have established the importance of adopting a more appropriate statistical approach: Bayesian analyses of published miRNA datasets qualitatively altered key phylogenetic conclusions and revealed considerable phylogenetic uncertainty in these estimates in four of the five cases that we examined.

Finally, we have demonstrated that the detection of miRNA families is prone to error—especially when using a mixture of detection methods—and this sampling error can substantially bias estimates of phylogeny. Accordingly, it is critical that we either extend existing stochastic models to accommodate this ascertainment bias, or take precautionary measures to minimize it. For example, models used to analyze both SNP data in population genetics (83) and discrete-morphological data in phylogenetics (84) explicitly model the associated ascertainment strategies to reduce the associated biases. The stochastic Dollo model might be similarly extended to accommodate the documented miRNA ascertainment bias. Although the complexity of the mixed genomic/RNA-library detection strategy would make such an extension challenging, the intense focus on miRNA detection methods (e.g., ref. 85) gives reason for optimism that these extensions may be possible. Alternatively, studies seeking to estimate phylogeny from miRNA presence/absence data should strictly use identical, genome-based detection methods in all lineages. This process may not always eliminate sampling error, but it should reduce bias arising from differential detection probabilities of the various miRNA discovery methods.

Although our appraisal of miRNA as a novel source of phylogenetic information is admittedly critical, we clearly recognize the potential of these data to inform phylogeny: inferences based on miRNA data often correspond broadly to those based on more conventional gene/omic data. We take issue, however, with the recent promotion of miRNA data as a phylogenetic panacea. New data are attended by new issues that need to be carefully resolved to realize their full potential.